Что это arctg: Арктангенс, арккотангенс, уравнения tg x = a, ctg x = a — урок. Алгебра, 10 класс.

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )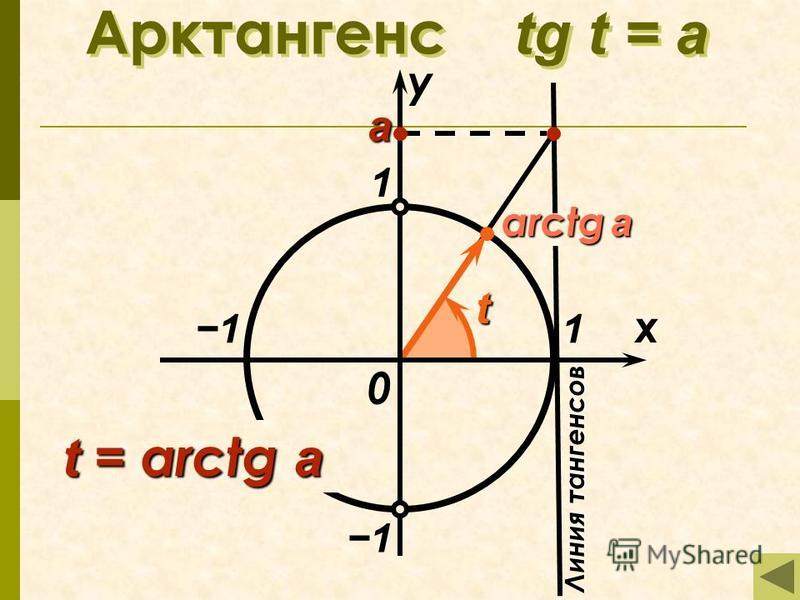
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )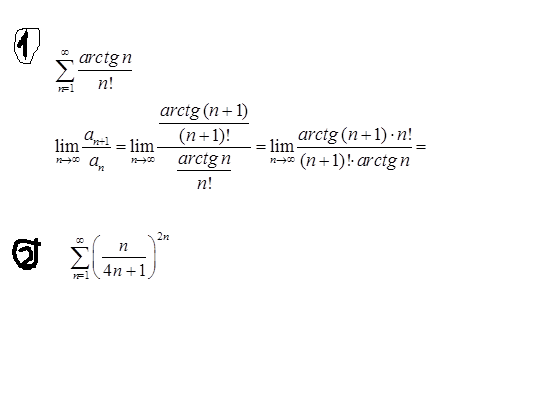
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )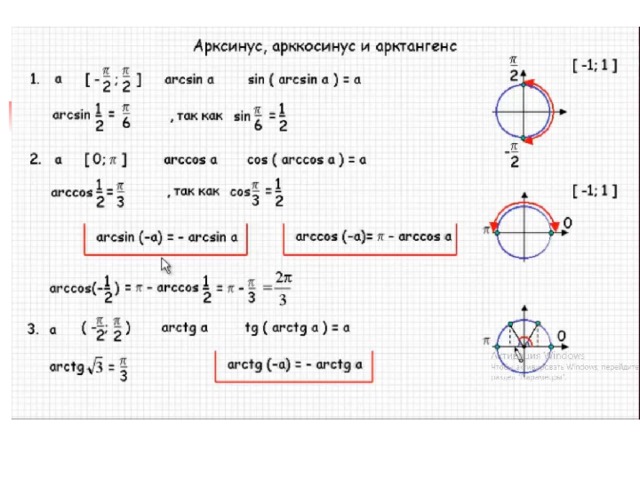
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

Что такое арктангенс?

Добавлено: 12.07.2016 18:52 Добавил: Авету

Тригонометрия – важный раздел математики, в переводе с греческого значит – «измерение треугольников».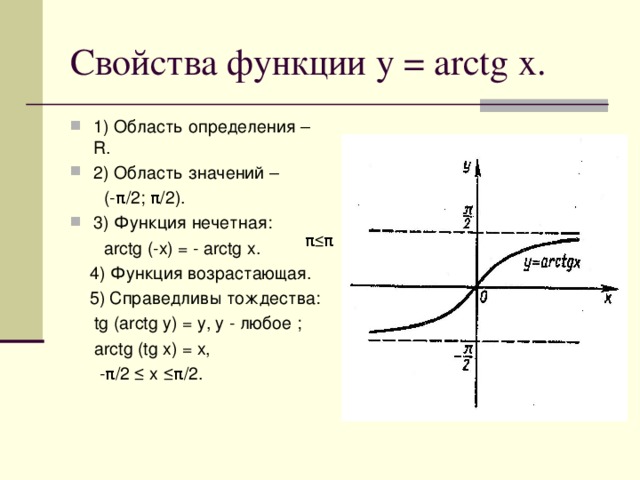 Она включает в себя такие понятия как арксинус, арккосинус, арктангенс, арккотангенс. Возникновение тригонометрии неразрывно связно со строительным делом, астрономией и землемерием. В школе знакомство с тригонометрическими функциями происходит, когда мы берем в руки транспортир. Позднее знание арктангенса, арксинуса и других обратных функций помогает в решении уравнений тригонометрии.

Существует несколько областей применения тригонометрии и свойств функций тригонометрии на практике. Ярким примером служит метод триангуляции в астрономии, он помогает определять расстояние до звезд в Космосе. Используют тригонометрию и в географии. Знание формул, свойств, особенностей тригонометрических функций помогает определить расстояние между объектами. Применяется этот раздел Алгебры и в спутниковой, морской, воздушной навигации, а также в акустике, оптике, в электронике, теории вероятностей, сейсмологии, океанографии, экономике, метеорологии, других науках и сферах жизни.

Как определяется арктангенс?

Арктангенс в алгебре – это обратная тригонометрическая функция к tg (тангенсу), его еще называют аркфункцией.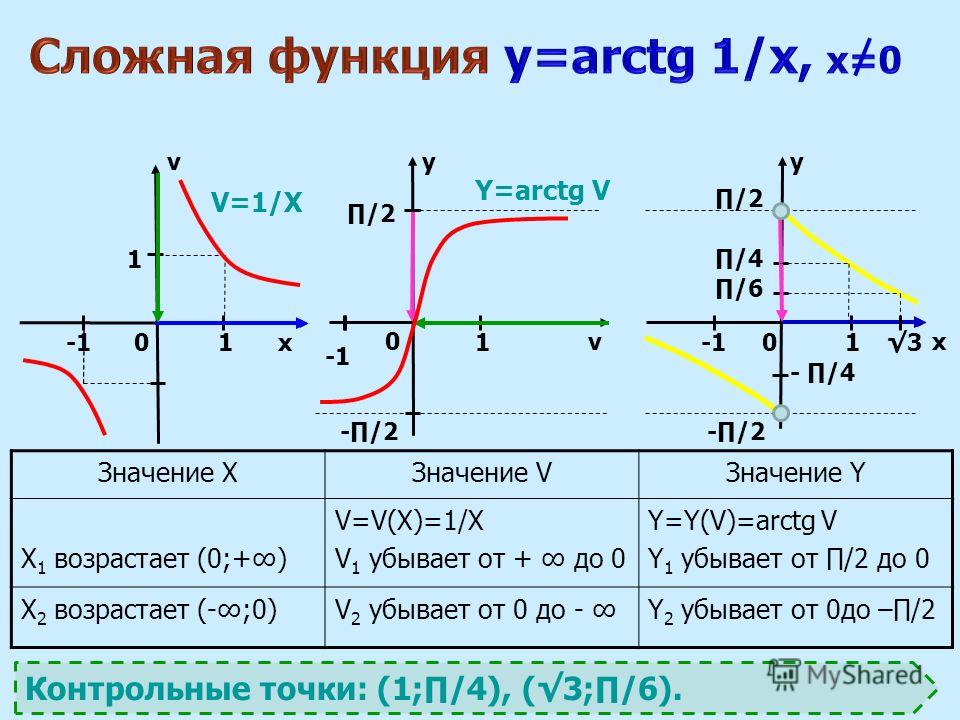 Область ее определения от — ∞ +∞. Обозначается он в математике как arctg x. Во многих учебниках и методической литературе зарубежных стран можно встретить другое обозначение: arctang x.
Из особенностей этой обратной функции выделяют то, что она является возрастающей. Функция y=arctg x ограничена и непрерывна на всей протяженности своей числовой прямой.
История происхождения названия обратных функций тоже имеет свою историю. Оно образовано при помощи приставки «арк», которая происходит от латинского слова arcus и переводится как дуга. Это объясняется тем, что значение обратной функции неразрывно связано с длиной дуги единичной окружности.

Обозначение обратных функций в тригонометрии при помощи приставки «arc» в математику привнес австрийский ученый Крал Шерфер, который жил в XVIII веке. Распространению этой приставки «arc» к обратным функциям мир математики обязан Лагранжу (он жил во Франции в это же время, Жозеф Луи Лагранж также известен известен, как и крупнейший математик XVIII Эйлер).

Позднее в XIX веке немецкие и английские математические школы использовали другие обозначения обратных функций: tg-1, 1/tg. Такие же обозначения как tg-1 встречаются в разных научных изданиях. С одной стороны это имеет место быть, а с другой – некорректно, возникает путаница с возведением функции в минусовую степень.

Понятие арктангенса в тригонометрии

В учебнике по алгебре школьного курса понятие арктангенса звучит следующим образом:
Арктангенсом числа m принято называть такое значение угла x с градусной мерой в радианах, тангенс которого равен m на отрезке -π/2 до π/2. Говоря математическим языком, это звучит так:
arctg m=x, следовательно, tg x =m. При условии, что x больше -π/2 , но меньше π/2, (числовое выражение: -π/2π/2).
График функции arctg выводят из графического отображения прямой функции тангенс. Для этого всего лишь меняют местами ось ординат и ось абсцисс. Для устранения многозначности необходимо ограничить интервалом множество значений: минус π/2 π/2.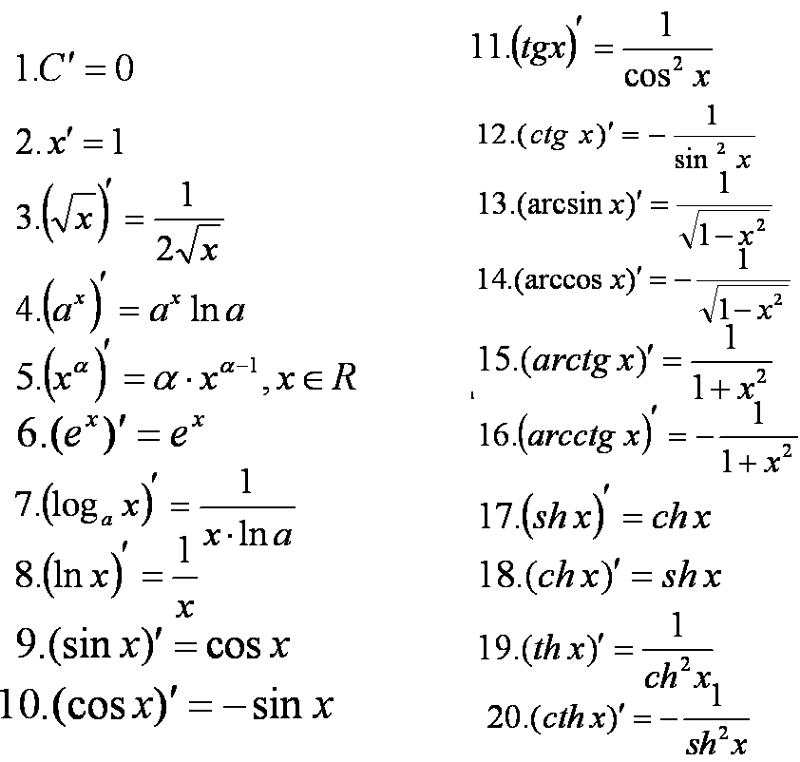 На этом отрезке функция монотонна. Это определение считают главным значением arctg.

Во всех математических справочниках и учебниках школьного курса вы найдете определение тангенса и котангенса, их графическое определение, формулы, свойства, графики. Также для решения тригонометрических уравнений вам понадобятся таблицы котангенсов, интегралы, производные и разложения в ряды, знание связи с гиперболическими функциями и умение выражать через комплексные переменные.

Остались вопросы?

Получить подробные ответы на свои вопросы в области обратных тригонометрических функций, узнать их особенности и свойства, изучить график арктангенса и грамотно подготовиться к ЕГЭ вы можете в режиме онлайн вы можете на сайте http://interneturok.ru/На этом портале найдете уроки как по алгебре, так и по другим предметам школьной программы.

Понравилось? Поделитесь с друзьями!

Похожие статьи

Почему многие выбирают онлайн игры 13. 10.2021 17:26

Количество азартных игр остается невероятно…

Какие возможности дают онлайн игры 30.07.2021 11:34

Есть в интернете местечко, где…

Взгляд эксперта на бейсбол 29.06.2021 14:03

Бейсбол — это вид спорта,…

Системы сбора данных клиентов 01.06.2021 13:35

Системы сбора данных клиентов включают…

В чем преимущества старого аккаунта в Фейсбуке 28.03.2021 20:26

Социальная сеть Фейсбук среди ныне. ..

5 полезных правил для организации сбора средств на благотворительные цели 26.03.2021 17:13

Во время организации сбора благотворительных…

Приятное времяпровождение в онлайн играх 30.01.2021 18:01

Если игрок ценит не только…

Где делают ставки на игры 22.01.2021 16:37

Букмеркер Париматч специализируется не только…

Пять советов по выбору букмекерской конторы 18.01.2021 12:43

От выбора букмекера зависит доход. ..

Чем привлекает букмекерская контора Фортуна лайв 12.01.2021 07:14

Букмекерская контора Фортуна лайв

Статья об Arctg из The Free Dictionary

(перенаправлено с Arctg )

обратная тригонометрическая функция

[¦in‚vərs ‚trig·ə·nə‚me·trik ′fəŋk·shən]

(математика)

Обратная функция тригонометрической функции; то есть арксинус, арккосинус, арктангенс, арккотангенс, арксеканс или арккосеканс. Также известна как антитригонометрическая функция.

Словарь научных и технических терминов McGraw-Hill, 6E, Copyright © 2003 The McGraw-Hill Companies, Inc.

Следующая статья взята из Большой советской энциклопедии (1979). Он может быть устаревшим или идеологически предвзятым.

Обратная тригонометрическая функция

 

функция, являющаяся решением задачи нахождения дуги (числа) по заданному значению ее тригонометрической функции.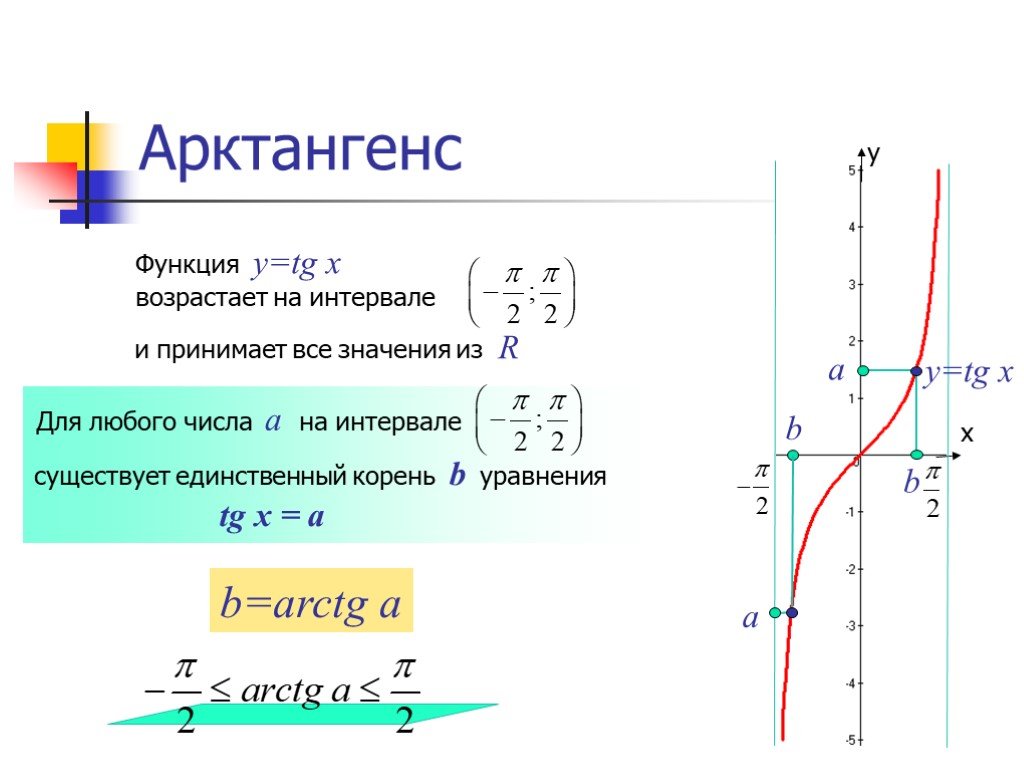 Шесть обратных тригонометрических функций соответствуют шести тригонометрическим функциям: (1) арксинус x , арксинус x ; (2) Arc cos x , арккосинус х ; (3) арктангенс x , арктангенс x ; (4) Arccot ​​ x , арккотангенс x ; (5) Arc sec x , арксеканс x ; и (6) Arc csc x , арккосеканс x .

Например, согласно этим определениям, x = Arcsin a является любым решением уравнения sin x = a ; то есть sin Arc sin a = и . Функции Arc sin x и Arc cos x определены в вещественной области для ǀ x ǀ ≤ 1, функции Arc tan x и Arc cot x определены для всех действительных x , а функции Arc sec x и Arc csc x определены для ǀ x ǀ ≥ 1. Последние две функции используются редко.

Поскольку тригонометрические функции периодические, их обратные функции многозначны. Некоторые однозначные ветви (главные ветви) этих функций обозначены как arc sin x , дуга cos x , …, дуга csc x .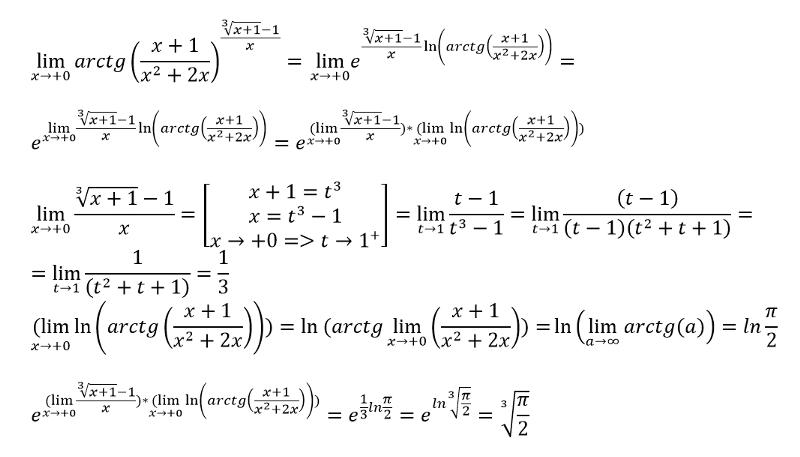 В частности, arcsin x : это ветвь функции Arcsin x , для которой –π/2 ≤ arcsin x ≤ π/2. Аналогично функции arc cos x , arc tan x и arc cot x определяются соответственно из условий 0 < arc cos x ≤ π, –π/2 < arc tan x < π/2 и 0 < arccot ​​ x < π. Обратные тригонометрические функции Arc sin x , … может быть легко выражено в терминах arc sin x , …; Например,

ARC SIN X = (–1) ^N ARC SIN x + π N

ARC COS X = ARC COS x + 2π N

ARC TAN x = ARC TAN x + π N

ARC COT x = ARC COT x + π N

, где N = 0, ± 1, 2,

, где N = 0, ± 1, 2, 2, 2, 2,

. ….

Из известных соотношений между тригонометрическими функциями получаются соотношения между обратными тригонометрическими функциями, например, из формулы

следует, что

Производные обратных тригонометрических функций имеют вид тригонометрические функции могут быть представлены в виде степенных рядов, например,

Эти ряды сходятся при – 1 ≤ x ≤ 1.

Обратные тригонометрические функции могут быть определены для произвольных комплексных значений независимой переменной, но значения из этих функций будут действительными только при указанных выше значениях независимой переменной. Обратные тригонометрические функции комплексной независимой переменной можно выразить с помощью логарифмической функции, например,

ЛИТЕРАТУРА

Новоселов С. И. Обратные тригонометрические функции , 3-е изд. М., 1950.

Большая советская энциклопедия, 3-е издание (1970-1979). © 2010 The Gale Group, Inc. Все права защищены.

Где на окружности arctg 1 3. Арксинус, формула, график функции арксинуса, урок и презентация

Ранее по программе учащиеся получили представление о решении тригонометрических уравнений, познакомились с понятиями арккосинуса и арксинус, примеры решений уравнений cos t = a и sin t = a. В этом видеоуроке мы рассмотрим решение уравнений tg x = a и ctg x = a.

В начале изучения данной темы рассмотрим уравнения tg x = 3 и tg x = — 3. Если решить уравнение tg x = 3 с помощью графика, то мы увидим, что пересечение графиков функции y = tg x и y = 3 имеет бесконечное число решений, где x = x 1 + πk. Значение x 1 есть координата x точки пересечения графиков функций y = tg x и y = 3. Автор вводит понятие арктангенса: arctg 3 — число, tg которого равно 3, и это число принадлежит интервал от -π/2 до π/2. Используя понятие арктангенса, решение уравнения tan x = 3 можно записать как x = arctan 3 + πk.

По аналогии решается уравнение tg x = — 3. По построенным графикам функций y = tg x и y = — 3 видно, что точками пересечения графиков, а значит, и решениями уравнений будут x = x 2 + πk. Используя арктангенс, решение можно записать в виде x = arctan (- 3) + πk. На следующем рисунке мы увидим, что arctg (- 3) = — arctg 3.

Общее определение арктангенса таково: арктангенс a — это такое число из интервала от -π/2 до π / 2, тангенс которого равен а. Тогда решением уравнения tg x = a является x = arctg a + πk.

Автор приводит пример 1. Найдите решение выражения arctg. Введем обозначения: арктангенс числа равен x, тогда tg x будет равно данному числу, где x принадлежит отрезку от -π/2 до π/2. Как и в примерах в предыдущих темах, мы будем использовать таблицу значений. Согласно этой таблице тангенс этого числа соответствует значению x = π/3. Запишем решение уравнения арктангенса заданного числа равным π/3, π/3 также принадлежит интервалу от -π/2 до π/2.

Пример 2. Вычисление арктангенса отрицательного числа. Используя равенство arctg (- a) = — arctg a, введите значение x. Аналогично примеру 2 запишем значение x, которое принадлежит интервалу от -π/2 до π/2. По таблице значений находим, что x = π/3, следовательно, — tg x = — π/3. Ответ на уравнение — π/3.

Рассмотрим пример 3. Решим уравнение tan x = 1. Запишем, что x = arctan 1 + πk. В таблице значению tg 1 соответствует значение x = π/4, следовательно, arctg 1 = π/4. Подставьте это значение в исходную формулу x и запишите ответ x = π/4 + πk .

Пример 4: расчет tg x = — 4. 1. В этом случае x = arctg (- 4.1) + πk. Поскольку в этом случае невозможно найти значение arctg, ответ будет иметь вид x = arctg (- 4.1) + πk.

В примере 5 рассматривается решение неравенства tg x > 1. Для его решения построим графики функций y = tg x и y = 1. Как видно из рисунка, эти графики пересекаются в точках x = π/4 + πk. Так как в этом случае tg x > 1, то на графике выделим площадь тангенсоиды, которая находится над графиком y = 1, где x принадлежит интервалу от π/4 до π/2. Запишем ответ как π/4 + πk

Далее рассмотрим уравнение ctg x = a. На рисунке показаны графики функций y = ctg x, y = a, y = — a, имеющих множество точек пересечения. Решения можно записать в виде x = x 1 + πk, где x 1 = arcctg a и x = x 2 + πk, где x 2 = arcctg (- a). Отмечено, что x 2 = π — x 1. Отсюда следует равенство arcctg(- a) = π — arcctg a. Далее дается определение арккотангенса: арккотангенсом а называется такое число из интервала от 0 до π, котангенс которого равен а. Решение уравнения сtg x = a записывается в виде: x = arcctg a + πk.

В конце видеоурока сделан еще один важный вывод — выражение ctg x = a можно записать в виде tg x = 1/a при условии, что a не равно нулю.

ИНТЕРПРЕТАЦИЯ ТЕКСТА:

Рассмотрим решение уравнений tg x = 3 и tg x = — 3. Решая первое уравнение графически, видим, что графики функций y = tg x и y = 3 имеют бесконечно много точек пересечения, абсциссы которых запишем в виде

х = х 1 + πk, где х 1 — абсцисса точки пересечения прямой у = 3 с главной ветвью тангенсоиды (рис. 1), для чего было придумано обозначение

arctan 3 (арктангенс трех).

Как понять arctg 3?

Это число, тангенс которого равен 3, и это число принадлежит интервалу (-;). Тогда все корни уравнения tg x = 3 можно записать по формуле x = arctg 3 + πk.

Аналогично решение уравнения tg x = — 3 можно записать в виде x = x 2 + πk, где x 2 — абсцисса точки пересечения прямой y = — 3 с главной ветвью тангеноида (рис. 1), для которого обозначение arctg (- 3) (арктангенс минус три). Тогда все корни уравнения можно записать по формуле: x = arctg(-3) + πk. Из рисунка видно, что arctg(- 3)= — arctg 3,

Сформулируем определение арктангенса. Арктангенсом а называется такое число из интервала (-;), тангенс которого равен а.

Часто используется равенство arctg(-a) = -arctg a, справедливое для любого a.

Зная определение арктангенса, делаем общий вывод о решении уравнения

tg x = a: уравнение tg x = a имеет решение x = arctg a + πk.

Рассмотрим примеры.

ПРИМЕР 1. Вычислить arctg.

Решение. Пусть arctg = x, тогда tgx = и xϵ (-;). Показать таблицу значений Следовательно, x =, так как tg = и ϵ (- ;).

Итак, arctg =.

ПРИМЕР 2 Рассчитать арктангенс (-).

Решение. Используя равенство arctg(- a) = — arctg a, запишем:

arctg(-) = — arctg . Пусть — arctg = x, тогда — tgx = и xϵ (-;). Следовательно, x =, так как tg = и ϵ (- ;). Показать таблицу значений

So — arctg=- tgх= — .

ПРИМЕР 3. Решить уравнение tgх = 1,

1. Запишем формулу решения: x = arctg 1 + πk.

2. Найти значение арктангенса

, так как tg = . Показать таблицу значений

Итак, arctg1= .

3. Подставить найденное значение в формулу решения:

ПРИМЕР 4. Решить уравнение tgx = — 4,1 (тангенс x равен минус четыре целых одна десятая).

Решение. Запишем формулу решения: x = arctg(- 4,1) + πk.

Мы не можем вычислить значение арктангенса, поэтому оставим решение уравнения как есть.

ПРИМЕР 5. Решить неравенство tgх 1.

Решение. Сделаем это графически.

1. Построим тангеноид

y = tgx и прямой y = 1 (рис. 2). Они пересекаются в точках вида x = + πk.

2. Выбрать интервал оси абсцисс, на котором главная ветвь тангенсоиды расположена над прямой у = 1, так как по условию tgх 1. Это интервал (;).

3. Используем периодичность функции.

Свойство 2. y = tg x — периодическая функция с основным периодом π.

Учитывая периодичность функции y = tgx, запишем ответ:

(;). Ответ можно записать в виде двойного неравенства:

Перейдем к уравнению ctg x = a. Приведем графическую иллюстрацию решения уравнения для положительных и отрицательных а (рис. 3).

Графики функций y=ctg x и y=a и

y=ctg x and y=-a

имеют бесконечно много общих точек, абсциссы которых имеют вид:

х = х 1 + , где х 1 — абсцисса точки пересечения прямой у = а с главной ветвью тангенсоиды и

x 1 = arcctg a;

х = х 2 +, где х 2 — абсцисса точки пересечения прямой

у = — но с главной ветвью тангенсоиды и х 2 = arcсtg (- а).

Заметим, что х 2 = π — х 1. Итак, запишем важное уравнение:

arcctg (-a) = π — arcctg a.

Сформулируем определение: арккотангенс числа а — это такое число из интервала (0; π), котангенс которого равен а.

Решение уравнения ctg x = a записывается как: x = arcсtg a +.

Обратите внимание, что уравнение ctg x = a можно преобразовать в форму

tg x = , за исключением случаев, когда a = 0.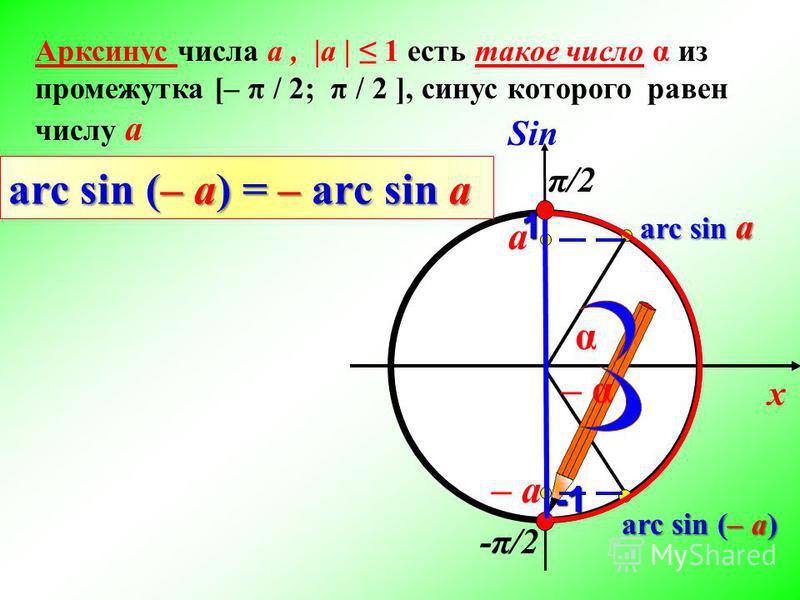

Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом , и арккотангенс. Одно является следствием другого, и пары функций одинаково важны для работы с тригонометрическими выражениями.

Рассмотрим рисунок единичной окружности, на котором графически отображаются значения тригонометрических функций.

Если рассчитать дуги OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Приведенные ниже формулы отражают связь между основными тригонометрическими функциями и соответствующими им дугами.

Чтобы лучше понять свойства арксинуса, необходимо рассмотреть его функцию. Расписание имеет вид асимметричной кривой, проходящей через центр координат.

Свойства арксинуса:

Если сравнить графики sin и arc sin , две тригонометрические функции могут найти общие закономерности.

Арккосинус

Арккосинус числа а есть значение угла α, косинус которого равен а.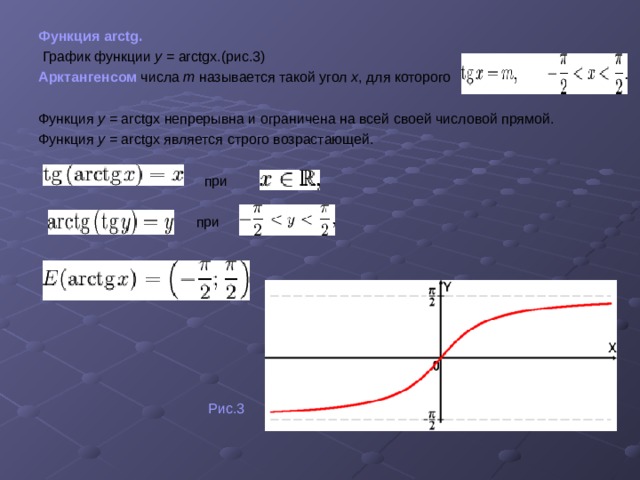

Кривая y = arcos x отражает график arcsin x с той лишь разницей, что она проходит через точку π/2 на оси OY.

Рассмотрим функцию арккосинуса более подробно:

1. Функция определена на отрезке [-1; один].
2. ОДЗ для arccos — .
3. График полностью расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
4. Y = 0 для x = 1.
5. Кривая уменьшается по всей длине. Некоторые свойства арккосинуса такие же, как у функции косинуса.

Некоторые свойства арккосинуса такие же, как у функции косинуса.

Возможно, такое «детальное» изучение «арок» покажется школьникам лишним. Однако в противном случае некоторые элементарные типовые задания ЕГЭ могут завести учащихся в тупик.

Упражнение 1. Задайте функции, показанные на рисунке.

Ответ: рис. 1 — 4, рис. 2 — 1.

В этом примере упор сделан на мелочи. Обычно студенты очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать форму кривой, если ее всегда можно построить по рассчитанным точкам. Не забывайте, что в тестовых условиях время, затраченное на рисование простой задачи, потребуется для решения более сложных задач.

Арктангенс

Arctg число а такое значение угла α, что его тангенс равен а.

Если рассматривать график арктангенса, то можно выделить следующие свойства:

1. График бесконечен и определен на интервале (- ∞; + ∞).
2. Арктангенс — нечетная функция, поэтому arctan (- x) = — arctan x.
3. Y = 0 для x = 0.
4. Кривая увеличивается по всей области определения.

Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.

Арктангенс

Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен a.

Свойства функции арккотангенса:

1. Интервал определения функции равен бесконечности.
2. Диапазон допустимых значений — интервал (0; π).
3. F(x) не является ни четным, ни нечетным.
4. На всем протяжении график функции убывает.

Сравнить ctg x и arctg x очень просто, нужно всего лишь нарисовать два рисунка и описать поведение кривых.

Задание 2. Соотнесите график и вид функции.

Логически графики показывают, что обе функции возрастают. Следовательно, оба рисунка отображают некоторую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,

Ответ: рис. 1 — 1, рис. 2-4.

Тригонометрические тождества arcsin, arcos, arctg и arcctg

Ранее мы уже определили связь между арками и основные функции тригонометрии. Эту зависимость можно выразить рядом формул, позволяющих выразить, например, синус аргумента через его арксинус, арккосинус или наоборот. Знание таких тождеств может оказаться полезным при решении конкретных примеров.

Существуют также соотношения для arctg и arcctg:

Другая полезная пара формул устанавливает значение суммы значений arcsin и arcos и arcctg и arcctg одного и того же угла.

Примеры решения задач

Задачи тригонометрии условно можно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить построение заданной функции, найти ее область определения или ОДЗ и выполнить аналитические преобразования для решения примера .

При решении первого типа задач необходимо придерживаться следующего плана действий:

При работе с графиками функций главное — знание их свойств и внешнего вида кривой. Таблицы тождеств нужны для решения тригонометрических уравнений и неравенств. Чем больше формул запоминает ученик, тем легче ему найти ответ на задание.

Допустим на экзамене необходимо найти ответ на уравнение вида:

Если правильно преобразовать выражение и привести его к нужному виду, то решить его очень просто и быстро. Во-первых, давайте переместим arcsin x в правую часть уравнения.

Если вспомнить формулу arcsin(sinα) = α , то поиск ответов можно свести к решению системы двух уравнений:

Ограничение на модель x возникло, опять же из свойств arcsin: ODZ for x [-1; один]. При a ≠ 0 часть системы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При а = 0 х будет равен 1,

Эта статья о нахождении значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала уточним, что называется величиной арксинуса, арккосинуса, арктангенса и арккотангенса. Далее получаем основные значения этих дуговых функций, после чего разберемся, как по таблицам синусов, косинусов, тангенсов находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса и котангенсы Брадиса. Наконец, поговорим о нахождении арксинуса числа, когда известны арккосинус, арктангенс или арккотангенс этого числа и т. д.

Навигация по страницам.

Значения арксинуса, арккосинуса, арктангенса и арккотангенса

Сначала нужно выяснить, что такое значение арксинуса, арккосинуса, арктангенса и арккотангенса ».

Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты. Здесь стоит упомянуть, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам для арксинуса, арккосинуса, арктг и arcctg противоположных чисел вида arcsin(−a)=−arcsin a , arccos(−a)=π−arccos a , arctg(−a)=−arctg a и arcctg(−a)=π−arcctg a .

Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса с помощью таблиц Брадиса. Мы сделаем это на примерах.

Предположим, нам нужно найти значение арксинуса 0,2857. Находим это значение в таблице синусов (случаи, когда этого значения нет в таблице, разберем ниже). Это соответствует синусу 16 градусов 36 минут. Следовательно, искомое значение арксинуса числа 0,2857 составляет угол 16 градусов 36 минут.

Часто необходимо учитывать поправки из трех столбцов справа от таблицы. Например, если нам нужно найти арксинус 0,2863. По таблице синусов это значение получается как 0,2857 плюс поправка 0,0006, то есть значение 0,2863 соответствует синусу 16 градусов 38 минут (16 градусов 36 минут плюс 2 минуты коррекции).

Если интересующее нас число, арксинус которого отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно найти два ближайших значения синусов к нему, между которыми заключено это число. Например, ищем значение арксинуса числа 0,2861573. Этого номера нет в таблице; с помощью поправок этот номер тоже получить нельзя. Затем находим два ближайших значения 0,2860 и 0,2863, между которыми заключено исходное число, эти числа соответствуют синусам 16 градусов 37 минут и 16 градусов 38 минут. Искомое значение арксинуса 0,2861573 лежит между ними, то есть любое из этих значений угла можно принять за приближенное значение арксинуса с точностью до 1 минуты.

Значения арккосинуса, значения арктангенса и значения арккотангенса абсолютно аналогичны (при этом, разумеется, используются таблицы косинусов, тангенсов и котангенсов, соответственно).

Нахождение значения arcsin через arccos, arctg, arcctg и т. д.

Например, предположим, что мы знаем, что arcsin a=−π/12 , но нам нужно найти значение arccos a . Вычислим значение арккосинуса, которое нам нужно: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12.

Гораздо интереснее ситуация, когда по известному значению арксинуса или арккосинуса числа а требуется найти значение арктангенса или арккотангенса этого числа а, или наоборот. К сожалению, мы не знаем формул, определяющих такие отношения. Как быть? Давайте разберемся с этим на примере.

Пусть нам известно, что арккосинус числа а равен π/10, и нам нужно вычислить значение арктангенса этого числа а. Решить задачу можно следующим образом: по известному значению арккосинуса найти число а, а затем найти арктангенс этого числа. Для этого нам понадобится сначала таблица косинусов, а затем таблица тангенсов.

Угол π/10 радиан — это угол 18 градусов, по таблице косинусов находим, что косинус 18 градусов примерно равен 0,9511, тогда число а в нашем примере равно 0,9511.

Осталось обратиться к таблице тангенсов, и с ее помощью найти значение нужного нам арктангенса 0,9511, он примерно равен 43 градусам 34 минуты.

Эту тему логически продолжает материал статьи вычисление выражений, содержащих arcsin, arccos, arctg и arcctg .

Библиография.

• Алгебра: Учеб. на 9 кл. среднее школа / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Эд. С. А. Теляковский.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
• Башмаков М.И. Алгебра и начало анализа: Учеб. на 10-11 кл. среднее школа — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
• Алгебра и начало анализа: Учеб. на 10-11 кл. общеобразовательные учреждения / А.Н. Колмогоров, А.М. Абрамов, Ю.В. П. Дудницын и др.; Эд. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
• И. В. Бойков, Л. Д. Романова. Сборник заданий для подготовки к ЕГЭ, часть 1, Пенза 2003.
• Брадис В. М. Четырехзначные математические таблицы: Для общеобразовательных целей. Учебные заведения. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2

Что такое арксинус, арккосинус? Что такое арктангенс, арктангенс?

Внимание!
Дополнительные материалы
содержатся в специальной секции 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень…»)

К понятиям Арксинус, арккосинус, арктангенс, арккотангенс студенческое население насторожено. Он не понимает этих терминов и, следовательно, не доверяет этому славному семейству.) А зря. Это очень простые понятия. Которые, кстати, сильно облегчают жизнь знающему человеку при решении тригонометрических уравнений!

Запутались в простоте? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.

Конечно, для понимания неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых ракурсов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.

Итак, мы удивлены, но помните: арксинус, арккосинус, арктангенс и арктангенс — это всего лишь некоторые углы. Ни больше, ни меньше. Есть угол, скажем, 30°. И есть угол arcsin0.4. или arctg(-1.3). Углы бывают всякие.) Просто писать углы можно по разному. Вы можете написать угол в градусах или радианах. А можно — через его синус, косинус, тангенс и котангенс…

Что означает выражение

arcsin 0.4?

Это угол, синус которого равен 0,4 ! Да Да. В этом смысл арксинуса. Специально повторяю: arcsin 0,4 — это угол, синус которого равен 0,4.

И все.

Чтобы надолго удержать эту простую мысль в голове, я даже приведу расшифровку этого страшного термина — арксинуса:

arc sin 0,4
впрыск, синус которого равен 0.4

Как написано, так и слышно.) Почти. Приставка дуга означает дуга (слово дуга знаете?), потому что древние люди использовали дуги вместо углов, но сути дела это не меняет. Запомните эту элементарную расшифровку математического термина! Причем для арккосинуса, арктангенса и арктангенса расшифровка отличается только названием функции.

Что такое arccos 0.8?
Это угол, косинус которого равен 0,8.

Что такое arctan(-1,3) ?
Это угол, тангенс которого равен -1,3.

Что такое arcctg 12?
Это угол, котангенс которого равен 12.

Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, вполне солидно выглядит выражение arccos1,8. Приступим к расшифровке: arccos1,8 — это угол, косинус которого равен 1,8… Хоп-хоп!? 1,8!? Косинус не может быть больше единицы!

Правильно. Выражение arccos1,8 не имеет смысла. А написание такого выражения в каком-нибудь ответе сильно позабавит проверяющего.)

Элементарно, как видите.) У каждого угла свои личные синус и косинус. И почти у каждого свой тангенс и котангенс. Следовательно, зная тригонометрическую функцию, можно записать и сам угол. Для этого предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я буду называть все это семейство уменьшительно-ласкательным — арки.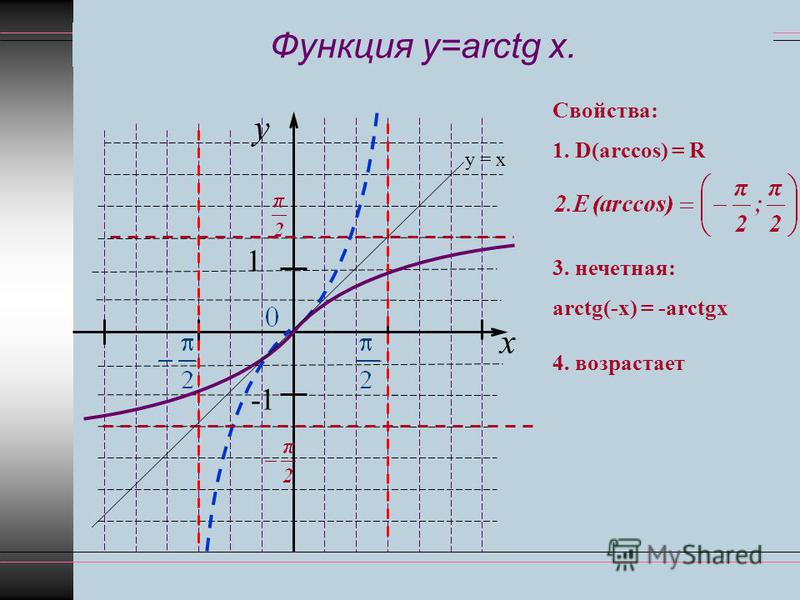 печатать меньше.)

Внимание! Элементарная словесная и сознательная расшифровка арок позволяет спокойно и уверенно решать самые разные задачи. А из необычных задач спасает только она.

Можно ли перейти с арок на обычные градусы или радианы? — слышу осторожный вопрос.)

Почему бы и нет!? Легко. Вы можете пойти туда и обратно. Более того, иногда это необходимо сделать. Арки вещь простая, но без них как-то спокойнее, правда?)

Например: что такое arcsin 0,5?

Посмотрим на расшифровку: arcsin 0.5 — это угол, синус которого равен 0.5. А теперь включите голову (или гугл)) и вспомните, у какого угла синус 0,5? Синус равен 0,5 y углу 30 градусов . Вот и все: arcsin 0,5 — это угол 30°. Можно смело писать:

arcsin 0.5 = 30°

Или, более солидно, в радианах:

Все, можно забыть про арксинус и работать дальше с обычными градусами или радианами.

Если ты понял что такое арксинус, арккосинус. .. Что такое арктангенс, арккотангенс… Тогда ты легко расправишься, например, с таким монстром.)

Несведущий человек отшатнется в ужасе, да…) А знающий вспомни расшифровку: арксинус — это угол, синус которого равен… Ну и тд. Если знающий человек знает еще и таблицу синусов… Таблицу косинусов. Таблица тангенсов и котангенсов, тогда вообще проблем нет!

Достаточно учесть, что:

Расшифрую, т.е. переведу формулу словами: угол, тангенс которого равен 1 (arctg1) угол 45°. Или, что то же самое, Пи/4. Аналогично:

и все… Заменяем все арки значениями в радианах, все сокращается, осталось посчитать сколько будет 1+1. Будет 2.) Это правильный ответ.

Вот так можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арктангенсов к обычным градусам и радианам. Это значительно упрощает страшные примеры!

Часто в таких примерах внутри арок находятся отрицательных значений .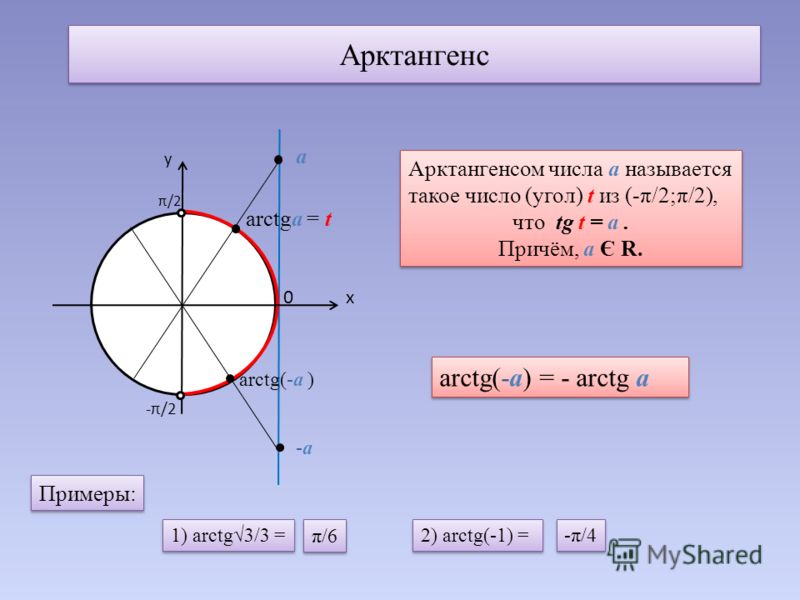 Например, arctg(-1.3) или, например, arccos(-0.8)… Это не проблема. Вот несколько простых формул для перехода от отрицательного к положительному:

Вам нужно, скажем, определить значение выражения:

Вы можете решить это, используя тригонометрический круг, но вы не хотите его рисовать. Ну ладно. Переход от отрицательных значений внутри арккосинуса к положительным по второй формуле:

Внутри арккосинуса справа уже положительный смысл. Что

вы просто должны знать. Осталось вместо арккосинуса подставить радианы и вычислить ответ:

Вот и все.

Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.

Проблемы с примерами 7–9? Ну да, там есть какая-то хитрость.)

Все эти примеры, с 1-го по 9-й, тщательно разложены по полочкам в Разделе 555. Что, как и почему. Со всеми секретными ловушками и уловками. Плюс способы кардинально упростить решение. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом.