Площадь прямоугольника как найти
Автор Ольга Андрющенко На чтение 5 мин. Просмотров 10.4k. Опубликовано
Площадь прямоугольника очень часто требуется найти в задачах по геометрии. И не только — в повседневной жизни очень многие плоскости имеют форму прямоугольника и надо найти площадь прямоугольника. Как это сделать? Давайте рассмотрим все формулы и примеры.
Мы учимся вычислять площадь прямоугольника или площадь прямоугольника в школе. Однако, когда вы станете старше, вполне возможно, что вы не будете помнить, как найти площадь прямоугольника. Для начала давайте вспомним, что такое прямоугольник.
Содержание
Что такое прямоугольник
Давайте не будем «срезать углы». Чтобы иметь возможность вычислить площадь прямоугольника, естественно, что мы сначала знаем, что это такое. Поэтому для начала необходимо помнить, что прямоугольник является четырехугольником. Другими словами, это геометрическая фигура, которая имеет четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.
Противоположные стороны прямоугольника имеют одинаковую длину. Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.
Не все четырехугольники являются прямоугольниками. Действительно, обязательно, чтобы они имели следующие свойства, чтобы мы могли сказать, что это действительно прямоугольник:
Характеристики прямоугольника
Противоположные стороны должны быть параллельны.
- Диагонали прямоугольника должны быть одинаковой длины. Они также пересекаются в своей середине.
- Точка пересечения диагоналей прямоугольника называется центром симметрии.
- Кроме того, прямоугольник также является параллелограммом, так как его стороны попарно параллельны. Однако это частный случай параллелограмма. На самом деле он имеет четыре прямых угла, и его две параллельные стороны не должны иметь одинаковую длину. В противном случае все четыре стороны имеют одинаковую длину — тогда мы говорим о квадрате.
Формула площади прямоугольника
Как рассчитать площадь прямоугольника? Обратите внимание, что базовую формулу для вычисления площади (или площади) прямоугольника очень легко запомнить. Вы просто должны умножить его длину на ширину.
Вы просто должны умножить его длину на ширину.
Площадь прямоугольника равна его длине, умноженной на ширину.
Например, площадь прямоугольника длиной 4 сантиметра и шириной 2 сантиметра равна 4 x 2 = 8 см².
Найти площадь прямоугольника по известным длине и ширине — онлайн калькулятор.
Введите длину a:
Введите ширину b:
Площадь прямоугольника:
Диагональ прямоугольника:
Площадь поверхности прямоугольника длиной L и шириной l равна: S = L x l
Принцип расчета площади прямоугольника
Чтобы вычислить площадь прямоугольника, мы посчитаем количество единиц областей, которые содержит прямоугольник:
В прямоугольнике выше 12 квадратов по 1 см². Его площадь составляет 12 см² (4 х 3).
Примечание. В этом расчете длина L и ширина l прямоугольника должны быть выражены в одной и той же единице длины. Результат будет выражен в той же единице измерения, возведенной в квадрат. Например, если длина прямоугольника выражена в метрах, ширина также должна быть выражена в метрах, а результат формулы для расчета площади прямоугольника даст результат в квадратных метрах (м²).
Площадь прямоугольника эквивалентна его территории. Территория — это термин, используемый для обозначения меры площади земли (мы используем единицу измерения гектар, а не м²). Гектар — это метрическая мера земельной площади, равная 10 000 м2.
Пример расчета
Рассмотрим прямоугольник длиной L = 4 см и шириной l = 2 см. Площадь S его поверхности равна:
A = L x l = 4 x 2 = 8 см².
Как рассчитать площадь прямоугольника, если мы знаем только одну сторону и диагональ
Можно определить площадь прямоугольника другим способом. Формула, которая была изложена ранее, не является единственным методом, который можно использовать. Действительно, вполне возможно сделать это по-другому. Для этого нам нужно будет, по крайней мере, измерить только одну сторону и необходимо знать длину диагонали. В этом случае мы делаем расчет, используя теорему Пифагора.
Что такое теорема Пифагора
Это формула, которая используется для определения длины третьей стороны прямоугольного треугольника, когда вы уже знаете значение двух других его сторон.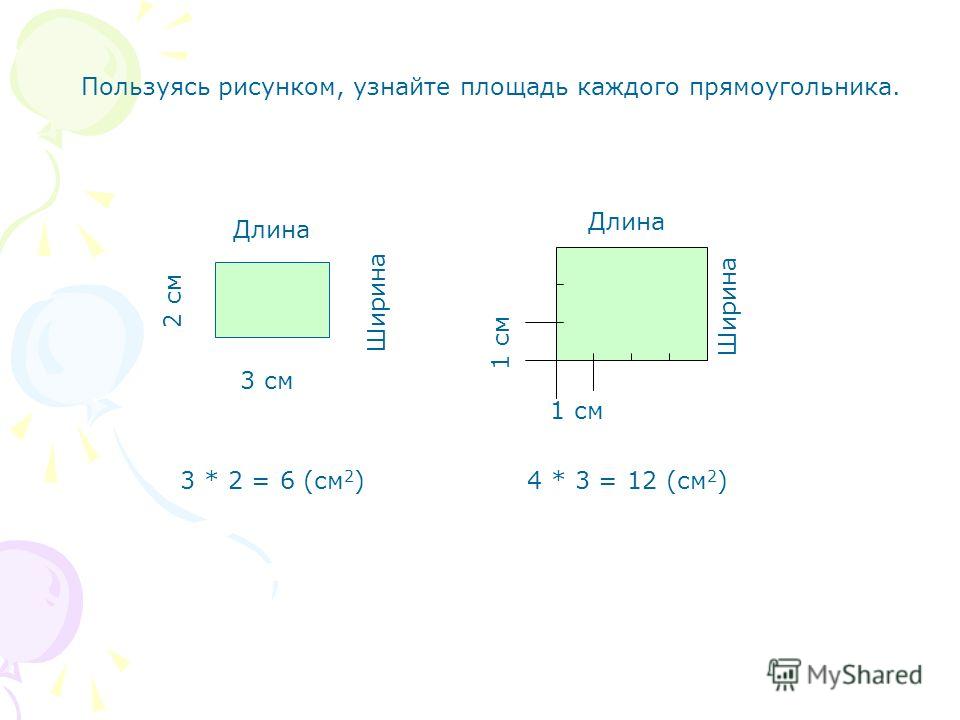
Обратите внимание, что прямоугольник состоит из двух прямоугольных треугольников. Действительно, диагональ представляет гипотенузу этого типа треугольника.
Теорема Пифагора
Кроме того, это также самая длинная сторона, которую можно найти на рисунке. Длина и ширина, с другой стороны, представляют две другие его стороны (скажем, смежные стороны). Это причина, почему можно использовать эту формулу для определения площади прямоугольника.
Теорема Пифагора основана на довольно простом уравнении, которое выглядит следующим образом: a² + b² = c². Где a и b используются для представления двух соседних сторон — катетов прямоугольного треугольника, а c представляет гипотенузу треугольника.
Чтобы полностью понять использование этой формулы, мы начнем с очень конкретного примера. Для этого предположим, что диагональ прямоугольника 10 см, а другая сторона 6 см. Если мы ссылаемся на формулу a² + b² = c², следовательно, сторона «a» составляет 6 см, а гипотенуза «c» — 10 см. Теперь нам нужно просто заменить буквенные значения числовыми значениями, которые у нас есть. Что дает нам:
Теперь нам нужно просто заменить буквенные значения числовыми значениями, которые у нас есть. Что дает нам:
a² + b² = c²
6² + b² = 10²
b² = 10² — 6²
b² = 100 — 36
b² = 64
b= 8
Мы получаем длину смежной стороны прямоугольника «b», которая равна 8 см. Теперь мы можем рассчитать площадь прямоугольника:
S = 8 см х 6 см
Следовательно, S = 48 см².
Нахождение площади. Как найти площадь прямоугольника
Урок на тему: «Формулы определения площади треугольника, прямоугольника, квадрата»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 5 класса
Тренажер к учебнику И.И.Зубаревой и А.Г.Мордковича
Тренажер к учебнику Г.В.Дорофеева и Л.Г.Петерсона
Определение и понятие площади фигуры
Чтобы лучше понять, что такое площадь фигуры, рассмотрим рисунок.
Эта произвольная фигура разбита на 12 маленьких квадратика. Сторона каждого квадратика равна 1 см. А площадь каждого квадратика равна 1 квадратному сантиметру, что записывается так: 1 см 2 .
Тогда площадь фигуры равна 12 квадратным сантиметрам. В математике площадь обозначается латинской буквой S.
Значит, площадь нашей фигуры равна: S фигуры = 12 см 2 .
Площадь фигуры равна площади всех маленьких квадратиков, из которых она состоит!
Ребята, запомните!
Площадь измеряется квадратными единицами длины.
Единицы измерения площади:
1. Квадратный километр — км 2 (когда площади очень большие, например, страна или море).
2. Квадратный метр — м 2 (вполне подходит для того, чтобы измерять площадь участка или квартиры).
3. Квадратный сантиметр — см 2 (обычно используется на уроках математики, когда рисуют фигуры в тетради).
4. Квадратный миллиметр — мм 2 .
Площадь треугольника
Рассмотрим два вида треугольников: прямоугольный и произвольный.
Чтобы найти площадь прямоугольного треугольника необходимо знать длину основания и высоту. В прямоугольном треугольнике высоту заменяет одна из сторон. Поэтому в формулу площади треугольника вместо высоты подставляем одну из сторон.
В нашем примере стороны равны 7 см и 4 см.
Формула для расчета площади треугольника записывается так:
S прямоугольного треугольника АВС = 7 см * 4 см: 2 = 14 см 2
Теперь рассмотрим произвольный треугольник.
Для такого треугольника необходимо провести высоту к основанию.
В нашем примере высота равна 6 см, а основание равно 8 см. Как и в предыдущем примере, рассчитываем площадь по формуле:
S произвольного треугольника АВС = ВС * h: 2.
Подставим в формулу наши данные и получим:
S произвольного треугольника АВС = 8 см * 6 см: 2 = 24 см 2 .
Площадь прямоугольника и квадрата
Возьмем прямоугольник АВСD со сторонами 5 см и 8 см.
Формула расчета площади прямоугольника записывается так:
S прямоугольника АВСD = 8 см * 5 см = 40 см 2 .
Теперь рассчитаем площадь квадрата. В отличии от прямоугольника и треугольника, для нахождения площади квадрата необходимо знать только одну сторону. В нашем примере сторона квадрата ABCD равна 9 см. S квадрата АВСD = АВ * ВС = АВ 2 .
Подставим в формулу наши данные и получим:
S квадрата АВСD = 9 см * 9 см = 81 см 2 .
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
В этой статье мы разберемся, как вычислить площадь фигуры.
Но не всегда можно сравнить площади фигур таким способом. Тогда можно разбить фигуру на равные квадраты и посчитать количество квадратов входящих в эту фигуру.
На
рисунке изображено две фигуры. Путем наложения эти фигуры сравнить
невозможно. Мы разбили эти фигуры на квадраты с одинаковой площадью. Теперь можно посчитать количество квадратов входящих в эти фигуры. В
первую фигуру вписалось 6 квадратов, а во вторую 8. Значит площадь
первой фигуры меньше площади второй.
Теперь можно посчитать количество квадратов входящих в эти фигуры. В
первую фигуру вписалось 6 квадратов, а во вторую 8. Значит площадь
первой фигуры меньше площади второй.
Фигуры равна числу единичных квадратов, составляющих эту фигуру.
Если у квадрата сторона равна 1 см, то площадь такого квадрата равна 1 квадратному сантиметру (см 2) .
Площадь квадрата сторона которого равна 1 дециметр равна 1 квадратному дециметру (дм 2) или 100 квадратным сантиметрам(см 2).
Площадь фигуры обозначается заглавной латинской буквой S.
Допустим
нам надо найти площадь прямоугольника, длины сторон которого равны 6 и 4
см. Разделим прямоугольник на квадратные сантиметры и вычислим его
площадь.
Итак, умножим длину прямоугольника на его ширину и получим площадь:
S = 6 × 4 = 24 см 2
Чтобы вычислить , надо измерить его длину и ширину в одинаковых единицах измерения и найти их произведение.
Если известна площадь прямоугольника и ширина, то найти длину просто, надо разделить площадь на известную длину.
Д = S ÷ Ш
или
Ш = S ÷ Д
Например, площадь прямоугольника равна 15 см 2 . Длина прямоугольника равна 5 см. Найдем его ширину:
Ш = 15 ÷ 5 = 3 см
Если фигура сложная, например, такая как на рисунке, то вычислить её площадь можно разбив фигуру на прямоугольники, вычислить их площадь, а затем сложить полученные площади.
Итак нашу фигуру мы можем разбить на два прямоугольника: первый площадью 2 см 2 , и второй площадью 8 см 2:
S = 2 × 1 + 4 × 2 = 10 см 2
А как найти . Для этого надо достроить треугольник до прямоугольника, так как показано на рисунке.
Теперь найдем площадь полученного прямоугольника и разделим её пополам:
S = (3 × 6) ÷ 2 = 9 см 2
Кажется все просто, когда треугольник прямоугольный. Если у треугольника нет прямого угла, то вычислить его площадь можно следующим образом:
На
следующем рисунке мы видим треугольник, площадь которого нам надо
вычислить, он выделен желтым цветом. Впишем его в прямоугольник, так как
показано на рисунке.
Теперь для того, чтобы найти площадь нашего треугольника, надо вычислить площади двух полученных прямоугольных треугольников и сложить их:
S1 = (3 × 4) ÷ 2 = 6 см 2
S2 = (2 × 4) ÷ 2 = 4 см 2
S = S1 + S2 = 6 + 4 = 10 см 2
Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.
Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении.
Формулы для нахождения площади любого треугольника представлены несколькими вариантами:
1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:
2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.
На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:
Прямоугольник
Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:
Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении. Такая формула площади прямоугольника имеет вид:
Такая формула площади прямоугольника имеет вид:
Квадрат
Площадь квадрата определяют как вторую степень длины стороны:
Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
Площадь квадрата можно найти другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.
Формулы площади параллелограмма таковы:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:
Трапеция
Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:
Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Цилиндр и параллелепипед
Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:
Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Площадь кольца, с использованием длин диаметров, определяют следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:
где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Как найти площадь прямоугольника пример. Как посчитать площадь
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
- Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определяемой величине.
 Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
- Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
- Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений.
 Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Что такое площадь и что такое прямоугольник
Площадь – это такая геометрическая величина, с помощью которой можно определить размер какой-либо поверхности геометрической фигуры.
На протяжении многих веков так повелось, что вычисление площади называли квадратурой. То есть, чтобы узнать площадь несложных геометрических фигур, достаточно было подсчитать количество единичных квадратов, которыми условно были покрыты фигуры. А фигуру, которая имела площадь, называли квадрируемой.
То есть, чтобы узнать площадь несложных геометрических фигур, достаточно было подсчитать количество единичных квадратов, которыми условно были покрыты фигуры. А фигуру, которая имела площадь, называли квадрируемой.
Поэтому, можно подвести итог, что площадь – это такая величина, которая показывает нам размер части плоскости, соединенной между собой отрезками.
Прямоугольник – это такой четырехугольник, у которого все углы прямые. То есть, четырехстороннюю фигуру, которая имеет четыре прямых угла и ее противоположные стороны равны, называют прямоугольником.
Как найти площадь прямоугольника
Самый простой способ нахождения площади прямоугольника – взять прозрачную бумагу, например кальку, или клеенку и расчертить ее на равные квадратики по 1 см, а потом приложить к изображению прямоугольника. Количество заполненных квадратиков и будет площадью в сантиметрах квадратных. Например, на рисунке видно, что прямоугольник попадает в 12 квадратов, значит, его площадь равна – 12 кв. см.
см.
Но для нахождения площади больших объектов, например квартиры, необходим более универсальный способ, поэтому была доказана формула, чтобы найди площадь прямоугольника необходимо умножить его длину на ширину.
А теперь давайте попробуем записать правило нахождения площади прямоугольника в виде формулы. Обозначим площадь нашей фигуры буквой S, буква а – будет обозначать его длину, а буква b – ширину.
В итоге получаем вот такую формулу:
S = а * b.
Если наложить эту формулу на рисунок прямоугольника выше, то мы получим те же 12 кв.см, т.к. а = 4 см, b = 3 см, а S = 4 * 3 = 12 кв.см.
Если взять две идентичные фигуры, и наложить их одну на другую, то они совпадут, а будут называться равными. У таких равных фигур будут также равны их площади и периметры.
Зачем уметь находить площадь
Во-первых, если вы знаете, как найти площадь какой-либо фигуры, то с помощью ее формулы вы без проблем сможете решать любые задачи по геометрии и тригонометрии.
Во-вторых, научившись находить площадь прямоугольника, вы сначала сможете решать простые задачки, а со временем перейдете к решению более сложных, и научитесь находить площади фигур, которые вписаны в прямоугольник или около него.
В-третьих, зная такую простую формулу, как S = а * b, вы получаете возможность без проблем решать любые простые бытовые задачи (например, находить S квартиры или дома), а со временем и сможете применить их к решению сложных архитектурных проектов.
То есть, если совсем упростить формулу нахождения площади, то она будет выглядеть так:
П = Д х Ш,
Что обозначает П – это искомая площадь, Д – это ее длина, Ш – обозначает ее ширину, а х – является знаком умножения.
А известно ли вам, что площадь любого многоугольника можно условно разбить на определенное количество квадратных блоков, которые находятся внутри этого многоугольника? Какая разница между площадью и периметром
Давайте на примере попробуем понять разницу между периметром и площадью. Например, наша школа находится на участке, который огражден забором – суммарная длина этого забора будет периметром, а то пространство, которое находится внутри ограждения и является площадью.
Например, наша школа находится на участке, который огражден забором – суммарная длина этого забора будет периметром, а то пространство, которое находится внутри ограждения и является площадью.
Единицы измерения площади
Если периметр одномерный измеряется в линейных единицах, которыми являются дюймы, футы и метры, то S относится к двумерным исчислениям и имеет свою длину и ширину.
И измеряется S в квадратных единицах, таких, как:
Один квадратный миллиметр, где S квадрата имеет сторону, равную одному миллиметру;
Квадратный сантиметр, имеет S такого квадрата, у которого сторона равна одному сантиметру;
Квадратный дециметр равен S этого квадрата со стороной в один дециметр;
Квадратный метр имеет S квадрата, сторона которого равна одному метру;
И наконец, квадратный километр имеет S квадрата, сторона которого равна одному километру.
Для измерения площадей больших участков на поверхности Земли используют такие единицы, как:
Один ар или сотка – если S квадрата имеет сторону десять метров;
Один гектар равен S квадрата, у которого сторона имеет сто метров.
Задачи и упражнения
А теперь давайте рассмотрим несколько примеров.
На рисунке 62 нарисована фигура, которая имеет восемь квадратов и каждая сторона этих квадратов равна одному сантиметру. Поэтому S такого квадрата будет квадратный сантиметр.
Если записать, то это будет выглядеть так:
1 см2. А S все этой фигуры, состоящей из восьми квадратов, будет равняться 8 кв.см.
Если взять какую-нибудь фигуру и разбить ее на «р» квадратов со стороной, равной одному сантиметру, то ее площадь будет равна:
Р см2.
Давайте рассмотрим прямоугольник, изображений на рисунке 63. Этот прямоугольник состоит из трех полос, а каждая такая полоска разбита на пять равных квадратов, имеющих сторону в 1 см.
Попробуем найти его площадь. И так берем пять квадратов, и умножаем на три полоски и получаем площадь равную 15 кв.см.:
Рассмотрим следующий пример. На рисунке 64 изображен прямоугольник ABCD, ломаной линией KLMN он разбит на две части.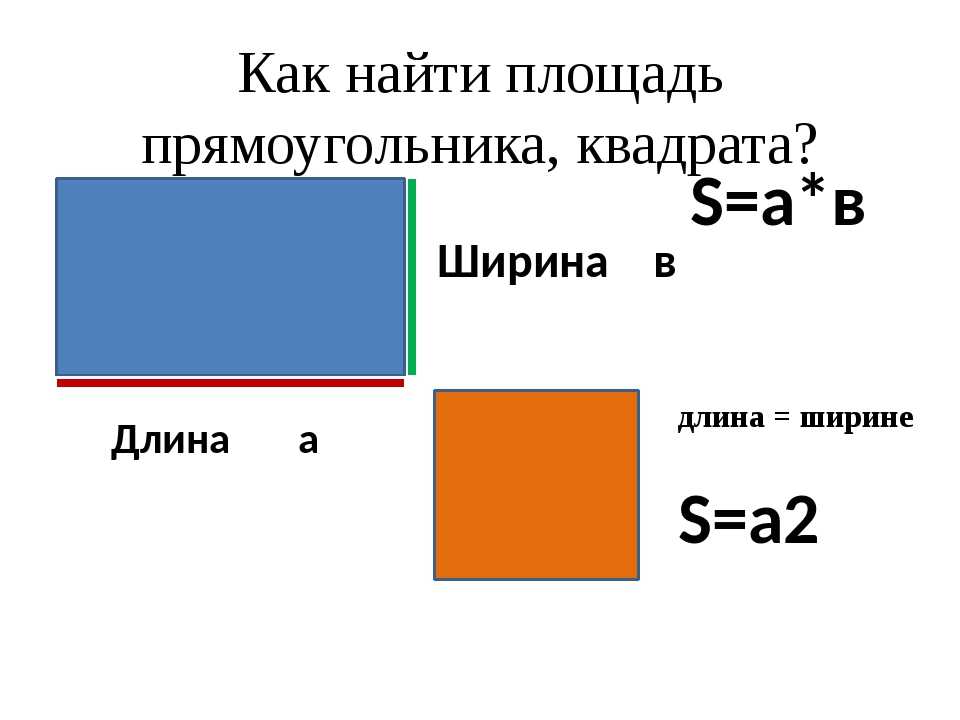 Первая его часть равна площади 12 см2, а вторая имеет площадь 9 см2.
Теперь давайте найдем площадь всего прямоугольника:
Первая его часть равна площади 12 см2, а вторая имеет площадь 9 см2.
Теперь давайте найдем площадь всего прямоугольника:
Итак, берем три и умножаем на семь и получаем 21 кв.см:
3 7 = 21 кв.см. При этом 21 = 12 + 9.
И приходим к выводу, что площадь всей нашей фигуры равна сумме площадей ее отдельных частей.
Рассмотрим еще один пример. И так на рисунке 65 изображен прямоугольник, который с помощью отрезка АС разбит на два равных треугольника ABC и ADC
А так, как нам уже известно, что квадрат – это такой же прямоугольник, только имеющий равные стороны, то площадь каждого треугольника будет равняться половине площади всего прямоугольника.
Представим, что сторона квадрата равна а, то:
S = a a = a2.
Делаем вывод, что формула площади квадрата будет иметь такой вид:
А запись a2 называется квадратом числа а.
И так, если сторона нашего квадрата равна четырем сантиметрам, то его площадь будет:
4 4, то есть 4 * 2 = 16 кв. см.
см.
Вопросы и задания
Найдите площадь фигуры, которая разбита на шестнадцать квадратов, сторона которых равна одному сантиметру.
Вспомните формулу прямоугольника и запишите ее.
Какие измерения нужно произвести, чтобы узнать площадь прямоугольника?
Дайте определение равным фигурам.
Могут ли иметь равные фигуры различные площади? А периметры?
Если вам известны площади отдельных частей фигуры, как узнать ее общую площадь?
Сформулируйте и запишите, чему равняется площадь квадрата.
Историческая справка
А известно ли вам, что древние люди в Вавилоне умели рассчитать площадь прямоугольника. Так же древние египтяне делали расчеты различных фигур, но так как точных формул они не знали, то вычисления имели небольшие погрешности.
В своей книге «Начала» знаменитый древнегреческий математик Евклид, описывает различные способы вычисления площадей разных геометрических фигур.
Инструкция
Чтобы найти длину стороны прямоугольника, если известна ширина и площадь , разделите числовое значение площади на числовое значение ширины. То есть воспользуйтесь формулой:Д = П / Ш, где:Д – длина стороны прямоугольника,
То есть воспользуйтесь формулой:Д = П / Ш, где:Д – длина стороны прямоугольника,
Ш – ширина прямоугольника,
П – его площадь .Например, если площадь прямоугольника равна 20 см², а его ширина – 5 см, то длина его стороны будет: 20 / 5 = 4 см.
Перед началом вычислений переведите ширину и площадь прямоугольника в одну систему измерений. То есть, площадь должна выражаться в соответствующих ширине квадратных единицах измерения. При этом, длина получится в тех же единицах, что и ширина . Так, если ширина задана в метрах, то площадь необходимо в . Особенно актуален такой при измерении земельных участков, где площадь обычно задана в гектарах, арах и «сотках».
Например, пусть площадь дачного участка равняется шести соткам, а его ширина – 30 метров. Требуется найти длину участка.
Так как «соткой» 100 , то площадь «стандартных» шести можно записать как 600 м². Отсюда длину земельного участка можно найти разделив 600 на 30. Получается – 20 метров.
Получается – 20 метров.
Иногда заданы площадь и ширина фигуры, имеющей не прямоугольную, а произвольную форму. При этом, также требуется найти ее длину . Как правило, в это случае подразумеваются габаритные фигуры, то есть параметры прямоугольника, в который эту фигуру можно заключить.
Если большая точность вычислений не требуется, то воспользуйтесь вышеприведенной формулой (Д = П / Ш). Однако, значение длины при этом получится заниженным. Чтобы получить более точное значение длины фигуры, оцените насколько полно фигура заполняет свой габаритный прямоугольник и разделите полученную длину на коэффициент заполнения.
Источники:
- Какова длина прямоугольника, если известна его ширина
Каждая геометрическая фигура обладает определенными характеристиками, которые, в свою очередь, связаны между собой. Поэтому для того, чтобы найти площадь прямоугольника, нужно знать, какова длина его сторон.
Прямоугольник — одна из самых распространенных геометрических фигур.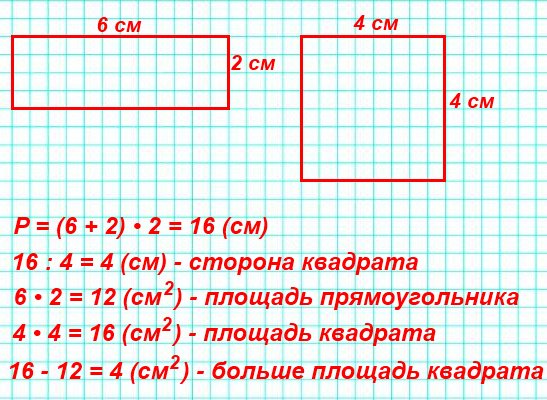 Он представляет собой четырехугольник, все углы которого равны между собой и составляют по 90 градусов. Эта характеристика, в свою очередь, влечет за собой определенные последствия в отношении других параметров рассматриваемой фигуры.
Он представляет собой четырехугольник, все углы которого равны между собой и составляют по 90 градусов. Эта характеристика, в свою очередь, влечет за собой определенные последствия в отношении других параметров рассматриваемой фигуры.
Во-первых, его стороны, располагающиеся друг напротив друга, будут параллельны. Во-вторых, эти стороны будут попарно равны между собой по длине. Эти характеристики оказываются очень важными для исчисления других его параметров, таких как площадь.
Порядок вычисления площади прямоугольника
Для того чтобы вычислить , необходимо иметь информацию о том, какова длина его сторон. Следует помнить, что стороны прямоугольника не равны по этому показателю: прямоугольник, все стороны которого равны между собой по длине, представляет собой другую геометрическую фигуру, которая носит название квадрата.
Поэтому для обозначения различающихся сторон прямоугольника приняты особые обозначения: так, сторону с большой протяженностью обычно называют длиной фигуры, а сторону с меньшей протяженностью — его шириной. При этом каждый прямоугольник в силу его свойств, описанных выше, имеет две длины и две ширины.
При этом каждый прямоугольник в силу его свойств, описанных выше, имеет две длины и две ширины.
Собственно алгоритм вычисления площади этой фигуры достаточно прост: необходимо лишь его одну длину умножить на одну его ширину. Полученное произведение будет представлять собой площадь прямоугольника.
Пример вычисления
Предположим, есть прямоугольник, одна сторона которого составляет 5 сантиметров, а другая — 8 сантиметров. Таким образом, согласно данному выше определению, длина этой фигуры, измеряемая как протяженностью большей стороны, будет равна 8 сантиметрам, а ширина — 5 сантиметрам.
Для нахождения площади фигуры необходимо ее ширину умножить на длину: таким образом, площадь рассматриваемого прямоугольника составит 40 квадратных сантиметров. Обратите внимание, что для осуществления вычислений оба используемых параметра должны измеряться в одинаковых единицах, например
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем жизненном пути встает очень часто и является важным не только для школьников.
Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем жизненном пути встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90°. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k
Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в старших классах, приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади прямоугольного треугольника. Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать радиус окружности. Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Прямоугольник – это частный случай четырехугольника. Это значит, что у прямоугольника четыре стороны. Его противоположные стороны равны: так например, если одна из его сторон равна 10 см, то противоположная ей будет так же равны 10 см. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.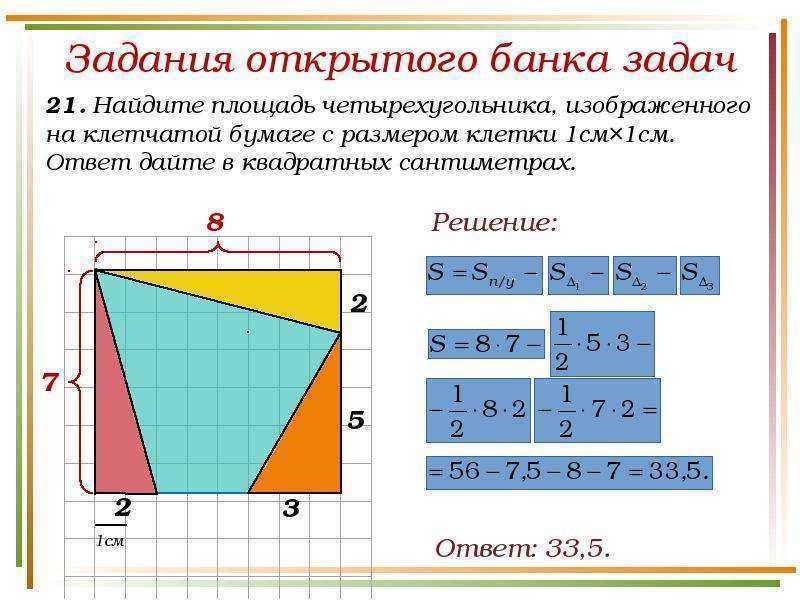 2 × sin(острого угла между диагоналями)/2.
2 × sin(острого угла между диагоналями)/2.
«Как найти площадь прямоугольника?» — Яндекс Кью
ПопулярноеСообщества
Стать экспертом Кью
Детский вопрос
МатематикаПлощадь
Анонимный вопрос
·
194,1 K
ОтветитьУточнитьДостоверно
Надежда Шихова
Математика
8,5 K
Редактор, автор и переводчик книг по математике · 18 авг 2019 · pilotlz.ru/books/287/11090
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину
Обрати внимание, что длина и ширина должны быть выражены в одних единицах. Если длина и ширина в сантиметрах, то площадь получится в сантиметрах квадратных; если длина и ширина в километрах, то площадь получится в квадратных километрах. Если длина и ширина выражены в разных единицах, сначала приведи к одинаковым, а потом уж умножай.
Если длина и ширина выражены в разных единицах, сначала приведи к одинаковым, а потом уж умножай.
Очень полезно познакомиться с площадями прямоугольников на практике. Давай я попробую угадать: площадь твоего стола меньше одного квадратного метра. Площадь твоей кровати больше одного квадратного метра, но меньше двух. Площадь твоей комнаты больше 10 квадратных метров и меньше 20 квадратных метров. Мне не видно, и я могла ошибиться. Так что измерь, посчитай и проверь, правильно ли я угадала.
2 эксперта согласны
116,8 K
Александра Кузнецова
23 декабря 2019
площадь- это длина умноженая на ширину
Комментировать ответ…Комментировать…
Рассчитать.рф — Калькуляторы онлайн!
176
Широкий список онлайн-калькуляторов для проведения самых разных вычислений · 6 окт 2020 · рассчитать.рф
Отвечает
Александр Дубасов
Самый простой способ заключается в перемножении значения длины и значения ширины прямоугольника. Онлайн калькулятор: https://рассчитать.рф/найти-площадь-прямоугольника-через-стороны/
Онлайн калькулятор: https://рассчитать.рф/найти-площадь-прямоугольника-через-стороны/
Онлайн-калькуляторы на все случаи жизни!
Перейти на рассчитать.рф/онлайн-калькуляторыКомментировать ответ…Комментировать…
Чарджбэк Легенда 112
132
Юридическая помощь по возврату денег от брокеров, онлайн-казино, букмекеров, финансовых… · 27 мая · chargeback-112.ru
Отвечает
Галина Визняк
Существует несколько способов найти площадь прямоугольника. Самый простой способ, если известны стороны прямоугольника, то достаточно их перемножить. Если стороны не известны, а имеется величины диагоналей прямоугольника и угла между ними, то нужно воспользоваться формулой, приведенной ниже:
1) через две стороны
S=a*b
2) через диагонали и угол
S=1/2*d(в квадрате)*sin(α). .. Читать далее
.. Читать далее
Поможем вернуть деньги от брокера, интернет-казино и финансовой пирамиды
Перейти на chargeback-112.ruКомментировать ответ…Комментировать…
Сауле Абдулина
9
Ученик 7 класса , кинокритик · 27 мар 2021
Надо длину умножить на ширину
Пример : 3*2 = 6 квадратных сантиметров ( квадратные сантиметры пишутся так : см и мелкая 2 на верху) так же есть и другие квадратные
Комментировать ответ…Комментировать…
Анонимный ответ22 июня 2021
Пример:
У прямоугольника есть 4 стороны. Первые 2 стороны равны друг другу, как и вторые 2 стороны.
Значит, прямоугольник делится на a и b. Представим, что сторона a — 3 сантиметра, а b — 2 сантиметра. Площадь будет буквой S. Чтобы вычислить площадь прямоугольника, нужно сторону a умножить на b. S=a*b. S=3*2. 3*2 это шесть. Площадь обозначается квадратными сантиметрами. S=6 см2
S=6 см2
varava falk
8 августа 2021
-Как найти площадь Ленина?
-Надо длину Ленина, умножить на ширину Ленина!
Комментировать ответ…Комментировать…
Тимофей Суханов
127
Геймер, програмер, учу английский, чуть-чуть ютубер · 4 мая 2021
У прямоугольника есть длина и ширина. Длину и ширину надо перемножить. Ответ надо записывать в квадратной величине (результат и маленькая двойка сверху) Пример: Ширина = 3 см Длина = 7 см 7*3 = 21(см2) Ответ: 21 см2. Читать далее
Женя Кац
5 мая 2021
Возьмите 2 игральных кубика. Бросьте оба. Первый показывает вам ширину прямоугольника, второй — длину. А площадь -… Читать дальше
Комментировать ответ…Комментировать…
Дарья Корикова
1
умею находить информацию · 26 февр 2021
Чтобы найти площадь прямоугольника надо умножить длину на ширину пример:
a-9 см
b-3 см
s-? см
s=a*b
9*3=27(см)
Ответ:27 сантиметров площадь прямоугольника. Читать далее
Читать далее
Комментировать ответ…Комментировать…
Андрей Иванов
112
Стаентист-клюкальщик. Профессионал. Лёгкая атлетика, среднее и тяжёлое машиностроения в… · 6 дек 2020
Никак не найти, если ты об этом. Во-первых, потому, что площадь не валяется где-то сама по себе под диваном. Во-вторых, потому, что площадь — понятие абстрактное, несмотря на то, что похожа на лошадь. Лошадь понятие не абстрактное, ее можно легко найти, например, в зоопарке. Есть ещё площадь, которая в городе площадь. Если бы был город «Прямоугольник», то и говорить не… Читать далее
Комментировать ответ…Комментировать…
Микаса Ван Лав
Привет! Я люблю обсуждать и смотреть аниме · 12 июн 2021
Площадь -S У нас есть две действующие стороны: a и b Формула нахождени площади такова: a×b=S Скажем, у а и b известны числа А-3 см B-6см 3×6=36 36 см²-это наша площадь Читать далее
Комментировать ответ…Комментировать…
Первый
Помогаю с математикой ✌ · 9 мая 2021
Что бы найти площадь треугольника, нужно воспольщоваться формулой: S= a•b Например: Длина прямоугольника равна 8 см Ширина прямоугольника равна 4см Площадь прямоугольника равна 8•4=32 Читать далее
Комментировать ответ…Комментировать…
Площадь прямоугольника в квадратных см.
 Как найти площадь прямоугольника. Что такое прямоугольник и квадрат
Как найти площадь прямоугольника. Что такое прямоугольник и квадратПлощадь многоугольника
Понятие площади многоугольника будем связывать с такой геометрической фигурой, как квадрат. За единицу площади многоугольника будем принимать площадь квадрата со стороной, равной единице. Введем два основных свойства, для понятия площади многоугольника.
Свойство 1: Для равных многоугольников значения их площадей равны.
Свойство 2: Любой многоугольник можно разбить на несколько многоугольников. При этом площадь исходного многоугольника равняется сумме площадей всех многоугольников, на которые разбит данный многоугольник.
Площадь квадрата
Теорема 1
Площадь квадрата определяется как квадрат длины его стороны.
где $a$ — длина стороны квадрата.
Доказательство.
Для доказательства нам необходимо рассмотреть три случая.
Теорема доказана.
Площадь прямоугольника
Теорема 2
Площадь прямоугольника определяется произведением длин его смежных сторон.
Математически это можно записать следующим образом
Доказательство.
Пусть нам дан прямоугольник $ABCD$, у которого $AB=b,\ AD=a$. Достроим его до квадрата $APRV$, длина стороны которого равняется $a+b$ (рис. 3).
Рисунок 3.
По второму свойству площадей имеем
\ \ \
По теореме 1
\ \
Теорема доказана.
Пример задач
Пример 1
Найти площадь прямоугольника со сторонами $5$ и $3$.
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
- Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников.
 Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
- Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
- Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Начиная с 5 класса, ученики начинают знакомиться с понятием площадей разных фигур. 2$.
2$.
Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.
Диагонали не является биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.
Что мы узнали?
Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также стоит не забывать, что если в задании разные единицы измерения сторон необходимо перевести их одну.
Тест по теме
Оценка статьи
Средняя оценка: 4.4 . Всего получено оценок: 292.
L * H = S чтобы найти площадь прямоугольника, необходимо перемножить ширину на длину. Другими словами её можно выразить так: площадь прямоугольника равна произведению сторон .
1. Приведём пример расчёта как найти площадь прямоугольника , стороны равны известным величинам, например ширина 4 см, длина 8 см.
Как найти площадь прямоугольника со сторонами 4 и 8 см: Решение простое! 4 х 8 = 32 см2 . Чтобы решить такую простую задачу нужно вычислить произведение сторон прямоугольника или просто умножить ширину на длину, это и будет площадь!
2. Частным случаем прямоугольника является квадрат, это тот случай когда стороны у прямоугольника равны, в этом случае найти площадь квадрата можно по выше приведённой формуле.
Чему равна площадь прямоугольника?
Умение рассчитывать площадь прямоугольника является базовым навыком для решения огромного количества бытовых или технических задач. Эти знания применяются практически во всех областях жизни! Например в тех случаях когда необходимы площади любых поверхностей в строительстве или недвижимости. При расчётах площадей земли, участков, стен домов, жилых помещений… не возможно назвать ни одной области деятельности человека, где это знание не может пригодиться!
Если расчёт площади прямоугольника вызывает у Вас сложности — просто воспользуйтесь нашим калькулятором! О моментально приведёт все необходимые вычисления и напишет текст решения с разъяснениями в деталях.
Мы уже познакомились с понятием площадь фигуры , узнали одну из единиц измерения площади — квадратный сантиметр . На уроке мы выведем правило, как вычислить площадь прямоугольника.
Мы уже умеем находить площадь фигур, которые разделены на квадратные сантиметры.
Например:
Мы можем определить, что площадь первой фигуры 8 см 2 , площадь второй фигуры 7 см 2 .
Как найти площадь прямоугольника, длины сторон которого 3 см и 4 см?
Для решения задачи разобьём прямоугольник на 4 полоски по 3 см 2 каждая.
Тогда площадь прямоугольника будет равна 3*4=12 см 2 .
Этот же прямоугольник можно разбить на 3 полоски по 4 см 2 .
Тогда площадь прямоугольника будет равна 4*3=12 см 2 .
В обоих случаях для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника.
Найдем площадь каждого прямоугольника.
Рассмотрим прямоугольник АКМО.
В одной полоске 6 см 2 , а таких полосок в этом прямоугольнике 2. Значит, мы можем выполнить следующее действие:
Значит, мы можем выполнить следующее действие:
Число 6 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Таким образом, мы перемножили стороны прямоугольника для того, чтобы найти площадь прямоугольника.
Рассмотрим прямоугольник KDCO.
В прямоугольнике KDCO в одной полоске 2см 2 , а таких полосок 3. Следовательно, мы можем выполнить действие
Число 3 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Мы их перемножили и узнали площадь прямоугольника.
Можно сделать вывод: чтобы найти площадь прямоугольника, не надо каждый раз разбивать фигуру на квадратные сантиметры.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (длины сторон прямоугольника должны быть выражены в одних и тех же единицах измерения), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади)
Обобщим: площадь прямоугольника равна произведению его длины и ширины.
Решите задачу.
Вычисли площадь прямоугольника, если длина прямоугольника 9см, а ширина — 2см.
Рассуждаем так. В данной задаче известны и длина и ширина прямоугольника. Поэтому действуем по правилу: площадь прямоугольника равна произведению его длины и ширины.
Запишем решение.
Ответ: площадь прямоугольника 18см 2
Как вы думаете, какими ещё могут быть длины сторон прямоугольника с такой площадью?
Можно рассуждать так. Поскольку площадь — это произведение длин сторон прямоугольника, поэтому надо вспомнить таблицу умножения. При умножении каких чисел получается ответ 18?
Правильно, при умножении 6 и 3 тоже получится 18. Значит, у прямоугольника могут быть стороны 6см и 3 см и его площадь тоже будет равна 18см 2 .
Решите задачу.
Длина прямоугольника 8см, а ширина 2см. Найди его площадь и периметр.
Нам известны длина и ширина прямоугольника. Необходимо вспомнить, что для нахождения площади необходимо найти произведение его длины и ширины, а для нахождения периметра нужно сумму длины и ширины умножить на два.
Запишем решение.
Ответ: площадь прямоугольника 16 см 2 , а периметр прямоугольника 20 см.
Решите задачу.
Длина прямоугольника 4см, а ширина — 3см. Чему равна площадь треугольника? (смотри рисунок)
Чтобы ответить на вопрос задачи, сначала надо найти площадь прямоугольника. Мы знаем, что для этого необходимо длину умножить на ширину.
Посмотрите на чертёж. Вы заметили, диагональ разделила прямоугольник на два равных треугольника? Следовательно, площадь одного треугольника в 2 раза меньше площади прямоугольника. Значит, надо 12 уменьшить в 2 раза.
Ответ: площадь треугольника 6 см 2 .
Сегодня на уроке мы познакомились с правилом, как вычислить площадь прямоугольника и учились применять это правило при решении задач на нахождение площади прямоугольника.
1. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. М., «Просвещение», 2012 год.
2. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. М., «Просвещение», 2012 год.
Математика: Учебник. 3 класс: в 2-х частях, часть 2. М., «Просвещение», 2012 год.
3. М.И.Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. М., «Просвещение», 2011 год.
5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
6. С.И.Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
7. В.Н.Рудницкая. Тесты. М., «Экзамен», 2012 (127с.)
2. Издательство «Просвещение» ()
1. Длина прямоугольника 7 см, ширина 4 см. Найдите площадь прямоугольника.
2. Сторона квадрата 5 см. Найдите площадь квадрата.
3. Начертите возможные варианты прямоугольников, площадь которых 18 см 2 .
4. Составьте задание по теме урока для своих товарищей.
Площадь трапеции abcd. Нахождение площади трапеции. Формула герона для площади трапеции.
Как найти площадь трапеции?
Складываем основания трапеции, делим сумму на два и умножаем все это на высоту, проведенную к большему основанию.
\(S=\frac{a+b}{2}h\)
Первое основание трапеции a:
Второе основание трапеции b:
Высота трапеции:
Также мы можем вычислить площадь трапеции зная все стороны трапеции (формула Герона):
\(s=\frac{a+b}{|a-b|}\sqrt{(p-a)(p-b)(p-a-c)(p-a-d)}\)
где: \(p=\frac{a+b+c+d}{2}\)
Первая сторона трапеции a:
Вторая сторона трапеции b:
Третья сторона трапеции c:
Четвертая сторона трапеции d:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Виктория Анатольевна Луковская
Репетитор по математике
Стаж (лет)
Образование:
Таганрогский педагогический институт им. А.П. Чехова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 4-11 классов. Математика дисциплинирует и воспитывает ум, это основа для всех наук. Очень люблю работать с детьми! Уроки проходят в комфортной обстановке, к каждому ученику подхожу индивидуально, объясняю доступно и понятно. На занятиях применяю игровые приемы, схемы, графики и презентации, для того, чтобы учащимся было интересно.
Математика дисциплинирует и воспитывает ум, это основа для всех наук. Очень люблю работать с детьми! Уроки проходят в комфортной обстановке, к каждому ученику подхожу индивидуально, объясняю доступно и понятно. На занятиях применяю игровые приемы, схемы, графики и презентации, для того, чтобы учащимся было интересно.
Анна Александровна Ваструхина
Репетитор по математике
Стаж (лет)
Образование:
Краснодарский государственный университет культуры и искусств
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Веду занятия по обществознанию с учениками 6-11 классов, готовлю к успешной сдаче ВПР/ОГЭ/ЕГЭ. В работе используются одобренные ФГОС материалы: как учебники, так и интернет ресурсы.
В работе используются одобренные ФГОС материалы: как учебники, так и интернет ресурсы.
Ирина Ивановна Ерыгина
Репетитор по математике
Стаж (лет)
Образование:
Армавирский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку для 5 — 11 классов. Подготовка к ОГЭ, ЕГЭ, ВПР. Индивидуальный подход к каждому учащемуся, использую опорные конспекты, алгоритмы рассуждения, что позволяет понять правила быстро и легко. Учащиеся приобретают практические навыки, действуют осмысленно, без тупой зубрежки абстрактных правил. К ЕГЭ, ОГЭ и ВПР готовлю на 5 и 4.
Учащиеся приобретают практические навыки, действуют осмысленно, без тупой зубрежки абстрактных правил. К ЕГЭ, ОГЭ и ВПР готовлю на 5 и 4.
Похожие статьи
- Многочлены
- Свойства интегралов
- Сложение векторов
- Действия с одночленами
- Как легко разделить на 0,5
- МИФИ: Прикладная Информатика
- Топ 20 бесполезных покупок к школе
- Пишем изложение: как запомнить больше информации?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Как рассчитать площадь | Что?, Вычисления, Единицы, Примеры
Примечание: эта страница содержит устаревшие ресурсы, которые больше не поддерживаются. Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.
Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.
Площадь сообщает нам размер формы или фигуры. Он сообщает нам размер квадратов, прямоугольников, кругов, треугольников, других многоугольников или любой замкнутой фигуры.
В реальном мире он говорит нам о размере листков бумаги, экранов компьютеров, комнат в домах, бейсбольных полей, городов, городов, стран и так далее. Знание местности может быть очень важным. Подумайте о том, чтобы постелить новый ковер в комнате вашего дома. Зная площадь комнаты, вы сможете убедиться, что ковер, который вы покупаете, достаточно большой, и в нем не останется лишнего.
Вычисление площадиПлощадь измеряется в квадратах (или квадратных единицах).
Сколько квадратов в этом прямоугольнике?
Мы можем посчитать квадраты или взять длину и ширину и использовать умножение. Прямоугольник выше имеет площадь 15 квадратных единиц.
Прямоугольник выше имеет площадь 15 квадратных единиц.
Площадь прямоугольника = длина x ширина
Примеры расчета площади прямоугольника
Единицы измерения площадиМы измеряем площадь квадратами. Мы используем разные размеры квадратов в зависимости от того, насколько велика или мала площадь.
| Пример | Длина стороны квадрата | Блок |
| Размер ногтя на большом пальце | Миллиметр | мм 2 |
| Размер листа бумаги | Сантиметр | см 2 |
| Размер комнаты | Счетчик | м 2 |
| Размер города | км | км 2 |
| Не забудь пи 2 |
Мы пишем квадратные размеры, используя маленькую 2 рядом с единицей измерения. Пишем мм 2 , см 2 , м 2 , км 2 , см 2 Мы можем сказать «63 квадратных миллиметра» или «63 квадратных миллиметра» |
Мы могли бы использовать маленькие квадраты для измерения больших площадей. Единственная проблема заключается в том, что в конечном итоге нам придется использовать очень большие числа. Например, поле может быть измерено в 5 000 000 000 квадратных миллиметров, тогда как 5000 квадратных метров было бы гораздо легче произносить, писать и визуализировать.
Возможно, вы услышите больше единиц измерения площади; квадратные дюймы, квадратные футы, квадратные ярды, квадратные мили, акры, гектары — все это единицы измерения площади.
Дополнительные примеры вычисления площади
Площадь квадратаДлина и ширина квадрата одинаковы, поэтому нам просто нужно умножить длину на длину.
Площадь круга Площадь круга = πr 2
, где r — радиус круга, а π — отношение длины окружности к ее диаметру.
π (произносится как «пирог» и часто пишется как «пи») — бесконечное десятичное число с общим приближением 3,14159. Вы можете узнать больше о Пи здесь . Обратите внимание, как по мере того, как сектора становятся меньше, форма становится больше похожей на прямоугольник. Примечание. Нет предела тому, насколько маленькими могут быть эти сектора и насколько близко они могут напоминать прямоугольник при расположении.
Предполагая, что мы знаем, что длина окружности равна 2πr, мы можем добавить размеры к «прямоугольнику», как показано ниже. Используя формулу площади прямоугольника, площадь = ширина x высота, мы можем увидеть, как можно показать, что наш круг, преобразованный в прямоугольник, имеет площадь, которая приблизительно равна 90 150 πr x r или πr . 2
Секторы круга переставлены Секторы круга переставлены – начинают выглядеть как прямоугольник Площадь составных фигур Во многих случаях для расчета общей площади необходимо вычислить более одной площади, а затем выполнить сложение, вычитание или какую-либо другую комбинацию операций для нахождения требуемой площади.
Примечание: В приведенных ниже примерах единицы измерения не показаны, а ответы и значение π (Пи) округлены до сотых.
Пример: простые составные формыПриведенный ниже пример расчета площади относительно прост. Форму можно рассматривать как треугольник в сочетании с прямоугольником.
Приведенный выше пример иллюстрирует распространенное требование при работе с составными формами — поиск размеров, которые не показаны. Обучая своих детей, при необходимости помогите найти эти «недостающие» измерения. Ниже приведен еще один пример.
Нахождение размеров Пример: вычитание одной площади из другойВ приведенном ниже примере фигура выглядит как прямоугольник с вырезанным треугольником.
Пример: Частичные площади Приведенный ниже пример аналогичен приведенному выше, но, поскольку у нас есть полукруг, нам нужно вычислить часть (половину) площади круга. Обратите внимание, что в этом примере показан диаметр, а не радиус.
Обратите внимание, что в этом примере показан диаметр, а не радиус.
Обычно имеется более одного способа вычисления конечной площади. В приведенных ниже примерах фигура может быть представлена как два объединенных прямоугольника или как один большой прямоугольник с меньшим прямоугольником, «вырезанным» из правого верхнего угла.
Рабочие листы для расчета площадиРаспечатайте приведенные ниже рабочие листы и используйте их для практики при обучении ваших детей.
- Вычисление площадей — прямоугольники и квадраты
- Вычисление площадей — прямоугольники
- Вычисление площадей — прямоугольники
- Вычисление составных площадей, например. с прямоугольными формами
- Вычисление составных площадей, например, с прямоугольниками, треугольниками и кругами
- Вычисление площадей, например, треугольников
- Площадь круга
- Расчет площади поверхности, например прямоугольных призм
Здесь вы найдете другие рабочие листы по геометрии для печати.
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Что такое площадь в математике? Определение, формулы, формы, примеры
Определение
Площадь определяется как общее пространство, занимаемое плоской (двухмерной) поверхностью или формой объекта.
Возьмите карандаш и нарисуйте квадрат на листе бумаги. Это двумерная фигура. Пространство, занимаемое фигурой на бумаге, называется площадью .
Теперь представьте, что ваш квадрат состоит из меньших квадратов. Площадь фигуры рассчитывается как количество единичных квадратов, необходимых для покрытия общей площади поверхности этой конкретной двумерной формы. Квадратные сантиметры, квадратные футы, квадратные дюймы, квадратные метры и т. д. являются одними из распространенных единиц измерения площади.
Чтобы узнать площади квадратных фигур, нарисованных ниже, начертите единичные квадраты со стороной в 1 сантиметр. Таким образом, форма будет измеряться в см² , также известных как квадратные сантиметры.
Здесь площадь фигур ниже будет измеряться в квадратных метрах (м²) и квадратных дюймах (дюйм²).
Происхождение термина: Площадь
Термин «область» происходит от латинского языка, что означает «простой кусок пустой земли». Это также означает «определенное количество пространства, содержащееся в наборе границ».
Подробнее о Зоне
Посмотрите на ковер в вашем доме. Чтобы купить ковер, подходящий к полу, нам нужно знать его площадь. Или ковер будет больше или меньше, чем пространство! Некоторые другие случаи, когда нам нужно знать площадь, — это при укладке плитки на пол, покраске стены или наклеивании на нее обоев или определении общего количества плиток, необходимых для строительства бассейна.
Формулы для вычисления площади
Нас окружает множество двумерных фигур: круг, треугольник, квадрат, прямоугольник, параллелограмм и трапеция. Вы можете нарисовать все эти фигуры на бумаге. Каждая фигура уникальна и уникальна, поэтому ее площадь также рассчитывается по-разному. Чтобы найти площадь, сначала определите форму. Затем используйте соответствующую формулу из списка, приведенного ниже, чтобы найти его площадь.
Площади составных фигур
Каждая плоская фигура не может быть классифицирована как простой прямоугольник, квадрат, треугольник или типичная форма в реальной жизни. Некоторые фигуры состоят из нескольких простых двумерных фигур. Соединим прямоугольник и полукруг.
Эти фигуры, образованные комбинацией двух или более простых фигур, называются « составные фигуры » или «составные фигуры ».
Чтобы найти площадь составной фигуры, мы должны найти сумму площадей всех фигур в ней. Таким образом, площадь фигуры, которую мы только что нарисовали, будет равна площади прямоугольника, l$\times$ b плюс половина площадь круга, ½ x πr² , где l и b — длина и ширина прямоугольника, r — радиус прямоугольника полукруг. 2$)
2$)
, где r — радиус полукруга, а b и h — основание и высота треугольника соответственно.
Применение в реальной жизни
Вот несколько способов применения знаний о площади фигур в повседневной жизни.
- Мы можем найти площадь подарочной бумаги, чтобы проверить, сможет ли она покрыть коробку или нет.
- Мы можем найти площадь квадрата или круга, чтобы найти площадь сигнального щита. 9{2}$
- Противоположные стороны параллельны.
- Все четыре стороны равны.
- Все углы равны 90º.
- Диагональ квадрата
- Площадь квадратов и прямоугольников Рабочие листы
- Периметр квадрата
- Площадь поверхности квадратной призмы
Пример 1: Какова площадь квадратного бассейна, одна сторона которого равна 8 м?
Решение:
Мы знаем, что одна сторона бассейна равна 8 м, поэтому воспользуемся формулой: Площадь квадрата = сторона × сторона = 8 × 8 = 64 м 2 .
 Следовательно, площадь бассейна составляет 64 квадратных метра.
Следовательно, площадь бассейна составляет 64 квадратных метра.Пример 2: Площадь квадратной доски составляет 3600 см 2 . Какова длина его стороны?
Решение:
Площадь квадратной доски = 3600 см 2 . Мы знаем, что Площадь = сторона × сторона = сторона 2 . Значит, сторона = √Площадь = √3600 = 60 см. Следовательно, сторона доски для каррома равна 60 см.
Пример 3: Найдите площадь квадратной комнаты на полу, состоящей из 100 квадратных плиток со стороной 15 дюймов.
Решение:
Площадь одной плитки = 15 дюймов × 15 дюймов = 225 квадратных дюймов. Мы знаем, что на полу комнаты 100 плиток. Таким образом, площадь, занимаемая 100 плитками, равна площади пола = 100 × 225 квадратных дюймов = 22500 квадратных дюймов. Следовательно, площадь пола составляет 22500 квадратных дюймов.
Пример 4: Найдите площадь квадратного ковра, диагональ которого равна 4 футам.

Решение:
Площадь квадрата, если дана его диагональ, равна D 2 /2. Дана диагональ d = 4 фута. Площадь ковра = (4 × 4)/2 = 16/2 = 8 квадратных футов. Следовательно, площадь ковра составляет 8 квадратных футов.
- Формулы периметра
- Формулы объема
- Формулы площади поверхности
- Формулы измерения
- У квадрата все стороны равны. Отсюда следует, что противолежащая и прилежащая стороны квадрата равны друг другу.
- Противоположные стороны квадрата параллельны, что делает его параллелограммом.
- Смежные стороны квадрата перпендикулярны друг другу. Это означает, что любые две смежные стороны имеют между собой угол 90 градусов.
- Квадрат разделен на два равных прямоугольных треугольника.
- Квадрат — это частный случай прямоугольника.

- Периметр квадрата: Расстояние, покрываемое границами квадрата, называется периметром квадрата. Он формулируется как:
- Когда указана чья-либо сторона:
- Шаг 1: Запишите значение стороны, скажем «а».
- Шаг 2: Подставьте значение a в формулу -> Площадь (со стороной) = (Сторона) 2 = (a) 2
- Шаг 3: Запишите ответ в квадратных единицах.

- Когда любой диагональный длина, скажите «d».
- Шаг 2: Подставьте значение d в формулу -> Площадь (с диагональю) = (d) 2 /2 =
- Шаг 3: Запишите результат в квадратных единицах.
Заключение
С помощью SplashLearn обучение становится частью жизни детей, и их поощряют учиться каждый день. Платформа делает это с помощью интерактивных игр и забавных рабочих листов. Для получения дополнительной информации об увлекательных математических играх посетите сайт www.splashlearn.com.
Связанный математический словарь Узнайте больше о таких понятиях, как ‘ Периметр , Многоугольник , Square Unit , Unit Square ’ и другие интересные математические темы на www.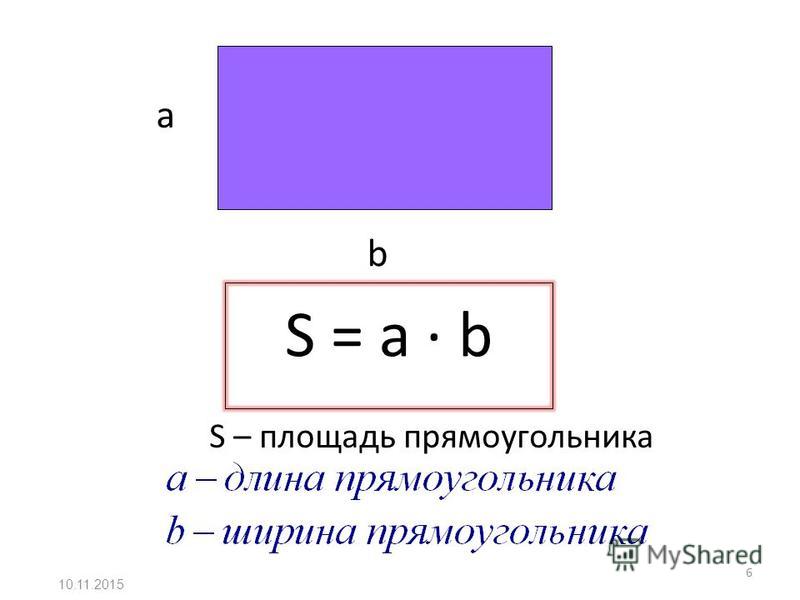 SplashLearn.com.
SplashLearn.com.
Часто задаваемые вопросы
Чем отличаются периметр и площадь фигуры?
Периметр и площадь связаны с двумерной геометрией форм. Периметр — это общая длина контура вокруг фигуры, а площадь — это общее пространство внутри фигуры.
Почему площадь измеряется в квадратных единицах, а периметр — нет?
Площадь — это мера количества единичных квадратов, вписывающихся в двумерную фигуру, поэтому она выражается в квадратных единицах. Периметр является мерой длины контура фигуры и выражается в линейных единицах.
В чем важность концепции области обучения?
Знание площади формы дает учащимся четкое представление об общем пространстве, охватываемом границами этой формы. Эта концепция имеет множество практических применений, таких как определение площади ковра в комнате, определение общего размера стены, которую нужно покрасить, и т. д.
д.
Как измеряется площадь неправильной формы?
Разделите неправильную форму на единичные квадраты и рассчитайте общее количество единичных квадратов. Если несколько единичных квадратов не заняты полностью, приблизьте их к 0 или 1 для каждого.
Площадь квадрата — формула, как найти площадь квадрата?
Площадь квадрата определяется как количество квадратных единиц, необходимых для заполнения этой фигуры. Другими словами, когда мы хотим найти площадь квадрата, мы учитываем длину его стороны. Поскольку все стороны фигуры равны, ее площадь равна произведению двух сторон. Общепринятыми единицами измерения площади квадрата являются квадратные метры, квадратные футы, квадратные дюймы и квадратные сантиметры.
Площадь квадрата также можно вычислить с помощью других измерений, таких как диагональ и периметр квадрата. Давайте попробуем понять больше о площади квадрата на этой странице.
1. | Какова площадь квадрата? |
| 2. | Площадь квадрата Формула |
| 3. | Как найти площадь квадрата? |
| 4. | Часто задаваемые вопросы о площади квадрата |
Какова площадь квадрата?
Квадрат представляет собой замкнутую двумерную фигуру с четырьмя равными сторонами и четырьмя равными углами. Четыре стороны квадрата образуют четыре угла при вершинах. Сумма всех длин сторон квадрата — это его периметр, а общее пространство, занимаемое фигурой, — это площадь квадрата. Это четырехугольник со следующими свойствами.
Квадраты можно найти повсюду. Вот некоторые часто встречающиеся объекты, имеющие форму квадрата. Шахматная доска, часы, школьная доска, плитка — все это примеры квадрата.
Площадь квадрата Определение
Площадь квадрата – это мера занимаемой им площади или поверхности.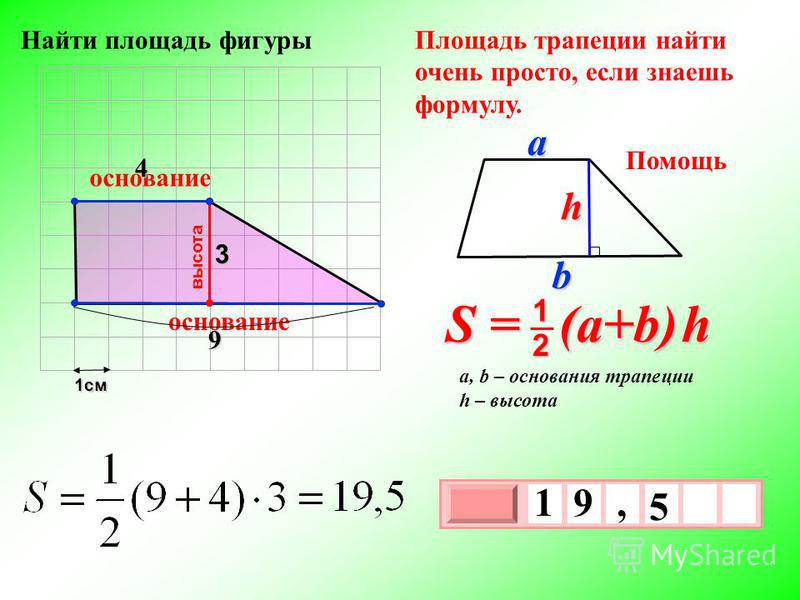 Он равен произведению длин двух его сторон. Поскольку площадь квадрата равна произведению двух его сторон, единица измерения площади выражается в квадратных единицах.
Он равен произведению длин двух его сторон. Поскольку площадь квадрата равна произведению двух его сторон, единица измерения площади выражается в квадратных единицах.
Обратите внимание на квадрат, показанный ниже. Он занял 25 кв. Следовательно, площадь квадрата равна 25 квадратных единиц. Из рисунка видно, что длина каждой стороны равна 5 единицам. Следовательно, площадь квадрата равна произведению его сторон. Площадь квадрата = сторона × сторона = 5 × 5 = 25 квадратных единиц.
Квадрат Определение
Квадрат представляет собой двумерный четырехугольник с четырьмя сторонами, равными и параллельными друг другу. Углы этой фигуры равны 90 градусов.
Площадь квадрата Формула
Формула площади квадрата, если даны стороны:
Площадь квадрата = сторона × сторона = S 2
Алгебраически площадь квадрата можно найти, возведя число в квадрат представляет собой меру стороны квадрата. Теперь воспользуемся этой формулой, чтобы найти площадь квадрата со стороной 7 см. Мы знаем, что площадь квадрата = Сторона × Сторона. Подставляя длину стороны как 7 см, 7 × 7 = 49. Следовательно, площадь данного квадрата равна 49 см 2 .
Мы знаем, что площадь квадрата = Сторона × Сторона. Подставляя длину стороны как 7 см, 7 × 7 = 49. Следовательно, площадь данного квадрата равна 49 см 2 .
Площадь квадрата также можно найти с помощью диагонали квадрата. Формула, используемая для нахождения площади квадрата по диагонали:
Площадь квадрата по диагоналям = Диагональ 2 /2.
Давайте разберемся в выводе этой формулы с помощью следующего рисунка, где «d» — диагональ, а «s» — стороны квадрата.
Здесь сторона квадрата ‘s’, а диагональ квадрата ‘d’. Применяя теорему Пифагора, мы имеем d 2 = s 2 + s 2 ; д 2 = 2s 2 ; д = √2с; с = d/√2. Теперь эта формула поможет нам найти площадь квадрата, используя диагональ. Площадь = s 2 = (d/√2) 2 = d 2 /2. Следовательно, площадь квадрата равна d 2 /2.
Как найти площадь квадрата?
В предыдущем разделе мы рассмотрели определение площади квадрата, а также формулу площади квадрата. В этом разделе давайте разберемся, как использовать формулу площади квадрата, чтобы найти ее площадь с помощью нескольких приложений или реальных примеров.
В этом разделе давайте разберемся, как использовать формулу площади квадрата, чтобы найти ее площадь с помощью нескольких приложений или реальных примеров.
Площадь квадрата по периметру квадрата
Пример: Найдите площадь квадратного парка, периметр которого равен 360 футов.
Решение:
Дано: периметр квадратного парка = 360 футов
Мы это знаем,
Периметр квадрата = 4 × сторона
⇒ 4 × сторона = 360
⇒ сторона = 360/4
⇒ сторона = 90 футов
Площадь квадрата = сторона 2
Следовательно, Площадь квадратного парка = 90 2 = 90 × 90 = 8100 футов 2
Таким образом, площадь квадратного парка с периметром 360 футов составляет 8100 футов 2 .
Площадь квадрата, если известна сторона квадрата
Пример: Найдите площадь квадратного парка, сторона которого равна 90 футов
Решение:
Дано: сторона квадратного парка = 90 футов
Мы это знаем,
Площадь квадрата = ft 2
Следовательно, Площадь квадратного парка = 90 2 = 90 × 90 = 8100 футов 2
Таким образом, площадь квадратного парка со стороной 90 футов составляет 8100 футов. .
.
Решение:
Дано: диагональ квадратного парка = 14 футов
Мы это знаем,
Формула площади квадрата при заданной диагонали = d 2 /2
Следовательно, площадь квадратного парка = (14 × 14)/2 = 98 футов 2
Таким образом, площадь квадратного парка с диагональю 14 м равна 98 футов 2 .
Площадь квадрата Советы:
Обратите внимание на следующие моменты, которые следует помнить при вычислении площади квадрата.
☛ Похожие статьи
Площадь квадрата Примеры
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может усвоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу с Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по площади квадрата
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади квадрата
Что такое площадь квадрата в геометрии?
В геометрии квадрат — это фигура с четырьмя равными сторонами. Площадь квадрата определяется как количество квадратных единиц, составляющих полный квадрат. Он рассчитывается по формуле площади квадрата Площадь = s × s = s 2 в квадратных единицах.
Какова площадь квадратной формулы?
Когда сторона квадрата известна, используется формула для нахождения площади квадрата со стороной s: Площадь = s × s = s 2 . Если дана диагональ d квадрата, то формула, используемая для нахождения площади, такова: Площадь = d 2 /2.
Как вычислить площадь квадрата?
Площадь квадрата рассчитывается по формуле: Площадь = s × s, где s — одна сторона квадрата. Поскольку площадь квадрата является двумерной величиной, она всегда выражается в квадратных единицах. Например, если мы хотим вычислить площадь квадрата со стороной 4 единицы, это будет: A = 4 × 4 = 16 единиц 2 . Проверьте сейчас калькулятор площади квадрата для быстрых расчетов.
Что такое периметр и площадь квадратных формул?
Периметр квадрата представляет собой сумму четырех сторон квадрата, то есть P = 4 × стороны. Она выражается в м, см, футах, дюймах.
Площадь квадрата = Площадь = s × s, где s — одна сторона квадрата. Дается в единицах м 2 , см 2 , фут 2 , в 2 .
Дается в единицах м 2 , см 2 , фут 2 , в 2 .
Чек:
Как найти площадь квадрата по диагонали квадрата?
Площадь квадрата также можно найти, если известна его диагональ. В этом случае используется следующая формула: Площадь квадрата по диагоналям = Диагональ²/2. Например, диагональ квадрата равна 6 единицам, Площадь = 6²/2 = 36/2 = 18 квадратных единиц.
Как найти площадь квадрата по периметру квадрата?
Площадь квадрата можно вычислить, если известен его периметр. Поскольку периметр квадрата: P = 4 × сторона, мы можем найти сторону квадрата ‘s’ = периметр/4. После получения стороны площадь квадрата можно вычислить по формуле: A = s × s. Например, если периметр квадрата равен 32 единицам, мы подставим это значение в формулу: P = 4 × сторона.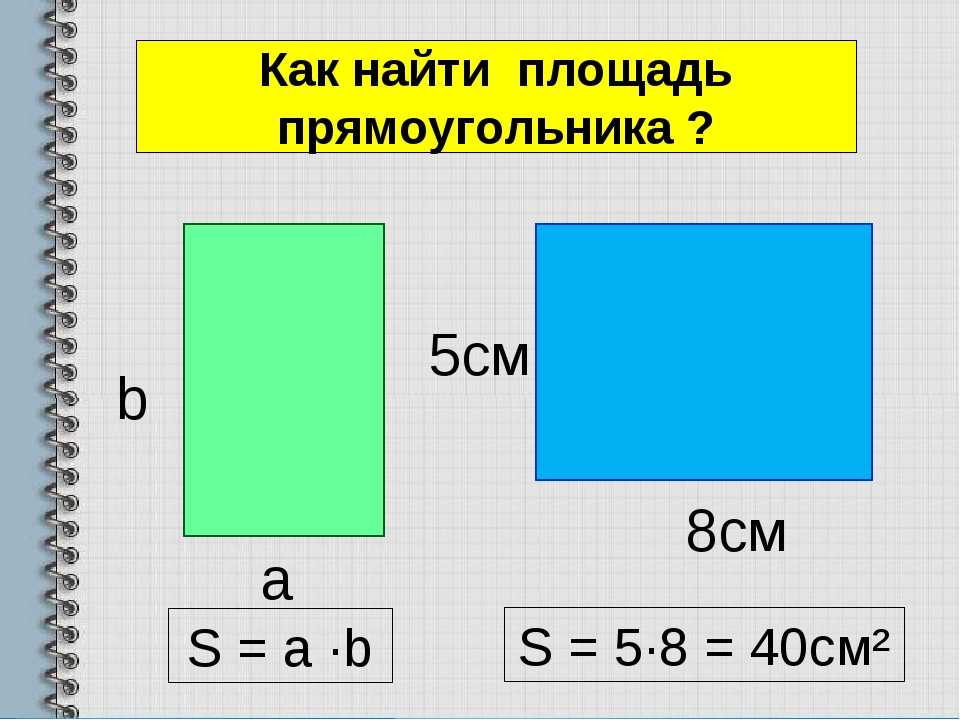 32 = 4 × сторона. Значит, сторона будет 8 единиц. Теперь мы можем вычислить площадь квадрата со стороной 8 единиц. Площадь = s × s = 8 × 8 = 64 кв.
32 = 4 × сторона. Значит, сторона будет 8 единиц. Теперь мы можем вычислить площадь квадрата со стороной 8 единиц. Площадь = s × s = 8 × 8 = 64 кв.
Каковы единицы площади квадрата?
Поскольку площадь квадрата представляет собой двумерную фигуру, она всегда выражается в квадратных единицах. Общепринятыми единицами площади квадрата являются м 2 , дюймы 2 , см 2 , футы 2 .
Какова площадь квадрата, вписанного в окружность?
Если квадрат вписан в круг, то диагональ квадрата равна диаметру круга. Итак, если диаметр круга дан, это значение можно использовать как диагональ квадрата, а площадь квадрата можно рассчитать по формуле: Площадь квадрата с использованием диагоналей = Диагональ²/2.
Как найти площадь квадрата?
Площадь квадрата можно определить по тому, сколько пространства занимает внутри него квадрат. Проще говоря, пространство, находящееся в пределах границы квадрата, известно как площадь квадрата. В этой статье вы узнаете основные параметры квадрата. Кроме того, вы узнаете, как найти площадь квадрата, площадь формулы квадрата и площадь поверхности квадратной пирамиды.
В этой статье вы узнаете основные параметры квадрата. Кроме того, вы узнаете, как найти площадь квадрата, площадь формулы квадрата и площадь поверхности квадратной пирамиды.
Все ли мы знаем, что такое квадрат? Квадрат – это замкнутый четырехугольник. Четырехугольники – фигуры, имеющие 4 стороны. Таким образом, квадрат — это четырехсторонняя фигура, у которой все четыре стороны равны. Если одна сторона квадрата равна 10 см, то и другие стороны равны 10 см. Давайте сначала изучим некоторые математические термины и понятия, связанные с квадратом:
Периметр (квадрат) = s + s + s + s = 4 x s = 4s {где s представляет сторону квадрата}
В нашей повседневной жизни мы можем найти квадраты везде. От наших домов до наших школ квадраты присутствуют на каждом углу. Плитка на вашей кухне квадратная. Шахматная доска представляет собой квадрат, состоящий из 64 черных и белых меньших квадратов. Самый простой пример — кубик Рубрика. Каждая поверхность кубика Рубика квадратная.
Другие измерения, такие как диагональ и периметр квадрата, также могут использоваться для вычисления площади квадрата. В этой статье мы попытаемся узнать больше о площади квадрата.
Какова площадь квадрата?
Теперь нам стало ясно, что такое квадрат! Прочтите раздел выше, чтобы прояснить все свои сомнения, если вы все еще не уверены. Давайте узнаем, что такое площадь? Пространство, заметаемое или покрываемое любой замкнутой фигурой, является площадью. Площадь фигуры определяется как пространство внутри границы фигуры. В результате площадь квадрата определяется как область, заметаемая или покрытая квадратом. Другими словами, площадь квадрата — это двумерное пространство внутри его границы.
Площадь фигуры определяется как пространство внутри границы фигуры. В результате площадь квадрата определяется как область, заметаемая или покрытая квадратом. Другими словами, площадь квадрата — это двумерное пространство внутри его границы.
Можно также сказать, что количество крошечных квадратов размером в 1 единицу, которые могут заполнить квадрат, называется площадью квадрата. Давайте разберемся в этой концепции с помощью иллюстрации, приведенной ниже.
Иллюстрация: Рассмотрим квадрат длины 4 единицы. Теперь рассмотрим меньшие квадраты длиной 1 единица каждый. Как мы видим на рисунке ниже, 4 квадрата по 1 единице заполняют первый ряд большего квадрата. Аналогично по 4 квадрата 1 единицы заполняют второй, третий и четвертый ряд. Теперь большой квадрат заполнен. Если мы посчитаем количество меньших квадратов, то получим, что 16 квадратов из 1 единицы заполняют квадрат из 4 единиц. Следовательно, 16 единиц — это площадь квадрата.
Отсюда мы можем сделать вывод, что площадь квадрата равна произведению двух его сторон. Как мы знаем, 16 = 4 х 4, а 4 единицы составляют одну сторону квадрата. В следующем разделе мы изучим и выведем формулу площади квадрата.
Как мы знаем, 16 = 4 х 4, а 4 единицы составляют одну сторону квадрата. В следующем разделе мы изучим и выведем формулу площади квадрата.
Площадь квадрата Формула
Из приведенного выше рисунка мы узнаем, что площадь квадрата равна произведению сторон. Это можно записать как «сторона х сторона». Следовательно, формула для любого квадрата с любой длиной стороны задается как
Площадь = (Сторона) 2
Давайте рассмотрим пример, чтобы понять эту формулу:
Пример: Найдите площадь квадрата со стороной 13 см.
Решение: При длине стороны = 13 см
Площадь квадрата = (Сторона) 2 = (13) 2 = 169 см 5 2,5
Площадь квадрата всегда выражается в квадратных единицах (квадратный сантиметр, квадратный метр, квадратный дюйм и т. д.)
Что если нам даны не стороны квадрата, а длина диагонали? Как в этом случае найти площадь квадрата?
Не волнуйтесь! Площадь квадрата можно вычислить, даже зная длину диагонали.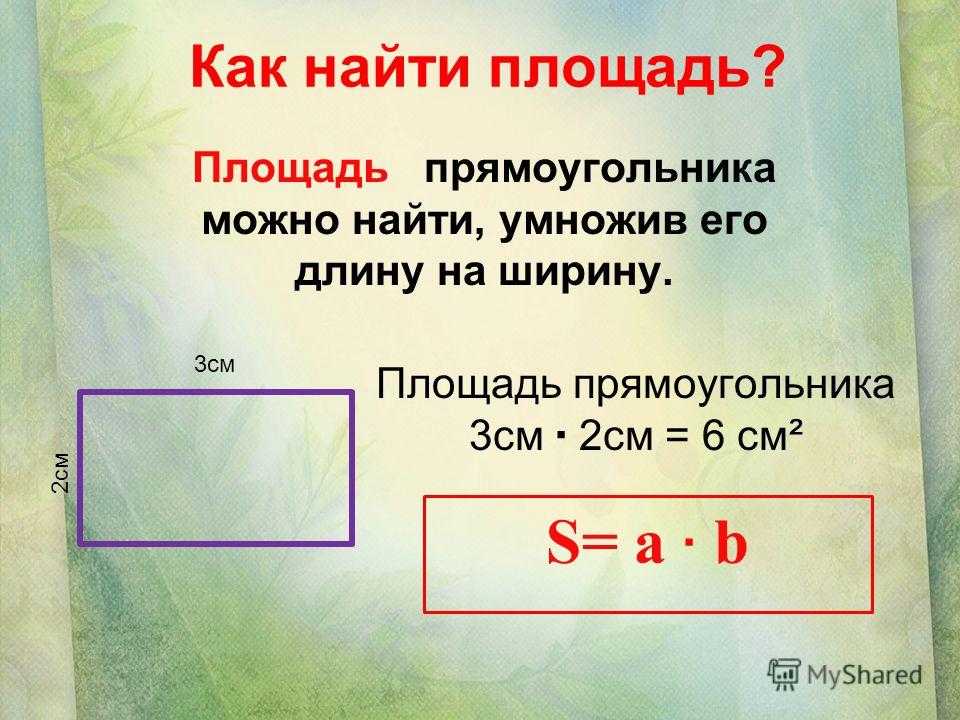 Вы можете найти площадь, используя формулу, написанную ниже:
Вы можете найти площадь, используя формулу, написанную ниже:
Площадь квадрата (с использованием диагоналей) = (D) 2 /2, где D представляет собой длину диагонали.
Примечание: Помните, что диагонали квадрата равны, поэтому площадь остается неизменной, если дана любая из диагоналей.
Пример: Найдите площадь квадрата, если длина диагонали равна 13 см.
Решение: Нас дается, диагональ = 13 см
Площадь квадрата = D 2 /2
= (13) 2 /2
= 169/2 CM 2
4. Как найти площадь квадрата
До сих пор мы выучили 2 формулы, связанные с нахождением площади квадрата. Давайте узнаем, как вы будете подходить к вопросам, связанным с площадью любого квадрата.
Пример: Найдите площадь пластика, необходимую для покрытия квадратного стола длиной 8 м.
Решение: Учитывая, что длина стола = 8 м
Поэтому площадь пластика, необходимая для покрытия стола, = площади стола.
Площадь таблицы = (сторона) 2 = 8 2 = 64 м 2
Пример: Найдите площадь квадрата с диагональю 4 см
Решение: Учитывая, что длина диагонали = 4 см = 16/2 = 8 см 2
Найти площадь квадрата, зная периметр квадрата
В предыдущих разделах мы научились вычислять площадь квадрата, зная сторону или диагональ. Но, предположим, вам не предоставлен ни один из этих параметров, но задан периметр квадрата. Как найти площадь, если известен периметр квадрата? Давайте узнаем:
Но, предположим, вам не предоставлен ни один из этих параметров, но задан периметр квадрата. Как найти площадь, если известен периметр квадрата? Давайте узнаем:
- Шаг 1: Запишите периметр данного квадрата.
- Шаг 2: Мы знаем, что периметр квадрата равен 4 с. Следовательно, 4s = периметр.
- Шаг 3: Подставьте значение периметра и найдите сторону по формуле s = Периметр/4
- Шаг 4: Теперь мы знаем сторону квадрата. Найдите площадь, используя s2.
- Шаг 5: Запишите ответ в квадратных единицах.
Пример: Квадратный сад имеет периметр 64 см. Макс хочет посадить цветы и найти площадь этого сада, но не знает, как это сделать? Помогите ему определить площадь сада.
Решение: Мы знаем: Периметр сада = 64 см
Сначала вычислим длину сторон сада.
Используя формулу из шага 3
Сторона (s) = периметр/4
= 64/4
= 16 см
Теперь,
Площадь сада = (s) 2
= 16 2
= 256 см 2
Некоторые советы с нашей стороны:
Примите конец следующих факторов к сохранению Факторов.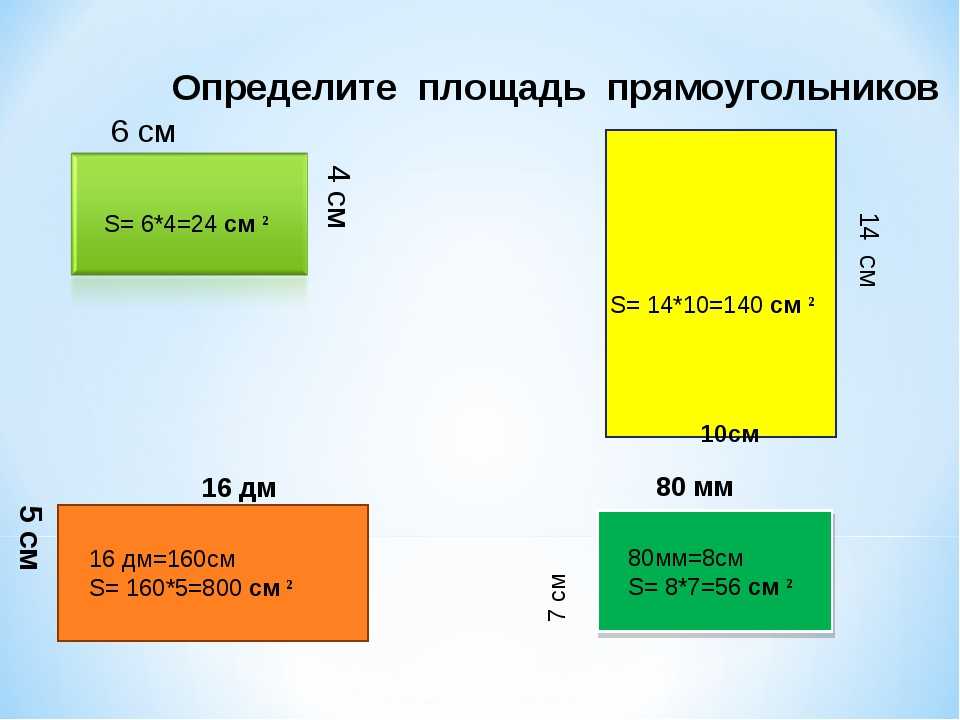 иметь в виду, когда вы вычисляете площадь квадрата.
иметь в виду, когда вы вычисляете площадь квадрата.
При вычислении площади квадрата мы часто ошибаемся, удваивая число. Это не тот случай! Имейте в виду, что площадь квадрата не равна удвоенной стороне. Это всегда либо «сторона х сторона», либо сторона 2 .
Мы должны не забыть указать единицу измерения площади при ее представлении. Площадь квадрата всегда двумерна; следовательно, мы используем квадратные единицы. Например см 2 , м 2 , дюйм 2 и т. д.
Часто задаваемые вопросы
1. Что такое площадь квадрата в геометрии?
Ответ. Площадь квадрата в геометрии — это измерение поверхности. Он рассчитывается путем умножения длины на ширину.
2. Что такое площадь квадратной формулы?
Ответ. Формула площади квадрата — это способ вычисления площади квадрата. Формула площади квадрата: A = s2, где s представляет собой длину каждой стороны квадрата.
3. Как вычислить площадь квадрата?
Ответ. Чтобы вычислить площадь квадрата, нужно умножить длину одной стороны на саму себя. Итак, если у вас есть квадрат со сторонами по 10 сантиметров, вы должны сделать: 10 * 10 = 100.
4. Каковы единицы измерения площади квадрата?
Ответ. Единицы измерения площади квадрата – это квадраты. Наиболее распространенной единицей измерения площади являются квадратные метры, но иногда вы также можете встретить квадратные футы или акры.
5. Что такое периметр и площадь квадратных формул?
Ответ. Формула для периметра квадрата: p = 4s
Формула площади квадрата: A = s2
Как найти объем и площадь поверхности для 6 обычных фигур
Как найти объем и площадь Место для 6 обычных форм
Эндрю Ли
23 мая 2021 г.
Онлайн-обучение
,
Геометрия
,
Математика
3 Наш мир наполнен трехмерными объектами.
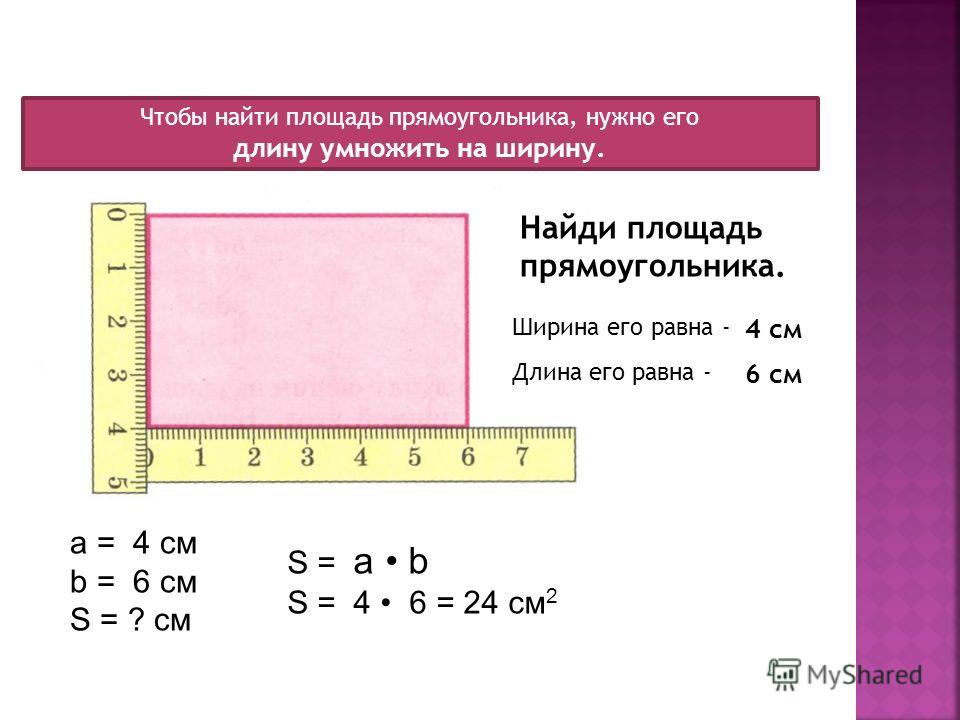 Когда дело доходит до знания объема и площади поверхности этих объектов, вам необходимо знать два определения. Площадь поверхности — это площадь всех внешних обращенных поверхностей объекта. Общая площадь поверхности рассчитывается путем сложения всех площадей на поверхности: площадей основания, вершины и боковых поверхностей (боков) объекта. Это делается с использованием различных формул площади и измеряется в квадратных единицах.
Когда дело доходит до знания объема и площади поверхности этих объектов, вам необходимо знать два определения. Площадь поверхности — это площадь всех внешних обращенных поверхностей объекта. Общая площадь поверхности рассчитывается путем сложения всех площадей на поверхности: площадей основания, вершины и боковых поверхностей (боков) объекта. Это делается с использованием различных формул площади и измеряется в квадратных единицах.Объем — это объем пространства, которое занимает трехмерный объект. Существуют также разные формулы для разных трехмерных фигур. Общий объем объекта измеряется в кубических единицах.
Общие формулы для объема и площади поверхности
У нас есть для вас шпаргалка — формулы объема и площади поверхности для обычных форм. Использовать его мудро!
Формулы площади поверхности
Площадь поверхности куба равна 6s² , где s — длина стороны.
Площадь поверхности прямоугольной призмы равна 2(wl + hl + hw) , где w — ширина, h — высота, а l — длина.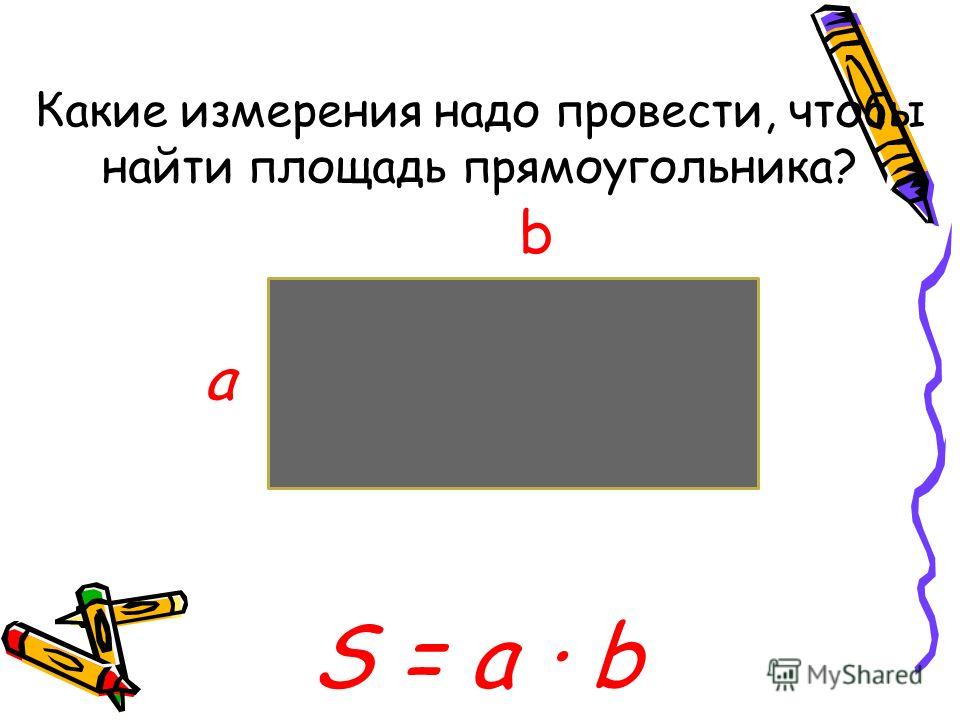
Площадь поверхности сферы равна 4πr² , где r — радиус сферы.
Площадь поверхности цилиндра равна 2πrh + 2πr² , где r — радиус цилиндра, а высота — высота.
Площадь поверхности конуса равна πrs + πr² , где r — радиус конуса, а s — наклон.
Формулы объема
Объем куба равен с³ , где s — длина стороны.
Объем прямоугольной призмы равен wlh , где w — ширина, h — высота, а l — длина.
Объем сферы равен ( 4πr³ ) / 3 , где r — радиус сферы.
Объем цилиндра равен πr²h , где r — радиус цилиндра, а высота — высота.
Объем конуса (πr²h) / 3 , где r — радиус конуса, а s — наклон.
Пример расчета объема и площади поверхности
Чтобы найти площадь поверхности объекта с криволинейной поверхностью, например сферы, нет другого выбора, кроме как запомнить формулы объема и площади поверхности. Но для других объектов мы часто можем разбить их на другие узнаваемые многоугольники и формы, объем или площадь поверхности которых мы можем легко найти. Например, в пирамиде вы просто вычисляете площадь основания и добавляете ее к площади поверхности каждой стороны треугольника.
Но для других объектов мы часто можем разбить их на другие узнаваемые многоугольники и формы, объем или площадь поверхности которых мы можем легко найти. Например, в пирамиде вы просто вычисляете площадь основания и добавляете ее к площади поверхности каждой стороны треугольника.
Найдем площадь поверхности и объем квадратной пирамиды с длиной основания 6 дюймов и высотой наклона 5 дюймов.
Площадь поверхности квадратной пирамиды
- Чтобы найти общую площадь поверхности, мы сначала исследуем площадь основания, которое представляет собой просто квадрат. Мы знаем, что площадь квадрата равна b² , где b — длина стороны. В этом случае площадь поверхности составляет 6² или 36 квадратных дюймов.
- Далее мы смотрим на четыре стороны, которые представляют собой просто треугольники. Мы знаем, что площадь треугольника равна (bh) / 2 , где b — основание, а h — высота. В этом случае основание треугольника совпадает с основанием пирамиды, б.
 Высота треугольника равна наклонной высоте пирамиды s. Таким образом, площадь только одной из этих треугольных сторон равна: .
Высота треугольника равна наклонной высоте пирамиды s. Таким образом, площадь только одной из этих треугольных сторон равна: .
- Когда мы складываем четыре из этих треугольников с площадью квадратного основания, мы получаем общую площадь поверхности b² + 4(bs) / 2 или b² + 2bs для квадратной пирамиды. Подставляя числа, мы получаем:
Объем квадратной пирамиды
Объем пирамиды определяется следующей формулой объема:
Мы можем подставить наши значения высоты и основания, чтобы получить:
Распознавание объема и площади15
Опять же, площадь поверхности измеряет площадь всех внешних поверхностей объекта, а объем измеряет внутреннее пространство, которое занимает объект.
Вы найдете много реальных случаев, когда полезно вычислить площадь поверхности или объем формы, например, количество воды, необходимое для заполнения бассейна (прямоугольная призма), или количество оберточной бумаги, необходимое для оберните свечу (цилиндр) или баскетбольный мяч (шар). Но всегда есть формулы для самых распространенных форм. Хотя полезно пройтись по формулам, прежде чем вам понадобится их использовать, не думайте, что вам нужно запоминать их все! Просто добавьте этот список в закладки, когда он вам понадобится.
Но всегда есть формулы для самых распространенных форм. Хотя полезно пройтись по формулам, прежде чем вам понадобится их использовать, не думайте, что вам нужно запоминать их все! Просто добавьте этот список в закладки, когда он вам понадобится.
Помощь с домашним заданием по математике
- Как найти радиус окружности тремя простыми способами
- Три способа найти объем пирамид
- Как определение площади поверхности применяется к 3D-объектам?
Площадь неправильных форм — расчеты, примеры и часто задаваемые вопросы
Неправильные формы — это многоугольники с пятью или более сторонами различной длины. Эти формы или фигуры могут быть далее разложены на известные формы, такие как треугольники, квадраты и четырехугольники, для оценки площади.
Вот некоторые примеры неправильных форм:
Предметы повседневной жизни неправильной формы
Как рассчитать площадь неправильной формы?
Определение площади неправильной формы
Различные методы оценки площади неправильной формы:
Оценка площади с использованием квадратов.

Разделение неправильной формы на две или более правильных фигур.
Разделение неправильной формы с помощью кривых на две или более правильных фигур.
Как найти площадь неровной фигуры?
Оценка площади с использованием единичных квадратов
Этот метод можно использовать для фигур с кривыми, кроме идеального круга или полукруга, а также для неправильных четырехугольников. В этом методе мы сначала делим фигуру на единичные квадраты. Общее количество единичных квадратов, попадающих в фигуру, используется для определения общей площади.
Например: Вычислите площадь путем подсчета квадратов на приведенном ниже рисунке 9.0100
Ответ: Если мы обозначим каждую единицу площади в сантиметрах, площадь будет равна 6 см2.
Вычисление площади неправильной формы с изогнутыми краями
Разделение неправильной формы на две или более правильных фигур
Используйте этот метод для вычисления площади неправильных фигур, которые представляют собой комбинацию треугольников и многоугольников. Используя предопределенные формулы, вычислите площадь таких фигур и сложите их вместе, чтобы получить общую площадь.
Используя предопределенные формулы, вычислите площадь таких фигур и сложите их вместе, чтобы получить общую площадь.
Например, в приведенной ниже неправильной форме мы разделим несколько ребер на треугольник и три многоугольника.
Общая площадь фигуры может быть рассчитана путем сложения отдельных площадей:
Общая площадь = площадь (ABIM) + площадь (BCGH) + площадь (CDEF) + площадь (JKL)
⇒ Общая площадь = (AB × BI ) + (BC × CG) + (CD × DE) + (12 × LJ × KO)
⇒Общая площадь = (10 × 5) + (3 × 3) + (2 × 2) + (1⁄2× 4 × 4)
⇒ Общая площадь = 50 + 9 + 4 + 8
⇒ Общая площадь = 71 см2
Расчет площади неправильной формы
Чтобы вычислить площадь неправильной формы, разделите фигуру с кривыми на две или более правильных фигур.
В этом методе разделите неправильную форму на несколько квадратов, треугольников или других четырехугольников. В зависимости от формы или кривых часть фигуры может быть также кругом, полукругом или квадрантом.
В зависимости от формы или кривых часть фигуры может быть также кругом, полукругом или квадрантом.
Найдите площадь заданной неправильной формы с 8 сторонами, включая одну кривую.
Решение: Определим неизвестные величины по заданным размерам сторон. Сначала нам нужно разделить фигуру на два прямоугольника и полукруг.
Площадь фигуры ABCDEF:
Общая площадь (ABCDEF) = Площадь (ABCG) + Площадь (GDEF) + Площадь (aob)
Общая площадь = (AB × AG) + (GD × DE) + (1/2 × π × ob2)
Общая площадь = (3 × 4) + (10 × 4) + (1/2 × 3,14 × 12)
Общая площадь = 12 + 40 + 1,57
Следовательно, общая площадь = 53,57 см2
Как найти площадь Неправильные формы с помощью миллиметровой бумаги?
Какова площадь неровной поверхности?
Найдите площадь данного листа.
Решение: Чтобы найти площадь неправильной поверхности в приведенном выше случае листа, мы должны положить лист на миллиметровую бумагу и провести его границу.
Форма листа неправильная. Таким образом, мы предположим, что более половины площади, покрытой листом, будет считаться 1, а менее половины будет считаться 0.
Теперь подсчитайте количество полностью закрытых фигур. Полностью покрыты 64 квадрата.
Кроме того, подсчитайте частично более чем наполовину закрытые квадраты, и каждый будет считать qs 1 квадрат. Есть 17 площади больше, чем половина площади.
Кроме того, подсчитайте частично менее половины закрытых Квадратов, и каждый из них будет считаться равным 0. Есть 16 Квадратов меньше половины Квадрата.
Теперь сложите все квадраты, чтобы найти площадь листа = 64 + 17 x 1 + 16 x 0 = 64 + 17 = 81 кв. единиц.
Отсюда Площадь листа будет 81 кв.ед.
Формула площади неправильных фигур
Чтобы найти площадь неправильных фигур, во-первых, нам нужно разделить неправильную форму на правильные фигуры, которые вы можете распознать, такие как треугольники, прямоугольники, круги, квадраты и так далее.
Затем найдите площадь этих отдельных фигур и сложите их, чтобы получить площадь неправильных фигур.
Пример решена
В. Найдите площадь заданной фигуры?
Решение: На рисунке выше есть три правильные фигуры. Начинайте делить сверху, у него есть треугольник, прямоугольник и трапеция.
Мы найдем площадь каждой из этих трех фигур и суммируем результаты, чтобы получить окончательную площадь фигуры.
Треугольник
Площадь треугольника = (основание × высота)/2
= (3 × 4)/2
= 12/2
= 6
Прямоугольник
Площадь прямоугольника = длина × ширина
= 3 × 10
= 30
Трапеция
Площадь трапеции = ((b1 + b2) × h)/2
= ((3 + 5) × 2) /2
= (8) × 2/2
= 16/2
= 8
Следовательно, площадь данной фигуры = 6 + 30 + 8 = 44.
Неправильные фигуры
Пространство, занимаемое фигурой известна как область неправильной формы; измеряется в квадратных единицах. Размер и длина фигур неправильной формы могут быть любыми. Существуют различные Неправильные Формы, которые мы можем видеть вокруг себя, такие как воздушные змеи, листья, алмазы и т. д. Следовательно, Неправильные Формы — это любые Формы, углы и длины которых не равны. Учащиеся могут изучать «Области неправильных форм» с предметными экспертами Vedantu, которые помогают учащимся понять каждую тему, чтобы было легче учиться и получать хорошие оценки.
Подробнее о неправильных формах
Область, покрываемая этой формой, известна как площадь неправильных форм. Стороны и углы неправильных фигур различны. чтобы найти площадь неправильной формы, мы должны разложить ее или разделить на несколько известных фигур, а затем будет добавлена площадь этих фигур, чтобы получить общую площадь неправильной формы. Неправильные формы можно увидеть повсюду вокруг нас в нашей повседневной жизни, например:
Неправильные формы можно увидеть повсюду вокруг нас в нашей повседневной жизни, например:
Лестница здания состоит из многоугольников, таких как прямоугольники и квадраты, площадь поверхности лестницы имеет неправильную форму.
Школьная игровая площадка с беговой дорожкой имеет неправильную форму, которая представляет собой комбинацию правильных форм.
Лист дерева или растения неправильной формы. И т. д.
Единица площади неправильной формы может быть выражена в м2, см2, дюйм2 или фут2.
Шаги по нахождению площади неправильных фигур
Шаг 1. Площадь неправильной формы нужно найти путем разложения неправильных фигур на знакомые формы.
Шаг 2. Учащиеся должны знать, как разложить неправильные фигуры.


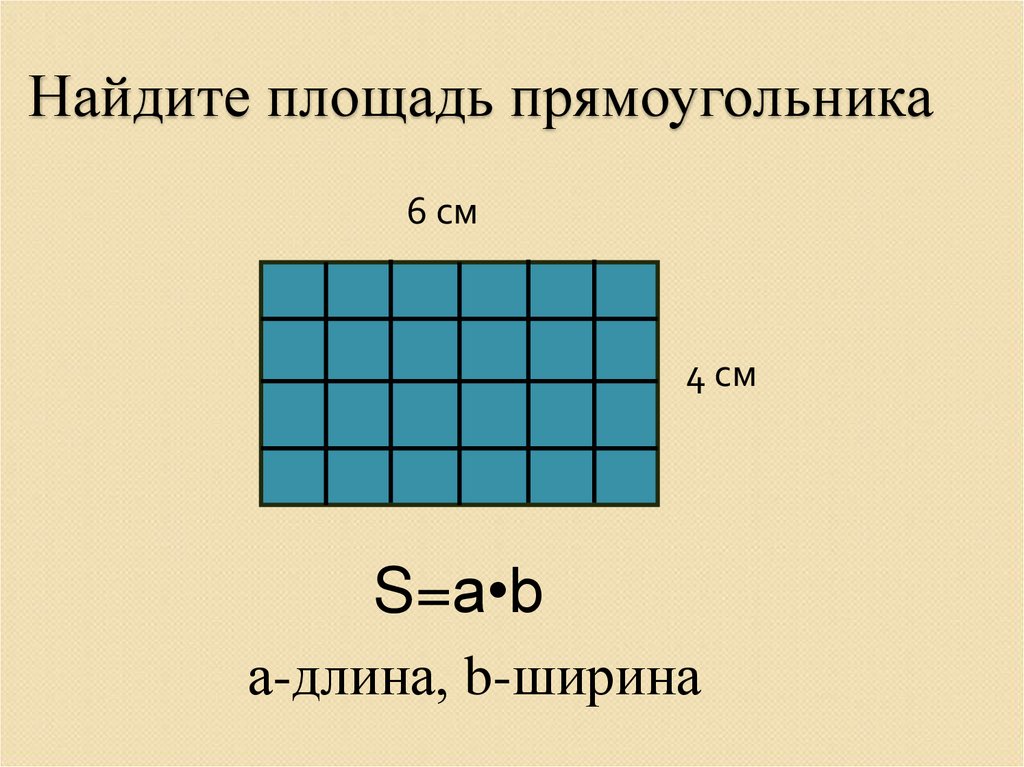
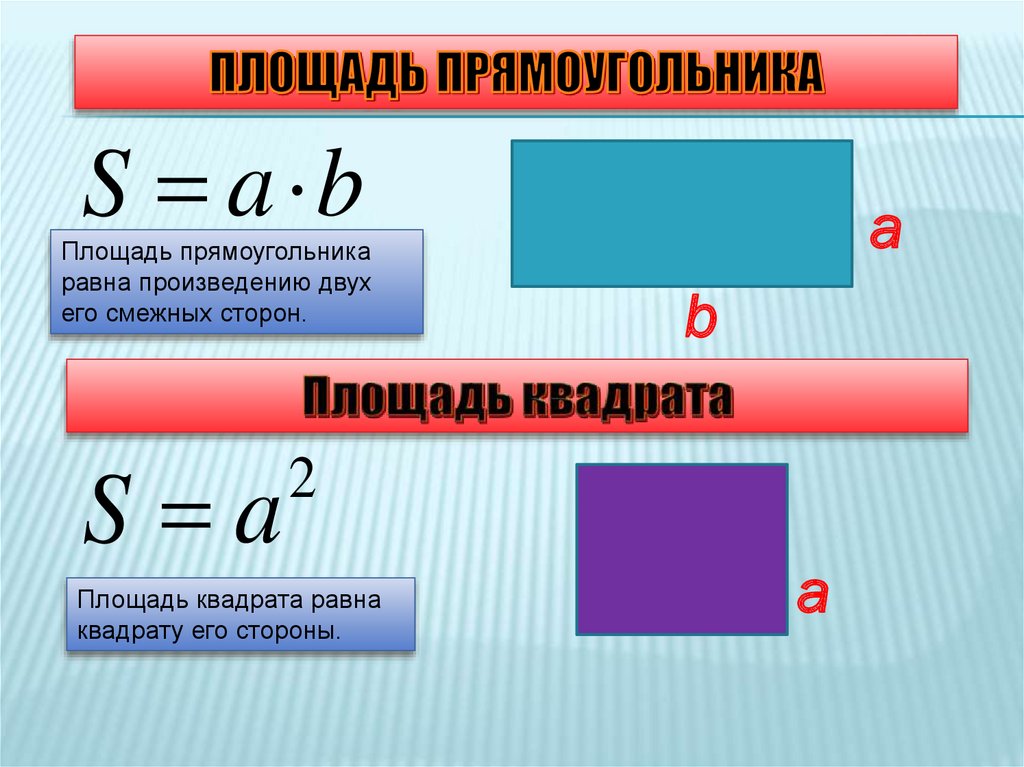 Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так: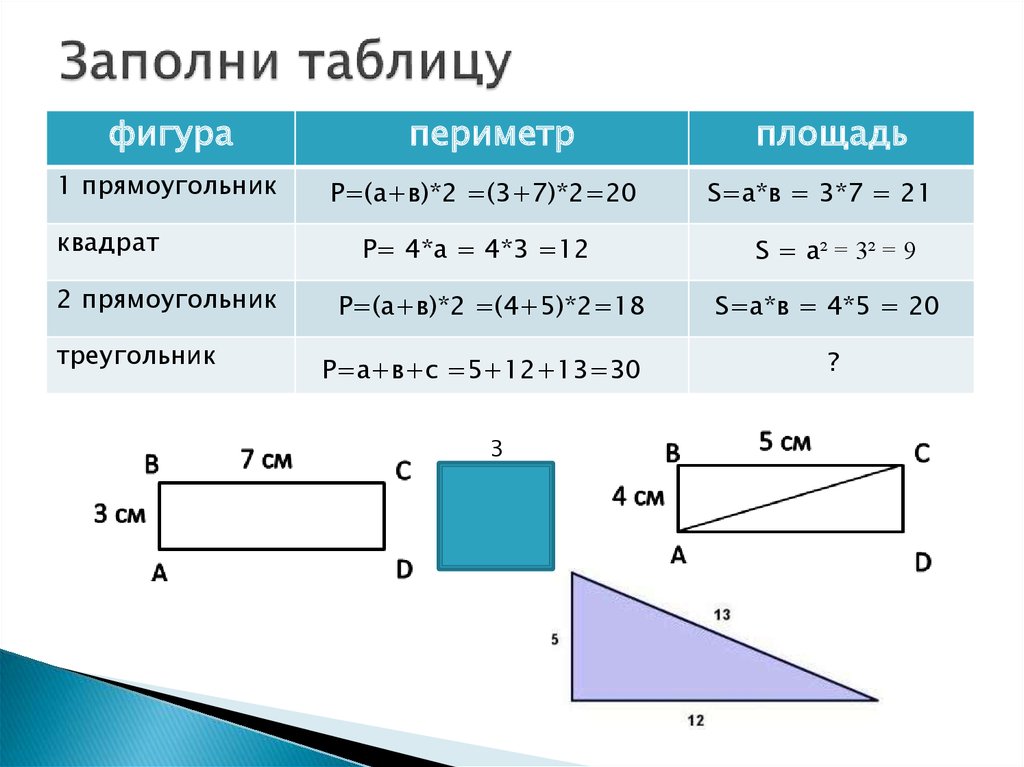 Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины. Следовательно, площадь бассейна составляет 64 квадратных метра.
Следовательно, площадь бассейна составляет 64 квадратных метра.

