“ Синус, косинус, тангенс и котангенс числового аргумента”
МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ ПМР
ГОУ «ДНЕСТРОВСКИЙ ТЕХНИКУМ ЭНЕРГЕТИКИ
И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ»
УТВЕРЖДАЮ
Зам. директора по учебной работе
__________________М.В. Питель
«_____»__________________2019 г
КОСы (экзаменационный материал)
по дисциплине: «МАТЕМАТИКА»
ВОПРОС:
“ Синус, косинус, тангенс и котангенс
числового аргумента”
Разработал преподаватель математики
ГОУ СПО «ДТЭ и КТ»
Демьянова Светлана Васильевна
РАССМОТРЕНО СОГЛАСОВАНО
на заседании ЦМК методист
_____________________ дисциплин ________ Левицкая И.
Н. Протокол №__ от «__»_____201__г. «__» _________201__г.
Председатель __________________
______________________________
г. Днестровск, 2019 г.
1. Определения:
а) Синусом угла а называется отношение ординаты точки к радиусу. Таким образом,
б) Косинусом угла а называется отношение абсциссы точки к радиусу. Таким образом,
2. Каждому углу а соответствует единственная точка , следовательно, единственное значение синуса и косинуса этого числа. Таким образом, а являются функциями числового аргумента. (Заметим, что в курсе геометрии мы рассматривали а как функции угловой величины а, а не числа а.)
3. Основное соотношение между а. Координаты любой точки единичной окружности удовлетворяют уравнению: (это следует из прямоугольного треугольника, катеты которого , а гипотенуза равна 1; см. рис. 98). Отсюда где
Из этой формулы следует, что: а)
4.
Значения синуса и косинуса некоторых чисел. В практических вычислениях часто используются значения синуса и косинуса, приведенные в таблице:
5. Знаки значений функций синуса и косинуса. Знаки а определяются знаками ординаты и абсциссы соответствующей точки единичной окружности. Если в первой координатной четверти), то числу а соответствует точка окружности координаты которой. Следовательно, на числовом промежутке. Если во второй координатной четверти), то, рассуждая аналогично, получаем (рис. 100).
Рис. 101 Рис. 102
Рис. 103
- ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА.
Определения:
1. Тангенсом числа а называется отношение ординаты точки к ее абсциссе (рис. 98). Таким образом,
2. Котангенсом числа а называется отношение абсциссы точки к ее ординате (рис. 98). Таким образом,
3. Значения тангенса и котангенса для чисел легко найти из формул .
Приведем таблицу этих значений:
4. Знаки значений функций тангенса и котангенса. Знаки значений тангенса и котангенса можно определить по знакам значений синуса и косинуса. Так как в I и III четвертях знаки значений синуса и косинуса одинаковые, а именно в I четверти , а в III четверти то в этих четвертях
Так как во II и IV четвертях знаки значений синуса и косинуса разные, а именно во II четверти ,а в IV четверти то в этих четвертях Заметим, что знаки значений тангенса и котангенса можно легко определить по знаку ординаты и абсциссы.
Лекция 12. Радианная мера угла. Синус, косинус, тангенс, котангенс числового аргумента. — Студопедия
Поделись
Радианная мера угла.
Отметим на оси Ох от начала координат точку А и проведем через нее окружность с центром в точке О. Радиус ОА будем называть начальным радиусом.
Угол Р (ОМ; ОЕ) можно описать как получившийся в результате вращения вокруг начала координат луча с началом в точке О от положения ОМ — начального до положения ОЕ — конечного.
Это вращение может происходить или против часовой стрелки или по часовой стрелке, причем
а) либо на неполный оборот,
б) либо на целое число полных оборотов;
в) либо на целое число полных оборотов и неполный оборот.
Меры углов, ориентированных против часовой стрелки, считаются положительными, а по часовой стрелки — отрицательными
Будем считать равными углами такие углы, для которых при совмещении каким либо образом их начальных лучей совмещаются и конечные лучи, причем движение от начального луча к конечному осуществляется в одну и ту же сторону на одно и то же количество полных и неполных оборотов вокруг точки О.
Нулевые углы считаются равными.
Свойства мер углов:
Существует угол, мера которого равна 1 — единица измерения углов. Равные углы имеют равные меры. Мера суммы двух углов равна сумме мер углов. Мера нулевого угла равна нулю.
Наиболее распространенные меры углов — градусная и радианная.
Единицей измерения углов в градусной мере является угол величины в один градус — 1/180 часть развернутого угла.
В качестве окружности с центром в начале координат мы будем брать окружность единичного радиуса, обозначая точки ее пересечения с координатными осями A(1;0), B(0;1), C(-1;0), D(0;-1). В качестве начального угла у рассматриваемых углов будет браться луч ОА.
Координатные оси абсцисс и ординат взаимно перпендикулярны и разбивают плоскость на четыре координатные четверти: I, II, III, IV (см. рисунок).
В зависимости от того, в какой координатной четверти окажется радиус ОМ, угол α будет так же углом этой четверти.
Так, если 00<α<900 , то угол α – угол первой четверти;
Если 900<α<1800 , то угол α – угол второй четверти;
Если 1800<α<2700 , то угол α – угол третьей четверти;
Если 2700<α<3600 , то угол α – угол четвертой четверти.
Очевидно, что при прибавлении к углу целого числа оборотов получается угол той же четверти.
Например, угол 4300 является углом I – ой четверти, так как 4300 = 3600 + 700 = 700;
Угол 9200 является углом III-ей четверти, так как 9200 = 3600 ·2 + 2000 = 2000
(т.
Углы 00, ± 900 , ± 1800, ± 2700, ± 3600 – не относятся ни к какой четверти.
Давайте определим, углом какой четверти является угол α, если:
α =2830 (IV) α = 1900 (III) α =1000 (II) α = -200 (IVч –отрицательное направление)
B курсе геометрии были определены синус, косинус, тангенс и котангенс угла α при 00 ≤ α ≤ 1800 . Теперь мы рассмотрим эти определения на случай произвольного угла α.
Пусть при повороте около точки О на угол α начальный радиус ОА переходит в радиус ОМ.
Синусом угла α называется отношение ординаты точки М к длине радиуса, т. е.
Косинусом угла α называется отношение абсциссы точки М к длине радиуса, т. е.
Тангенсом угла α называется отношение ординаты точки М к ее абсциссе, т. е.
Котангенсом угла α называется отношение абсциссы точки М к ее ординате, т. е.
Рассмотрим примеры вычисления тригонометрических функций с помощью таблиц значений некоторых углов.
Прочерки сделаны в том случае, когда выражение не имеет смысла.
| α (град) | ||||||||
| (рад) | π | 2π | ||||||
| sin α | -1 | |||||||
| cos α | -1 | |||||||
| tg α | - | - | ||||||
| ctg α | - | - | - |
Пример №1.
Найти sin300; cos450; tg600.
Решение: а) находим в столбике таблицы sinα и в строчке 300, на пересечении столбца и строчки находим значение sin 300- это число . Пишут так: sin 300 =
б) находим в столбике таблицы cosα и в строчке 450, на пересечении столбца и строчки находим значение cos 450 — это число . Пишут так: cos 450 =
в) находим в столбике таблицы tgα и в строчке 600, на пересечении столбца и строчки находим значение tg 600- это число . Пишут так: tg 600 = .
Пример №2
Вычислитьа) 2сos 600 + cos 300 = 2·
б)3tg 450 ·tg 600 = 3·1· = 3
Вычислите самостоятельно: а) 5sin 300 — ctg 450 б) 2sin 300 + 6cos 600 – 4tg 450
в) 4tg 600·sin 600 в) 2cossin 900 + 5tg 1800
Как использовать функцию COT
- Дом
- Функции
- Формулы
- Функции
Основы Excel Таблица Excel Расширенный фильтр Валидация данных Выпадающие списки Именованные диапазоны Решатель
- Графики
- Условное форматирование
- Сводная таблица
- VBA
Функции VBA Методы Характеристики Заявления Макросы Пользовательские функции Файлы и папки Флажки
- Архив
Все статьи отсортированы по дате Категории Продукты Продвинутый курс Excel
- Контакт
Обо мне Блоги, которые я прочитал
Автор: Оскар Кронквист Последнее обновление статьи: 04 мая 2022 г.
Функция COT вычисляет котангенс угла, указанного в радианах.
Формула в ячейке C3:
=COT(B3)
Синтаксис функции Excel
COT( число )
Аргументы
| Обязательный. Угол в радианах. |
Комментарии
Используйте функцию РАДИАНЫ для преобразования градусов в радианы.
=COT(РАДИАНЫ(30))
Рекомендуемые артикулы
Как использовать функцию РАДИАНЫ
Функция РАДИАНЫ преобразует градусы в радианы. Формула в ячейке C3: =RADIANS(B3) Синтаксис функции Excel RADIANS(угол) Аргументы angle Обязательный. […]
Функции в этой статье
COTRADIANS
Функции в категории «Математика и тригонометрия»
Функция COT function — одна из многих функций в категории «Математика и тригонометрия».
Функция ABS
Преобразует отрицательные числа в положительные числа.
Функция ACOS
Вычисляет арккосинус или арккосинус числа.
Функция ACOSH
Вычисляет гиперболический арккосинус числа.
Функция ACOT
Вычисляет арккотангенс числа.
Функция ACOTH
Вычисляет аркгиперболический котангенс числа.
Функция АГРЕГАТ
Выполнение различных конкретных функций для списка или базы данных.
Функция ASIN
Вычисляет арксинус числа.
Функция ASINH
Вычисляет арктический гиперболический синус числа.
Функция ATAN
Вычисляет арктангенс числа.
Функция ATAN2
Вычисляет арктангенс угла, используя определенные координаты x и y.
Функция ATANH
Вычисляет гиперболический арктангенс числа.
Функция BASE
Преобразует число в текстовое представление с заданной системой счисления (основанием).
Функция CEILING
Округляет число до ближайшего кратного.
Функция COMBIN
Возвращает количество комбинаций для определенного количества элементов из большей группы.
Функция COMBINA
Вычисляет количество комбинаций для заданного количества элементов из большей группы элементов.
Функция COS
Вычисляет косинус угла.
Функция COSH
Вычисляет гиперболический косинус числа.
Функция COT
Вычисляет котангенс угла, указанного в радианах.
Функция COTH
Вычисляет гиперболический котангенс гиперболического угла.
Функция CSC
Вычисляет косеканс угла (в радианах).
Функция DECIMAL
Преобразует текстовое представление числа с заданной системой счисления в десятичное число.
Функция ГРАДУСЫ
Вычисляет градусы в радианах.
ЧЕТНАЯ функция
Округляет число до ближайшего четного целого числа.
Функция EXP
Возвращает e, возведенное в степень числа, e равно 2,71828182845904.
Функция FACT
Возвращает факториал числа.
Функция FACTDOUBLE
Возвращает двойной факториал числа.
ИСПРАВЛЕННАЯ функция
Округляет число до указанного количества десятичных знаков, форматирует число в десятичном формате с использованием точки и запятых и возвращает результат в виде текста.
Функция FLOOR.MATH
Округляет число в меньшую сторону до ближайшего целого числа или до ближайшего кратного значения.
Функция FLOOR.PRECISE
Округляет число в меньшую сторону до ближайшего целого числа или ближайшего кратного значения.
Функция НОД
Вычисляет наибольший общий делитель, который делит все заданные аргументы без остатка.
Функция INT
Удаляет десятичную часть из положительных чисел и возвращает целое число (целое), за исключением того, что отрицательные значения округляются в меньшую сторону до ближайшего целого числа.
Функция LCM
Вычисляет наименьшее общее кратное. Наименьшее общее кратное — это наименьшее положительное целое число, кратное всем целым аргументам. Используйте функцию НОК, чтобы найти дроби с разными знаменателями.
Функция LET
Позволяет назвать результаты промежуточных вычислений, что может значительно сократить формулы и повысить производительность.
Функция LN
Вычисляет натуральный логарифм числа.
Натуральные логарифмы основаны на константе e.
Функция LOG
Вычисляет логарифм числа по определенному основанию.
Функция LOG10
Вычисляет логарифм числа по основанию 10.
Функция MINVERSE
Вычисляет обратную матрицу для заданного массива.
Функция МУМНОЖ
Вычисляет матричное произведение двух массивов, массива с тем же количеством строк, что и массив1, и столбцов, как массив2.
Функция MOD
Возвращает остаток после деления числа на делитель.
Функция ОКРУГЛ
Вычисляет число, округленное до заданного кратного.
МНОГОНОМНАЯ функция
Вычисляет отношение факториала суммы значений к произведению факториалов.
Функция MUNIT
Вычисляет единичную матрицу для заданного измерения
Функция PI
Возвращает число пи (¶).
Функция POWER
Вычисляет число, возведенное в степень.
Функция ПРОДУКТ
Возвращает произведение чисел, указанных в аргументе.
Функция ЧАСТНОЕ
Возвращает целую часть деления.
Функция RADIANS
Преобразует градусы в радианы.
Функция СЛУЧАЙ
Вычисляет случайное действительное число, большее или равное 0 и меньшее 1.
Функция СЛУЧАЙ
Создает массив случайных чисел .
Функция ОКРУГЛ
Округляет число на основе указанного вами количества цифр.
Функция ОКРУГЛВНИЗ
Округляет число в меньшую сторону на основе количества цифр, до которого вы хотите округлить число.
Функция ОКРУГЛВВЕРХ
Вычисляет число, округленное в большую сторону, на основе количества цифр, до которого вы хотите округлить число.
Функция SEC
Вычисляет секанс угла.
Функция SECH
Вычисляет гиперболический секанс угла.
Функция ПОСЛЕДОВАТЕЛЬНОСТЬ
Создает список порядковых номеров.
Функция SERIESSUM
Вычисляет сумму степенного ряда на основе формулы.
Функция ЗНАК
Возвращает знак числа.
1 для положительного числа, 0 (ноль) для 0 (ноль) и -1 для отрицательного числа.
Функция SIN
Вычисляет синус угла.
Функция SINH
Вычисляет гиперболический синус числа.
Функция SQRT
Вычисляет положительный квадратный корень.
Функция ПРОМЕЖУТОЧНЫЙ ИТОГ
Возвращает промежуточный итог из списка или базы данных, вы можете выбрать один из множества аргументов, которые определяют, что вы хотите, чтобы функция делала.
Функция СУММ
Позволяет добавлять числовые значения, функция возвращает сумму в ячейке, в которую она введена. Функция СУММ умно разработана, чтобы игнорировать текст и логические значения, добавляя только числа.
Функция СУММЕСЛИ
Суммирует числовые значения на основе условия.
Функция СУММЕСЛИМН
Складывает числа на основе критериев.
Функция СУММПРОИЗВ
Вычисляет произведение соответствующих значений, а затем возвращает сумму каждого умножения.
Функция СУММСК
Вычисляет сумму квадратов аргументов.
Функция SUMX2MY2
Вычисляет сумму разности квадратов соответствующих значений в двух массивах.
Функция SUMX2PY2
Вычисляет сумму суммы квадратов соответствующих значений в двух массивах.
Функция SUMXMY2
Вычисляет сумму квадратов разностей соответствующих значений в двух массивах.
Функция TAN
Вычисляет тангенс угла.
Функция TANH
Вычисляет гиперболический тангенс числа.
Функция TRUNC
Удаляет дробную часть числа до целого числа.
Категории функций Excel
Работа с массивами
Функции Excel, позволяющие изменять размер, комбинировать и формировать массивы.
Совместимость
Функции обратной совместимости с более ранними версиями Excel. Функции совместимости заменены более новыми функциями с повышенной точностью. Используйте новые функции, если совместимость не требуется.
База данных
Выполнение основных операций со структурой, подобной базе данных.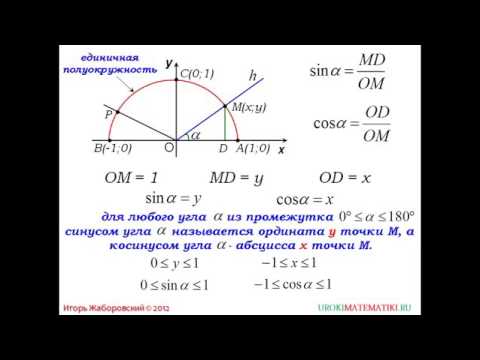
Дата и время
Функции, позволяющие выполнять вычисления со значениями даты и времени в Excel.
Инженерное дело
Позволяет работать с двоичными числами, преобразовывать значения между различными системами счисления и вычислять мнимые числа.
Финансовый
Расчет приведенной стоимости, процентов, накопленных процентов, основной суммы, накопленной основной суммы, амортизации, платежа, цены, роста, доходности по ценным бумагам и других финансовых расчетов.
Информация
Функции, позволяющие получать информацию из ячейки, форматирования, формулы, листа, книги, пути к файлу и других объектов.
Логический
Функции, позволяющие возвращать логические значения и управлять ими, а также управлять расчетами формул на основе логических выражений.
Поиск и ссылка
Эти функции позволяют сортировать, искать, получать внешние данные, такие как котировки акций, фильтровать значения на основе условий или критериев и получать относительное положение заданного значения в определенном диапазоне ячеек.
Они также позволяют вычислять строки, столбцы и другие свойства ссылок на ячейки.
Математика и тригонометрия
В этой категории вы найдете функции, которые вычисляют случайные значения, округляют числовые значения, создают последовательные числа, выполняют тригонометрию и многое другое.
Статистический
Расчет распределений, биномиальных распределений, экспоненциального распределения, вероятностей, дисперсии, ковариации, доверительного интервала, частоты, среднего геометрического, стандартного отклонения, среднего, медианы и других статистических показателей.
Текст
Функции, которые позволяют вам манипулировать текстовыми значениями, заменять строки, находить строку в значении, извлекать подстроку в строке, преобразовывать символы в код ANSI среди других функций.
Web
Получение данных из Интернета, извлечение данных из строки XML и многое другое.
Категории Excel
Домашняя страница
Последние обновленные статьи.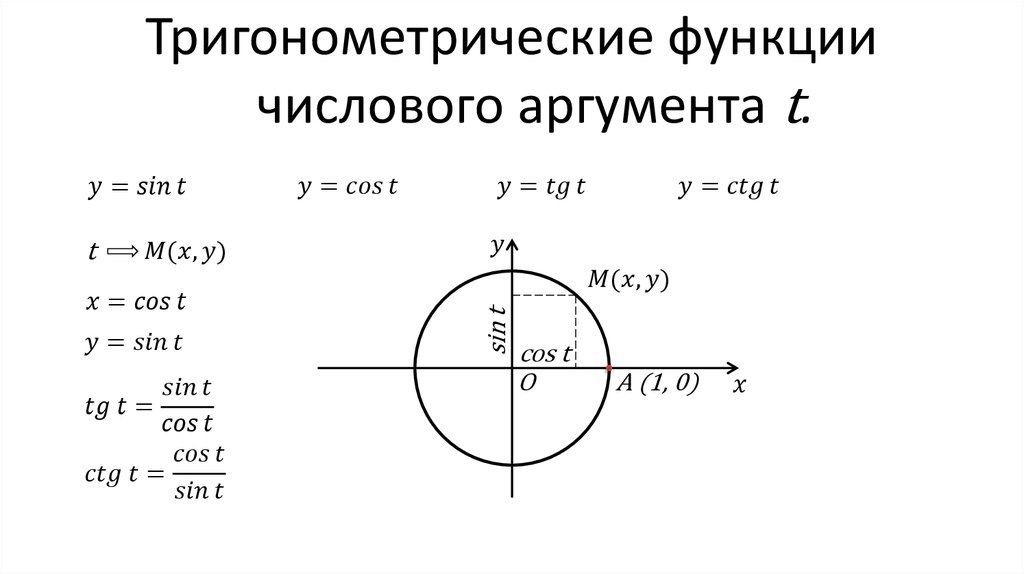
Функции Excel
Более 300 функций Excel с подробной информацией, включая синтаксис, аргументы, возвращаемые значения и примеры для большинства функций, используемых в формулах Excel.
Формулы Excel
Более 1300 формул, организованных в подкатегории.
Таблицы Excel
Таблицы Excel упрощают работу с данными, добавляя или удаляя данные, фильтруя, суммируя, сортируя, улучшая читаемость с помощью форматирования ячеек, ссылок на ячейки, формул и многого другого.
Расширенный фильтр
Позволяет фильтровать данные на основе выбранного значения, заданного текста или других критериев. Он также позволяет фильтровать существующие данные или перемещать отфильтрованные значения в новое место.
Проверка данных
Позволяет контролировать, что пользователь может вводить в ячейку. Это позволяет вам указать условия и показать собственное сообщение, если введенные данные недействительны.
Раскрывающийся список
Позволяет пользователю работать более эффективно, отображая список, из которого пользователь может выбрать значение.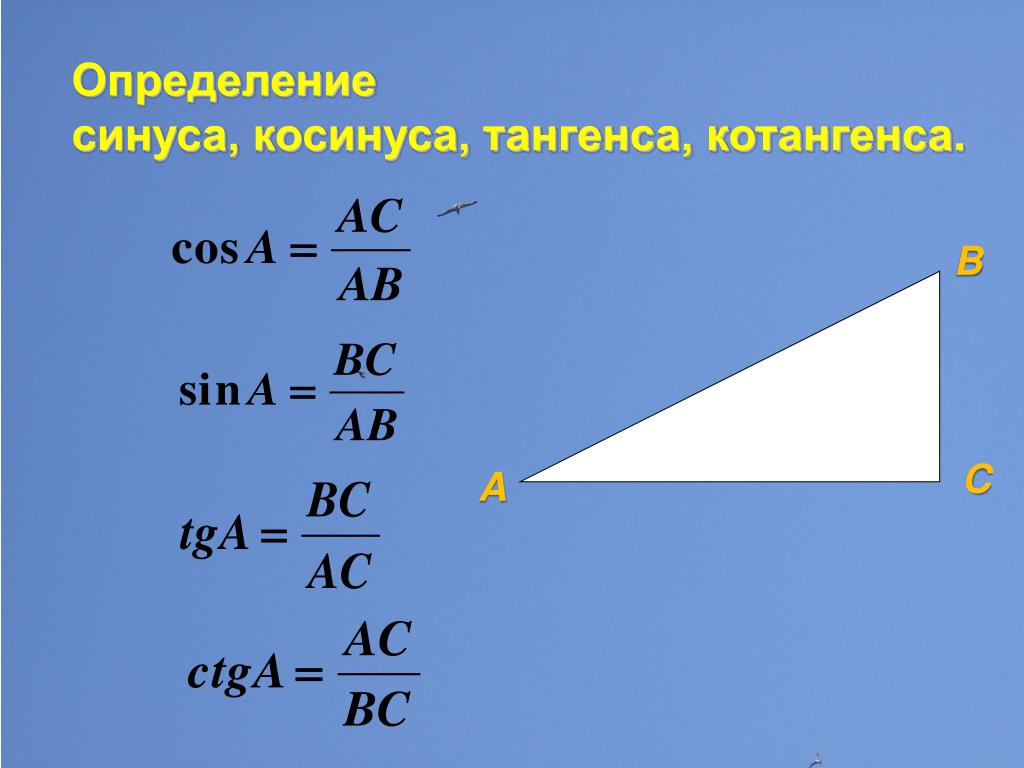
Это позволяет вам контролировать то, что отображается в списке, и это быстрее, чем ввод в ячейку.
Именованные диапазоны
Позволяет дать имя одной или нескольким ячейкам, это упрощает поиск ячеек с помощью поля Имя, чтение и понимание формул, содержащих имена вместо ссылок на ячейки.
Excel Solver
Excel Solver — это бесплатная надстройка, которая использует целевые ячейки, ограничения, основанные на формулах на листе, для выполнения анализа «что, если» и других проблем принятия решений, таких как перестановки и комбинации.
Диаграммы
Функция Excel, позволяющая визуализировать данные в виде графика.
Условное форматирование
Форматирование ячеек или значений ячеек на основе условия или критерия. Существует несколько встроенных инструментов условного форматирования, которые можно использовать, или использовать пользовательскую формулу условного форматирования.
Сводные таблицы
Позволяет быстро суммировать большие объемы данных в удобной для пользователя форме.
Эта мощная функция Excel позволяет эффективно анализировать, упорядочивать и классифицировать важные данные.
VBA
VBA означает Visual Basic для приложений и представляет собой язык программирования, разработанный Microsoft. Он позволяет автоматизировать трудоемкие задачи и создавать пользовательские функции.
Макросы
Программа или подпрограмма, созданная на языке VBA, которую может создать любой. Используйте средство записи макросов, чтобы быстро создавать собственные макросы VBA.
UDF
UDF расшифровывается как User Defined Functions и представляет собой настраиваемые функции, которые может создать каждый.
Архив
Список всех опубликованных статей.
Функции
ФункцииДалее: Генератор случайных чисел Up: выражения Предыдущий: Выражения Содержание Индекс Функции в gnuplot такие же, как и соответствующие функции в математической библиотеке Unix, за исключением того, что все функции принимают целые, действительные и сложные аргументы, если не указано иное.
Для тех функций, которые принимают или возвращают углы, которые могут быть заданы в любом градусы или радианы (sin(x), cos(x), tan(x), asin(x), acos(x), atan(x), atan2(x) и arg(z)), единица измерения может быть выбрана с помощью заданных углов , которые по умолчанию в радианах.
| Функции математических библиотек | ||
| Функция | Аргументы | Возвращает |
| абс(х) | любой | абсолютное значение 7#7, 8#8; тот же тип |
| абс(х) | комплекс | длина 7#7, 9#9 |
| акос(х) | любой | |
| акош(х) | любой | 11#11 (арктический гиперболический косинус) в радианах |
| аргумент(х) | комплекс | фаза 7#7 |
| асин(х) | любой | 12#12 (обратный синус) |
| asinh(x) | любой | 13#13 (обратный гиперболический синус) в радианах |
| атан(х) | любой | 14#14 (арктангенс) |
| атан2(у,х) | целое или реальное | 15#15 (арктангенс) |
| атан(х) | любой | 16#16 (арктический гиперболический тангенс) в радианах |
| besj0(x) | целое или реальное | 17#17 Функция Бесселя 7#7, в радианах |
| besj1(x) | целое или реальное | 18#18 Функция Бесселя 7#7, в радианах |
| бесы0(х) | целое или реальное | 19#19 Функция Бесселя 7#7, в радианах |
| бесы1(х) | целое или реальное | 20#20 Функция Бесселя 7#7, в радианах |
| потолок(х) | любой | 21#21, наименьшее целое не меньше 7#7 (действительная часть) |
| соз(х) | любой | 22#22, косинус 7#7 |
| кош(х) | любой | 23#23, гиперболический косинус 7#7 в радианах |
| эрф(х) | любой | 24#24, функция ошибки реального (7#7) |
| erfc (х) | любой | 25#25, 1. 0 — функция ошибки реального(7#7) |
| ехр(х) | любой | 26#26, экспоненциальная функция 7#7 |
| этаж(х) | любой | 27#27, наибольшее целое число, не больше чем 7#7 (действительная часть) |
| гамма(х) | любой | 28#28, гамма-функция реального (7#7) |
| ибета (р, д, х) | любой | 29#29, ibeta функция реального(30#30,31#31,7#7) |
| инвертировать(х) | любой | обратная функция ошибки вещественного числа (7#7) |
| игамма (а, х) | любой | 32#32, игамма-функция реального(33#33,7#7) |
| изображение(х) | комплекс | мнимая часть 7#7 как действительное число |
| инвнорм(х) | любой | обратная функция нормального распределения вещественного числа (7#7) |
| интервал (х) | настоящий | целая часть 7#7, усеченная до нуля |
| ламберт (х) | настоящий | W-функция Ламберта |
| лгамма(х) | любой | 34#34, гамма-функция реального (7#7) |
| журнал (х) | любой | 35#35, натуральный логарифм (по основанию 36#36) числа 7#7 |
| лог10(х) | любой | 37#37, логарифм (основание 38#38) от 7#7 |
| норма(х) | любой | функция нормального распределения (Гаусса) действительного (7#7) |
| ранд(х) | любой | 39#39, генератор псевдослучайных чисел |
| реальный(х) | любой | действительная часть 7#7 |
| знак (х) | любой | 1, если 40#40, -1, если 41#41, 0, если 42#42. изображение (7 # 7) игнорируется |
| грех(х) | любой | 43#43, синус 7#7 |
| грех(х) | любой | 44#44, гиперболический синус 7#7 в радианах |
| кврт(х) | любой | 45#45, квадратный корень из 7#7 |
| загар(х) | любой | 46#46, тангенс 7#7 |
| танх(х) | любой | 47#47, гиперболический тангенс 7#7 в радианах |
| Строковые функции | ||
| Функция | Аргументы | Возвращает |
| gprintf(«формат»,x) | любой | строковый результат применения анализатора формата gnuplot |
спринтф(«формат»,х,. ..) | несколько | строковый результат от языка C sprintf |
| стрлен(«строка») | строка | целая длина строки |
| strstrt(«строка»,»ключ») | строк | int индекс первого символа подстроки «key» |
| substr(«строка»,начало,конец) | несколько | строка «строка»[начало:конец] |
| система («команда») | строка | строка, содержащая поток вывода команды оболочки |
| слово(«строка»,n) | строка, целое число | возвращает n-е слово в «строке» |
| слова («строка») | строка | возвращает количество слов в «строке» |
| другие функции gnuplot | ||
| Функция | Аргументы | Возвращает |
| столбец (х) | интервал | столбец 7#7 во время обработки файла данных. |
| определено(X) | имя переменной | [УСТАРЕЛО] возвращает 1, если X определен, иначе 0. |
| существует («Х») | «имя переменной» | возвращает 1, если определена переменная с именем X, иначе 0. |
| строкастолбец(х) | интервал | содержимое столбца 7#7 в виде строки. |
| столбец времени (х) | интервал | временной столбец 7#7 во время обработки файла данных. |
| тм_час(х) | интервал | час |
| tm_mday(x) | интервал | день месяца |
| tm_min(x) | интервал | минута |
| тм_мон(х) | интервал | месяц |
| тм_сек(х) | интервал | второй |
| тм_вдай(х) | интервал | день недели |
| tm_yday(x) | интервал | день года |
| тм_год(х) | число | год |
| действительный(х) | интервал | проверка достоверности
48#48 во время манипулирования файлом данных. |