Что происходит со степенями при умножении: Свойства степеней, действия со степенями

Открытый урок по теме «Умножение и деление степеней с натуральным показателем», алгебра 7 класс

Конспект открытого урока по теме:

«Умножение и деление степеней с натуральным показателем»

(алгебра 7 класс)

Выполнила учитель математики

Лазарева Вера Николаевна

Аннотация

Урок «Умножение и деление степеней» является первым уроком в данной теме и третьим уроком в теме «Степень с натуральным показателем». На начало урока учащиеся владеют понятием степени, знают степень отрицательного числа с четным и нечетным показателем, степень положительного числа, умеют записывать произведение в виде степени, степень в виде произведения, вычислять значение степени, пользоваться таблицей степеней на стенде. Опираясь на это, и вводится новый материал.

И фонетическая зарядка, и актуализация знаний направлены на повторение учениками прошлого материала для введения нового материала.

На этих этапах повторяется теоретический материал и практические действия со степенями. Используются в работе интерактивная доска, презентация с заданием для фонетической зарядки.

При постановке темы урока и его цели используется проблемно-поисковый метод.

Ребятам экспериментальным путем предлагается определиться в действиях со степенями. В результате ребята получают возможность самостоятельно определить тему и сформулировать цель своей работы. На данном этапе урока предполагается совместное обсуждение полученных результатов.

Введение нового материала происходит в форме диалога с учащимися. Ребята по возможности самостоятельно выдвигают свои предположения. Учитель их корректирует, переводит полученные результаты от частных примеров к общим случаям. На этом этапе урока предполагается работа с учебником.

Первичное закрепление изученного материала происходит при работе в тетрадях и у доски.

Для определения достижения целей в конце урока проводится самостоятельная работа с последующей взаимопроверкой. В результате которой учащиеся определяют уровень полученных умений и понять в чем еще они испытывают затруднения.

Заключительным этапом урока является рефлексия. В ходе этого этапа учащиеся получают возможность оценить свою деятельность на уроке, высказать свое мнение о результатах прошедшего урока.

Домашнее задание предполагает работу с теоретическим материалом и практическое выполнение заданий.

Конспект открытого урока по теме:

«Умножение и деление степеней с натуральным показателем»

(алгебра 7 класс)

Цель урока:  

Формировать умение умножать и делить степени с одинаковыми основаниями   

Задачи:                                                                                                             

Образовательные: на основе имеющихся знаний учащихся вывести правила умножения и деления степеней с одинаковыми основаниями; ввести понятие нулевой степени числа ≠ 0; используя эти правила, учить умножать и делить степени с одинаковыми основаниями и способствовать выработке их практического применения.
Развивающие: развивать умение работать с текстом учебника, способствовать развитию кратковременной памяти, концентрации внимания, логического мышления, вычислительных навыков, формировать навыки познавательной деятельности.

Коррекционные: способствовать развитию монологической речи и её выразительности, развитию слухового восприятия

Воспитательные: воспитывать познавательную активность, взаимоконтроль, самооценку, аккуратность ведения записей в тетрадях.

Тип урока: урок изучения нового материала.

Словарь: Степень, основание степени, показатель степени.

Оборудование: ПК, И/доска, проектор, USB носитель, презентация

Карточки для самостоятельной работы

План урока:

Организационный момент. (3 мин.)

Актуализация знаний (5 мин)

Устный счет (3 мин)

Сообщение темы и цели урока (1 мин)

Изучение нового материала с первичным закреплением (17мин)

Самостоятельная работа (3мин)

Рефлексия и домашнее задание. (5 мин)

Выставление оценок (2мин)

Ход урока

I. Организационный момент

1)ПРИВЕТСТВИЕ:

Здравствуйте, ребята! Здравствуйте, гости!

Ребята, поприветствуйте наших гостей: Доброе утро! Здравствуйте! Привет всем! Мы рады вас видеть! Доброе утро!

2)ПРОВЕРКА готовности к уроку.

Ответьте ДА или НЕТ на мои вопросы: Слушайте внимательно!

(обращаюсь по имени к каждому ученику и задаю вопрос)

У тебя 2 аппарата?

Сейчас урок геометрии?

Учебники есть у всех?

Мы на алгебре изучаем треугольники?

Сейчас зима?

Все здоровы?

Вопрос ко всем: ВСЕ ГОТОВЫ К УРОКУ?

МОЛОДЦЫ, К УРОКУ ГОТОВЫ

3)ФОНЕТИЧЕСКАЯ ЗАРЯДКА: Ц-Ч

Назовите дежурные звуки. (один ученик произносит)

Ребята, произнесите правильно дежурные звуки.

(Каждый произносит дежурные звуки)

Не забывайте все остальные звуки тоже говорить правильно.

Прочитайте словосочетания с дежурными звуками: ОТРИЦАТЕЛЬНЫЕ ЧИСЛА, ЧЁТНЫЕ ЧИСЛА, НЕЧЁТНЫЕ ЧИСЛА, ПРЕЖНЕЕ.

(читают словосочетания и приводят примеры)

В каком слове нет дежурных звуков? – ПРЕЖНЕЕ

Что оно означает? (ученики не знают)

Учитель даёт толкование этого слова в контексте изучаемой темы: ПРЕЖНЕЕ = ТО ЖЕ САМОЕ,

Дополните недостающим словом следующие два правила, изученные на прошлом уроке:

( с выходом к И/ доске) ( сначала вставляют недостающее слово)

(слайд 1)

СТЕПЕНЬ ОТРИЦАТЕЛЬНОГО ЧИСЛА С ЧЁТНЫМ ПОКАЗАТЕЛЕМ ЕСТЬ ЧИСЛО ……. (положительное)

СТЕПЕНЬ ОТРИЦАТЕЛЬНОГО ЧИСЛА С НЕЧЁТНЫМ ПОКАЗАТЕЛЕМ ЕСТЬ ЧИСЛО ……. (отрицательное)

Прочитайте с правильным логическим ударением.

(Один или два ученика читают)

II. Актуализация знаний

Учитель: — Ребята, какую тему мы изучали на прошлом уроке?

-Определение степени с натуральным показателем.

Учитель: — Что было задано?

— Учить правила.

У: Давайте вспомним, что мы знаем:

1.Составьте предложения, которые являются правилами и прочитайте с правильным логическим ударением.

(Работа на И/доске)

(Выполняют по цепочке с выходом к доске и находят окончания предложений и читают с правильным логическим ударением)

1 часть:

Повторяющийся множитель степени называется…(основанием степени)

Число повторяющихся множителей степени называется…(показателем степени)

Степенью числа а с показателем 1 называется …(само число а)

При возведении в степень положительного числа получается …. (положительное число).

При возведении в степень нуля получается (нуль)

Квадрат любого числа есть…(положительное число или нуль)

2 часть: …. основанием.

…. показателем.

…. само число а.

….. положительное число.

….. нуль.

….. положительное число или нуль.

Всё ли верно? Ошибки есть? Посмотрите внимательно…

Если всё верно, – МОЛОДЦЫ!

III. Устный счет. (слайд 2)

1. Вычислите:

2³ = 2∙2∙2 = 8 (- 2)² = 4

4³ = 64 (- 1)⁵ = — 1 2³ + 2² = 8 + 4 = 12

2. Представьте в виде степени: а) 8= б) 9= в) 16=

(Учащиеся выполняют устные вычисления). Ситуация успеха.

(Создание проблемной ситуации:)

А представьте в виде степени такие выражения…

г) 2³∙ 2² = ??? д) 3⁵ : 3² = ???

Как посчитать?

(Ученики могут сказать ответ в г) 4⁵ или 4⁶или 8∙4 = 32; но в задании д) у них ответа не будет)

Посмотрите внимательно, какие действия надо выполнить ?

В г) – УМНОЖЕНИЕ, а в д) — ДЕЛЕНИЕ

А как их выполнить? Не знаете? Хотите узнать?

IV. Постановка темы и определение цели урока.

Это и будет темой нашего урока.

Откройте, пожалуйста, тетради, напишите в них число, классная работа и тему урока: Умножение и деление степеней. (Слайд 3)

(и фиксируем на доске)

Пишите красиво и аккуратно

Какую мы поставим цель? Что будем делать?

Ученики: — УЧИТЬСЯ УМНОЖАТЬ И ДЕЛИТЬ СТЕПЕНИ

Учитель: — Правильно, УЧИТЬСЯ УМНОЖАТЬ И ДЕЛИТЬ СТЕПЕНИ при помощи правил. (фиксируем эту цель на доске)

V. Изучение нового материала

Вернёмся к нашим примерам: (пишу сама на доске)

2³ ∙ 2² = (2∙2∙2)∙(2∙2) =2∙2∙2∙2∙2 = 2⁵

Что вы заметили?

Чему равно основание? : везде 2 и было 2 и осталось 2

А что стало с показателем?

Как мы его получили? З + 2 = 5 — Мы их сложили.

2³ ∙ 2² = 2^{3 + 2} = 2⁵

Т. е.(учитель говорит слово, — ученики дополняют) основание, мы оставили… прежним, а показатели степеней ……сложили.

Откройте учебник на стр. 93 и посмотрите, такое ли там правило?

Прочитайте его. (Все читают правило в учебнике)

ПРИ УМНОЖЕНИИ СТЕПЕНЕЙ С ОДИНАКОВЫМИ ОСНОВАНИЯМИ ОСНОВАНИЕ ОСТАВЛЯЮТ ПРЕЖНИМ, А ПОКАЗАТЕЛИ СКЛАДЫВАЮТ

В тетрадях запишем это правило в буквенном выражении:

аⁿ ∙ а^m = а^{n + m} для любого а и натуральных m и n

(на доску вывешиваю таблицу с правилом)

Приведите по одному примеру на это правило и запишите их в тетради.

(Ребята записывают примеры, затем несколько учеников зачитывают свои примеры.)

Это правило можно применять при умножении двух и более степеней

Например: 5⁴ ∙5³ ∙ 5 = 5⁴⁺³⁺¹ = 5⁸

Давайте решим у доски несколько примеров:

1. 2⁶ ∙2³ ∙ 2 = 2⁶⁺³⁺¹ = 2¹⁰

2. 3¹⁰ ∙3⁵ = 3¹⁰⁺⁵= 3¹⁵

3. х⁷ ∙ х⁵ ∙ х² = х⁷⁺⁵⁺² = х¹⁴ (трое учеников по очереди выходят к доске, решают и читают свои примеры)

Кто не понял? Кому трудно вычислять? У кого есть вопросы?

Какое действие мы учились выполнять? (жду ответа, потом показываю на цель урока на слово УМНОЖАТЬ)

— Ребята, как умножаются степени, мы с вами теперь знаем?

Чему еще сегодня будем учиться?

-ДЕЛИТЬ СТЕПЕНИ.

Вернёмся к нашему примеру на деление степеней.

3⁵ : 3² = (запишем в виде дроби: в числителе делимое, а в знаменателе делитель) = = и сократим = 3∙3∙3 = 3³

Посмотрите внимательно, основание степени у нас изменилось?

Ученики: — НЕТ, оно осталось прежним

А чему равен показатель степени?

Ученики: 5-2 = 3

Какое у нас получается правило?

Вы начните его, а я помогу закончить:

ПРИ ДЕЛЕНИИ СТЕПЕНЕЙ С ОДИНАКОВЫМИ ОСНОВАНИЯМИ ОСНОВАНИЯ ОСТАВЛЯЮТ ПРЕЖНИМ, А….. ИЗ ПОКАЗАТЕЛЯ ДЕЛИМОГО ВЫЧИТАЮТ ПОКАЗАТЕЛЬ ДЕЛИТЕЛЯ

Откройте учебник на стр. 94 и посмотрите, такое ли там правило?

Прочитайте его.

В тетрадях запишем это правило в буквенном выражении:

аⁿ : а^m = а^{n — m} при условии, что а ≠ 0 m n

(на доске фиксирую таблицу с правилом)

Приведите по одному примеру на это правило и запишите их в тетради.

(Одного ученика попросить прочитать свой пример)

Если m=n, то можно записать: а^m : а^m = а^{m – m} = а⁰ = 1 при а ≠ 0 (т.к. 0⁰ не имеет смысла)

Например: 6⁰ = 1 2,7⁰ = 1 х⁰ = 1 (х≠0)

(фиксируем на доске и в тетрадях)

Какое ещё действие мы учились выполнять? – ДЕЛИТЬ степени

(жду ответ и показываю на цель урока на слово ДЕЛИТЬ)

Самостоятельно: Подойдите и возьмите карточки для самостоятельной работы. (в карточках по 4 примера на умножение и деление степеней)

Выполните задания в тетрадях: (работа в парах)

Поменяйтесь тетрадями и проверьте, правильно ли решили?

У кого есть ошибки?

Объясните соседу по парте как исправить ошибку.

Давайте ещё раз прочитаем правила: (обращаемся к таблицам с правилами, которые расположены на доске или (слайд 4))

VI. ИТОГ:

— Итак, ребята, подходит к концу наш урок. Давайте подведем итог:

Какую цель мы с вами ставили сегодня на уроке?

УЧИТЬСЯ УМНОЖАТЬ И ДЕЛИТЬ СТЕПЕНИ

Смогли ли мы ее достичь?

Что мы умеем? УМНОЖАТЬ И ДЕЛИТЬ СТЕПЕНИ

Что было трудно? Кому что непонятно?

Рефлексия:

Поделитесь своими мыслями по данному уроку. Выскажите свое мнение одним предложением, взяв за начало следующие фразы: (Слайд 5)

1. Сегодня я узнал…

2. Было трудно…

3. Я понял, что…

4. Теперь я умею…

5. Я научился…

6. У меня получилось …

7. Урок дал мне…

8. Мне захотелось…

Оцените свою работу на уроке:

Кристина, у тебя были ошибки? Какую бы ты сама поставила себе оценку?

Даша, ты работала хорошо? Какую бы ты сама поставила себе оценку?

Саша, у тебя были ошибки? Какую бы ты сам поставил себе оценку?

Домашнее задание: (слайд 6)

Выписать в справочник из учебника стр. 93, 94 все правила, № 408

Спасибо за урок!!! (слайд 7)

Разработка урока математики по теме «Умножение и деление степеней» | Презентация к уроку по алгебре (7 класс) по теме:

Муниципальное образовательное учреждение

«Козлецкая основная общеобразовательная школа»

Разработка урока

по теме:

 «Умножение и деление степеней с натуральным показателем»

(алгебра 7 класс)

Выполнила учитель математики

Бутусова Ирина Александровна

Пояснительная записка

   Урок «Умножение и деление степеней» является первым уроком в данной теме и третьим  уроком в теме «Степень с натуральным показателем». На начало урока учащиеся владеют понятием степени, знают степень отрицательного числа с четным и нечетным показателем, степень положительного числа, умеют записывать произведение в виде степени, степень в виде произведения, вычислять значение степени, пользоваться таблицей степеней в учебнике. Опираясь на этот аппарат, и вводится новый материал.

     В начале урока целесообразно провести устный счет. Так как  довольно часто учащиеся делают ошибки на действия с рациональными числами, то именно эти примеры и включены в счет. Чтобы внести элемент занимательности предлагается по полученным ответам открыть буквы и составить слово.

    Следующий этап урока направлен на актуализацию знаний с целью повторения для введения нового материала. На этом этапе повторяется теоретический материал и практические действия со степенями. Элемент занимательности — отгадать имя ученого- математика.

     При постановке темы урока и его цели используется проблемно-поисковый метод.

Ребятам  экспериментальным путем предлагается определиться в действиях со степенями. В результате ребята получают возможность самостоятельно определить тему и сформулировать цель своей работы. На данном этапе урока предполагается  работа в группах и совместное обсуждение полученных результатов.

Введение нового материала происходит в форме диалога с учащимися.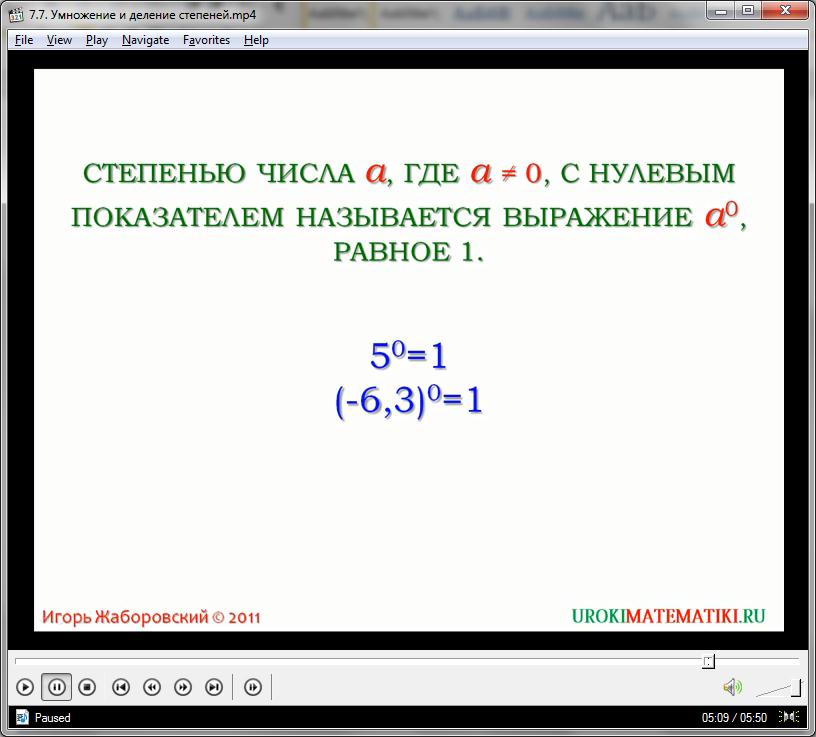 Ребята по возможности самостоятельно выдвигают свои предположения.  Учитель их корректирует, переводит полученные результаты от частных примеров к общим случаям. На данном этапе урока предполагается работа с материалом учебника.

     Первичное закрепление изученного материала происходит по заданиям в учебнике,  ведется работа у доски.

    Для определения достижения целей  в конце урока проводится самостоятельная работа с последующей самопроверкой по образцу. В результате которой учащиеся  определяют уровень полученных умений и понять в чем еще они испытывают затруднения. Оценки за самостоятельную работу выставляются в журнал по желанию учеников.

 Заключительным этапом урока является рефлексия. В ходе этого этапа учащиеся получают возможность оценить свою деятельность на уроке, высказать свое мнение о результатах прошедшего урока.

   Домашнее задание предполагается дифференцированное, с нарастающим уровнем сложности.

Цели урока :                                                                                                                 

Образовательные — формирование умения умножать и делить степени с натуральным показателем

Воспитательные — воспитание познавательной активности, чувства ответственности, культуры общения.                                                                                                                                          Развивающие — развитие математически грамотной речи, логического мышления.

Задачи:

— организовать деятельность учащихся по изучению свойств и правил умножения и деления степеней;

-вызвать у учащихся интерес к занятию;

-развивать у учащихся потребность в творческой деятельности.

Тип урока: урок изучения нового материала.

Структура урока:

1. Организационный момент. (1 мин.)

2 Устный счет (3 мин)

3. Актуализация знаний (5 мин)

4. Постановка темы и цели урока (5 мин)

5. Введение нового материала (10 мин)

6 Первичное закрепление(13 мин)

7 Самостоятельная работа(4 мин)

8.Рефлексия и постановка домашнего задания.(4 мин)

Оборудование:

Учебник «Алгебра 7 класс»   Ю.Н.Макарычев

Карточки  ответов для устного счета

Карточки для задания «Составь фразу»

Карточки с самостоятельной работой

Карточки ответов к самостоятельной работе

Презентация

Оформление доски

Таблица ответов для этапа актуализации знаний

Ход урока

Организационный момент

Здравствуйте, ребята! Я рада вас видеть. Надеюсь, что сегодня на уроке вы вновь ощутите радость новых открытий.

Устный счет. (слайд 2)

-2,8-3,2=

-6,8:3,4=

5*1,6=

0,8-7=

8,2:0,41=

(Учащиеся выполняют устные вычисления. Затем открывают карточки с полученными ответами, на обратной стороне которых написаны буквы. Из них они составляют слово: удача.)

— Я желаю, чтоб каждому из вас улыбнулась удача на сегодняшнем уроке. Пожелайте и вы друг другу удачи.

Откройте, пожалуйста, тетради, подпишите в них число, классная работа.

Актуализация знаний

— Ребята, какую тему мы с вами сейчас изучаем?

— Степень с натуральным показателем.

— Давайте вспомним, что мы с вами уже знаем. (Оба задания выполняются одновременно)

1. Выполните вычисления. Заполните таблицы буквами, учитывая найденные ответы, прочитайте текст (Выполняют  по цепочке, записывают в таблицу, заранее подготовленную на доске) (слайд 3)

Н   0,4=                                                                                                         М   0,2=

О   (-0,6) =                                                                                                    В  (-0,1)  =

А   1,1=                                                                                                         И  (-1,2)=

С   (-1,5)=                                                                                                      Р  -1,4=

Т   (2/7)=                                                                                                       К   (-1/2) =

Д   (-2/3) =                                                                                                     Е   (1/3) =

2. 25	1.44	0.008	0,36	0.16		2.25	4/49	1/9	-0.001	1.44	0.16

(Симон Стевин)

-нидерландский математик, который в конце 16 века предпринял шаги к построению современной теории степеней. Он обозначал неизвестную величину кружком, а внутри его указывал показатели степени. Например, хон обозначал как              (слайд4)

2.Составь фразы. (Выполняет 1 ученик)

1 часть

Повторяющийся множитель степени называется…

Число повторяющихся множителей степени называется…

Степенью числа а с натуральным показателем n , большим 1, называется ….

Степенью числа а с показателем 1 называется ……

При возведении в стенень положительного числа получается …..

При возведении в степень отрицательного числа получается……

Степенью отрицательного числа с четным показателем является…..

Степенью отрицательного числа с нечетным показателем является…..

Квадрат любого числа есть…

2 часть

….основанием.

…. показателем.

….. выражение a, равное произведению n множителей, каждый из которых равен а.

…. само число а.

….. положительное число.

….. нуль.

…..положительное число.

….. отрицательное число.

….. положительное число или нуль.

Постановка темы и определение целей урока.

— Ребята, какие действия с числами вы умеете выполнять?

— Сложение, вычитание, умножение и деление.

— А как вы думаете, какие из этих действий можно выполнять со степенями?

-( перечисляют)

— Давайте попробуем поэкспериментировать.

Работа в группах:

Используя таблицу степеней, найдите значение выражения и представьте (если возможно) это значение в виде степени с основанием 2. (слайд 5)

1 группа: 2+2

                2-2

2 группа: 2*2

                 2:2

(Ответы фиксируются на доске)

— Что вы заметили?

— При умножении и делении степеней значение также является степенью исходного числа, а при сложении и вычитании так не получается.

— Так может быть нам стоит более глубоко рассмотреть действия умножения и деления степеней с одинаковыми основаниями?

— Да

— Тогда давайте сформулируем тему нашего урока.

— Умножение и деление степеней. (слайд 6)

— Запишите в тетради  тему урока « Умножение и деление степеней».

— Какую цель мы перед собою ставим?

— Научиться умножать и делить степени. (слайд 7)

Введение нового материала

Вернемся  к выражению 2*2

Запишем, что получается в результате вычислений 2*2=2

Ребята, посмотрите внимательно,  что произошло с основанием степени и что произошло с ее показателем?

— Основание  не изменилось, показатель равен сумме показателей степеней.

— Молодцы! Покажем это свойство для степеней для любых степеней с одинаковым основанием.

Работаем в тетради:

Для любого числа а и произвольных натуральных чисел m  и n  aa=a.(слайд 8)

Доказательство: aa=(ааа…аа)*(ааа…а)=аааа…..ааа= a.

                                           раз         раз        раз

Таким образом,   aa=a.

Это равенство выражает основное свойство дроби. Оно распространяется на произведение трех и более степеней.

Итак, давайте теперь сформулируем правило умножения степеней. Я начну, а вы продолжите.

При умножении степеней с одинаковыми основаниями основание….

— оставляют прежним,

— а показатели…..

-складывают.

— Замечательно, повторите каждый сам про себя. Приведите по одному примеру на это правило в тетради.

Ребята записывают  примеры, затем несколько учеников зачитывают свои примеры.

Первичное закрепление

№ 403 а,в,д,ж, стр 94 (ведется работа в тетрадях и на доске)

— Ребята, как умножаются степени,  мы с вами теперь знаем? Чему еще нам осталось сегодня научиться?

-Делить степени.

— Давайте посмотрим на пример 2:2=2. Кто попытается самостоятельно сформулировать правило деления степеней?

-При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Работа с учебником

— Хорошо, а теперь откройте учебник на странице 94 и прочитайте правило. Запишите свойство частного степеней в тетрадь, приведите пример.  (слайд9)

№ 414 а,в,д, стр 95 (ведется работа в тетрадях и на доске)

Резерв: № 408а,в,д

             № 416 а,в

Самостоятельная работа с последующей самопроверкой

1 вариант                                                                                2 вариант

                          Представьте произведение в виде степени                                                                                

х*х=                                                                                       у*у=

х*х =                                                                                      у:у=

х:х=                                                                                      у*у=

3*3*3=                                                                              5*5*5=

х*х:х=                                                                               у:у*у=

(Карточки для самопроверки:

1 вариант                                                                                 2 вариант

х*х=   х =х                                                                      у*у= у=у

х*х =х=  х                                                                        у:у=у=у

х:х= х = х                                                                       у*у=у=у

3*3*3=3=3                                                                 5*5*5=5=5

х*х:х=  х =х                                                                у:у*у=у=у)

Оцените свою работу: «5» -верно все

                                       «4»-допущена одна ошибка

                                       «3»- допущены две ошибки

Рефлексия, постановка домашнего задания

— Итак, ребята, подходит к концу наш урок. Давайте подведем итог. Какую цель мы с вами ставили сегодня на уроке? Смогли ли мы ее достичь?

Поделитесь своими мыслями по данному уроку. Выскажите свое мнение одним предложением, взяв за начало следующие фразы:

1. Сегодня я узнал…
2. Было интересно…
3. Было трудно…
4. Я понял, что…
5. Теперь я могу…
6. Я научился…
7. У меня получилось …
8. Я  попробую…
9. Меня удивило…
10. Урок дал мне…
11. Мне захотелось…

-Запишите задание на дом: п.19, выучить правила,

№ 404 г,з, 415 в,д    на оценку «3»

№ 404 г,з, 415 в,д , 405 а,б на оценку «4»

№ 404 г,з, 415 в,д ,407  на оценку «5»

Выставление оценок за урок.

-Спасибо за урок! (слайд10)

Подробная информация об умножении показателей степени — Получить образование

Показатели степени — это степени или индексы. Показатель степени или степень означает, сколько раз число многократно увеличивается само по себе. Например, когда мы сталкиваемся с числом, созданным как 53, это просто предполагает, что пять увеличивается само по себе три раза. Другими словами, 53 = 5 х 5 х 5 = 125. Давайте подробнее об умножении показателей.

Экспоненциальное выражение состоит из 2 частей, а именно основания, представленного как b, и показателя степени, представленного как n. Основной вид экспоненциального выражения — b n.

Умножение показателей степени является жизненно важной частью математики высокого уровня. Тем не менее, многие стажеры изо всех сил пытаются понять, как именно выполнять эту операцию. Хотя выражения, включающие отрицательные значения, а также множественные показатели степени, кажутся сложными.

В этой короткой статье мы, скорее всего, узнаем о размножении бэкеров, и по этой причине это поможет вам чувствовать себя намного комфортнее при решении проблем с бэкерами.

Умножение показателей степени требует соблюдения подтем:

• Реплика подложек на той же основе
• Увеличение покровителей с разными основаниями
• Воспроизведение неблагоприятных показателей
• Увеличение частей с показателями
• Репродукция дробных подложек
• Увеличение переменных с показателями
• Умножение начала квадрата с показателями
• Увеличение числа сторонников с той же базой

При воспроизведении показателей с одинаковым основанием показатели суммируются. Правило умножения сложения показателей степени при одинаковых основаниях можно обобщить как x a m = a n + m.

Пример

м ⁵ × м ³ = (м × м × м × м × м) × (м × м × м).

= м5 + 3.

= м ⁸.

3 ⁴ × 3 ² = (3 × 3 × 3 × 3) × (3 × 3) = 3 4+ 3= 3 ⁶.

(-3) ³ × (-3) ⁴ = [(-3) × (-3) × (-3)] × [(-3) × (-3) × (-3) × (-3 )]= (-3) 3 +4.

= (-3)7.

Пять ³ × пять ⁶.

= (5 х 5 х 5) х (5 х 5 х 5 х 5 х 5 х 5).

и, = 53 +6.

= 5 ⁹.

(-7)10 × (-7) ¹².

= [(-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × ( -7)] × [(-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7)]

= (-7) ²².

Умножение показателей с разными основаниями

При увеличении двух переменных с разными основаниями, но с одинаковыми показателями, мы просто умножаем основания и позиционируем одного и того же покровителя. Это руководство можно резюмировать следующим образом:

a n ⋅ b n = (a ⋅ b) n.

Пример

(x3) *( y3) = xxx * yyy = (x y) 3.

3 2 x 4 2= (3 x 4) 2= 122 = 144.

как и базы, разные. После этого каждое число рассчитывается индивидуально, а после этого результаты перемножаются друг с другом. В этом случае формула представлена ​​an ⋅ bm.

Пример

32x 43 = 9 x 64 = 576.

Как умножать отрицательные степени?

Для чисел с одинаковым основанием и противоположными показателями степени мы просто добавляем показатели степени. В общем случае: a -n x a -m = a–(n + m) = 1/ a n + m.

Читайте также: Что такое градиент концентрации? Определение

Умножение квадратных корней с показателями

Home > Математика > Разделы по математике > Квадратные корни > Умножение квадратных корней с показателями

При умножении квадратных корней, содержащих показатели степени, мы должны понимать, как работают вместе степени и показатели степени.

Когда показатель степени содержится в квадратном корне, мы можем переписать член с рациональным показателем степени. Для этого рационального показателя мы будем использовать текущий показатель в качестве числителя и корень из 2 в качестве знаменателя.

Пример:

√3 ² x √4 ⁴

3 ^2/2 x 4 ^4/2 3

30106 1 x 4 ²

3 x 16

48

Обратите внимание, что наша новая степень по основанию 3 стала 1, а новая степень по основанию 4 стала 2. Следовательно, наша задача стала 3, умноженной на 16.

Иногда наши показатели степени не делятся без остатка на наш корень из 2. Когда это произойдет, основание со степенью 1 должно остаться в радикале. Чтобы решить эти проблемы, мы разделим нашу базу на два члена, один со степенью, которая делится без остатка на два, и один со степенью, равной 1.

Пример:

√5 ³ x √2 ⁷

√ (5 ² x 5 ¹ ) x √ (2 ⁶ x 2 ¹ )

^2/2 x 2 ¹ ) 9000 3 ^{2/2906 2/29066 2/2} x 2 ¹ ) 9000 3 ^{2/ 2/ x 2 1 ) 9000 5 2 2 1 ) 2} √ 5 x 2 ^6/2 √2

5 ¹ √ 5 x 2 ³ √2

5 √ 5 x 8√2

(5 x 8) √ (5 x 2)

40 √ 10

Обратите внимание, что √5 и √2 должны были остаться в радикалах, потому что их силы не делятся поровну на наш корень из двух.

Наконец, мы должны сделать это и с переменными.

Пример:

2√ (5 ⁶ Z ) x 3√ (3 ⁷ Y ³ )

2√ (5 ⁶ Z ⁸ Z ^{1 907) x 3√(3 6 3 1 y 2 y 1 )}

2(5 ^6/2 )(z ^{8/2 9 х} )√ 2 )(y ^2/2 )√(3y)

2(125)(z ⁴ ) √(5z) x 3(27)(y ¹ ) √(3y)

250 z ⁴ √5z x 81y ¹ √3y

(250 x 81)y ¹ z ⁴ √( 5z x 3y)

20,250 y ¹ z ⁴ √ 15yz

Нам пришлось разбить числа, а также переменные, чтобы получить как можно больше. Обратите внимание, что после упрощения мы объединили два члена, перемножив вместе коэффициенты, а также наши базы.

Практические задачи

Упрощение.

1. √6 ⁴ x √3 ⁸

2. √7 ³ x √3 ⁵

3. 4√ (2 ⁶ Y ³ ) x 5√ (2 ⁶ Y ³ ) x 5? (2 ⁶ Y ³ ) x 5? 4 ⁵ z ⁵ )

Answers

1. √6 ⁴ x √3 ⁸

6 ^4/2 x 3 ^8/2

6 ² x 3 ⁴

36 x 81

2916

2. √7 ³ x √3 ⁵

√7 ² 7 ¹ x √3 ⁴ 3 ¹

7 ^2/2 √7 x 3 ^4/2

7 ^2/2 √7 x 3 ^4/2 √3 √3 √3 ^2/2 √7 x 3 4/2

a

7 ¹ √7 x 3 ² √3

(7 x 9) √ (7 x 3)

63 √21

3. 4√ (2 ⁶ Y ³ ) X 5√ (4 ⁵ Z ⁵ )

4√ (2

6 Y ² Y ¹ ) x 5√ (4 ⁴ 4 ¹ Z 9?0106 4 z ¹ )

4(2 ^6/2 )(y ^2/2 )√y x 5(4 ^4/2 )(z ^{10 4z √2 90)}

4 (8) (y) √y x 5 (16) (z ² ) √ (4z)

32y √y x 80z ² √4z

(32 x 80) y z ² √ (y x x x.