Модуль числа | Презентация к уроку по алгебре (7 класс) по теме:
Модуль числа
Цель:
изучение понятия модуля,
применение определения модуля при выполнении задач.
Задачи:
развивать умение применять теоретический материал при решении практических задач;
развивать интерес к математике через поиск примеров по данной теме;
расширить математический кругозор;
приобрести навыки исследовательской работы.
Считаю, что выбранная тема является актуальной:
Задачи, связанные с абсолютной величиной, часто встречаются на математических олимпиадах и вступительных экзаменах.
Понятие модуля широко применяется в различных разделах школьного курса математики.
Это понятие является одним из основных понятий элементарной математики. Осмысленное владение модулем позволяет воспринимать алгебру и геометрию, как единое целое. “Расстояние между точками” позволяет оценивать правильность найденных решений ряда уравнений, содержащих модуль, строить графики функций.
В ходе работы я использовала следующие методы:
Исследование литературы по теме.
Проведение поиска задач по теме.
Основная часть
Существенной характеристикой числа является понятие его абсолютной величины (модуля).
Модулем числа называют расстояние от точки, изображающей число на координатной прямой до начала отсчета.
В различных учебниках первоначальное понятие модуля вводится по-разному: как расстояние от точки, изображающей число, до начала отсчёта (Математика. Н.Я. Виленкин), как длина вектора (Математика. П.М. Эрдниев), как число “без знака” (Математика. Г.В. Дорофеев) и др.
В архитектуре – это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике – это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например, модуль зацепления, модуль упругости и т.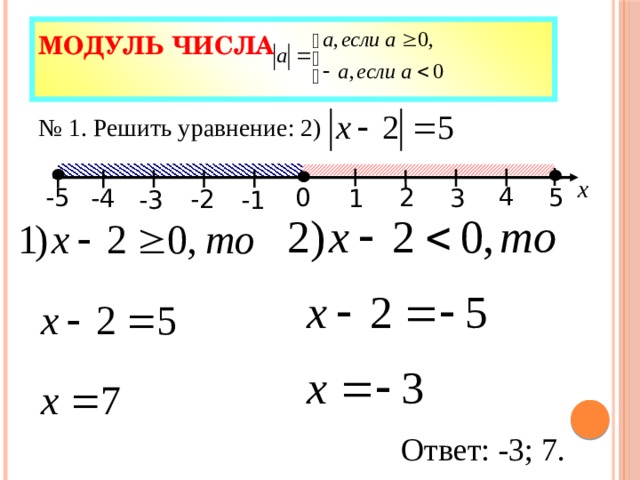 п.
п.
Понятие модуля
Модуль (modulus) в переводе с латинского языка означает “мера, размер”.
Модуль числа а обозначают | а |. Этот термин “модуль” ввёл в 1806 г. французский математик Жорж Аргон.
Геометрический смысл модуля
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).
Модуль числа 5 равен 5, так как точка В(5) удалена от начала отсчета на 5 единичных отрезков. Пишут: |5| = 5.
Расстояние точки М(-6) от начала отсчета О равно 6 единичным отрезкам. Число 6 называют модулем числа -6.
Пишут: |-6| = 6.
Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули.
|-а| = |а|
Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета О, т.е. удалена от нее на 0 единичных отрезков.
|0| = 0
Так как модуль числа – это расстояние, он никогда не будет отрицательным.
Изучая понятие модуля, я рассмотрела доказательство следующей теоремы:
Абсолютная величина действительного числа a ≠ 0 равна большему из двух чисел a или -a.
Доказательство:
Если число a положительно, то -a отрицательно, т.е. –a
Например, число 5 положительно, тогда -5 – отрицательно и -5
В этом случае |a| = a, т.е. |a| совпадает с большим из двух чисел a и -a.
Если a отрицательно, тогда -a положительно и a
Для нахождения модуля числа можно использовать следующую блок-схему.
Отработка алгоритма. Допустим, необходимо найти модуль чисел -3 и 7.
В учебниках приводятся различные упражнения с использованием модуля числа. Вот некоторые из них:
Запишите число, противоположное данному: 4; -4; +3; -3; -6,3; 6,3.
2. Найдите модуль каждого из чисел: |- 6 |, | 9 |, | — 5 |, | 0 |, |0,8 |.
3. Найти расстояние от М(-7) и N(6) до начала отчета на координатной прямой.
При решении задач, содержащих модуль числа, основным приемом является раскрытие знака модуля в соответствии с его свойствами.
В некоторых случаях модуль раскрывается однозначно.
Например: |x2 + y2| = x2 + y2, так как выражение под знаком модуля неотрицательно при любых х и у. Или |–z2 – 1| = z2 + 1, так как выражение под модулем отрицательно при любых z.
Уравнения, содержащие знак модуля, решаются следующими способами:
алгебраический,
графический,
последовательное раскрытие модулей,
метод интервалов.
Рассмотрим некоторые примеры решения уравнений и неравенств, содержащих знак модуля.
Решить уравнение: |x| = 3. Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и -3. Значит, у уравнения |x| = 3 есть два решения:
x = 3 и x = -3.
Решить уравнение: |x — 3| = 4.
Это уравнение можно прочитать так: расстояние от точки до точки равно 4. С помощью графического метода можно определить, что уравнение имеет два решения: — 1 и 7.
Решить неравенство: |x + 7|
Можно прочитать как: расстояние от точки до точки меньше четырёх. Ответ: (-11; -3).
Ответ: (-11; -3).
Решить неравенство: |10 — x| ≥ 7.
Расстояние от точки 10 до точки х больше или равно семи.
Ответ: (-∞; 3]U [17, +∞)
Рассматривая модуль числа, я познакомилась с функцией y = |x|, графиком которой является ломаная линия, состоящая из двух лучей, являющихся биссектрисами I и II координатных четвертей.
Действительно,
Для x ≥ 0 имеем y = x.
Для x
ЗАКЛЮЧЕНИЕ
В результате работы я:
повторила школьный материал по данной теме,
изучила решение уравнений и неравенств, содержащих знак модуля,
научилась строить график функции вида y = |x|,
Так как изучение модуля числа продолжается в старших классах, где рассматриваются свойства модуля, а также задачи различного уровня сложности, исследование данной темы будет продолжено. В следующем году я проведу исследование задач различного уровня сложности, а также олимпиадные и экзаменационные задачи.
«Абсолютная величина числа, или Этот «коварный» модуль».
 Программа элективного курса, алгебра, 9-й класс «Абсолютная величина числа, или Этот «коварный» модуль». Программа элективного курса, алгебра, 9-й класс
Программа элективного курса, алгебра, 9-й класс «Абсолютная величина числа, или Этот «коварный» модуль». Программа элективного курса, алгебра, 9-й класс- Погонец Наталия Сергеевна, учитель математики
Разделы: Математика, Общепедагогические технологии
Класс: 9
Элективный курс рассчитан на учащихся 9
классов и посвящен систематическому изложению
материала , связанного с понятием модуля числа и
его применения при решении задач на экзаменах.
Программа курса рассчитана на 17 учебных часов.
Цели курса.
- Образовательная (обучающая):
- Научить разным методам решения задач, в которых
присутствует модуль числа.

- Научить разным методам решения задач, в которых
присутствует модуль числа.
- Развивающая.
- Развивать умение преодолевать трудности при решении задач разного уровня сложности, формировать логическое мышление.
- Воспитательная.
- Формирование логического, абстрактного, эвристического, системного мышления.
Потребность в проведении курса возникла в связи с тем , что:
- в учебных пособиях мало заданий с модулем числа.
- не разобраны в системе методы и приёмы решения задач с модулем.
- нет развернутых тем в стандартах образования по модулю числа.
- задачи с модулем систематически встречаются на ЕГЭ и при поступлении в различные учебные заведения.
Курс в основном предназначен для учащихся,
увлекающихся математикой, но благодаря
содержанию курс может быть интересен и другим
категориям школьников.
Курс построен на материале “Алгебра 7 – 9 кл.”.
Содержание курса качественно отличается от
базового тем , что в нем будут изучаться многие
замечательные задания с модулем числа , т.к. у них
своя специфика. Это и уравнения, неравенства,
графики, которых нет в учебниках.
Основные задачи проведения курса:
- проведение правильного отбора содержания;
- проведение доступного изложения материала и составление системы упражнений;
- выявлялся тот материал и те задания, которые вызывали наибольшие затруднения у учеников.
- определение эффективности усвоения материала посредством второй диагностической работы
- выявить заинтересованность учащихся в изучении данной темы.
Курс обеспечен следующей литературой. (Приложение 1)
Возможны следующие виды деятельности учащихся:
- устное сообщение;
- написание рефератов, докладов, творческих работ;
- проекты.

Учащимся можно самостоятельно выбирать вид
отчетной работы; литературу.
Критерии успешной работы учащихся: при
выполнении не менее 3 работ ученик получает
зачет.
Динамика интереса в процессе обучения:
- анкетирование
- диагностические работы
- собеседования в процессе работы.
Форма итоговой отчетности: «МАТЕМАТИЧЕСКИЙ БОЙ» (Приложение 2)
Содержание курса
№ |
Название темы |
Кол-во часов всего |
Кол-во лекций |
Практика |
Форма занятия |
Образовательный продукт |
| 1 | Модуль действительного числа. |
1 |
1 |
|
Анкета, диагностическая работа № 1. | Устные сообщения |
| 2 | Основные свойства модуля числа. Геометрический смысл модуля числа. | 1 |
1 |
|
Лекция с элементами практики. | Таблица “Свойства модуля» |
| 3 | Модуль числа в алгебраических преобразованиях. | 2 |
1 |
1 |
Практикум. | Творческие работы учащихся |
| 4 | Решение уравнений вида: |х| = а, |х – b| = а, |f(х)| = а, |f(х)| = g(х) | 3 |
1 |
2 |
Лекция, практикумы. |
Выступление в парах. |
| 5 | Решение уравнений вида |х – b| + |х – с| = а | 2 |
1 |
1 |
Занятие-исследование, урок одной задачи | Работа с литерат., доклад. |
| 6 | Решаем неравенства вида |х| < а, |х| > |
2 |
1 |
1 |
||
| 7 | Построение множества точек на коорд. прямой, плоскости, содержащих знак модуля числа. | 2 |
1 |
1 |
Занятие-эксперимент. |
Таблицы с множ-вами. |
| 8 | Построение графиков функций: у = |х, у = а|х|, у = а|х – m| + b, у = |f(х)| | 3. |
1. |
2. |
Диагностическая работа № 2на 3 занятии. | Таблицы с модулями графиков. |
| 9 | Итоговое занятие. | 1 |
|
1 |
Математический бой. | Различные способы решения задач. |
Требования к умениям и навыкам учащихся.
- должны знать определение модуля числа и его геометрическую интерпретацию.
- уметь решать простейшие уравнения и
неравенства с модулем.

- уметь строить графики функций с модулем.
- уметь выполнять алгебраические преобразования с модулем числа.
Время проведения: наименее загруженный день.
Дополнительные материалы издательства
«Учитель», которые использовались для работы
по данной теме. (
Содержание программы
Модуль действительного числа, урок по алгебре в 8 классе, презентация
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Модуль действительного числа (PPTX)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Мультимедийное учебное пособие «Алгебра за 10 минут»
Ребята, с модулем числа мы встречались и раньше.
5. $|a|=|-a|$.
Геометрический смысл модуля действительного числа
Числовая прямая служит хорошим примером множества действительных чисел. Давайте отметим на числовой прямой две точки a и b и постараемся найти расстояние $ρ(a; b)$ между этими точками. Очевидно, что это расстояние равно $b-a$, если $b>a$.
Если $a>b$, то расстояние будет равно $a-b$.
Если $a=b$, то расстояние равно нулю, так как получается единая точка.
Все три случая мы можем описать единообразно: $ρ(a;b)=|a-b|$.
Пример.
Решите уравнение:
а) $|x-3|=6$;
б) $|x+5|=3$;
в) $|x|=2,8$;
г) $|x-\sqrt{3}|=2$.
Решение.
а) Надо найти на координатной прямой такие точки, которые удалены от точки 3 на расстояние равное 6.
$ρ(x;3)=6$.
Это точки – 9 и -3 (прибавили и отняли шестерку от тройки).
Ответ: $х=9$ и $х=-3$.
б) $|x+5|=3$, перепишем уравнение в виде $|x-(-5)|=3$.
$ρ(x;-5)=3$.
Найдем расстояние от точки -5, удаленное на 3. Такое расстояние, получается от двух точек: $х=2$ и $х=-8$.
Ответ: $х=2$ и $х=-8$.
в) $|x|=2,8$ можно представить в виде $|х-0|=2,8$ или $ρ(x;0)=2,8$.
Очевидно, что $х=-2,8$ или $х=2,8$.
Ответ: $х=-2,8$ и $х=2,8$.
г) $|x-√3|=2$ эквивалентно $ρ(x; \sqrt{3})=2$.
Очевидно, что $х=\sqrt{3}-2$ или $х=\sqrt{3}+2$.
Ответ: $x=\sqrt{3}-2$ или $x=\sqrt{3}+2$.
Пример.
Решить уравнения:
а) $|2x-8|=4$;
б) $|3-3x|=6$;
в) $|10x+5|=-2$.
Решение.
а) Преобразуем левую часть уравнения: $|2x-8|=|2(x-4)|=|2||x-4|=2|x-4|$.
Тогда уравнение можно переписать в виде: $|x-4|=2$.
Или $ρ(x;4)=2$.
Ответ: $х=6$ или $х=2$.
б) Опять же преобразуем левую часть: $|3-3x|=|-3(x-1)|=|-3||(x-1)|=3|x-1|$.
Тогда уравнение можно переписать в виде: $|x-1|=2$.
Или $ρ(x;1)=2$.
Ответ: $х=3$ или $х=-1$.
в)$|10x+5|=-2 $.
Модуль не может быть отрицательным числом, тогда, очевидно, что корней нет.
Ответ: нет корней.
График функции $y=|x|$.
Вычислить модуль мы можем из любого числа.
 2}$.
{-1}}$
$\renewcommand{\Im}{\operatorname{Im}}$
$\DeclareMathOperator{\Mod}{Mod}$
$\DeclareMathOperator{\Ker}{Ker}$
$\DeclareMathOperator{\Coker}{Coker}$
$\DeclareMathOperator{\Coim}{Coim}$
2}$.
{-1}}$
$\renewcommand{\Im}{\operatorname{Im}}$
$\DeclareMathOperator{\Mod}{Mod}$
$\DeclareMathOperator{\Ker}{Ker}$
$\DeclareMathOperator{\Coker}{Coker}$
$\DeclareMathOperator{\Coim}{Coim}$Ан Абелева группа с дистрибутивным действием кольца. Модуль является обобщением (линейного) векторное пространство над поле $K$, когда $K$ заменяется звенеть.
Пусть дано кольцо $A$. Аддитивная абелева группа $M$ называется левым $A$-модулем, если существует отображение $A\times M \to M$, значение которого на паре $(a, m)$ при $a \in A$ , $m \in M$, записанное как $am$, удовлетворяет аксиомам: 9\text{opp}$-модули и наоборот. Когда $A$ коммутативен, любой левый $A$-модуль можно рассматривать как правый $A$-модуль, и различие между левым и правым модулями исчезает. Ниже обсуждаются только левые $A$-модули.
Простейшие примеры модулей (конечные абелевы группы, они же $\ZZ$-модули) были известны еще К.Ф. Гаусса как группы классов бинарных квадратичных форм. Общее понятие модуля впервые встречается в 60—80-х гг.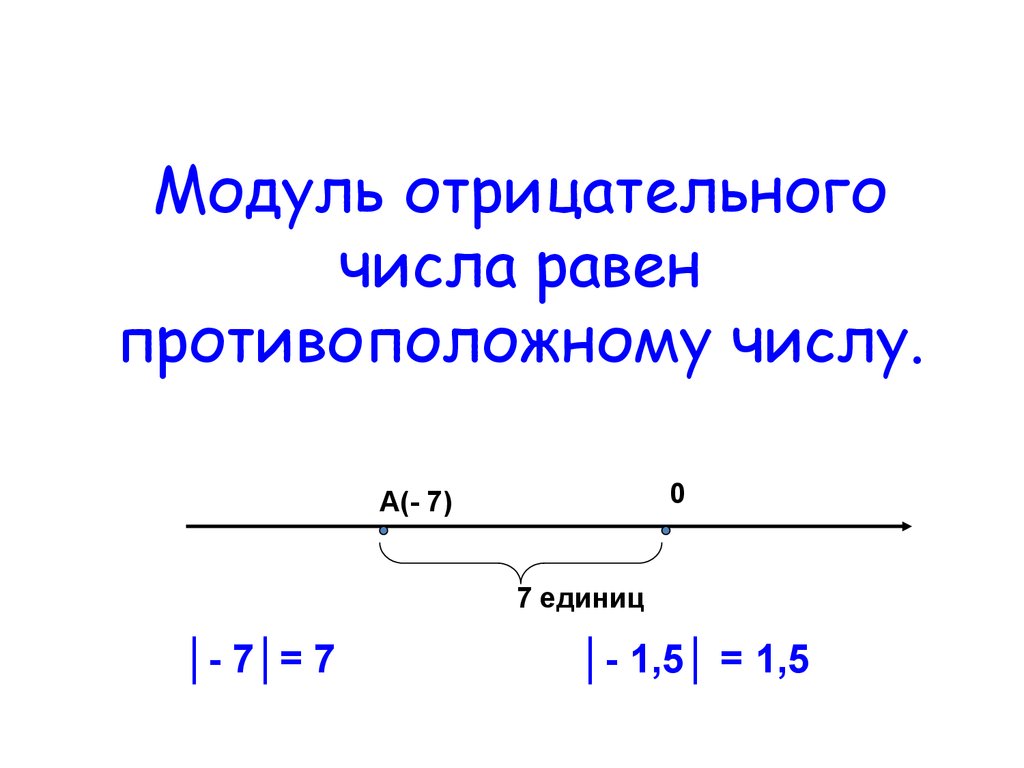 19 в. в работах Р. Дедекинда и Л. Кронекера, посвященных арифметике алгебраических чисел и полей функций. Примерно в то же время исследования конечномерных ассоциативных алгебр, в частности групповых алгебр конечных групп (Б. Пирс, Ф. Фробениус), привели к изучению идеалов некоторых некоммутативных колец. Сначала теория модулей развивалась преимущественно как теория идеалов кольца. Лишь позднее, в работах Э. Нётер и В. Крулля, было замечено, что многие результаты удобнее формулировать и доказывать в терминах произвольных модулей, а не только идеалов. Дальнейшее развитие теории модулей было связано с применением методов и идей теории категорий (ср.
категории), в частности, методы
гомологическая алгебра.
19 в. в работах Р. Дедекинда и Л. Кронекера, посвященных арифметике алгебраических чисел и полей функций. Примерно в то же время исследования конечномерных ассоциативных алгебр, в частности групповых алгебр конечных групп (Б. Пирс, Ф. Фробениус), привели к изучению идеалов некоторых некоммутативных колец. Сначала теория модулей развивалась преимущественно как теория идеалов кольца. Лишь позднее, в работах Э. Нётер и В. Крулля, было замечено, что многие результаты удобнее формулировать и доказывать в терминах произвольных модулей, а не только идеалов. Дальнейшее развитие теории модулей было связано с применением методов и идей теории категорий (ср.
категории), в частности, методы
гомологическая алгебра.
Содержание
- 1 Примеры модулей.
- 2 $G$-модуля.
- 2.1 Примеры $K$-модулей.
- 3 модуля над алгеброй Ли.
- 4 Построения в теории модулей.
- 5 Генераторы и отношения.
- 6 Замена колец.
- 7 Категория модулей.

- 7.1 Каталожные номера
Примеры модулей.
1) Любая абелева группа $M$ является модулем над кольцом целых чисел $\ZZ$. Для $a \in \ZZ$ и $m \in M$ произведение $am$ определяется как результат прибавления $m$ к самому себе $a$ раз.
2) Когда $A$ — поле, понятие унитарного $A$-модуля в точности эквивалентно понятию линейного векторного пространства над $A$.
3) $n$-мерное векторное пространство $V$ над полем $K$ (с координатами) можно рассматривать как модуль над кольцом $M_n(K)$ всех $(n\times n) $-матрицы с коэффициентами в $K$. Для $v \in V$ и $X \in M_n(K)$ произведение $Xv$ определяется как произведение матрицы $X$ на столбец координат вектора $v$.
4) Ассоциативное кольцо (ср. Ассоциативные кольца и алгебры) $A$ — левый $A$-модуль. Умножение элементов кольца на элементы модуля есть обычное умножение в $A$.
5) Множество дифференциальных форм на гладком многообразии $X$ имеет естественную структуру модуля над кольцом всех гладких функций на $X$.
6) С любой абелевой группой $M$ связано ассоциативное кольцо с единицей $\End(M)$ всех эндоморфизмов группы $M$. Группа $M$ имеет естественную структуру $\End(M)$-модуля.
Если на $M$ существует $A$-модульная структура для некоторого кольца $A$, то отображение $m \maps в am$ является эндоморфизмом $M$ для любого $a \in A$. Сопоставляя элементу $a \in A$ порождаемый им эндоморфизм $M$, мы получаем гомоморфизм $\phi$ элемента $A$ в $\End(M)$. Обратно, любой гомоморфизм $\phi: A \to \End(M)$ определяет структуру $A$-модуля на $M$. Таким образом, задание структуры $A$-модуля на абелевой группе $M$ эквивалентно заданию гомоморфизма колец $\phi: A \to \End(M)$. Такой гомоморфизм также называется представлением кольца $A$, а $M$ — модулем представления. С любым представлением $\phi$ связан двусторонний идеал $\Ann(M) = \Ker\phi$, состоящий из таких $a \in A$, что $am = 0$ для всех $m \in M $. Этот идеал называется аннулятором модуля $M$. Когда $\Ann(M) = 0$, представление называется точным, а $M$ называется точным модулем (или точным представлением).
Очевидно, что модуль $M$ можно рассматривать и как модуль над факторкольцом $A/\Ann(M)$. В частности, хотя определение модуля не предполагает ассоциативности $A$, кольцо $A/\Ann(M)$ всегда ассоциативно. Поэтому в большинстве случаев можно ограничиться модулями над ассоциативными кольцами. Везде ниже, если не оговорено противное, $A$ предполагается ассоциативным.
$G$-модули.
Пусть $G$ будет группа. Аддитивная абелева группа $M$ называется левым $G$-модулем, если существует отображение $G\times M \to M$, значение которого в паре $(g, m)$, где $g \in G$ , $m \in M$, записывается как $gm$, и где для любого $g \in G$ отображение $m \maps в gm$ является эндоморфизмом $M$; для любых $g_1, g_2 \in G$, $m \in M$ $(g_1 g_2)m = g_1(g_2 m)$; и для всех $m \in M$ $1m = m$, где 1 — единица $G$. Для любого $g \in G$ отображение $m \maps в gm$ является автоморфизмом группы $M$.
Аналогично могут быть определены правые $G$-модули.
Примеры $K$-модулей.
1) Пусть $k$ будет
Расширение Галуа поля $G$ с
Группа Галуа $K$. g$, т. е. то есть действие $G$ записывается экспоненциально.
g$, т. е. то есть действие $G$ записывается экспоненциально.
Пусть задан $G$-модуль $M$. Сопоставляя элементу $g \in G$ автоморфизм $m \mapsto gm$ кольца $M$, получается гомоморфизм $G$ в группу обратимых элементов кольца $\End(M)$. Обратно, любые гомоморфизмы $G$ в группу обратимых элементов $\End(M)$ задают $M$ структуру $G$-модуля.
Понятия модуля над кольцом и $G$-модуля тесно связаны. А именно, любой $G$-модуль $M$ можно рассматривать как модуль над групповым кольцом (ср. групповой алгебры) $\ZZ G$, если действие $G$ на $M$ продолжается линейно, т. е. если положить
$$\left(\sum a_i g_i\right) m = \sum a_i (g_i m),$$ где $a_i \in \ZZ$, $g_i \in G$, $m \in M$. Наоборот, при наличии унитарной структуры $\ZZ G$-модуля на $M$ $M$ можно рассматривать как $G$-модуль.
Когда $M$ является одновременно $K$-модулем над коммутативным кольцом $K$ и $G$-модулем, где действие элементов $G$ на $M$ коммутирует с действием элементов $K$, то $M$ можно придать структуру $KG$-модуля, линейно продолжив действие с $G$ на $KG$. Например, если $V$ — линейное векторное пространство над полем $K$, то спецификация структуры $KG$-модуля на $V$ эквивалентна заданию представления $G$ в $V$.
Например, если $V$ — линейное векторное пространство над полем $K$, то спецификация структуры $KG$-модуля на $V$ эквивалентна заданию представления $G$ в $V$.
Используя стандартную инволюцию $g\maps в g\inv$ в $G$, любой левый $G$-модуль $M$ можно превратить в правый $G$-модуль, положив $mg = g\inv m$ для $m \in M$, $g \in G$. Аналогично любой правый $G$-модуль можно превратить в левый $G$-модуль.
Модули над алгеброй Ли.
Пусть $\lieg$ будет Алгебра Ли над коммутативным кольцом $K$, и пусть $M$ — $K$-модуль. Спецификация структуры $\lieg$-модуля на $M$ состоит из спецификации $K$-эндоморфизма $m\mapsto gm$ группы $M$ для каждого $g\in\lieg$, где аксиома
$$[g_1, g_2] м = g_1(g_2 м) — g_2(g_1 м)$$
верно для $g_1, g_2 \in \lieg$, $m \in M$. Это определение отличается от определения $A$-модуля, данного ранее. Задание структуры $\lieg$-модуля на $M$ эквивалентно заданию гомоморфизма алгебры Ли $\lieg$ в алгебру Ли кольца $\End(M)$. Модуль над алгеброй Ли $\lieg$ можно также рассматривать как модуль в обычном смысле над алгеброй Ли. универсальная обертывающая алгебра $\lieg$.
универсальная обертывающая алгебра $\lieg$.
Построения в теории модулей.
Начиная с данного $A$-модуля можно получить новые $A$-модули с помощью ряда стандартных конструкций. Таким образом, любому модулю $M$ соответствует решетка его подмодулей. Например, если $A$ рассматривать как левый модуль над собой, то его левые подмодули являются в точности левыми идеалами в $A$. Ряд важных типов модулей определяется в терминах решетки подмодулей. Например, условие обрыва нисходящей (восходящей) цепочки подмодулей определяет артиновы модули (соответственно нётеровы модули, ср. артинов модуль; нётеров модуль). Условие отсутствия нетривиальных подмодулей, т. е. подмодулей, отличных от 0 или $M$, определяет неприводимые или простые модули (ср. неприводимый модуль).
Для модуля $M$ и любого подмодуля $N$ факторгруппе $M/N$ можно придать структуру $A$-модуля. Этот модуль называется фактормодулем $M$ над $N$.
Гомоморфизм $A$-модулей определяется как абелева группа
гомоморфизм $f : M \to N$, коммутирующий с умножением на элементы из $A$, т. е. $f(am) = af(m)$ для всех $m \in M$, $a \in A$. Если заданы два гомоморфизма $f_1, f_2 : M \to N$, то их сумма, определяемая равенством $(f_1 + f_2)(m) = f_1(m) = f_2(m)$, снова является гомоморфизмом $A $-модули. Это добавление придает абелеву групповую структуру множеству $\Hom_A(M, N)$ всех гомоморфизмов $M$ в $N$. Для любого гомоморфизма $f : M \to N$ подмодули $\Ker f$ (ядро $f$) и $\Im f$ (образ $f$), а также фактор-модули $\Coker f = N / \Im f$ (коядро $f$) и $\Coim f = M/\Ker f$ (кообраз $f$). Модули $\Im f$ и $\Coim f$ канонически изоморфны и поэтому обычно отождествляются. Например, для любого левого идеала $J$ в $A$ определен фактор-модуль $A/J$. Модуль $A/J$ неприводим тогда и только тогда, когда $J$ — максимальный левый идеал (ср.
Максимальный идеал). Если $M$ — неприводимый $A$-модуль, не аннулирующий кольцо $A$, то $M$ изоморфен $A/J$ для некоторого максимального левого идеала $J$.
е. $f(am) = af(m)$ для всех $m \in M$, $a \in A$. Если заданы два гомоморфизма $f_1, f_2 : M \to N$, то их сумма, определяемая равенством $(f_1 + f_2)(m) = f_1(m) = f_2(m)$, снова является гомоморфизмом $A $-модули. Это добавление придает абелеву групповую структуру множеству $\Hom_A(M, N)$ всех гомоморфизмов $M$ в $N$. Для любого гомоморфизма $f : M \to N$ подмодули $\Ker f$ (ядро $f$) и $\Im f$ (образ $f$), а также фактор-модули $\Coker f = N / \Im f$ (коядро $f$) и $\Coim f = M/\Ker f$ (кообраз $f$). Модули $\Im f$ и $\Coim f$ канонически изоморфны и поэтому обычно отождествляются. Например, для любого левого идеала $J$ в $A$ определен фактор-модуль $A/J$. Модуль $A/J$ неприводим тогда и только тогда, когда $J$ — максимальный левый идеал (ср.
Максимальный идеал). Если $M$ — неприводимый $A$-модуль, не аннулирующий кольцо $A$, то $M$ изоморфен $A/J$ для некоторого максимального левого идеала $J$.
Для любого семейства $A$-модулей $\{M_i\}$, где $i$ проходит через некоторое множество индексов $J$, прямая сумма и прямое произведение $\{M_i\}$ существуют в категории $A$-модулей. Здесь элемент прямого произведения $\prod_{i \in J} M_i$ можно интерпретировать как вектор $(ldots, m_i, \ldots)$, компоненты которого пронумерованы $J$ и где для каждого $i $, $m_i \in M_i$. Сумма таких векторов и их произведение на элементы кольца определяются покомпонентно. Прямая сумма $\sum_{i \in J} M_i$ семейства $\{M_i\}$ может быть интерпретирована как подмодуль прямого произведения, состоящего из векторов, все компоненты которых, кроме конечного числа, равны до нуля.
Здесь элемент прямого произведения $\prod_{i \in J} M_i$ можно интерпретировать как вектор $(ldots, m_i, \ldots)$, компоненты которого пронумерованы $J$ и где для каждого $i $, $m_i \in M_i$. Сумма таких векторов и их произведение на элементы кольца определяются покомпонентно. Прямая сумма $\sum_{i \in J} M_i$ семейства $\{M_i\}$ может быть интерпретирована как подмодуль прямого произведения, состоящего из векторов, все компоненты которых, кроме конечного числа, равны до нуля.
Для проективной (индуктивной) системы $A$-модулей проективный (индуктивный) предел этой системы естественным образом снабжается структурой $A$-модуля. Прямое произведение и прямая сумма могут рассматриваться как частные случаи понятий проективного и индуктивного предела.
Генераторы и отношения.
Пусть $X$ — подмножество $A$-модуля $M$. Подмодуль, порожденный $X$, является пересечением подмодулей $M$, содержащих $X$. Если этот подмодуль совпадает с $M$, то $X$ называется семейством (системой) образующих модуля $M$. Модуль, допускающий конечное семейство образующих, называется конечно порожденным модулем. Например, в нётеровом кольце любой идеал является конечнопорожденным модулем. Прямая сумма конечного числа конечно порожденных модулей снова конечно порождена. Любой фактормодуль конечно порожденного модуля также конечно порожден. Для построения системы образующих модуля $M$
Часто оказывается полезной лемма Накаямы: для любого идеала $\frakA$, содержащегося в радикале кольца $A$, условие $\frakA M = M$ влечет $M = 0$. В частности, в условиях леммы Накаямы элементы $m_1, \ldots, m_r$ образуют систему образующих для $M$, если их образы порождают модуль $M/\frakA M$. Это особенно часто используется, когда $A$ является
локальное кольцо, а $\frakA$ — максимальный идеал в $A$.
Модуль, допускающий конечное семейство образующих, называется конечно порожденным модулем. Например, в нётеровом кольце любой идеал является конечнопорожденным модулем. Прямая сумма конечного числа конечно порожденных модулей снова конечно порождена. Любой фактормодуль конечно порожденного модуля также конечно порожден. Для построения системы образующих модуля $M$
Часто оказывается полезной лемма Накаямы: для любого идеала $\frakA$, содержащегося в радикале кольца $A$, условие $\frakA M = M$ влечет $M = 0$. В частности, в условиях леммы Накаямы элементы $m_1, \ldots, m_r$ образуют систему образующих для $M$, если их образы порождают модуль $M/\frakA M$. Это особенно часто используется, когда $A$ является
локальное кольцо, а $\frakA$ — максимальный идеал в $A$.
Пусть $M$ — модуль с системой образующих $\{x_i\}_{i \in J}$. Тогда отображение $\phi : y_i \to x_i$ определяет эпиморфизм свободного $A$-модуля $F$ с образующими $\{y_i\}_{i \in I}$ на $M$ ($F$ можно определить как множество формальных конечных сумм $\sum a_i y_i$, $a_i \in A$ и $\phi$ продолжается с образующих до $F$ по линейности). Элементы $R = \Ker\phi$ называются отношениями между образующими $\{x_i\}$ $M$. Если $M$ можно представить как фактор-модуль конечно-порожденного свободного модуля $F$ так, что модуль отношений $R$ также конечно-порожден, то $M$ называется конечно-представленным модулем. Например, над нётеровым кольцом $A$ любой конечно порожденный модуль конечно определен. В общем, быть конечно порожденным не означает быть конечно представленным.
Элементы $R = \Ker\phi$ называются отношениями между образующими $\{x_i\}$ $M$. Если $M$ можно представить как фактор-модуль конечно-порожденного свободного модуля $F$ так, что модуль отношений $R$ также конечно-порожден, то $M$ называется конечно-представленным модулем. Например, над нётеровым кольцом $A$ любой конечно порожденный модуль конечно определен. В общем, быть конечно порожденным не означает быть конечно представленным.
Смена колец.
Существуют стандартные конструкции, позволяющие рассматривать $A$-модуль $M$ как модуль над некоторым другим кольцом. Например, пусть $\phi : B \to A$ — гомоморфизм колец. Тогда, полагая $bm = \phi(b) m$, $M$ можно рассматривать как $B$-модуль. Полученный $B$-модуль называется полученным заменой базы или, в частности, в случае, когда $B$ является подкольцом в $A$, ограничением скаляров. Если $M$ — унитарный $A$-модуль и $\phi$ переводит тождество в тождество, то $M$ становится унитарным $B$-модулем.
Пусть задан гомоморфизм колец $\phi: A \to B$ и $A$-модуль $M$. Тогда $B$ можно задать структуру $(B, A)$-модуля (ср.
бимодуль), полагая $ba = b\phi(a)$ для $b\in B$, $a \in A$, и можно рассматривать левый $B$-модуль $B\tensor_A M$. Говорят, что этот модуль получается из $M$ расширением скаляров.
Тогда $B$ можно задать структуру $(B, A)$-модуля (ср.
бимодуль), полагая $ba = b\phi(a)$ для $b\in B$, $a \in A$, и можно рассматривать левый $B$-модуль $B\tensor_A M$. Говорят, что этот модуль получается из $M$ расширением скаляров.
Категория модулей.
Класс всех модулей над данным кольцом $A$ с гомоморфизмами модулей как морфизмов образует Абелева категория, обозначаемая, например, $A$-mod или $\Mod_A$. Наиболее важными функторами, определенными в этой категории, являются $\Hom$ (гомоморфизм) и $\tensor$ (тензорное произведение). Функтор $\Hom$ принимает значения в категории абелевых групп и ставит в соответствие паре $A$-модулей $M, N$ группу $\Hom_A(M, N)$. Для $f : M_1 \to M$ и $\phi : N \to N_1$ отображения
$$f’ : \Hom_A(M, N) \to \Hom_A(M_1, N)$$ а также
$$\phi’ : \Hom_A(M, N) \to \Hom_A(M, N_1)$$
определяются очевидным образом; т. е. функтор $\Hom$ контравариантен по первому аргументу и ковариантен по второму. Когда $M$ или $N$ несут бимодульную структуру, группа $\Hom_A(M,N)$ имеет дополнительную модульную структуру. Если $N$ — $(A, B)$-модуль, $\Hom_A(M,N)$ — правый $B$-модуль, а если $M$ — $(A,B)$-модуль, тогда $\Hom_A(M, N)$ — левый $B$-модуль.
Если $N$ — $(A, B)$-модуль, $\Hom_A(M,N)$ — правый $B$-модуль, а если $M$ — $(A,B)$-модуль, тогда $\Hom_A(M, N)$ — левый $B$-модуль.
Функтор $\tensor_A$ переводит пару $M, N$, где $M$ — правый $A$-модуль, а $N$ — левый $A$-модуль, в тензорное произведение $M\tensor_A N$ из $M$ и $N$ над $A$. Этот функтор принимает значения в категории абелевых групп и ковариантен как по отношению к $M$, так и к $N$. Когда $M$ или $N$ — бимодуль, группа $M \tensor_A N$ может быть снабжена дополнительной структурой. А именно, если $M$ — $(B, A)$-модуль, $M\tensor_A N$ — $B$-модуль и если $N$ — $(A, B)$-модуль, то $M\tensor_A N$ — правый $B$-модуль. Изучение функторов $\Hom$ и $\tensor$, а также их производных функторов является одной из основных задач гомологической алгебры.
Многие важные типы модулей можно охарактеризовать в терминах $\Hom$ и $\tensor$. Таким образом,
проективный модуль $M$ определяется требованием точности функтора $\Hom_A(M, X)$ (как функтора в $X$) (ср.
Точный функтор). Точно так же
инъективный модуль $N$ определяется требованием точности $\Hom_A(X, N)$ (в $X$). А
плоский модуль $M$ определяется требованием точности функтора $M \tensor_A X$.
Точно так же
инъективный модуль $N$ определяется требованием точности $\Hom_A(X, N)$ (в $X$). А
плоский модуль $M$ определяется требованием точности функтора $M \tensor_A X$.
Модуль над данным кольцом $A$ можно рассматривать с двух точек зрения.
A) Модули можно изучать с точки зрения их внутренней структуры. Основной проблемой здесь является полная классификация модулей, т. е. построение для каждого модуля системы инвариантов, характеризующей модуль с точностью до изоморфизма, и возможность по набору инвариантов построить модуль с этими инвариантами. . Для некоторых типов колец такое описание возможно. Например, если $M$ — конечно порожденный модуль над групповым кольцом $KG$ конечной группы $G$, где $K$ — поле взаимно простой характеристики порядка $G$, то $M$ представим в виде конечной прямой суммы неприводимых подмодулей ($M$ вполне приводим, ср.
Вполне приводимый модуль). Это представление единственно с точностью до изоморфизма (выбор неприводимых модулей, вообще говоря, неоднозначен).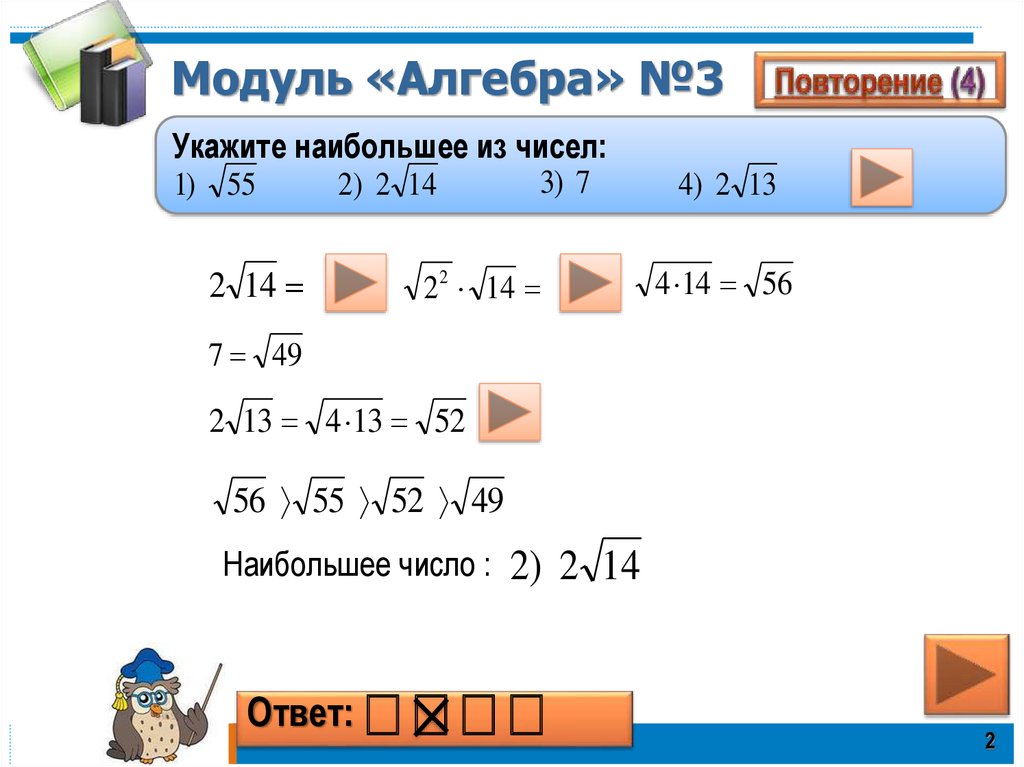 Все неприводимые подмодули также допускают простое описание: все они содержатся в
регулярное представление $G$ и находятся во взаимно однозначном соответствии с неприводимыми характерами группы. Модули над кольцами главных идеалов и кольцами Дедекинда также имеют простое описание. А именно, любой конечно порожденный модуль $M$ над
Кольцо главных идеалов $A$ изоморфно конечной прямой сумме модулей вида $A/\frakA_i$, где $\frakA_i$ — идеалы кольца $A$ (возможно, нулевые), а $\frakA_1 \subseteq \cdots \subseteq \frakA_m \ne A$. Идеалы $\frakA_i$ однозначно определяются этим последним условием. Таким образом, множество инвариантов $\{\frakA_i\}$ полностью определяет $M$. Если $M$ — конечно порожденный модуль над
Кольцо Дедекинда $A$, тогда $M = M_1 \oplus M_2$, где $M_2$ — модуль кручения (периодический модуль), а $M_1$ —
модуль без кручения (выбор $M_1$ неоднозначен). Модуль $M_2$ аннулируется некоторым идеалом $\frakA$ кольца $A$ и, следовательно, является модулем над кольцом главных идеалов $A/\frakA$ и допускает приведенное выше описание; $M_1$ представим в виде $(\bigoplus^n A)\oplus \frakB$, где $\frakB$ — идеал $A$, а $\bigoplus^n$ — $n$-кратная прямая сумма .
Все неприводимые подмодули также допускают простое описание: все они содержатся в
регулярное представление $G$ и находятся во взаимно однозначном соответствии с неприводимыми характерами группы. Модули над кольцами главных идеалов и кольцами Дедекинда также имеют простое описание. А именно, любой конечно порожденный модуль $M$ над
Кольцо главных идеалов $A$ изоморфно конечной прямой сумме модулей вида $A/\frakA_i$, где $\frakA_i$ — идеалы кольца $A$ (возможно, нулевые), а $\frakA_1 \subseteq \cdots \subseteq \frakA_m \ne A$. Идеалы $\frakA_i$ однозначно определяются этим последним условием. Таким образом, множество инвариантов $\{\frakA_i\}$ полностью определяет $M$. Если $M$ — конечно порожденный модуль над
Кольцо Дедекинда $A$, тогда $M = M_1 \oplus M_2$, где $M_2$ — модуль кручения (периодический модуль), а $M_1$ —
модуль без кручения (выбор $M_1$ неоднозначен). Модуль $M_2$ аннулируется некоторым идеалом $\frakA$ кольца $A$ и, следовательно, является модулем над кольцом главных идеалов $A/\frakA$ и допускает приведенное выше описание; $M_1$ представим в виде $(\bigoplus^n A)\oplus \frakB$, где $\frakB$ — идеал $A$, а $\bigoplus^n$ — $n$-кратная прямая сумма .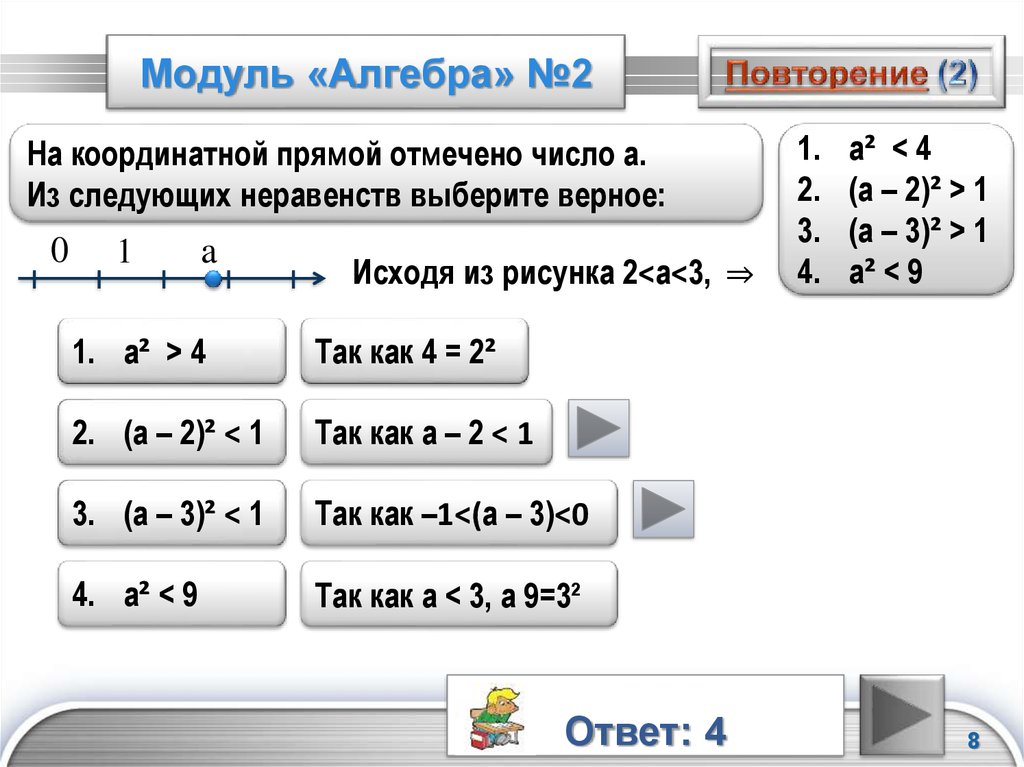 Модуль $M_1$ с точностью до изоморфизма определяется двумя инвариантами: числом $n$ и классом $\frakB$ в группе идеальных классов.
Модуль $M_1$ с точностью до изоморфизма определяется двумя инвариантами: числом $n$ и классом $\frakB$ в группе идеальных классов.
Б) Другой подход к изучению модулей состоит в изучении категории $A$-mod и в рассмотрении данного модуля $M$ как объекта этой категории. Такое исследование является целью гомологическая алгебра и алгебраическая $K$-теория. На этом пути было получено много важных и глубоких результатов.
Часто рассматриваются модули, несущие некоторую дополнительную структуру. Таким образом, рассматриваются градуированные модули, фильтрованные модули, топологические модули, модули с полуторалинейная форма и т. д. (ср. Градуированный модуль; Топологический модуль; фильтруемый модуль).
Каталожные номера
| [1] | Н. Бурбаки, «Элементы математики. Алгебра: алгебраические структуры. Линейная алгебра», 1 , Addison-Wesley (1974), стр. Глава 1; 2 (перевод с французского) MR0354207 |
| [2] | Н. Бурбаки, «Элементы математики. Коммутативная алгебра», Addison-Wesley (1972) (перевод с французского) MR0360549 Zbl 0279.13001 Бурбаки, «Элементы математики. Коммутативная алгебра», Addison-Wesley (1972) (перевод с французского) MR0360549 Zbl 0279.13001 |
| [3] | Н. Бурбаки, «Элементы математики. Группы Ли и алгебры Ли», Addison-Wesley (1975) (Перевод с французского) MR0682756 Zbl 0319.17002 |
| [4] | С. Ланг, «Алгебра», Addison-Wesley (1984) MR0783636 Zbl 0712.00001 |
| [5] | Б.Л. van der Waerden, «Algebra» , 1–2 , Springer (1967–1971) (Translated from German) MR1541390 Zbl 1032.00002 Zbl 1032.00001 Zbl 0903.01009 Zbl 0781.12003 Zbl 0781.12002 Zbl 0724.12002 Zbl 0724.12001 Zbl 0569.01001 Zbl 0534.01001 Zbl 0997.00502 Zbl 0997.00501 Zbl 0316.22001 Збл 0297.01014 Збл 0221.12001 Збл 0192.33002 Збл 0137.25403 Збл 0136.24505 Збл 0087.25903 Збл 0192.33001 Збл 0067.00502 |
| [6] | А.И. Кострикин, «Введение в алгебру», Springer (1982) (перевод с русского) MR0661256 Zbl 0482.00001 Кострикин, «Введение в алгебру», Springer (1982) (перевод с русского) MR0661256 Zbl 0482.00001 |
| [7] | Н. Якобсон, «Структура колец», амер. Мат. соц. (1956) MR0081264 Збл 0073.02002 |
| [8] | И.Н. Герштейн, «Некоммутативные кольца», Матем. доц. амер. (1968) MR1535024 MR0227205 Збл 0177.05801 |
| [9] | К. Фейт, «Алгебра: кольца, модули и категории», 1–2 , Springer (1981–1976) MR0551052 MR0491784 MR0366960 Zbl 0508.16001 Zbl 0266.16001 |
| [10] | Х. Картан, С. Эйленберг, «Гомологическая алгебра», Princeton Univ. Пресс (1956) MR0077480 Zbl 0075.24305 |
| [11] | С. Маклейн, «Гомология», Springer (1963) Zbl 0818.18001 Zbl 0328.18009 |
| [12] | Х. Басс, «Алгебраическая $K$-теория», Бенджамин (1968) MR249491 |
| [13] | Дж. В. Милнор, «Введение в алгебраическую $K$-теорию», пер. Пресс (1971) MR349811 В. Милнор, «Введение в алгебраическую $K$-теорию», пер. Пресс (1971) MR349811 |
Как процитировать эту запись:
Модуль. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Module&oldid=43388
Эта статья адаптирована из оригинальной статьи Л.В. Кузьмин (создатель), появившийся в Математической энциклопедии — ISBN 140200609.2): Математика обучения и обучения для средних школ
Перейти к основному содержанию
Нажмите здесь для получения информации и обновлений о реакции университета на COVID-19.
В рамках проекта MODULE(S 2 ) создаются учебные материалы, которые предоставляются преподавателям математики бакалавриата.
способ предоставить будущим учителям возможность развивать математическую
знания для обучения (MKT), в то время как они изучают содержание университетской алгебры, геометрии,
курсы моделирования и статистики. | |||||
Как вы можете принять участие Мы ищем преподавателей для тестирования материалов MODULE(S 2 ) в университетских курсах математики, которые будущие учителя старших классов
брать. Мы ищем пилотов на 2021-2022 учебный год. Факультет пилотирования будет
получать компенсацию стипендией за: участие в летнем институте; участие
в учебном сообществе в течение учебного года; обучение с материалами для
полный семестр; и участвовать в мероприятиях в течение всего срока, в течение которого
курс преподается, включая сбор домашних заданий, видеозапись занятий,
и проведение мероприятий в начале и в конце срока. | |||||
Совместная работаМы поощряем сотрудничество между заинтересованными сторонами, включая пилотный факультет, учебную программу дизайнеры, профессиональные разработчики, исследователи, руководство и члены правления. Мы собираем отзывы, анализируем преподавание и обучение с помощью материалов и координируем профессиональные мероприятия по развитию для преподавателей с использованием MODULE(S 2 ) материалы. | |||||
Кто мы
|
| ||||
МОДУЛЬ(S2 ) Особенности Подготовка студентов к вкладу в области науки, статистики, техники
математика и технологии имеют решающее значение для того, чтобы наша страна оставалась мировым лидером. В последние десятилетия накопились данные о том, что для внедрения качественного обучения математике
преподаватели должны обладать пониманием содержания, которое конкретно применяется в
работа по обучению (математические знания для обучения — МКТ). Разработать МКТ, перспективный
учителям нужны возможности использовать математические знания, чтобы распознавать, реагировать,
и понимать математические вопросы, которые возникают в контексте обучения. | |||||
Образцы материаловЗдесь вы можете найти образцы материалов Geometry MODULE (S 2 ). Здесь вы можете найти образцы материалов для МОДУЛЯ по алгебре (S 2 ). Здесь вы можете найти образцы материалов МОДУЛЯ СТАТИСТИЧЕСКОГО МОДУЛЯ (S 2 ). Здесь вы можете найти образцы материалов для моделирования MODULE(S 2 ). | |||||
Вопросы?Если у вас есть вопросы о МОДУЛЕ (S 2 ), свяжитесь с Джереми Стрейером. | |||||
| |||||
Любые мнения, выводы и выводы или рекомендации, изложенные в этом материале
принадлежат автору (авторам) и не обязательно отражают точку зрения Национального
Научный фонд. | |||||
Государственный университет Среднего Теннесси © 2020 Условия политики недискриминации
алгебра.модуль.базовый — mathlib docs
алгебра.модуль.базовый — mathlib docsВ этом файле мы определяем
-
модуль RM: аддитивный коммутативный моноидMявляетсямодулемнадполукольцо Rесли дляr : Rиx : Mопределено их «скалярное умножениеr • x : M, и операция•удовлетворяет некоторым естественным аксиомам ассоциативности и дистрибутивности, аналогичным на кольце.
Замечания по реализации #
В типичном математическом использовании наше определение модуля соответствует «полумодулю», а
слово «модуль» зарезервировано для модуля RM , где R — кольцо , а M — add_comm_group . Если
Если R является полем и M add_comm_group , M будет называться R -векторным пространством.
Поскольку эти предположения можно сделать, изменив классы типов, применяемые к R и M ,
без изменения аксиом в модуле , mathlib называет все модулем .
В старых версиях mathlib у нас были отдельные сокращения semimodule и vector_space .
В некоторых случаях это вызывало проблемы с выводом, но не давало никаких реальных преимуществ, поэтому мы решили
использовать канонический модуль typeclass повсюду.
Теги #
полумодуль, модуль, векторное пространство
источник
источник
source
@[protected, instance]
Модуль над полукольцом автоматически наследует структуру mul_action_with_zero .
- module.to_mul_action_with_zero = {to_mul_action := {to_has_smul := mul_action.to_has_smul infer_instance, one_smul := _, mul_smul := _}, smul_zero := _, zero_smul := _}
источник
@[защищено, экземпляр]
Уравнения- add_comm_monoid.nat_module = {to_distrib_mul_action := {to_mul_action := {to_has_smul := add_monoid.has_smul_nat (add_comm_monoid.to_add_smuloid: _= mul_add_monoid M), one , smul_zero := _, smul_add := _}, add_smul := _, zero_smul := _}
источник
источник
источник
источник
источник
источник
@[simp]
источник
@[защищенный, приводимый]
Обратный перенос структуры модуля вдоль инъективного аддитивного моноидного гомоморфизма. См. примечание [сокращаемые неэкземпляры].
См. примечание [сокращаемые неэкземпляры].
- function.injective.module R f hf smul = {to_distrib_mul_action := {to_mul_action := {to_has_smul := {smul := has_smul.smul _inst_5}, one_smul := _, mul_smul := _}, smul_zero := _, smul_add := _}, add_smul := _, zero_smul := _}
source
@[protected]
Продвинуть структуру модуля вдоль сюръективного аддитивного моноидного гомоморфизма.
- function.surjective.module R f hf smul = {to_distrib_mul_action := {to_mul_action := {to_has_smul := {smul := has_smul.smul _inst_5}, one_smul := _, mul_smul := _}, smul_zero := _, smul_add := _}, add_smul := _, zero_smul := _}
source
@[reducible]
Продвинуть действие R на M по совместимой сюръективной карте f : R →+* S .
См. также function.surjective.mul_action_left и function. . surjective.distrib_mul_action_left
surjective.distrib_mul_action_left
- function.surjective.module_left f hf hsmul = {to_distrib_mul_action := {to_mul_action := {to_has_smul := {smul := has_smul.smul _inst_8}, one_smul := _, mul_smul := _}, smul_zero := _ , smul_add := _}, add_smul := _, zero_smul := _}
source
@[reducible]
Составьте модуль с ring_hom , с действием fs • m .
См. примечание [сокращаемые неэкземпляры].
Уравнения- module.comp_hom M f = {to_distrib_mul_action := {to_mul_action := {to_has_smul := {smul := has_smul.comp.smul ⇑f}, one_smul := _, mul_smul := _}, smul_zero := _ , smul_add := _}, add_smul := _, zero_smul := _}
источник
@[simp]
источник
@[simp]
источник
источник
источник
источник
источник
@[сокращаемый]
add_comm_monoid , который является модулем по кольцу , содержит естественный add_comm_group структура. См. примечание [сокращаемые неэкземпляры].
См. примечание [сокращаемые неэкземпляры].
- module.add_comm_monoid_to_add_comm_group R = {add := add_comm_monoid.add infer_instance, add_assoc := _, zero := add_comm_monoid.zero infer_instance, zero_add := _, add_zero := _, nsomul_insmul_insmul := add_nsomulfermon := add_nsomulfermon ‘ := _, nsmul_succ’ := _, neg := λ (a : M), (-1) • a, sub := add_group.sub._default add_comm_monoid.add module.add_comm_monoid_to_add_comm_group._proof_6 add_comm_monoid.zero module.add_comm_monoid_to_add_comm_group ._proof_7 module.add_comm_monoid_to_add_comm_group._proof_8 add_comm_monoid.nsmul module.add_comm_monoid_to_add_comm_group._proof_9module.add_comm_monoid_to_add_comm_group._proof_10 (λ (a : M), (-1) • a), sub_eq_add_neg := _, zsmul := add_group.zsmul._default add_comm_monoid.add module.add_comm_monoid_to_add_comm_group._proof_12 add_comm_monoid_to_add_monoid_1 add_comm_monoid_1 tommm.zero module.add_comm module.add_comm_monoid_to_add_comm_group._proof_14 add_comm_monoid.
 nsmul module.add_comm_monoid_to_add_comm_group._proof_15 module.add_comm_monoid_to_add_comm_group._proof_16 (λ (a : M), (-1) • a), zsmul_zero’ := _, ‘smul_succ’ := _, ‘smul_succ’ : _, add_left_neg := _, add_comm := _}
nsmul module.add_comm_monoid_to_add_comm_group._proof_15 module.add_comm_monoid_to_add_comm_group._proof_16 (λ (a : M), (-1) • a), zsmul_zero’ := _, ‘smul_succ’ := _, ‘smul_succ’ : _, add_left_neg := _, add_comm := _}
источник
@[защищено, экземпляр]
Уравнения- add_comm_group.int_module M = {to_distrib_mul_action := {to_mul_action := {to_has_smul := sub_neg_monoid.has_smul_int (add_group.to_smul_sub_neg_monoid:= mul_neg_monoid M), one }, smul_zero := _, smul_add := _}, add_smul := _, zero_smul := _}
источник
источник
@[nolint]
- to_has_smul : has_smul RM
- smul_add : ∀ (r : R) (x y : M), r • (x + y) = r • x + r • y
- add_smul : ∀ (rs : R) (x : M), (r + s) • x = r • x + s • x
- mul_smul : ∀ (rs : R) (x : M), (r * s) • x = r • s • x
- one_smul : ∀ (x : M), 1 • x = x
Структура, содержащая большую часть информации, как в модуле, за исключением полей zero_smul и smul_zero . Поскольку эти поля можно вывести из других, когда
Поскольку эти поля можно вывести из других, когда M является add_comm_group ,
это дает возможность построить структуру модуля, проверяя меньше свойств, в module.of_core .
module.core - module.core.has_sizeof_inst
источник
Определить модуль без доказательства zero_smul и smul_zero с помощью вспомогательного
структура module.core , когда базовым пространством является add_comm_group .
- module.of_core H = let _inst : has_smul R M := H.to_has_smul in {to_distrib_mul_action := {to_mul_action := {to_has_smul := H.to_has_smul, one_smul := _, mul_smul := _}, smul_zero := _, smul_add := _}, add_smul := _, zero_smul := _}
источник
source
Вариант module., удобный для терминального режима. ext
ext
источник
@[simp]
источник
@[simp]
источник
@[simp]
источник
источник
source
@[protected]
Полукольцо является нетривиальным при условии, что над этим полукольцом существует нетривиальный модуль.
источник
@[защищено, экземпляр]
Equations- semiring.to_module = {to_distrib_mul_action := {to_mul_action := monoid.to_mul_action R (monoid_with_zero.to_monoid R), smul_zero := _, smul_add := _}, add = _, zero_smul := _}
source
@[protected, instance]
Аналогично semiring.to_module , но умножается справа.
- semiring.to_opposite_module = {to_distrib_mul_action := {to_mul_action := mul_action_with_zero.to_mul_action (monoid_with_zero.to_opposite_mul_action_with_zero R), smul_zero := _, smul_add := 2mul_zero}, add_smul :=} :90,smul :=} :90,smul :=}
source
Кольцевой гомоморфизм f : R →+* M определяет модульную структуру как r • x = f r * x .
- f.to_module = module.comp_hom S f
source
@[protected, instance]
Тавтологическое действие R →+* R на R .
Обобщает function.End.apply_mul_action .
- ring_hom.apply_distrib_mul_action = {to_mul_action := {to_has_smul := {smul := λ (_x : R →+* R) (_y : R), ⇑_x _y}, one_smul := _, mul_smul := _ }, smul_zero := _, smul_add := _}
источник
@[защищенный, упрощенный]
source
nsmul аналогичен любой другой модульной структуре посредством приведения.
source
Конвертировать любой экзотический ℕ -smul обратно в канонический экземпляр. Это не должно быть необходимо, так как в
mathlib все add_comm_monoid обычно должны иметь ровно одну ℕ — модульная структура по дизайну.
источник
@[защищено, экземпляр]
source
zsmul аналогичен любой другой модульной структуре посредством приведения.
source
Преобразование обратно любого экзотического ℤ -smul в канонический экземпляр. Это не должно быть необходимо, так как в
mathlib все add_comm_group обычно должны иметь только один ℤ — модульная конструкция по конструкции.
источник
источник
источник
источник
источник
источник
источник
Если E является векторным пространством над двумя делителями R и S , затем скалярные умножения
согласовать инверсии целых чисел в R и S .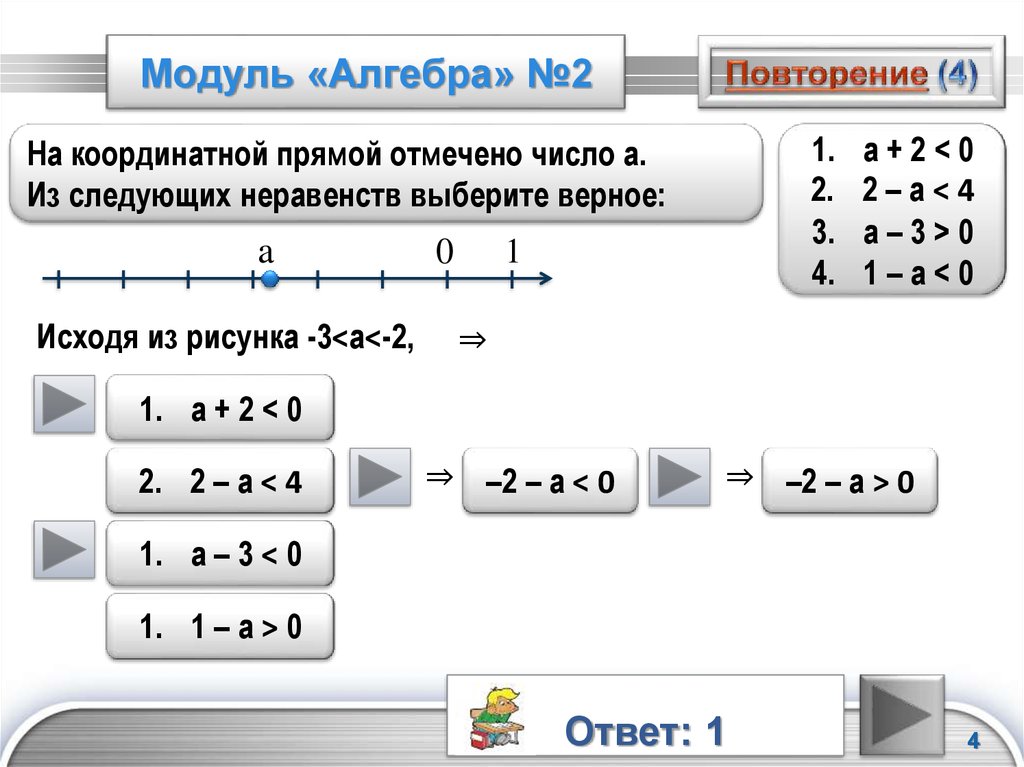
источник
Если E является векторным пространством над двумя телами R и S , то скалярные умножения
договориться об инверсиях натуральных чисел в R и S .
источник
Если E векторное пространство над делительными кольцами R и обладает моноидным действием по α , то
действие коммутирует скалярным умножением обратных целых чисел в R
источник
Если E является векторным пространством над телом R и имеет моноидное действие посредством α , то это
действие коммутирует скалярным умножением обратных натуральных чисел в R .
источник
Если E — векторное пространство над двумя телами R и S , затем скалярные умножения
согласовать рациональные числа в R и S .
источник
@[защищено, экземпляр]
источник
@[защищено, экземпляр]
источник
@[защищено, экземпляр]
источник
@[защищено, экземпляр]
no_zero_smul_divisors # Этот раздел определяет класс no_zero_smul_divisors и включает некоторые тесты
для исчезновения элементов (особенно в модулях над разделительными кольцами).
источник
@[защищено, экземпляр]
источник
источник
@[simp]
источник
источник
источник
@[simp]
источник
Если M является R -модулем с единицей и M имеет нулевую характеристику, то R имеет характеристику
также ноль.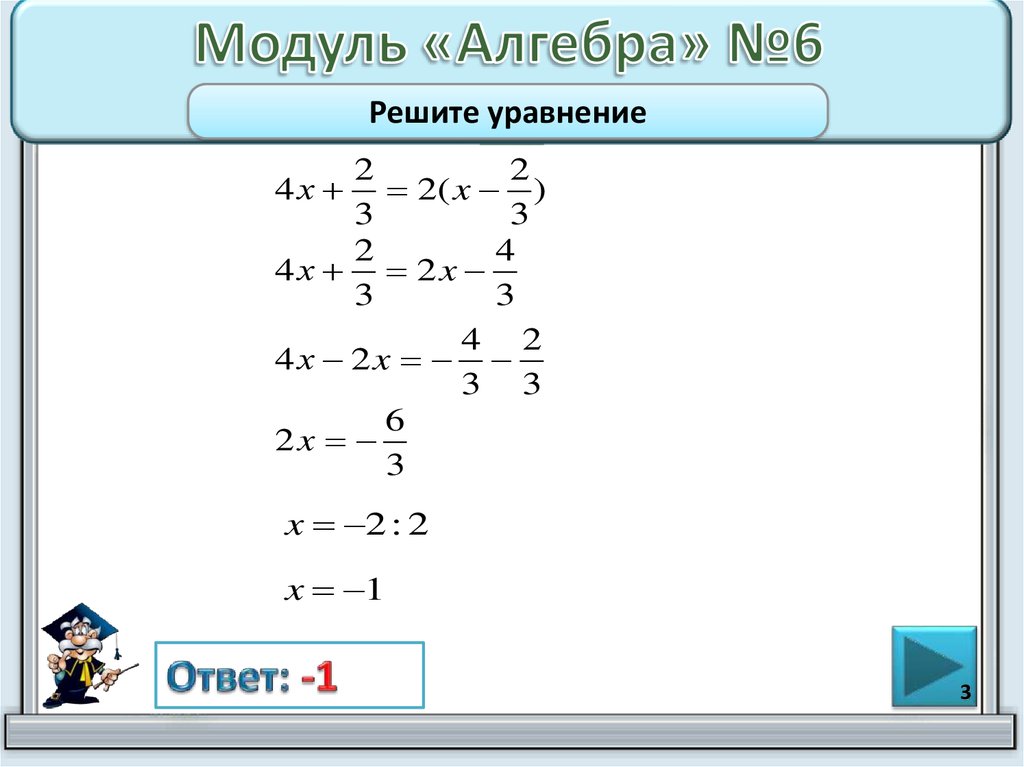



 Материалы предназначены для преподавания с использованием методов обучения, основанных на справедливости, в том числе
углубление в математику и подтверждение личности изучающих математику.
Материалы предназначены для преподавания с использованием методов обучения, основанных на справедливости, в том числе
углубление в математику и подтверждение личности изучающих математику. Пожалуйста, укажите ваш
интерес, заполнив форму здесь.
Пожалуйста, укажите ваш
интерес, заполнив форму здесь. Для этого учителям математики средних и старших классов важно
быть хорошо подготовленным к обучению математике. Математика действия, понимания,
Обучение и образование для средних школ (МОДУЛЬ(S 2 )) проект создает учебные материалы, которые предоставляют возможности для будущих учителей
развивать математические знания, поскольку они относятся конкретно к работе преподавателя
геометрия, статистика, алгебра и моделирование. Эти модули могут быть использованы в университете
курсы математики на факультетах в университетах и колледжах всех типов по всему миру.
Соединенные Штаты. Проект способствует эффективному обучению, предлагая профессиональные
развивающие мероприятия для преподавателей с использованием модулей летом и в школе
год.
Для этого учителям математики средних и старших классов важно
быть хорошо подготовленным к обучению математике. Математика действия, понимания,
Обучение и образование для средних школ (МОДУЛЬ(S 2 )) проект создает учебные материалы, которые предоставляют возможности для будущих учителей
развивать математические знания, поскольку они относятся конкретно к работе преподавателя
геометрия, статистика, алгебра и моделирование. Эти модули могут быть использованы в университете
курсы математики на факультетах в университетах и колледжах всех типов по всему миру.
Соединенные Штаты. Проект способствует эффективному обучению, предлагая профессиональные
развивающие мероприятия для преподавателей с использованием модулей летом и в школе
год. Кроме того, проект исследует влияние обучения с модулями
о знаниях будущих учителей, тем самым информируя общенациональные усилия учителей
образование. Этот пятилетний проект основан на усилиях Центра подготовки учителей математики.
Партнерство (MTE-P) для создания золотого стандарта подготовки к средней математике
учителей более 90 университетов-участников.
Кроме того, проект исследует влияние обучения с модулями
о знаниях будущих учителей, тем самым информируя общенациональные усилия учителей
образование. Этот пятилетний проект основан на усилиях Центра подготовки учителей математики.
Партнерство (MTE-P) для создания золотого стандарта подготовки к средней математике
учителей более 90 университетов-участников. Результаты
из циклов «планируй-делай-изучай-действуй», в которых использовались первоначальные модули, разработанные проектом, указывают
увеличение MKT будущих учителей средних школ. МОДУЛЬ(S 2 ) сейчас расширяет эти материалы и изучает условия обучения, которые
влияние на MKT будущих учителей, развитие MKT, а также ожидания и ценность в
использование MKT в качестве ресурса для обучения. В проекте используются смешанные методы для предоставления эмпирически обоснованных данных.
отчеты о том, как факторы качества обучения и учебных ресурсов влияют
МКТ будущих учителей. Кроме того, результаты используются несколько раз в год для
улучшить МОДУЛЬ(S 2 ) материалы через циклы улучшения, проводимые в рамках сетевого улучшения
Дизайн сообщества.
Результаты
из циклов «планируй-делай-изучай-действуй», в которых использовались первоначальные модули, разработанные проектом, указывают
увеличение MKT будущих учителей средних школ. МОДУЛЬ(S 2 ) сейчас расширяет эти материалы и изучает условия обучения, которые
влияние на MKT будущих учителей, развитие MKT, а также ожидания и ценность в
использование MKT в качестве ресурса для обучения. В проекте используются смешанные методы для предоставления эмпирически обоснованных данных.
отчеты о том, как факторы качества обучения и учебных ресурсов влияют
МКТ будущих учителей. Кроме того, результаты используются несколько раз в год для
улучшить МОДУЛЬ(S 2 ) материалы через циклы улучшения, проводимые в рамках сетевого улучшения
Дизайн сообщества.

 nsmul module.add_comm_monoid_to_add_comm_group._proof_15 module.add_comm_monoid_to_add_comm_group._proof_16 (λ (a : M), (-1) • a), zsmul_zero’ := _, ‘smul_succ’ := _, ‘smul_succ’ : _, add_left_neg := _, add_comm := _}
nsmul module.add_comm_monoid_to_add_comm_group._proof_15 module.add_comm_monoid_to_add_comm_group._proof_16 (λ (a : M), (-1) • a), zsmul_zero’ := _, ‘smul_succ’ := _, ‘smul_succ’ : _, add_left_neg := _, add_comm := _}