Область существования функции
1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = 3 • x2-6 • x+9
Находим нули функции. Для этого приравниваем производную к нулю
3 • x2-6 • x+9 = 0
Для данного уравнения корней нет.
16.Дана функция . Тогда
(Укажите интервал выпуклости вверх (вниз) функции).
Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
f»(x) = 6 • x-6
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
6 • x-6 = 0
Откуда точки перегиба:
x1 = 1
| (-∞ ;1) | (1; +∞) |
| f»(x) < 0 | f»(x) > 0 |
| функция выпукла | функция вогнута |
17.Найти наибольшее значение функции в интервале [4,5].
y = x^2-11*x+28
[4;5]
Необходимое условие экстремума функции одной переменной.
Уравнение f’0(x*) = 0 — это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f’0(x*) = 0
f»0(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f’0(x*) = 0
f»0(x*) < 0
то точка x* — локальный (глобальный) максимум.
Решение.
Находим первую производную функции:
y’ = 2 • x-11
Приравниваем ее к нулю:
2 • x-11 = 0
Вычисляем значения функции на концах отрезка
f(4) = 0
f(5) = -2
Ответ:
fmin = -2, fmax = 0
18.
Пусть функции — непрерывны на интервале . Тогда (Основные свойства неопределенного интеграла).
Если функция f ( x ) имеет первообразную на промежутке X, и k – число, то
Короче: постоянную можно выносить за знак интеграла.
Если функции f ( x ) и g ( x ) имеют первообразные на промежутке X , то
Короче: интеграл суммы равен сумме интегралов.
Если функция f ( x ) имеет первообразную на промежутке X , то для внутренних точек этого промежутка:
Короче: производная от интеграла равна подынтегральной функции.
Если функция f ( x ) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:
Короче: интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.
19.Таблица интегралов. ( ).
Sinx+C
20.Найдите интеграл , , , ,
21.Вычислить , , ,
22.Пусть функции — непрерывны на интервале . Тогда (Основные свойства определенного интеграла, 9 свойств).
Основные свойства интеграла. Установим ряд важных свойств определенного интеграла. Большая часть этих свойств присуща интегралам от любых интегрируемых функций, но мы будем формулировать их для функций непрерывных.
Теорема 1. Если f(x
т. е. интеграл суммы равен сумме интегралов слагаемых.
В самом деле, составляя интегральную сумму для функции f(x) + g(x), очевидно, будем иметь
после чего остается перейти к пределу при λ → 0.
Аналогично доказывается
Теорема 2. Если f(x) — непрерывная функция, а c — постоянное число, то
т.
е. постоянный множитель можно выносить за знак интеграла.
Теорема 3. Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.
В самом деле, будем при раздроблении промежутка [ a, b] на части включать c в число точек деления. Если c = xm, то
Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [a, b], [a, c] и [c, b]. Остается перейти к пределу при λ → 0.
Доказанную теорему можно высказать в более общей форме. Для этого нам понадобится расширить смысл символа интеграла.
Если f(x) — любая функция, определенная в точке a, то по определению полагаем
(11)
Таким образом, интеграл с совпадающими пределами равен нулю.
Пусть функция f(x) интегрируема на промежутке [a, b]. Тогда по определению полагаем
(12)
Таким образом, при перестановке пределов интегрирования определенный интеграл меняет знак.
Теперь можем привести упомянутую более общую форму теоремы 3:
Теорема 4. Пусть функция f(x) непрерывна в промежутке [A, B]. Если a, b, c суть точки этого промежутка, то
(13)
В самом деле, если из точек a, b и c две (а тем более три) совпадают, то равенство (13) очевидно. Пусть же все эти точки различны. Если a < c < b, то дело сводится к теореме 3. Прочие случаи взаимного расположения точек a, b, c тоже легко свести к той же теореме. Пусть, например, c < b < a. Тогда
откуда
и остается дважды применить формулу (12).
Свойство интеграла, выражаемое теоремами 3 и 4, называется аддитивностью его, как функции промежутка интегрирования.
Теорема 5. Если f(x) — непрерывная функция, заданная на промежутке [a, b], то существует такая точка , что
(14)
В самом деле, пусть M и m наибольшее и наименьшее значения f(x) на промежутке [a, b]. Составим для f(x) какую-нибудь интегральную сумму
Так как при всех k будет m ≤ f(ξk) ≤ M, а xk+1 > xk, то m(xk+1 — xk) ≤ M(xk+1 — xk). Складывая такие неравенства и замечая, что
получим:
m(b — a) ≤ σ ≤ M(b — a).
Переходя в этом неравенстве к пределу при λ → 0, приходим после деления на b — a к новому неравенству
Таким образом, частное
есть число, лежащее между наибольшим и наименьшим значениями непрерывной функции.
Как известно, тогда и само это число должно являться одним из значений той же функции. Поэтому в [a, b] обязательно существует такая точка ξ, что h = f(ξ), а это равносильно равенству (14).
Заметим, что равенство (14) справедливо не только при a < b, но и при a = b (тогда обе части этого равенства нули), а также и при a > b (этот случай приводится к рассмотренному изменением знаков). В первом из этих случаев будет ξ = a, а во втором a ≥ ξ ≥ b.
Теорему 5 обычно называют теоремой о среднем значении. Из нее вытекает ряд свойств интеграла, выражающихся неравенствами.
Теорема 6
. Если f(x) — неотрицательная непрерывная функция и нижний предел интеграла не больше верхнего*, то и сам интеграл будет числом неотрицательнымДействительно, в этом случае оба сомножителя правой части формулы (14) неотрицательны.
___________________________________
* Если в интеграле будет a ≤ b, то будем говорить, что порядок пределов интегрирования — нормальный.
Последний результат можно несколько уточнить.
Теорема 7. Если a < b, а f(x) — непрерывная неотрицательная функция, которая хотя бы в одной точке [a, b] отлична от нуля, то
В самом деле, пусть x0 (a < x0 < b) — такая точка, что f(x0) > 0. Возьмем столь малое
Первый и третий интегралы правой части по предыдущей теореме неотрицательны, а второй интеграл по теореме о среднем представим в форме
и потому строго положителен.
Теорему 7 можно, очевидно, формулировать и так:
Теорема 8. Пусть f(x) — неотрицательная непрерывная функция, заданная в [a, b], причем a < b. Если
то f(x) всюду на [a, b] равна нулю.
В обеих теоремах 7 и 8 (в отличие от теоремы 6) нельзя отбросить условия непрерывности подинтегральной функции. Например, функция, которая в конечном числе точек [ a, b] равна единице, а в остальных точках этого промежутка равна нулю, будет неотрицательной и нетождественной нулю, а интеграл от нее (как показано в пунктеОпределенный интеграл) равен нулю.
Теорема 9. Если a ≤ b, а f(x) и u·g(x) — две непрерывные функции, которые на [a, b] удовлетворяют условию f(x) ≤ g(x), то
(15)
т. е. при нормальном порядке пределов интегрирования неравенство можно интегрировать почленно.
Действительно,
Если бы мы допустили, что a < b и что хоть в одной точке оказывается f(
Теорема 10. Если a ≤ b и f(x) непрерывна на [a, b], то
(16)
т. е. при нормальном порядке пределов интегрирования абсолютная величина интеграла не превосходит интеграла от абсолютной величины подинтегральной функции.
В самом деле, интегрируя неравенств
— | f(x) | ≤ f(x) ≤ | f(x) |,
находим:
а это равносильно неравенству (16).
23.Пусть — площадь фигуры, ограниченной линиями , . Тогда значение лежит в интервале
Приводим подобные:
2Решаем уравнение:
3Решаем уравнение:
4Решаем уравнение:
5Графики уравнений:
Ответ:
(Решение уравнения с учётом ОДЗ )
24.
3/log(x)
Находим частные производные по формулам:
Для нашей функции F(x,y,z):
При нахождении ∂F/∂x считаем y и z постоянными:
При нахождении ∂F/∂y считаем x и z постоянными:
При нахождении ∂F/∂z считаем x и y постоянными:
По формулам находим частные производные:
∂z∂x=−6⋅x⋅y⋅z8−y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x)∂z∂x=−6⋅x⋅y⋅z8−y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x)
или
∂z∂x=−6⋅x⋅y⋅z8+y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x)∂z∂x=−6⋅x⋅y⋅z8+y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x)
или
Полный дифференциал функции.
dz=(−6⋅x⋅y⋅z8+y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x))dx+(−3⋅x2⋅z8−2⋅y⋅z3ln(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x))dydz=(−6⋅x⋅y⋅z8+y2⋅z3x⋅ln2(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x))dx+(−3⋅x2⋅z8−2⋅y⋅z3ln(x)24⋅x2⋅y⋅z7+3⋅y2⋅z2ln(x))dy
28. Ответ понравился автору вопроса
Посмотреть всех экспертов из раздела Учеба и наука > Математика Боря купил 4 книги. Может ли у каждого из учащихся в классе быть ровно трое друзей в этом классе, если
в классе: 1) 25 учащихся; 2) 18 учащихся ? ответ с решением Решено В пакете лежат несколько леденцов с разными вкусами, произведенных в разных странах. любые два леденца в пакете различаются либо вкусом, либо страной Решено На дне рождения у Пети нашлось трое гостей, которые вместе съели не менее 21
конфеты. Все присутствующие (гости и Петя) съели 60 конфет, причём не Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30. Пользуйтесь нашим приложением Вот формулировки признаков: Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо: Найти промежутки возрастания и убывания функции . Решение. Первым шагом является нахождение обрасти определения функции. В нашем примере выражение в знаменателе не должно обращаться в ноль, следовательно, . Переходим к производной функции: Для определения промежутков возрастания и убывания функции по достаточному признаку решаем неравенства и на области определения. Воспользуемся обобщением метода интервалов. Единственным действительным корнем числителя является x = 2, а знаменатель обращается в ноль при x = 0. Эти точки разбивают область определения на интервалы, в которых производная функции сохраняет знак. Отметим эти точки на числовой прямой. Плюсами и минусами условно обозначим интервалы, на которых производная положительна или отрицательна. Стрелочки снизу схематично показывают возрастание или убывание функции на соответствующем интервале. Таким образом, и . В точке x = 2 функция определена и непрерывна, поэтому ее следует добавить и к промежутку возрастания и к промежутку убывания. В точке x = 0 функция не определена, поэтому эту точку не включаем в искомые интервалы. Приводим график функции для сопоставления с ним полученных результатов. Ответ: функция возрастает при , убывает на интервале (0; 2]. — Точки экстремума функции одной переменной. Достаточные условия экстремума Пусть функция f(x), определенная и непрерывная в промежутке [a,b], не является в нем монотонной. Найдутся такие части [ , ] промежутка [a,b], в которых наибольшее и наименьшее значение достигается функцией во внутренней точке, т.е. между и . Говорят, что функция f(x) имеет в точке максимум (или минимум), если эту точку можно окружить такой окрестностью (x0— ,x0+ ), содержащейся в промежутке, где задана функция, что для всех её точек выполняется неравенство. f(x) < f(x0)(или f(x)>f(x0)) Иными словами, точка x0 доставляет функции f(x) максимум (минимум), если значение f(x0) оказывается наибольшим (наименьшим) из значений, принимаемых функцией в некоторой (хотя бы малой) окрестности этой точки. Если существует такая окрестность, в пределах которой (при x=x0) выполняется строгое неравенство f(x)<f(x0)(или f(x)>f(x0) то говорят, что функция имеет в точке x0 собственный максимум (минимум), в противном случае – несобственный. Если функция имеет максимумы в точках x0 и x1 , то, применяя к промежутку [x0,x1] вторую теорему Вейерштрасса, видим, что наименьшего своего значения в этом промежутке функция достигает в некоторой точке x2 между x0 и x1 и имеет там минимум. Аналогично, между двумя минимумами непременно найдется максимум. В том простейшем (и на практике – важнейшим) случае, когда функция имеет вообще лишь конечное число максимумов и минимумов, они просто чередуются. Заметим, что для обозначения максимума или минимума существует и объединяющий их термин – экстремум. Понятия максимум (max f(x)) и минимум (min f(x)) являются локальными свойствами функции и имеют место в определенной точке х0. Понятия наибольшего (sup f(x)) и наименьшего (inf f(x)) значений относятся к конечному отрезку [a,b] и являются глобальными свойствами функции на отрезке. Из рисунка 1 видно, что в точках х1 и х3 локальные максимумы, а в точках х2 и х4 – локальные минимумы. Однако, наименьшего значения функция достигает в точке х=а, а наибольшего – в точке х=b. Поставим задачу о разыскании всех значений аргумента, доставляющих функции экстремум. При решении ее основную роль будет играть производная. Предположим сначала, что для фунции f(x) в промежутке(a,b) существует конечная производная. Если в точке х0 функция имеет экстремум, то, применяя к промежутку (х0— ,х0+ ), о которой была речь выше, теорему Ферма, заключаем, что f(x)=0 этом состоит необходимое условие экстремума. Не следует, думать, однако, что каждая точка, в которой производная равна нулю, доставляет функции экстремум : указанное только что необходимое условие неявляется достаточным В рамках исследования того, как изменяются функции, мы можем определить интервалы, в течение которых функция изменяется определенным образом. Мы говорим, что функция возрастает на интервале, если значения функции увеличиваются по мере увеличения входных значений в этом интервале. Точно так же функция убывает на интервале, если значения функции уменьшаются по мере увеличения входных значений на этом интервале. Средняя скорость изменения возрастающей функции положительна, а средняя скорость изменения убывающей функции отрицательна. На рис. 3 показаны примеры увеличения и уменьшения интервалов функции. 9{\text{}}\left(2,\infty\right)(-∞,−2)∪ (2,∞) и уменьшается на (−2,2)\left(-2\text {,}2\справа)(−2,2) . В то время как некоторые функции возрастают (или убывают) во всей своей области определения, многие другие этого не делают. Значение входа, при котором функция изменяется с возрастающей на убывающую (по мере движения слева направо, то есть по мере увеличения входной переменной), называется локальный максимум . Если функция имеет более одного, мы говорим, что она имеет локальные максимумы. Точно так же значение входа, при котором функция изменяется с убывающей на возрастающую по мере увеличения входной переменной, называется локальным минимумом . Форма множественного числа — «локальные минимумы». Вместе локальные максимумы и минимумы называются локальными экстремумами или локальными экстремальными значениями функции. (Форма единственного числа — «экстремум». Ясно, что функция не возрастает и не убывает на интервале, где она постоянна. Функция также не возрастает и не убывает в экстремумах. Обратите внимание, что мы должны говорить о локальных экстремумах, потому что любой данный локальный экстремум, как определено здесь, не обязательно является самым высоким максимумом или самым низким минимумом во всей области определения функции. Для функции на рисунке 4 локальный максимум равен 16, и он приходится на х=-2х=-2х=-2 . Локальный минимум равен −16-16−16 и приходится на x=2x=2x=2 . Рисунок 4 Чтобы найти локальные максимумы и минимумы на графике, нам нужно наблюдать за графиком, чтобы определить, где график достигает своей самой высокой и самой низкой точки, соответственно, в пределах открытого интервала. Рис. 5. Определение локального максимума. Эти наблюдения приводят нас к формальному определению локальных экстремумов.
-x — Учеба и наука Лучший ответ по мнению автора
07. 
11.16Лучший ответ по мнению автора
Андрей Андреевич
Читать ответы
Eleonora Gabrielyan
Читать ответы
Галина Владимировна
Читать ответы
Похожие вопросы 
Все книги без первой стоят 42 р., без второй — 40 р., без третьей — 38 р., без четвёртой — 36 р. Сколько стоит каждая книга?Достаточные признаки возрастания и убывания функции — Мегаобучалка
На основании достаточных признаков находятся промежутки возрастания и убывания функции.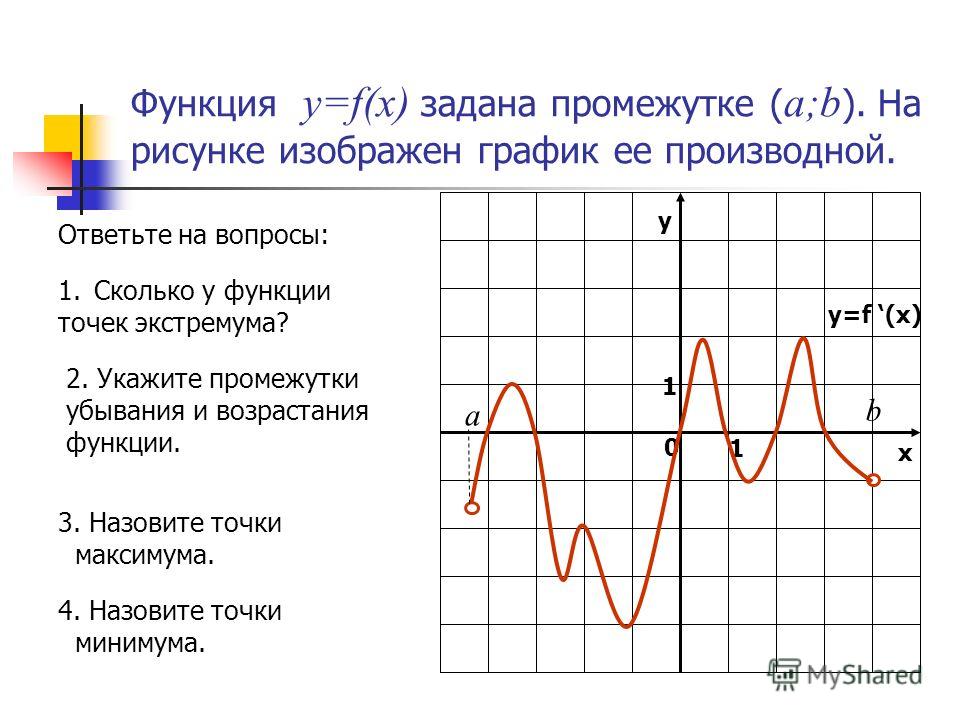
Рассмотрим пример для разъяснения алгоритма.
Пример.
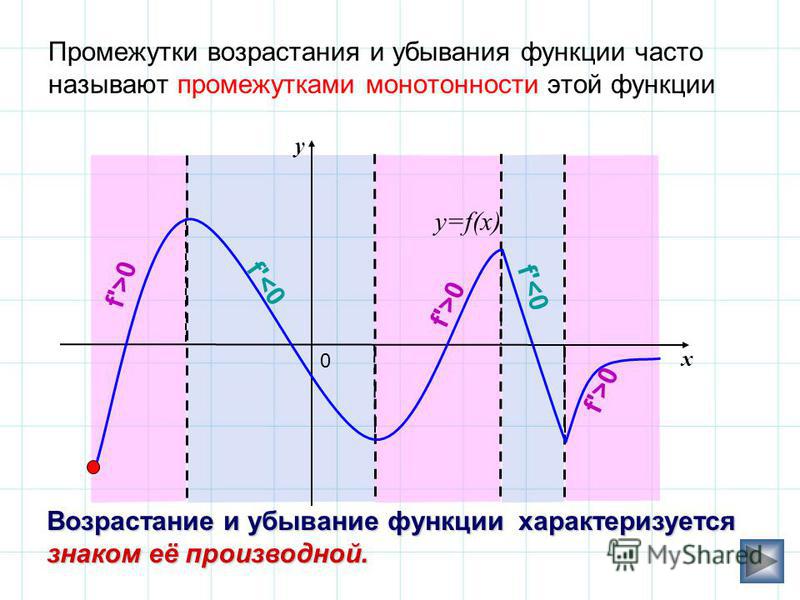Отметим, что самое определение максимума (минимума) предполагает, что функция задана по обе стороны от точки x0.
Экстремум следует искать только в тех точках, где производная равна нулю. Используйте график, чтобы определить, где функция увеличивается, уменьшается или постоянна | Колледж Алгебра |
В этом видео также объясняется, как найти, где функция увеличивается или уменьшается.
) Часто термин местный заменяется термином относительный 9.0030 . В этом тексте мы будем использовать термин локальный .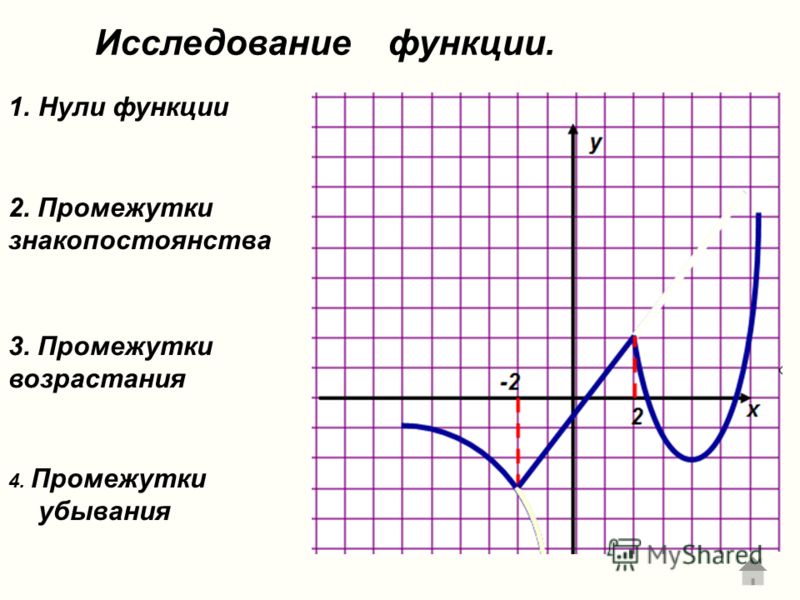
Подобно вершине американских горок, график функции в локальном максимуме выше, чем в соседних точках с обеих сторон. График также будет ниже в локальном минимуме, чем в соседних точках. Рисунок 5 иллюстрирует эти идеи для локального максимума. A Общее примечание: локальные минимумы и локальные максимумы >f\left(a\right)f(b)>f(a)
для любых двух входных значений
aaa
и
bbb
в заданном интервале, где
б>аб>аб>а
.
Функция
fff
является убывающей функцией на открытом интервале, если
f(b) для любых двух входных значений aaa и bbb в заданном интервале, где b>ab>ab>a . Функция fff имеет локальный максимум на x=bx=bx=b , если существует интервал (a,c)\left(a,c\right)(a,c) с a такое, что для любых xxx в интервале (a,c)\left(a,c\right)(a,c) , f(x) ≤f(b)f\влево(x\вправо)\le f\влево(b\вправо)f(x)≤f(b) . Аналогично, fff имеет локальный минимум в точке x=bx=bx=b , если существует интервал (a,c)\left(a,c\right)(a,c) с a такое, что для любого xxx в интервале (a,c)\left(a,c\right)(a,c) , f(x)≥f(b)f\left(x\right)\ge f \left(b\right)f(x)≥f(b) . Учитывая функцию p(t)p\left(t\right)p(t) на графике ниже, определите интервалы, на которых функция кажется возрастающей. Рис. 6 Мы видим, что функция не постоянна на любом интервале. Функция увеличивается там, где она наклонена вверх, когда мы движемся вправо, и уменьшается там, где она наклонена вниз, когда мы двигаемся вправо. Функция увеличивается с t=1t=1t=1 до t=3t=3t=3 и с t=4t=4t=4 . В обозначении интервала мы бы сказали, что функция возрастает на интервале (1,3) и интервале (4,∞)\влево(4,\infty \вправо)(4,∞) . График функции f(x)=2x+x3f\left(x\right)=\frac{2}{x}+\frac{x}{3 }f(x)=x2+3x . Затем используйте график, чтобы оценить локальные экстремумы функции и определить интервалы, на которых функция возрастает. Используя технологию, мы обнаруживаем, что график функции выглядит так, как показано на рисунке 7. Похоже, что существует нижняя точка или локальный минимум между 9{2}-15x+20\\f(x)=x3−6×2−15x+20 для оценки локальных экстремумов функции. Используйте их, чтобы определить интервалы, на которых функция увеличивается и уменьшается.
Решение Для функции fff , график которой показан на рисунке 9, найти все локальные максимумы и минимумы. Рисунок 9 См. график fff . График достигает локального максимума на x=1x=1x=1 , потому что это самая высокая точка в открытом интервале около x=1x=1x=1 . Локальным максимумом является yyy -координата x=1x=1x=1 , что равно 222 . График достигает локального минимума в точке x=−1 \text{ }x=-1\text{ } x=−1 , потому что это самая нижняя точка открытого интервала около х=-1х=-1х=-1 . Локальным минимумом является координата y в точке x=−1x=-1x=−1 , что равно −2-2−2 . f(x)=cf\left(x\right)={c}f(x)=c (−∞,0)\left(-\infty,0\right)(−∞,0) По убыванию (0,∞)\left(0,\infty\right)(0, ∞) f(x)=x3f\left(x\right)=\sqrt[3]{x}f(x)=3x f(x)=xf\left(x\right)=\sqrt{x}f(x)=x (0,∞)\left(0,\infty\right)(0,∞) f(x)=∣x∣f\left(x\right)=|x|f(x)=∣x∣ (0,∞)\left(0,\infty\right)(0,∞) Уменьшение на (−∞,0)\left(-\infty,0\right)(−∞, 0) увеличивается, остается постоянным или уменьшается. В этом объяснении мы будем использовать обозначение интервала для описания интервалов
увеличения и уменьшения. Начнем с того, что вспомним, что мы подразумеваем под интервалом
обозначение. Интервал чисел между 𝑎 и 𝑏,
включая 𝑎 и 𝑏, обозначается
[𝑎,𝑏], где 𝑎 и 𝑏
называются концами отрезка. Чтобы указать, что одна из конечных точек должна быть исключена из набора, соответствующий
квадратная скобка изменена. Таким образом, в нотации конструктора наборов это выражается следующим образом:
]𝑎,𝑏[={𝑥∈ℝ∣𝑎𝑥𝑏},[𝑎,𝑏[={𝑥∈ℝ∣𝑎≤𝑥𝑏},]𝑎,𝑏]={𝑥∈ℝ∣𝑎𝑥≤𝑏},[𝑎,𝑏} ]={𝑥∈ℝ∣𝑎≤𝑥≤𝑏}. Теперь определим условия, при которых любая функция будет возрастающей, убывающей,
или постоянна на заданном интервале. Функция 𝑓(𝑥) является возрастающей на интервале
]𝑎,𝑏[ если для любого
𝑥𝑥 в
]𝑎,𝑏[∶𝑓(𝑥)𝑓(𝑥). Поскольку нам нужно сравнить 𝑓(𝑥)
к 𝑓(𝑥), функция 𝑓 должна
быть определено на ]𝑎,𝑏[. Когда функция возрастает на интервале, ее выходы увеличиваются на этом интервале.
интервал, поэтому его кривая должна расти на этом интервале. Функция 𝑓(𝑥) убывает интервал ]𝑎,𝑏[ если для любого
𝑥𝑥 в
]𝑎,𝑏[∶𝑓(𝑥)>𝑓(𝑥). Когда функция убывает на интервале, ее выходы уменьшаются на этом интервале.
интервал, поэтому его кривая должна падать на этот интервал. Также принято называть функции строго возрастающими или строго
уменьшение; однако мы не будем использовать эту терминологию в данном объяснении. Мы также можем описать функции, которые не изменяют выходы на интервале, как
следует. Функция 𝑓(𝑥) равна константа на интервале
]𝑎,𝑏[ если для любого 𝑥
в ]𝑎,𝑏[: 𝑓(𝑥)=𝑐, для некоторых
постоянная 𝑐. Когда функция постоянна на интервале, ее выходы постоянны на этом интервале.
интервал, поэтому его график будет горизонтальным на этом интервале. Если функция 𝑓(𝑥) возрастает на всем своем протяжении
домен, мы просто говорим, что функция возрастает. Аналогично, если функция
𝑓(𝑥) убывает на всей своей области определения, мы просто
говорят, что функция убывает. Теперь мы рассмотрим различные графики и определим, на каких интервалах в
в их области функции возрастают, убывают или постоянны. Во-первых
Например, мы будем определять эту информацию по заданному графику функции. График функции приведен ниже. Какое из следующих утверждений
про функцию верно? Начнем с того, что вспомним, что означают слова возрастание, убывание и константа.
Расскажите о графиках функции. Во-первых, функция 𝑓(𝑥) возрастает
на интервале ]𝑎,𝑏[
если для любого 𝑥𝑥 в
]𝑎,𝑏[∶𝑓(𝑥)𝑓(𝑥). Если мы сравним эти определения с нашим графиком, мы увидим, что у нас есть
горизонтальная линия, поэтому наша функция должна быть постоянной. Для каждого значения
𝑥, мы видим, что выход, 𝑦,
равно −4. Если мы посмотрим на горизонтальную линию, представляющую нашу функцию, мы увидим, что она
имеет стрелки на обоих концах. Это означает, что линия должна проходить от
−∞ до ∞. Интервал ]−∞,∞[
множество всех действительных чисел; следовательно, функция должна быть постоянной для
все действительные числа. Следовательно, наш ответ — вариант А; функция постоянна на ℝ. В следующем примере мы будем использовать график функции для определения
интервалы, в которых она возрастает, убывает или постоянна. Какое из следующих утверждений правильно описывает монотонность
функция, представленная на рисунке ниже? Монотонность функции описывает, является ли она возрастающей или
уменьшается на заданном интервале. В этом примере нам дано четыре
возможные варианты. Напомним, что функция 𝑓(𝑥) является возрастающей на интервале ]𝑎,𝑏[ если для любого
𝑥𝑥 в ]𝑎,𝑏[∶𝑓(𝑥)𝑓(𝑥). Функция
𝑓(𝑥) равно уменьшению на отрезке
]𝑎,𝑏[ если для любого 𝑥𝑥
в ]𝑎,𝑏[∶𝑓(𝑥)>𝑓(𝑥). Наш график состоит из трех основных частей. Между 𝑥=−2 и 𝑥=−1, так как
значение 𝑥 увеличивается, выход, 𝑦,
также увеличивается. Это означает, что функция возрастает на
]−2,−1[. Поскольку в опционах используются открытые интервалы,
нам не нужно беспокоиться о концах интервалов в этом вопросе. Между 𝑥=−1 и 𝑥=5 выход,
𝑦, всегда равно 3, поэтому функция постоянна
на этом интервале. Это означает, что функция постоянна на
]−1,5[. И снова наш интервал открыт
на обоих концах. Между 𝑥=5 и 𝑥=8, как значение
𝑥 увеличивается, выход 𝑦 уменьшается. Этот
означает, что функция убывает на
]5,8[. Монотонность функции можно описать как возрастающую на
]−2,−1[ постоянная на
]−1,5[ и убывает по
]5,8[. Следовательно, наш ответ — вариант C; функция возрастает на
]−2,−1[ постоянная на
]−1,5[ и убывает по
]5,8[. В нашем следующем примере мы будем определять возрастающие и убывающие области из
взаимный график. График функции приведен ниже. Какое из следующих утверждений
про функцию верно? В каждом из утверждений рассматривается монотонность функции; то есть,
увеличивается или уменьшается на заданном интервале. Мы помним, что
функция 𝑓(𝑥) есть , увеличивая на интервале ]𝑎,𝑏[
если для любого 𝑥𝑥 в
]𝑎,𝑏[∶𝑓(𝑥)𝑓(𝑥). Наш график имеет две асимптоты. Мы видим, что 𝑦-ось
(𝑥=0) — вертикальная асимптота
и у нас есть горизонтальная асимптота при 𝑦=−5. Это означает
что 0 не находится в домене 𝑓. Поскольку 0 не находится в домене 𝑓, нам нужно рассмотреть
монотонность функции на области определения, интервалы
]−∞,0[ и
]0,∞[. Теперь посмотрим, что происходит с нашим графиком при увеличении 𝑥. При переходе от −∞
к 0 по оси 𝑥 значение
𝑓(𝑥) увеличивается. Это означает, что на интервале
]−∞,0[ функция возрастает. То же самое происходит при движении от 0 к ∞ по
𝑥-ось; выходы 𝑓(𝑥) равны
увеличение. Это означает, что на интервале ]0,∞[
функция также увеличивается. Важно отметить, что происходит при 𝑥=0. 0 не входит в область определения 𝑓(𝑥), что
означает, что он не находится в интервалах, где
𝑓(𝑥) увеличивается или уменьшается. Можно сделать вывод, что функция возрастает на
]−∞,0[ и
]0,∞[. Так как 0 не находится в домене 𝑓, нам нужно было рассмотреть
монотонность функции только на интервалах
]−∞,0[ и
]0,∞[. Таким образом, функция
возрастает на всей своей области. Следовательно, наш ответ — вариант А; функция возрастает на
]−∞,0[ и
]0,∞[. Теперь мы рассмотрим критерии экспоненциальной функции, которые сделали бы ее
увеличение. Какое условие должно быть на 𝑧 для
𝑓(𝑥)=𝑧7,
где 𝑥 — положительное число, которое должно быть
возрастающая функция? Функция 𝑓(𝑥) равна , увеличивая на
интервал ]𝑎,𝑏[ если для любого
𝑥𝑥 в
]𝑎,𝑏[∶𝑓(𝑥)𝑓(𝑥). Чтобы наша функция 𝑓(𝑥)=𝑧7 возрастала для всех положительных значений
𝑥, нам нужно признать, что у нас есть экспоненциальная
функция. Начиная с 0𝑥𝑥, нам нужно найти
значения 𝑎 такие, что 𝑓(𝑥)𝑓(𝑥). Мы можем написать
𝑥=𝑥+𝑝,𝑝>0.где Мы можем использовать это для сравнения размеров
𝑓(𝑥) и 𝑓(𝑥)𝑓(𝑥)=𝑎=𝑎=𝑎×𝑎=𝑎𝑓(𝑥)
𝑝>0, поэтому
𝑎>0. Мы также знаем 𝑥, 𝑥>0, поэтому
𝑓(𝑥),𝑓(𝑥)>0. Для возрастающей функции нам понадобится неравенство
𝑓(𝑥)𝑓(𝑥)
для всех этих возможных значений 𝑥 и
𝑥. Подставив в выражение для
𝑓(𝑥), мы можем переписать это неравенство в виде
𝑓(𝑥)𝑎𝑓(𝑥). С 𝑓(𝑥) и 𝑎
положительны, это неравенство будет верным, только если 𝑎>1,
для любого положительного значения 𝑝. Мы можем найти значения
𝑎, которые удовлетворяют этому неравенству, логарифмируя оба
стороны:
logloglogloglog(𝑎)>(1),𝑝(𝑎)>(1),𝑝(𝑎)>0. Поскольку 𝑝 положительно, мы должны иметь
журнал (𝑎)> 0,
что верно, когда 𝑎>1. Следовательно, функция 𝑎 возрастает, для положительных
𝑥, когда 𝑎>1. В этом вопросе
𝑎=𝑧7 поэтому имеем неравенство
𝑧7>1(7)𝑧>7.умножая обе стороны на Следовательно, если 𝑧>7, то
𝑓(𝑥)=𝑧7 является
возрастающая функция для положительных значений 𝑥. В нашем последнем примере мы рассмотрим возрастающую и убывающую области
обратную функцию, не зная ее графика. Какое из следующих утверждений верно для функции
ℎ(𝑥)=−17−𝑥−5? Мы видим, что наша функция является обратной функцией. Мы можем найти увеличение
и убывающие области функции от ее графика, поэтому один из способов ответа
этот вопрос заключается в том, чтобы набросать кривую,
ℎ(𝑥)=−17−𝑥−5. Начнем с рисования графика, 𝑓(𝑥)=1𝑥. Этот график имеет горизонтальные и вертикальные
асимптоты, составленные из 𝑥- и 𝑦-осей. Теперь рассмотрим ряд преобразований, отображающих функцию
𝑓(𝑥)=1𝑥 на
ℎ(𝑥). Во-первых, график 1(−𝑥) является
отражение 1𝑥 в
𝑦-ось и имеет одинаковые горизонтальную и вертикальную асимптоты. Далее мы можем отобразить 1(−𝑥) на
17−𝑥, переместив график на 7 единиц вправо. Поскольку 17−𝑥=1−(𝑥−7),
что означает, что вертикальная асимптота теперь является линией с уравнением
𝑥=7, а так как горизонтальное смещение не влияет на
положение горизонтальной асимптоты, это остается как
𝑥-ось. Функция ℎ(𝑥) содержит отрицательное значение этого,
так что мы можем отобразить 17−𝑥 на
−17−𝑥 по
отражая его по оси 𝑥. Вертикаль и горизонталь
асимптоты не меняются при этом преобразовании, так как
𝑦=0 — горизонтальная асимптота. Наконец, чтобы отобразить −17−𝑥 на
ℎ(𝑥)=−17−𝑥−5, выполняем
вертикальное перемещение на 5 единиц вниз. Это переводит горизонтальное
асимптотирует вниз на 5 единиц и оставляет
вертикальная асимптота не изменилась. Итак, теперь у нас есть горизонтальная асимптота при
𝑦=−5. Функция ℎ(𝑥)=−17−𝑥−5 является
обратная функция с вертикальной асимптотой при 𝑥=7
и горизонтальная асимптота при 𝑦=-5. Теперь нам нужно установить, где эта функция возрастает и где она
уменьшается. Напомним, что функция 𝑓(𝑥) является возрастающей на интервале ]𝑎,𝑏[ если для любого
𝑥𝑥 в
]𝑎,𝑏[∶𝑓(𝑥)𝑓(𝑥). При движении от −∞ к 7 по
𝑥-ось, выходные значения ℎ(𝑥)
уменьшаются. Это означает, что на интервале ]−∞,7[
функция убывает. Аналогично, при движении от 7 к ∞ по
𝑥-ось, выходные значения ℎ(𝑥)
уменьшаются. Это означает, что на интервале
]7,∞[ функция также убывает. Важно отметить, что происходит при 𝑥=7. 7 не входит в домен 𝑓(𝑥), что
означает, что она не может находиться в промежутках, где
𝑓(𝑥) увеличивается или уменьшается. Можно заключить, что функция ℎ(𝑥)=−17−𝑥−5 убывает на отрезках
]−∞,7[ и
]7,∞[; другими словами,
это убывающая функция. Следовательно, наш ответ — вариант D; ℎ(𝑥) убывает на
интервалы ]−∞,7[ и
]7,∞[. Мы закончим это объяснение повторением некоторых ключевых моментов. Функция f (строго) увеличивает на
интервал, если всякий раз и a и b являются точками в интервале. Функция f (строго) уменьшает на
интервал, если всякий раз и a и b являются точками в интервале. Это означает
что граф идет вниз слева направо . Теорему о среднем значении можно использовать, чтобы определить, когда функция возрастает.
и когда она уменьшается. Если — дифференцируемая функция на отрезке
, тогда: 1. f увеличивает на если на . 2. f уменьшает на если на . Это имеет смысл, так как производная дает наклон касательной
линию к графику. Положительный наклон означает, что график идет вверх слева
вправо, а отрицательный наклон означает, что график идет вниз слева направо.
Правильно. Таким образом, я могу использовать производную для получения информации о
форма графика. В качестве дополнительного преимущества я могу сказать, является ли
критическая точка – это локальный максимум или локальный минимум. Пример. Найдите интервалы, на которых увеличивается и интервалы
на котором она уменьшается. Найдите и классифицируйте любые локальные экстремумы. Эскиз
график. Производная определяется для всех x, а также для и . я поставил таблица знаков для
используя критические точки в качестве точек останова. На
каждый интервал определяется критическими точками, я выбираю точку в
случайно и подключите его к . Если точка дает положительное значение для , то я знаю, что оно положительно на интервале, и, следовательно, что
функция увеличивает . Ставлю «+» над интервалом
и нарисуйте под ним линию с наклоном вверх. Точно так же, если точка дает отрицательное значение для , то я знаю, что оно отрицательно на интервале, и, следовательно, что
функция убывает . Ставлю «-» над интервалом
и нарисуйте наклонную вниз линию под ним. Читая мою диаграмму знаков, я вижу, что функция возрастает при и при . Восходящие и нисходящие линии дают схематическое изображение графика
функции. Обратите внимание на форму графика: Он показывает, что это локальный максимум. Кроме того, форма схемы показывает, что это локальный мин. Использование для классификации критической точки как максимальной или
min часто называют первым производным тестом .
Нарисовав схематический рисунок с восходящими и нисходящими линиями, вы
убрать необходимость запоминать тест: можно посмотреть из схематического изображения, является ли точка максимальной или минимальной. Вот
заявление о тесте. Теорема. ( Первая производная
Тест ) Предположим, что f непрерывна на интервале. Предположим, что и c является критической точкой f. (a) Если f увеличивается слева от c и убывает справа от c,
тогда c — локальный максимум. (b) Если f убывает слева от c и возрастает справа от c,
тогда c — локальный мин. Я не буду приводить доказательства, но вы можете понять, почему это имеет смысл, нарисовав
диаграмма знаков для интервалов по обе стороны от c. Пример. Найдите интервалы, на которых она возрастает, и интервалы, на которых она убывает.
Найдите и классифицируйте любые локальные экстремумы. Производная У людей часто возникают проблемы с выводом таких деривативов на рынок.
правильная форма. Вот общая процедура для производных с дробями
или отрицательные силы: (a) Запишите отрицательные степени x в виде дробей. Не используйте корни для
дробные полномочия — это сбивает с толку. б) Приведите дроби к общему знаменателю. Вы хотите
производная в «одном куске». (c) Факторизируйте все, что может быть факторизовано (например, верх и низ
полученная дробь). Если производная является дробью, она будет равна 0, когда вершина равна 0
и он будет неопределенным, когда дно равно 0. В этом случае не определено в ; это не критическая точка (потому что y не
определено в ), но считается точкой останова
на моей таблице знаков. Точки разрыва на вашей таблице знаков включают все
точки, где или где не определено, независимо от того, является ли функция
определены в этих точках. Наконец, для . Функция возрастает при и при . Уменьшается для и для . является локальным максимумом и является локальным минимумом. Пример. Найдите промежутки, на которых возрастает и
промежутки, на которых она уменьшается. Найдите и классифицируйте любые местные
экстремумы. Производная не определено в ; поскольку y определено в , это является критической точкой. за . Функция возрастает при и при . Он уменьшается для .
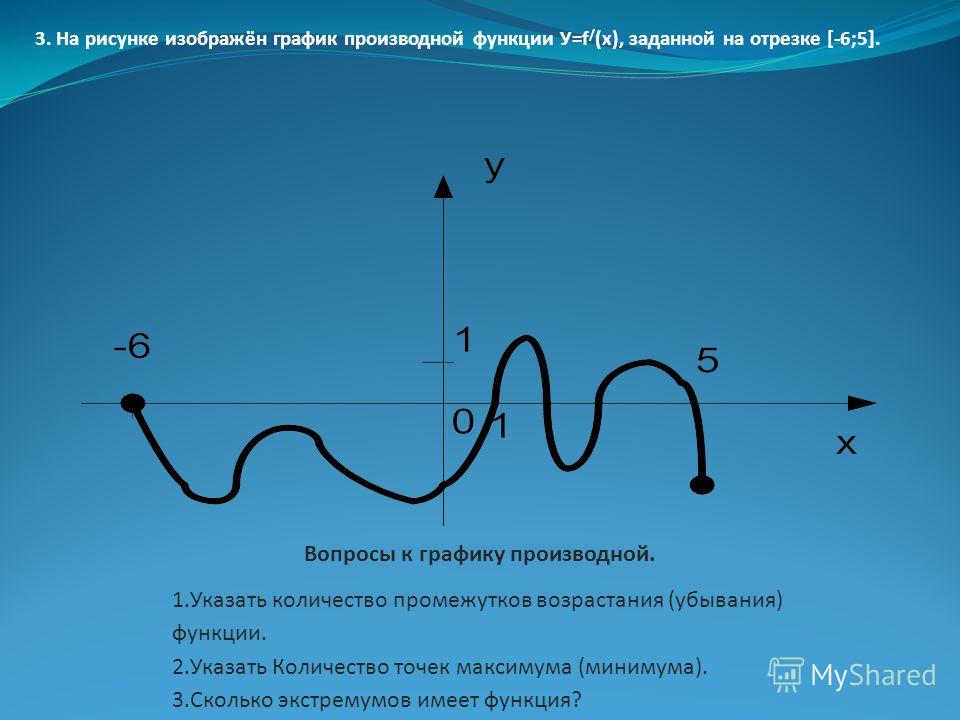
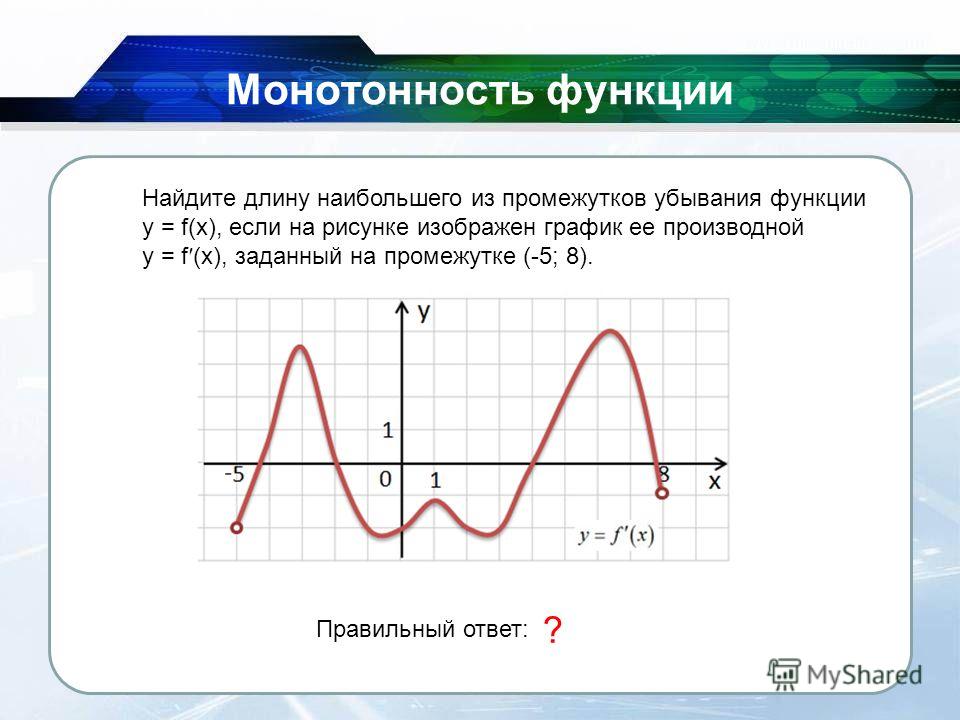
Пример 7. Поиск возрастающих и убывающих интервалов на графике
Решение
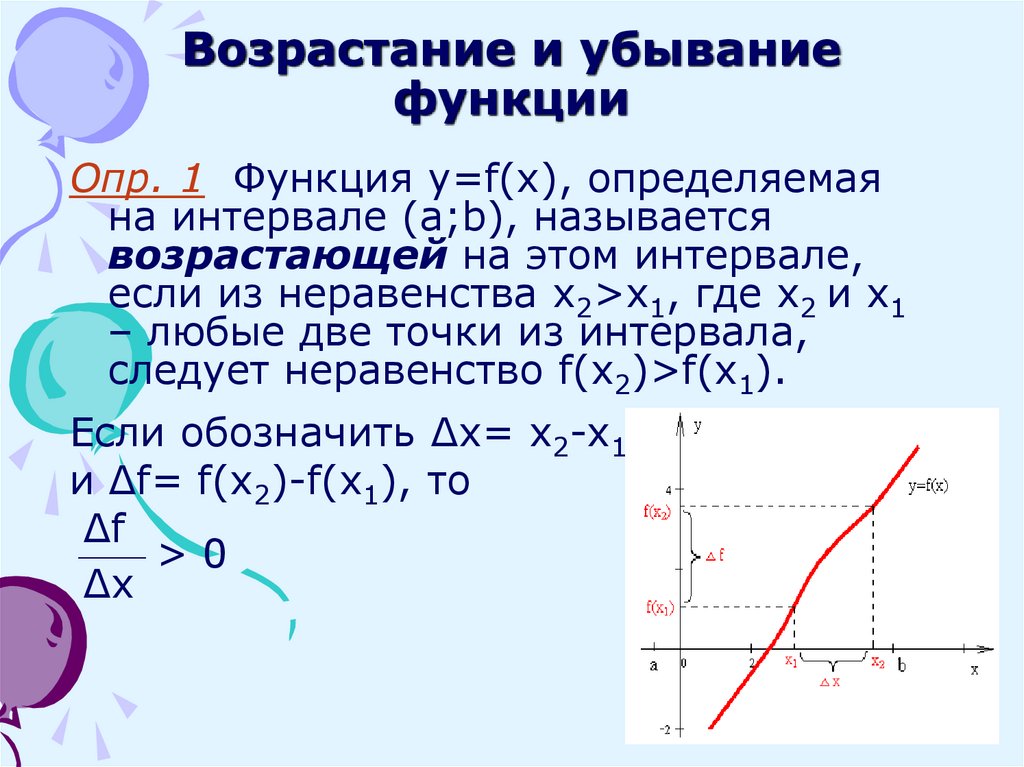
Пример 8. Поиск локальных экстремумов на графике
Раствор
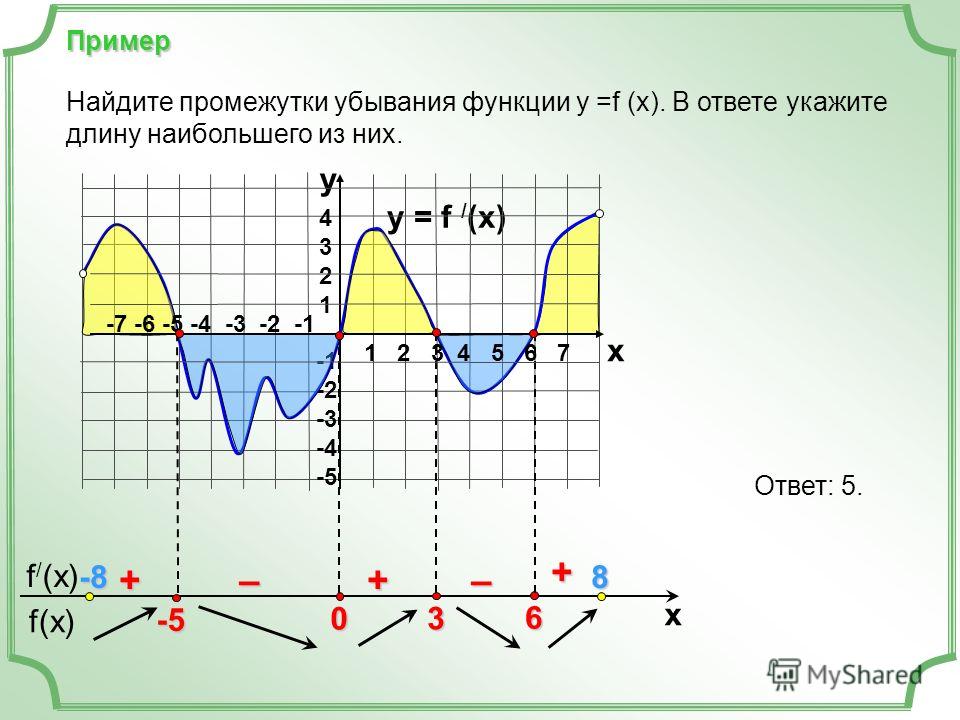
Пример 9. Поиск локальных максимумов и минимумов на графике
Решение
Функция Увеличение/уменьшение Пример Постоянная функция 9{2}}f(x)=x21 По возрастанию Кубический корень Увеличение Квадратный корень Увеличение по Абсолютное значение Возрастание на Лицензии и атрибуты
Контент по лицензии CC, совместно используемый ранее
Автор : Джей Абрамсон и др. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу: http://cnx.org/contents/[email protected] Все права защищены.
Автор : Mathispower4u. Лицензия : Все права защищены . Условия лицензии : Стандартная лицензия YouTube Объяснение урока: Интервалы возрастания и убывания функции
Определение: Обозначение интервала
Определение: возрастающие функции
Определение: убывающие функции
Определение: постоянная функция на интервале
Определение: возрастающие, убывающие или постоянные функции
Наконец, если функция
𝑓(𝑥) постоянна на всей своей области определения, мы просто
говорят, что функция постоянна. Пример 1. Определение возрастающей функции на данном графике,
Убывающая или Ни одна из них
Ответ
Во-вторых, функция
𝑓(𝑥) убывает на отрезке
]𝑎,𝑏[ если для любого
𝑥𝑥 в
]𝑎,𝑏[∶𝑓(𝑥)>𝑓(𝑥). Наконец, функция
𝑓(𝑥) постоянно на отрезке
]𝑎,𝑏[ если для любого 𝑥
в ]𝑎,𝑏[∶𝑓(𝑥)=𝑐,
для некоторой постоянной 𝑐.
Пример 2. Описание монотонности кусочной функции с помощью графика
Ответ
Наконец, функция
𝑓(𝑥) равно константе на интервале
]𝑎,𝑏[ если для любого 𝑥
в ]𝑎,𝑏[: 𝑓(𝑥)=𝑐, для некоторой константы 𝑐.
Пример 3. Определение областей возрастания и убывания графика
Ответ
Функция 𝑓(𝑥) уменьшение на интервале
]𝑎,𝑏[ если для любого
𝑥𝑥 в
]𝑎,𝑏[∶𝑓(𝑥)>𝑓(𝑥).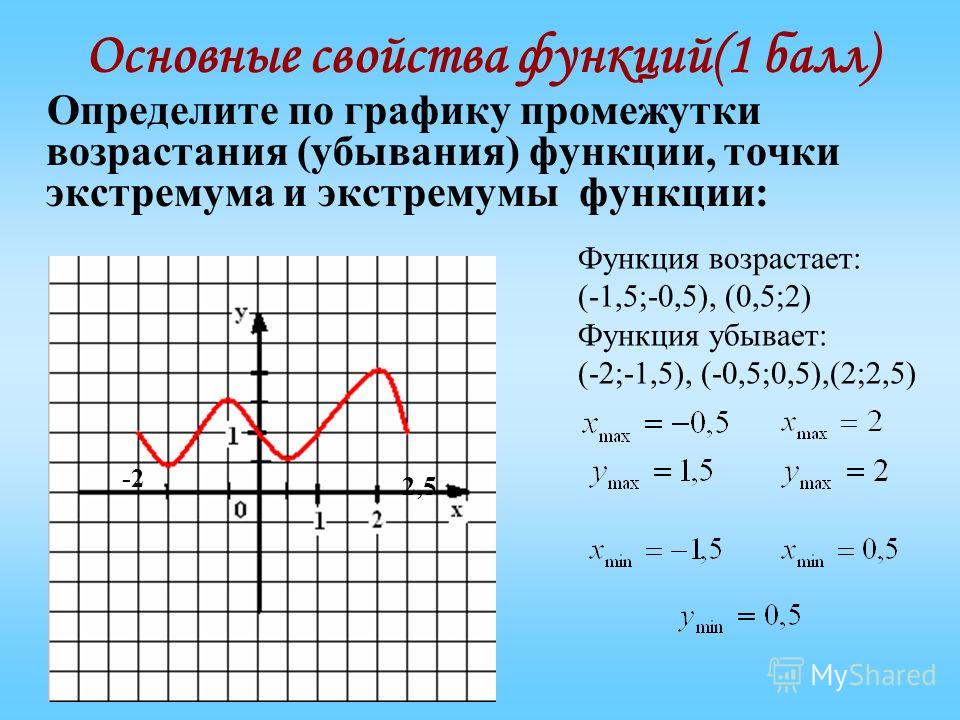
Пример 4. Определение условия возрастания экспоненциальной функции
Ответ
Общая форма экспоненциальной функции:
𝑓(𝑥)=𝑎. Если
𝑎>1, функция возрастает, и если
0𝑎1,
функция снижается. Частично это можно показать следующим образом.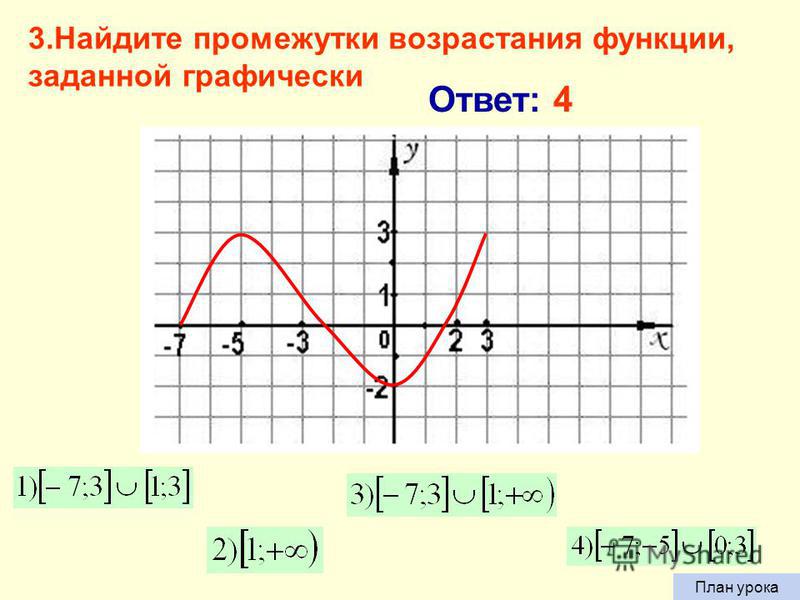
Пример 5. Определение областей возрастания и убывания обратной функции
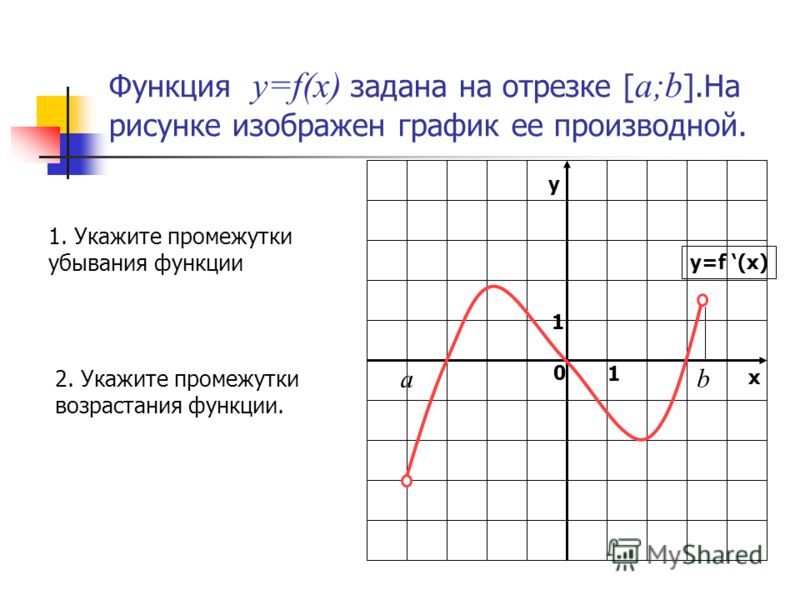
Ответ
Функция 𝑓(𝑥)
равно убыванию на интервале ]𝑎,𝑏[
если для любого 𝑥𝑥 в
]𝑎,𝑏[∶𝑓(𝑥)>𝑓(𝑥).
Ключевые точки
Функции возрастания и убывания
Функции возрастания и убывания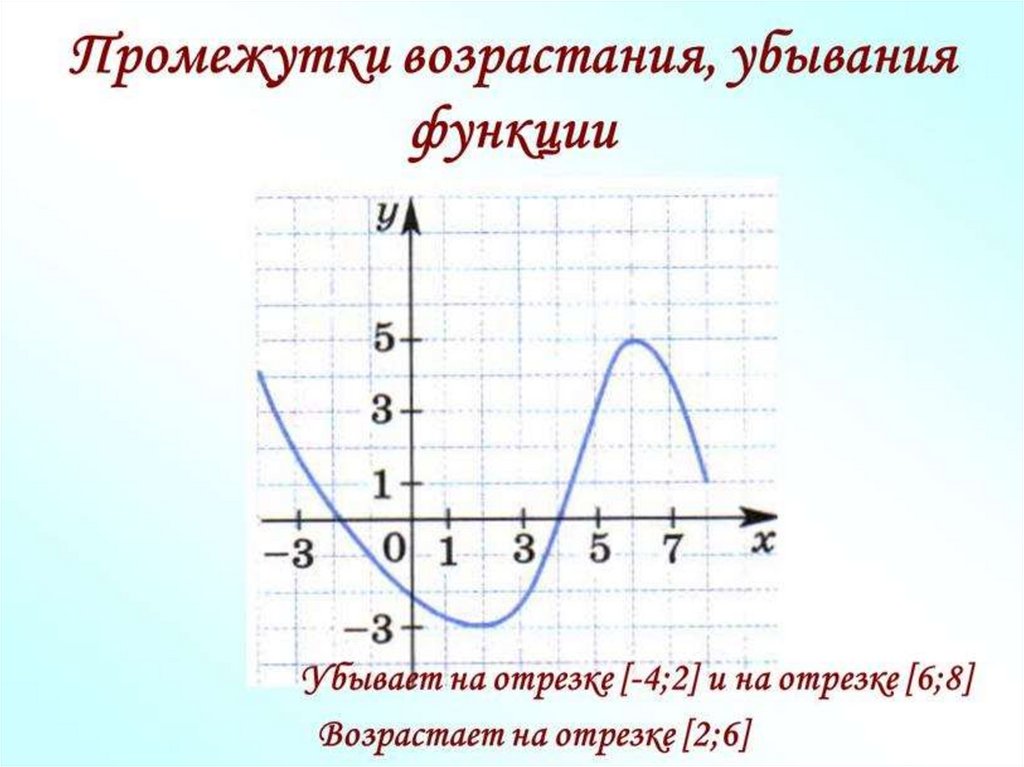
Это означает
что график идет вверх слева направо .
Он уменьшается для
.
(Могут быть другие
неопределенные места, если у вас есть такие вещи, как корни или бревна, конечно.)