| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Физический справочник/ / Электрические и магнитные величины/ / Понятия и формулы для электричества и магнетизма. / / Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.
| |||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||
TehTab. Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||
Формулы нахождения периметра всех фигур. Как найти периметр и площадь прямоугольника. Постановка учебной задачи
Урок и презентация на тему: «Периметр и площадь прямоугольника»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые.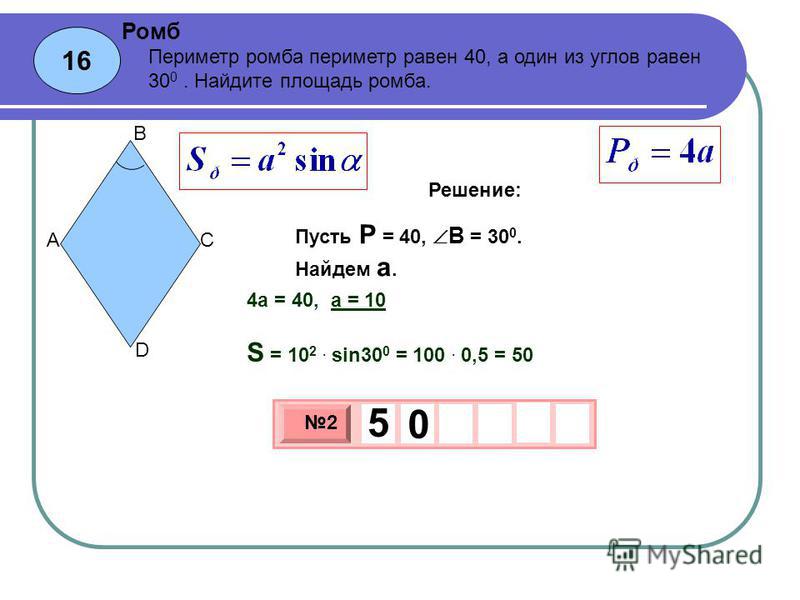
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
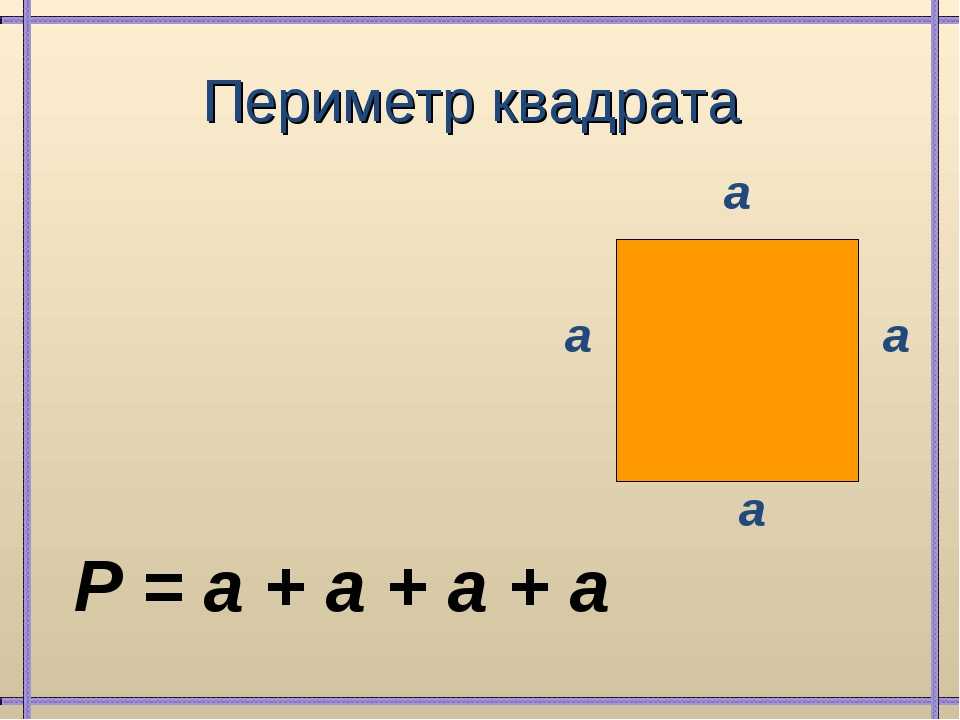
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.
Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
P ABCD = 2 * (AB + BС)
P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: P ABCD = 16 см.
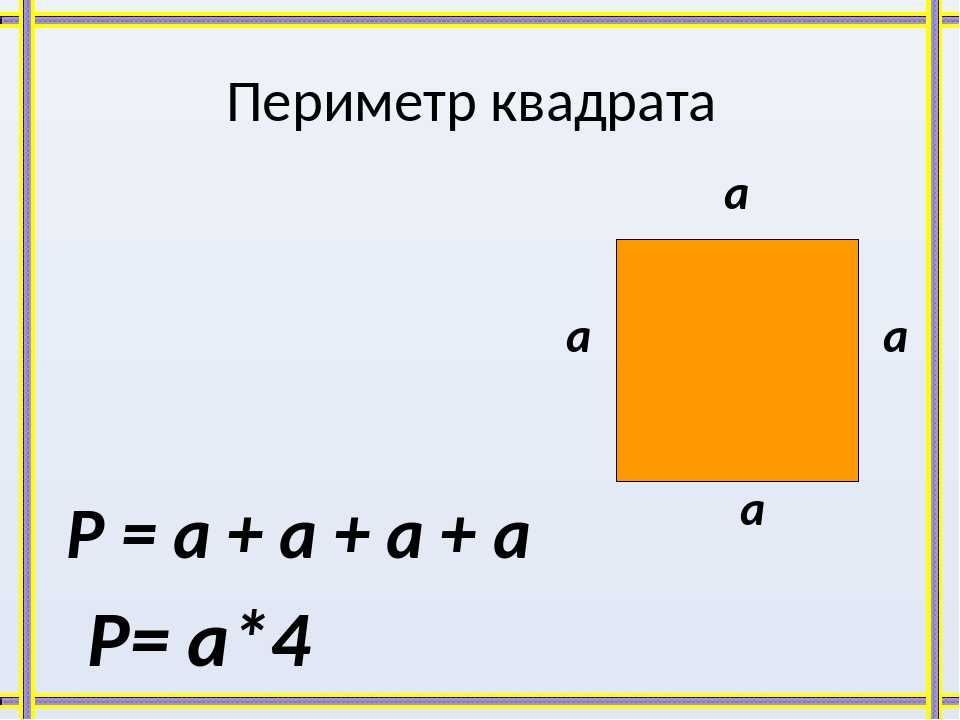
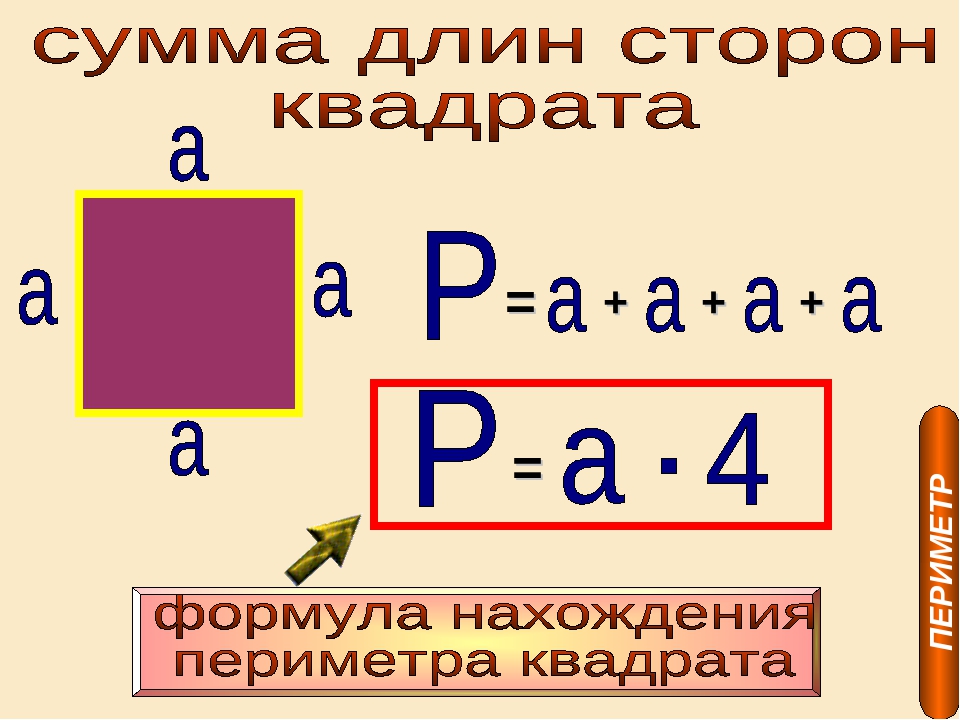
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
P ABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
P ABCD = 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
P ABCD = 4 * AB
3. Подставим в формулу наши данные:
Подставим в формулу наши данные:
P ABCD = 4 * 6 см = 24 см
Ответ: P ABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .
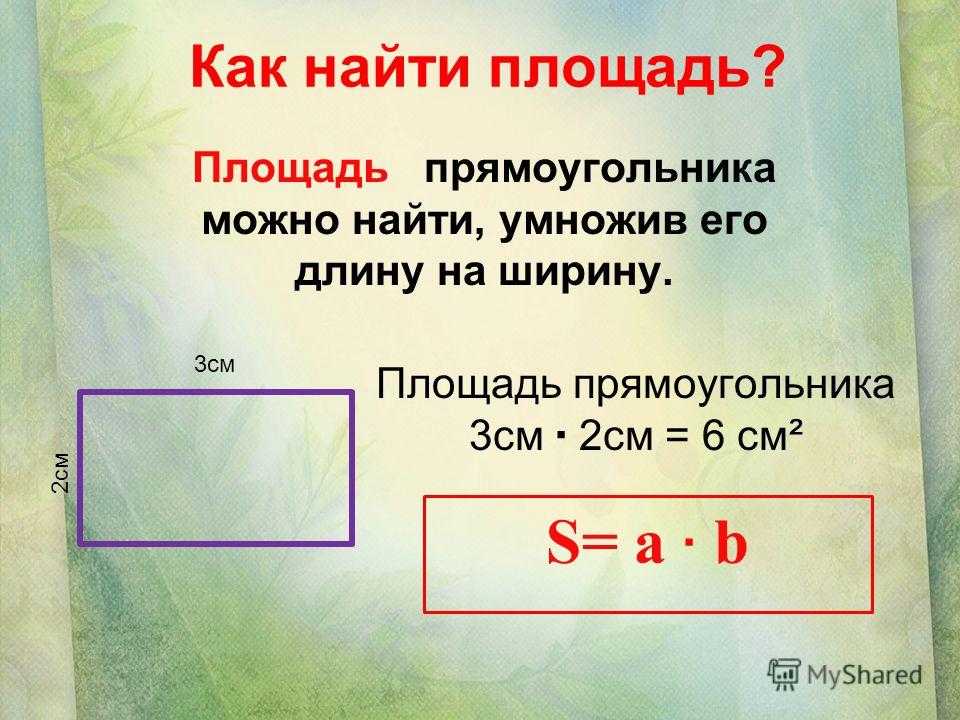
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .
Ответ: 14 см 2 .
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.
Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см 2
Ответ: 64 см 2 .
Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Разделы: Начальная школа
Класс: 3
Тема урока: формулы периметра и площади прямоугольника.
Тип урока: урок введения нового знания.
Цель урока: построение формулы нахождения стороны прямоугольника по его периметру и другой стороне.
1) сформировать представление о
формуле, как о равенстве, устанавливающем
взаимосвязь между величинами. Научить, в
простейших случаях, выражать зависимость между
величинами с помощью формул. Отрабатывать навыки
устных и письменных вычислений.
2) Развивать способности анализировать, сравнивать, обобщать.
3) Воспитывать коммуникативные способности, культуру речи.
Оборудование: бланк с задачами
Ход урока
1. Самоопределение к деятельности.
Математика пришла,
Занимай свои места.
Найди для головы полезное занятье!
Чтоб от безделья не зевать,
Полезно “голову ломать”!
Как понимаете фразеологический оборот “ломать голову”?
2. Актуализазия знаний.
1) Что общего в записях?
2 · x = 480
Y – 56 = 64
A = S: b
d: 5=12
S = a · b
540: z = 18
P = (a+b) · 2
(Это равенства, содержащие переменные.)
2) На какие группы их можно разделить?
(Уравнения и формулы.)
3) Что называют уравнением? (Равенство с переменной, значение которой надо найти.)
4) Найдите корни уравнений и запишите
их через запятую в тетради. (240, 120, 60, 30.)
(240, 120, 60, 30.)
5) Что интересного вы заметили? (Все числа круглые, каждое следующее уменьшается в 2 раза.)
6) Какое число следующее? (15)
7) Запишите его, мысленно уберите запятые и прочитайте полученное число.(240 120 603 015.)
8) Посмотрите на равенства второго столбика. Что показывает первая формула? Вторая? А третья?
9) Чем отличаются формулы от уравнений? (В уравнениях буквы обозначают некоторые числа, а в формулах — значения величин; формулы верны для всех значений букв, а уравнения — только для корней)
10) Для чего нужны формулы?
11) На какое слово похоже слово “формула”? (Слово “формула” похоже на слово “форма”. Формочка для песка помогает лепить из него пирожки, а формулы помогают решать задачи, задавая форму связей между величинами)
12) Попробуйте сформулировать определение формулы.
(Формула – это верное равенство, устанавливающее взаимосвязь между величинами)
3. Постановка учебной задачи.

Используя данные формулы, решите задачи № 1, № 2, № 3 из бланка задач. Работать будете в парах.
1) Найти площадь прямоугольника со сторонами 30 см и 80 см.
2) Найти сторону прямоугольника, площадь которого равна 1800 кв. см, а вторая сторона 20 см.
3) Ширина прямоугольника 8 см. Чему равна длина, если периметр равен 40 см?
4) Длина прямоугольника 3м, а ширина 2 дм. Чему равен периметр?
5) Ширина прямоугольника 6 см. Чему равна длина, если периметр равен 44 см?
6) Длина прямоугольника 5 см, а ширина на 10 мм короче. Чему равен его периметр?
Проверка решения.
Какая формула помогла решить первую задачу? Вторую?(S = a · b), (a =S: b)
Почему не смогли решить третью задачу? (Нужной формулы нет в списке изученных нами формул)
Так чем же мы будем заниматься на уроке? (Мы будем выводить формулу нахождения стороны прямоугольника через периметр и другую сторону)
Тема нашего урока: “Формулы периметра
и площади прямоугольника”.
4. “Открытие” детьми нового знания.
1) С чего начнём? (Построим чертёж и введём обозначения)
Дети могут вывести формулу на основе логических рассуждений, опираясь на чертёж. Сумма длины и ширины – это половина периметра, а чтобы найти одну из сторон, из этой половины надо вычесть другую сторону: a = P: 2 — b
Второй способ.
2) Что напоминает эта формула: P= (a+b) · 2? (Уравнение)
3) Какое это уравнение? (Это составное уравнение)
4) Чем является сумма a и b?(Первым множителем)
5) Как найти неизвестный множитель?(a+b=P:2)
6) Что теперь у нас неизвестно? (Слагаемое)
7) Как найти неизвестное слагаемое? (a=P:2-b)
Итак, мы вывели формулу нахождения длины прямоугольника. А как будет выглядеть формула нахождения ширины прямоугольника?(b=P:2-a)
Что же такое формула? (Формула – это верное равенство, устанавливающее взаимосвязь между величинами)
Прочтите полученную формулу. (Длина
стороны прямоугольника равна разности половины
периметра и длины другой стороны)
(Длина
стороны прямоугольника равна разности половины
периметра и длины другой стороны)
А теперь, используя новую формулу, давайте решим задачу, с которой вы не смогли справиться.
b=P: 2-a=40:2-8=12(см)
5. Физминутка.
Солнце заглянуло в класс
Отдыхать зовёт всех нас.
Раз, два, три, четыре, пять
Надо нам присесть и встать.
Руки вытянуть пошире,
Раз, два, три, четыре, пять
Наклониться – три-четыре,
И на месте поскакать.
На носок, потом на пятку,
Все мы делаем зарядку.
6. Первичное закрепление во внешней
речи.
1)Посмотрите на оставшиеся задачи. Какую из них мы сможем решить, используя вновь выведенную формулу? (№ 4)
b = P: 2 – a = 44: 2- 6 = 16 (см)
А есть ли другой способ решения этой задачи? (Подставим известные величины в формулу)
P= (a+b) · 2
44= (6+b) · 2
(6+b) · 2=44
6 + b = 44: 2
6+b=22
b=22-6
b=16
Ответ: длина прямоугольника 16 см.
7. Самостоятельная работа с
самопроверкой по вариантам:
Работа по учебнику: Петерсон Л. Г. Математика. 3 класс. Часть 2. – М.: Издательство “Ювента”, 2005. – 96 с.: ил. :
1 вариант № 4 (стр. 86)
2 вариант № 6 (стр. 87)
На доске:
3 м =30 дм
Р=(30+2) · 2=64 (дм)
10 мм =1 см
5-1=4(см)
Р=(5+4) · 2=18(см)
8. Включение в систему знаний и
повторение.
Решение уравнений из № 7(а, е) с опорой на выведенный ранее алгоритм.
9. Рефлексия деятельности.
Какова цель нашего урока?
Достигли ли мы поставленной цели?
Как оцениваете свою работу?
10. Домашнее задание.
Выучить формулы из опорного конспекта в учебнике на стр. 86 и решить задачи из № 3, стр. 87.
Литература
1. Петерсон Л.Г. Математика. 3 класс.
Часть 2. – М.: Издательство “Ювента”, 2005. – 96 с.:
ил.
3 класс.
Часть 2. – М.: Издательство “Ювента”, 2005. – 96 с.:
ил.
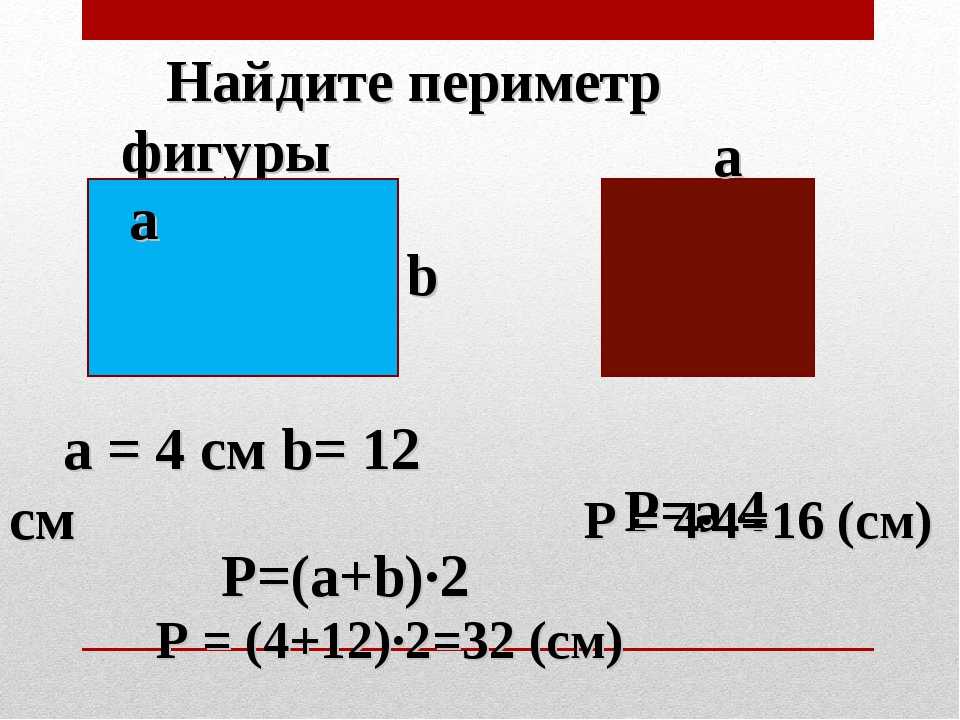
Периметр — это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.
- Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.
Существует 2 способа его нахождения:
- 1 способ. Складываем все стороны. P = a + а + b + b
- 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2.
 ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
«a» — длина прямоугольника, более длинная пара его сторон.
«b» — ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.
Запомни формулы вычисления периметра прямоугольника!
Полупериметр — это сумма одной длины и одной ширины.
- Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
- Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.
- : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
Одним из базовых понятий математики является периметр прямоугольника. На эту тему существует множество задач, при решении которых не обойтись без формулы периметра и навыков его вычисления.
Основные понятия
Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны. В нашей жизни многие фигуры имеют форму прямоугольника, например, поверхность стола, тетрадь и прочее.
Рассмотрим пример: по границам земельного участка необходимо поставить забор. Для того чтобы узнать длину каждой из сторон необходимо их измерить.
Для того чтобы узнать длину каждой из сторон необходимо их измерить.
Рис. 1. Земельный участок формой прямоугольника.
Земельный участок имеет стороны длиной 2 м., 4 м., 2 м., 4 м. потому чтобы общую узнать длину забора необходимо сложить длины всех сторон:
2+2+4+4= 2·2+4·2 =(2+4)·2 =12 м.
Именно эта величина в общем случае и называется периметром. Таким образом, для нахождения периметра необходимо сложить все стороны фигуры. Для обозначения периметра используют букву P.
Для вычисления периметра прямоугольной фигуры не нужно разделять её на прямоугольники, нужно измерить линейкой (рулеткой) лишь все стороны данной фигуры и найти их сумму.
Периметр прямоугольника измеряется в мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одинаковую систему измерения.
Периметр прямоугольника измеряется в различных единицах: мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одну систему измерения.
Формула периметра фигуры
Если принять к вниманию тот факт, что противоположные стороны прямоугольника равны, то можно вывести формула периметра прямоугольника:
$P = (a+b) * 2$, где а, b – стороны фигуры.
Рис. 2. Прямоугольник, с обозначенными противоположными сторонами.
Существует и другой способ найти периметр. Если в задание дано лишь одну сторону и площадь фигуры, можно использовать выразить другую сторону через площадь. Тогда формула будет выглядеть следующим образом:
$P = {{2S + 2a2}\over{a}}$, где S – площадь прямоугольника.
Рис. 3. Прямоугольник с сторонами a, b .
Задание : Вычислить периметр прямоугольника, если его стороны равны 4 см. и 6 см.
Решение:
Используем формулу $P = (a+b)*2$
$P = (4+6)*2=20 см$
Таким образом, периметр фигуры $P = 20 см$.
Так как периметр – это сумма все сторон фигуры, то полупериметр это сумма только одной длины и ширины. Чтобы получить периметр необходимо полупериметр умножить на 2.
Площадь и периметр – это два основных понятия измерения любой фигуры. Их нельзя путать, хоть они и связаны между собой. Если увеличить, либо уменьшить площадь, то, соответственно, увеличится либо уменьшится его периметр.
Что мы узнали?
Мы узнали, как найти периметр прямоугольника. А также ознакомились с формулой его вычисления. С этой темой можно столкнуться не только при решении математических задач, но и в реальной жизни.
Тест по теме
Оценка статьи
Средняя оценка: 4.5 . Всего получено оценок: 320.
Среди неиссякаемого многообразия геометрических фигур есть те, которые наиболее применимы в нашей жизни, например, параллелограмм, круг, овал и др. Геометрические фигуры повсюду, в связи с этим зачастую возникает необходимость определения их числовых характеристик: площадь, периметр, объем.
Прямоугольник обладает многими отличительными особенностями, исходя из которых выработаны правила вычисления его различных числовых характеристик.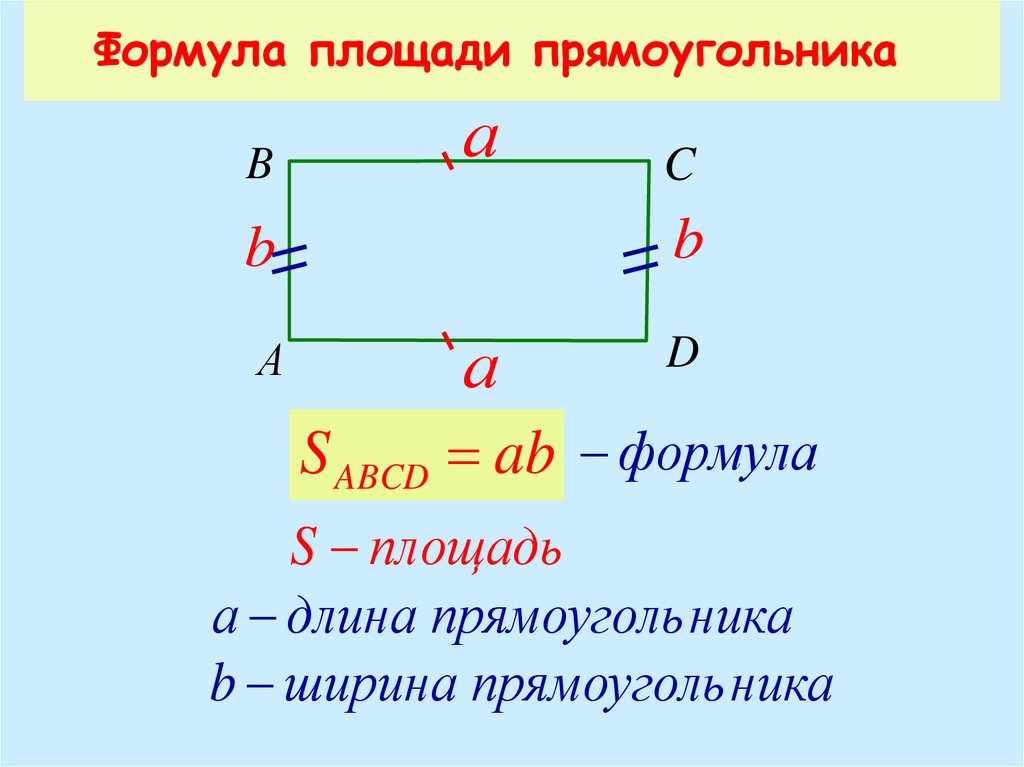 Итак, прямоугольник:
Итак, прямоугольник:
- это плоская геометрическая фигура;
- это четырехугольник;
- это фигура, у которой противоположные стороны равны и параллельны, все углы прямые, т.е. по 90°.
Рассмотрим нахождение значений периметра и площади прямоугольника на конкретном примере:
- имеется прямоугольник ABCD;
- стороны AB и CD равны 5 см;
- стороны BC и AD равны 7 см.
Периметр или длина границы прямоугольника – это сумма длин всех сторон фигуры. Исходя из этого, периметр прямоугольника вычисляется суммированием числовых значений всех четырех его сторон. Периметр ABCD = 5+7+5+7= 2× 5 + 2× 7 = 24 см.
Для вычисления площади прямоугольника существует простая формула: площадь фигуры равна произведению значений любых двух смежных сторон, имеющих общий угол. Площадь ABCD = AB × AC = 5 × 7 = 35 см.
Объясняем p-значения для начинающих Data Scientist’ов / Хабр
Я помню, когда я проходил свою первую зарубежную стажировку в CERN в качестве практиканта, большинство людей все еще говорили об открытии бозона Хиггса после подтверждения того, что он соответствует порогу «пять сигм» (что означает наличие p-значения 0,0000003).
Тогда я ничего не знал о p-значении, проверке гипотез или даже статистической значимости.
Я решил загуглить слово — «p-значение», и то, что я нашел в Википедии, заставило меня еще больше запутаться…
При проверке статистических гипотез p-значение или значение вероятности для данной статистической модели — это вероятность того, что при истинности нулевой гипотезы статистическая сводка (например, абсолютное значение выборочной средней разницы между двумя сравниваемыми группами) будет больше или равна фактическим наблюдаемым результатам.
— Wikipedia
Хорошая работа, Википедия.
Ладно. Я не понял, что на самом деле означает р-значение.
Углубившись в область науки о данных, я наконец начал понимать смысл p-значения и то, где его можно использовать как часть инструментов принятия решений в определенных экспериментах.
Поэтому я решил объяснить р-значение в этой статье, а также то, как его можно использовать при проверке гипотез, чтобы дать вам лучшее и интуитивное понимание р-значений.
Также мы не можем пропустить фундаментальное понимание других концепций и определение p-значения, я обещаю, что сделаю это объяснение интуитивно понятным, не подвергая вас всеми техническими терминами, с которыми я столкнулся.
Всего в этой статье четыре раздела, чтобы дать вам полную картину от построения проверки гипотезы до понимания р-значения и использования его в процессе принятия решений. Я настоятельно рекомендую вам пройтись по всем из них, чтобы получить подробное понимание р-значений:
- Проверка гипотезы
- Нормальное распределение
- Что такое P-значение?
- Статистическая значимость
Это будет весело.
Давайте начнем!
1. Проверка гипотез
Прежде чем мы поговорим о том, что означает р-значение, давайте начнем с разбора проверки гипотез, где р-значение используется для определения статистической значимости наших результатов.
Наша конечная цель — определить статистическую значимость наших результатов.
И статистическая значимость построена на этих 3 простых идеях:
- Проверка гипотезы
- Нормальное распределение
- P-значение
Проверка гипотез используется для проверки обоснованности утверждения (нулевой гипотезы), сделанного в отношении совокупности с использованием выборочных данных. Альтернативная гипотеза — это та, в которую вы бы поверили, если бы нулевая гипотеза оказалась неверной.
Другими словами, мы создадим утверждение (нулевая гипотеза) и используем пример данных, чтобы проверить, является ли утверждение действительным. Если утверждение не соответствует действительности, мы выберем альтернативную гипотезу. Все очень просто.
Чтобы узнать, является ли утверждение обоснованным или нет, мы будем использовать p-значение для взвешивания силы доказательств, чтобы увидеть, является ли оно статистически значимым. Если доказательства подтверждают альтернативную гипотезу, то мы отвергнем нулевую гипотезу и примем альтернативную гипотезу. Это будет объяснено в следующем разделе.
Это будет объяснено в следующем разделе.
Давайте воспользуемся примером, чтобы сделать эту концепцию более ясной, и этот пример будет использоваться на протяжении всей этой статьи для других концепций.
Пример. Предположим, что в пиццерии заявлено, что время их доставки составляет в среднем 30 минут или меньше, но вы думаете, что оно больше чем заявленное. Таким образом, вы проводите проверку гипотезы и случайным образом выбираете время доставки для проверки утверждения:
- Нулевая гипотеза — среднее время доставки составляет 30 минут или меньше
- Альтернативная гипотеза — среднее время доставки превышает 30 минут
- Цель здесь состоит в том, чтобы определить, какое утверждение — нулевое или альтернативное — лучше подтверждается данными, полученными из наших выборочных данных.
Мы будем использовать односторонний тест в нашем случае, так как нам важно только, чтобы среднее время доставки превышало 30 минут. Мы не будем учитывать эту возможность в другом направлении, поскольку последствия того, что среднее время доставки будет меньше или равно 30 минутам, еще более предпочтительны. Здесь мы хотим проверить, есть ли вероятность того, что среднее время доставки превышает 30 минут. Другими словами, мы хотим посмотреть, не обманула ли нас пиццерия.
Мы не будем учитывать эту возможность в другом направлении, поскольку последствия того, что среднее время доставки будет меньше или равно 30 минутам, еще более предпочтительны. Здесь мы хотим проверить, есть ли вероятность того, что среднее время доставки превышает 30 минут. Другими словами, мы хотим посмотреть, не обманула ли нас пиццерия.
Одним из распространенных способов проверки гипотез является использование Z-критерия. Здесь мы не будем вдаваться в подробности, так как хотим лучше понять, что происходит на поверхности, прежде чем погрузиться глубже.
2. Нормальное распределение
Нормальное распределение — это функция плотности вероятности, используемая для просмотра распределения данных.
Нормальное распределение имеет два параметра — среднее (μ) и стандартное отклонение, также называемое сигма (σ).
Среднее — это центральная тенденция распределения. Оно определяет местоположение пика для нормальных распределений. Стандартное отклонение — это мера изменчивости. Оно определяет, насколько далеко от среднего значения склонны падать значения.
Оно определяет, насколько далеко от среднего значения склонны падать значения.
Нормальное распределение обычно связано с правилом 68-95-99.7 (изображение выше).
- 68% данных находятся в пределах 1 стандартного отклонения (σ) от среднего значения (μ)
- 95% данных находятся в пределах 2 стандартных отклонений (σ) от среднего значения (μ)
- 99,7% данных находятся в пределах 3 стандартных отклонений (σ) от среднего значения (μ)
Помните порог «пять сигм» для открытия бозона Хиггса, о котором я говорил в начале? 5 сигм — это около 99,99999426696856% данных, которые должны быть попасть до того, как ученые подтвердили открытие бозона Хиггса. Это был строгий порог, установленный, чтобы избежать любых возможных ложных сигналов.
Классно. Теперь вы можете задаться вопросом: «Как нормальное распределение относится к нашей предыдущей проверке гипотез?»
Поскольку мы использовали Z-тест для проверки нашей гипотезы, нам нужно вычислить Z-баллы (которые будут использоваться в нашей тестовой статистике), которые представляют собой число стандартных отклонений от среднего значения точки данных. В нашем случае каждая точка данных — это время доставки пиццы, которое мы получили.
В нашем случае каждая точка данных — это время доставки пиццы, которое мы получили.
Обратите внимание, что когда мы рассчитали все Z-баллы для каждого времени доставки пиццы и построили стандартную кривую нормального распределения, как показано ниже, единица измерения на оси X изменится с минут на единицу стандартного отклонения, так как мы стандартизировали переменную, вычитая среднее и деля его на стандартное отклонение (см. формулу выше).
Изучение стандартной кривой нормального распределения полезно, потому что мы можем сравнить результаты теста с ”нормальной» популяцией со стандартизированной единицей в стандартном отклонении, особенно когда у нас есть переменная, которая поставляется с различными единицами.
Z-оценка может сказать нам, где лежат общие данные по сравнению со средней популяцией.
Мне нравится, как Уилл Кёрсен выразился: чем выше или ниже Z-показатель, тем менее вероятным будет случайный результат и тем более вероятным будет значимый результат.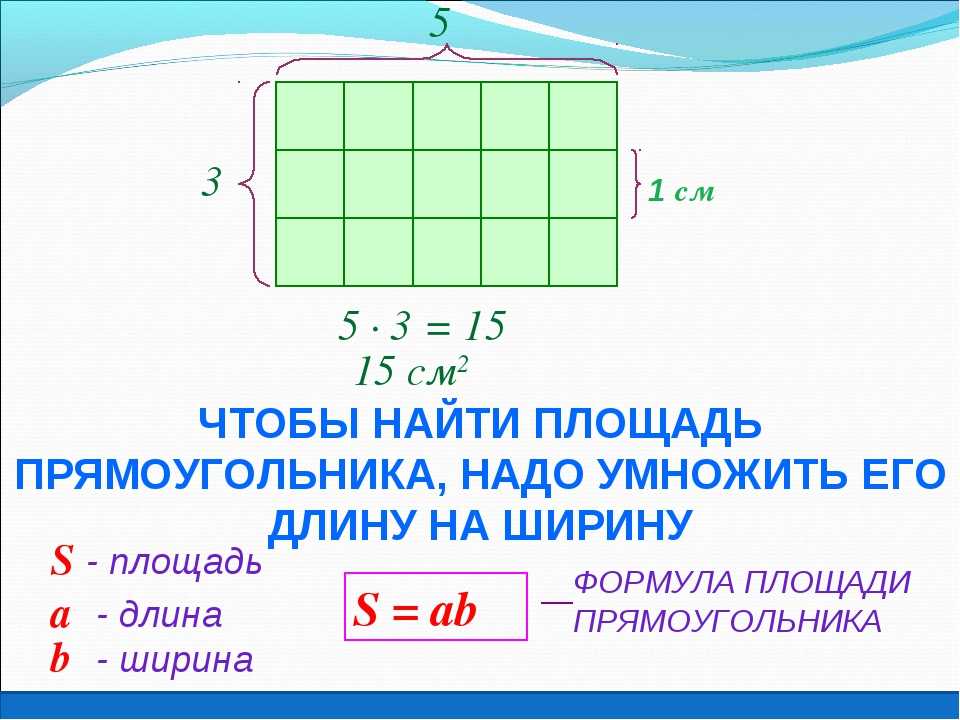
Но насколько высокий (или низкий) показатель считается достаточно убедительным, чтобы количественно оценить, насколько значимы наши результаты?
Кульминация
Здесь нам нужен последний элемент для решения головоломки — p-значение, и проверить, являются ли наши результаты статистически значимыми на основе уровня значимости (также известного как альфа), который мы установили перед началом нашего эксперимента.
3. Что такое P-значение?
Наконец… Здесь мы говорим о р-значении!
Все предыдущие объяснения предназначены для того, чтобы подготовить почву и привести нас к этому P-значению. Нам нужен предыдущий контекст и шаги, чтобы понять это таинственное (на самом деле не столь таинственное) р-значение и то, как оно может привести к нашим решениям для проверки гипотезы.
Если вы зашли так далеко, продолжайте читать. Потому что этот раздел — самая захватывающая часть из всех!
Вместо того чтобы объяснять p-значения, используя определение, данное Википедией (извини Википедия), давайте объясним это в нашем контексте — время доставки пиццы!
Напомним, что мы произвольно отобрали некоторые сроки доставки пиццы, и цель состоит в том, чтобы проверить, превышает ли время доставки 30 минут.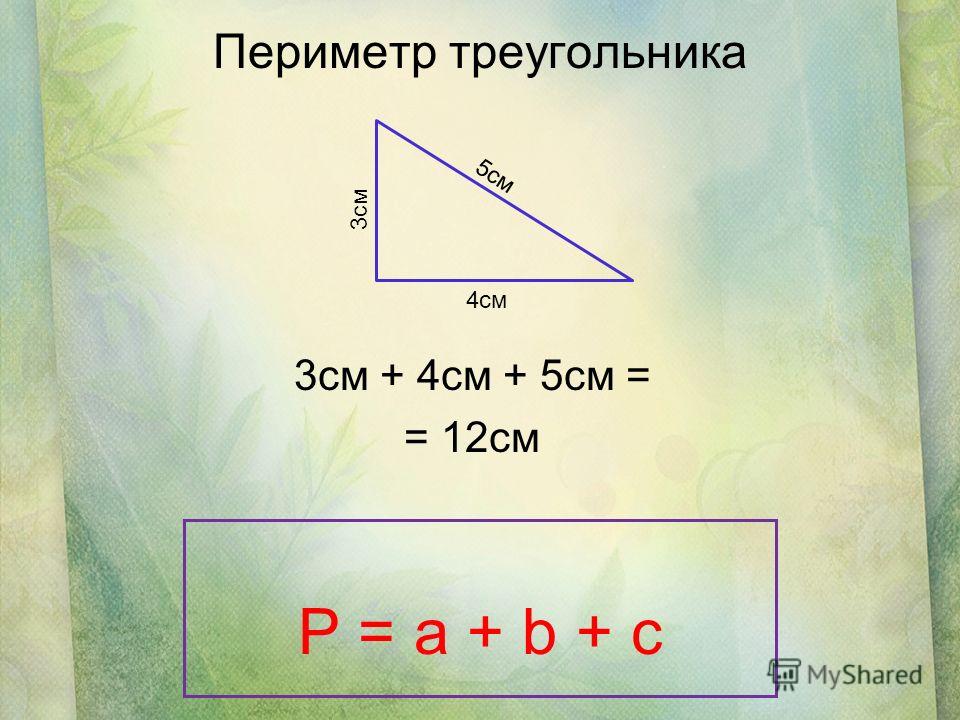 Если окончательные доказательства подтверждают утверждение пиццерии (среднее время доставки составляет 30 минут или меньше), то мы не будем отвергать нулевую гипотезу. В противном случае мы опровергаем нулевую гипотезу.
Если окончательные доказательства подтверждают утверждение пиццерии (среднее время доставки составляет 30 минут или меньше), то мы не будем отвергать нулевую гипотезу. В противном случае мы опровергаем нулевую гипотезу.
Поэтому задача p-значения — ответить на этот вопрос:
Если я живу в мире, где время доставки пиццы составляет 30 минут или меньше (нулевая гипотеза верна), насколько неожиданными являются мои доказательства в реальной жизни?
Р-значение отвечает на этот вопрос числом — вероятностью.
Чем ниже значение p, тем более неожиданными являются доказательства, тем более нелепой выглядит наша нулевая гипотеза.
И что мы делаем, когда чувствуем себя нелепо с нашей нулевой гипотезой? Мы отвергаем ее и выбираем нашу альтернативную гипотезу.
Если р-значение ниже заданного уровня значимости (люди называют его альфа, я называю это порогом нелепости — не спрашивайте, почему, мне просто легче понять), тогда мы отвергаем нулевую гипотезу.
Теперь мы понимаем, что означает p-значение. Давайте применим это в нашем случае.
P-значение в расчете времени доставки пиццы
Теперь, когда мы собрали несколько выборочных данных о времени доставки, мы выполнили расчет и обнаружили, что среднее время доставки больше на 10 минут с p-значением 0,03.
Это означает, что в мире, где время доставки пиццы составляет 30 минут или меньше (нулевая гипотеза верна), есть 3% шанс, что мы увидим, что среднее время доставки, по крайней мере, на 10 минут больше, из-за случайного шума.
Чем меньше p-значение, тем более значимым будет результат, потому что он с меньшей вероятностью будет вызван шумом.
В нашем случае большинство людей неправильно понимают р-значение:
Р-значение 0,03 означает, что есть 3% (вероятность в процентах), что результат обусловлен случайностью — что не соответствует действительности.
Люди часто хотят получить определенный ответ (в том числе и я), и именно поэтому я долго путался с интерпретацией p-значений.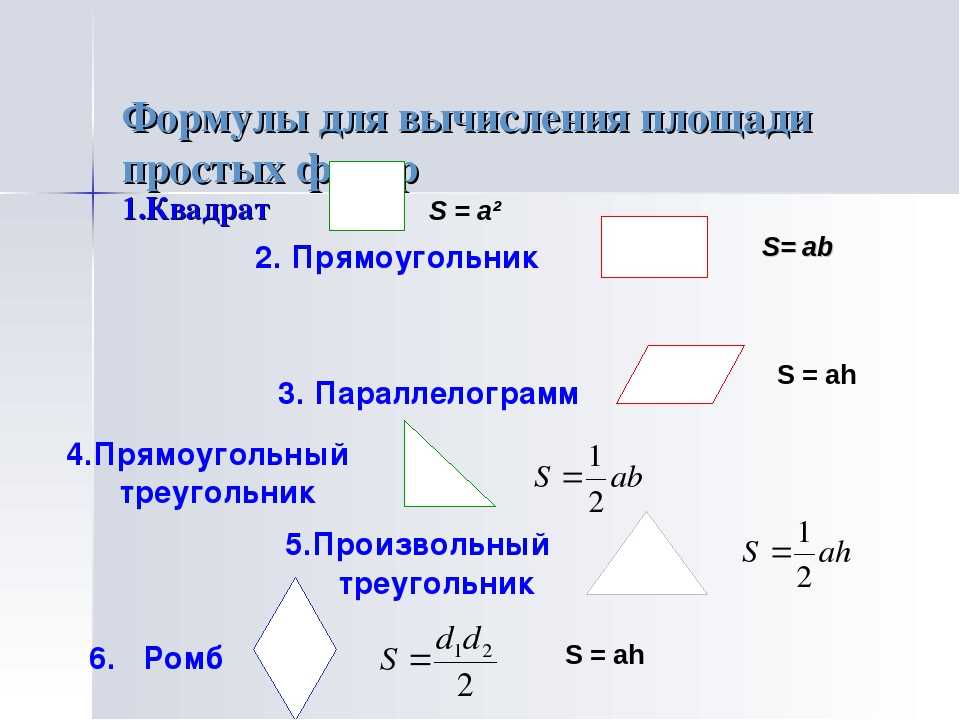
Р-значение ничего не *доказывает*. Это просто способ использовать неожиданность в качестве основы для принятия разумного решения.
— Кэсси Козырков
Вот как мы можем использовать p-значение 0,03, чтобы помочь нам принять разумное решение (ВАЖНО):
- Представьте, что мы живем в мире, где среднее время доставки всегда составляет 30 минут или меньше — потому что мы верим в пиццерию (наше первоначальное убеждение)!
- После анализа времени доставки собранных образцов р-значение на 0,03 ниже, чем уровень значимости 0,05 (предположим, что мы установили это значение перед нашим экспериментом), и мы можем сказать, что результат является статистически значимым.
- Поскольку мы всегда верили пиццерии, что она может выполнить свое обещание доставить пиццу за 30 минут или меньше, нам теперь нужно подумать, имеет ли это убеждение смысл, поскольку результат говорит нам о том, что пиццерия не выполняет свое обещание и результат является статистически значимым.

- Так что же нам делать? Сначала мы пытаемся придумать любой возможный способ сделать наше первоначальное убеждение (нулевая гипотеза) верным. Но поскольку пиццерия постепенно получает плохие отзывы от других людей и часто приводит плохие оправдания, которые привели к задержке доставки, даже мы сами чувствуем себя нелепо, чтобы оправдать пиццерию, и, следовательно, мы решаем отвергнуть нулевую гипотезу.
- Наконец, следующее разумное решение — не покупать больше пиццы в этом месте.
К настоящему времени вы, возможно, уже что-то поняли… В зависимости от нашего контекста, p-значения не используются, чтобы что-либо доказать или оправдать.
По моему мнению, p-значения используются в качестве инструмента для оспаривания нашего первоначального убеждения (нулевая гипотеза), когда результат является статистически значимым. В тот момент, когда мы чувствуем себя нелепо с нашим собственным убеждением (при условии, что р-значение показывает, что результат статистически значим), мы отбрасываем наше первоначальное убеждение (отвергаем нулевую гипотезу) и принимаем разумное решение.
4. Статистическая значимость
Наконец, это последний этап, когда мы собираем все вместе и проверяем, является ли результат статистически значимым.
Недостаточно иметь только р-значение, нам нужно установить порог (уровень значимости — альфа). Альфа всегда должна быть установлена перед экспериментом, чтобы избежать смещения. Если наблюдаемое р-значение ниже, чем альфа, то мы заключаем, что результат является статистически значимым.
Основное правило — установить альфа равным 0,05 или 0,01 (опять же, значение зависит от вашей задачи).
Как упоминалось ранее, предположим, что мы установили альфа равным 0,05, прежде чем мы начали эксперимент, полученный результат является статистически значимым, поскольку р-значение 0,03 ниже, чем альфа.
Для справки ниже приведены основные этапы всего эксперимента:
- Сформулируйте нулевую гипотезу
- Сформулируйте альтернативную гипотезу
- Определите значение альфа для использования
- Найдите Z-показатель, связанный с вашим альфа-уровнем
- Найдите тестовую статистику, используя эту формулу
- Если значение тестовой статистики меньше Z-показателя альфа-уровня (или p-значение меньше альфа-значения), отклоните нулевую гипотезу.
 В противном случае не отвергайте нулевую гипотезу.
В противном случае не отвергайте нулевую гипотезу.
Если вы хотите узнать больше о статистической значимости, не стесняйтесь посмотреть эту статью — Объяснение статистической значимости, написанная Уиллом Керсеном.
Последующие размышления
Здесь много чего нужно переваривать, не так ли?
Я не могу отрицать, что p-значения по своей сути сбивают с толку многих людей, и мне потребовалось довольно много времени, чтобы по-настоящему понять и оценить значение p-значений и то, как они могут быть применены в рамках нашего процесса принятия решений в качестве специалистов по данным.
Но не слишком полагайтесь на p-значения, поскольку они помогают только в небольшой части всего процесса принятия решений.
Я надеюсь, что мое объяснение p-значений стало интуитивно понятным и полезным в вашем понимании того, что в действительности означают p-значения и как их можно использовать при проверке ваших гипотез.
Сам по себе расчет р-значений прост. Трудная часть возникает, когда мы хотим интерпретировать p-значения в проверке гипотез. Надеюсь, что теперь трудная часть станет для вас немного легче.
Трудная часть возникает, когда мы хотим интерпретировать p-значения в проверке гипотез. Надеюсь, что теперь трудная часть станет для вас немного легче.
Если вы хотите узнать больше о статистике, я настоятельно рекомендую вам прочитать эту книгу (которую я сейчас читаю!) — Практическая статистика для специалистов по данным, специально написанная для data scientists, чтобы разобраться с фундаментальными концепциями статистики.
Узнайте подробности, как получить востребованную профессию с нуля или Level Up по навыкам и зарплате, пройдя платные онлайн-курсы SkillFactory:
- Обучение профессии Data Science с нуля (12 месяцев)
- Профессия аналитика с любым стартовым уровнем (9 месяцев)
- Курс по Machine Learning (12 недель)
- Курс «Python для веб-разработки» (9 месяцев)
- Курс по DevOps (12 месяцев)
- Профессия Веб-разработчик (8 месяцев)
Читать еще
- Тренды в Data Scienсe 2020
- Data Science умерла.
 Да здравствует Business Science
Да здравствует Business Science - Крутые Data Scientist не тратят время на статистику
- Как стать Data Scientist без онлайн-курсов
- 450 бесплатных курсов от Лиги Плюща
- Data Science для гуманитариев: что такое «data»
- Data Scienсe на стероидах: знакомство с Decision Intelligence
Как найти значение P: процесс и расчеты
Значения P повсюду в статистике. Они есть во всех типах проверки гипотез. Но как рассчитать p-значение? Неудивительно, что точные расчеты зависят от теста. Однако существует общий процесс, применимый к нахождению значения p.
В этом посте вы узнаете, как найти значение p. Я начну с того, что покажу вам общий процесс проверки всех гипотез. Затем я перейду к пошаговому примеру, показывающему расчеты для значения p. Этот пост включает в себя калькулятор, чтобы вы могли применить то, что вы узнали.
Общий процесс определения значения P
Чтобы найти значение p для вашего образца, выполните следующие действия:
- Определите правильную статистику теста.

- Рассчитайте статистику теста, используя соответствующие свойства вашего образца.
- Укажите характеристики выборочного распределения тестовой статистики.
- Поместите тестовую статистику в выборочное распределение, чтобы найти значение p.
Прежде чем перейти к примеру с расчетами, я резюмирую цель каждого шага. Эта часть говорит вам «почему». В разделе примеров расчетов я показываю «как».
Определите правильную тестовую статистику
Все тесты гипотез сводят ваши выборочные данные к одному числу, известному как тестовая статистика. T-тесты используют t-значения. F-тесты используют F-значения. Тесты хи-квадрат используют значения хи-квадрат. Выбор правильного зависит от типа данных, которые у вас есть, и от того, как вы хотите их анализировать. Прежде чем вы сможете найти значение p, вы должны определить, какой тест гипотезы и тестовую статистику вы будете использовать.
Статистика тестов оценивает, насколько данные выборки согласуются с нулевой гипотезой. По мере того, как тестовая статистика становится более экстремальной, она указывает на большую разницу между данными вашей выборки и нулевой гипотезой.
По мере того, как тестовая статистика становится более экстремальной, она указывает на большую разницу между данными вашей выборки и нулевой гипотезой.
Расчет статистики теста
Способ расчета статистики теста зависит от того, какой из них вы используете. Неудивительно, что метод расчета тестовой статистики зависит от типа теста. Следовательно, чтобы рассчитать значение p для любого теста, вам нужно знать правильную формулу статистики теста.
Чтобы узнать больше о тестовой статистике и о том, как ее рассчитать для других тестов, прочитайте мою статью Test Statistics.
Укажите свойства выборочного распределения тестовой статистики
Статистика тестов не имеет единиц измерения, поэтому их сложно интерпретировать самостоятельно. Вам нужно поместить их в более широкий контекст, чтобы понять, насколько они экстремальны.
Распределение выборки для тестовой статистики обеспечивает этот контекст. Распределения выборки — это тип распределения вероятностей. Следовательно, они позволяют вам рассчитать вероятности, связанные с экстремальностью вашей тестовой статистики, что позволяет нам найти значение p!
Следовательно, они позволяют вам рассчитать вероятности, связанные с экстремальностью вашей тестовой статистики, что позволяет нам найти значение p!
Например, что означает значение t, равное двум? Это важно? Как вы увидите в примере, t-распределение отвечает на этот вопрос и позволяет нам рассчитать p-значение.
Как и любое распределение, одно и то же выборочное распределение (например, t-распределение) может иметь различные формы в зависимости от его параметров. На этом шаге вам необходимо определить характеристики выборочного распределения, которые соответствуют вашему дизайну и данным.
Обычно это влечет за собой указание степеней свободы (меняет свою форму) и является ли тест одно- или двусторонним (влияет на направления, в которых тест может обнаруживать эффекты). По сути, вы берете общее распределение выборки и адаптируете его к своему исследованию, чтобы оно обеспечивало правильные вероятности для нахождения значения p.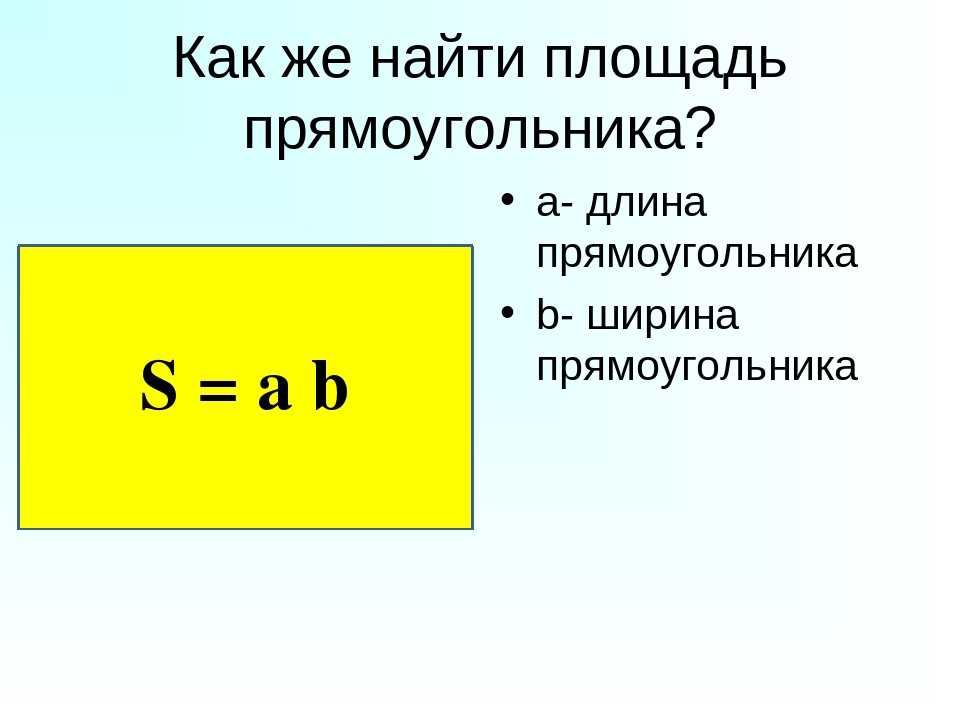
Распределение выборки каждой тестовой статистики имеет уникальные свойства, которые необходимо указать. В конце этого поста я даю ссылки на несколько.
Узнайте больше о степенях свободы и односторонних и двусторонних тестах.
Размещение тестовой статистики в распределении выборки для определения значения P
Наконец, пришло время найти значение p, потому что у нас все готово. Мы рассчитали нашу тестовую статистику и определили правильные свойства для ее выборочного распределения. Теперь нам нужно найти вероятность значений, более экстремальных, чем наша наблюдаемая тестовая статистика.
В этом контексте более экстремальный означает большее расстояние от нулевого значения в обоих направлениях для двустороннего теста или в одном направлении для одностороннего теста.
На данный момент существует два способа использования тестовой статистики и распределения для расчета значения p. Формулы для распределения вероятностей относительно сложны. Следовательно, вы не будете вычислять его напрямую. Вместо этого вы будете использовать либо онлайн-калькулятор, либо статистическую таблицу для тестовой статистики. Я покажу вам оба подхода на пошаговом примере.
Вместо этого вы будете использовать либо онлайн-калькулятор, либо статистическую таблицу для тестовой статистики. Я покажу вам оба подхода на пошаговом примере.
Таким образом, вычисление p-значения включает в себя идентификацию и вычисление статистики теста, а затем размещение ее в распределении выборки, чтобы найти вероятность более экстремальных значений!
Давайте посмотрим весь этот процесс в действии на примере!
Пошаговый пример того, как найти значение P для Т-критерия
В этом примере предположим, что нам нужно определить, отличается ли среднее значение выборки от гипотетического значения. Нам дана примерная статистика ниже, и нам нужно найти значение p.
- Среднее значение: 330,6
- Стандартное отклонение: 154,2
- Размер образца: 25
- Значение нулевой гипотезы: 260
Давайте рассмотрим пошаговый процесс расчета p-значения.
Во-первых, нам нужно определить правильную тестовую статистику. Поскольку мы сравниваем одно среднее значение с нулевым значением, нам нужно использовать t-критерий с одной выборкой. Следовательно, t-значение — это наша тестовая статистика, а t-распределение — это наше распределение выборки.
Поскольку мы сравниваем одно среднее значение с нулевым значением, нам нужно использовать t-критерий с одной выборкой. Следовательно, t-значение — это наша тестовая статистика, а t-распределение — это наше распределение выборки.
Во-вторых, посчитаем тестовую статистику. Формула t-значения для t-критерия с 1 выборкой выглядит следующим образом:
Где:
- x̄ — выборочное среднее.
- µ 0 — значение нулевой гипотезы.
- с — стандартное отклонение выборки.
- n — размер выборки
- В совокупности знаменатель представляет собой стандартную ошибку среднего значения.
Давайте введем наши выборочные значения в уравнение для расчета t-значения.
В-третьих, нам нужно указать свойства выборочного распределения, чтобы найти значение p. Нам понадобятся степени свободы.
Степени свободы для одновыборочного t-критерия равны n – 1. Размер нашей выборки равен 25. Следовательно, у нас есть 24 DF.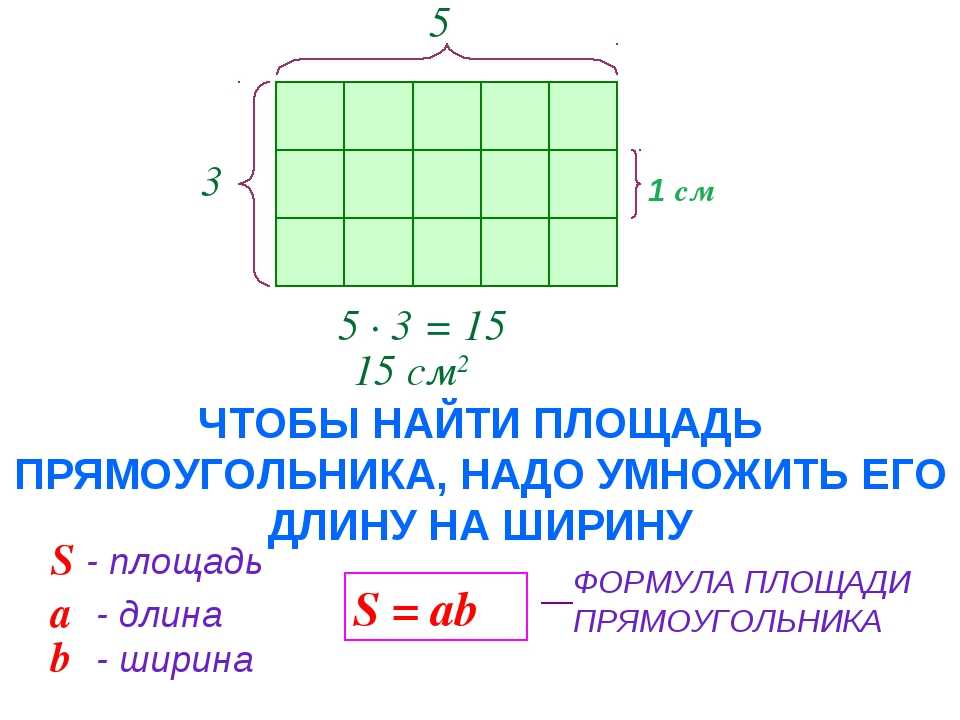 Мы будем использовать двусторонний тест, который является стандартным.
Мы будем использовать двусторонний тест, который является стандартным.
Теперь у нас есть вся необходимая информация для расчета p-значения. Я покажу вам два способа сделать последний шаг!
Калькулятор P-значения
Одним из способов является использование онлайн-калькулятора p-значения, подобного приведенному ниже.
Введите следующее в калькулятор для нашего примера t-критерия.
- В Что тебе нужно? , выберите Двустороннее p-значение (по умолчанию).
- В Что у тебя есть? , выберите t-score .
- В Степени свободы (d) введите 24 .
- В Ваш t-значение введите 2,289 .
Калькулятор показывает результат 0,031178.
Ну вот! Используя стандартный уровень значимости 0,05, наши результаты статистически значимы!
Использование статистической таблицы для определения значения P
Другим распространенным методом является использование статистической таблицы. В этом случае нам нужно использовать t-таблицу. В этом примере я обрежу строки. Вы можете найти мой полный стол здесь: T-Table.
В этом случае нам нужно использовать t-таблицу. В этом примере я обрежу строки. Вы можете найти мой полный стол здесь: T-Table.
Этот метод не найдет точное значение p, но вы найдете диапазон и узнаете, являются ли ваши результаты статистически значимыми.
Начните с поиска в строке 24 степеней свободы, выделенных светло-зеленым цветом. Нам нужно найти, где наш t-показатель 2,289подходит. Я выделяю два табличных значения, между которыми находится наше t-значение, 2,064 и 2,492. Затем мы смотрим на двустороннюю строку вверху, чтобы найти соответствующие значения p для двух t-значений.
В этом случае наше значение t, равное 2,289, дает значение p между 0,02 и 0,05 для двустороннего теста. Наши результаты статистически значимы и согласуются с более точными результатами калькулятора.
Отображение значения P на диаграмме
В приведенном выше примере вы видели, как рассчитать значение p, исходя из выборочной статистики. Мы рассчитали t-значение и поместили его в применимое t-распределение. Я нахожу, что расчеты и цифры сами по себе сухие. Я люблю рисовать графики, когда это возможно, поэтому я буду использовать график распределения вероятностей, чтобы проиллюстрировать пример.
Я нахожу, что расчеты и цифры сами по себе сухие. Я люблю рисовать графики, когда это возможно, поэтому я буду использовать график распределения вероятностей, чтобы проиллюстрировать пример.
Используя статистическое программное обеспечение, я создам графический эквивалент вычисления p-значения выше.
На этой диаграмме две заштрихованные области, потому что мы провели двусторонний тест. Каждый регион имеет вероятность 0,01559. Когда вы суммируете их, вы получаете p-значение 0,03118. Другими словами, вероятность попадания t-значения в любую заштрихованную область, когда нулевая гипотеза верна, составляет 0,03118.
Я показал вам, как найти значение p для t-критерия. Нажмите на ссылки ниже, чтобы увидеть, как это работает для других тестов гипотез:
- F-критерий однофакторного дисперсионного анализа
- Критерий независимости хи-квадрат
Теперь, когда мы нашли значение p, как его точно интерпретировать? Если вы выходите за рамки значимого/незначимого решения и действительно хотите понять, что это значит, прочитайте мой пост «Интерпретация значений P».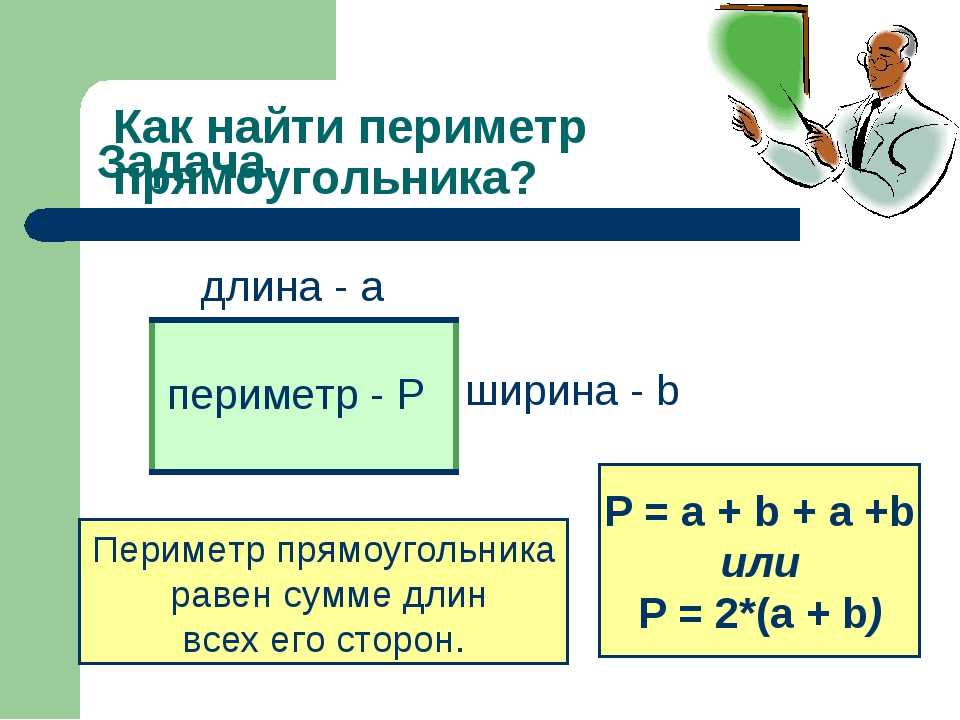
Если вы изучаете проверку гипотез и вам нравится подход, который я использую в своем блоге, ознакомьтесь с моей книгой «Проверка гипотез»! Вы можете найти его на Amazon и других розничных магазинах.
Калькулятор p-значения | Формула | Интерпретация
Создано Bogna Szyk и Anna Szczepanek, PhD
Отзыв от Jack Bowater
Последнее обновление: 19 июля 2022 г.
Содержание:- Что такое p-значение?
- Как рассчитать p-значение из тестовой статистики?
- Как интерпретировать p-значение?
- Как использовать калькулятор p-значения, чтобы найти p-значение из тестовой статистики?
- Как найти значение p по z-значению?
- Как найти p-значение по t?
- p-значение по показателю хи-квадрат (показатель χ2)
- p-значение по F-показателю
- Часто задаваемые вопросы
Добро пожаловать в наш калькулятор p-значения! Вам больше никогда не придется задаваться вопросом, как найти p-значение, так как здесь вы можете определить одностороннее и двустороннее p-значения из тестовой статистики, следуя всем наиболее популярным распределениям: нормальному, t-Стьюдента, хи-квадрат и P-значения Snedecor F.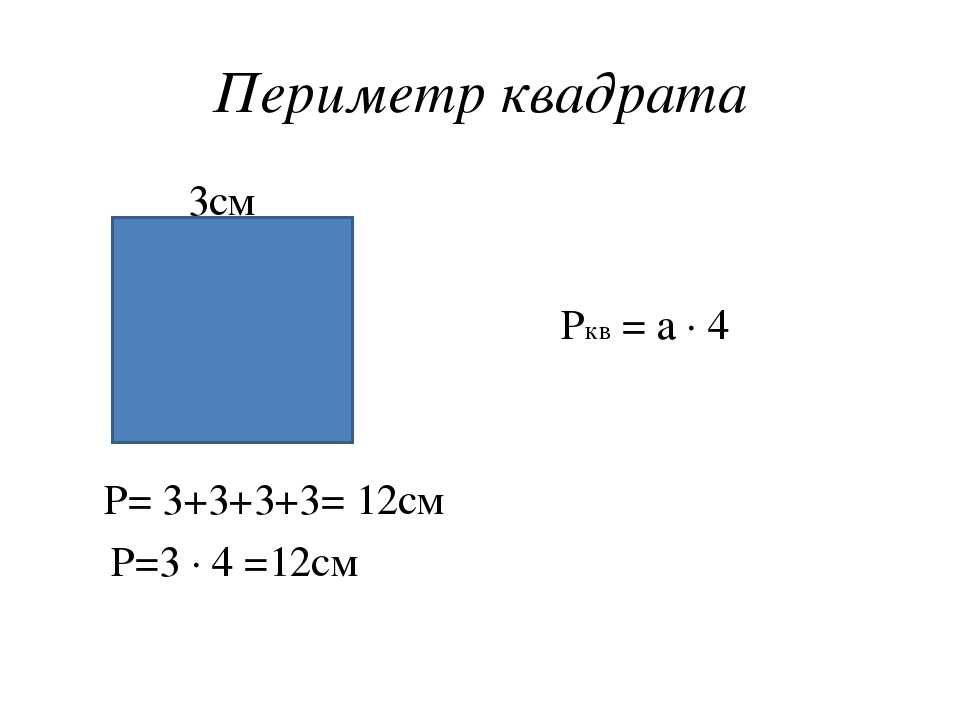
встречаются во всех науках, но многие люди находят эту концепцию немного пугающей. Не волнуйтесь — в этой статье мы объясним не только значение p, но и как правильно интерпретировать p-значения . Вам когда-нибудь было интересно, как рассчитать p-значение вручную? Мы также предоставляем вам все необходимые формулы!
Что такое р-значение?
Формально p-значение представляет собой вероятность того, что тестовая статистика выдаст значения, по крайней мере столь же экстремальные, как значение, полученное для вашей выборки . Важно помнить, что эта вероятность рассчитывается в предположении, что нулевая гипотеза верна !
Более интуитивно, р-значение отвечает на вопрос:
Предполагая, что я живу в мире, где верна нулевая гипотеза, насколько вероятно, что для другой выборки тест, который я выполняю, сгенерирует значение на по крайней мере столь же экстремально, как тот, который я наблюдал для образца, который у меня уже есть?
Это альтернативная гипотеза , которая определяет, что на самом деле означает «экстремальный» , поэтому p-значение зависит от альтернативной гипотезы, которую вы формулируете: левосторонней, правосторонней или двусторонней.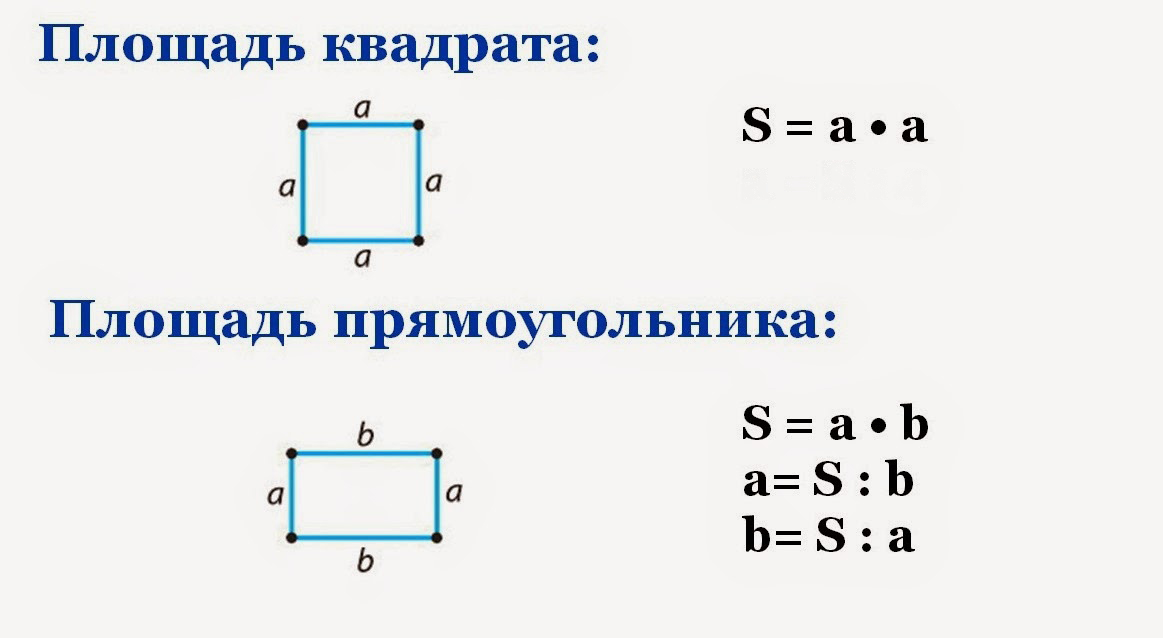 В формулах ниже
В формулах ниже S означает тестовую статистику, x — значение, полученное для данной выборки, а Pr(event | H 0 ) — вероятность события, рассчитанную в предположении, что H 0 верно:
Левосторонний тест:
p-значение = Pr(S ≤ x | H 0 )Правосторонний тест:
p-значение = Pr(S ≥ x | H 0 )Двусторонний тест:
p-значение = 2 * min{Pr(S ≤ x | H 0 ), Pr(S ≥ x | H 0 )}(через
min{a,b}мы обозначаем меньшее число изaиb.)Если распределение тестовой статистики при H 0 является симметричным относительно 0 , то
p-значение = 2 * Pr(S ≥ |x| | H 0 )или, что то же самое,
p-value = 2 * Pr(S ≤ -|x| | H 0 )
Поскольку картинка стоит тысячи слов, давайте проиллюстрируем эти определения.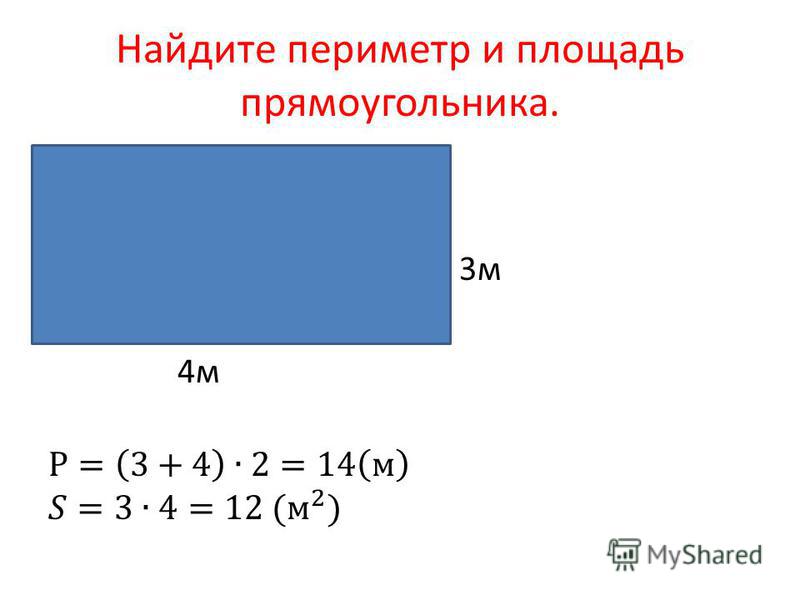 Здесь мы используем тот факт, что вероятность можно четко изобразить как площадь под кривой плотности для данного распределения. Мы даем два набора картинок: один для симметричного распределения, а другой для асимметричного (несимметричного) распределения.
Здесь мы используем тот факт, что вероятность можно четко изобразить как площадь под кривой плотности для данного распределения. Мы даем два набора картинок: один для симметричного распределения, а другой для асимметричного (несимметричного) распределения.
- Симметричный случай: нормальное распределение
- Несимметричный случай: распределение хи-квадрат
На последнем рисунке (двустороннее значение p для асимметричного распределения) площадь левой части равна площади правой части.
Чтобы определить p-значение, вам нужно знать распределение статистики вашего теста в предположении, что нулевая гипотеза верна . Затем с помощью кумулятивной функции распределения ( cdf ) этого распределения мы можем выразить вероятность того, что тестовая статистика будет не менее экстремальной, чем ее значение x для выборки:
Левосторонний тест:
p-value = cdf(x)Правосторонний тест:
p-значение = 1 - cdf(x)Двусторонний тест:
p-значение = 2 * min{cdf(x) , 1 - cdf(x)}Если распределение тестовой статистики по H 0 является симметричным относительно 0 , то двустороннее p-значение может быть упрощено до
p-value = 2 * cdf(-|x|), или, эквивалентно, какp-value = 2 - 2 * cdf(|x|)
Распределения вероятностей, наиболее распространенные при проверке гипотез, как правило, имеют сложные формулы cdf, и поиск p-значения вручную может быть невозможен. Вам, вероятно, придется прибегнуть к помощи компьютера или статистической таблицы, где люди собрали приблизительные значения cdf.
Вам, вероятно, придется прибегнуть к помощи компьютера или статистической таблицы, где люди собрали приблизительные значения cdf.
Ну, теперь вы знаете, как вычислить p-значение, но… зачем вообще нужно вычислять это число? При проверке гипотез подход 90 122 p-значения является альтернативой подходу 90 123 критического значения. Напомним, что последний требует, чтобы исследователи заранее установили уровень значимости α, который представляет собой вероятность отклонения нулевой гипотезы, когда она верна (то есть ошибка I типа ). Когда у вас есть p-значение, вам просто нужно сравнить его с любым заданным α, чтобы быстро решить, отклонять нулевую гипотезу или нет на этом уровне значимости α. Подробнее см. в следующем разделе, где мы объясняем, как интерпретировать p-значения.
Как интерпретировать p-значение?
Как мы упоминали выше, p-значение является ответом на следующий вопрос:
Если предположить, что я живу в мире, где верна нулевая гипотеза, насколько вероятно, что для другой выборки тест, который я выполнение будет генерировать значение, по крайней мере, столь же экстремальное, как то, которое я наблюдал для образца, который у меня уже есть?
Что это значит для вас? Итак, у вас есть два варианта:
- Высокое значение p означает, что ваши данные хорошо совместимы с нулевой гипотезой; и
- Небольшое значение p свидетельствует против нулевой гипотезы , так как это означает, что ваш результат был бы очень маловероятным, если бы нулевая гипотеза была верна.

Однако может случиться так, что нулевая гипотеза верна, но ваша выборка очень необычна! Например, представьте, что мы изучили действие нового лекарства и получили p-значение 0,03 . Это означает, что в 90 240 3 % 90 241 подобных исследований только случайный случай все еще мог бы дать значение тестовой статистики, которое мы получили, или даже более экстремальное значение, даже если бы лекарство вообще не действовало!
На вопрос «что такое p-значение» можно также ответить следующим образом: p-значение — это наименьший уровень значимости, при котором нулевая гипотеза будет отвергнута. Итак, если вы теперь хотите принять решение относительно нулевой гипотезы на каком-то уровне значимости α , просто сравните свое значение p с α :
- Если
значение p ≤ α, то вы отклонить нулевую гипотезу и принять альтернативную гипотезу; и - Если
p-значение ≥ α, то у вас недостаточно доказательств, чтобы отвергнуть нулевую гипотезу.
Очевидно, судьба нулевой гипотезы зависит от α . Например, если бы p-значение было 0,03 , мы бы отклонили нулевую гипотезу на уровне значимости 0,05 , но не на уровне 0,01 . Вот почему уровень значимости должен быть указан заранее, а не удобно адаптирован после того, как p-значение установлено! Уровень значимости 0.05 — самое распространенное значение, но в нем нет ничего волшебного. Здесь вы можете увидеть, к чему может привести слишком сильная вера в порог 0,05 . Всегда лучше указать p-значение и позволить читателю сделать собственные выводы.
Кроме того, имейте в виду, что знания предметной области (и общая причина) имеют решающее значение. В противном случае, бездумно применяя статистические принципы, можно легко прийти к статистически значимым, несмотря на то, что вывод будет на 100% неверным.
Поскольку наш калькулятор p-значения к вашим услугам, вам больше не нужно задаваться вопросом, как найти p-значение из всех этих сложных тестовых статистических данных! Вот шаги, которые вам нужно выполнить:
Выберите альтернативную гипотезу : двустороннюю, правостороннюю или левостороннюю.

Расскажите нам распределение вашей тестовой статистики при нулевой гипотезе: это N(0,1), t-Стьюдент, хи-квадрат или F Снедекора? Если вы не уверены, проверьте разделы ниже, так как они посвящены этим дистрибутивам.
При необходимости укажите степени свободы распределения тестовой статистики.
Введите значение тестовой статистики , рассчитанной для вашей выборки данных.
Наш калькулятор определяет p-значение из тестовой статистики и предоставляет решение, которое необходимо принять относительно нулевой гипотезы. Стандартный уровень значимости по умолчанию равен 0,05.
Перейти к расширенный режим , если вам нужно увеличить точность , с которой выполняются вычисления, или изменить уровень значимости .
Как найти значение p по z-значению?
С точки зрения кумулятивной функции распределения (cdf) стандартного нормального распределения, которое традиционно обозначается как Φ , p-значение задается следующими формулами:
Левосторонний z-критерий:
p-значение = Φ(Z оценка )Правосторонний z-критерий:
p-значение = 1 - Φ(Z оценка )Двусторонний z-критерий:
значение p = 2 * Φ(−|Z оценка |)
или
значение p = 2 - 2 * Φ(|Z оценка |)
Мы используем Z-оценку , если статистика теста примерно соответствует стандартному нормальному распределению N(0,1) .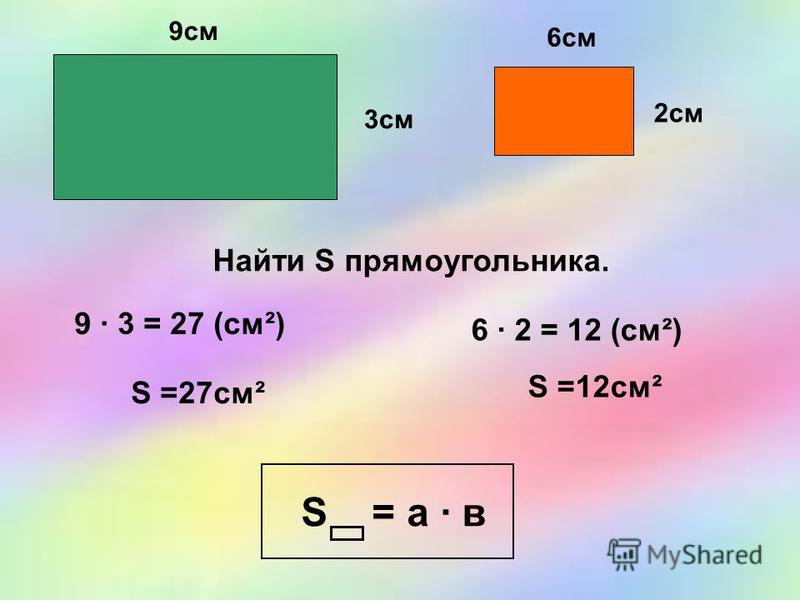 Благодаря центральной предельной теореме вы можете рассчитывать на аппроксимацию, если у вас есть большая выборка (скажем, не менее 50 точек данных) и вы относитесь к своему распределению как к нормальному.
Благодаря центральной предельной теореме вы можете рассчитывать на аппроксимацию, если у вас есть большая выборка (скажем, не менее 50 точек данных) и вы относитесь к своему распределению как к нормальному.
Z-критерий чаще всего относится к проверке среднего значения совокупности или разницы между двумя средними значениями совокупности, в частности между двумя пропорциями. Вы также можете найти Z-тесты в оценках максимального правдоподобия.
СтефанПоль / CC0 wikimedia.org
Как найти p-значение по t?
Значение p из t-показателя определяется следующими формулами, в которых cdf==t,d== обозначает кумулятивную функцию распределения t-распределения Стьюдента с d степенями свободы:
Левосторонний t-критерий:
p-значение = cdf t, d (t оценка )Правосторонний t-критерий:
p-значение = 1 - cdf t,d (t оценка )Двусторонний t-критерий:
p-значение = 2 * cdf t,d (−|t оценка |)
или
p-значение = 2 - 2 * cdf t, d (|t оценка |)
Используйте параметр t-score , если ваша тестовая статистика следует распределению t-Стьюдента .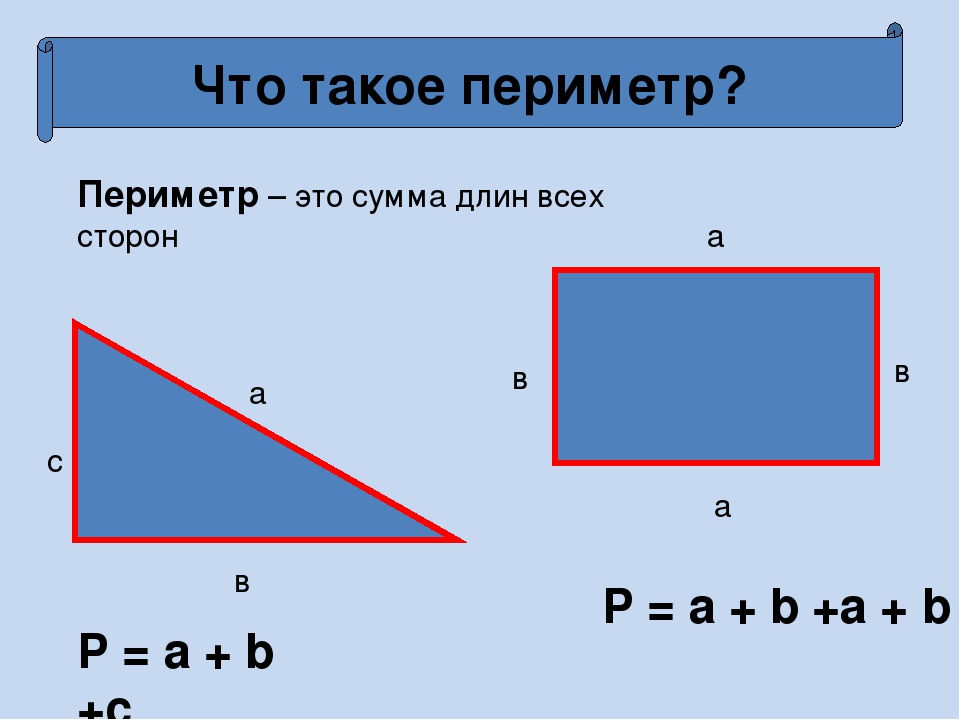 Это распределение имеет форму , похожую на N(0,1) (колоколообразную и симметричную), но имеет более тяжелые хвосты — точная форма зависит от параметра, называемого степенями свободы . Если число степеней свободы велико (> 30), что обычно происходит для больших выборок, распределение t-Стьюдента практически неотличимо от нормального распределения N (0,1).
Это распределение имеет форму , похожую на N(0,1) (колоколообразную и симметричную), но имеет более тяжелые хвосты — точная форма зависит от параметра, называемого степенями свободы . Если число степеней свободы велико (> 30), что обычно происходит для больших выборок, распределение t-Стьюдента практически неотличимо от нормального распределения N (0,1).
Скбкекас / CC BY wikimedia.org
Наиболее распространенными t-тестами являются тесты для популяции означает с неизвестным стандартным отклонением популяции или для разницы между средними значениями двух популяций с равными или неравными, но неизвестными стандартными отклонениями популяции. Существует также t-критерий для парных (зависимых) выборок .
значение p из показателя хи-квадрат (значение χ2)
Используйте параметр χ²-значение при выполнении теста, в котором статистика теста соответствует χ²-распределению .
Это распределение возникает, если, например, взять сумму квадратов переменных, каждая из которых соответствует нормальному распределению N(0,1). Не забудьте проверить количество степеней свободы χ²-распределения вашей тестовой статистики!
Geek3 / CC BY wikimedia.org
Как найти p-значение по показателю хи-квадрат ? Это можно сделать с помощью следующих формул, в которых cdf χ²,d обозначает кумулятивную функцию распределения χ²-распределения с d степенями свободы:
Левосторонний χ²-критерий:
p-value = cdf χ²,d (χ² оценка )Правосторонний χ²-тест:
p-value = 1 - cdf χ²,d (χ² оценка )Помните, что χ²-критерии согласия и независимости являются правосторонними тестами! (см.
 ниже)
ниже)Двусторонний χ²-критерий:
p-значение =2 * min{cdf χ²,d (χ² оценка ), 1 - cdf χ²,d (χ² оценка )}(через
min{a,b}обозначим меньшее из чиселaиb.)
Наиболее популярными тестами, дающими оценку χ², являются следующие:
Проверка того, имеет ли дисперсия нормально распределенных данных некоторое заранее определенное значение. В этом случае тестовая статистика имеет χ²-распределение с 90 240 n — 1 90 241 степенями свободы, где 90 240 n 90 241 — объем выборки. Это может быть односторонний или двусторонний тест .
Тест на пригодность проверяет, согласуется ли эмпирическое (выборочное) распределение с некоторым ожидаемым распределением вероятностей. В этом случае тестовая статистика следует χ²-распределению с 90 240 k — 1 90 241 степенями свободы, где 90 240 k 90 241 — число классов, на которые разбита выборка.
 Это правосторонний тест .
Это правосторонний тест .Тест на независимость используется для определения наличия статистически значимой связи между двумя переменными. В этом случае его тестовая статистика основана на таблице непредвиденных обстоятельств и следует χ²-распределению с
(r - 1)(c - 1)степеней свободы, гдеr— количество строк, аc— количество столбцов в этой таблице непредвиденных обстоятельств. Это также правосторонний тест .
p-значение из F-показателя
Наконец, параметр F-показателя следует использовать при выполнении теста, в котором статистика теста соответствует F-распределению , также известному как распределение Фишера-Снедекора. Точная форма F-распределения зависит от две степени свободы .
IkamusumeFan / CC BY-SA wikimedia.
 org
org Чтобы увидеть, откуда берутся эти степени свободы, рассмотрим независимые случайные величины X и Y , которые следуют χ²-распределениям со степенями свободы d 1 и d 2 (X/d 1 )/(Г/д 2 ) следует F-распределению с (d 1 , d 2 ) - степенями свободы. По этой причине два параметра d 1 и d 2 также называются степенями свободы в числителе и знаменателе .
Значение p из F-показателя дается следующими формулами, где мы позволяем cdf F,d 1 ,d 2 обозначать кумулятивную функцию распределения F-распределения, где (д 1 , д 2 ) -степени свободы:
Левосторонний F-критерий:
p-value = cdf F,d 1 ,d 2 (F оценка )Правосторонний F-критерий:
p-value = 1 - cdf F,d 1 ,d 2 (F оценка )Двусторонний F-критерий:
p-значение =2 * мин{cdf F,d 1 ,d 2 (F счет ), 1 - cdf F,d 1 ,d 2 (F счет ) }(через
min{a,b}мы обозначаем меньшее из чиселaиb. )
)
Ниже мы перечисляем наиболее важные тесты, которые дают F-показатели. Все они правосторонние тесты .
Критерий равенства дисперсий в двух нормально распределенных совокупностях . Его тестовая статистика соответствует F-распределению с 90 240 (n - 1, m - 1) 90 241 степенями свободы, где 90 240 n 90 241 и 90 240 m 90 241 - соответствующие размеры выборки.
Дисперсионный анализ используется для проверки равенства средних в трех или более группах, полученных из нормально распределенных совокупностей с равными дисперсиями. Приходим к F-распределению с 90 240 (k - 1, n - k) 90 241 -степеней свободы, где 90 240 k 90 241 - число групп, а
n– общий объем выборки (по всем группам вместе).Тест для общей значимости регрессионного анализа . Статистика теста имеет F-распределение с 90 240 (k - 1, n - k) 90 241 -степеней свободы, где 90 240 n 90 241 - размер выборки, а 90 240 k 90 241 - количество переменных (включая точку пересечения).

С наличием линейной зависимости , установленной в вашей выборке данных с помощью вышеуказанного теста, вы можете рассчитать коэффициент детерминации, R², который указывает на сила этой связи .
Тест для сравнения двух вложенных регрессионных моделей . Статистика теста следует F-распределению с
(k 2 - k 1 , n - k 2 )-степеней свободы, гдеk 1 1иk 29092 число переменных в меньшей и большей моделях соответственно, аn— размер выборки.Вы можете заметить, что F-тест общей значимости — это особая форма F-теста для сравнения двух вложенных моделей: он проверяет, значительно ли наша модель работает лучше, чем модель без предикторов (т. ).
Часто задаваемые вопросы
Может ли p-значение быть отрицательным?
Нет, p-значение не может быть отрицательным. Это связано с тем, что вероятности не могут быть отрицательными, а p-значение — это вероятность того, что тестовая статистика удовлетворяет определенным условиям.
Это связано с тем, что вероятности не могут быть отрицательными, а p-значение — это вероятность того, что тестовая статистика удовлетворяет определенным условиям.
Что означает высокое значение p?
Высокое значение p означает, что при нулевой гипотезе существует высокая вероятность того, что для другой выборки тестовая статистика будет генерировать значение, по крайней мере столь же экстремальное, как наблюдаемое в уже имеющейся выборке. Высокое значение p не позволяет отвергнуть нулевую гипотезу.
Что означает низкое значение p?
Низкое p-значение означает, что при нулевой гипотезе маловероятно, что для другой выборки статистика теста сгенерирует значение, по крайней мере столь же экстремальное, как наблюдаемое для уже имеющейся выборки. Низкое p-значение свидетельствует в пользу альтернативной гипотезы — оно позволяет отвергнуть нулевую гипотезу.
Богна Шик и Анна Щепанек, доктор философии
Что вы хотите?
Что у тебя есть?
Ваш Z-показатель
Z-показатель : статистика теста соответствует стандартному нормальному распределению N(0,1).
Ознакомьтесь с 29 похожими калькуляторами логической статистики 📉
Тест ABКоэффициент детерминацииДоверительный интервал… Еще 26
Как рассчитать P-значение при проверке нулевой гипотезы
08-10-2022
Из книги: Статистика для чайников
Статистика для чайников
Исследовать книгу Купить на Amazon
В статистике, когда вы проверяете гипотезу о населении, вы находите p-значение и используете свою тестовую статистику, чтобы решить, следует ли отклонить нулевую гипотезу, H 0 . р-значение — это вероятность, связанная с вашим критическим значением. Критическое значение зависит от вероятности, которую вы допускаете для ошибки типа I. Он измеряет вероятность получения результатов, по крайней мере, таких же сильных, как ваши, если утверждение (H 0 ) были правдой.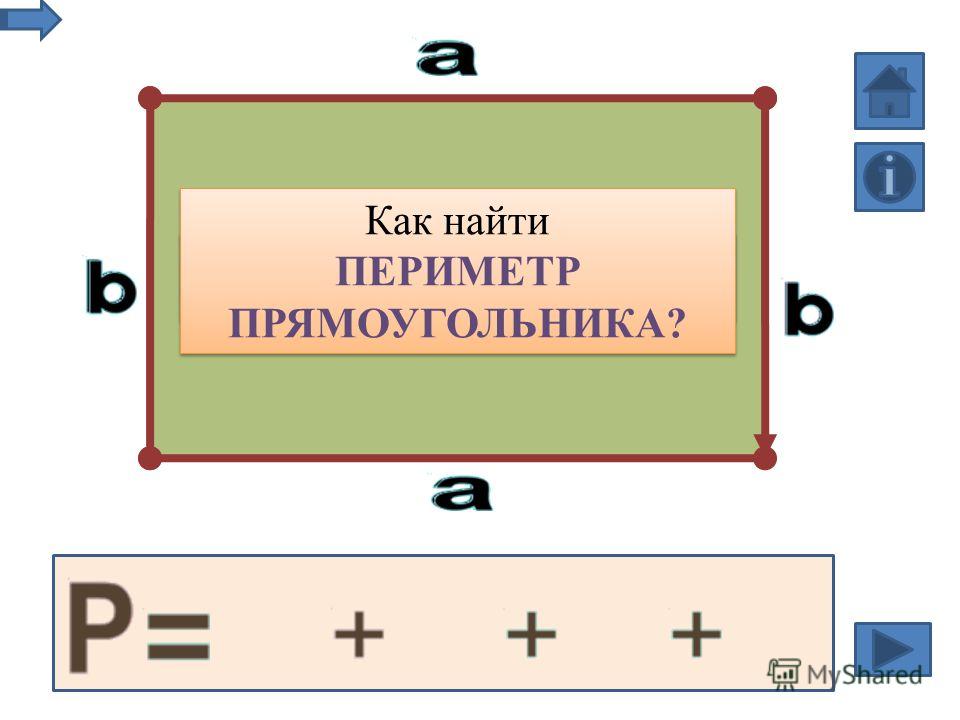
На следующем рисунке показано расположение тестовой статистики и соответствующие выводы.
Решения для га: не равно
Обратите внимание, что если альтернативная гипотеза меньше альтернативы, вы отклоняете H 0 только в том случае, если тестовая статистика попадает в левый хвост распределения (ниже –2). Точно так же, если H a является альтернативой «больше чем», вы отклоняете H 0 только в том случае, если тестовая статистика попадает в правый конец (выше 2).Чтобы найти значение p- для вашей тестовой статистики:
Найдите тестовую статистику по соответствующему распределению — в данном случае по стандартному нормальному ( Z-) распределению (см. следующие таблицы Z ).
Найдите вероятность того, что Z превышает (более экстремально) вашу тестовую статистику:
Если H a содержит альтернативу меньше, найти вероятность того, что Z меньше вашей тестовой статистики (то есть посмотрите свою тестовую статистику в таблице Z и найдите соответствующую вероятность).
 Это значение p-. (Примечание: в этом случае статистика вашего теста обычно отрицательна.)
Это значение p-. (Примечание: в этом случае статистика вашего теста обычно отрицательна.)Если H a содержит альтернативу «больше чем», найдите вероятность того, что Z больше вашей тестовой статистики (поищите свою тестовую статистику в таблице Z , найдите соответствующую вероятность и вычтите ее из единицы). ). Результат ваш p- значение . (Примечание: в этом случае статистика вашего теста обычно положительная.)
Если H a содержит альтернативу, не являющуюся равной, найдите вероятность того, что Z выходит за пределы вашей тестовой статистики, и удвойте ее. Есть два корпуса:
Если ваша тестовая статистика отрицательна, сначала найдите вероятность того, что Z меньше вашей тестовой статистики (посмотрите свою тестовую статистику в таблице Z и найдите соответствующую вероятность). Затем удвойте эту вероятность, чтобы получить p- значение .
Если ваша тестовая статистика положительна, сначала найдите вероятность того, что Z больше, чем ваша тестовая статистика (найдите свою тестовую статистику в таблице Z , найдите соответствующую вероятность и вычтите ее из единицы).
 Затем удвойте этот результат, чтобы получить значение p-.
Затем удвойте этот результат, чтобы получить значение p-.
Эти расчеты дают тестовую статистику (стандартный балл) –0,05, деленную на 0,04 = –1,25. Это говорит вам о том, что результаты вашей выборки и утверждение генеральной совокупности в H 0 отличаются друг от друга на 1,25 стандартной ошибки; в частности, результаты вашего образца на 1,25 стандартных ошибки ниже заявленного.
При тестировании H 0 : p = 0,25 по сравнению с H a : p < 0,25 вы обнаружите, что значение p- равно -1,25, найдя вероятность того, что Z меньше -1,25.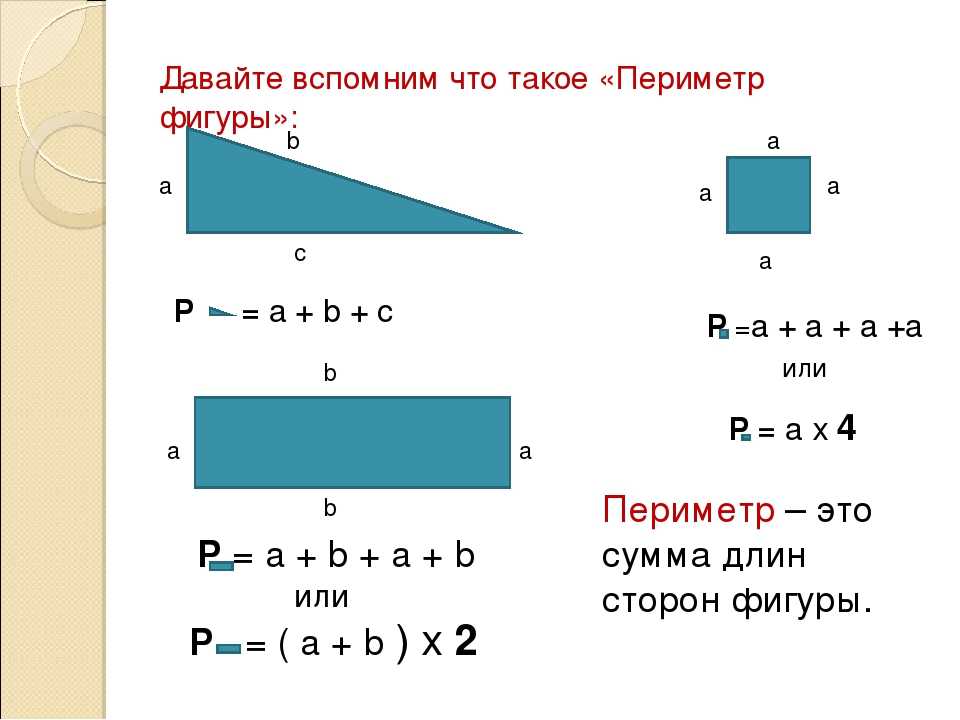 Когда вы посмотрите на это число выше Z -table, вы найдете вероятность 0,1056 того, что Z меньше этого значения.
Когда вы посмотрите на это число выше Z -table, вы найдете вероятность 0,1056 того, что Z меньше этого значения.
Примечание. Если бы вы тестировали двусторонний вариант
, значение p было бы 2 ∗ 0,1056 или 0,2112.
Если результаты, вероятно, произошли по иску, то вы не можете отклонить H 0 (как присяжные признают невиновным). Если маловероятно, что результаты были получены по иску, то вы отклоняете H 0 (подобно тому, как присяжные признают виновным).
Эта статья взята из книги:
- Статистика для чайников,
Об авторе книги:
Дебора Дж. Рамси, доктор философии, , является младшим профессором и специалистом по статистике в Университете штата Огайо. Она является автором книг «Статистика для чайников», «Статистика II для чайников», «Рабочая тетрадь по статистике для чайников», «» и «Вероятность для чайников».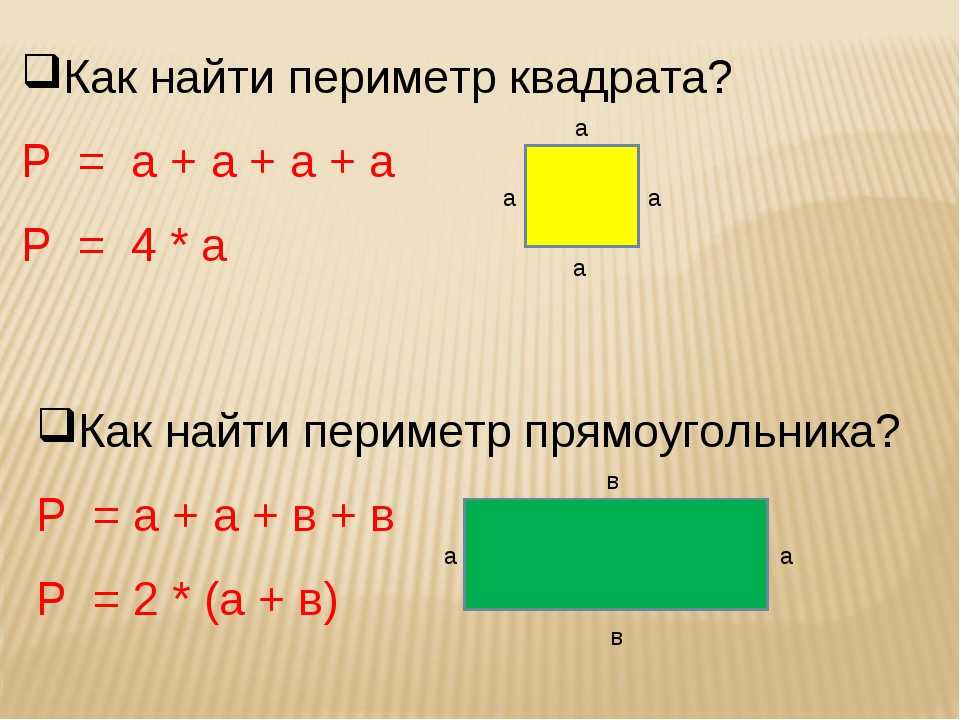



 ru
ru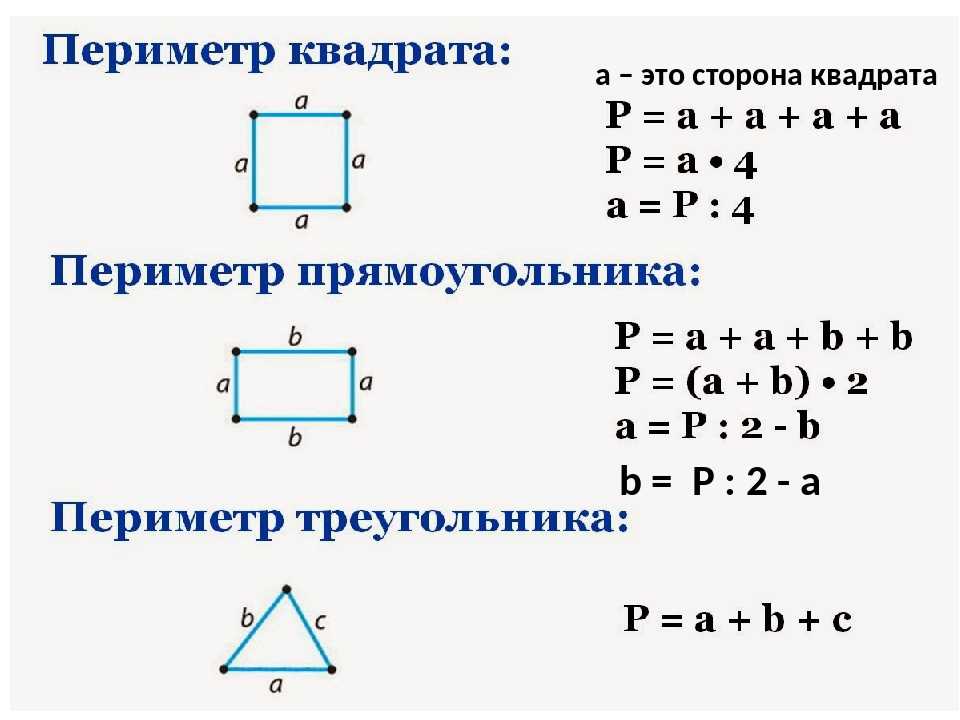 ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
 В противном случае не отвергайте нулевую гипотезу.
В противном случае не отвергайте нулевую гипотезу. Да здравствует Business Science
Да здравствует Business Science


 ниже)
ниже)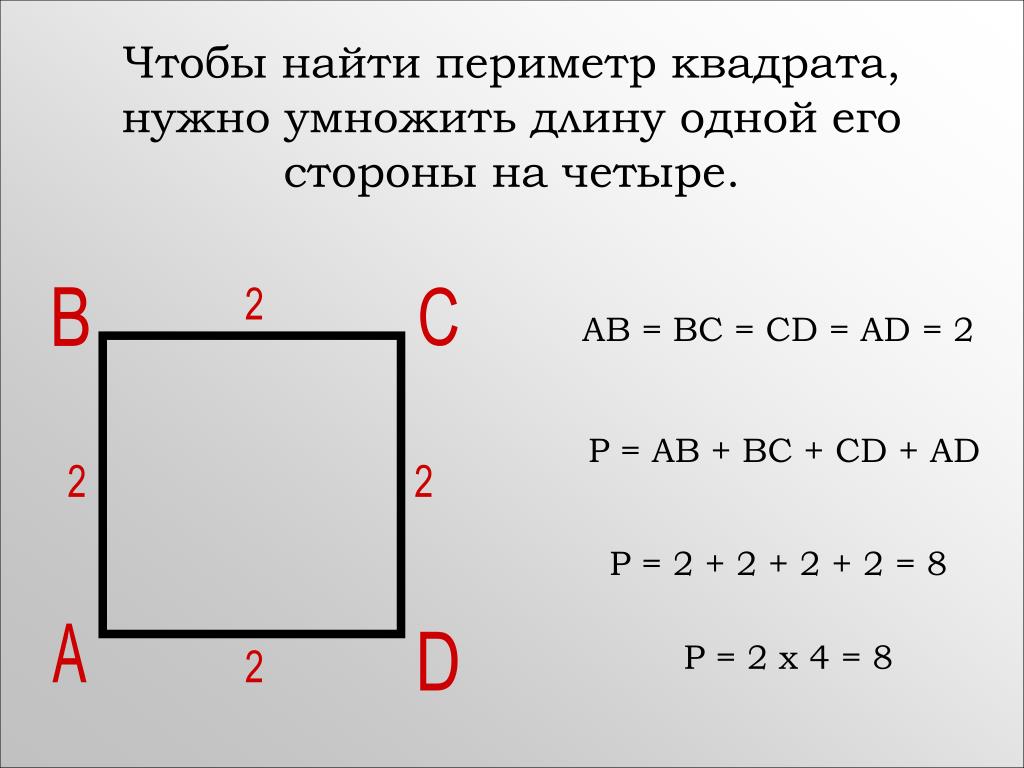 Это правосторонний тест .
Это правосторонний тест . )
)
 Это значение p-. (Примечание: в этом случае статистика вашего теста обычно отрицательна.)
Это значение p-. (Примечание: в этом случае статистика вашего теста обычно отрицательна.) Затем удвойте этот результат, чтобы получить значение p-.
Затем удвойте этот результат, чтобы получить значение p-.