Двойное неравенство — Большая Энциклопедия Нефти и Газа, статья, страница 3
Cтраница 3
Множество всех таких действительных чисел х, каждое из которых удовлетворяет двойному неравенству а х Ь, обозначают ] а, Ь [ и называют интервалом. На рис. 4 дано геометрическое изображение интервала. [31]
Множество всех таких действительных чисел х, каждое из которых удовлетворяет двойному неравенству адс &, обозначается ] а, Ь [ и называется интервалом. На рис. 3 дано геометрическое изображение интервала. [32]
Если х О, то я х и правое неравенство в двойном неравенстве ( 7) выполнено в силу ( 6), а левое очевидно, так как — а0 и х О. [33]
Последняя группа неравенств соответствует первой группе неравенств ( 43), а двойные неравенства равнозначны второму и третьему неравенствам. [34]
Формула Пуассона дает возможность установить для гармонических функций, неотрицательных в круге, двойное неравенство, которое, очевидно, справедливо для всех ограниченных снизу гармонических функций, так как эти функции становятся неотрицательными, если прибавить к ним некоторые постоянные.
Запись аЬс означает, что а b и b с одновременно, и называется двойным неравенством. [36]
Запись а b с означает, что а b и b с одновременно, и называется двойным неравенством. [37]
На указанном интервале изменения аргумента х 0 25тг х 0 5тг значения функции tg x изменяются по закону двойного неравенства 1 tg х оо. [38]
В зависимости от этих изменений значений функции tg x значения функции Igtgrc — функции от функции тоже подчиняются двойному неравенству 0 Igtga: оо. Поэтому областью изменения значений исходной данной функции у sinl 57r lgtg на указанном интервале от 0 25тг до 0 5тг значений аргумента х является область: О 1 lg tg x оо. [39]
Замечание: Записывая дугу в виде а-необходимо следить за тем, чтобы выполнялось неравенство а fi, иначе это двойное неравенство окажется противоречивым. [40]
Заметим теперь, что и в случае, когда а Ф 2а 1, мькне можем записать решения неравенства ( 17) в виде двойного неравенства, поскольку неизвестно, какое из чисел а и 2а 1 больше. Поэтому рассмотрим два возможных случая.
[41]
Поэтому рассмотрим два возможных случая.
[41]
На рис. 7 и 8 приведены графики коэффициентов усиления на втором и третьем этапах в этом случае. Для п, удовлетворяющих двойному неравенству 0 5 пЛ, переходный процесс не заканчивается на четвертом этапе, однако колебания не имеют периодического характера. [42]
УРЗ, когда открываются или закрываются определенные транзисторы. Худшим случаем для удовлетворения левой части
Неравенства, входящие в систему, объединяются фигурной скобкой. Иногда системы неравенств записывают в виде двойного неравенства. [44]
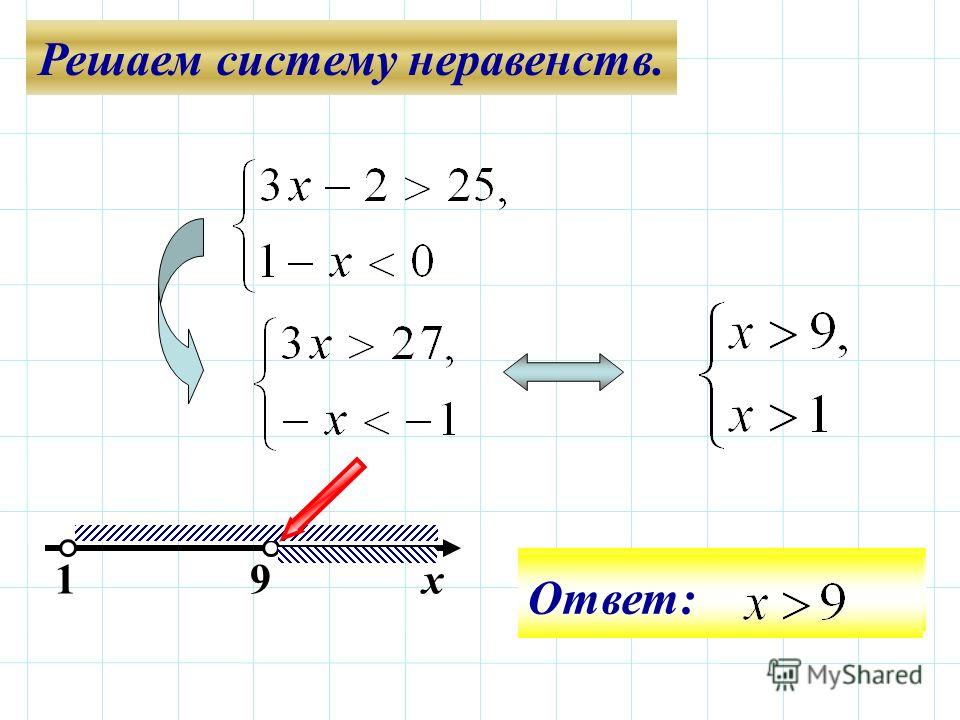
Именно это место многих поставило в тупик — уравнение пропало.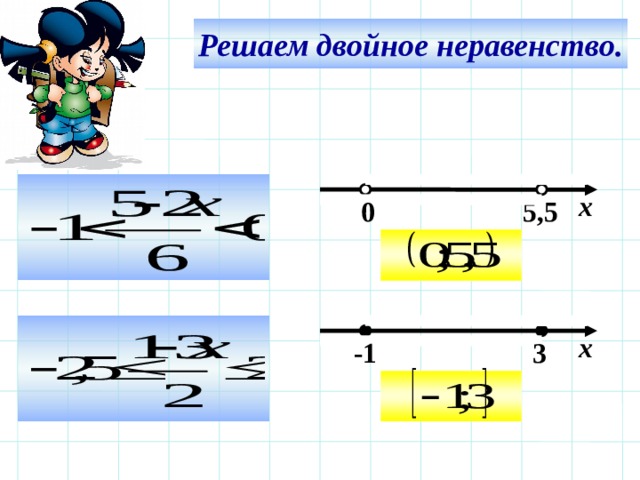 Таким образом, любое х, удовлетворяющее условию 4 х2 9, является решением уравнения. Теперь остается решить это двойное неравенство.
[45]
Таким образом, любое х, удовлетворяющее условию 4 х2 9, является решением уравнения. Теперь остается решить это двойное неравенство.
[45]
Страницы: 1 2 3 4
Школа: КГУ ШГ №118 | |||||||||
Дата: «____»____________20___г. | ФИО учителя: Гончарова А.А. | ||||||||
Класс: 5 «____» класс. | Количество присутствующих: отсутствующих: | ||||||||
Тема урока: | Двойное неравенство | ||||||||
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу): | |||||||||
5. устанавливать порядок действий и находить значения числовых выражений со скобками и без скобок, содержащих более четырёх действий; 5.1.2.3 использовать свойства сложения и умножения для нахождения значений числовых выражений; | |||||||||
Цели урока: | Выявить и осмыслить получение двойных неравенств, их запись и решение | ||||||||
Критерии успеха | Научиться записывать и решать двойные неравенства повысить познавательную активность. Развивается внимание, мышление, речь , умение обобщать, делать выводы | ||||||||
Привитие ценностей | Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни. | ||||||||
Межпредметные связи | Взаимосвязь с предметами: обучение грамоте на родном языке, самопознание, познание мира, естествознание, музыка. | ||||||||
Навыки использования ИКТ | На данном уроке учащиеся используют ИКТ – для индивидуальной работы – задание: флеш-презентация | ||||||||
Предварительные знания | Учащиеся могут сравнивать группы предметов, соединяя их в пары и наблюдая. | ||||||||
Ход урока | |||||||||
Этапы урока | Запланированная деятельность на уроке | Ресурсы | |||||||
Начало урока |
Число — это понятие, отражающее количество. Цифра — это знак (символ) для обозначения чисел.
| ||||||||
Критерии успеха | Работая в группах, ученики самостоятельно изучают новый материал. Ученики делают выводы по увиденному | Стикеры или фишки | |||||||
Середина урока | 1. Вводная беседа.К 1. 2. При взвешивании арбуза оказалось, что он тяжелее одной 5-килограммовой гири, но легче двух таких гирь. Обозначив массу арбуза х кг, можно записать: Значит, масса арбуза заключена в промежутке от 5 кг до 10 кг. Вместо двух неравенств 5 Решениями неравенства 5 3. Прочитай неравенства 4.Можно ли заменить данные неравенства двойным неравенством? Если да, то запиши подходящее двойное неравенство. а) 2 б) у 2 и у в) 2 г) у | Учебник: Больше, меньше, равно, Рабочая тетрадь: Рабочий лист «Больше, меньше, равно», Рабочий лист 8 «Сравни», стр. 12 Ресурсы
| |||||||
Критерии успеха | Учащиеся знают, что если количество предметов в группах не равно, то говорят, что одних предметов больше, а других меньше. вырабатывают навыки чтения двойных неравенств -учатся записывать неравенства | Стикеры или фишки | |||||||
Конец урока | Первичное закрепление. 1. Запиши двойные неравенства: а) t больше 4 и меньше 9 ———————— б) k больше или равно 5 и меньше 18 —————————— в) m больше 10 и меньше или равно 25 —————————— г) n больше или равно 6 и меньше или равно 15 —————————- 6. Отметь на луче множество решений двойного неравенства и запиши его с помощью фигурных скобок. 2. Напиши двойные неравенства, множество решений которых совпадает с множеством чисел, отмеченных на луче: 8. Реши уравнения. Что ты замечаешь? х + 389 = 2076 х — 1687 = 389 2076 -х = 1687
Самостоятельная работа в тетради. (Если останется время.) РТ Взаимопроверка. | ||||||||
Критерии успеха | Учащиеся могут оперировать понятиями «больше», «меньше»; умеют сравнивать группы предметов; способствовать развитию навыков разбиения предметов на группы по их признакам. | Стикеры или фишки | |||||||
Дифференциация Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание Как Вы планируете проверить уровень усвоения материала учащимися? Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока. | Здоровье и соблюдение техники безопасности Здоровьесберегающие технологии. Используемые физминутки и активные виды деятельности. | |||||||
http://files.school-collection.edu.ru/dlrstore/4999b6cb-9e71-11dc-8314-0800200c9a66/iz2.swf | Итог урока. – Вот мы и дома. Понравилась ли вам прогулка? Что учились делать на прогулке? (Учились сравнивать группы предметов.) Какие слова помогли нам сравнивать? («Больше» и «меньше».) Когда говорят, что предметов больше или меньше? (Если их количество не равно, то есть при соотнесении остается «лишний» предмет.) | №1 Пять домовых Пять веселых домовых праздничною ночью (вытянув руку с раскрытыми пальцами вперед, поворачивают кисть вправо и влево) Разгулялись чересчур, расшалились очень. (Энергичные движения руками в стороны – вверх,в стороны – вниз. Встав на цыпочки, один закружился в вальсе (кружатся на месте), А второй споткнулся и – нос себе расквасил. (Присесть, прикрыть нос рукой.) Третий прыгал до небес, с неба звезды цапал (прыжки вверх без продвижения вперед), А четвертый топал, как мишка косолапый. (Шаги па месте.) Пятый пел до хрипоты песенку за песенкой… (Руки развести в стороны, имитируя позу певца.) Этой ночью домовым было очень весело! (Хлопки в ладоши.) №2: Раз, два, три, четыре, пять – вышли дети погулять. (Ходьба на месте.) Остановились на лугу – я вперед быстрей бегу. (Бег на месте.) Лютики, ромашки, розовые кашки Собирал наш первый класс: вот какой букет у нас! (Разведение рук в стороны.) | |||||||
Выберите и составьте эквивалентную форму выражения, чтобы раскрыть и объяснить свойства величины, представленной выражением.
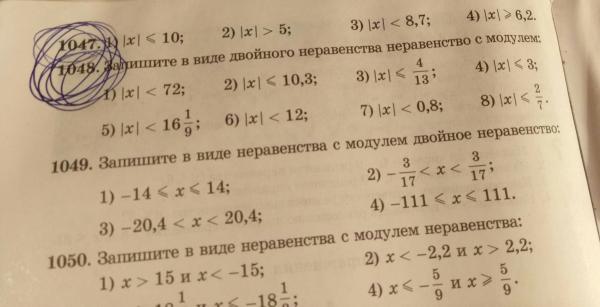 | СС | ЧСА | HSA-SSE | HSA-SSE.B
| СС | ЧСА | HSA-SSE | HSA-SSE.BДополнительные темы
в Выберите и создайте эквивалентную форму выражения, чтобы выявить и объяснить свойства величины, представленной выражением.Popular Tutorials
in Выберите и создайте эквивалентную форму выражения, чтобы раскрыть и объяснить свойства величины, представленной выражением.Какова сила частного правила?
Возвели дробь в степень? Узнайте, как разделить этот показатель степени и поместить его в числитель и знаменатель вашей дроби, используя силу правила частного. Этот урок покажет вам, как!
Что такое экспоненциальная функция?
Ищете уравнение с переменной в показателе степени? У вас есть экспоненциальная функция! Узнайте об экспоненциальных функциях в этом руководстве.
Как разложить трехчлен на множители?
Разложение трехчленов на множители может быть сложным, но это руководство может помочь! Следите за тем, как прямо на ваших глазах вычисляется трехчлен! Затем проверьте свой ответ, используя метод FOIL, чтобы снова перемножить двучлены и посмотреть, получится ли исходный трехчлен.

Как решить квадратное уравнение с помощью факторинга?
Одним из многих способов решения квадратного уравнения является его разложение на множители. В этом уроке вы увидите, как факторизовать квадратное уравнение, используя метод факторинга «догадка и проверка». Затем используйте свойство нулевого произведения, чтобы найти решение!
Как использовать ярлык для разложения на множители идеального квадратного трехчлена?
Разложение на множители совершенного квадратного трехчлена? Знаете ли вы, что существует короткий путь к разложению на множители этого специального вида трехчлена? Проверьте это! Это довольно круто, и это может сделать этот процесс немного быстрее!
Что такое произведение правила степеней?
Работа с экспонентами может быть очень увлекательной, если вы понимаете, как они работают. В этом уроке вы увидите, как складываются показатели степени, когда вы умножаете одно и то же число, возведенное в разные степени!
В чем сила силового правила?
Иногда вы видите число с показателем степени, возведенным в другую степень, и, увидев его впервые, вы, вероятно, подумаете, что это опечатка! Но это не опечатка, это реальная вещь, и есть действительно хороший трюк, чтобы упростить ее, который вы увидите в видео.

В чем сила правила продукта?
Есть отличный трюк для возведения произведения двух чисел в степень, и этот урок покажет вам, как именно этот трюк работает.
Что такое правило отношения сил?
Работа с экспонентами может быть очень увлекательной, если вы понимаете, как они работают. В этом уроке вы увидите, как складываются показатели степени, когда вы делите одно и то же число, возведенное в разные степени!
Как разложить полином на множители, используя разность квадратов?
Пытаетесь разложить на множители двучлен с вычитаемыми множителями с идеальным квадратом? У вас есть задача на разность квадратов! Узнайте, как факторизовать такой бином, как этот, посмотрев этот урок.
Что такое свойство нулевого продукта?
Свойство нулевого произведения позволяет разделить произведение факторов на отдельные уравнения.
 Затем вы можете решить каждое уравнение, чтобы получить решения исходного уравнения! Узнайте все об этом очень полезном свойстве, посмотрев этот урок.
Затем вы можете решить каждое уравнение, чтобы получить решения исходного уравнения! Узнайте все об этом очень полезном свойстве, посмотрев этот урок.Как разложить полином на множители, угадывая и проверяя?
Разложение трехчленов на множители может быть сложным, но это руководство может помочь! Следите за тем, как трехчлен факторизуется с использованием метода догадок и проверок. Что, никакие возможности не работают? Трехчлен должен быть простым! Посмотрите этот урок и посмотрите, что получится!
Как разложить полином на множители с помощью метода A-C?
Разложение трехчленов на множители может быть сложным, но это руководство может помочь! Посмотрите, как использовать метод A-C для разложения трехчлена на произведение двух двучленов. Затем используйте метод FOIL, чтобы снова перемножить два бинома, чтобы проверить свой ответ.
Как найти все возможные делители трехчлена?
При разложении трехчлена на произведение двух двучленов иногда полезно знать все возможные варианты.
 В этом уроке используется метод «угадай и проверь», чтобы сделать именно это! Взглянем!
В этом уроке используется метод «угадай и проверь», чтобы сделать именно это! Взглянем!Как найти шаблон для разложения трехчлена на множители?
Знаете ли вы, что при разложении трехчлена знаки трехчлена определяют знаки произведения двучленов? Эта информация действительно полезна, когда вы факторизуете трехчлены! Посмотрите этот урок и изучите различные случаи знаков.
Как выделить общий делитель из разности квадратов?
Пытаетесь разложить бином? Посмотрите, сможете ли вы выделить наибольший общий множитель. В этом руководстве показано, как разложить бином на множители, сначала выделив наибольший общий множитель, а затем используя разность квадратов. Проверьте это!
Как узнать, есть ли у вас разница квадратов?
Не уверены, что бином, который вы разложили на множители, представляет собой задачу на разность квадратов? Этот урок покажет вам, какими характеристиками должен обладать бином, чтобы быть задачей на разность квадратов.

Как преобразовать квадратичную форму из стандартной формы в вершинную, заполнив квадрат?
Вершинная форма квадратного уравнения может помочь вам быстро определить вершину этого квадратного уравнения. Следуйте этому руководству, чтобы узнать, как использовать метод завершения квадрата, чтобы изменить квадратное уравнение из стандартной формы в вершинную форму!
Как преобразовать квадрат из стандартной формы в форму вершины, дополнив квадрат, если a≠1?
Вы можете преобразовать квадратное уравнение из стандартной формы в вершинную форму, заполнив квадрат! Этот учебник шаг за шагом проведет вас через процесс.
Составные неравенства — решение, график, примеры
Составное неравенство представляет собой комбинацию двух неравенств, которые объединяются с помощью «и» или «или». Процесс решения каждого из неравенств в составных неравенствах такой же, как и для обычного неравенства, но только при объединении решений обоих неравенств зависит от того, объединяются ли они с помощью «и» или «или».
Давайте посмотрим, как решаются сложные неравенства, а также как их изображать на числовой прямой.
| 1. | Что такое сложное неравенство? |
| 2. | График сложного неравенства |
| 3. | Решение сложных неравенств |
| 4. | Часто задаваемые вопросы о сложном неравенстве |
Что такое сложное неравенство?
Составное неравенство — это неравенство, объединяющее два неравенства с помощью «и» или «или». Иногда «и» не упоминается конкретно, но понимается. Например, 1 < x < 3 — это не что иное, как «x > 1 и x < 3». С другой стороны, сложное неравенство с «или» всегда упоминается с использованием «или». Два типа составных неравенств — это конъюнкция и дизъюнкция, и различия между ними заключаются в следующем:
| Соединение | Разделение |
|---|---|
Это составное неравенство, в котором неравенства соединяются с помощью «И».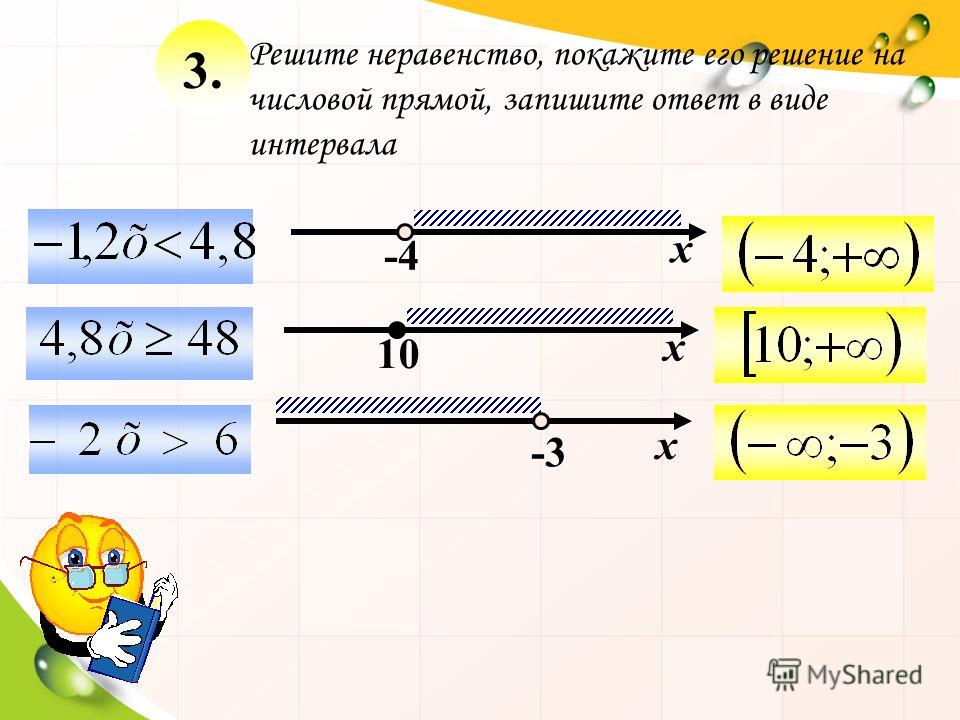 | Это составное неравенство, в котором неравенства соединяются с помощью «ИЛИ». |
| Пример : -2 < x < 3 [или эквивалентно "x > -2 AND x < 3"] | Пример: x < -2 ИЛИ x > 3 |
| Их можно объединить, используя символ «пересечения» (∩) между представляющими их интервалами. Например, x > -2 И x < 3 можно записать как (-2, ∞) ∩ (-∞, 3). | Их можно объединить, используя символ «союза» (∪) между представляющими их интервалами. Например, x < -2 ИЛИ x > 3 можно записать как (-∞, -2) ∪ (3, ∞). |
| Так как это «И», решение должно содержать значения, которые удовлетворяют «ОБОИМ» неравенствам. | Так как это «ИЛИ», решение может содержать значения, которые удовлетворяют «одному или обоим» неравенствам. |
График сложного неравенства
Составные неравенства можно изобразить на числовой прямой. При построении сложных неравенств учитывайте следующее.
- Сначала найдите число на числовой прямой, которое имеет неравенство. Например, если у нас есть x > 2, нам нужно увидеть, где 2 находится на числовой прямой.
- Поставьте открытую точку (чтобы показать, что значение НЕ включено), если неравенство равно «>» или «<".
Поставьте закрытую точку (чтобы показать, что значение включено), если неравенство либо «≥», либо «≤».
Например, если у нас есть x > 2, поставьте открытую точку у 2, так как неравенство является строгим и не включает «=». - Для знака «>» или «≥» нарисуйте стрелку справа от числа.
- Для знака «<" или "≤" нарисуйте стрелку слева от числа.
- Для нахождения окончательного решения просто используйте пересечение или объединение в зависимости от того, задано ли соответственно «И» или «ИЛИ».
Пример графического отображения сложного неравенства с помощью И
Изобразите составное неравенство x > 1 AND x ≤ 4.
Мы изобразим каждое неравенство на числовой прямой следующим образом:
- x > 1: Поскольку мы не Если у 1 есть «=», мы получаем открытую точку в 1.
 Кроме того, мы рисуем стрелку справа от 1, так как у нас есть «>».
Кроме того, мы рисуем стрелку справа от 1, так как у нас есть «>». - x ≤ 4: Так как у нас есть «=» в 4, мы получаем закрытую точку в 1. Кроме того, мы рисуем стрелку слева от 4, так как у нас есть «≤».
Наконец, мы ищем значения на числовой прямой, которые удовлетворяют «ОБОИМ» неравенствам, поскольку в данном составном неравенстве есть «И». Из обеих стрелок выше очень ясно, что область пересечения (общая область) обеих стрелок составляет от 1 до 4, где 1 не включена, а 4 включена. т. е. решение данного сложного неравенства есть 1 < x ≤ 4 и показано «оранжевой» линией в числовой строке ниже. В интервальной записи решение можно записать в виде (1, 4].
Пример графического построения составного неравенства с помощью OR
Начертите составное неравенство x ≤ -1 OR x > 2.
Каждое неравенство изобразим на числовой прямой следующим образом:
- x ≤ -1: Поскольку у нас есть «=» в 1, мы получаем закрытую точку в 1.
 Кроме того, мы рисуем стрелку слева от 1, так как у нас есть «≤».
Кроме того, мы рисуем стрелку слева от 1, так как у нас есть «≤». - x > 2: Так как у нас нет «=» в 2, мы получаем открытую точку в 2. Кроме того, мы рисуем стрелку справа от 2, так как у нас есть «>».
Поскольку в данном неравенстве есть «ИЛИ», мы просто используем «объединение» между ними в решении. Следовательно, решение есть x ≤ -1 ИЛИ само x > 2. В интервальных обозначениях решение имеет вид (-∞, -1] ∪ (2, ∞). Решение показано «оранжевой» линией в числовой строке ниже.
Решение сложных неравенств
Мы знаем, что составное неравенство представляет собой слияние двух простых неравенств. Следовательно, каждое из них может быть решено так же, как мы решаем простое неравенство (чтобы узнать, как решить простое неравенство, щелкните здесь), а затем мы объединяем их в соответствии с тем, что они дали (И / ИЛИ), точно так же, как это было объяснено в предыдущем разделе. Вот пошаговое объяснение Решение сложных неравенств.
- Шаг 1: Определите два неравенства, которые даны в данном неравенстве.
- Шаг 2: Решите каждое из них так же, как мы решаем обычное неравенство. Обратите внимание, что процедура решения неравенства такая же, как и решение уравнения, но просто меняйте знак неравенства, когда вы умножаете или делите неравенство на отрицательное число.
- Шаг 3: Нарисуйте решение каждого неравенства на числовой прямой (как описано в предыдущем разделе).
- Шаг 4: Возьмите «пересечение» решений, если задано «И»; и возьмите «объединение» решений, если дано «ИЛИ».
Если мы сможем проанализировать решение без построения графика, то мы сможем избежать шага 3 . Графики составных неравенств не являются обязательными, если это специально не указано. Вышеупомянутая процедура поясняется примерами (по одному из «И» и «ИЛИ») ниже.
Пример решения составного неравенства с И
Решите составное неравенство -2 < 2x - 3 < 5.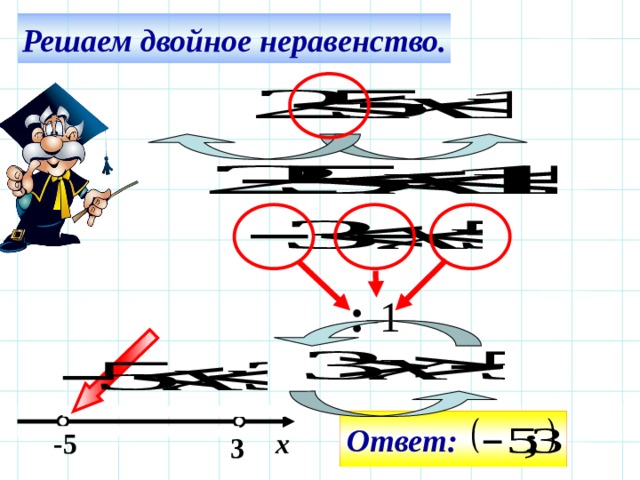
Мы можем решить его двумя способами: один без разбиения на два; а другой — путем разделения на два. Давайте посмотрим на оба пути.
Метод 1: Данное составное неравенство: -2 < 2x - 3 < 5.
Прибавление 3 со всех сторон,
-2 + 3 < 2x - 3 + 3 < 5 + 3
1 < 2x < 8
Деление всех сторон на 2,
1/2 < 2x/2 < 8/2
1/2 < x < 4,
Следовательно, прямым решением является 1/2 < x < 4 (или) интервал (1/2, 4).
Способ 2: Разобьем данное неравенство на два неравенства. Тогда мы получим
2x — 3 > -2 И 2x — 3 < 5
Прибавляя по 3 к обеим сторонам каждого неравенства,
2x > 1 И 2x < 8
Деля каждое неравенство с обеих сторон на 2,
x > 1/2 И x < 4
Снова объединяя их обратно,
1/2 < x < 4.
Следовательно, решение 1/2 < x < 4 (или) интервал (1/2, 4).
Пример решения составного неравенства с оператором ИЛИ
Решите составное неравенство -3x — 1 > -7 ИЛИ -5x + 2 < -12.
Прибавьте 1 к обеим сторонам первого неравенства и вычтите 2 из обеих сторон второго неравенства.
-3x > -6 ИЛИ -5x < -14
Разделите первое неравенство с обеих сторон на -3, а второе неравенство на -5. Обратите внимание, что знак неравенства меняется при делении на отрицательное число.
х < 2 ИЛИ х > 2,8
Следовательно, решение равно (-∞, 2) U (2.8, ∞).
Важные примечания о составных неравенствах:
- Составное неравенство включает более одного неравенства, объединенного с помощью «И» или «ИЛИ».
- Если два неравенства объединяются с помощью «И», то объединяют их решения, взяв пересечение.
- Если два неравенства объединяются с помощью «ИЛИ», то объединяют их решения, взяв объединение.
- Составные неравенства, построенные на графике, очень упрощают процесс нахождения объединения или пересечения.
- Составное неравенство иногда «не имеет решения», а иногда имеет в качестве решения «множество всех действительных чисел».

☛ Связанные темы:
- Линейные неравенства
- Квадратные неравенства
- Неравенства абсолютного значения
- Калькулятор неравенства
Часто задаваемые вопросы о сложном неравенстве
Что такое сложные неравенства?
Составные неравенства – это комбинации двух неравенств, объединенных с помощью «и» или «или». Например, 1 < x < 3 — это не что иное, как «x > 1 и x < 3».
Пример сложного неравенства?
Составное неравенство , как следует из его названия, содержит два неравенства с операторами «И» или «ИЛИ» между ними. Например, -2 < x OR x > 5 является составным неравенством.
Как решать сложные неравенства?
Чтобы решить сложные неравенства, просто решите каждое из двух неравенств в нем по отдельности и объедините их, используя союз
- , если между ними есть «ИЛИ». Пересечение
- , если между ними есть «И».

Как определить, является ли составное неравенство И или ИЛИ?
Для составных неравенств «И» или «ИЛИ» обычно упоминаются явно, как «x < 2 AND x > -1». Но иногда может быть неравенство вида -2 < x < 1, и это, очевидно, означает x > -2 И x < 1.
Что такое график сложного неравенства?
График сложного неравенства — это график, показывающий решение сложного неравенства. Чтобы нарисовать график сложного неравенства:
- Сначала нарисуйте решение каждого неравенства, используя начальную точку, а затем стрелку от нее (влево или вправо в зависимости от знака неравенства).
- Затем найти их пересечение, если в данном сложном неравенстве есть «И» (или) найти их объединение, если в данном сложном неравенстве есть «ИЛИ».
Что такое процесс графического построения сложных неравенств?
Для графического построения сложных неравенств
- мы сначала решаем каждое неравенство в нем.
- , затем изобразите каждое неравенство на числовой прямой.


 1.2.2
1.2.2

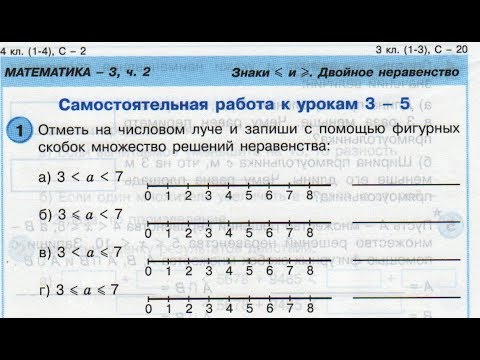
 Отметь на числовом луче множество чисел, которое одновременно больше 3 и меньше 7. Предложи свой вариант записи этого множества с помощью знаков неравенства.
Отметь на числовом луче множество чисел, которое одновременно больше 3 и меньше 7. Предложи свой вариант записи этого множества с помощью знаков неравенства.


 )
)


 В этом уроке используется метод «угадай и проверь», чтобы сделать именно это! Взглянем!
В этом уроке используется метод «угадай и проверь», чтобы сделать именно это! Взглянем!
 Кроме того, мы рисуем стрелку справа от 1, так как у нас есть «>».
Кроме того, мы рисуем стрелку справа от 1, так как у нас есть «>». Кроме того, мы рисуем стрелку слева от 1, так как у нас есть «≤».
Кроме того, мы рисуем стрелку слева от 1, так как у нас есть «≤».