Что такое функция в алгебре определение: Что такое функция — материалы для подготовки к ЕГЭ по Математике

Содержание

Что такое функция — материалы для подготовки к ЕГЭ по Математике

Понятие функции – одно из основных в математике.

На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.

Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.

1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.

Любой физический закон, любая формула отражает такую взаимосвязь величин. Например, формула – это зависимость давления жидкости от глубины .

Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.

Знакомое вам обозначение как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины по определенному закону, или правилу, обозначаемому .

Другими словами: меняем (независимую переменную, или аргумент) – и по определенному правилу меняется .

Совсем необязательно обозначать переменные и . Например, – зависимость длины от температуры , то есть закон теплового расширения. Сама запись означает, что величина зависит от .

2. Можно дать и другое определение.

Функция – это определенное действие над переменной.

Это означает, что мы берем величину , делаем с ней определенное действие (например, возводим в квадрат или вычисляем ее логарифм) – и получаем величину .

В технической литературе встречается определение функции как устройства, на вход которого подается – а на выходе получается .

Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.

3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.

Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

Например, функция каждому действительному числу ставит в соответствие число в два раза большее, чем .

Повторим еще раз: каждому элементу множества по определенному правилу мы ставим в соответствие элемент множества . Множество называется областью определения функции. Множество – областью значений.

Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.

Рассмотрим в качестве примера соответствие между двумя множествами – гражданами России, у которых есть паспорта, и номерами их паспортов. Ясно, что это соответствие взаимно-однозначное – у каждого гражданина только один российский паспорт. И наоборот – по номеру паспорта можно найти человека.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция . Каждому значению соответствует одно и только одно значение . И наоборот – зная , можно однозначно найти .

Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:

Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.

Пример такого соответствия в математике – функция . Один и тот же элемент второго множества соответствует двум разным элементам первого множества: и .

А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:

Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.

Очень сложно было бы описать такое соответствие математически, не правда ли?

Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?

Ответ очевиден. Первая кривая – это график некоторой функции, а вторая – нет. Ведь на ней есть точки, где каждому значению соответствует не одно, а целых три значения .

Перечислим способы задания функции.

1. С помощью формулы. Это удобный и привычный для нас способ. Например:

Это примеры функций, заданных формулами.

2. Графический способ. Он является самым наглядным. На графике сразу видно все – возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума. В следующей статье будет рассказано об исследовании функции с помощью графика.

К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.

3. С помощью таблицы. С этого способа вы когда-то начинали изучение темы «Функция» — строили таблицу и только после этого – график. А при экспериментальном исследовании какой-либо новой закономерности, когда еще неизвестны ни формула, ни график, этот способ будет единственно возможным.

4. С помощью описания. Бывает, что на разных участках функция задается разными формулами. Известная вам функция задается описанием:

Читайте также: Чтение графика функции

§ Что такое функция в математике

Что такое функция в математике Как решать задачи на функцию Функция «y = kx» и её график Линейная функция
«y = kx + b» и её график Как построить график функции вида
«y = 7» или «x = 2»

Понятие функции в математике появилось не просто так. Давайте разберемся, зачем придумали функцию и как с ней можно работать.

Разберём пример из жизни. Рассмотрим движение автомобиля. Предположим, что он двигается с постоянной скоростью 60 км/ч.

То, что автомобиль двигается с постоянной скоростью 60 км/ч означает, что автомобиль проезжает 60 км за 1 час.

Зададим себе вопрос: «Сколько километров проедет автомобиль за 2 часа?».

Очевидно, чтобы найти, сколько километров пройдет автомобиль за 2 часа, нужно 60 умножить на 2. Мы получим, что за 2 часа автомобиль проедет 120 км.

Составим таблицу, в которой укажем какое расстояние проедет автомобиль за разное время при постоянной скорости 60 км/ч.

Сколько времени двигается автомобиль	Сколько км проедет автомобиль
1 час	60 км
2 часа	120 км
3 часа	180 км

Если внимательно изучить таблицу станет очевидно, что между временем автомобиля в пути и пройденным расстоянием есть четкая зависимость.

Обозначим за «x» время автомобиля в пути.

Обозначим за «y» расстояние, пройденное автомобилем.

Запишем зависимость «y» (расстояния) от «x» (времени в пути автомобиля).

y = 60 · x

Давайте убедимся, что мы правильно записали зависимость пройденного расстояния от времени в пути.

Рассчитаем по записанной формуле, сколько пройдет автомобиль за 1 ч. То есть подставим в формулу «y = 60 · x» значение x = 1.

y = 60 · 1 = 60(км) — пройдёт автомобиль за 1 час. Это совпадает с нашими расчетами ранее.

Теперь рассчитаем для x = 2.
y = 60 · 2 = 120(км) — пройдёт автомобиль за 2 часа.

Теперь вместо «y» запишем обозначение «y(x)». Такая запись означает, что «y» зависит от «x».

Окончательная запись нашей функции, которая показывает зависимость пройденного автомобилем расстояния от времени в пути, выглядит следующим образом:

y(x) = 60x

Запомните!

Функцией называют зависимость «y» от «x».

«x» называют переменной или аргументом функции.

«y» называют зависимой переменной или значением функции.

Запись функции в виде «y(x) = 60x» называют формульным способом задания функции.

Конечно, нужно понимать, что функция «y(x) = 60x» — это не единственная в мире функция. В математике бесконечное множество самых разнообразных функций.

Примеры других функций:

y(x) = 2x
y(x) = −5x + 2
y(x) = 12x²−1

Единственное, что объединяет все функции, это то, что они показывают зависимость значения функция («y») от её аргумента («x»).

Существуют три основных способа задания функции. Все способы задания функции в математике тесно связаны друг с другом .

Задание функции формулой

Через формульный способ задания функции всегда можно сразу по конкретному значению аргумента «x» найти значение функции «y».

Например, рассмотрим функцию, заданную формульным способом.

y(x) = 32x + 5

Найдем значение функции «y» при x = 0. Для этого подставим в формулу вместо «x»
число «0».

Запишем расчет следующим образом.

y(0) = 32 · 0 + 5 = 5

Таким же образом найдем значения «y» при x = 1 и при x = 2.

Найдем значение «y» при x = 1.

y(1) = 32 · 1 + 5 = 37

Теперь найдем значение «y» при x = 2.

y(2) = 32 · 2 + 5 = 64 + 5 = 69

Табличный способ задания функции

С табличным способом задания функции мы уже встречались, когда расписывали таблицу для функции, которая описывает движение автомобиля «y(x) = 60x».

Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений «y» для произвольно выбранных значений «x».

Рассмотрим функцию

y(x) = −x + 4

Найдем значения «y» при x = −1, x = 0 и x = 1.

Важно!

Будьте внимательны, когда подставляете значение «x» в функцию,
у которой перед «x» есть минус.

Нельзя терять знак минуса, который стоит перед «x».

При подстановки отрицательного числа в функцию вместо «x» обязательно заключайте отрицательное число в скобки. Не забывайте использовать правило знаков.

Подставим в функцию «y(x) = −x + 4» вместо «x» отрицательное число «−1».

Неправильно

Правильно

Теперь для функции «y(x) = −x + 4» найдем значения «y» при x = 0 и x = 1.

y(0) = −0 + 4 = 4

y(1) = −1 + 4 = 3

Запишем полученные результаты в таблицу. Таким образом мы получили табличный способ задания функции «y(x) = −x + 4».

x	y
−1	5
0	4
1	3

Графический способ задания функции

Теперь давайте разберемся, что называют графиком функции и как его построить.

Прежде чем перейти к изучению графического способа задания функции обязательно вспомните, что называют прямоугольной системой координат.

Рассмотрим функцию «y(x) = −2x + 1».

Найдем несколько значений «y» для произвольных «x». Например, для x = −1,
x = 0 и x = 1.

Результаты запишем в таблицу.

x	Расчет
−1	y(−1) = −2 · (−1) + 1 = 2 + 1 = 3
0	y(0) = −2 · 0 + 1 = 0 + 1 = 1
1	y(1) = −2 · 1 + 1 = −2 + 1 = −1

Каждая пара значений «x» и «y» — это координаты точек по оси «Ox» (абсцисса точки) и «Oy» (ордината точки) соответственно.

Назовем каждую полученную точку и запишем их координаты в новую таблицу.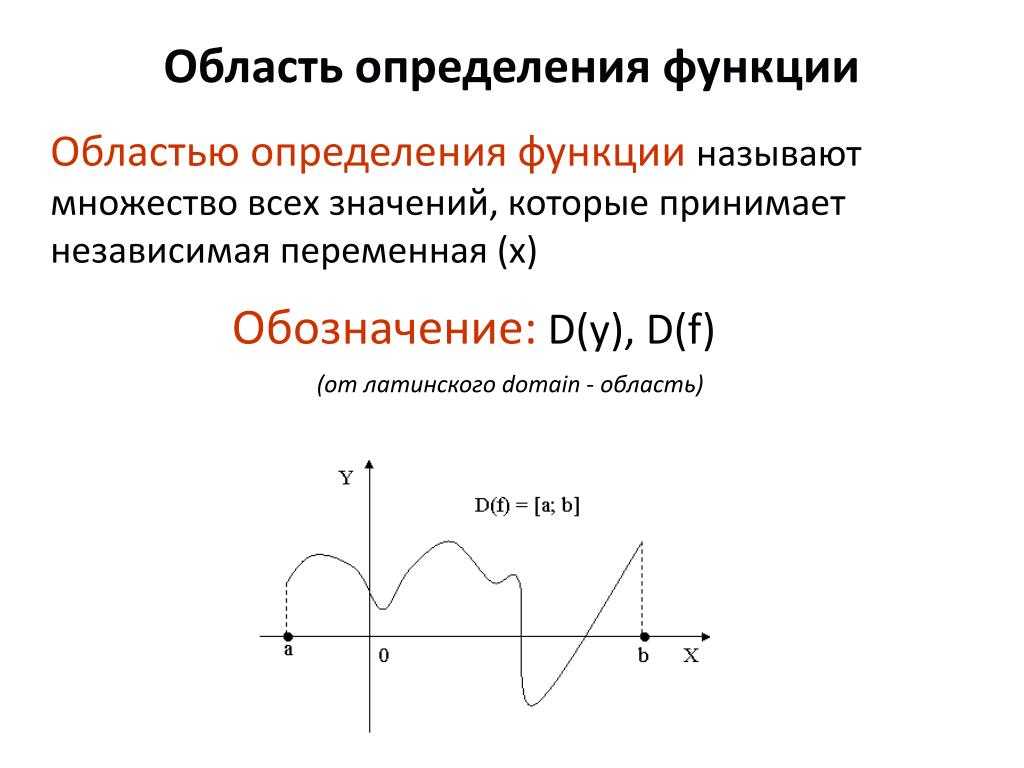

Имя точки	x	y
(·) A	−1	3
(·) B	0	1
(·) C	1	−1

Отметим точки А(−1;3), B(0;1) и С(1;−1) на прямоугольной системе координат.

Соединим отмеченные точки прямой. Проведенная прямая будет графиком функции «y(x) = −2x + 1».

Запомните!

График функции — это объединение всех точек, координаты которых мы можем найти, подставляя в функцию произвольные числовые значения вместо «x».

Другими словами можно сказать, что под графиком функции мы понимаем множество всех точек, координаты которых мы можем найти, подставляя в функцию любые числовые значения вместо «x».

Полученный график функции «y(x) = −2x + 1» это бесконечное множество точек, которые лежат на одной прямой.

При многократном увеличении графика функции мы увидим, что в самом деле вся прямая состоит из рядом стоящих точек.

Точки располагаются максимально близко к друг другу, поэтому по расчетам получается, что графиком функции будет являться прямая.

Урок 48. функции. свойства функций и их графики. исследование функций — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №48. Функции. Свойства функций и их графики. Исследование функций.

Перечень вопросов, рассматриваемых в теме:

функция, аргумент функции, значение функции
график функции, преобразование графика функции
свойства функции, исследование свойств функции

Глоссарий по теме урока

Определение

Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.

х – независимая переменная, аргумент,

у — зависимая переменная, значение функции

Определение

Множество значений аргумента функции называется областью определения функции и обозначается D(y).

Определение

Множество значений, которые принимает сама функция, называется множеством значений функции и обозначается Е(у).

Определение

Функция у = f(х) называется четной, если она обладает двумя свойствами:

область определения этой функции симметрична относительно 0;
для любого х из области определения выполняется равенство f(-х)=f(х).

Функция у = f(х) называется нечетной, если она обладает двумя свойствами:

область определения этой функции симметрична относительно 0;

для любого х из области определения выполняется равенство f(-х)=-f(х).

Определение

Значения аргумента, при которых значение функции равно 0, называются корнями (нулями) функции.

Определение

Функция у=f(x) возрастает на промежутке (а; в), если для любых х₁, х₂ из этого промежутка, таких, что х₁<х_2, выполняется неравенство у₁<у₂.

Функция у=f(x) убывает на промежутке (а; в), если для любых х₁, х₂ из этого промежутка, таких что, х₁<х_2, выполняется неравенство у₁>у₂.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2015. С. 98-118, 271-307.

Дополнительная литература:

Шахмейстер А.Х. Построение и преобразование графиков. Параметры. Ч.2-3. СПб.: Петроглиф; М.: МЦНМО, 2016. 392 с. С.73-307.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”.

https://mathb-ege.sdamgia.ru/test?theme=177

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей.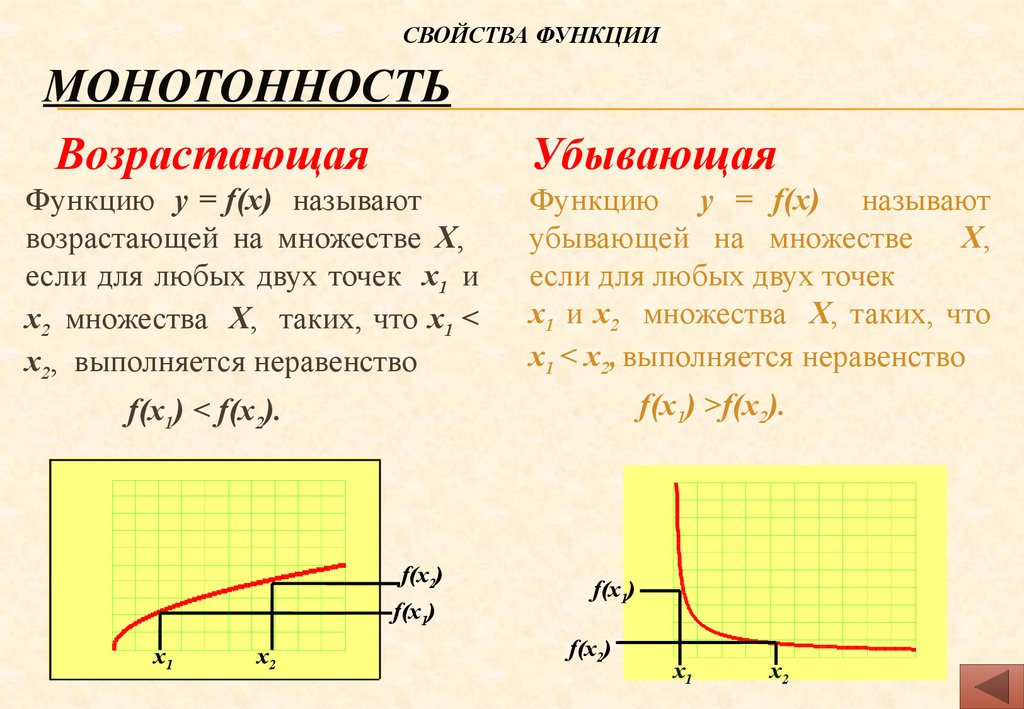 Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

1. Исследование функции и построение графика

Схема исследования функции на примере функции

1) Область определения функции

Знаменатель дроби не равен нулю:

Получили область определения

D(y)=

Множество значений функции

Отыскание Е(у) можно свести к решению уравнения с параметром у. Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).

Получили

Четность / нечетность функции

D(y)= — симметрична относительно нуля

следовательно, функция четная и ее график симметричен относительно оси ОУ

Нули функции

Для нахождения нулей функции необходимо решить уравнение

Уравнение не имеет действительных корней, значит, нулей у данной функции нет, ее график не пересекает ось ОХ

Промежутки знакопостоянства

у>0 при

у<0 при

Монотонность

Найдем производную

Найдем точки, в которых производная равна нулю или не существует: х=0, х=-1, х=1.

Определим знаки производной в полученных промежутках.

точки -1, 1 – выколоты, 0 — закрашена

Производная положительна, а значит, функция возрастает при .

Производная отрицательна, а значит, функция убывает при

Экстремум

х=0 – стационарная точка.

В ней производная меняет знак с плюса на минус, следовательно, х=0 – точка максимума.

Значение функции в точке максимума

Дополнительные точки

у(0,5)= у(-0,5)=-5/3; у(2)=у(-2)=5/3; у(3)= у(-3)=5/4

Отразим найденные свойства графически, построим график функции

2. Решение задачи на оптимизацию

Задачи на отыскание наибольших или наименьших значений величин решаются по определенному плану.

В решении таких задач выделяют 3 основных этапа:

1 этап. «Перевод» задачи на язык функций:

вводят независимую переменную х
выявляют оптимизируемую величину у, для которой надо найти наибольшее или наименьшее значение
выражают у через х и другие известные величины
устанавливают по условию задачи границы изменения переменной х

2 этап. Исследуют составленную функцию на наибольшее или наименьшее значение (в зависимости от условия задачи) с помощью производной или элементарными средствами.

3 этап. Интерпретация найденного решения для поставленной задачи – «перевод» полученного математического результата на язык задачи.

Рассмотрим план решения на примере задачи.

Задача. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t² у.е. Если на втором объекте работает t человек, то их суточная зарплата составляет t² у.е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у.е. в этом случае придется заплатить рабочим?

Решение:

1 этап. Ведем переменную, выразим нужные компоненты, составим искомую функцию.

Пусть на 1 объект направлено х рабочих, суточная зарплата которых составит 4x² у. е.

Тогда на 2 объект направлено (24 — x) рабочих – суточная заработная плата (24 — x)² (у.е.)

Всем рабочим нужно заплатить 4x²+(24 — x)² = 5x²-48x+576 (у.е.)

Причем 0≤ x ≤ 24, x ϵ N.

2 этап.

Рассмотрим функцию f(x)=5x²-48x+576.

Функция квадратичная, старший коэффициент положителен, следовательно, наименьшее значение в вершине при x₀ = 4,8 .

3 этап. Перевод на язык задачи

Поскольку x ϵ N, подходящим будет ближайшее к вершине натуральное значение, x=5 (рабочих) – на 1 объекте.

24-5=19 (рабочих) – на 2 объекте.

Наименьшее значение f(5)=125+240-576=461 (у.е.) – наименьшая суточная выплата.

Примечание: исследовать функцию также можно было с помощью производной.

Ответ: 5 рабочих на 1 объекте, 19 – на втором, 461 у.е. – наименьшая суточная выплата.

Примеры и разбор решения заданий тренировочного модуля

1. Исследуйте функции на четность.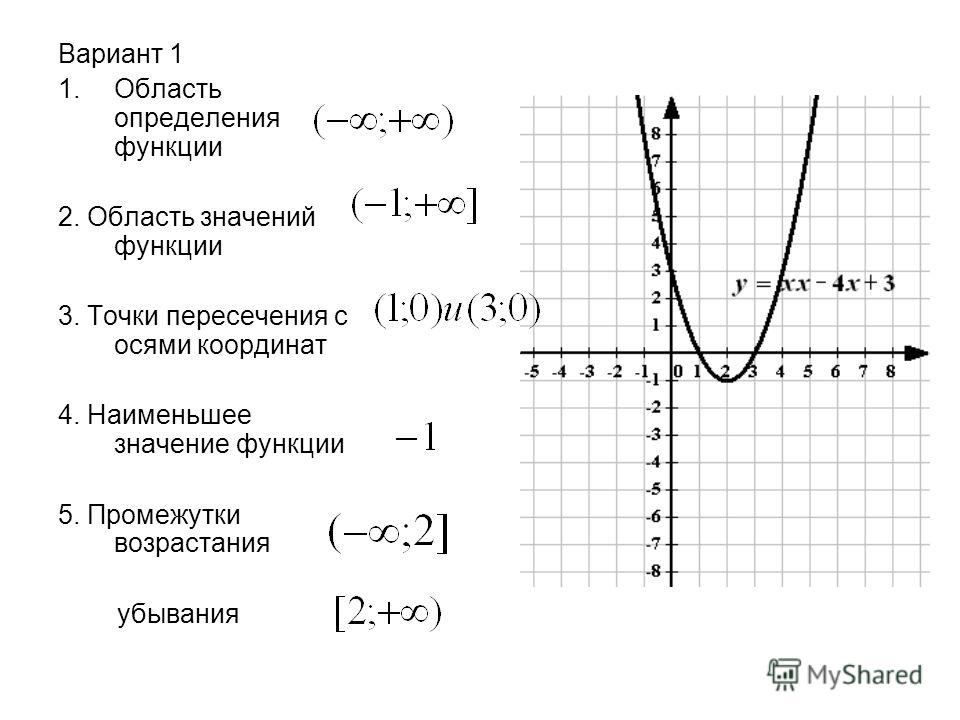

Функции

у=0

у=sin(x+5π/2)

у=lg(x+10)

Решение:

у=0

область определения – множество действительных чисел – симметрична относительно нуля

у(-х)=0, что можно интерпретировать и как у(х), и как –у(х). К тому же график этой функции – прямая, совпадающая с осью ОХ, — симметричен относительно оси ОУ и относительно начала координат.

Данная функция одновременно четна и нечетна.

у=sin(x+5π/2)

область определения – множество действительных чисел – симметрична относительно нуля

преобразуем функцию, применив формулы приведения: sin(x+5π/2)=cos x

у= cos x – четная функция, значит, исходная функция также четная

у=lg(x+10)

логарифмируемое выражение должно быть положительным

x+10>0; x>-10

D(y): x>-10

Область определения несимметрична относительно 0, значит, в проверке второго условия нет необходимости, — функция общего вида.

Найдем область определения D(f)

Проверим второе условие

Полученное в результате подстановки –х в функцию выражение, очевидно, не равно f(x), не дает пока понимания о выполнении условия нечетности.

Зайдем с другого конца, выразим -f(x):

домножим на сопряженное

Теперь можем сделать вывод: f(-x)=-f(x), функция нечётная.

Ответ:

Функции	Четность / нечетность
у=0	и четная, и нечетная
у=sin(x+5π/2)	четная
у=lg(x+10)	общего вида
	нечетная

Решение:

Используем функциональный подход при решении данной задачи. Представим каждое из уравнений как функции. Построим их графики. Единственное решение системы будем интерпретировать как единственную точку пересечения графиков функций первого и второго уравнений.

Второе уравнение проще, но содержит параметр. Перепишем его в явном виде для функции, выразив у: у=-х+а.

В таком виде понятно, что данное уравнение задает множество прямых, параллельных у=-х.

Первое уравнение содержит квадратные корни, что накладывает ограничения: х≥-4, у<7

Сгруппируем в скобках первое, третье и пятое слагаемые, второе и четвертое, получим:

Приравнивая каждый из множителей числителя к нулю, получаем прямые: у=4, у=х+3, х=-4, точнее, с учетом ограничений, части прямых.

Выполним построения выделенных функций.

Условию задачи удовлетворяют только такие прямые второго уравнения у=-х+а, которые пересекают графики первого уравнения только в одной точке.

Анализируя рисунок, получаем: а ≤ -5, а ≥11, а=5.

Ответ:

Что такое значение функции в алгебре – Значение функции это

Функции по алгебре это

Функции: понятие функция и аргумент, функциональная зависимость

Если две переменные величины находятся между собой в такой зависимости, что каждому значению одной переменной соответствует строго определённое значение другой, то первая величина называется аргументом, а вторая его функцией.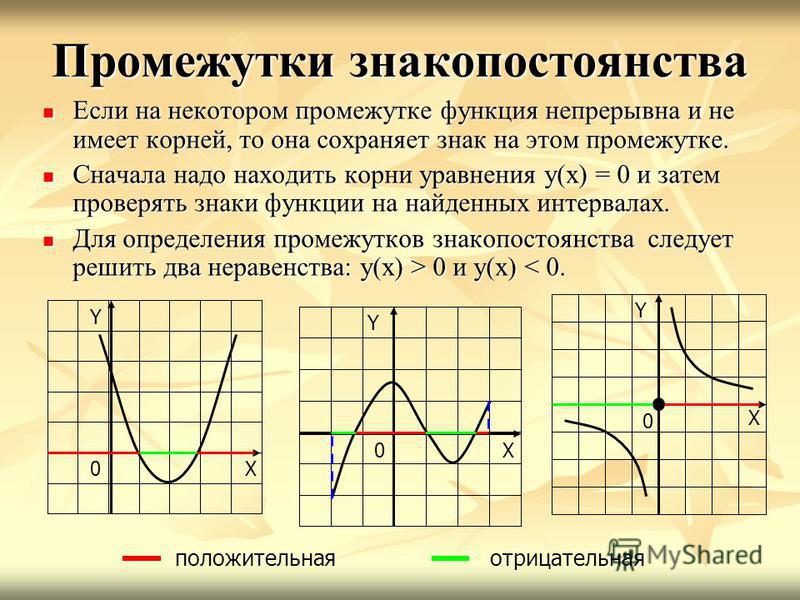

Функция – это зависимая переменная величина. Аргумент – это независимая переменная. Зависимость функции от аргумента называется Функциональной зависимостью.

Если нужно указать на тот факт, что y функция от x, не акцентируя внимания на то, в какой именно зависимости находится функция от аргумента, то пишут просто:

Где f (начальная буква слова function – функция) заменяет слово функция, y – это функция, а x – аргумент.

Иногда чтобы показать, что y зависит от x пишут просто:

Обратите внимание, что вместо y и x могут использоваться любые другие буквы.

Значение y, соответствующее заданному значению x называют Значением функции. Все значения, которые принимает аргумент, образуют Область определения функции. Все значения, которые принимает зависимая переменная, образуют Множество значений функции. Для функции f приняты следующие обозначения:

D(f) – область определения функции
(множество значений аргумента)

E(f) – множество значений функции

Пример.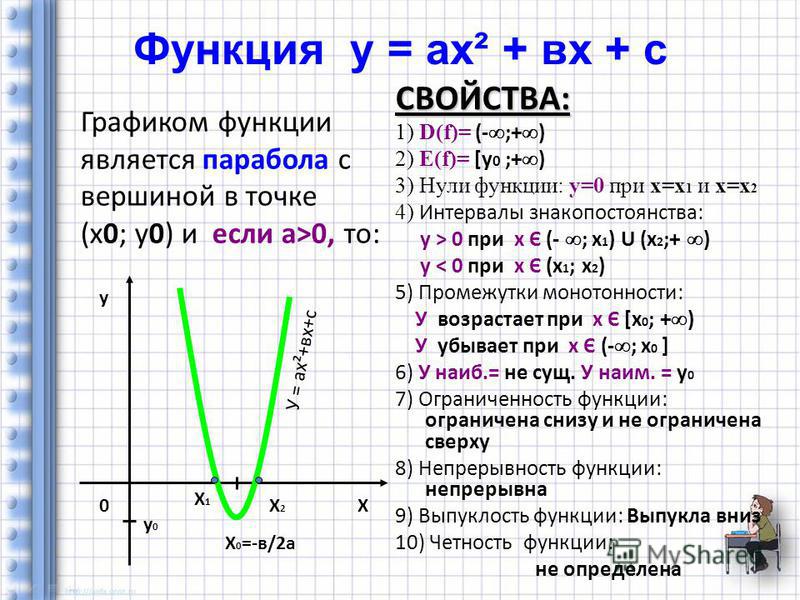 Возьмём формулу нахождения расстояния по скорости и времени:

Где S – это расстояние, v – скорость, а t – время. Если взять скорость равную 50 км/ч, то каждому неотрицательному значению

T (ч) S (км)

1	1,5	2	2,5	3
50	75	100	125	150

Следовательно, S является функцией от t – S(t) , область определения функции – D(S) &ges; 0, так как время не может быть отрицательным, но при этом можно не затратить времени вообще если не двигаться, в этом случае t = 0. Значение этой функции в точке t0 можно обозначить в виде S(t0), то есть записать таблицу со значениями в таком виде:

Что такое алгебра?! Функция и аргумент в алгебре.

В данной статье разберемся, Что такое алгебра. Узнаем о таких понятиях, как Функция и аргумент в алгебре и дадим простые и понятные определения.

Один из разделов математики это алгебра, которая подразумевает выполнение различных операций с числами, так как сложение, умножение и т. д. Можно сказать, что алгебра это нечто вроде расширения арифметики до более высокого уровня. Понять, что такое алгебра и откуда она взялась, помогут исторические факты. Первые предпосылки алгебры появились в разных уголках мира, людям нужна была алгебра для того, чтобы решить определенные уравнения. Например, в Древней Греции впервые об уравнениях заговорил Диофант, это был 2-3 век нашей эры.

В Китае примерно 2 тысячи лет до нашей времени уже было умение решать квадратные уравнения и уравнения первой степени. Также некоторые предпосылки алгебры встречались у индийского народа и жителей арабских стран. Согласно историческому прошлому, также отличилось издание «Алгебра» аль-Хваризми, которое стало популярным в 12-ом веке благо переводу на латинском языке. Человечество нуждалось в проведение расчетов, так появилась алгебра. Что такое алгебра для вас и нужна или нет, каждый решает сам. Потребность в алгебре появилась, как необходимость решать однотипные задачи. В школе алгебра всегда была и остается обязательным предметом.

Когда начинают учить алгебру в школе?

Разделение математики на несколько областях определило для алгебры решение определенных уравнений, под названием Алгебраические уравнения. Что такое алгебра как предмет можно узнать только в 7-ом классе. Именно тогда вместе привычной математики появляется два отдельных предмета: алгебра и геометрия. Изучение начинается с простых понятий, также как и в случае других учебных процессов, все строится от простого материала к сложному.

7 класс оптимальное время для того, чтобы узнать, что такое алгебра. Вместо обычных операций с числами осуществляется переход на переменные. Так проще понять общие законы арифметики, научиться работать с неизвестными и функциями. Алгебру можно разделить на 5 отдельных категорий:

Школьная программа подразумевает изучение исключительно элементарной категории. Элементарная алгебра занимается изучением операций с вещественными числами. Перемененные и постоянные обозначены в алгебре символами в виде букв. С их помощью происходит преображение уравнений и математических выражений на основе четких правил.

Функция в алгебре

Понимание алгебры как предмет требует знание определенных элементов, так как функция, аргумент и определение. Что такое функция в алгебре и чем она определена? Функция является одним из основных понятий и определяет зависимость между переменными с неодинаковой величиной.

Что такое функция?:

Функция в алгебре представляет собой сопоставимость между двумя множествами. Согласно этому каждый элемент множества соответствует по одному единственному элементу другого множества.

Функция задается различным образом:

— согласно словесной формулировке (описание словами)

— аналитическим образом (используя формулу).

Школьная алгебра всецело сосредоточена над изучением числовых функций. Функция и аргумент указаны в виде чисел. Пример: Y=f(x), где

X перемена независимого типа, а Y функция наоборот зависимая. У функции есть еще такие параметры как: область определения (D) и область значения (E). Первый параметр представляет собой совокупность значений для переменной «х», в то время как второй обозначает множество значений для «у».

Аргумент в алгебре

Что такое аргумент в алгебре? Это не что иное, как перемена х, от которой зависит у, то есть функция. Аргумент функции в алгебре это независимая перемена с помощью которой определяется значение функции.

Значение аргумента можно определить по значению функции. Для определения аргумента по функции y=f(x), надо заменить y заданным значением. Остается только решить уравнение относительно x для того, чтобы значение стало известным. Существует возможность определения данного параметра и по графику функции.

Определение алгебры и ее практическая польза

Определение, что такое алгебра, позволяет понять какая от нее практическая польза. Только понимая область деятельности этой части математики, появляется стремление ее изучать. Благодаря алгебре, можно шагать на более высокий уровень познания математики. Алгебра это та простая ступень, которая позволяет делать прогресс в процессе изучения современной математики. Благодаря ней, появилась возможность взглянуть иначе на множества.

Постепенно элементарные значения алгебры перешли в более сложные понятия. Так появилась универсальная алгебра, которая стала основой для развития топологии. Алгебра это ступень, которая позволяет ступать дальше, и без нее не быть некоторым явлений прогресса. Знания некоторых людей, может завершиться на элементарных основ дисциплины, но в определенных областях глубокое изучение обязательно.

Если материал был полезен, вы можете Отправить донат или поделиться данным материалом в социальных сетях:

Значение функции

Область значений функции

Область значений (или Множество значений) Функции — множество, состоящее из всех значений, которые принимает функция[1][2][3].

Определение

Пусть на множестве X задана функция f, которая отображает множество X в Y, то есть: f : X → Y. Тогда Областью (или Множеством) Значений функции f называется совокупность всех её значений, которая является подмножеством множества Y и обозначается f ( X ) :

Множество значений функции f обозначается также символами E ( f ) , R ( f ) или r a n f \,f> (от англ.

Терминология

В некоторых источниках различаются понятия Области значений и Множества значений функции. При этом Областью значений функции называют её кодомен, то есть множество Y в обозначении функции f : X → Y [4], сохраняя термин Множество значений для обозначения совокупности всех значений функции f.

Множество значений f ( X ) называется также образом множества X при отображении f.

Иногда Множество значений функции называют Множеством всех значений или Областью изменения функции[3].

Понятие и свойства функции. Область определения и область значения

Основные данные о работе

Версия шаблона	2. 1
ЦДОР
Вид работы	Творческое эссе
Название дисциплины	Математика (курс 13)
Тема	Понятие и свойства функции. Область определения и область значения.
Фамилия
Имя
Отчество
№ контракта

Содержание

Понятие и свойства функции. Область определения и область значения……………3

Список использованных интернет-ресурсов……………………………………………9

Основная часть

Понятие и свойства функции. Область определения и область значения

1.Фукция и её свойства.

Функция (отображение, оператор, преобразование) — это математическое понятие, отражающее связь между элементами множеств. Так же можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной однозначно определяет значение выражения, а значение месяца однозначно определяет значение следующего за ним месяца, а также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Термин «функция» (в некотором более узком смысле) был впервые использован Лейбницем в 1692 год. В свою очередь, Иоганн Бернулли в письме к Лейбницу употребил этот термин в смысле, более близком к современному.

Первоначально, понятие функции было неотличимо от понятия аналитического представления. Впоследствии появилось определение функции, которое дал Эйлер в 1751 год, затем — Лакруа в 1806 год — уже практически в современном виде. Наконец, общее определение функции (в современной форме, но для числовых функций) было дано Лобачевским в 1834 году и Дирихле в 1837 году.

К концу XIX века понятие функции переросло рамки числовых систем. Первыми это сделали векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.

Часто под термином «функция» понимается числовая функция; то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.

Функция – это одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.

Функция — это зависимость переменной у от переменной х, если каждому значению х соответствует единственное значение у.

Переменная х – это независимая переменная или аргумент.

Переменная у – это зависимая переменная.

Значение функции – это значение у, соответствующее заданному значению х.

Область определения функции – это все значения, которые принимает независимая переменная.

Область значений функции (множество значений)- это все значения, которые принимает функция.

Функция является четной — если для любого х из области определения функции выполняется равенство f(х)=f(-х)

Функция является нечетной — если для любого х из области определения функции выполняется равенство f(-х)=-f(х)

Возрастающая функция — если для любых х1 и х2, таких, что х1

Убывающая функция — если для любых х1 и х2, таких, что х1F(х2)

2. Способы задания функции.

Как найти значение функции 🚩 значение функции это 🚩 Математика

27 декабря 2018

Под понятием функции в математике понимают связь между элементами множеств. Если говорить более точно, это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Знания в области алгебры и математического анализа.

Значения Функции это некая область, значения из которой может принимать функция. Например область значения функции f(x)=|x| от 0 до бесконечности. Чтобы найти Значение функции в конкретной точке необходимо подставить вместо аргумента функции его числовой эквивалент, полученное число и будет значением функции. Пусть дана функция f(x)=|x| — 10 + 4x. Найдем значение функции в точке x=-2. Подставим вместо x число -2: f(-2)=|-2| — 10 + 4*(-2) = 2 — 10 — 8 = -16. То есть значение функции в точке -2 равно -16.

Прежде чем искать значение функции в точке — убедитесь, что она входит в область определения функции.

Аналогичным способом можно найти значение функции нескольких аргументов. Отличие в том, что вместо одного числа необходимо будет подставить несколько — по числу аргументов функции.

Распечатать

Как найти значение функции

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

Значение функции. Поясните Значение функции это есть значения У (игрек) Так?

Значение зависимой переменной называют значениями функции

Линейная функция — y=kx+b

Наибольшее и наименьшее значение формулы

У — это значение функции, или можно назвать результат функции, или ответ функции

Где f (начальная буква слова function – функция) заменяет слово функция, y – это функция, а x – аргумент.

Иногда чтобы показать, что y зависит от x пишут просто:

Обратите внимание, что вместо y и x могут использоваться любые другие буквы.

D(f) – область определения функции
(множество значений аргумента)

E(f) – множество значений функции

Пример. Возьмём формулу нахождения расстояния по скорости и времени:

T (ч)S (км)

1	1,5	2	2,5	3
50	75	100	125	150

Область определения и область значения.

Xn—-8sbanwvcjzh9e. xn--p1ai

11.09.2019 8:54:47

2019-09-11 08:54:47

Источники:

Https://xn—-8sbanwvcjzh9e. xn--p1ai/raznoe-2/chto-takoe-znachenie-funkcii-v-algebre-znachenie-funkcii-eto. html

Функции и их свойства | Материал по алгебре: | Образовательная социальная сеть » /> » /> .keyword { color: red; }

Функции по алгебре это

Функция — одно из важнейших математических понятий. Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.

Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.

Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: y=f(x ). (Читают: у равно f от х. ) Символом f(x) обозначают значение функции, соответствующее значению аргумента, равному х.

Все значения независимой переменной образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.

Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.

Способы задания функции:

1. аналитический способ (функция задается с помощью математической формулы;

2. табличный способ (функция задается с помощью таблицы)

3. описательный способ (функция задается словесным описанием)

4. графический способ (функция задается с помощью графика).

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

2. Промежутки знакопостоянства функции

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

3. Возрастание (убывание) функции.

Возрастающая в некотором промежутке функция — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Функция у = f (x) называется возрастающей на интервале (а; b), если для любых x 1 и x 2 из этого интервала таких, что x 1 2 , справедливо неравенство f(x 1 ) 2 ).

Убывающая в некотором промежутке функция — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Функция у = f (x) называется убывающей на интервале (а; b) , если для любых x 1 и x 2 из этого интервала таких, что x 1 2 , справедливо неравенство f(x 1 )>f(x 2 ).

4. Четность (нечетность) функции

Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x) . График четной функции симметричен относительно оси ординат.

Например, у = х 2 — четная функция.

Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.

Например: у = х 3 — нечетная функция.

Функция общего вида не является четной или нечетной ( у = х 2 +х ).

Свойства некоторых функций и их графики

1. Линейной функцией называется функция вида, где k и b – числа.

Область определения линейной функции – множество R действительных чисел.

Графиком линейной функции у = kx + b (k ≠ 0) является прямая проходящая через точку (0; b ) и параллельная прямой у = kx.

Прямая, не параллельная оси Оу, является графиком линейной функции.

Свойства линейной функции.

1. При k > 0 функция у = kx + b возрастающая в области определения.

2. При k 0 функция у = kx + b убывающая в области определения.

3. Множеством значений функции y = kx + b(k ≠ 0 ) является вся числовая прямая, т. е. множество R действительных чисел.

При k = 0 множество значений функции у = kx + b состоит из одного числа b.

3. При b = 0 и k = 0 функция не является ни четной, ни нечетной.

При k = 0 линейная функция имеет вид у = b и при b ≠ 0 она является четной.

При k = 0 и b = 0 линейная функция имеет вид у = 0 и являете одновременно четной и нечетной.

Графиком линейной функции у = b является прямая, проходящая через точку (0; b ) и параллельная оси Ох. Заметим, что при b = 0 график функции у = b совпадаете осью Ох.

5. При k > 0 имеем, что у > 0, если и у 0, если. При k 0 имеем, что у > 0, если и у

2. Функция y = x 2

Область определения этой функции — множество R действительных чисел.

Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле y = x 2 , изображаем график функции.

График функции y = x 2 называется параболой.

Свойства функции у = х 2 .

1. Если х = 0, то у = 0, т. е. парабола имеет с осями координат общую точку (0; 0) — начало координат.

2. Если х ≠ 0 , то у > 0, т. е. все точки параболы, кроме начала координат, лежат над осью абсцисс.

3. Множеством значений функции у = х 2 является промежуток [0; + ∞).

4. Если значения аргумента отличаются только знаком, то значения функции равны, т. е. парабола симметрична относительно оси ординат (функция у = х 2 — четная).

5. На промежутке [0; + ∞) функция у = х 2 возрастает.

6. На промежутке (-∞; 0] функция у = х 2 убывает.

7. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.

Область определения этой функции — промежуток [0;+∞), т. е. все неотрицательные числа.

Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле, изображаем график функции.

1. Если х = 0, то у = 0, т. е. график функции имеет с осями координат общую точку (0; 0) — начало координат.

2. Если х > 0, то у > 0, т. е. все точки графика функции, кроме начала координат, лежат над осью абсцисс.

3. Множеством значений функции является промежуток [0;+∞) .

4. Функция не является ни четной, ни нечетной.

5. Функция возрастающая в области определения.

6. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.

4. Функция y = x 3

Область определения этой функции — множество R действительных чисел,

Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле у = х 3 , изображаем график функции.

График функции у= х 3 называется кубической параболой.

Свойства функции y = x 3 .

1. Если х = 0, то у = 0, т. е. кубическая парабола пересекает оси координат в точке (0; 0) — начале координат.

2. Если х > 0, то у > 0, а если х 0, то у

3. Множеством значений функции у = х 3 является вся числовая прямая.

4. Если значения аргумента отличаются только знаком, то и значения функции отличаются только знаком, т. е. кубическая парабола симметрична относительно начала координат (функция у = х 3 — нечетная).

4. Функция у = х 3 возрастающая в области определения.

Область определения этой функции — множество R действительных чисел.

Пользуясь определением модуля числа х при х > О получим у = х, а при х у = — х. Таким образом, имеем:

График функции состоит из двух частей: части прямой у = х при х ≥ 0 и из части прямой у =- х при х

1. Если х = 0, то у = 0, т. е. график пересекает оси координат в точке (0; 0) — начале координат.

2. Если х ≠ 0, то у > 0, т. е. все точки графика функции y = |x|, кроме начала координат, лежат над осью абсцисс.

3. Множеством значений функции y = |x| является промежуток [0;+∞).

4. Если значения аргумента отличаются только знаком, то значения функции равны, т. е. график функции симметричен относительно ординат (функция y = |x| — четная).

5. На промежутке [0;+∞) функция y = |x| возрастает.

6. На промежутке (-∞;0] функция y = |x| убывает.

7. Наименьшее значение функция принимает в точке х, оно равно 0. Наибольшего значения не существует.

Область определения функции: .

Область значений функции: .

2. Промежутки знакопостоянства,

Если k > 0, то у > 0 при х > 0; у х

Если k у х > 0; у > 0 при х

3. Промежутки возрастания и убывания.

Если k > 0, то функция убывает при.

4. Четность (нечетность) функции.

Уравнение вида ax 2 +bx+c = 0, где a, b и с — некоторые числа, причем а≠ 0, называется квадратным.

В квадратном уравнении ax 2 +bx+c = 0 коэффициент а называется первым коэффициентом, b — вторым коэффициентам, с — свободным членом.

Формула корней квадратного уравнения имеет вид:

Выражение называется дискриминантом квадратного уравнения и обозначается через D.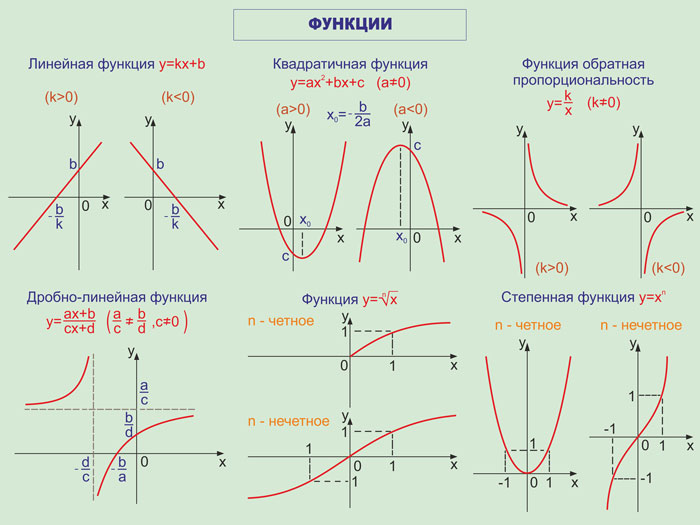

Если D = 0, то существует только одно число, удовлетворяющее уравнению ax 2 +bx+c = 0. Однако условились говорить, что в этом случае квадратное уравнение имеет два равных действительных корня, а само число называют двукратным корнем.

Если D > 0, то квадратное уравнение имеет два различных действительных корня.

Пусть дано квадратное уравнение ax 2 +bx+c = 0. Так как а≠ 0, то, разделив обе части данного уравнения на а, получим уравнение. Полагая и, приходим к уравнению, в котором первый коэффициент равен 1. Такое уравнение называется приведенным.

Формула корней приведенного квадратного уравнения имеет вид:

Аx 2 +bx = 0, ax 2 + с = 0, аx 2 = 0

Называются неполными квадратными уравнениями. Неполные квадратные уравнения решаются разложением левой части уравнения на множители.

Сумма корней квадратного уравнения равна взятому с противоположным знаком отношению второго коэффициента к первому, а произведение корней — отношению свободного члена к первому коэффициенту, т.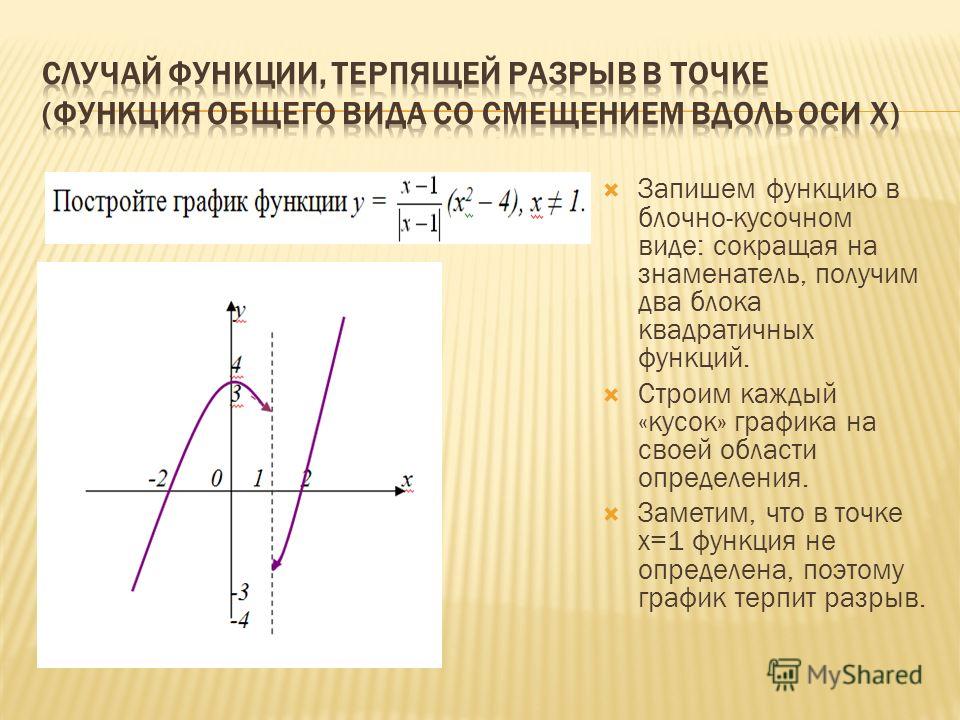 е.

Если сумма каких-нибудь двух чисел х 1 и х 2 равна, а их произведение равно, то эти числа являются корнями квадратного уравнения ах 2 + bх + с = 0.

Функция вида ах 2 +bх + с называется квадратным трехчленом. Корни этой функции являются корнями соответствующего квадратного уравнения ах 2 + bх + с = 0.

Если дискриминант квадратного трехчлена больше нуля, то этот трехчлен можно представить в виде:

Ах 2 +bх + с =а(х-х 1 )(х-х 2 )

Где х 1 и х 2 — корни трехчлена

Если дискриминант квадратного трехчлена равен нулю, то этот трехчлен можно представить в виде:

Ах 2 +bх + с =а(х-х 1 ) 2

Где х 1 — корень трехчлена.

Например, 3х 2 — 12х + 12 = 3(х — 2) 2 .

Уравнение вида ах 4 + bх 2 + с = 0 называется биквадратным. С помощью замены переменной по формуле х 2 = y оно приводится к квадратному уравнению аy 2 + by + с = 0.

Квадратичной функцией называется функция, которую можно записать формулой вида y = ax 2 + bx + c, где x – независимая переменная, a, b и c – некоторые числа, причем a≠ 0.

Свойства функции и вид ее графика определяются, в основном, значениями коэффициента a и дискриминанта.

Свойства квадратичной функции

— Область определения: R;

При b = 0 функция четная

При b≠ 0 функция не является ни четной, ни нечетной

При D > 0 два нуля: ,

При D = 0 один нуль:

Если, а > 0, D > 0, то

Если, а > 0, D = 0, то

Графиком квадратичной функции является парабола – кривая, симметричная относительно прямой, проходящей через вершину параболы (вершиной параболы называется точка пересечения параболы с осью симметрии).

Чтобы построить график квадратичной функции, нужно:

1) найти координаты вершины параболы и отметить ее в координатной плоскости;

2) построить еще несколько точек, принадлежащих параболе;

3) соединить отмеченные точки плавной линией.

Координаты вершины параболы определяются по формулам:

Преобразование графиков функции

1. Растяжение графика у = х 2 вдоль оси у в |а| раз (при |а| 1 — это сжатие в 1/ |а| раз).

Если, а х (ветви параболы будут направлены вниз).

Результат: график функции у = ах 2 .

2. Параллельный перенос графика функции у = ах 2 вдоль оси х на |m| (вправо при

M > 0 и влево при т 0).

Результат: график функции у = а(х — т) 2 .

3. Параллельный перенос графика функции вдоль оси у на |n| (вверх при п > 0 и вниз при п 0).

Результат: график функции у = а(х — т) 2 + п.

Неравенства вида ах 2 + bх + с > 0 и ах 2 + bх + с 0, где х — переменная, a, b и с — некоторые числа, причем, а≠ 0, называют неравенствами второй степени с одной переменной.

Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.

Для решения неравенств вида ах 2 + bх + с > 0 и ах 2 + bх + с 0 поступают следующим образом:

1) находят дискриминант квадратного трехчлена и выясняют, имеет ли трехчлен корни;

2) если трехчлен имеет корни, то отмечают их на оси х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а > 0 или вниз при а 0; если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а > 0 или в нижней при а

3) находят на оси х промежутки, для которых точки параболы расположены выше оси х (если решают неравенство ах 2 + bх + с > 0) или ниже оси х (если решают неравенство ах 2 + bх + с

Ее графиком является парабола, ветви которой направлены вниз (т.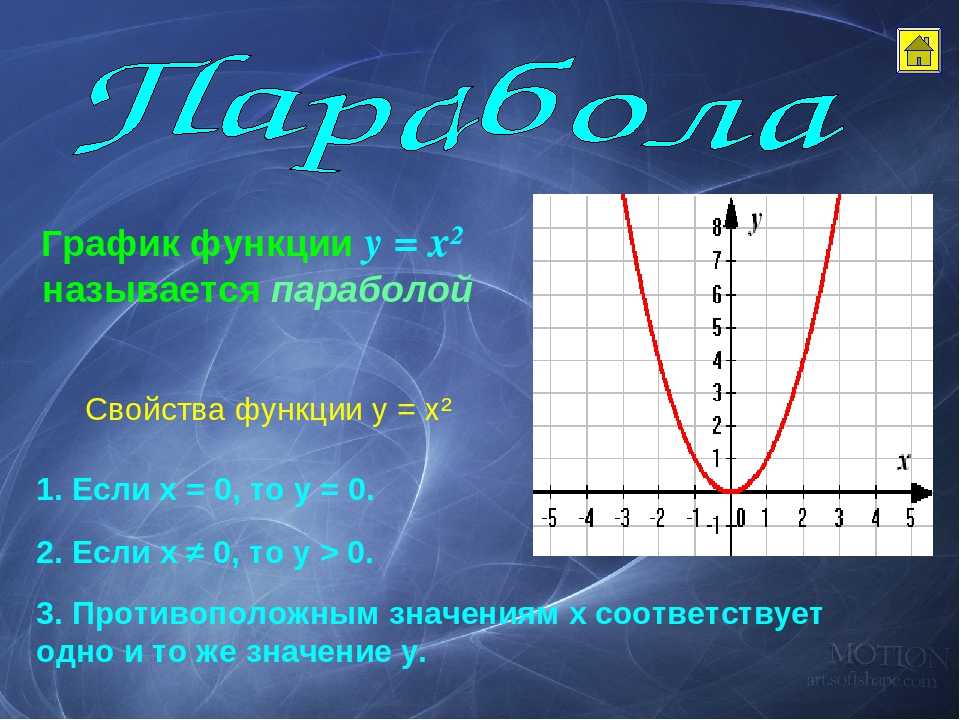 к. ).

Выясним, как расположен график относительно оси х. Решим для этого уравнение. Получим, что х = 4. Уравнение имеет единственный корень. Значит, парабола касается оси х.

Изобразив схематически параболу, найдем, что функция принимает отрицательные значения при любом х, кроме 4.

Ответ можно записать так: х — любое число, не равное 4.

Решение неравенств методом интервалов

1. Найти нули функции, стоящей в левой части неравенства.

2. Отметить положение нулей на числовой оси и определить их кратность (если k i четное, то нуль четной кратности, если k i нечетное — то нечетной).

3. Найти знаки функции в промежутках между ее нулями, начиная с крайнего правого промежутка: в этом промежутке функция в левой части неравенства всегда положительна для приведенного вида неравенств. При переходе справа налево через нуль функции от одного промежутка к соседнему следует учитывать:

• если нуль нечетной кратности, знак функции изменяется,

• если нуль четной кратности, знак функции сохраняется.

4. Записать ответ.

( х + 6) ( х + 1) ( х — 4)

Найден нули функции. Они равны: х 1 = -6; х 2 = -1; х 3 = 4.

Отметим на координатной прямой нули функции f(x) = ( х + 6) ( х + 1) ( х — 4).

Найдем знаки этой функции в каждом из промежутков (-∞; -6), (-6; -1), (-1; 4) и

Из рисунка видно, что множеством решений неравенства является объединение промежутков (-∞; -6) и (-1; 4).

Ответ: (-∞ ; -6) и (-1; 4).

Рассмотренный способ решения неравенств называют методом интервалов.

По теме: методические разработки, презентации и конспекты

Урок-презентация. Тригонометрические функции и их свойства.

Данная презентация поможет закрепить свойства тригонометрических функций в решении сложных задач.

Открытый урок по алгебре «Графики функций и их свойства» с презентацией 10 класс

Урок обобщения и систематизации знаний по теме «Графики функций и их свойства» с применением ИКТ. Формирование конструктивных навыков, эстетичности и аккуратности при выполнении графических работ чере.

Урок в 9 классе на тему: «Квадратичная функция и ее свойства»

Урок обобщения свойств функции на примере квадратичной функции с использованием дифференцированного подхода в обучении математике и элементов тестирования, что способствует подготовки учащихся к ГИА п.

Квадратичная функция и ее свойства. С применением электронных образовательных ресурсов

Дать определение квадратичной функции и по графику определять ее основные свойства, научить использовать свойства квадратичной функции при решать задач; развитие познавательного интереса к обуче.

Презентация «Линейная функция, её график, свойства».

Презентация к уроку.

Конспект урока с презентацией «Функции. Графики функции и их свойства» 10 класс

Конспект урока по теме «Функции. Графики функции и их свойства» в 10 классе. Тип урока: Обобщение и систематизация знаний. К учебнику Алимова и др. Основная работа на уроке идет по презентации, т.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты соответствующим значениям функции.

Nsportal. ru

15.05.2017 5:46:41

2017-05-15 05:46:41

Источники:

Https://nsportal. ru/shkola/algebra/library/2019/05/31/funktsii-i-ih-svoystva

Что такое Функция в Алгебре? » /> » /> .keyword { color: red; }

Функции по алгебре это

Мы знаем, как соответствовать определенным чертам: быть вежливым, опрятным, инициативным. А как быть соответствиям между числовыми множествами — узнаем в этой статье про математические функции.

О чем эта статья:

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение Y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина У зависит от величины Х по определенному закону, или правилу, которое обозначается F.

Вывод: меняя Х (независимую переменную, или аргумент) — меняем значение У.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину Х, как-то над ней поколдовать — и получить соответствующую величину У.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, функция У = 2х каждому действительному числу X ставит в соответствие число Y, которое в два раза больше, чем Х.

Область определения — множество Х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

Область определения выглядит так:

х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество У, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению Х соответствует одно и только одно значение У. И наоборот — зная У, можно сразу найти Х.

О чем эта статья.

Skysmart. ru

02.10.2020 6:09:54

2020-10-02 06:09:54

Источники:

Https://skysmart. ru/articles/mathematic/chto-takoe-funkciya

Определение, понятие, свойства и значение функций в алгебре

Одним из основных понятий в математике, если не самым основным, является понятие функции. Для понимания этого термина, его значения, смысла и необходимости, обратимся к следующему примеру:

Вообразим себе обыкновенный автомобиль. Предположим, что он постоянно двигается со скоростью 80 км/ч и не меняет её на протяжении всего пути. А теперь попробуем выяснить: сколько километров проедет автомобиль, если в пути он будет находиться 5 часов? Итак, нам известна скорость и время. Попробуем составить зависимость:

…

Оглавление:
Смысл
Способы задания
Свойства

Сколько времени находится в пути автомобиль?	Сколько километров автомобиль проехал?
1 ч	80 км
2 ч	160 км
3 ч	240 км
4 часа	320 км
5 часов	400 км

Нам были известны всего две величины: скорость автомобиля и время, которое он находился в пути. Взглянув на таблицу, можно понять, что между временем, которое находился автомобиль в пути, и пройденным им расстоянием есть чёткая зависимость — каждый час автомобиль проезжает на 80 километров больше. Что ж, давайте немного приблизимся к алгебре и введём две переменные: y и x.

Y — это наше расстояние, а x — время пути. Составим уравнение: y = 80 * x. Теперь вместо x подставим время:

Y = 80 * 1. Получается 80 — значение расстояния, которое автомобиль пройдёт за 1 час.
Теперь вместо x подставим 2. Получается: y = 80 * 2 = 160. Это значение расстояния, которое пройдёт автомобиль при условии, что он будет ехать 2 часа.

Теперь введём следующую запись: y(x). Эта запись означает зависимость первой переменной от второй, а наше окончательное уравнение для движения автомобиля будет выглядеть следующим образом: y(x)=80x. Y в алгебре принято называть функцией, а x — аргументом.

Это интересно: какой вектор называется разностью двух векторов?

Смысл

Пользуясь приведённым примером, мы чётко и ясно можем понять, что определение функции — это зависимость одной переменной от другой.

Очень важно понимать, что y = 80 * x — не единственная зависимость. Стоит нам лишь изменить скорость автомобиля, то все ý при тех же значениях аргумента будут совсем другие. Кроме того, существует огромное множество зависимостей, которые могут иметь другой вид.

Способы задания

Всего в математике существует три способа задания функции:

«Формульный способ». С помощью формулы мы всегда можем определить ý. Допустим, что у нас есть зависимость y = 5x + 1. Чтобы найти все y, нам просто нужно подставить вместо x любое число, например: если x = 0, y = 1, если x = 5, y = 26. В этой функции мы можем принимать любые значения аргумента, но если нам встретится следующая зависимость: y = √x, то мы сможем взять за x все числа, кроме отрицательных, так как число под корнем не может быть с минусом.
Табличный способ задания также очень сильно распространён. Мы уже встречались с таблицей, когда приводили пример про автомобиль. Для того чтобы составить таблицу, необходимо всего лишь найти несколько значений y при нескольких значениях аргумента.
Графический способ задания. Когда только начинают знакомятся с функциями, обязательно вводят такое понятие, как график. Давайте рассмотрим, что же он из себя представляет.

Перед вами координатная плоскость — основа для графика. Она состоит из вертикальной оси Y — оси значений, и из горизонтальной оси X — аргумента. У координатной плоскости обязательно есть начало отсчёта, которая обозначается нулём, и единичный отрезок (в данном примере единичный отрезок равен одной клетке).

На координатной плоскости мы можем взять любой единичный отрезок. Например, если нам удобно, значение одной клетки будет ни 1, а 100. Следовательно, две клетки — 200 и так далее. Здесь мы можем построить любой график и, соответственно, увидеть любую зависимость.

На координатной плоскости мы видим график 2x — 1. Графиком является прямая. Как же определить зависимость? Давайте приметим любое значение аргумента, например, 0. Когда x = 0, значение равно 1, что чётко видно на графике. Когда аргумент = -1, значение также равно -1.

Свойства

В алгебре есть невообразимое количество свойств функции, но основными и действительно важными являются лишь некоторые.

«Область определения». Это понятие очень простое: оно подразумевает собой абсолютно все числа, которые может принимать переменная x. Например, в функции y = x — 2, переменная x может принимать все значения, то есть от минус бесконечности до плюс бесконечности. Другое дело, например, такая функция: y = √x. Так как под корнем не может стоять отрицательное число, допустимыми значениями аргумента могут быть все числа от нуля до плюс бесконечности.
Если область определения все значения аргумента, то следующее свойство функции, называемое «область значений» — это все значения, которые может принимать переменная y. Поскольку значения функции зависимы от аргумента, то тут ничего выдумывать не надо, а просто вычислять.
«Ограниченность» определить очень просто: если в рассматриваемой функции существует максимальное или минимальное значение y, то мы говорим, что функция будет называться ограниченной либо сверху, либо снизу.
«Непрерывность» —тоже очень простое свойство. Например, зависимость ý = 2x — 1, которую мы уже рассматривали, непрерывна, так как её график нигде не прерывается. Если же в какой-либо функции график будет прерываться, можно говорить, что она прерывается на определённом промежутке.
«Выпуклость» также присуща не всем графикам. У линейной зависимости её быть не может, поскольку это прямая и она не может быть выпуклой. А, например, парабола может быть выпуклой либо вверх, либо вниз.
Нули функции — это пересечение с осями. То есть, если нам необходимо описать данное свойство, нужно будет найти, в каком месте график пересекается с осью абсцисс и в каком месте с осью ординат.

Подводя итог, мы можем сказать, что функция — это важнейшее понятие в математике, ведь, по сути, ею можно описать любые процессы.

алгебра все о функциях

Вы искали алгебра все о функциях? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгебра все функции, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «алгебра все о функциях».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как алгебра все о функциях,алгебра все функции,алгебра график,алгебра графики,алгебра графики функций,алгебра функции,алгебра функции виды,алгебра функции все,алгебра функции их свойства и графики,алгебра функция,алгебра функция это,алгебра что такое функция,в алгебре функция,вид функции,виды графики функций,виды графиков все,виды графиков функции,виды графиков функций,виды графиков функций и их формулы,виды парабол и их графики,виды функции алгебра,виды функции графиков,виды функций,виды функций в математике,виды функций графики,виды функций и их графики,виды функция,все виды графиков,все виды графиков функции и их формулы,все виды функций и их графики,все графики и их функции,все графики функции,все графики функции и их формулы,все графики функций,все графики функций и их формулы,все графики функций и их формулы таблица,все о функциях алгебра,все о функциях и графиках,все функции,все функции алгебра,все функции в алгебре,все функции графики,все функции и их графики,все функции и их графики и свойства,все функции и их графики и свойства таблица,все функции и их графики и свойства таблица 9 класс,все функции и их свойства и графики,высшая математика графики функций,геометрические функции,график алгебра,график и их функции,график общего вида функции,график функции как находить,график функции как решать,график функции как читать,график функции общего вида,график функции определение,график функции примеры,график функции тема,график функции функция,график функции четверти,график функции что это,график функции это,график функции это определение,график функции это что,график функций как решать,графика простая,графика функция,графики алгебра,графики в математике,графики всех функций,графики и их названия,графики и их свойства,графики и их формулы,графики и их функции,графики и их функции и формулы,графики и их функция,графики и формулы,графики и формулы функции,графики и функции,графики и функции все,графики и функции формулы,графики как понять как,графики какие бывают,графики математика,графики математические,графики математических функций,графики основных и обратных функций,графики основных функций,графики по алгебре,графики по математике,графики пример,графики примеры,графики произвольных функций,графики простейших функций,графики простых функций,графики различных функций,графики формулы,графики функции все,графики функции и их графики таблица,графики функции и их свойства,графики функции и их формулы,графики функции и их формулы 9 класс шпаргалка,графики функции и их формулы все,графики функции и формулы,графики функции как строить,графики функции какие бывают,графики функции примеры,графики функций 9 класс и их формулы,графики функций алгебра,графики функций виды,графики функций виды функций,графики функций все,графики функций всех,графики функций высшая математика,графики функций и их,графики функций и их название,графики функций и их названия,графики функций и их свойства,графики функций и их уравнения,графики функций и их формулы,графики функций и их формулы 8 класс алгебра,графики функций и их формулы 9 класс,графики функций и их формулы все,графики функций и их формулы шпаргалка,графики функций и их формулы шпаргалка 9,графики функций и их формулы шпаргалка 9 класс,графики функций и формулы,графики функций как понять,графики функций как строить и решать,графики функций какие бывают,графики функций картинки,графики функций математика,графики функций примеры,графики функций различных,графики функций таблица,графики функций формулы,графиков примеры,графиков функций примеры,графические функции,графіки функції,графіки функцій,для функции y,как изобразить график функции,как называется функция,как найти график функции,как определить график функции по формуле,как определить по формуле график функции,как по формуле определить график функции,как понять графики функций,как решать функции,как решать функции по алгебре,как строить графики функций,как чертить графики функций,как читать график функции,как читать графики функций,как читать функцию,какая функция,какие бывают графики,какие бывают графики функции,какие бывают графики функций,какие бывают функции,какие бывают функции в алгебре,какие бывают функции в алгебре и их графики,какие графики бывают,какие графики функции бывают,какие графики функций бывают,какие есть функции,какие функции,какие функции бывают,какие функции бывают в алгебре,какие функции в,какие функции есть,какой график,какую функцию,картинки графики функций,математика высшая функции,математика графики,математика графики функций,математика функции,математика функции их свойства и графики,математика функция,математика функция это,математика что такое функция,математическая функция,математические графики,математические основные функции,математические функции,название графиков,название графиков функций,название функций,названия графиков,названия графиков функций,названия функций,названия функций графиков,названия функций и их графики,называется графиком функции,описание функций графиков,определение график функции,определение графика функции,определение по графику функции,определение функции,определение функции в алгебре,определение функции график,определение функции графика,определение функции по графику,определение что такое функция в алгебре,определения функция,основные графики и их функции,основные графики функций,основные функции и их графики,основные функции математические,парабола гипербола и другие графики,парабола гипербола и другие графики формулы,понятие графика функции,понятие функции графика функции,построить график функции что значит,приведите пример функции удовлетворяющей следующим условиям графиком является парабола,пример график,пример графика,пример функции,примеры график функции,примеры графики функции,примеры графики функций,примеры графиков,примеры графиков функций,примеры функции,примеры функций,примеры функций графиков,простая графика,простейшие графики и их функции,простейшие функции и их графики,простейшие функции их графики и свойства,простейшие функции их свойства и графики,таблица графики функций,таблица графиков функций и их формулы,таблица функций,тема график функции,типы графиков функций,укажите график функции,уравнения графиков функций,уравнения функций и их графики,формула графика прямой,формула графика функции,формула параболы на графике функции,формула прямой на графике функции,формула функции,формула функции y x,формула функции графика,формулы графики,формулы графики функций,формулы графиков функций,формулы графиков функций 9 класс,формулы и графики,формулы и графики функции,формулы и графики функций,формулы и их графики,формулы и их функции,формулы и функции графики,формулы функции,формулы функции и графики,формулы функций,формулы функций графиков,формулы функций графиков 9 класс,формулы функция,фукция,функ,функции,функции алгебра,функции алгебра все,функции в алгебре,функции в алгебре и их графики,функции в алгебре определение,функции в математике,функции в математике виды и их графики,функции виды,функции виды графиков,функции виды математика,функции все,функции все алгебра,функции геометрические,функции график формулы,функции графика,функции графики,функции графики и формулы,функции графики примеры,функции графиков и их формулы,функции графические,функции и графики,функции и графики формулы,функции и графики шпаргалка,функции и их график,функции и их графики,функции и их графики и свойства,функции и их графики и свойства таблица,функции и их свойства и графики,функции и их формулы,функции и их формулы и графики,функции и формулы,функции и формулы графики,функции их свойства и графики,функции какие есть,функции математика,функции математики,функции математические,функции название,функции определения,функции по алгебре,функции пример,функции примеры,функции таблица,функции формула,функции формулы,функции формулы и графики,функций виды в алгебре,функций их названия и графики,функция алгебра,функция алгебра это,функция в алгебре,функция в алгебре это,функция в математике,функция в математике это,функция виды,функция график функции,функция графика,функция и ее график,функция и их свойства и графики,функция и не функция картинки,функция математика,функция математика что такое,функция математика это,функция математическая,функция формулы,функция это алгебра,функция это в алгебре,функция это в математике,функция это математика,четверти график функции,четверти графика,четверти графика функции,что называется графиком функции,что называют графиком функции,что такое график функции,что такое график функции в алгебре,что такое график функций,что такое значение функции в алгебре,что такое функция в алгебре,что такое функция в алгебре определение,что такое функция в математике,что такое функция определение в алгебре,что является графиком функции. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и алгебра все о функциях. Просто введите задачу в окошко и нажмите «решить» здесь (например, алгебра график).

Решить задачу алгебра все о функциях вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Алгебраическая функция — определение, примеры, типы

Алгебраическая функция, как следует из ее названия, представляет собой функцию, состоящую только из алгебраических операций. В математике мы изучаем различные типы функций. Наиболее распространенные функции:

Алгебраические функции
Тригонометрические функции
Логарифмические функции
Экспоненциальные функции

Давайте узнаем больше об алгебраических функциях, их типах и примерах.

1.	Что такое алгебраическая функция?
2.	Типы алгебраических функций
3.	Графики алгебраических функций
4.	Часто задаваемые вопросы по алгебраическим функциям

Что такое алгебраическая функция?

Алгебраическая функция является числом функция, которая включает только алгебраические операции. К таким операциям относятся сложение, вычитание, умножение, деление и возведение в степень. Основываясь на этом определении, давайте посмотрим на некоторые примеры алгебраических функций и неалгебраических функций.

Примеры алгебраических функций

Вот несколько примеров алгебраических функций. Обратите внимание, что алгебраические функции должны включать только операции +, -, ×, ÷, целые и рациональные степени. Эти обозначения приводят к алгебраическим функциям, таким как полиномиальная функция, кубическая функция, квадратичная функция, линейная функция, и основаны на степени задействованных уравнений.

f(x) = x ² — 5x + 7
г(х) = √х
ч(х) = (3х + 1) / (2х — 1)
к(х) = х ³

Идентификация алгебраических функций

Если функция включает только вышеупомянутые операции (+, -, ×, ÷, показатели степени (также корни)), то мы можем сказать, что это алгебраическая функция. Давайте взглянем и на неалгебраические функции, чтобы избежать путаницы.

Примеры неалгебраических функций

К неалгебраическим функциям относятся тригонометрические функции, логарифмические функции, функции абсолютного значения, экспоненциальные функции и т. д. Вот несколько примеров.

f(x) = sin (3x + 2)
г(х) = журнал х
ч(х) = 3 ^х

Типы алгебраических функций

Основываясь на приведенных выше примерах, у вас, возможно, уже возникла идея разделить типы алгебраических функций. Вот основные виды.

Полиномиальные функции
Рациональные функции
Силовые функции

Давайте посмотрим больше примеров каждого из этих типов.

Полиномиальные функции

Полиномиальные функции (которые являются одним из типов алгебраических функций) — это функции, определением которых является полином. Полиномиальные функции включают линейную функцию, квадратичную функцию, кубическую функцию, биквадратичную функцию, функцию пятого числа и т. д. Вот несколько примеров.

f(x) = 3x + 7 (линейная функция)
f(x) = x ² — 2x + 5 (квадратичная функция)
f(x) = x ³ — 7x + 7 (кубическая функция)
f(x) = x ⁴ — 5x ² + 2x — 8 (биквадратная функция)
f(x) = x ⁵ — 7x + 3 (функция пятой степени)

Область определения всех полиномиальных функций — это набор всех действительных чисел, а диапазон зависит от значений y, которые охватывает график. Чтобы узнать больше о полиномиальных функциях, нажмите здесь.

Рациональные функции

Рациональные функции (которые являются одним из типов алгебраических функций) — это функции, определение которых включает дробь с переменной в знаменателе (они также могут иметь переменную в числителе). т. е. они имеют вид f(x) = p(x)/q(x), где p(x) и q(x) — многочлены от x. Вот несколько примеров:

f(x) = (x — 1) / (3x + 2)
f(x) = (5x — 7) / (x ² — 7x + 9)
f(x) = (4x ² + 1) / (х + 2)

Чтобы найти область рациональных функций, мы используем знаменатель правила ≠ 0, а чтобы найти диапазон, мы решаем функцию для x, а затем применяем тот же знаменатель правила ≠ 0. Чтобы узнать больше о рациональных функциях, нажмите здесь.

Степенные функции

Степенные функции имеют вид f(x) = k x ^a , где «k» и «a» — любые действительные числа. Поскольку «а» — действительное число, показатель степени может быть как целым, так и рациональным числом. Вот несколько примеров.

f(x) = x ²
f(x) = x ^-1 (обратная функция)
f(x) = √(x — 2) = (x — 2) ^1/2
f(x) = $\sqrt[3]{x-3}$ = (x-3) ^1/3

Область применения всех силовых функций может не совпадать. Это зависит от значений x, в которых определена функция. Диапазон степенных функций зависит от значений y, которые будет охватывать график.

Графики алгебраических функций

Графики всех алгебраических функций НЕ одинаковы. Это зависит от уравнения функции. Общая процедура для построения графика любого y = f(x):

Найдите точки пересечения x (установив y = 0)
Найдите точки пересечения с осью y (установив x = 0)
Найдите все асимптоты и начертите их.
Найдите критические точки и точки перегиба.
Найдите несколько дополнительных точек между каждыми двумя пересечениями по оси x и между каждыми двумя асимптотами.
Нанесите все эти точки на график и соедините их кривыми, соблюдая асимптоты.

Для получения дополнительной информации о графических функциях нажмите здесь.

Важные замечания по алгебраическим функциям

Алгебраические функции включают только алгебраические операции.
Алгебраические операции: сложение, вычитание, умножение, деление, степени и корни.
Любая функция, которая имеет логарифм, ln, тригонометрические функции, обратные тригонометрические функции или переменную в показателе степени, НЕ является алгебраической функцией.
Область определения и область значений любой алгебраической функции можно найти, построив ее график на графическом калькуляторе и увидев значения x и значения y соответственно, которые покрывает график.

☛ Связанные темы:

Отношения и функции
Домен и область действия
Четная функция
Постоянная функция

Часто задаваемые вопросы по алгебраическим функциям

Что такое определение алгебраической функции?

Алгебраическая функция – это тип функций, который образуется только с помощью следующих операций:

Сложение
Вычитание
Умножение
Подразделение
Показатель степени (целочисленный или рациональный)

Что такое список алгебраических функций?

Алгебраические функции строятся только с использованием алгебраических операций. Здесь есть 3 типа:

Полиномиальные функции
Силовые функции
Рациональные функции

Что такое алгебраические типы функций?

Алгебраические функции используют только операции: +, -, ×, ÷ и показатель степени (любой рациональный показатель степени) и бывают 3 типов:

Рациональные функции
Полиномиальные функции
Силовые функции

Является ли log x алгебраической функцией?

Нет, log x НЕ является алгебраическим. Это логарифмическая функция.

Как определить алгебраические функции?

Алгебраическая функция должна включать только следующие операции:

+
—
×
÷
Степени типа x ² , (x — 1) ^1/2 и т. д.

Если у нас есть что-то кроме этих операций, то функция НЕ является алгебраической.

Является ли Sin x алгебраической функцией?

Нет, sin x НЕ является алгебраическим. Это тригонометрическая функция.

Какие функции НЕ являются алгебраическими?

Функции, включающие в себя все, кроме +, -, ×, ÷ и показателя степени, НЕ являются алгебраическими. Некоторые примеры неалгебраических функций:

f(x) = sin (x + 2)
f(x) = ln (x ³/3) и т. д.

Предварительное исчисление по алгебре — Что такое функция?

Резюме

Функция — это то, что принимает число, изменяет его в соответствии с некоторым правилом и выдает другое число. Вот и все. Это все. Остальное — обозначения.

Simpler Definition

Когда я учился в 4-м и 5-м классах, когда мы говорили о функциях, мы говорили о них в контексте функциональных «машин» — тех милых штучек, которые принимали число и выдавали другое, что-то вроде как эти таблицы:

Позже правила станут жестче. А правила были тем, что называлось «функциями». Вот что такое функция на самом фундаментальном уровне: что-то, что принимает число и выдает другое число в соответствии с заранее определенным правилом.

Средний Определение

Затем, в 6-м или 7-м классе, мы начали говорить о функциях как об уравнениях. Эти правила функциональных машин могут быть записаны в виде уравнений, которые принимают на вход $x$ и выдают результат $y$. Эти функции можно изобразить на декартовой плоскости следующим образом:

Мы узнали, что точки на этой линии представляют входы и выходы — координата x представляет вход, а координата y представляет выход. Уравнения, конечно, могли быть и более сложными, и их также можно было записать в виде $f(x) = x$ (вместо $y=x$), и нам сказали, что это обозначение функции , и это будет полезно позже.

Определение теории множеств

Совсем недавно, вне школы, я выучил более формальное определение функции, используя теорию множеств. Во-первых, несколько быстрых терминов/обозначений, и мы будем в пути.

«Наивное» определение множества состоит в том, что множество представляет собой совокупность любого количества объектов, обычно чисел, но иногда и других вещей. На самом деле это оказывается не совсем правильным, и если вы будете следовать этому достаточно далеко, это приведет к парадоксу, называемому парадоксом Рассела, но для наших целей мы можем придерживаться этого определения. Таким образом, у нас может быть набор $A = \{4,5\}$ и набор $B = \{4,5,6\}$.

Во-первых, мы можем определить элемент набора, т. е. число или объект, входящий в этот конкретный набор. Например, здесь мы можем сказать $4\in A$ или что $4$ находится в $A$. Мы также можем определить 90 337 подмножеств 90 338 набора. Чтобы быть подмножеством другого множества, все элементы предполагаемого подмножества должны находиться в другом множестве. Например, $A$ — это подмножество $B$ (обозначаемое как $A \subset B$), потому что $4$ и $5$ принадлежат $B$.

Далее мы можем определить умножение наборов. Для этого я хотел бы использовать в примере два разных множества, поэтому мы определим множества $A = \{a,b\}$ и $B = \{c,d\}$. Ответ здесь не совсем такой, как вы могли бы ожидать — это $A \times B = \{(a,c),(a,d),(b,c),(b,d)\}$. Другими словами, это набор упорядоченных пар, которые могут быть созданы из двух наборов таким образом, что упорядоченная пара имеет вид $(x, y)$, где $x \in X$ и $y \in Y$. 9n$ — множество всех действительных координат в $n$-м измерении. Круто, да?

Продолжая, давайте определим отношение , еще один ключевой элемент головоломки. Отношение $R$ между двумя множествами $X$ и $Y$ называется подмножеством $R \subset Y \times X$. Чтобы сказать, что $x \in X$ связано с $y \in Y$, мы можем написать $yRx$. Итак, что именно это означает? Итак, рассмотрим отношение $=$ на $\mathbb{R}$. Это строка $y=x$! Имеет ли это смысл? Мы имеем дело с множеством всех действительных чисел и эффективно установили связь между некоторым значением $x$ в множестве всех действительных чисел и некоторым значением $y$ в множестве всех действительных чисел. Мы создали почти функцию!

Итак, теперь мы переходим к функциям. Функция $f$ между $X$ и $Y$ записывается как $f: X\rightarrow Y$. Это отношение на $Y \times X$ такое, что $yfx$ и $y’fx$ влекут $y=y’$ — другими словами, функция — это отношение, которое «отображает» или связывает каждый $x$ с уникальный $y$.

Использование

О, чувак. Есть так много применений для этих вещей, что я не знаю, с чего начать! Они используются для всего, что включает в себя ввод числа, изменение его в соответствии с правилом и, очевидно, выплевывание нового числа. Подобным образом занимаются многие дисциплины, такие как физика, экономика, инженерия, компьютерное программирование, финансы, и я мог бы продолжать. Функции можно рассматривать как один из наиболее широко используемых математических инструментов. 92$. Это функция! Он принимает число $r$ и выдает число $A$.

Пример

Здесь я собираюсь определить функцию расстояния, метрику . Представьте множество $X$ с функцией $d: X\times X \rightarrow \mathbb{R}$, такой что

$d(x,y) = d(y, x)$ для всех $x,y \in X$ — другими словами, расстояние между двумя числами одинаково, независимо от того, перечислены они так или иначе.
$d(x, y) \geq 0$, где $d(x,y)$ равно нулю, только если $x=y$ — в принципе, расстояние не может быть отрицательным, и расстояние может быть равно нулю, только если оно это одна и та же точка.
$d(x,y) \leq d(x,z) + d(z,y)$ для всех $x, y, z \in X$ — это известно как неравенство треугольника, сделать это довольно ясно.

Извините, довольно неравносторонний треугольник, ну да ладно. Расстояние между $x$ и $y$ не может быть больше, чем расстояние между $y$ и $z$ плюс расстояние между $y$ и $x$, что действительно имеет большой смысл. Вы можете только увеличить расстояние, добавив еще одну точку.

Итак, мы только что определили функцию расстояния! Не так уж и плохо, правда. 92$, если хотите. Это просто еще один способ написать основную концепцию.

Я буду обновлять ответ на этот вопрос.

Наконец-то…

Есть несколько вещей, которые можно сделать с помощью функций, таких как композиция, и все виды других вещей, которые требуют некоторого времени для рассмотрения здесь (хм… может быть, я добавлю кое-что из этого впоследствии). А пока я бы порекомендовал заглянуть на страницу википедии, посвященную функциям, и на такие сайты, как Khan Academy, и, конечно же, задавать вопросы, когда они у вас есть.

Надеюсь, это поможет!

Определение функции | Алгебра среднего уровня

Результаты обучения

Определение функции с помощью таблиц
Определите, создает ли набор упорядоченных пар функцию
Определить домен и диапазон функции, представленной в виде таблицы или набора упорядоченных пар

Есть много видов отношений. Отношения — это просто соответствие между наборами значений или информации. Подумайте о членах вашей семьи и их возрасте. Сопряжение каждого члена вашей семьи и их возраста является отношением. Каждому члену семьи можно сопоставить возраст в наборе возрастов членов вашей семьи. Другим примером отношения является соединение штата с его сенаторами США. Каждому штату могут быть сопоставлены два человека, каждый из которых был избран сенатором. В свою очередь, каждому сенатору можно сопоставить одно конкретное государство, которое он или она представляет. Оба они являются реальными примерами отношений.

Первое значение отношения является входным значением, а второе значение — выходным значением. Функция представляет собой особый тип отношения, в котором каждое входное значение имеет одно и только одно выходное значение. Вход — это независимое от значение , а выход — это зависимое от значение , поскольку оно зависит от значения на входе.

Обратите внимание, что в первой таблице ниже, где входными данными являются «имя», а выходными данными — «возраст», каждый вход соответствует ровно одному выходу. Это пример функции.

Имя члена семьи (ввод)	Возраст члена семьи (Вывод)
Нелли	[латекс]13[/латекс]
Маркос	[латекс]11[/латекс]
Эстер	[латекс]46[/латекс]
Сэмюэл	[латекс]47[/латекс]
Нина	[латекс]47[/латекс]
Пол	[латекс]47[/латекс]
Катрина	[латекс]21[/латекс]
Андрей	[латекс]16[/латекс]
Мария	[латекс]13[/латекс]
Ана	[латекс]81[/латекс]

Сравните это со следующей таблицей, где вводом является «возраст», а выводом — «имя». Некоторые из входов приводят к более чем одному выходу. Это пример соответствия, которое является , а не функцией.

Возраст члена семьи (ввод)	Имя члена семьи (выход)
[латекс]11[/латекс]	Маркос
[латекс]13[/латекс]	Нелли, Мария
[латекс]16[/латекс]	Андрей
[латекс]21[/латекс]	Катрина
[латекс]46[/латекс]	Эстер
[латекс]47[/латекс]	Самуэль, Нина, Пол
[латекс]81[/латекс]	Ана

Теперь давайте посмотрим на некоторые другие примеры, чтобы определить, являются ли отношения функциями или нет, и при каких обстоятельствах. Помните, что отношение является функцией, если для каждого входа имеется только один выход.

Пример

Заполните таблицу.

Вход	Выход	Функция?	Почему или почему бы и нет?
Имя сенатора	Название штата
Название штата	Имя сенатора
Прошедшее время	Высота подбрасываемого мяча
Высота подброшенного мяча	Время истекло
Количество вагонов	Количество шин
Количество шин	Количество вагонов

Показать решение

Отношения могут быть записаны как упорядоченные пары чисел или как числа в таблице значений. Изучив входные данные ( x -координаты) и выходные данные ( y -координаты), вы можете определить, является ли отношение функцией. Помните, что в функции каждый вход имеет только один выход.

Существует одно имя для набора входных значений и другое имя для набора выходных значений для функции. Набор входных значений называется домен функции . Набор выходных значений называется диапазоном функции .

Если у вас есть набор упорядоченных пар, вы можете найти домен, перечислив все входные значения, которые представляют собой координаты x . Чтобы найти диапазон, перечислите все выходные значения, которые являются координатами y .

Рассмотрим следующий набор упорядоченных пар:

[латекс]\{(−2,0),(0,6),(2,12),(4,18)\}[/латекс]

Вы есть следующее:

[латекс]\begin{array}{l}\text{Домен:}\{−2,0,2,4\}\\\text{Диапазон:}\{0,6,12,18\} \end{array}[/latex]

Теперь попробуйте сами.

Пример

Перечислите домен и диапазон для следующей таблицы значений, где x — входные данные, а y — выходные.

х	у
[латекс]−3[/латекс]	[латекс]4[/латекс]
[латекс]−2[/латекс]	[латекс]4[/латекс]
[латекс]−1[/латекс]	[латекс]4[/латекс]
[латекс]2[/латекс]	[латекс]4[/латекс]
[латекс]3[/латекс]	[латекс]4[/латекс]

Показать решение

В следующем видео мы приводим еще один пример определения того, представляет ли таблица значений функцию, а также определения домена и диапазона каждого из них.

Пример

Определите домен и диапазон для следующего набора упорядоченных пар и определите, является ли заданное отношение функцией.

[латекс]\{(−3,−6),(−2,−1),(1,0),(1,5),(2,0)\}[/латекс]

Показать решение

В следующем видео мы покажем, как определить, является ли отношение функцией, и как найти домен и диапазон.

Пример

Найдите домен и диапазон отношения и определите, является ли оно функцией.

[латекс]\{(−3, 4),(−2, 4),(−1, 4),(2, 4),(3, 4)\}[/латекс]

Показать решение

Определите входные значения — это ваш домен.
Определите выходные значения — это ваш диапазон.
Если каждое значение в домене приводит только к одному значению в диапазоне, классифицируйте связь как функцию. Если какое-либо значение в домене приводит к двум или более значениям в диапазоне, не классифицируйте связь как функцию.

Что такое функция? — Математический обзор (видео)

TranscriptFAQsPractice

Здравствуйте, добро пожаловать в этот обзор функций! В этом видео мы рассмотрим природу математических отношений между переменными. Когда мы работаем с некоторыми примерами, наша цель — определить, соблюдаются ли критерии для определения особого отношения, известного как «функция».

Давайте рассмотрим основы математических правил или «отношений». Когда мы работаем с уравнением, значение переменной $x$ помогает определить значение переменной $y$.

$y=2x+3$

Значение $x$ можно рассматривать как ввод в математическое правило, определяемое уравнением, а $y $-значения, которые получаются в результате, являются выходными данными . Технические термины для всех $x$-значений и $y$-значений: домен и диапазон соответственно. Таким образом, в этом уравнении диапазон $y$ будет таким же, как $2x+3$.

Мы можем использовать таблицу, чтобы представить некоторые из различных результатов уравнения.

Домен	Диапазон $\hspace{20px}y=2x+3$
$20-20$ 9 $-20-20$ 9 = -1\)
$-1$	$2(-1)+3=1$
$0$	$2(0)+3= 3$
$1$	$2(1)+3=5$
$2$	$2(2)+3=7$

Итак, у нас есть наше уравнение и различные значения, которые $x$ могут быть перечислены здесь. Например, если мы обнаружим, что $x$ равно -2, наша задача будет выглядеть как $2(-2)$ (что равно -4) плюс 3, что равно -1.

Набор упорядоченных пар также можно использовать для отображения математической взаимосвязи. Здесь показаны пять элементов домена и диапазона из таблицы:

$(-2,-1), (-1,1), (0,3), (1,5), ( 2, 7)$

Словами каждое $x$-значение отображается как упорядоченная пара с соответствующим ему $y$-значением. Эти упорядоченные пары можно изобразить на координатной плоскости, чтобы визуально показать взаимосвязь.

Отношение $y=2x+3$ изображено здесь:

Значения домена находятся на оси $x$, а график принимает форму в соответствии со значениями диапазона на оси $y$.

Другое удобное визуальное представление отношения называется отображением , которое показывает прямое соответствие между элементами домена и диапазона. Вот два примера:

На карте A каждое входное значение соответствует одному выходному значению, а на карте B значение домена «2» соответствует двум выходным значениям, 20 и 40. На этом простом изображении четко показаны критерии. определить, является ли заданное отношение функцией.

По определению отношение определяется как функция, если каждый элемент домена отображается на один и только один элемент диапазона. Не все отношения являются функциями, но функции являются подмножеством отношений. В этом видео мы рассмотрели несколько репрезентаций отношений. На следующем изображении показаны четыре представления, которые показывают отношение, которое не квалифицируется как функция:

На этом этапе мы сосредоточимся на графике этого отношения, чтобы ввести тест вертикальной линии, который позволяет быстро определить функцию. статус любого графа, который вам дан.

Короче говоря, если вы проведете вертикальную линию через график и попадете только в ОДНУ точку, то этот график представляет собой функцию. В примере, который мы только что показали, если вы проведете вертикальную линию через значение домена -2, линия пройдет через значения диапазона 2 и -2.

Следовательно, отношение не проходит тест вертикальной линии. Вот еще примеры этого удобного инструмента для определения функции по графику.

Думаете, у вас получилось?

Что такое функция?

Давайте вместе решим несколько задач и посмотрим.

Это функция?

\(\{(−2 , 2), (−3 , 3), (−4 , 4)\}[/latex

В этом наборе упорядоченных пар значения домена равны [латекс ]{-2, -3, -4}\), а значения диапазона равны ${2, 3, 4}$. Поскольку каждое значение домена связано только с одним значением диапазона, это отношение является функцией. Что с этим набором?

$\{(3, 2), (3, 3), (2, 4)\}$

В этом наборе значения домена равны ${3, 2}$, а значения диапазона равны ${2, 3, 4}$. Поскольку значение домена 3 связано с 2 и 3 в диапазоне, это отношение НЕ является функцией.

Вот еще один набор, чтобы разобраться:

$\{(1, 2), (2, 2), (3, 2), (4, 2), (5, 2)\}$

Что вы думаете? Это функция или просто отношение?

Домен этого отношения — ${1, 2, 3, 4, 5}$, а диапазон — ${2}$. Поскольку каждый элемент домена связан с «2», он удовлетворяет определению функции. Допускается, чтобы каждый элемент домена сочетался с ТАКИМ ЖЕ элементом диапазона.

Помните тест на вертикальную линию? Какой из этих графиков пройдет этот тест, если мы проведем через него вертикальную линию?

Первый график здесь проходит тест, потому что вертикальная линия проходит только через одну точку. На втором графике вертикальная линия проходит через две точки, поэтому это не функция.

Теперь, когда мы рассмотрели несколько различных представлений функций, вы должны быть на пути к составлению более сложных уравнений.

Спасибо за просмотр и удачной учебы!

Часто задаваемые вопросы

Q

Что такое функция в математике?

A

Функция – это отношение, в котором одна величина зависит от другой.

Q

Как найти домен функции?

A

Найдите область определения функции, рассмотрев, какие числа могут быть входными данными для функции.
Пример. Какова область определения $f(x)=\frac{x+7}{x-3}$? 92+х+4\)?
Диапазон равен [4,∞), поскольку наименьшее значение f(x) для любого заданного значения x равно 4, но f(x) может принимать любое значение больше 4.

Q

Что такое линейная функция?

A

Линейная функция — это любая функция, график которой представляет собой линию.

Практические вопросы

Вопрос № 1:

Какой набор упорядоченных пар показывает отношение, которое является функцией?

$(1,-3), (2,-4), (0,2), (-1,5), (-2,8)$

$(1,1), (1,2), (1,3), (1,4), (1,5)$

$(0,-3), (1,4 ), (2,-5), (3,-6), (0,3)$

$(-5,-5), (-4,-4), (-5,-3) , (-4,-2), (-5,-1)$

Показать ответ

Ответ:

По определению отношение является функцией, если каждый элемент домена отображается только в один элемент в диапазон. Другими словами, отношение является функцией, если каждое $х$-значение имеет только одно $у$-значение. Глядя на отношения в каждом выборе, единственное отношение, в котором значение домена ($x$-значение) не повторяется, это $(1,-3), (2,-4), (0,2), (-1,5), (-2,8)$. 92+5\)

$(-3{,}2),(-2{,}1),(-1{,}0),(0{,}0),(-1{,} 1)$

900

$\mathbf{x}$	$\mathbf{y}$
$-2$	$6-$

$-1$	$-3$
$0$	$0$
$1$ 9001\)

Показать ответ

Ответ:

График уравнения в варианте А и график в варианте D представляют собой параболы с боковыми сторонами, которые не проходят тест на вертикальную линию. В варианте B $-1$ отображается как в $0$, так и в $1$, что означает, что это не функция. Вариант C — единственное отношение, в котором каждое значение домена соответствует одному уникальному значению в диапазоне.

Скрыть ответ

Вопрос № 4:

В какой таблице значений показано отношение, являющееся функцией?

33339119 \ (0 \)3333 \ (0 \)333

\ (\ mathbf {x} \)	\ (\ mathbf {y} \)
\ (0 \)	\ (2 \)
\ (0 \)	\ (2 \)
\ (2 \)
18
\ (2 \)
8
\ (0 \)	. \)	$3$
$2$	$4$
$2$	$5$

\ (\mathbf{х}\)	$\mathbf{y}$
$2$	$2$
$3$	$3$
\ (4\)	$4$
$5$	$5$

$\mathbf4\4\2) {у}$
$-1$	$4$
$-2$	$6$	9001 )	$-6$
$-1$	$-4$

$\mathbf{x4}2) 0 y}$
$7$	$3$
$5$	$1$
$3$	\ (-1\)
$7$	$-3$

Показать ответ

Ответ:

мы смотрим на значения домена (значения x), чтобы увидеть, соответствуют ли они одному уникальному значению диапазона. Единственным отношением, удовлетворяющим этому требованию, является вариант B, где каждое значение домена сопоставляется с уникальным значением диапазона.

Скрыть ответ

Вопрос № 5:

Что показывает график функции?

Показать ответ

Ответ:

Поскольку нам уже были даны графики отношений, мы можем применить тест вертикальной линии, чтобы определить, какое отношение является функцией. Единственным графом, прошедшим тест на вертикальную линию, является график Choice D.

Скрыть ответ

0642 784611822500

Функции в алгебре: это ваши правильные отношения

Домен и диапазон

Purplemath

Существуют разные взгляды на функции. Мы рассмотрим несколько. Но сначала нам нужно обсудить некоторую терминологию.

Что такое отношение в алгебре?

«Отношение» — это просто отношение между наборами информации. Подумайте обо всех людях в одном из ваших классов и подумайте об их росте. Сочетание имен и высот является отношением.

Содержание продолжается ниже

MathHelp.com

Функции и отношения

В отношениях и функциях пары имен и высот «упорядочены», что означает, что одно идет первым, а другое вторым. Иными словами, мы могли бы организовать эту пару таким образом, чтобы либо вы давали мне имя, а затем я давал вам рост этого человека, либо вы давали мне рост, а я давал вам имена всех людей, которые такой высокий.

Каковы домен и диапазон отношения?

Набор всех начальных значений отношения называется «домен», а набор всех конечных значений — «диапазон». Домен — это то, с чего вы начинаете; диапазон — это то, что вы получите в итоге; домен x , диапазон y . (Я объясню больше о доменах и диапазонах позже.)

Функция — это «хорошо работающее» отношение, под которым мы подразумеваем, что, имея начальную точку, мы знаем ровно одну конечную точку, к которой нужно перейти. ; учитывая x -значение, мы получаем только и ровно одно соответствующее y -значение. (Примечание: это означает, что, хотя все функции являются отношениями [поскольку функции передают информацию о парах], , а не , все отношения являются функциями. Члены семьи с хорошим поведением являются подмножеством всех ваших отношений; так же и функции [хорошее поведение] являются подмножеством всех математических отношений.)

Каков реальный пример отношения, которое не является функцией?

Вернемся к нашему соотношению ваших одноклассников и их роста, и предположим, что домен есть множество всех ростом. Предположим, что в коридоре вас ждет доставщик пиццы; все, что доставщик знает, это то, что пицца предназначена для ученика в вашем классе ростом пять футов пять дюймов.

Теперь впустите парня. К кому он идет? Что, если никто не ростом пять футов пять дюймов? Что, если в комнате шесть человек, которых пять-пять? Они все должны платить? Что делать, если вы пять футов пять дюймов? А что, если у вас закончились наличные? А аллергия на анчоусы? Вы все еще на крючке? ак! Какой беспорядок!

Отношение «высота указывает имя» некорректно. Это не функция. Учитывая отношение ( x , y ) = (пять футов пять дюймов, имя), может быть шесть различных вариантов для y = «имя». Чтобы отношение было функцией, должно быть только и ровно , одно и , соответствующее данному x .

Какие изображения функций и отношений?

Выше показана функция. Вы можете сказать, что это функция, проследив от каждого x до каждого y . На каждые x приходится только один х ; из каждого x выходит только одна стрелка.

Ха! Держу пари, я обманул некоторых из вас на этом! это — это функция! Из каждого x выходит только одна стрелка; есть только один y для каждого x . Так уж получилось, что это всегда одно и то же y для каждого x , но только одно y . Итак, это функция; это просто чрезвычайно скучная функция!

Это не функция: есть две стрелки, исходящие из числа 1; число 1 связано с двумя разными элементы диапазона. Итак, это отношение, но не функция.

Ладно, это вопрос с подвохом. Каждый элемент домена, у которого есть пара в диапазоне, хорошо себя ведет. А как же эти 16? Это — это в домене, но у него нет соответствующего элемента диапазона! Это не сработает! Тогда это не функция. Черт возьми, это даже не отношения!

Что такое тест вертикальной линии?

Тест вертикальной линии предоставляет графический способ проверки того, является ли отношение функцией. Если на графике нет места, где вертикальная (то есть восходящая и нисходящая) линия пересекалась бы дважды, то отношение проходит проверку и является функцией. Теперь, что все это значит?

Глядя на эту функцию графически, что, если бы у нас было отношение, состоящее из множества, состоящего всего из двух точек: {(2, 3), (2, −2)}? Мы уже знаем, что это не функция, поскольку x = 2 соответствует каждому из y = 3 и y = −2.

Если изобразить это отношение на графике, оно будет выглядеть так:

Обратите внимание, что через две точки можно провести вертикальную линию, вот так:

Эта характеристика не-функций была замечена Я-не-знаю-кто , и был кодифицирован в «Тесте вертикальной линии»: если на графике отношения вы можете нарисовать вертикальную линию, пересекающую график более чем в одном месте, то отношение не является функцией.

Какой пример применения теста вертикальной линии?

Рассмотрим график ниже:

На этом графике показана функция, потому что нет вертикальной линии, которая пересекала бы этот график дважды.

Теперь рассмотрим эллипс, изображенный ниже:

На этом графике не показана функция, потому что любое количество вертикальных линий будет дважды пересекать этот овал. Например, ось y пересекает (пересекает) прямую дважды.

Как быстро определить, функция это или нет?

Самый быстрый способ определить, представляет ли данная формула или уравнение функцию, — это взглянуть на свой калькулятор. Если формулу можно ввести в калькулятор (чтобы калькулятор мог изобразить ее на графике, оценить или сделать что-то еще), то это функция; иначе нет. Что это значит?

Принимая во внимание все построенные вами графики, самый простой способ для заданного уравнения — найти « y =», построить T-диаграмму, выбрать несколько значений для x , найти соответствующие значения y , отметьте точки и соедините точки, бла-бла-бла-бла.

Это полезно не только для построения графиков, но и дает еще один способ идентификации функций: если вы можете найти « y =», то это функция. Другими словами, если вы можете ввести его в свой графический калькулятор, то это функция. Калькулятор может обрабатывать только функции. Например, 2 y + 3 x = 6 — это функция, потому что вы можете найти y :

2 у + 3 х = 6
2 у = -3 х + 6
y = (−3/2) x + 3

С другой стороны, y ² + 3 x = 6 не является функцией, потому что вы не можете найти уникальных y :

Я имею в виду, да, это решено для » y =» , но это не уникальный . Вы берете положительный квадратный корень или отрицательный? Кроме того, где клавиша «±» на вашем графическом калькуляторе? Таким образом, в этом случае отношение не является функцией.

Кстати, вы также можете проверить это отношение, используя наше первое определение сверху. Подумайте о подключении « x = −1». Тогда мы получаем y ² − 3 = 6, поэтому y ² = 9, и тогда y может быть либо −3, либо +3. То есть, если бы мы сделали стрелочную диаграмму, было бы две стрелки, исходящие из 90 337 x 90 338 = −1. Это еще раз показывает, что отношение не является функцией.

URL: https://www.purplemath.com/modules/fcns.htm

Вы можете использовать приведенный ниже виджет Mathway, чтобы попрактиковаться в определении того, является ли отношение функцией. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Определить, является ли отношение функцией», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок).

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления. )

Page 2

Функциональная терминология | Brilliant Math & Science Wiki

Содержание

Терминология
Дальнейшие подробности
Примеры проблем

Функция : Функция — это отношение между каждым элементом в домене и уникальным элементом в домене кода. Это обозначается как f ⁣:X→Y f \colon X \rightarrow Y f:X→Y.
Домен : Домен функции — это набор входов функции. Обозначается ХХХ.
Кодовый домен : Кодовый домен функции — это набор всех допустимых выходных данных. Это обозначается Y.Y.Y.
Диапазон : Диапазон функции задается всеми достигнутыми выходами. По определению диапазон является подмножеством кодового домена. Это обозначается f(X)f(X)f(X).
Образ ААА : Образ набора ААА – это набор всех достигнутых результатов, чьи входы являются элементами набора ААА. Это обозначается Im(A)={ y∈Y∣∃a∈A,f(a)=y }. \text{Im}(A) = \{\, y \in Y \mid \существует a \in A, f(a) = y \, \}.Im(A)={y∈Y∣∃a∈ А,f(а)=у}. 9{-1} (y) = \{\, x \in X \mid f(x) = y \, \} f−1(y)={x∈X∣f(x)=y}.
График : График функции представляет собой набор всех упорядоченных пар (x,f(x)) (x, f(x) ) (x,f(x)).
Инъективный : Инъективная функция — это функция, которая сопоставляет каждое значение в домене с уникальным значением в домене кода, так что для любого заданного значения в диапазоне есть только одно соответствующее значение в домене. Инъективные функции также называют функциями «один к одному».
Surjective : Сюръективная функция — это функция, которая покрывает каждый элемент в домене кода, так что в домене кодов нет элементов, которые не являются значением функции. В сюръективной функции диапазон и кодовый домен будут идентичными.
Биективная : Биективная функция одновременно инъективна и сюръективна.

Обратите внимание, что домен и кодовый домен не всегда должны быть набором действительных чисел. Другими часто используемыми наборами являются комплексные числа, положительные целые числа, люди, матрицы, графики и т. д. Например, рассмотрим функцию Citizen(⋅) \text{Citizen} (\cdot) Citizen(⋅), которая принимает в качестве входных данных имя блестящего ученика и выводит страну гражданства этого ученика. В данном случае домен — это набор имен блестящих учеников, а кодомен — это набор стран. Чтобы это было действительно функцией, мы должны сделать предположение, что студент является гражданином только 1 страны. Чтобы иметь дело с возможностью двойного гражданства, мы должны добавить пары стран в наш домен.

Конечно, мы можем добавить в кодовый домен ненужные элементы, такие как {alligator}, {purple} и {Calvin}. Таким образом, мы определяем диапазон функции (также называемой изображением ) как набор всех выходных данных. Обратите внимание, что по определению диапазон функции должен быть подмножеством домена кода.

Математическое сокращение (поскольку математики ленивы) для утверждения, что f ff является функцией от множества A AA до множества B BB, это f ⁣:A→B f\двоеточие A \to Bf:A→B. Например, поскольку C \mathbb{C}C обозначает комплексные числа, Z \mathbb{Z}Z обозначает целые числа, а N \mathbb{N}N обозначает положительные целые числа, f ⁣:C→N f \colon \ mathbb{C} \to \mathbb{N}f:C→N относится к функции из множества комплексных чисел в множество положительных целых чисел. Поскольку мы в основном имеем дело с функциями действительных чисел, если домен и кодовый домен не указаны явно (или сразу очевидны из установки), предполагается, что они являются набором действительных чисел,

Хотя обычно домен и кодовый домен являются одним и тем же набором, важно проводить четкое различие между ними. Функция тождества — это уникальная функция на множестве, которая отображает каждый элемент в себя. Обозначим эту функцию как IdA ⁣:A→A \text{Id}_A \colon A \to AIdA:A→A, где IdA(a)=a \text{Id}_A (a) = a IdA( а)=а для всех элементов ааа из ААА.

Если бы мы изменили домен функции, то мы получили бы другую функцию. Например, IdR ⁣:R→R \text{Id}_\mathbb{R} \colon \mathbb{R} \to \mathbb{R} IdR:R→R — это функция, сильно отличающаяся от IdN ⁣:N. →N \text{Id}_\mathbb{N} \colon \mathbb{N} \to \mathbb{N}IdN:N→N. Это потому, что у нас IdR(0,5)=0,5 \text{Id}_\mathbb{R} (0,5) = 0,5IdR(0,5)=0,5, а IdN(0,5) \text{Id}_\mathbb{N } (0.5)IdN(0.5) не имеет никакого смысла. Таким образом, мы говорим, что 2 функции f ⁣:A→B f\colon A \to Bf:A→B и g ⁣:C→D g\colon C \to Dg:C→D равны, если A=C A= CA=C и для всех значений a aa в A AA f(a)=g(a) f(a) = g(a)f(a)=g(a). Кодовый домен менее важен, так как по нашему предыдущему наблюдению мы можем добавлять в него произвольные элементы, не затрагивая сути функции.

Для функции f ⁣:A→B f\colon A \to Bf:A→B и любого подмножества C⊂A C \подмножества AC⊂A мы говорим, что образ C CC есть множество всех значений f( в) f(c)f(c), где c cc — элемент из C CC. Для подмножества D⊂B D \подмножества BD⊂B мы говорим, что прообразом D DD называется множество всех значений x xx, где f(x) f(x)f(x) — элемент D DD. Используя эту терминологию, мы говорим, что диапазон — это образ домена. По сути, диапазон — это та часть кодового домена, которая нас действительно волнует, поэтому мы хотели бы ограничить наше внимание только диапазоном.

Когда домен представляет собой набор действительных чисел, нам нравится думать о f(x) f(x)f(x) как о графике функции. И наоборот, для любого графика это функция, если каждое значение xxx соответствует не более чем одному значению yyy. Такой график должен пройти тест вертикальной линии: каждая вертикальная линия пересекает график не более чем на 1 точку.

Что, если мы хотим найти все возможные входы, дающие определенный результат? Например, если я хочу знать, кто все блестящие студенты, являющиеся гражданами Индии, я прошу список студентов, которые удовлетворяют требованиям Гражданин (⋅) = Индия. \text{Гражданин} (\cdot) = \text{Индия}.Гражданин(⋅)=Индия. Обратная функция не всегда должна быть функцией (как в этом примере). Чтобы обратная функция была реальной функцией, исходная функция должна пройти тест горизонтальной линии: каждая горизонтальная линия пересекает график не более чем на 1 точку. 9{-1} (\text{Кальвин}) Гражданин-1(Кальвин) недействителен. Таким образом, мы часто ограничиваем наше внимание просто диапазоном исходной функции (которая, как вы помните, является образом области определения). Каков домен обратного? Это будет прообраз диапазона. Обратите внимание, что прообраз диапазона не обязательно должен быть всей областью f ff.

В случае, если обратная функция не является функцией, мы можем ограничить наше внимание подмножеством домена. В частности, если f ⁣:A→B f\colon A \to Bf:A→B и C⊂A C \subset AC⊂A, мы определяем функцию f∣C ⁣:C→B f|_C \colon C \to Bf∣C:C→B как f∣C(c)=f(c) f|_C (c) = f(c)f∣C(c)=f(c) для всех значений c cc в C СС. Например, функция S ⁣:R→R S \colon \mathbb{R} \to \mathbb{R}S:R→R, заданная как S(x)=x2 S(x) = x^2S(x)= x2 не имеет обратной функции, потому что не удовлетворяет критерию горизонтальной линии. {-1} (x) = -\sqrt{x} S∣R≤0−1(x)=−x.

Функция является инъективной (или однозначной), если f(a1)≠f(a2) f(a_1) \neq f(a_2)f(a1)=f(a2) для любые 2 различных элемента a1,a2 a_1, a_2a1, a2 в домене. Функция сюръективна (или на), если для каждого элемента b bb в области кодов существует элемент a aa в области, такой что f(a)=b f(a) = bf(a)=b. Функция биективна, если она одновременно инъективна и сюръективна. С этой терминологией инъективная функция имеет обратную, которая является функцией. Биективная функция f ⁣:A→B f\colon A\to Bf:A→B имеет обратную (которая по предыдущему наблюдению является функцией), областью определения которой является B BB.

Теперь, когда мы создали этот словарь, мы можем поговорить о композиции функций. Вы не всегда можете составить 2 функции. Например, Гражданин∘Гражданин \text{Гражданин} \circ \text{Гражданин}Гражданин∘Гражданин не будет иметь никакого смысла, что бы мы ни пытались сделать. Давайте разберемся, как заставить работать композицию функций.

Предположим, что у нас есть 2 функции f ⁣:A→B f \двоеточие A \to Bf:A→B и g ⁣:C→D g\двоеточие C \to Dg:C→D, когда g∘f g \ circ fg∘f имеет смысл? Для любого значения a aa в области A мы должны иметь возможность применить g gg к значению f(a) f(a)f(a). Отсюда следует, что B BB должно быть подмножеством C CC. С этим условием мы можем определить g∘f ⁣:A→D g \circ f\colon A \to D g∘f:A→D равным (g∘f)(a)=g(f(a )) (g \circ f) (a) = g ( f(a) ) (g∘f)(a)=g(f(a)). Обратите внимание, что порядок композиции важен, так как мы не сможем определить f∘g f \circ gf∘g, если не будем дополнительно знать, что D DD является подмножеством A AA.

Пусть X={1,2,3,4,5,6,7,8}X = \{1, 2, 3, 4, 5, 6, 7, 8\}X={1,2,3, 4,5,6,7,8} и Y={2,4,6,8,10}.Y = \{2, 4, 6, 8, 10\}.Y={2,4,6, 8,10}. Для данной пары (a,b)(a, b)(a,b) чисел пусть f(a)=b.f(a) = b.f(a)=b. Является ли fff функцией f ⁣:X→Y f\colon X \to Y f:X→Y для следующего набора пар:
{(1,2),(2,10),(3,4),(4,4),(5,3),(6,3),(7,4),(8,2)} ?\{(1, 2), (2, 10), (3, 4), (4, 4), (5, 3), (6, 3), (7, 4), (8, 2) \}?{(1,2),(2,10),(3,4),(4,4),(5,3),(6,3),(7,4),(8,2 )}?
Чтобы fff была функцией, должны быть выполнены следующие условия:
fff оценивается для каждого элемента домена;
⇒f\Стрелка вправо f⇒f от 1 до 8 имеют собственные оценки (удовлетворены).
fff имеет только одну оценку для каждого элемента в домене;
⇒f\Rightarrow f⇒f от 1 до 8 имеют только один выход (удовлетворено).
Выходные данные fff должны быть элементами кодового домена;
⇒f(5)=f(6)=3∉Y\стрелка вправо f(5)=f(6)=3\notin Y⇒f(5)=f(6)=3∈/Y (неудовлетворено) .
Условие 3 не выполняется, поэтому fff не является функцией f:X→Y. □ f: X \rightarrow Y. \ _\square f:X→Y. □

Пусть X={ x∣0≤x≤3,x∈Z }X =\{ \, x \mid 0 \le x \le 3, x \in \mathbb{Z} \, \}X={x∣ 0≤x≤3,x∈Z} и Y=Z,Y = \mathbb{Z},Y=Z, где Z\mathbb{Z}Z — множество целых чисел. Когда f(x)=2x+1,f(x) = 2x + 1,f(x)=2x+1, какова сумма всех элементов в образе f?f?f?
У нас есть
f(0)=1f(1)=3f(2)=5f(3)=7.\begin{выровнено} f(0)&=1\\ f(1)&=3\\ f(2)&=5\\ f(3)&=7. \end{align}f(0)f(1)f(2)f(3)=1=3=5=7. 9{+} \cup \{0\} R+∪{0} {0,1,2}\{0,1,2\}{0,1,2}
Если функция f(x)f(x)f(x) определена как f(x)=1−x , f(x)= \sqrt{1 — \sqrt{x}},f(x)=1−x, какой у него домен?
Рассмотрим функцию g(x,y)=x×y g(x, y) = x \times y g(x,y)=x×y в области −5≤x≤10 -5 \leq x \leq 10 −5≤x≤10 и −5≤y≤10 -5 \leq y \leq 10 −5≤y≤10.
No related posts.

Домен	Диапазон \(\hspace{20px}y=2x+3\)
\(20-20\) 9 \(-20-20\) 9 = -1\)
\(-1\)	\(2(-1)+3=1\)
\(0\)	\(2(0)+3= 3\)
\(1\)	\(2(1)+3=5\)
\(2\)	\(2(2)+3=7\)

\(\mathbf{x}\)	\(\mathbf{y}\)
\(-2\)	\(6-\)

\(-1\)	\(-3\)
\(0\)	\(0\)
\(1\) 9001\)

\ (\mathbf{х}\)	\(\mathbf{y}\)
\(2\)	\(2\)
\(3\)	\(3\)
\ (4\)	\(4\)
\(5\)	\(5\)

\(\mathbf4\4\2) {у}\)
\(-1\)	\(4\)
\(-2\)	\(6\)	9001 )	\(-6\)
\(-1\)	\(-4\)

\(\mathbf{x4}2) 0 y}\)
\(7\)	\(3\)
\(5\)	\(1\)
\(3\)	\ (-1\)
\(7\)	\(-3\)