Что такое иррациональное число: суть, примеры, свойства
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Что такое иррациональное число: суть, примеры, свойства
Бесконечные дроби бывают периодическими и непериодическими. Последние называются иррациональными числами.
Их суть, как следует из названия, заключается в том, что они не является рациональным, т.е. не могут быть представлены в виде обыкновенной дроби
m/n
, где m и n – это целые числа, а n ≠ 0.
Самый распространенный вид иррациональных чисел (но не единственный) – квадратный корень из любого натурального числа, которое не является точным квадратом.
Примеры:
- √2 = 1,414213562373…
- √3 = 1,732050807568…
- e = 2,718281828459…
Множество иррациональных чисел обозначается латинской буковой “I“.
Свойства:
1. Суммой двух иррациональных чисел может быть рациональное число.
2. Между двумя любыми числами есть иррациональное.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Какие все иррациональные числа?
Действительные числа, которые не могут быть представлены в виде отношения, называются иррациональными числами. Хотя рациональные числа также являются действительными числами, они отличаются от иррациональных чисел. В V веке до нашей эры Гиппас, философ-пифагорейец, открыл иррациональные числа. Продолжайте читать, чтобы узнать больше об иррациональных числах и различиях между иррациональными и рациональными числами.
Хотя рациональные числа также являются действительными числами, они отличаются от иррациональных чисел. В V веке до нашей эры Гиппас, философ-пифагорейец, открыл иррациональные числа. Продолжайте читать, чтобы узнать больше об иррациональных числах и различиях между иррациональными и рациональными числами.
Что такое иррациональные числа?
Десятичное расширение иррационального числа не заканчивается и не повторяется. Например, 2,59265… не заканчивается, поэтому это иррациональное число. Иррациональные числа — это действительные числа, которые нельзя представить в виде простой дроби. Они не могут быть выражены как отношение, подобное p/q, где p и q — целые числа, а q ≠ 0.
Что такое десятичные дроби?
Что такое завершающие и повторяющиеся десятичные дроби?
Несмотря на то, что повторяющаяся десятичная дробь имеет бесконечное число цифр, все они известны. Цифры после запятой не могут быть все равны 0, чтобы десятичная запятая считалась повторяющейся. Для незавершающихся десятичных знаков, которые не повторяются, известны не все цифры. Сколько бы чисел ни было известно, после нее всегда будет цифра, которую нужно определить.
Для незавершающихся десятичных знаков, которые не повторяются, известны не все цифры. Сколько бы чисел ни было известно, после нее всегда будет цифра, которую нужно определить.
Стоит отметить, что 1/3 — это повторяющаяся десятичная дробь, а также неконечная десятичная дробь. Крайне важно понять разницу между рациональными и иррациональными десятичными знаками, чтобы различать их. Все десятичные дроби, оканчивающиеся цифрой, являются рациональными числами. Как конечные, так и повторяющиеся десятичные дроби могут быть выражены в форме дроби .
Существуют непрерывающиеся и неповторяющиеся иррациональные числа, наиболее заметным из которых является pi . Два экземпляра пи (3,14159…) и квадратный корень из 2 (1,4142135…). Независимо от того, сколько цифр мы вычисляем, ни одна из них никогда не закончится и не повторится.
Что такое рациональные числа?
В арифметике рациональных чисел — это число, которое мы обычно изучаем после целых чисел. Рациональные числа можно представить как частное двух целых чисел. Они выражаются в виде дроби a / b, где a и b — целые числа, а b отлично от нуля.
Рациональные числа можно представить как частное двух целых чисел. Они выражаются в виде дроби a / b, где a и b — целые числа, а b отлично от нуля.
В то время как целые числа составляют дроби, например, 2 равно 2/1, целое число представляет собой обозначение внутри дроби, т. е. 2 внутри 2/1. Это может немного сбивать с толку, но знайте, что целые числа — это общий термин, который охватывает все числа.
Свойства иррациональных чисел
Свойства иррациональных чисел помогают нам идентифицировать иррациональные числа среди группы действительных чисел:
- Неконечные и неповторяющиеся десятичные дроби составляют иррациональные числа.
- Используются только действительные числа.
- Произведение иррационального числа x и рационального числа y является иррациональным числом.
- Произведение любого иррационального числа на любое ненулевое рациональное число является иррациональным числом. Произведение иррационального числа x с рациональным числом y иррационально.

- Наименьшее общее кратное (НОК) любых двух иррациональных чисел может существовать, а может и не существовать.
- Сложение, вычитание, умножение и деление двух иррациональных чисел могут быть рациональными числами, а могут и не быть.
Как узнать, является ли число иррациональным?
Рациональные числа могут быть представлены в виде отношения или дроби. Дроби нельзя использовать для представления иррациональных чисел. Если число может быть записано или переведено в форму p/q, где p и q — целые числа, а q — ненулевое число, то оно называется рациональным. Если это невозможно, то говорят, что оно иррационально.
Объяснение
Любое число, которое может быть представлено или записано в форме p/q, где p и q — целые числа, а q — ненулевое число, является рациональным числом.
Пример: 12/5, -9/13, 8/1
С другой стороны, иррациональное число не может быть представлено в форме p/q, и его десятичное представление не повторяется и не завершается.
Пример: √2, √7, √11
Мы можем распознавать и классифицировать числа как рациональные или иррациональные, используя эти определения. Форма p/q является ключом к определению и классификации рациональных и иррациональных чисел. Если число соответствует форме p/q, то оно рационально, если не соответствует, то иррационально.
Символ иррационального числа
Давайте рассмотрим символы для различных типов чисел, прежде чем изучать иррациональные числа.
- N означает натуральные числа
- I обозначает мнимые числа
- Q обозначает рациональные числа
И рациональные, и иррациональные числа составляют действительные числа. Иррациональные числа можно получить, вычитая рациональные числа (Q) из действительных чисел, как определено (R-Q) (R). Его также можно записать как (R\Q).
Рациональные и иррациональные числа
Рациональное число — это любое число, которое может быть выражено в виде отношения или дроби (p/q). Числитель (p) и знаменатель (q), если q не равно нулю, могут быть включены. Целое число или целое число может быть рациональным числом.
Числитель (p) и знаменатель (q), если q не равно нулю, могут быть включены. Целое число или целое число может быть рациональным числом.
Возьмем, например, 2/3 = 0,6666 = 0,67. Поскольку десятичное значение повторяется, мы вычислили 0,67. √4 равно 2 и -2, где 2 — положительное целое число, а -2 — отрицательное целое число.
Rational
Может быть представлено в виде дроби или отношения, например p/q, где q меньше нуля. Десятичное расширение повторяется и либо заканчивается, либо не заканчивается (повторяется).
Пример: 0,33333, 0,656565.., 1,75
Иррациональное
Не может быть представлено в виде дроби или отношения. В любой момент времени десятичное расширение является непрерывным и неповторяющимся.
Пример: π, √13, e
Примеры иррациональных чисел
Какое из следующих чисел является иррациональным?
2, √ 16, 1/2, √5
Иррациональные числа — это действительные числа, которые не могут быть выражены простой дробью, а их десятичное представление не завершается и не повторяется. Таким образом, давайте просмотрим указанные числа:
Таким образом, давайте просмотрим указанные числа:
- 2 — это целое число, поэтому оно не является иррациональным числом.
- √16 выглядит так, как будто это иррациональное число, но квадратный корень из 16 равен 4 без остатка. Следовательно, это не иррационально.
- 1/2, выраженное в виде десятичного числа, равно 0,5, которое заканчивается и не повторяется. Следовательно, это также не иррациональное число.
- √5 является иррациональным числом, поскольку квадратный корень равен 2,2360679774997896964091736, который не заканчивается.
Какое из следующих иррациональных чисел является самым большим?
π, √5, 4,64378123…, √21
Преобразование всех этих чисел в десятичные числа позволит нам сравнить и сопоставить эти числа. Поскольку все это иррациональные числа, приводящие к бесконечному числу десятичных чисел, мы ограничим их до 3 знаков после запятой.
- π в виде десятичной дроби равно 3,143.
- √5 равно 2,236
- 4.
 644 можно оставить как есть.
644 можно оставить как есть. - √21 равно 4,582
Глядя на все приведенные выше десятичные дроби, мы можем сравнить их, чтобы определить, какая из них самая большая.
От большего к меньшему иррациональные числа располагаются в следующем порядке:
4,64378123…, √21, √5, π
Является ли 7/12 иррациональным?
Чтобы понять это, мы должны преобразовать эту дробь в десятичную:
0,5833…
12) 7.0000
60
100
96
40
36
40
36
4
Как таковой, 7/12 = 0,58333…
Это не концевое значение. является иррациональным числом.
Репетиторство по математике
Многие дети испытывают трудности с математикой, и наверстать упущенное может быть непросто. Tutorax предлагает услуги репетиторства на дому и онлайн для учащихся начальной, средней, старшей школы и даже университета. Наши репетиторы могут помочь вам с домашним заданием, подготовкой к экзаменам и поддержкой в классе, среди прочего, если у вас возникли проблемы с математикой.
Найти репетитора
Разница между рациональными и иррациональными числами на примерах
0
Сохранить
Скачать публикацию в формате PDFРазница между рациональными и иррациональными числами важна для решения примеров, основанных на классификации рациональных и иррациональных чисел. Они полная противоположность друг другу. Хотя между рациональными и иррациональными числами есть сходство, поскольку есть различия.
В этой статье мы в первую очередь сосредоточимся на изучении разницы между рациональными и иррациональными числами, понимая их определения и сходства между ними с помощью решенных примеров и часто задаваемых вопросов
Что такое рациональные и иррациональные числа?
Давайте сначала посмотрим, что подразумевается под рациональными и иррациональными числами.
Рациональные числа
Число получается путем деления двух целых чисел (целое число — это число без дробной части).
- «Отношение» — корень слова.
 В арифметике рациональное число — это число, которое может быть выражено как частное p/q двух чисел с q ≠ 0.
В арифметике рациональное число — это число, которое может быть выражено как частное p/q двух чисел с q ≠ 0. - Множество рациональных чисел также включает все целые числа, которые могут быть выражены как частное с целым числом как числитель и 1 в знаменателе.
- Рациональные числа — это либо завершающие, либо повторяющиеся десятичные дроби в десятичной форме. 1/7 = 0,142857, например, где 142857 не повторяется бесконечно.
- Все целые числа, а также все дроби, конечные десятичные дроби и повторяющиеся десятичные дроби входят в число рациональных чисел.
Также прочтите эту статью о наборах после прочтения этой статьи.
Иррациональные числа
Иррациональное число — это действительное число, которое не может быть выражено как отношение двух целых чисел. Иррациональное число, выраженное в десятичной системе счисления, никогда не заканчивается и не повторяется. Именно потому, что рациональные числа счетны, а действительные числа несчетны, можно сказать, что иррациональные числа составляют почти все действительные числа.
- Иррациональные числа в некотором роде противоположны рациональным. Это действительные числа, которые мы не можем записать в виде отношения \({p\over{q}}\), где p и q — целые числа, где q не может быть равно нулю.
- Например, \(\sqrt{2} = 1,414213….\) иррационально, потому что мы не можем записать это в виде дроби целых чисел.
- Иррациональные числа, следовательно, являются повторяющимися числами. Давайте теперь посмотрим, как мы можем определить иррациональные числа.
Разница между рациональными и иррациональными числами заключается в следующем: 9

Классификация рациональных и иррациональных чисел
Выполните шаги, указанные ниже, чтобы классифицировать число как рациональное или иррациональное.
Рациональное число — это число, которое можно записать в виде p/q, где p,q — целые числа. Итак, сначала проверьте номер, можно ли его так записать. Если его можно записать в виде p/q, то его можно классифицировать как рациональное число. Если нет, то это иррациональное число.
Давайте посмотрим на пример.
Классифицируйте следующее число как рациональное или иррациональное с обоснованием: 3\sqrt{18}
Рациональное число — это число, которое можно записать в виде p/q, где p,q — целые числа.
\(3\sqrt{18} = 3\sqrt{9\times2} = 3\times3\sqrt{2} = 9\sqrt{2}\)
Изучите различные концепции биномиальной теоремы здесь.
Решенные примеры различий между рациональными и иррациональными числами
Давайте посмотрим на некоторые примеры различий между рациональными и иррациональными числами, которые приходят на экзаменах.
Решено Пример: Классифицируйте следующее число как рациональное или иррациональное с обоснованием:
1.010010001….
Решение:
Если десятичные дроби оканчиваются десятичными дробями, число является рациональным числом; если десятичные дроби не заканчиваются, а повторяются (повторяя один и тот же шаблон снова и снова), число также является рациональным числом. 1.010010001… в данном случае — это бесконечное и неповторяющееся десятичное расширение. В результате это иррациональное число.
Решено Пример: Классифицируйте следующее число как рациональное или иррациональное с обоснованием \((1 + \sqrt{5}) – (4 + \sqrt{5})\)
Решение:
\((1 + \sqrt{5}) – (4 + \sqrt{5}) = -3 = -3/1\)
Итак, \((1 + \sqrt{ 5}) – (4 + \sqrt{5})\) можно записать в виде p/q
Итак, это рациональное число.
Надеюсь, эта статья о разнице между рациональными и иррациональными числами была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Разница между рациональными и иррациональными числами Часто задаваемые вопросы
В.1 Что такое пример рационального числа?
Ответ 1 Число получается путем деления двух целых чисел (целое число — это число без дробной части). «Отношение» — это корень слова. В арифметике рациональное число — это число, которое может быть выражено как частное p/q двух чисел с q = 0. Множество рациональных чисел также включает все целые числа, которые могут быть выражены как частное с целым числом в качестве числителя и 1 в качестве знаменателя. Рациональные числа — это либо завершающие, либо повторяющиеся десятичные дроби в десятичной форме. 1/7 = 0,142857, например, где 142857 не повторяется бесконечно. Каждое рациональное число можно представить в виде дроби a/b, где a и b — целые числа.
Q.2 Что означает иррациональное в математике?
Ответ 2 Иррациональные числа являются частным случаем чисел во всей системе счисления. Иррациональные числа в некотором роде противоположны рациональным. Это действительные числа, которые мы не можем записать в виде отношения \({p\over{q}}\), где p и q — целые числа, где q не может быть равно нулю. Например, \(\sqrt{2} = 1,414213….\) иррационально, потому что мы не можем записать это как часть целых чисел. Следовательно, иррациональные числа являются повторяющимися числами. Давайте теперь посмотрим, как мы можем определить иррациональные числа.
Q.3 Как узнать, является ли число рациональным?
Ответ 3 Число получается путем деления двух целых чисел (целое число — это число без дробной части).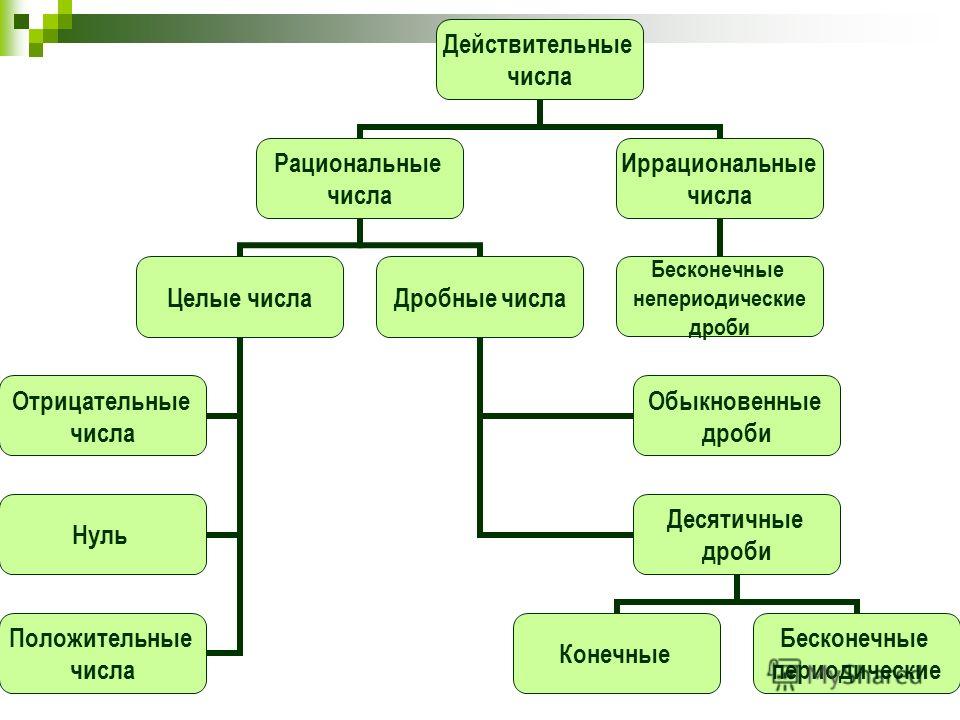 «Отношение» — это корень слова. В арифметике рациональное число — это число, которое может быть выражено как частное p/q двух чисел с q = 0. Множество рациональных чисел также включает все целые числа, которые могут быть выражены как частное с целым числом в качестве числителя и 1 в качестве знаменателя. Рациональные числа — это либо завершающие, либо повторяющиеся десятичные дроби в десятичной форме. 1/7 = 0,142857, например, где 142857 не повторяется бесконечно.
«Отношение» — это корень слова. В арифметике рациональное число — это число, которое может быть выражено как частное p/q двух чисел с q = 0. Множество рациональных чисел также включает все целые числа, которые могут быть выражены как частное с целым числом в качестве числителя и 1 в качестве знаменателя. Рациональные числа — это либо завершающие, либо повторяющиеся десятичные дроби в десятичной форме. 1/7 = 0,142857, например, где 142857 не повторяется бесконечно.
Q.4 Является ли 5,676677666777 иррациональным числом?
Ответ 4 Рациональное число — это число, которое можно записать в виде p/q, где p, q — целые числа. Итак, сначала проверьте число, можно ли его так записать. Если его можно записать в виде p/q, то его можно классифицировать как рациональное число. Если нет, то это иррациональное число. Нет, несмотря на наличие десятичных точек, это не иррациональное число, поскольку числа после десятичной точки не продолжаются вечно. Следовательно, 5,676677666777 — рациональное число.
Следовательно, 5,676677666777 — рациональное число.
Q.5 Что такое правила рациональных и иррациональных чисел?
Q.6 Каковы некоторые реальные примеры рациональных и иррациональных чисел?
Ответ 6 Ниже приведены некоторые примеры реальных ситуаций, в которых можно применять рациональные числа: Возможно дробное представление налогов.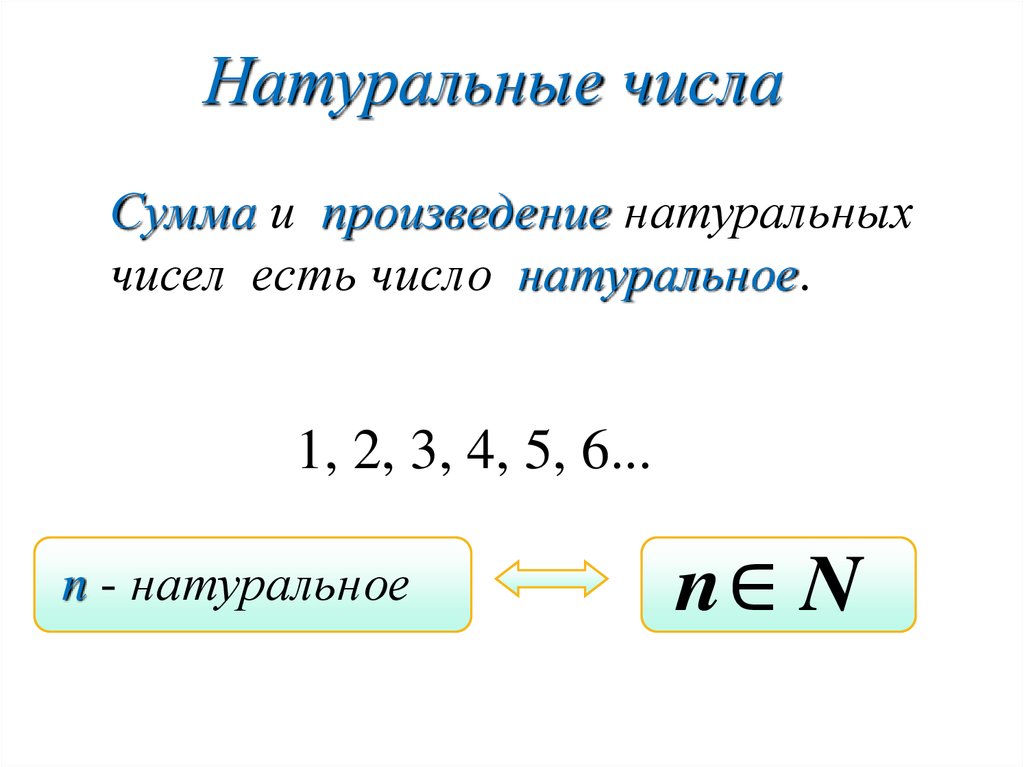


 644 можно оставить как есть.
644 можно оставить как есть. В арифметике рациональное число — это число, которое может быть выражено как частное p/q двух чисел с q ≠ 0.
В арифметике рациональное число — это число, которое может быть выражено как частное p/q двух чисел с q ≠ 0.