Что такое максимум функции: Максимумы, минимумы и экстремумы функций

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют

экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т. е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки \(-13\), \(-11\), \(-9\),\(-7\) и \(3\). Количество точек экстремума функции – \(5\).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).

         

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.

— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с \(-13\): до \(-13\) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что \(-13\) – точка максимума.

\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.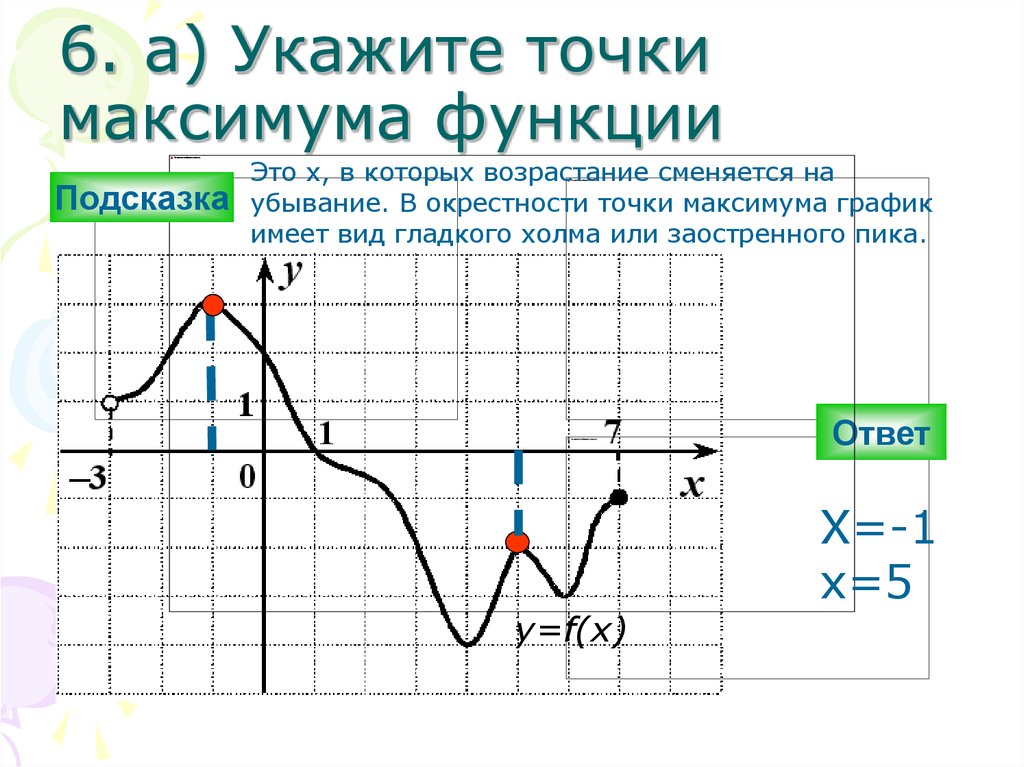

\(- 9\): функция возрастает, а потом убывает – максимум.

\(-7\): минимум.

\(3\): максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.

— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

1. Найдите производную функции \(f'(x)\). 
2. Найдите корни уравнения \(f'(x)=0\). 
3. Нарисуйте ось \(x\) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью \(f'(x)\), а под осью \(f(x)\).
4. Определите знак производной в каждом промежутке (методом интервалов). 
5. Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью). 
6. Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
   — если \(f’(x)\) изменила знак с «\(+\)» на «\(-\)», то \(x_1\) – точка максимума;
   — если \(f’(x)\) изменила знак с «\(-\)» на «\(+\)», то \(x_3\) – точка минимума;
   — если \(f’(x)\) не изменила знак, то \(x_2\) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). 2-4=0\)
               \(x=±2\)

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является \(-2\).

Ответ. \(-2\).

Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов

Скачать статью

как найти по уравнению, поиск минимума

Содержание:

• Минимум и максимум функции
  • Точка минимума, минимум функции
  • Точка максимума, максимум функции
• Исследование функций на экстремумы
• Примеры задач

Содержание

• Минимум и максимум функции
  • Точка минимума, минимум функции
  • Точка максимума, максимум функции
• Исследование функций на экстремумы
• Примеры задач

Минимум и максимум функции

Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом: 

• \(y_{min}, y_{max}\) — минимум, максимум функции или экстремумы;
• \(x_{min}, x_{max}\) — точки минимума, максимума функции;
• \(y_{наиб}, y_{наим}\) — наибольшее (максимальное), наименьшее (минимальное) значение функции.

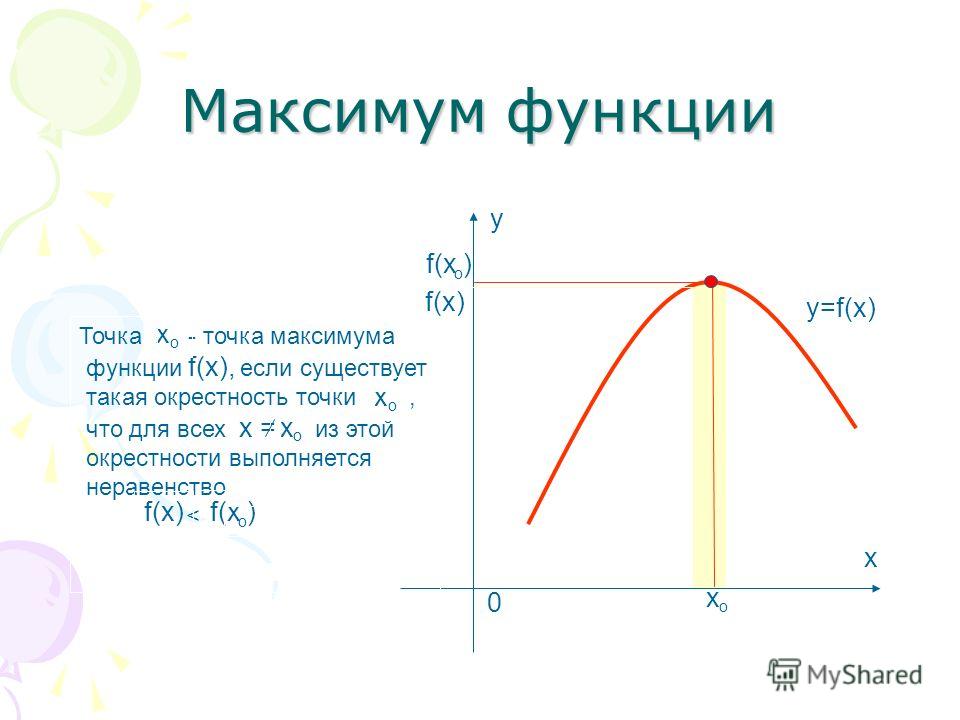
Точка минимума, минимум функции

Точка минимума — такая точка \(x_0\), если у неё существует окрестность, для всех точек которой выполняется неравенство \(f(x)\geq f(x_0)\)

Минимум функции — значение функции в точке минимума \(x_0\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.

Точка максимума, максимум функции

Точка максимума — такая точка \(x_0\), если у неё существует окрестность, для всех точек которой выполняется неравенство \(f(x)\leq f(x_0)\)

Максимум функции — значение функции в точке максимума \(x_0\)

Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание. 4+6x\)

3) Приравняем f'(x) к 0 и найдем корень: x = 0. Отметим 0 на числовой прямой и определим знак производной на промежутках \((-\infty;0)\) и \((0;+\infty)\). Получим, что производная положительна на обоих промежутках, следовательно функция возрастает на всей числовой прямой.

Утверждение доказано

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 3)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Нахождение максимума и минимума с использованием производных

Где находится функция в верхней или нижней точке? Расчет может помочь!

Максимум — это верхняя точка, а минимум — нижняя точка:

В плавно изменяющейся функции максимум или минимум всегда находится там, где функция сглаживает   (за исключением седловой точки ).

Где он выравнивается?  Где наклон равен нулю .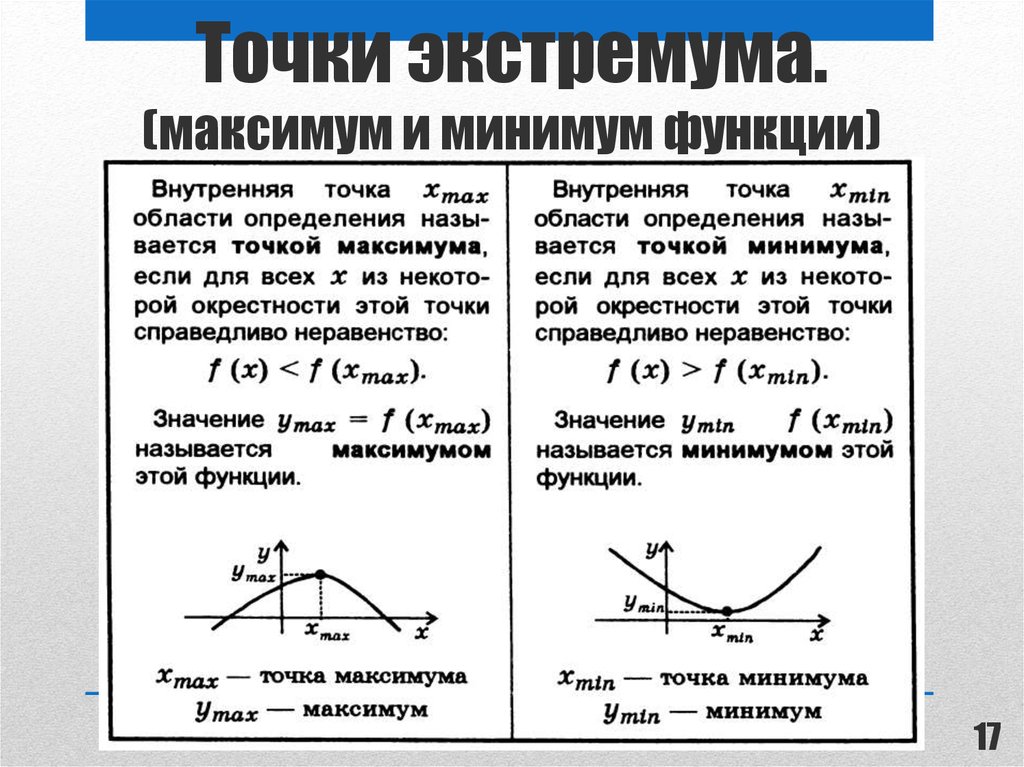

Где нулевой наклон?   Производная говорит нам!

Давайте рассмотрим пример:

Пример: Мяч подброшен в воздух. Его высота в любой момент времени t определяется как:

h = 3 + 14t − 5t ²

Какова его максимальная высота?

 

Используя производные, мы можем найти наклон этой функции:0003

(см. Ниже примером, как мы обнаружили, что производная.)

Теперь обнаружите, когда наклон равен нулю :

14 — 10t = 0

10t = 14

T = 14/10. = 1,4

Наклон равен нулю при t = 1,4 секунды

А высота в это время равна:

h = 3 + 14×1,4 − 5×1,4 ²

3 9 − 9,8 = 12,8

Итак:

Максимальная высота 12,8 м (при t = 1,4 с)

 

Краткий обзор производных

Производная в основном находит наклон функции.

В предыдущем примере мы взяли это:

h = 3 + 14t − 5t ²

и получили следующую производную:

d dt

0 h = 0 5 + 24 = 14 − 10t

Что говорит нам о наклоне функции в любой момент времени

t

 

Мы использовали следующие производные правила:

• Наклон константы (например, 3) равен 0
• Наклон линии , например, 2x равен 2, поэтому 14t имеет наклон 14
• Функция квадрата , такая как t ² , имеет наклон 2t, поэтому 5t ² имеет наклон 5(2t)
• А потом мы сложили их: 0 + 14 − 5(2t)

 

Откуда мы знаем, что это максимум (или минимум)?

Мы видели это на графике! Но в остальном. .. на помощь снова приходят производные.

Возьмите производную от наклона (вторая производная исходной функции):

Производная от 14 − 10t равна −10

Это означает, что наклон постоянно уменьшается (-10): при перемещении слева направо наклон начинается с положительного значения (функция возрастает), проходит через ноль (плоская точка), а затем наклон становится отрицательным (функция падает). :

Наклон, который становится меньше (и проходит через 0), означает максимум.

Это называется тестом второй производной

На графике выше я показал наклон до и после, но на практике мы делаем тест в точке, где наклон равен нулю :

Проверка второй производной

Когда наклон функции равен нулю при x , а вторая производная при x :

• меньше 0, это локальный максимум
• больше 0, это локальный минимум
• равно 0, то тест не пройден (хотя могут быть и другие способы выяснить это)

 

«Вторая производная: меньше 0 — максимум, больше 0 — минимум»

 

Пример: найдите Maxima и Minima для:

y = 5x ³ + 2x ² — 3x

Производное (наклон):

D DX Y = 15x ^{2 DX Y = 15x 2 D DX Y = 15x 20038 + 4x − 3}

Что является квадратичным с нулями:

• x = −3/5
• х = +1/3

 

Могут ли они быть максимальными или минимальными? (Пока не смотрите на график!)

 

Вторая производная равна y» = 30x + 4

При x = −3/5:

y» = 30(−3/5 ) + 4 = −14

меньше 0, поэтому −3/5 является локальным максимумом

При x = +1/3:

y» = 30(+1/3) + 4 = + 14

больше 0, поэтому +1/3 — локальный минимум

(Теперь вы можете посмотреть на график. )

слов

Высшая точка называется максимум (множественное число максимум ).

Нижняя точка называется минимум (множественное число минимум ).

Общее слово для обозначения максимума или минимума: экстремум (множественное число экстремум ).

Мы говорим местное максимальное (или минимальное), когда могут быть более высокие (или более низкие) точки в другом месте, но не поблизости.

Еще один пример

Пример: найдите Maxima и Minima для:

y = x ³ — 6x ² + 12x — 5

Производная:

D DX Y = 3x ² 88 88 88 88 88 88 88 88 88 888. 12

Какое квадратичное число имеет только один нуль в x = 2

Это максимум или минимум?

 

Вторая производная равна y» = 6x − 12

При x = 2:

y» = 6(2) − 12 = 0

это 0, поэтому тест не пройден

И вот почему:

Это точка перегиба («седловая точка»). .. наклон становится нулевым, но это не максимум и не минимум.

 

Должен быть дифференцируемым

И есть важный технический момент:

Функция должна быть дифференцируемой (производная должна существовать в каждой точке своей области определения).

Пример: Как насчет функции f(x) = |x| (абсолютная величина) ?

|х| выглядит так:

При x=0 очень резкое изменение!

На самом деле он там не дифференцируем (как показано на дифференцируемой странице).

Таким образом, мы не можем использовать метод производной для функции абсолютного значения.

Функция также должна быть непрерывной, но любая дифференцируемая функция также непрерывна, так что мы защищены.

 

 

Как найти максимальное и минимальное значение функции

Следующие шаги были бы полезны, чтобы найти максимальное и минимальное значение функции, используя первую и вторую производные.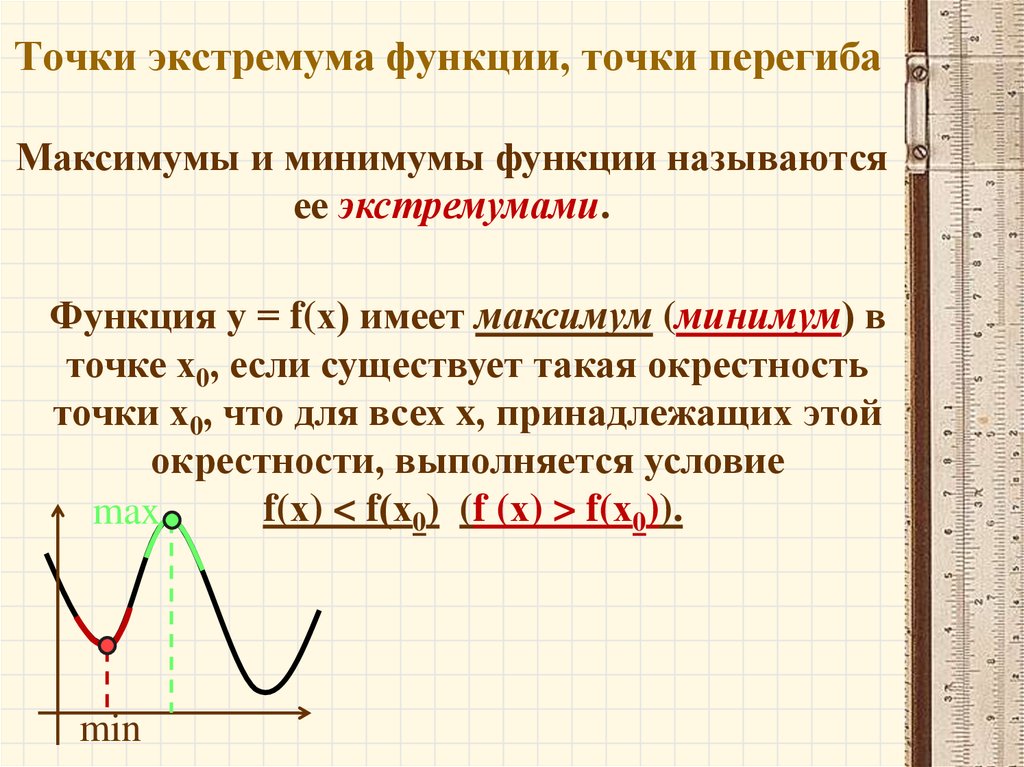

Шаг 1: 

Пусть f(x) — функция. Найдите первую производную от f(x), которая равна f'(x).

Шаг 2 : 

Приравняйте первую производную f'(x) к нулю и найдите x, которые называются критическими числами.

Шаг 3 :

Найдите вторую производную f(x), которая равна f»(x). 

Шаг 4: 

Подставьте критические числа, найденные на шаге 2, во вторую производную f»(x).

Шаг 5:

Если f»(x) < 0 для некоторого значения x, скажем, x = a, то функция f(x) максимальна при x = a. 

Если f»(x) > 0 для некоторого значения x, скажем, x = b, тогда функция f(x) минимальна при x = b.

Шаг 6: 

Чтобы получить максимальное и минимальное значения функции, подставьте x = a и x = b в f(x).

Максимальное значение = f(a)

Минимальное значение = f(b)

Пример 1:

Определить максимальное значение функции:

f(x) = 4x — x ^{83 + 83 3}

Решение:

Найдите первую производную f(x).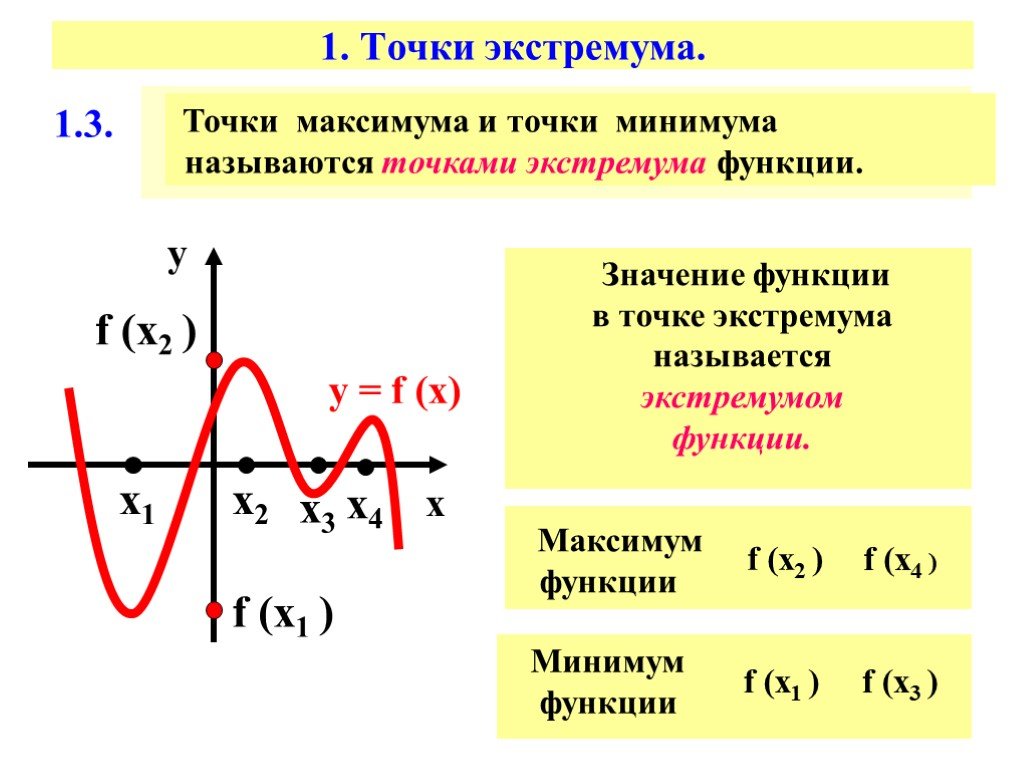

f'(x) = 4(1) — 2x + 0

= 4 — 2x

Приравнять первую производную к нулю, то есть f'(x) = 0.

4 — 2x = 0

2(2 — х) = 0

2 — х = 0

x = 2

Найдите вторую производную f(x).

f'(x) = 4 — 2x

f»(x) = 0 — 2(1)

f»(x) = -2

Подставить критическое число x = 2 в f»(x) .

f»(2) = -2 < 0

Итак, f(x) максимальна при x = 2.

Чтобы найти максимальное значение, подставьте x = 2 в f(x).

f(2) = 4(2) — 2 ² + 3

= 8 — 4 + 3

= 11 — 4

= 7

Следовательно, максимальное значение функции ) составляет 7,

Обоснование :

Мы можем обосновать наш ответ, построив график функции f(x).

f(x) = 4x — x ² + 3

Данная функция является уравнением параболы. Замените f(x) на y.

y = -x ² + 4 x + 3

Запишите приведенное выше уравнение параболы в вершинной форме.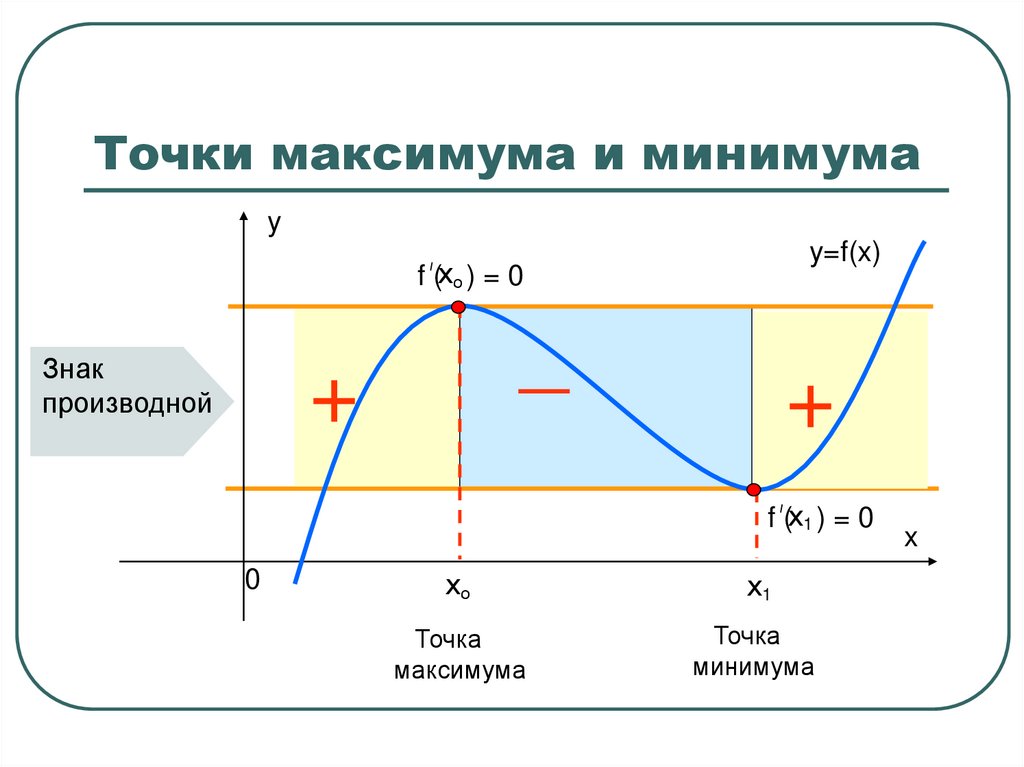

y = -(x ² — 4 x — 3)

y = -[x ²  — 2(x)(2) + 2 ²  — 2 ² 0 — 0 3] 9 0 = -[(х — 2) ² — 4 — 3]

y = -[(x — 2) ²  — 7]

y = -(x — 2) ²  + 7

Приведенное выше уравнение имеет вид y = а(х — h) ²  + k.

a = -1

Вершина (h, k) = (2, 7)

Поскольку ‘a’ отрицательно, парабола раскрывается вниз. Итак, у нас есть только максимальное значение y, то есть координата y в вершине, равная 7.

Ответ обоснован.

Пример 2:

Определить максимальное и минимальное значения функции:

f(x) = 2x ³ + 3x ² — 36x + 1

Решение:

Найдите первую производную f(x).

f'(x) = 2(3x ² ) + 3(2x) — 36(1) + 0

= 6x ²  + 6x — 36 f'(x) = 0,

6x ²  + 6x — 36 = 0

Разделите обе части на 6.

x ²  + x — 6 = 0

Сомножите и решите.

No related posts.