Больше примеров решений Решение интегралов онлайн
Таким образом, если функция $y=f(x)$ имеет первообразную, то она имеет бесконечное множество первообразных.
Теорема
(Об общем виде первообразной для функции)
Если функции $F(x)$ и $\Phi(x)$ — две любые первообразные функции $y=f(x)$, то их разность равна некоторой постоянной, то есть
$$\Phi(x)-F(x)=C=\text { const }$$
Последнюю теорему можно сформулировать иначе: каждая функция, которая является первообразной для функции $f(x)$, может быть представлена в виде $F(x)+C$.
Неопределенный интеграл
Определение
Совокупность всех первообразных функции $y=f(x)$, определенных на заданном промежутке, называется неопределенным интегралом от функции $y=f(x)$ и обозначается символом $\int f(x) d x$. То есть
$\int f(x) d x=F(x)+C$
Знак $\int$ называется интегралом, $f(x) d x$ — подынтегральным выражением
Операция нахождения первообразной или неопределенного интеграла от функции $f(x)$ называется интегрированием функции $f(x)$. Интегрирование представляет собой операцию, обратную дифференцированию.
Геометрическая интерпретация неопределенного интеграла
Неопределенный интеграл представляет собой семейство параллельно расположенных кривых $F(x)+C$, где каждому конкретному числовому значению постоянной $C$ соответствует определенная кривая из указанного семейства.
График каждой кривой из семейства называется интегральной кривой.
Теорема
Каждая непрерывная на промежутке $(a ; b)$ функция, имеет на этом интервале первообразную.
Читать дальше: свойства неопределенного интеграла.
19.2. Неопределенный интеграл и его свойства
Совокупность всех первообразных к функции называется неопределенным интегралом
от функцииФункция
называетсяподынтегральной
функцией,
переменной
интегрирования.
Другими словами, неопределенный интеграл – это общая первообразная, содержащая произвольную постоянную, при каждом численном значении которой получается частная первообразная.
Восстановление функции по ее производной (отыскание неопределенного интеграла) называется интегрированием этой функции. Интегрирование – операция обратная дифференцированию.
Из определения неопределенного интеграла вытекают его свойства.
1)Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
2)Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
3)Постоянный множитель можно вынести из-под знака интеграла, т.е. если то
4)Неопределенный
интеграл от алгебраической суммы двух
функций равен алгебраической сумме
интегралов от этих функций в отдельности,
т.
е.
19.3. Таблица основных интегралов
Приведем таблицу основных интегралов. Часть формул следует из определения интегрирования как операции, обратной дифференцированию, и таблицы производных. В таблице произвольная постоянная,– функция от переменнойчисло.
Таблица 6
Неопределенный интеграл | Первообразная | Неопределенный интеграл | Первообразная |
Неопределенный интеграл | Первообразная | Неопределенный интеграл | Первообразная |
+ |
Рассмотрим
основные методы интегрирования.
Метод непосредственного интегрирования основан на непосредственном использовании формул таблицы интегралов и свойств неопределенного интеграла.
Заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим пример. Требуется найти значение интеграла
На основе известной формулы дифференцирования
можно сделать вывод, что искомый интеграл равен гденекоторое постоянное число. С другой стороны,
Окончательно можно сделать вывод:
В
отличие от дифференцирования, где для
нахождения производной использовались
четкие приемы и методы, правила нахождения
производной, определение производной,
для интегрирования такие методы
недоступны. При нахождении первообразной
следует в основном опираться на знания
таблиц производных и первообразных.
Метод непосредственного интегрирования применим только для весьма ограниченных классов функций. Поэтому в большинстве случаев применяются способы, описанные ниже.
19.4. Интегрирование методом замены переменной
Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла, т.е. перейти к непосредственному интегрированию. Такой метод называют методом подстановки или методом замены переменной.
Данный метод основан на теореме: пусть функция определена и дифференцируема на некотором промежутке и пустьмножество значений этой функции, на котором определена функция. Тогда на множествефункцияимеет первообразную, на множествесправедлива формула
Пусть первообразная дляна множествеРассмотрим на множествесложную функциюПо правилу дифференцирования сложной функции, учитывая, что
получаем
т.
е.
функция
имеет на множествепервообразную,
следовательно
Замечая, что
.
Рассмотрим пример. Найти неопределенный интеграл
Сделаем замену Получим
Рассмотрим еще один пример. Найти интеграл
Сделаем замену Получим
Пример. Найти интеграл
Сделаем замену Получим
Рассмотрим пример. Найти интеграл и проверить ответ дифференцированием
Проверим
Рассмотрим пример. Найти интеграл и проверить ответ дифференцированием
Проверим
Рассмотрим
пример.
Найти
интеграл
Рассмотрим пример. Найти интеграл
Контрольные вопросы
Какая функция называется первообразной?
Что представляет собой неопределенный интеграл?
Какими свойствами обладает неопределенный интеграл?
Какова идея метода замены переменной?
Лекция №20. Интегрирование по частям
20.1. Интегрирование по частям.
20.2. Интеграл от функций, содержащих квадратный трехчлен.
Неопределенный интеграл
Неопределенный интеграл (также называемый первообразной , а иногда примитивным интегралом ) связан с определенным интегралом через фундаментальную теорему исчисления — тему, которую мы будем более подробно исследовать в другом месте этой статьи.
раздел. Мы знаем, что определенный интеграл даст нам площадь области под кривой для непрерывной функции на замкнутом интервале. Таким образом, он оценивается как число. Неопределенный интеграл
Название первообразной на самом деле довольно хорошо описывает природу неопределенного интеграла. По сути, это против производной. Предположим, у нас есть функция ƒ( x ), для которой мы хотим найти неопределенный интеграл. Мы уже установили, что ищем функцию. Оказывается, ƒ( x ) на самом деле является производной функции, которую мы ищем. Давайте посмотрим на пример. Предположим, мы хотим найти неопределенный интеграл функции ƒ( x ) = x 2 + 2 x . Мы знаем, что ƒ( x ) является производной искомой функции, но как нам обратить процесс дифференцирования, чтобы получить неопределенный интеграл? Давайте подумаем, что нам нужно было сделать, чтобы получить производную в первую очередь.
Рассмотрим терм x 2 . Когда мы дифференцируем степень x , мы умножаем коэффициент x на показатель степени, в который возводится x , а затем уменьшаем показатель степени на единицу. Чтобы обратить процесс вспять, нам нужно увеличить показатель степени на единицу и разделить коэффициент x на новый показатель степени. Таким образом, новый показатель степени x будет равен три (3), а новый коэффициент x будет одна треть ( 1 / 3 ). Таким образом, интеграл от x 2 равен 1 / 3 x 3 . Применяя ту же процедуру к терму 2 x , мы видим, что интеграл от 2 x должен быть равен x 2 . Искомая функция, которую мы назовем F ( x ), будет выглядеть следующим образом:
Ф ( x ) = 1 / 3 x 3 + x 2
Если это верно, то нахождение производной этой функции должно дать нам исходную функцию ƒ( x ) = x 2 + 2 x .
Применение основных правил дифференцирования к F ( x ) подтвердит, что это так:Ф ′( x ) = x 2 + 2 x
В общих чертах, мы можем определить неопределенный интеграл от ƒ( x ) как любую функцию F ( x ), такую, что:
F ′( x ) = ƒ( x )
Однако здесь есть потенциальная проблема. Рассмотрим следующие возможности для F ( x ):
F ( x ) = 1 / 3 x 3 + x + 2
F ( x ) = 1 / 3 x 3 + x 2 6
F ( x ) = 1 / 3 x 3 + х 2 + π
F ( x ) = 1 / 3 x 3 + x 2 + E 2
.
Теперь подумайте, какой будет производная для каждой из этих функций. Вы, конечно, обнаружите, что все они будут иметь одну и ту же производную, т.е.
Ф ′( x ) = x 2 + 2 x
Почему? Потому что последний член в каждом случае является константой . Всякий раз, когда мы дифференцируем константу, мы получаем ноль. Поэтому на самом деле не имеет значения, какой постоянный член у нас есть в конце функции при дифференцировании. Любой набор функций, отличающихся друг от друга только постоянным членом, будет иметь одну и ту же производную. Если подумать, это совершенно логично. Почему? Поскольку производная функции просто дает нам наклон этой функции для заданного значения x . Добавление постоянного значения к функции не изменяет ее наклон , а только ее вертикальную ориентацию. Мы можем видеть это на иллюстрации ниже.
Добавление постоянного члена к функции не меняет ее наклон
На самом деле существует бесконечное количество функций, которые дадут нам точно такую же производную.
Единственная разница между ними будет заключаться в постоянном члене. Поэтому мы, возможно, могли бы записать неопределенный интеграл функции ƒ( x ) = x 2 + 2 x следующим образом:
F ( x ) = 1 / 3 x 3 + x + 2
где знак вопроса представляет неизвестное постоянное значение. Вскоре мы вернемся к вопросу о том, как поступить с этой неизвестной величиной. А пока обратим внимание на обозначения, которые мы должны использовать здесь для неопределенного интеграла. Вы, наверное, помните, как писать определенный интеграл для функции ƒ( x ):
| ∫ | B | ƒ ( x ) D x |
| A |
Интегральный символ (это длинный символ ‘s’ над левой частью) говорит нам, что мы рассматриваем интеграл, а символы a и b сразу справа от интеграла.
символ интеграции нижний и верхний пределы интегрирования соответственно. Функция ƒ( x ) — это подынтегральная функция (то есть то, что мы интегрируем), а d x в конце говорит нам, что x — это наша переменная интегрирования (это также можно увидеть как представляющие бесконечно малые приращения x ). Теперь посмотрите, как мы записываем неопределенных интегралов от ƒ( x ):
| ∫ | ƒ( x ) d x |
На первый взгляд это выглядит так же, как запись определенного интеграла. Обратите внимание, однако, что верхний и нижний пределы интегрирования отсутствуют. Это потому что там есть нет домена интеграции . В то время как определенный интеграл приводит нас к числу, представляющему площадь ограниченной области под графиком функции, неопределенный интеграл есть просто другая функция — функция, которую мы фактически получаем, обращая процесс дифференцирования, который дал воспользуемся функцией ƒ( х ).
Этот процесс, обратный дифференцировке, называется антидифференцировкой (или неопределенной интеграцией ).
Нам все еще нужно что-то сделать с постоянным членом, который был потерян при дифференцировании (для упрощения мы будем работать, исходя из предположения, что было постоянным членом, даже если это не так). Конечно, невозможно определить значение постоянного члена. Как только оно было устранено в процессе дифференциации, оно исчезло навсегда. Но как показать эту отсутствующую константу в наших обозначениях? Ответ на самом деле очень прост. Мы просто используем букву C в качестве заполнителя. Вот как мы записываем неопределенный интеграл функции ƒ( x ) = x 2 + 2 x :
| ∫ | x 2 + 2 x d x = 1 / 3 x 3 + x 2 + C |
Буква C представляет все возможные значения отсутствующей константы, в том числе ноль .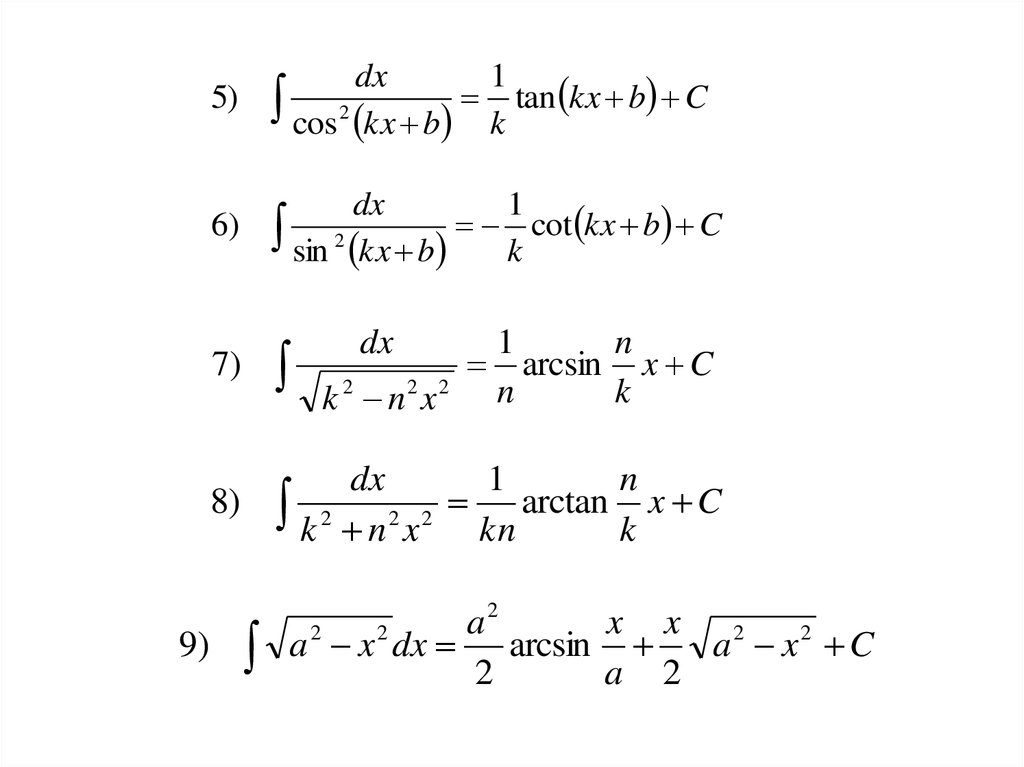
Мы называем C константой интегрирования . d x , следующее за интегралом, является дифференциалом . На самом деле вы уже должны быть хорошо знакомы с ним из изучения дифференциального исчисления. Это очень важно, и никогда нельзя опускать . Почему? Во-первых, он сообщает нам, где заканчивается выражение, которое нужно проинтегрировать (подынтегральная функция и ). В приведенном выше примере его отсутствие не вызвало бы особых проблем, но рассмотрим следующий неопределенный интеграл:
| ∫ | 3 x 2 + 2 x D x + 3 = x 3 + x 2 + + 3 9038 + 3 + 3 9038 9038 + 3 + 3  е.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вторая часть, которую иногда называют второй фундаментальной теоремой исчисления , говорит нам, что мы можем вычислить определенный интеграл для функции, используя один из ее неопределенных интегралов (которых, помните, существует бесконечное число ).
0003 C 
В двух словах, это говорит нам, что если функция непрерывна на некотором замкнутом интервале, то определенный интеграл для этого интервала (или область интегрирования ) может быть вычислен путем нахождения значений неопределенного интеграла (который это функция, помните) на каждом конце интервала. Определенным интегралом будет разница между этими двумя величинами. Другими словами, если функция F ( x ) — неопределенный интеграл функции ƒ( x ), а ƒ( x ) непрерывен на отрезке [ a , b ], тогда:
График этой функции показан ниже. Как видите, определенный интеграл будет иметь как положительную, так и отрицательную составляющие.
Если вам когда-нибудь понадобится проверить результат ваших вычислений, вы можете использовать множество онлайн-калькуляторов определенных интегралов, например, этот в Number Empire 9.Сайт 0004:
Вы также исследуете нахождение первообразных графически и аналитически. 
Приняв за = 0, мы получим одну первообразную из семейства первообразных.
