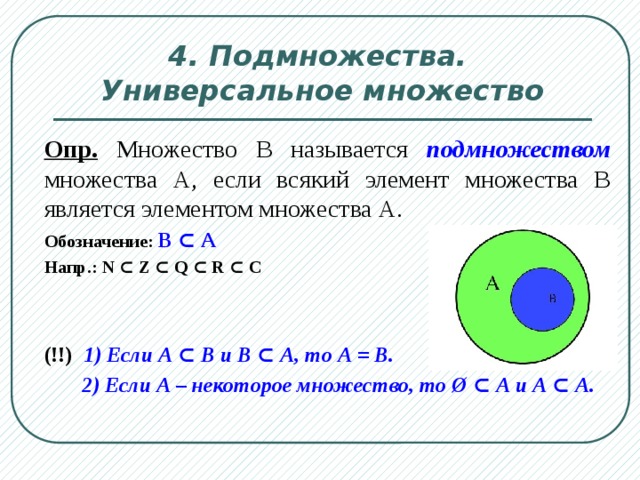
Что такое подмножество в информатике: Урок информатики по теме «Множество. Подмножество. Пересечение множеств»

Содержание

Урок информатики по теме «Множество. Подмножество. Пересечение множеств»

Щепина Зинаида Николаевна

Разделы: Начальная школа

Цели урока.

Повторить понятия “множество”, “элементы множества”.
Закрепить представления о множествах, подмножествах, пересечении двух множеств.
Закрепить умение определять принадлежность элементов множеству и характер отношений между множествами.
Развитие быстроты реакции, сообразительности, гибкости мышления.
Тренировка внимания.

Задачи урока.

Закрепить у детей начальные представления о множествах.
Научить определять принадлежность объектов заданным множествам, в том числе подмножествам и пересекающимся множествам.
Учить делать выводы с помощью простейших схем рассуждений.

Оборудование. Учебник “Информатика в играх и задачах 4 класс” (часть 2), цветные карандаши, карточки-ребусы.

I. Оргмомент. Интеллектуальная разминка

Учитель. Быстро сообразите и ответьте Что это? Кто это?
Девочка, вступившая в борьбу с самой снежной королевой (Герда).

Ребенок собаки (Щенок).

Начало дня (Утро).

Самая большая вкусная ягода (Арбуз).

Северная ездовая и охотничья собака (Лайка).

Главный обитатель цветочного города (Незнайка).

Часть одежды, куда кладут деньги (Карман).

Самая любимая пора школьников и студентов (Каникулы).

Причина гибели “Титаника” (Айсберг).

Метательное орудие, возвращающееся к охотнику (Бумеранг).

II. Проверка домашнего задания
№61, №62 (Часть I Учебника)

III. Сообщение темы урока. Игра “Собери слово”
Учитель. Тему сегодняшнего урока узнаете, когда разгадаете ребусы, которые лежат у вас на партах. Первые буквы из отгаданных вами ребусов составят название темы урока (см. Рис.№1 – МНОЖЕСТВА).

IV. Актуализация опорных знаний.
Учитель. Сегодня на уроке мы будем решать задачи, главными героями которых будут МНОЖЕСТВА.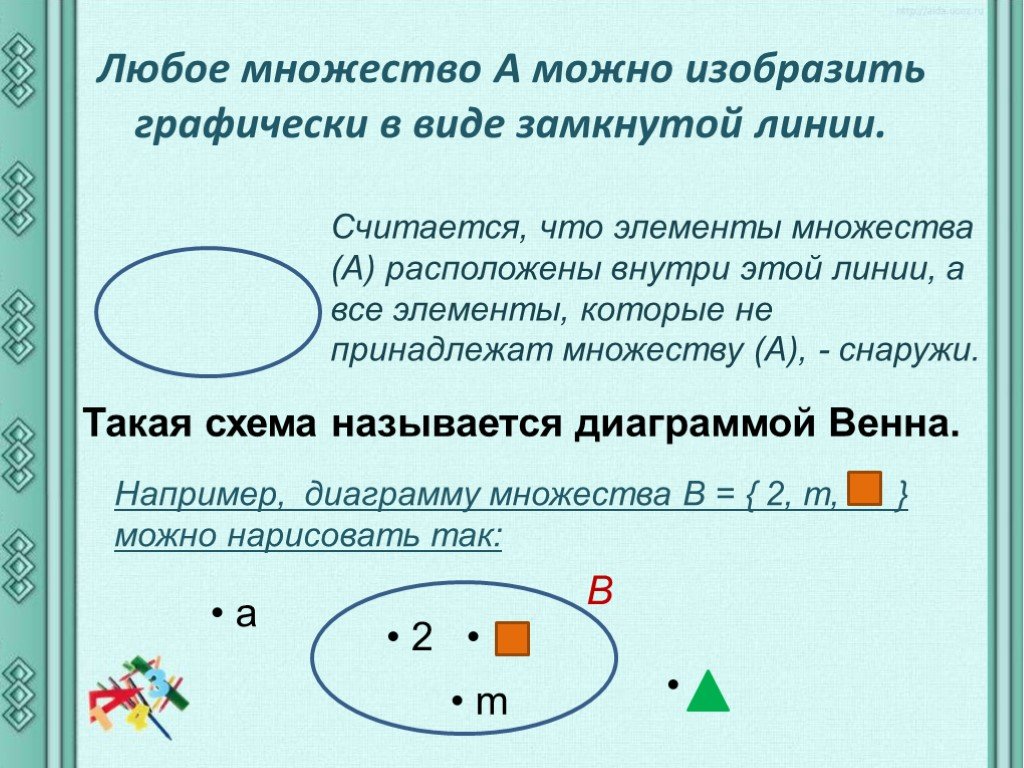

Давайте вспомним, что вы уже знаете о множествах и элементах множеств:

Назовите элементы множества “Месяцы года” (Январь, февраль и т.д.)
Сколько всего элементов в этом множестве? (12)
Назовите элементы множества “Времена года” (4 элемента – зима, весна, лето, осень).
Назовите элементы множества “Материки” (6 элементов: Евразия, Африка,Сев.Америка, Юж.Америка, Австралия, Антарктида).
Назовите элементы множества “Летающие бегемоты”
(пустое множество).
Многоугольники (бесконечное множество). Учитель. Таким образом, можно сделать вывод о том, что “множество”, в отличие от всех других слов, выражающих идею объединения объектов (сервиз, табун, эскадра, стая и т.д.), может применяться к обитателям любой природы. Объекты, собранные во множество, называются элементами множества.
Учитель. Раскрывая смысл термина “множество”, один из создателей теории множеств, немецкий ученый Георг Кантер (1845-1918) писал: “Множество есть многое, мыслимое нами, как единое.”

Существенный признак множеств – объединение в одно целое.

Как назвать:

Множество людей, поющих вместе ( Хор).

Множество детей, которые вместе учатся (Класс).

Множество книг, собранных вместе (Библиотека).

V. Физкультминутка.
Руки в стороны и вверх
Повторяем дружно.
Засиделся ученик –
Разминаться нужно.
(руки к плечам, потом вверх, потом снова к плесам и т. д.)
Мы сначала всем в ответ
Головой покружим: Нет!
(Вращение головой в стороны)
Энергично, как всегда,
Головой покажем: Да!
(подбородок прижат к груди, затем запрокинуть голову назад)
Чтоб колени не скрипели,
Чтобы ножки не болели,
Приседаем глубоко,
Поднимаемся легко.
(приседание)
Раз, два, три, чеканим шаг.
(ходьба на месте)
Подает учитель знак.
Это значит, что пора
Нам за парты сесть. Ура!
(дети садятся за парты).

VI. Работа в учебнике.
Стр.2-4, №1-5.

VII. Итог урока.
Учитель. О чем говорили на уроке? (о множествах)
Мы вспомнили, что множества состоят из различного числа элементов, что встречаются пустые, бесконечные множества. Мы вспомнили, что существуют 3 схемы расположения множеств.

Множества не пересекаются

Горячев А.В., Горина К.И. “Информатика в играх и задачах 4 класс” Методические рекомендации для учителя, М. “Баласс”, 2004

Винокурова Н. “Подумаем вместе”, М. “РОСТ”, 1997

11.02.2008
Информатика — Множества. Основные сведения.
1. Множества и их элементы.
Множества являются «основными» математическими объектами. Они лежат в основе всей математики, все математические объекты (числа, точки и другие) можно рассматривать как множества и их элементы. Вот основные свойства множеств и отношения между множествами и составляющими их элементами («элемент» здесь общее слово для тех объектов, которые составляют множество; это могут быть яблоки, люди, гномы, числа, точки и т. д.). Ниже при описании свойств и отношений множества обозначаются большими латинскими буквами, а их элементы – маленькими латинскими буквами .
Свойства: «множество A — пустое«, т.е. A не содержит ни одного элемента. Пустое множество обозначается так: Ø.
Отношения:
1) » x принадлежит A», т.е. x является элементом множества A; синоним: x лежит в A. Пример высказывания: » число ½ принадлежит множеству целых чисел». Это высказывание ложно. Принадлежность элемента множеству обозначается знаком ∈. Пример: «½∈Z » (здесь Z обозначает множество целых чисел).
2) «A — подмножество B» (синонимы: «A включено в B «, » A — часть B«). Смысл: каждый элемент первого множества одновременно является и элементом второго множества. Пример: «множество натуральных чисел — подмножество множества целых чисел»; это высказывание истинно. Отношение «быть подмножеством обозначается знаком ⊆ . Пример: «N ⊆ Z» (здесь N обозначает множество натуральных чисел, а Z обозначает множество целых чисел).
2. Операции над множествами.
Основные операции над множествами — это объединение (обозначение: A ∪ B), пересечение (обозначение: A ∩ B), и разность (обозначение: A \ B), . Часто удобно считать, что все рассматриваемые в задаче множества являются подмножествами одного универсального множества U. В зависимости от решаемой задачи в качестве универсального множества может выступать множество всех целых чисел, множество всех точек прямой, множество всех точек плоскости и т.п. Разность между универсальным множеством и данным множеством A называется дополнением множества A.

3. Операции над множествами и логические операции.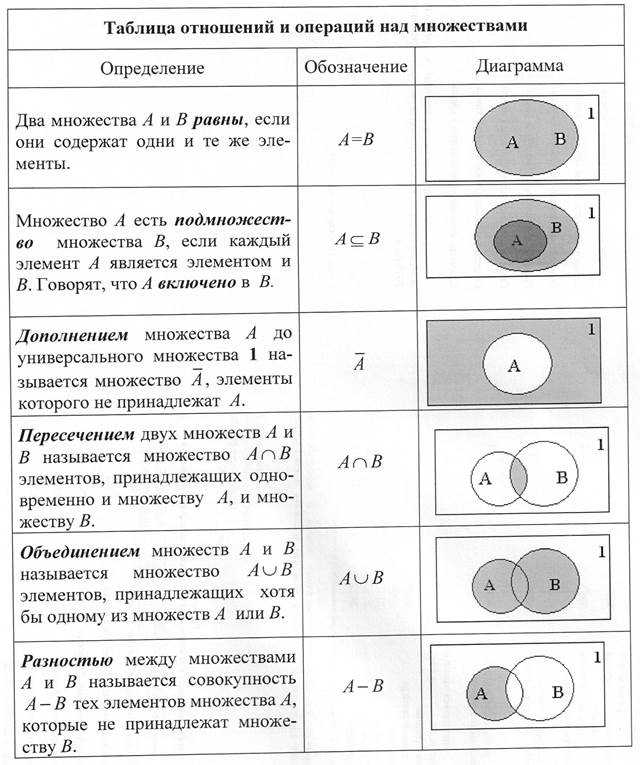
Логические выражения над элементарными высказываниями о множествах (высказывания вида «A=∅», «x∈A» «A⊆B» ) можно преобразовывать, используя не только общие правила преобразования логических выражений, но и свои правила, связанные со свойствами операций над множествами. Ниже U — это универсальное множество; x — его произвольный элемент, A, B, X — множества. Верны следующие утверждения.
1. Следующие высказывания эквивалентны, т.е. имеют одинаковые логические значения при любых x, A, B (это обозначено знаком ⇔)
1а) (x∈A)∧(x∈B) ⇔ x∈A∩B
1б) (x∈A)∨(x∈B) ⇔ x∈A∪B
1в) ¬(x∈A) ⇔ x∈U\A
1г) (x∈A)∧ (¬(x∈B)) ⇔ x∈A\B
2. Следующие высказывания эквивалентны, т. е. имеют одинаковые логические значения при любых X, A, B (это обозначено знаком ⇔)
2а) (X∩A ≠Ø ) ∨ (X∩B ≠Ø ) ⇔ (X∩ (A∪B) ≠Ø )
2б) (X∩A = Ø ) ∧ (X∩B = Ø ) ⇔ (X∩ (A∪B) = Ø )
3. (а) Пусть A ⊆ B, т.е.  A — подмножество B; x — элемент универсального множества U. Тогда истинно высказывание:
(x ∈ A) → (x∈ B)
(б) Пусть высказывание (x ∈ A) → (x∈ B) истинно при любом x ∈ U. Тогда  A ⊆ B.
4.  (а) Пусть A ⊆ B, т.е.  A — подмножество B; X ⊆ U — произвольное множества. Тогда истинно высказывание:
(X∩A ≠Ø ) → (X∩B ≠Ø )
(б) Пусть высказывание (X∩A ≠Ø ) → (X∩B ≠Ø )  истинно для любого множества X ⊆ U. Тогда  A ⊆ B.
5. Следующее высказывания истинны для любых множеств A, B, X
( (X∩A ≠ Ø ) ∧ (X∩B = Ø ) ) → (X∩ (B) ≠ Ø )

4. Подсчет количества элементов в пересекающихся множествах.
См. здесь

Учебник по теории множеств. «Никто не изгонит нас из… | Брэндон Скеррит | Заметки по информатике
SpaceX
«Никто не изгонит нас из рая, созданного для нас Кантором». — Гильберт о создании Кантором теории множеств
В Quizlet появилась колода карточек для теории множеств:
Карточки по теории множеств | Quizlet
Начните изучать теорию множеств. Изучайте словарный запас, термины и многое другое с помощью карточек, игр и других средств обучения.
quizlet.com
Теория множеств — это нотация, используемая для описания множеств. Набор — это список объектов, где повторение не имеет значения и порядок не имеет значения .
Для обозначения набора используйте фигурные скобки. Чтобы обозначить набор всего хорошего британского чая, вы можете написать что-то вроде Tea = {чаевые PG, Tetley, Yorkshire Tea, Twinnings}.
Если вам очень нравятся чаевые PG, вы можете переписать это как чай = {чаевые PG, чаевые PG, чаевые PG}, что приведет к простому равенству чай = {чаевые PG} как повторение не имеет значения.
Что, если мы хотим обозначить набор всего плохого британского чая? Это легко. Вы бы сделали это, чай = {} или чай = ∅ , что является символом пустого набора.
Вы можете создавать наборы внутри наборов, например, у вас может быть набор британских чаев с хорошим британским чаем. Чай = { {Типсы ПГ, Типсы ПГ черные}, {Тетлы} }.
Два набора равны, если содержимое равно. Например, {2, 3, 3} равно {2, 3}, но {{2}} не равно {2}.
С помощью математики можно создавать бесконечные множества. Например, чтобы создать набор всех положительных четных чисел, можно составить набор:
X = {y | y — все положительные четные числа}
Вам не нужно выписывать все положительные четные числа, просто покажите, что это подразумевается, используя символ вертикальной черты «|», чтобы показать математическую формулу, применяемую к набору.
Здесь можно применить любую математическую формулу. Например, чтобы получить набор всех положительных целых чисел от 0 до 100, можно сделать так:
Х = {с | 0 < s < 100}
Все множества обозначаются с большой буквы.
Выполнение операций над множествами
Подмножество — это множество, полностью существующее в родительском или исходном множестве. Например, для набора x = {1, 2, 3, 4} подмножество может быть y = {1, 2} или q = {4}.
Подмножество содержит любые элементы (не все), существующие в родительском наборе. Просто повторю: x = {Tetley, PG Tips} является подмножеством Tea = {PG Tips, Tetley, Yorkshire Tea, Twinnings}.
Подмножество обозначается символом ⊆. Чтобы сказать, что x является подмножеством Tea, можно сказать, что x ⊆ Tea.
Другими словами, ∅ ⊆ X, где X вообще любое множество.
Битовый вектор — это нотация, используемая для описания размещения элементов в подмножестве. Допустим, у нас есть набор x = {1, 2, 3, 4, 5, 6, 7, 8, 9}, и у нас есть подмножество y = {1, 3, 6}, мы могли бы обозначить y, используя битовые векторы как :
Y = (1, 0, 1, 0, 0 , 1, 0, 0 , 0)
Это означает, что y является подмножеством x с элементами 1, 3, 6. Если порядок a набор имеет значение, это также было бы удобной записью для представления того, где находятся элементы в обоих списках.
Два набора равны, если первый набор является подмножеством второго набора, а второй набор является подмножеством первого шага, по существу, они содержат одни и те же элементы. В математических терминах это:
A ⊆ B и B ⊆ A, тогда A = B
Объединение двух множеств — это множество, содержащее все элементы первого множества и все элементы второго множества.
Обозначение для описания этого объединения A и B равно A ∪ B.
Математическая формула для этого объединения множеств: A ∪ B = {x | x ∈ A или x ∈ B}
Опять же, все, что есть в A и B, появится в наборе, который является объединением двух наборов.
Объединение двух наборов, при котором все, что есть в обоих наборах, суммируется. Автор Watchduck (он же Тилман Писк) — собственная работа, общественное достояние, https://commons. wikimedia.org/w/index.php?curid=11149747
Объединение A (где A — любой набор) и ∅ ( пустой набор) — это просто A, поскольку ∅ не имеет элементов, которые можно было бы добавить в набор.
Объединение A = {1, 2} и B = {3, 4} есть A ∪ B = {1, 2, 3, 4]
Попробуем создать объединение двух наборов в битовой записи.
C = (1, 0, 0, 0, 1) и B = (1, 1, 0, 1, 1)
Объединение C и B (C ∪ B) есть {1, 1, 0, 1, 1}
Пересечение двух множеств — это подмножество, содержащее только те элементы, которые есть как в A, так и в B. Математический символ для этого — ∩. Пересечение A и B есть A ∩ B.
Если A содержит элементы {1, 2, 3}, а B содержит элемент {2}, то A ∩ B (пересечение A и B) есть подмножество {2 } так как 2 существует в обоих этих множествах.
Пересечение любого множества A с пустым множеством является просто пустым множеством, потому что пустое множество не имеет элементов. A ∩ ∅ = ∅
Пересечение 2 множеств. Красная часть представляет собой пересечение. Автор Watchduck (он же Тилман Писк) — собственная работа, общественное достояние, https://commons.wikimedia.org/w/index.php?curid=11149747
. Математическое обозначение пересечения: A ∩ B = {x : x ∈ A и X ∈ B}.
Если A является подмножеством B, A ⊆ B, то A ∩ B.
Пересечение двух наборов, представленных битовыми векторами.
Пусть C = (1, 0, 0, 0 ,1) и D = (1, 1, 0, 0, 1 ), тогда C ∩ D равно
C ∩ D = (1, 0, 0, 0, 1)
Относительное дополнение — это множество A ∪ B минус B. Другими словами, это все числа в множестве A, которых нет в множестве B.
Автор Watchduck (также известный как Tilman Piesk) — собственная работа, Public Domain, https://commons.wikimedia.org/w/index.php?curid=11149747
Другой способ, которым мы можем взглянуть на это, состоит в том, что если A является множеством, то относительная комплементарность A — это все, что не находится в A.
Математическое обозначение относительного дополнения — символ «\».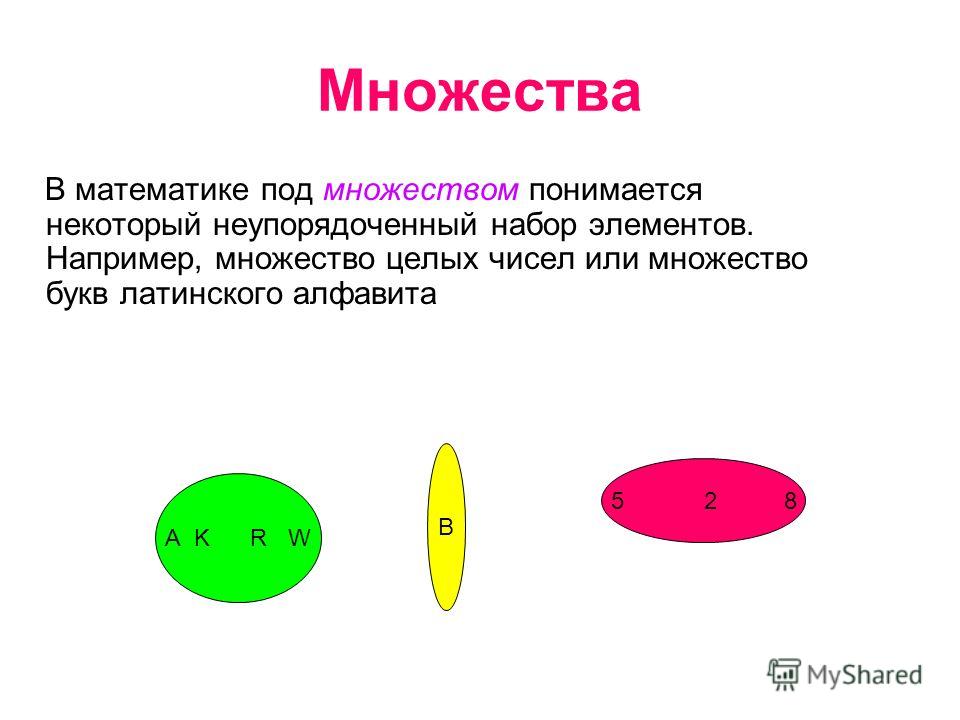 Чтобы обозначить A как относительное дополнение B, можно было бы сказать A \ B.
Математическая формула для относительного дополнения: A \ B = {X | X ∈ A и ∉ B}
Предположим, например, что существует множество A = {4, 7, 8}, а также множество B = {4, 9, 10}, тогда A \ B = {7, 8}
A \ ∅ = A для любого множества A, потому что пустому множеству нечего выносить.
Другой хороший пример:
A = {1, 2, 3} и B = натуральные числа, тогда A \ B приводит к пустому множеству, ∅. Это потому, что при удалении B из A мы ничего не добавляем, мы не можем ничего добавить к исходному набору A.
Давайте попробуем это с битовыми векторами.
Положим C = (1, 0, 0, 0, 1) и D = (1, 1, 0, 0, 1), тогда C \ D = (0, 0, 0, 0, 0)
Существует набор в рамках теории множеств, называемый универсальным набором, обозначаемый как U. Универсальный набор — это набор каждого отдельного объекта.
Дополнение — это универсальный набор, забрать данный набор.
Автор Watchduck (также известный как Tilman Piesk) — собственная работа, общественное достояние, https://commons.wikimedia.org/w/index.php?curid=11149747
При наличии набора, обозначенного красным кружком, мы можем найти комплимент этого набора, удалив его из универсального набора; белый квадрат.
Автор Watchduck (также известный как Tilman Piesk) — собственная работа, общественное достояние, https://commons.wikimedia.org/w/index.php?curid=11149747
На изображении выше представлен универсальный набор, из которого удален предыдущий красный кружок. , таким образом, дополнение A, где A — красный кружок, показано выше. 9с или ~ а.
Математическая формула для дополнения: (0, 1, 1, 1, 0). По сути, инвертирование битового вектора.
Дополнением к универсальному набору является универсальный набор, за исключением универсального набора ∅.
Некоторым читателям может быть привычнее называть комплимент «нет». Не А есть множество всего, что не А.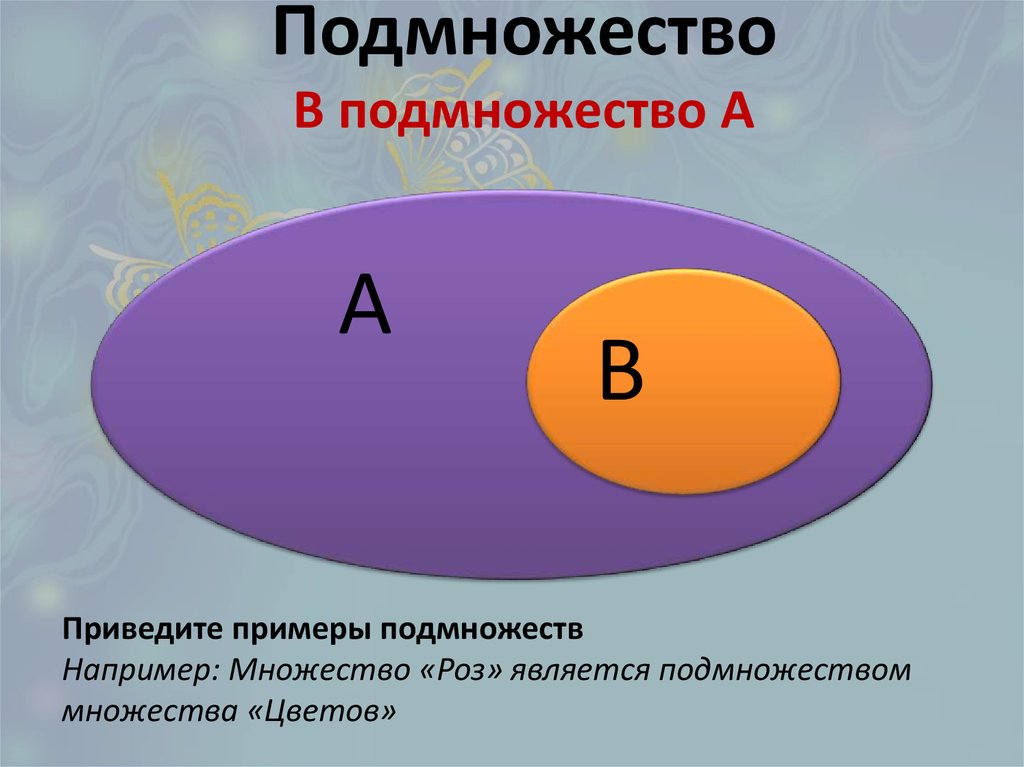
Симметричная разность двух множеств — это все, что есть в множестве А, и все, что есть в множестве В, но не в обоих, за исключением универсального множества.
Public Domain, https://commons.wikimedia.org/w/index.php?curid=3437442
Математическая формула для этого:
a∆b = {x | (a ∈ a и x ∉ b) или (x ∉ a и x ∈ b)}
Короче говоря, это объединение двух множеств за вычетом общих элементов.
Вот пример: A = {4, 7, 8} и B = {4, 9, 10}, поэтому A ∆ B = {7, 8, 9, 10}
Не
Коммуникативный закон
Коммуникативный закон гласит, что мы можем поменять числа местами и получить тот же результат.
Мы можем использовать алгебру в рамках теории множеств, такой как коммуникативный закон. В алгебре a * b = b * a и a + b = b + a. Следовательно, объединение двух множеств A ∪ B = B ∪ A.
Закон ассоциаций
Закон ассоциаций гласит, что не имеет значения, как мы группируем числа.
Предположим, что множества A, B, C, U такие, что A⊆U, B⊆U, C⊆U, тогда:
Объединение (B ∪ c) = (a ∪b) ∪ c, a ∩b (b ∩ c) = a ∩ b ∩ c
В алгебре это просто
a+(b+c) = ( a+b)+c или a * (b*c) = (a*b)*c
Распределительный закон
Распределительный закон утверждает, что число a в уравнении a(b+c) = ab+ac равно что a отдельно применяется к каждому члену уравнения b + c, что дает ab + ac.
Простыми словами, этот закон показывает, что результат сначала сложения нескольких чисел вместе, а затем умножения конечной суммы на некоторое число такой же, как сначала умножение каждого члена по отдельности на число, а затем сложение произведений.
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Объединение A с (B пересечением C) является пересечением (объединения b) и (объединения c).
Законы Деморгана — это набор преобразующих правил, созданных Августом Де Морганом, многие люди пишут Законы Де Моргана как законы Деморгана, поэтому здесь используются обозначения.
Примечание. Преподаватели Ливерпульского университета используют «~» для обозначения комплимента.
Один из законов Деморгана гласит, что если вы возьмете объединение двух множеств, то дополнение этого будет таким же, как если взять дополнение A и дополнение B и найти пересечение A и B.
В обозначениях теории множеств:
~(A ∪ B) = ~A ∩ ~B
Второй закон гласит, что дополнение пересечения является объединением дополнения этих двух множеств
~(A ∩ B ) = ~A ∪ ~ B
Ниже приведено изображение, показывающее применение законов Деморгана к двум различным диаграммам Венна.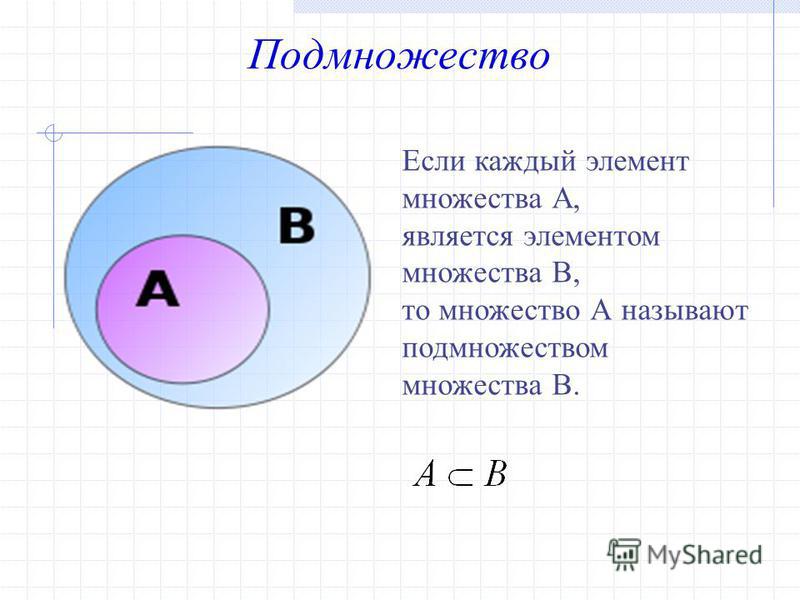 Примечание: черточка над буквами обозначает комплимент.
Автор Teknad — собственная работа, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=36768081
Количество элементов — это количество элементов набора в наборе. Допустим, S = {1, 2, 3, 3}, тогда |S| равно 3, так как повторение не имеет значения.
Допустим, S = {{a, {a, b}, {d}, e}. Мощность S, |S| равно 4, потому что на верхнем уровне существует 4 элемента.
Что такое |N| где N — натуральные числа? Бесконечность. Или в теории множеств, алеф-ноль.
|Р| где r — действительные числа — алеф-1.
Если вы хотите узнать больше об Алефе и о том, как считать до бесконечности, посмотрите это видео.
Если A и B множества, то |A| + |Б| = |А ∪ В|
Если множества A и B, то |A ∪ B| = |А| + |Б| — |А ∩ В|
Это называется наивным, потому что страдает парадоксами.
Например:
Парикмахер бреет всех и только тех мужчин, которые не бреются сами.
Кто бреет парикмахера?
Мы можем записать это в теории множеств. Примечание: => означает поэтому.
Пусть B будет парикмахером. Если B бреется сам, то B ∈ {те, кто брился посредством B}=> B ∈ {те, кто не бреется}=> B не бреется сам.
Если B не бреется, то B ∈ {те, кто не бреется} => B ∈ {те, кто бреется B}=> B бреется.
Это парадокс. В более общем случае это называется парадоксом Рассела.
Парадокс Рассела показывает, что объект {x | P(x) } не всегда имеет смысл. Ниже символически показан парадокс Рассела.
Пусть X= {R | R ∉ R}, то X ∈ X < = > R ∉ R.
Используйте их для проверки. Ответы в конце.
Предположим, есть 100 студентов третьего курса. 40 из них сдают модуль «Последовательные алгоритмы» и 80 — модуль «Многоагентные системы». 25 из них взяли оба модуля. Сколько студентов не взяли ни того, ни другого?
Является ли Ø ∈ Ø?
Ø ⊆ {5}?
Каков результат {x : x ∈ N, 5 < x < 6}? (Примечание: N состоит из всех натуральных чисел)
Какие числа содержатся в множестве A = {x | x ∈ N, X > 1 и X < 10}?
Evaluate U — Ø
Medium не поддерживает таблицы, поэтому это выглядит неуклюже. Для лучшей и более полной таблицы перейдите сюда.
5
Нет, пустой набор — это набор, который ничего не содержит, поэтому пустой набор не входит в набор пустого набора.
Да, пустой набор является подмножеством каждого набора.
Ø
{2, 3, 4, 5, 6 ,7, 8, 9}
Универсальный набор Уберите пустой набор, он останется универсальным.
Определение подмножества | ПКМаг
Группа команд или функций, которые не включают все возможности исходной спецификации. Программные или аппаратные компоненты, разработанные для подмножества, также будут работать с оригиналом. Однако любой компонент, разработанный для полной исходной спецификации, не будет работать с подмножеством продуктов. Контраст с суперсетом.
Реклама
Истории PCMag, которые вам понравятся
{X-html заменен}
Выбор редакции
ЭТО ОПРЕДЕЛЕНИЕ ПРЕДНАЗНАЧЕНО ТОЛЬКО ДЛЯ ЛИЧНОГО ИСПОЛЬЗОВАНИЯ. Любое другое воспроизведение требует разрешения.

Copyright © 1981-2023. The Computer Language(Opens in a new window) Co Inc. Все права защищены.
Информационные бюллетени PCMag
Информационные бюллетени PCMag
Наши лучшие истории в вашем почтовом ящике
Подпишитесь на PCMag
Фейсбук (Открывается в новом окне)
Твиттер (Откроется в новом окне)
Флипборд (Открывается в новом окне)
Гугл (откроется в новом окне)
Инстаграм (откроется в новом окне)
Pinterest (Открывается в новом окне)
PCMag.com является ведущим авторитетом в области технологий, предоставляющим независимые лабораторные обзоры новейших продуктов и услуг. Наш экспертный отраслевой анализ и практические решения помогут вам принимать более обоснованные решения о покупке и получать больше от технологий.

Как мы тестируем Редакционные принципы
(Открывается в новом окне) Логотип Зиффмедиа
(Открывается в новом окне) Логотип Аскмен
(Открывается в новом окне) Логотип Экстримтек
(Открывается в новом окне) Логотип ИНГ
(Открывается в новом окне) Логотип Mashable
(Открывается в новом окне) Предлагает логотип
(Открывается в новом окне) Логотип RetailMeNot
(Открывается в новом окне) Логотип Speedtest
(Открывается в новом окне) Логотип Спайсворкс
(Открывается в новом окне)
PCMag поддерживает Group Black и ее миссию по увеличению разнообразия голосов в СМИ и прав собственности на СМИ.
No related posts.