Что такое рациональное число и иррациональное число примеры: Рациональные и иррациональные числа

2

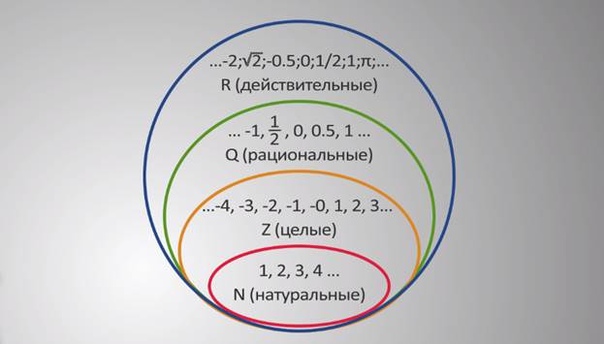
1.4 Натуральные, рациональные, иррациональные числа

О. Множество М называется индуктивным, если

.

О. Множество натуральных чисел – это наименьшее индуктивное множество, содержащее 1. Обозначается N .

О. Множество целых чисел – это множество

Z N .

О. Множество рациональных чисел – это множество

Q целое, натуральное .

Числа, которые не являются рациональными, называются иррациональными.

Любое рациональное число можно представить в виде конечной или бесконечной периодической десятичной дроби. Например, . Иррациональное число – это всегда бесконечная непериодическая десятичная дробь.

Принцип Архимеда Множество N не ограничено сверху.

Доказательство. Допустим, N – ограничено сверху. Тогда оно имеет точную верхнюю грань. Обозначим . Тогда для числа . Но тогда , т.е. М не является . Противоречие. ■

Следствие 1 из принципа Архимеда .

Доказательство. Возьмем . Рассмотрим число . Оно не является верхней гранью для N (так как N не ограничено сверху). Значит, . Следовательно, .■

Следствие 2 Если и , то .

Доказательство. Допустим, . Тогда .

Противоречие с условием. ■

Следствие 3 Для : .

1.5 Принцип Кантора

Примеры числовых множеств: отрезок, интервал, полуинтервал, луч, прямая, пустое множество, N, Q и т. п. Из множеств можно образовывать системы множеств. Например, , .

Утверждение Для системы интервалов не существует точки, общей для всех интервалов, т.е. Ø.

Доказательство. Допустим, существует общая точка. Это число не может быть отрицательным. Это и не ноль. Допустим, существует число . По следствию 1 из принципа Архимеда, . Но тогда . Противоречие. ■

Пусть имеется система множеств . Если , т.е. , то эта система называется системой вложенных множеств.

Принцип Кантора Для любой системы вложенных отрезков существует точка, общая для всех отрезков, т.е. . Если, кроме того, система отрезков такова, что существует отрезок, длина которого меньше , то точка

с – единственная.

Доказательство. Пусть .

Рассмотрим два множества: и (А – левые концы , В – правые концы ). Нетрудно доказать (от противного), что (иначе бы , и они бы не пересекались). Значит, по аксиоме полноты, , в том числе и для случая тоже.

Значит, , .

Допустим теперь, , общие для всех отрезков. Пусть . Возьмем в качестве . Тогда существует отрезок длины меньше . Так как и , то длина равна . Но, по построению, длина меньше . Противоречие. ■

1.6 Правило построения отрицания

Пусть некоторое свойство, обозначим противоположное к нему свойство.

Утверждение	Отрицание (противоположное утверждение)

2 Числовые последовательности

2.

1 Определения

Функцией называется правило (закон), по которому каждому элементу множества Х ставится в соответствие единственный элемент множества Y.

Обозначается или . Множество Х при этом называется областью определения, а множество Y – областью значений.

Последовательность

– это функция, область определения которой есть множество N всех натуральных чисел.

– n—ый член последовательности, номер члена .

Примеры .

О. Последовательность называется ограниченной сверху, если

: .

О. Последовательность называется ограниченной снизу, если

: .

О. Последовательность называется ограниченной, если

: .

О. Последовательность называется возрастающей с номера , если .

О. Последовательность называется убывающей с номера , если

.

Рациональные числа и иррациональные числа

Рациональные числа включают целых числа , дроби или десятичных знака , которые заканчиваются или повторяются. Иррациональное число — это любое число, которое нельзя преобразовать в дробь .

Содержание

• Рациональные числа:
• Иррациональные числа:
• Десятичное представление рациональных и иррациональных чисел:
  • Конечные десятичные знаки:
  • Повторяющиеся десятичные знаки:
  • Неконечные десятичные дроби:
  • Неповторяющиеся десятичные дроби:
• Докажите, что √2 является иррациональным числом
• Теорема:
•               Докажите, что сумма рациональных чисел иррациональна.
• Часто задаваемые вопросы-FAQ
  • Что такое рациональные числа? Приведи примеры.
  • Является ли 0 рациональным числом?
  • Какой знаменатель у рационального числа?
  • что такое иррациональное число?
  • Является ли Pi(π) рациональным числом?

Рациональные числа:

Те числа, которые можно представить в виде P/q, где p, q ∈ Z и q≠0.Числа √16, 3.7,4 являются рациональными числами. √16 можно привести к виду p/q, где p, q ∈ Z и q≠0, поскольку √16=4=4/1. Рациональные числа, обозначаемые Q.

Q= {x|x=p/q, где p, q ∈ Z и q≠0.}

Иррациональные числа:

Те числа, которые нельзя представить в виде p/q, где p, q ∈ Z и q≠0.числа

√2, √3    7/ (√5) — иррациональные числа. Иррациональное число обозначается Q’.

Q’ = {х| x ≠p/q, где p, q ∈ Z и q≠0.}

Десятичное представление рациональных и иррациональных чисел:

Существует четыре типа десятичного представления рациональных и иррациональных чисел:

Конечные десятичные дроби:

                               Десятичное число, которое имеет только конечное число цифр в своих десятичных частях, называется завершающим десятичным числом. Таким образом, 203,05, 0,00415, 1,456 являются примерами завершающих десятичных знаков.

 Поскольку конечная десятичная дробь может быть преобразована в обыкновенную дробь, каждая конечная десятичная дробь представляет собой рациональное число.

Повторяющиеся десятичные числа

:

                               Это еще один тип рациональных чисел.

Хорошо видно, что повторяющаяся десятичная дробь может быть преобразована в обыкновенную дробь. Таким образом, каждая повторяющаяся десятичная дробь представляет собой рациональное число.

Неконечные десятичные числа:

                               Десятичное число, в десятичных частях которого содержится бесконечное количество цифр, называется неконечным десятичным числом. Таким образом, 1,4235……, 0,013246…. , 2.33333333…, являются примерами неконечной десятичной дроби.

Неповторяющиеся десятичные дроби:

                          В общем случае неповторяющиеся десятичные дроби — это десятичные дроби, в которых цифры в десятичной части не повторяются. Таким образом, 1,5673….. являются примером конечного десятичного числа.

Неконечная, неповторяющаяся десятичная дробь — это десятичная дробь, которая не завершается и не повторяется.

Невозможно преобразовать такую ​​десятичную дробь в обыкновенную.

Таким образом, непрерывающаяся и неповторяющаяся десятичная дробь представляет собой иррациональное число.

Пример:

1. O.34=34/100 — рациональное число.
2. 0,3333….=1/3 — повторяющееся десятичное число, рациональное число
3. 0,142857142857…..=1/7 — повторяющееся десятичное число — рациональное число.
4. 1.4142135… — иррациональное число.
5. 7.3205080….. является иррациональным числом.
6. 3.141592……. — это важное иррациональное число, называемое (пи), которое обозначает постоянное отношение длины окружности любого круга к длине диаметра, т.е.

   Приблизительное значение π (пи) равно 22/7, более точное приближение равно 355/113, а еще более точное приближение равно 3,14159. … значение π с точностью до 5 знаков после запятой было определено с помощью компьютера.

   Докажите, что √2 – иррациональное число.

   Доказательство: предположим, что √2 – рациональное число.

   Чем,

   √2=p/q → (a)

    Где p, q ∈ Z и q≠0. Также пусть p/q является низшей формой.

   Возводя в квадрат обе части уравнения (а), получаем,

   P x p — четное число.

   (Четное x четное=четное)

   (Нечетное x нечетное=нечетное)

   Итак, p — это четное число . Тогда это можно записать как

   P=2m → (2)

   Используя (2) в (1)

   2q2= (2m) ²

   2q ² =4m 909137 2 2 = 2m ² → (3)

   Отсюда следует, что q ² — четное число.

   Итак, q тоже четное число. Мы можем записать это как

    q=2n → (4)

   Из (2) и (4)

   P/q=2m/2n

   Что не в самой низкой форме. Это противоречит нашему предположению, что p/q находится в низшей форме. Следовательно, √2  не является рациональным числом. Это иррациональное число.

   Таким же методом можно доказать иррациональность √3, √5, √7,…….√n, где n — любое простое число,

   Простое число обозначается через P.

   P= {2 , 3, 5, 7, 11,…….}

   Теорема:

                Докажите, что сумма рационального и иррационального чисел есть иррациональное число.

   Доказательство: предположим, что

   Rational + Irration = Rational

   P/Q + X = M/N → (1)

   ∴ По определению рациональное и иррациональное число.

   Из (1)

   x = M/N-P/Q

   x = MQ-NP/NQ

   x = (Integer-Integer)/Integer

   , где P, Q, M, n ∈Z

   x =integer/integer

   X должно быть рациональным числом.

   Противоречащее нашему предположению неверно.

   Итак, сумма рационального и иррационального чисел должна быть иррациональным числом.

   Часто задаваемые вопросы

   Что такое рациональные числа? Приведи примеры.

   

   Рациональное число — это число, которое может быть выражено в виде дроби p/q, где p и q — целые числа, а q не равно 0. Некоторые примеры рациональных чисел включают 1/3, 2/4, 1/5. , 9/3 и так далее.

   Является ли 0 рациональным числом?

   Да, 0 — рациональное число, потому что это целое число, которое можно записать в любой форме, например 0/1, 0/2, где b — целое число, отличное от нуля. Его можно записать в виде: p/q = 0/1.
   Следовательно, мы можем заключить, что 0 — рациональное число.

   Какой знаменатель у рационального числа?

   Знаменатель рационального числа может быть любым действительным числом, кроме 0.

   что такое иррациональное число?

   Иррациональное число — это любое действительное число, которое не может быть выражено рациональным числом. Это число, которое не может быть представлено как конечное или завершающее десятичное число.

   Является ли Pi(π) рациональным числом?

   Нет, Пи (π) не является рациональным числом, поскольку его значение равно 3,142857…

   Определения и примеры рациональных чисел

   Определения и примеры рациональных чисел

   Введение

   , 900 число, которое может быть выражено как частное или дробь p/q двух целых чисел, числителя p и ненулевого знаменателя q. Набор всех рациональных чисел, часто называемый «рациональными числами», обычно обозначается жирным шрифтом Q (или жирным шрифтом на доске?). Десятичное разложение рационального числа всегда либо заканчивается после конечного числа цифр, либо начинает снова и снова повторять одну и ту же конечную последовательность цифр. Более того, любое повторяющееся или заканчивающееся десятичное число представляет собой рациональное число. Эти утверждения справедливы не только для основания 10, но и для любого другого целого числа с основанием b ? 2. Вещественное число, не являющееся рациональным, называется иррациональным. К иррациональным числам относятся ?2 (квадратный корень из 2, алгебраическое число), ? (пи, трансцендентное число) и постоянная Эйлера e.

   Что такое рациональные числа?

   Рациональные числа — это любые числа, которые могут быть выражены в виде дроби p/q, где p и q — целые числа, а q не равно 0. Все целые и целые числа — рациональные числа, так как они могут быть выражены в виде дробей с знаменатель 1. Например:

   1/1 = 1
   2/1 = 2
   -3/1 = -3

   Все десятичные числа также могут быть выражены как рациональные числа. Например:

   0,5 = 1/2
   -0,75 = -3/4
   2,25 = 9/4

   Некоторые иррациональные числа, например ? (пи), также могут быть выражены как рациональные числа с использованием бесконечного десятичного расширения. Например:

   ? = 3,141592653589979323846264338327950288419716939937510582097494459230781640628620898628034825421170679. Один из способов заключается в том, как они представлены, включая дроби, десятичные числа и проценты. Другой способ — по их свойствам, таким как положительность или отрицательность, а также то, являются ли они простыми числами.

   Дроби — самый распространенный тип рациональных чисел. Они создаются, когда одно число делится на другое число, в результате чего получается частное и остаток. Частное — это целая часть дроби, а остаток — десятичная часть. Например, если кто-то попросит вас разделить 7 на 3, ответ будет 2 с остатком 1 (2,333…). Следовательно, дробь 7/3 будет записана как 2 1/3.

   Десятичные числа — это еще одна форма рационального числа, которую можно легко преобразовать в дроби. Десятичное число — это просто число с десятичной точкой где-то внутри него. Например, 0,5, 1,25 и 2,75 — все десятичные числа. Все десятичные числа можно преобразовать в дроби, перемещая десятичную точку до тех пор, пока слева от нее не останется только одна цифра, и подсчитывая, сколько всего цифр, включая нули по обе стороны от исходной десятичной точки. Таким образом, 0,5 станет 5/10, потому что слева от исходной десятичной точки (0) находится одна цифра, а всего две цифры, включая нули (0 и 5). Десятичные также могут быть

   Как определить рациональные числа?

   Рациональные числа — это любые числа, которые могут быть представлены в виде дроби, где и числитель, и знаменатель являются целыми числами. Набор рациональных чисел включает в себя все целые числа, поскольку каждое целое число может быть представлено в виде дроби со знаменателем 1.

   Чтобы определить, является ли данное число рациональным, вы можете проверить, может ли оно быть представлено в виде дроби. Если можно, то это рационально. Если нет, то это не рационально.

   Например, число 3 можно выразить как 3/1, что является дробью с целым числителем и целым знаменателем. Следовательно, 3 — рациональное число. С другой стороны, число пи (3,14159…) не может быть выражено в виде дроби с целыми числами как в числителе, так и в знаменателе. Следовательно, число пи нерационально.

   Рациональные числа в десятичной форме

   Рациональные числа в десятичной форме всегда имеют конечное или повторяющееся десятичное представление. Например, 3/4 = 0,75, 8/5 = 1,6, 11/13 = 0,84615384615…9.0011

   Чтобы преобразовать рациональное число в десятичную форму, разделите числитель на знаменатель. Ответ будет либо завершающим десятичным числом (тот, который в конечном итоге заканчивается), либо повторяющимся десятичным числом (тот, в котором цифры повторяются в шаблоне).

   При записи дробей в виде десятичных дробей мы можем использовать разрядное значение в наших интересах. Значение разряда идет справа налево, начиная со столбца единиц, затем столбца десятков и так далее. Из-за этого мы можем выстроить столбцы дробей друг под другом и просто разделить прямо поперек:

   Например:
   1/4 = ?
   3/8 = ?

   1 | 4 3 | 8
   – – –
   4 | 4 8 | 8 Таким образом, 1/4 = 0,25 и 3/8 = 0,375

   Список рациональных чисел

   Рациональное число — это число, которое может быть представлено дробью p/q, где p и q — целые числа, а q ? 0. Другими словами, рациональное число — это число, которое можно представить как отношение двух целых чисел.

   Множество всех рациональных чисел обозначается Q. Ниже приведены некоторые примеры рациональных чисел:

   -3/5
   2/3
   7/4
   -10/7

   Как видите, рациональное число может быть положительным или отрицательным, быть целым или нецелым.

   Сложение и вычитание рациональных чисел

   При сложении и вычитании рациональных чисел важно помнить, что они ничем не отличаются от любых других чисел. Разница лишь в том, что их можно записать в виде дроби. Чтобы складывать или вычитать рациональные числа, нужно сначала найти ЖК. ЖК-дисплей является наименьшим общим знаменателем. Это наименьшее число, на которое можно разделить обе дроби. Когда у вас есть ЖК-дисплей, вы можете изменить каждую дробь так, чтобы они обе имели одинаковый знаменатель. Когда у них одинаковый знаменатель, вы можете складывать или вычитать их, как обычные числа.

   Умножение и деление рациональных чисел

   Рациональные числа — это любые числа, которые могут быть представлены в виде дроби, включая все целые числа. В математике дробь определяется как деление двух целых чисел, где делимое называется числителем, а делитель называется знаменателем. Например, 3/4 будет читаться как «три четверти».

   Целые числа являются рациональными числами, но не все рациональные числа являются целыми числами. Любое число, которое нельзя представить в виде дроби, является иррациональным числом. Например, ?2 (квадратный корень из 2) — иррациональное число.

   При умножении и делении рациональных чисел необходимо учитывать как числитель, так и знаменатель. Сначала рассмотрим пример умножения двух рациональных чисел:

   3/4 x 1/2 = 3/8

   В этом примере мы умножаем числители (3 и 1) вместе, чтобы получить 3, а затем умножаем знаменатели (4 и 2) вместе, чтобы получить 8. Ответ 3/8. Теперь рассмотрим пример деления двух рациональных чисел:

   1/2 ÷ 1/4 = 2/1 или 2 (ответ будет в наименьшем выражении)

   В этом примере мы делим числители (1 и 1), чтобы получить 1, а затем делим знаменатели (2 и 4), чтобы получить 2. Ответ: 2/1 или 2 (ответ будет в наименьшем выражении) .

   Рациональные и иррациональные числа

   Рациональные числа определяются как числа, которые могут быть выражены как отношение двух целых чисел. Рациональное число можно записать в виде дроби, и в этом случае оно называется обыкновенной дробью. Например, число 3 можно записать как 3/1, что является обыкновенной дробью.

   No related posts.