Онлайн построение графиков в полярных координатах: Построить график в полярных координатах на плоскости

Полярные координаты в геометрии

Полярные координаты — это альтернативный способ представления точек в пространстве. В отличие от декартовых координат, которые используют пару перпендикулярных осей (оси x и оси y) для точного определения местоположения, полярные координаты выражают точки с помощью одной радиальной оси (ось r) и оси вращения (тета-ось). ось).

 

Полярные координаты могут быть полезны для построения графиков некоторых типов функций или для представления точек в пространстве, которые не подходят для традиционных осей x и y. Например, траекторию снаряда легче представить с помощью полярных координат, чем декартовых. В этом сообщении блога мы более подробно рассмотрим, как работают полярные координаты и как их можно использовать для построения графиков точек и функций.

 

Как работают полярные координаты

 

Как мы упоминали ранее, каждая полярная координата состоит из двух компонентов: радиальной координаты (r) и угловой координаты (тета).

Радиальная координата соответствует расстоянию от начала координат (0,0), а угловая координата соответствует углу между положительной осью x и отрезком линии, соединяющим точку с началом. Этот угол измеряется в градусах или радианах; чаще всего радианы используются в математических и физических приложениях.

 

Один из способов представить это так: радиальная координата соответствует тому, насколько «далеко» находится точка от начала координат, а угловая координата соответствует тому, в каком «направлении» находится эта точка от начала координат. Давайте рассмотрим пример, чтобы увидеть, как это работает на практике.

 

Пример: преобразование декартовых координат в полярные

 

Предположим, у нас есть точка (3,4). Чтобы преобразовать эту точку из декартовых координат в полярные координаты, нам нужно вычислить радиальную координату и угловую координату. 92)

 

р = 5

 

Теперь нам нужно вычислить угловую координату.

Напомним, что это угол между положительной осью x и отрезком, соединяющим точку с началом координат. Мы можем использовать тригонометрию, чтобы вычислить это:

 

тета = арктан((4-0)/(3-0))

 

тета = 53,13 градуса

 

Следовательно, полярные координаты точки нашего примера равны (5, 53,13 градуса).

 

Графические точки в полярных координатах

 

Теперь, когда мы знаем, как преобразовывать декартовы координаты в полярные, давайте посмотрим, как наносить точки на график с использованием полярных координат.

 

Существует два распространенных способа графического отображения точек в полярных координатах. Первый называется «прямоугольным методом», и это просто вопрос построения точки с соответствующими значениями r и тета. Итак, для точки нашего примера (5, 53,13 градуса) мы нанесем на график точку (5,53,13).

 

Второй метод называется «полярным методом». Чтобы использовать этот метод, мы начинаем с построения начала координат (0,0). Затем мы используем линейку, чтобы нарисовать отрезок линии от начала координат наружу под углом, соответствующим тета. Наконец, мы измеряем длину этого отрезка и отмечаем его в точке, соответствующей r.

 

Для точки нашего примера (5, 53,13 градуса) полярный метод будет выглядеть так:

 

Начнем с построения начала координат (0,0).

 

Далее мы проводим отрезок от начала координат под углом 53,13 градуса.

 

Наконец, мы измеряем длину этого отрезка и отмечаем его на уровне 5 единиц. Это дает нам нашу точку (5, 53,13 градуса).

 

Полярные координаты и графики функций

 

Мы также можем использовать полярные координаты для графических функций. Для этого мы просто наносим ряд точек, удовлетворяющих уравнению функции, а затем соединяем эти точки плавной кривой.

 

Давайте рассмотрим пример.

 

Пример: построение графика функции в полярных координатах

 

Предположим, мы хотим построить график следующей функции в полярных координатах:

 

r = 2 + cos(тета)

 

Для этого нам нужно вычислить несколько точек, удовлетворяющих уравнению, а затем нанести эти точки на график. Начнем с поиска трех точек, удовлетворяющих уравнению.

 

Если мы установим тета = 0, мы получим r = 2 + cos(0) = 2 + 1 = 3. Итак, наша первая точка — (3, 0).

 

Если мы установим theta = pi/2, мы получим r = 2 + cos(pi/2) = 2 + 0 = 2. Итак, наша вторая точка (2, pi/2).

 

Если мы установим theta = pi, мы получим r = 2 + cos(pi) = 2 — 1 = 1. Итак, наша третья точка это (1, pi).

 

Теперь, когда у нас есть три точки, мы можем нанести их на график и соединить плавной кривой. Это дает нам следующий график:

 

Как видите, это довольно простой график. Однако мы также можем использовать полярные координаты для построения графиков более сложных функций.

 

Полярные координаты — очень полезный инструмент в математике, и их можно использовать для построения графиков самых разных функций. Надеюсь, это введение дало вам хорошее представление о том, как они работают и как их использовать.

Полярные координаты — узнайте и поймите это онлайн

Представьте, что вы с другом направляетесь к кофейне в центре большого города. Глядя на карту, ваш друг говорит, что вы находитесь примерно в \(1\) миле (\(1,61 км\)) к юго-западу от кофейни. Вы смотрите на ту же карту и видите, что находитесь в \(4\) кварталах поперек и \(4\) кварталах вниз от кофейни.

Рисунок 1. Схема расположения кофейни

В этом сценарии вы и ваш друг обмениваетесь одинаковой информацией о том, где вы находитесь относительно кофейни. Разница в том, что, в то время как вы использовали прямоугольную систему координат или декартовых координат , ваш друг использовал полярную систему координат . В этой статье будут представлены полярные координаты, как отображать полярные координаты на графике, как преобразовывать полярные координаты в прямоугольные, а также обобщения полярных координат в трех измерениях.

Полярная система координат

Вероятно, вы привыкли говорить о точках на плоскости, ссылаясь на их координаты \(x\) и \(y\). Эта система маркировки точек называется прямоугольной системой координат , также известной как декартовых координат .

Рис. 2. Прямоугольная система координат

Полярные координаты — это просто другой способ обозначения точек на плоскости. Вместо использования координат \(x\) и \(y\) полярная система координат помечает точки по их удалению от начала координат \(r\) и их углу \(\theta\) по отношению к положительной оси \(x\), измеренному против часовой стрелки. Этот угол \(\theta\) обычно измеряется в радианах.

Ниже в этой статье вы можете узнать, как конвертировать градусы в радианы, если вы забыли!

Рис. 3. Полярная система координат

В принципе, как угол \(\theta\), так и радиальное расстояние \(r\) может принимать любое действительное значение. На практике значения \(r\) выражаются с использованием только неотрицательных значений, то есть

\[ r \in [0,\infty). \]

Если \(r\) равно нулю, то независимо \(\theta\), точка \((r,\theta)\) находится на полюсе.

Рис. 4. Начало, или полюс, в полярных координатах

Обычным соглашением является выражение \(\theta=0\), чтобы избежать двусмысленности.

Как упоминалось ранее, \(r\) может принимать отрицательные значения, но обычно это не выражается так. Вместо записи точки \((-r,\theta)\) с отрицательной координатой \(r\) вы записываете отражение точки \((r,\theta)\), добавляя \(\pi\ ) до угла.

Рисунок 5. Точка и ее отражение в полярных координатах

Угловая координата \(\theta\) обычно выражается с помощью значений между \(0\) и \(2\pi\), то есть

\[ \theta \in [0,2\pi].\]

Так же, как и радиальная координата, также возможно получить точку \((r,-\theta)\) с отрицательным значением \(\theta \) координата. Вы можете получить эту точку, повернув по часовой стрелке от положительной оси x на \(\theta\) вместо против часовой стрелки.

Рис. 6.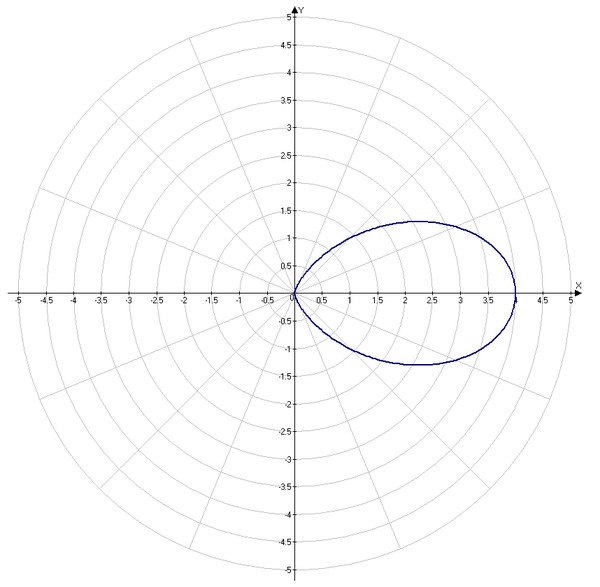 Две точки с противоположными знаками \(\theta\)

Полярные и декартовы координаты неявно вводят понятие различных метрик и различных способов говорить о расстоянии. Возвращаясь к нашему сценарию с кофейней, вы можете либо сказать, что вы и ваш друг находитесь в \(8\) кварталах от кофейни (4 квартала в ширину и \(4\) кварталов вниз), либо вы \(1\ ) мили (\(1,61 км\)) от кофейни. Оба понятия расстояния имеют свои преимущества. «Кварталное расстояние», называемое метрикой такси , говорит вам, сколько вам нужно пройти, чтобы добраться до кафе, если вы вынуждены оставаться на тротуаре. «Диагональное расстояние», или Евклидова метрика показывает вам кратчайший путь, который вы могли бы выбрать, чтобы добраться до кофейни, при условии, что вы можете пересекать городские кварталы по диагонали.

Метрики и связанные с ними метрические пространства становятся все более важными по мере того, как вы продолжаете изучать математику и находите невероятное практическое применение в различных областях, от науки о данных до обработки сигналов и квантовой механики.

Терминология полярных координат

Существует несколько терминов, которые важно знать при работе с полярными координатами. Точка, которую мы называем начало координат при работе с прямоугольными координатами называется полюсом при работе с полярными координатами. То, что мы называем осью x при работе с прямоугольными координатами, называется полярной осью при работе с полярными координатами.

Полярная ось также известна как опорное направление .

Расстояние от начала координат, обозначаемое как координата \(r\), также упоминается как радиус , радиальная координата или радиальное расстояние . Координата \(\theta\) называется угловой координатой , полярным углом или азимутом .

Таблица 1. Терминология, используемая в полярных координатах

Градусы и

Имя (ы) в прямоугольных координатах	Имя (S) в полярных координатах
Origin	44845424542454545424545454245424545454545424542454545454545424542454245424542454545424542454245424542454245424245424542424542454242424245424542454. \)-ось	Полярная ось или опорное направление
Расстояние от начала координат	Радиальная координата, радиус или радиальное расстояние
Угол против часовой стрелки от положительной оси \(x\)	Угловая координата, полярный угол или азимут

3 902 Радианы

Угловая координата \(\theta\) обычно задается либо в градусах, либо в радианах. Градусы и радианы — это просто разные способы измерения углов.

Алгебраически соотношение между градусами и радианами выглядит следующим образом: 9{\circ}\) можно записать в радианах. Используя преобразование

\[k\text{градусы} = \dfrac{k\pi}{180}\text{ радианы}, \]

вы получите

\[ \begin{align} 30\text {градусы} &= \dfrac{30\pi}{180}\text{радианы} \\ &= \dfrac{\pi}{6}\text{радианы}. \end{align}\]

И наоборот, угол \(\tfrac{\pi}{4}\) радиан можно записать в градусах. Используя преобразование

\[k\pi\text{ радианы} = 180k \text{градусы}, \]

вы получите это

\[\begin{align} \frac{\pi}{4}\text{радианы} &= \frac{1 \, \pi \text{радианы}}{4} \\ & = \dfrac{180\text{ градусов}}{4} \\ &= 45 \text{ градусов}. \end{align}\]

Множественные представления точек в полярных координатах

Одним из интересных аспектов работы с полярными координатами является то, что каждая точка имеет бесконечное множество полярных координат, описывающих ее. Вы заметили это ранее для полюса, который, как мы сказали, представлен \((0,\theta)\) для любого значения \(\theta\). Например, координаты \((0,0)\), \((0,-\pi)\) и \(\left(0,\tfrac{\sqrt{\pi}}{17}\right )\) все представляют полюс.

Стоит отметить, что этого многозначного представления обычно избегают и координаты показывают в диапазоне

\[ r \in [0,\infty)\]

и

\[ \theta \in [0, 2\pi).\]

Однако для некоторых специальных сценариев, таких как описание движения в физике, эти области расширяются, так что обе включают все действительные числа.

В общем случае точки \((r,\theta)\) и \((r,\theta+2n\pi)\) для любого целого числа \(n\) описывают одну и ту же точку. Точки \((-r,\theta)\) и \((r,\theta+m\pi)\), где \(m\) — нечетное целое, также опишите ту же точку.

Геометрически \((r,\theta)\) и \((r,\theta+2n\pi)\) представляют одну и ту же точку, поскольку добавление \(2n\pi\) соответствует повороту точки на \( 2n\pi\) радиан или кратное 360 градусам. Вращение на число, кратное \(2\pi\), фактически не меняет положение точки, поэтому \((r,\theta)\) и \((r,\theta+2n\pi)\) представляют собой тот же пункт.

Рис. 7. Несколько изображений одной и той же точки в полярных координатах

Координаты \(\left(1,\tfrac{\pi}{4}\right)\) и \(\left(1,\tfrac{9\pi}{4}\right)\) описывают та же точка с

\[ \begin{align} \frac{9\pi}{4} &=\frac{\pi}{4}+\frac{8\pi}{4}\\ &=\frac {\пи} {4}+2\пи. \end{align}\]

Аналогично, координаты \(\left(-10,\tfrac{5\pi}{6}\right)\) и \(\left(10,\tfrac{11\pi {6}\right)\) описывают одну и ту же точку, поскольку

\[\begin{align} \frac{11\pi}{6} &= \frac{5\pi}{6}+\frac{ 6\pi}{6} \\ &=\frac{5\pi}{6}+\pi. \конец{выравнивание}\] 9{-1}{\left( \frac{y}{x}\right)}.\]

Чтобы увидеть, откуда взялись эти формулы, скажем, вам дана точка \((x,y)\) в прямоугольной координаты, и вы хотите знать соответствующие полярные координаты \((r,\theta)\).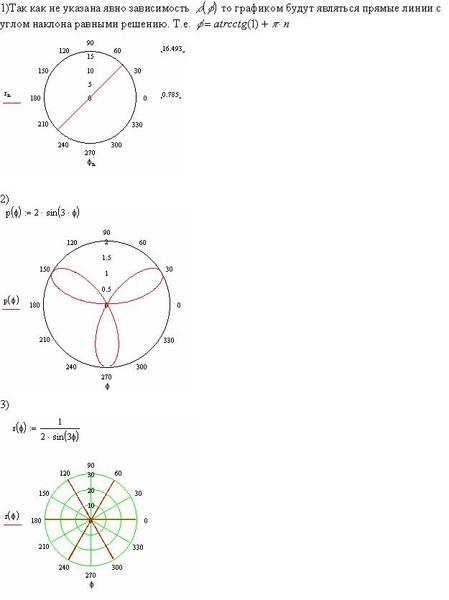 Если бы вы построили точку на графике, вы бы получили что-то вроде следующего изображения.

Рис. 8. Точка на плоскости, представленная в полярных и прямоугольных координатах

Вы можете использовать известные факты о прямоугольных треугольниках, чтобы записать отношения между \(\тета\). Во-первых, обратите внимание, что вы можете использовать теорему Пифагора, чтобы записать 92}.\]

Вы также можете использовать тот факт, что тангенс угла \(\theta\) в прямоугольном треугольнике является отношением его противоположной стороны к прилежащей, так что вы можете написать

\[ \ tan{\theta} = \frac{y}{x}.\]

Теперь вы можете использовать функцию арктангенса, чтобы изолировать \(\theta\), то есть

\[ \theta = \arctan{\left ( \frac{y}{x}\right)}.\]

Точка

\[ P=(3, 4)\]

задана в декартовых координатах. Запишите \(P\) в полярных координатах. 92} \\ &= \sqrt{ 9 +16} \\ &= \sqrt{25} \\ &= 5. \end{align}.\]

Затем найдите угол, используя

\[\ theta = \arctan{\left(\frac{y}{x}\right)}\]

с помощью калькулятора, то есть

\[ \begin{align} \theta &= \arctan{\ frac{y}{x}} \\ &= \arctan{\left(\frac{4}{3} \right)} \\ &= 0,9272. \end{align} \]

Помните, что этот угол обычно дается в радианах, поэтому убедитесь, что ваш калькулятор использует их!

Это означает, что точка \(P\) в полярных координатах равна

\[ P =(5,0.9272).\]

Поскольку вам нужно использовать функцию арктангенса, чтобы найти угол \(\theta\), лучше обсудить это немного подробнее.

Тангенс и арктангенс

При использовании формулы

\[\theta=\arctan{\left(\frac{y}{x}\right)},\]

вы должны знать некоторые технические детали, связанные с функции тангенса и арктангенса.

Во-первых, обратите внимание, что это выражение не определено, когда \(x=0\). В этом случае точка \((x,y)\) должна лежать на оси \(y\). Таким образом, \(\theta\) должно быть либо \(\tfrac{\pi}{2}\), либо \(-\tfrac{\pi}{2}\), в зависимости от того, положительно ли \(y\) или отрицательный.

Рисунок 9. Две точки в полярных координатах, когда \(x=0\)

Далее, для любого \(\tfrac{y}{x}\) на самом деле есть два значения \(\theta\) в \([-\pi,\pi]\), удовлетворяющие \(\tan(\theta)=\tfrac{y}{x}\).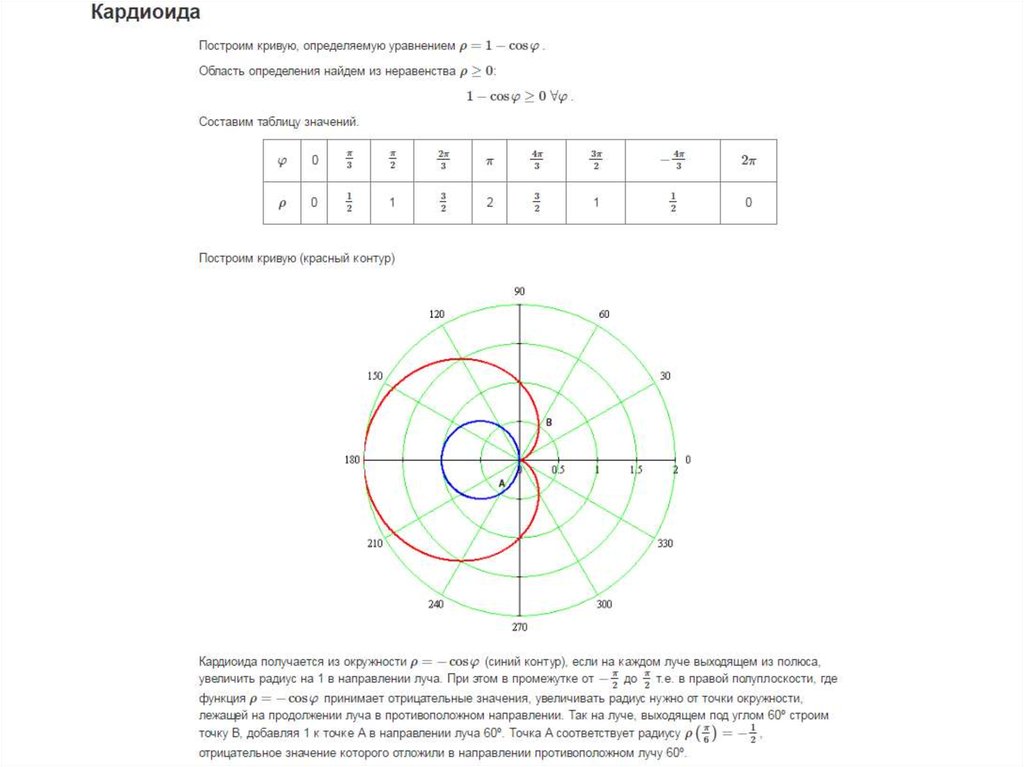

Даны \(y=1\) и \(x=1\), оба угла \(\tfrac{\pi}{4}\) и \(-\tfrac{3\pi}{4}\ ) удовлетворяют этому

\[ \begin{align} \tan\left(\dfrac{\pi}{4}\right) &=\tan\left(-\dfrac{3\pi}{4}\right) \\ &=\dfrac{y}{x} \\ &=\dfrac{1}{1} \\&=1. \конец{выравнивание}\]

Обратите внимание, что эти углы являются отражением друг друга; это всегда так.

Чтобы убедиться, что вы указываете правильную точку при записи точки в полярных координатах, вы должны убедиться, что угол \(\theta\), который вы используете, находится в правильном квадранте. Функция арктангенса возвращает только углы между \(-\tfrac{\pi}{2}\) и \(\tfrac{\pi}{2}\), поэтому \(\arctan\left(\tfrac{y}{ x}\right)\) возвращает правильное значение для \(\theta\) только в том случае, если точка \((x,y)\) находится в первом или четвертом квадранте.

Рисунок 10. График функции арктангенса

Кроме того, поскольку значения \(\theta\) обычно даются между \(0\) и \(2\pi\), вам также необходимо выполнить коррекцию, если угол вы получаете от калькулятора отрицательно. В следующей таблице показано, как найти \(\theta\).

Таблица 2. Связь между знаком \(x\) и углом \(\theta\)

Квадрант	Знак \(x\)	Знак \(y\)	\(\тета\)
I	\(+\)	\(+\)	\(\theta=\arctan\left(\dfrac{y}{x}\right)\)
II	\(-\)	\(+\)	\(\theta=\arctan\left(\dfrac{y}{x}\right)+\pi\)
III	\( -\)	\(-\)	\(\theta=\arctan\left(\dfrac{y}{x}\right)+\pi\)
IV	\(+\)	\(-\)	\(\theta=\arctan\left(\dfrac{y}{x}\right)+2\pi\)

Рассмотрим точку \( P= (-2,1) \).

1. В каком квадранте находится \(P\)?
2. Найдите его координату \(r\).
3. Найдите его координату \(\theta\).

Решение:

1. Поскольку координата \(x\) отрицательна, а ее координата \(y\) положительна, точка \(P\) лежит во втором квадранте (II) . 2} \\&= \sqrt{4+1} \\&= \sqrt{5}.\end{align} \]
2. Вы только что обнаружили, что \(P\) находится во втором квадранте, поэтому используйте калькулятор и найдите, что \[\begin{align} \theta &= \arctan{\left( \frac{1}{-2} \right)}+\pi \\ &= \arctan{\left(-0,5\right)}+\pi \\ &= -0,463647+3,141592 \\ &= 2,677945.\end{align}\]

Как преобразовать полярные координаты в прямоугольные

Теперь предположим, что вам дана точка в полярных координатах, и вы хотите знать, как выразить эту точку, используя прямоугольные координаты. В этом случае вы также можете использовать ту же диаграмму прямоугольного треугольника, которая связывает \(x\), \(y\), \(r\) и \(\theta\).

Рис. 11. Точка на плоскости, представленная в полярных и прямоугольных координатах

Фокус на угле \(\theta\). Поскольку у вас есть прямоугольный треугольник, вы можете записать синус угла как:

\[ \sin{\theta} = \frac{y}{r}\]

Аналогично, косинус угла равен:

\[ \cos{\theta} = \frac{x}{r}\]

Решение каждого выражения для \(x\) и \(y\) даст вам:

\[ x=r\, \cos{\theta}\]

и

\[y=r\,\sin{\theta}\]

В отличие от перехода от прямоугольных координат к полярным, приведенные выше выражения не требуют от вас каких-либо особых соображений.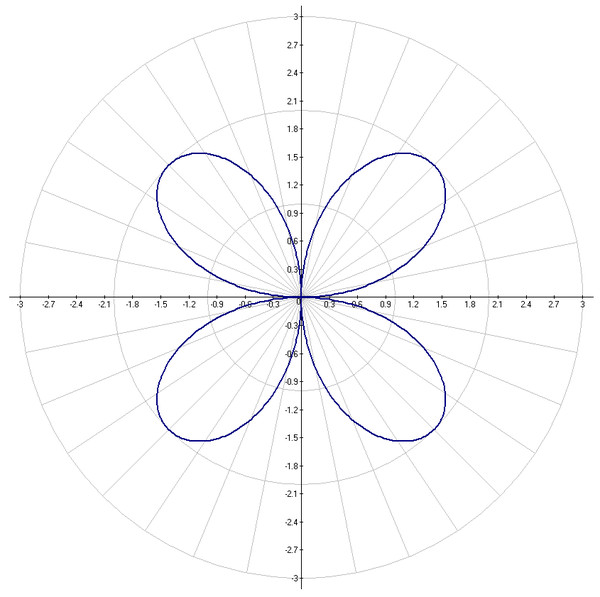 Это настолько просто, насколько это возможно!

Ранее вы обнаружили, что точка \(P=(-2,1) \) имеет:

\[ r = \sqrt{5}\]

и

\[ \theta = 2.677945 \]

Убедитесь, что приведенные выше значения верны.

Решение:

Чтобы найти координату \(x\), используйте:

\[ x = r \, \cos{\theta},\]

поэтому используйте калькулятор и найдите:

\[ \begin{align} x &= \sqrt{5} \cdot \cos{2.677945} \\ &= -2. \end{align}\]

Вместо \(y\)-координаты используйте:\[ y = r\, \sin{\theta}\]

, то есть

\[ \begin{align} y &= \sqrt{5} \cdot \sin{2.677945} \\ &= 1. \end{align}\]

Приведенные выше значения являются точно прямоугольными координатами точки \(P\).

Полярные координатные самописцы

Вы можете использовать несколько электронных ресурсов для отображения точек в полярных координатах. Например, в Geogebra можно изобразить точку \((r,\theta)\), набрав \((r;\theta)\). Многие графические калькуляторы также позволяют отображать точки с использованием полярных координат, как и программы и языки программирования, такие как Python, Octave и Matlab. Для получения информации о том, как графически отображать полярные кривые, см. статью Полярные кривые.

Примеры преобразования полярных координат в прямоугольные координаты

Здесь вы можете посмотреть примеры конвертации между обеими системами координат!

Примеры преобразования прямоугольных координат в полярные

Для этих примеров предположим, что вам дана точка в прямоугольных координатах, и вы хотите, чтобы она была записана в полярных координатах.

Преобразование точки \[ P= \left(-2\sqrt{3},-2\right)\]

из прямоугольных в полярные координаты.

Решение:

Во-первых, обратите внимание, что эта точка находится в третьем квадранте, так как и \(x\), и \(y\) отрицательны. 92} \\ &=\sqrt{4(3)+4} \\ &= \sqrt{12+4} \\ &= \sqrt{16}\\ &=4.\end{align}\]

Далее найдите тета. Поскольку точка находится в третьем квадранте, вам нужно будет использовать \[\theta=\arctan\left(\frac{y}{x}\right)+\pi,\]

, то есть

\[\begin {align}\theta&=\arctan\left(\frac{-2}{-2\sqrt{3}}\right)+\pi \\ &=\arctan\left(\dfrac{1}{\sqrt{ 3}}\right)+\pi \\ &=\dfrac{\pi}{6}+\pi \\ &=\dfrac{7\pi}{6}. \end{align}\]

Таким образом , точка \(\left(-2\sqrt{3},-2\right)\) в полярных координатах равна \(\left(4,\tfrac{7\pi}{6}\right)\). 92} \\ &= \sqrt{\dfrac{9\cdot2}{4}+\dfrac{9\cdot2}{4}} \\ &=\sqrt{\dfrac{9}}{2}+\dfrac{ 9}{2}}\\ &=\sqrt{9} \\ &=3.\end{align}\]

Ранее вы обнаружили, что точка находится в четвертом квадранте, поэтому вам нужно будет использовать

\[ \theta = \arctan{\left( \frac{y}{x} \right)}+2\pi.\]

Прежде чем продолжить, обратите внимание, что значения \(x\) и \(y\) одинаковые, только с противоположными знаками. Это означает, что

\[ \frac{y}{x}=-1,\]

, поэтому вам не нужно записывать всю огромную дробь, так как она упростится до \(-1\). Зная это,

\[ \begin{align} \theta &= \arctan{-1}+2\pi \\ &= -\frac{\pi}{4}+2\pi \\ &= \frac{7\ pi}{4}.\end{align}\]

Это означает, что точка \(Q\), записанная в полярных координатах, равна

\[ Q = \left(3, \frac{7\pi}{4 }\right).\]

Примеры преобразования полярных координат в прямоугольные

В следующем примере предположим, что вам дана точка в полярных координатах, и вы хотите знать, как она записывается в прямоугольных координатах.

Конвертировать точку

\[\left(4,-\tfrac{\pi}{3}\right)\]

из полярных координат в прямоугольные.

Решение:

Начните с нахождения \(x\) по формуле \(x=r\cos(\theta)\).

\[\begin{align} x&=4\cos\left(-\dfrac{\pi}{3}\right) \\ &= 4\left(\dfrac{1}{2}\right) \ \ &=2.\end{align}\]

Затем найдите \(y\), используя формулу \(y=r\sin(\theta)\).

\[\begin{align} y&=4\sin\left(-\dfrac{\pi}{3}\right) \\ &= 4\left(-\dfrac{\sqrt{3}}{2 }\right) \\ &=-2\sqrt{3}.\end{align}\]

Итак, точка \(\left(4,-\tfrac{\pi}{3}\right)\) в декартовых координатах равна \((2,-2\sqrt{3})\).

Вот последний пример.

Преобразование точки

\[\left(5,\tfrac{3\pi}{4}\right)\]

из полярных координат в прямоугольные.

Решение:

Сначала найдите \(x\) по формуле \(x=r\cos(\theta)\).

\[\begin{align} x&=5\cos\left(\dfrac{3\pi}{4}\right) \\ &= 5\left(-\dfrac{\sqrt{2}}{2 }\right) \\ &=-\dfrac{5\sqrt{2}}{2}.