Что такое развернутый угол: определение, свойства, пример задачи
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Что такое развернутый угол
В данной публикации мы рассмотрим, что такое развернутый угол, перечислим его основные свойства, а также разберем пример задачи по этой теме.
- Определение развернутого угла
- Свойства развернутого угла
- Пример задачи
Определение развернутого угла
Угол является развернутым, если его градусная мера равняется 180 градусам.
Т.е. стороны угла образуют прямую.
Свойства развернутого угла
1. Луч, берущий начало в вершине развернутого угла, делит его на два угла, которые называются смежными.
- точка O – вершина угла;
- α и β – смежные углы.
2. Биссектриса развернутого угла делит его на два угла по 90° (т.е. прямых).
α = β = 90°
3. Если луч, который делит развернутый угол, не является его биссектрисой, то один из образованных углов меньше 90° (острый), а другой находится в промежутке от 90° до 180° (тупой).
Пример задачи
Дан развернутый угол, поделенный лучом на два угла, один из которых в три раза больше другого. Найдем градусные меры этих углов.
Решение
Пусть меньший угол будет “x”, тогда больший равен “3x”. Сумма этих углов равняется 180 градусам. Составим соответствующее уравнение и решим его:
x + 3x = 180
4x = 180
x = 180 : 4 = 45
Таким образом, первый угол равен 45°, а второй – 135° (45° умножаем на 3).
Проверка: 45° + 135° = 180° (верно).
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Угол называется развернутым если его стороны.
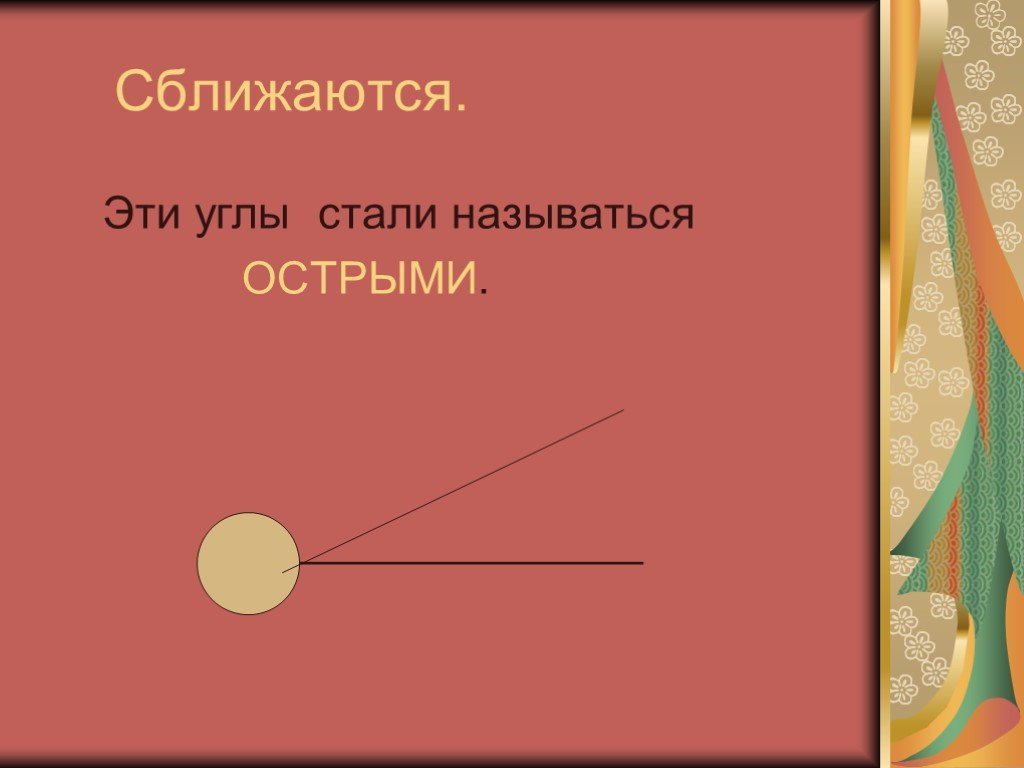 Развернутый угол в геометрии
Развернутый угол в геометрииДавайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о.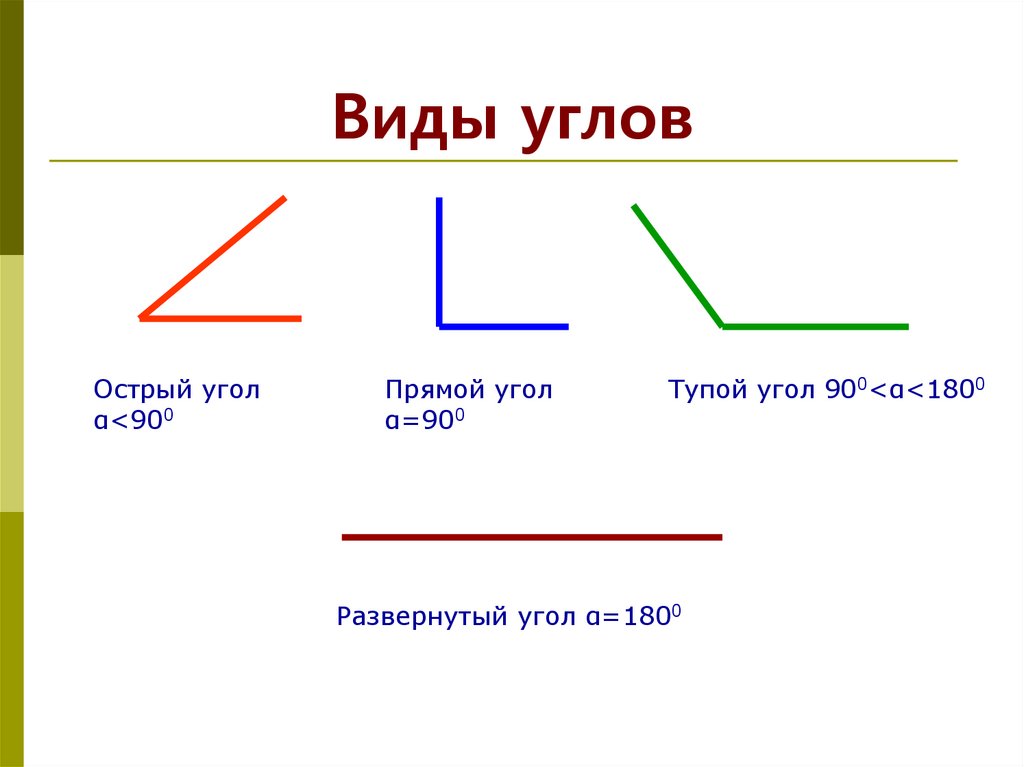 Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О.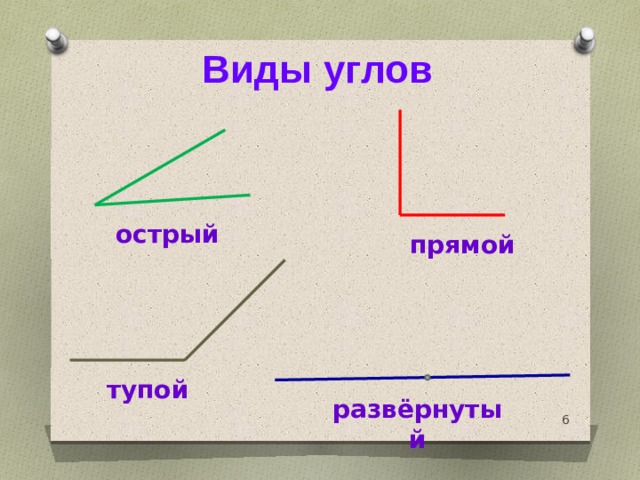
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 ABC = MNK.
Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Прямой и развернутый угол
Два дополнительных друг другу
 164).
164).Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Чертежный треугольник
Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.
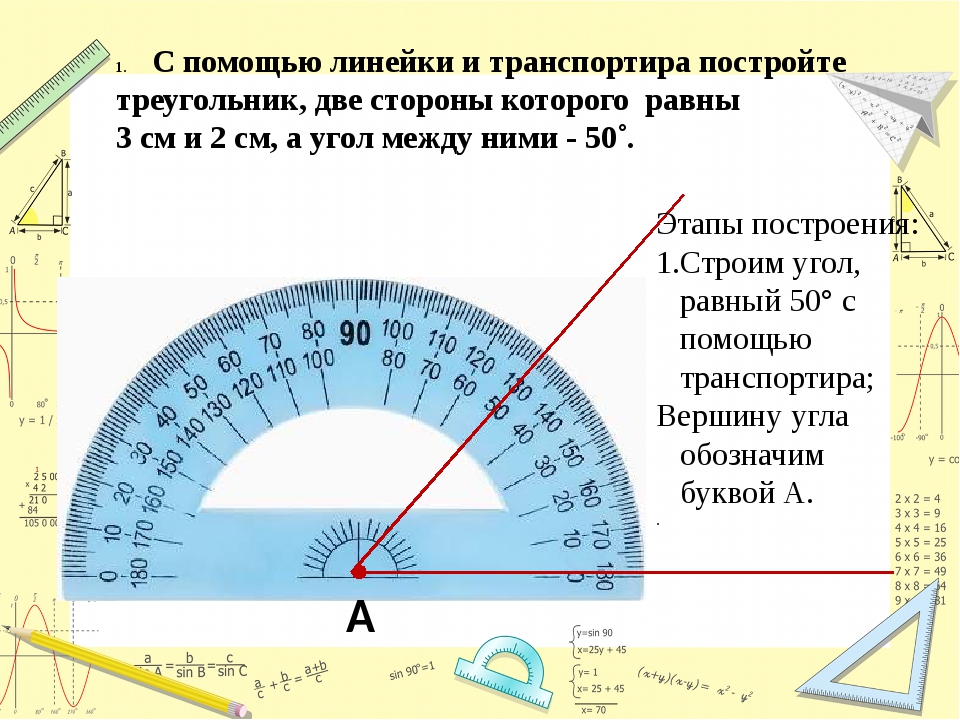
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид: « ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°.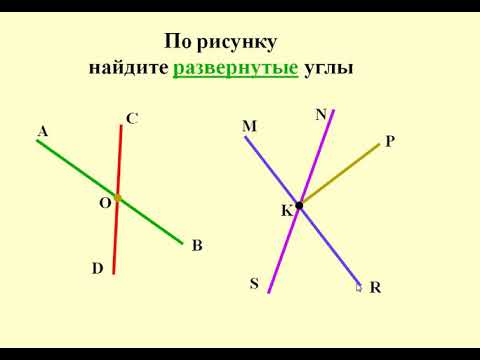 Это и есть развернутый угол.
Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ?
1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.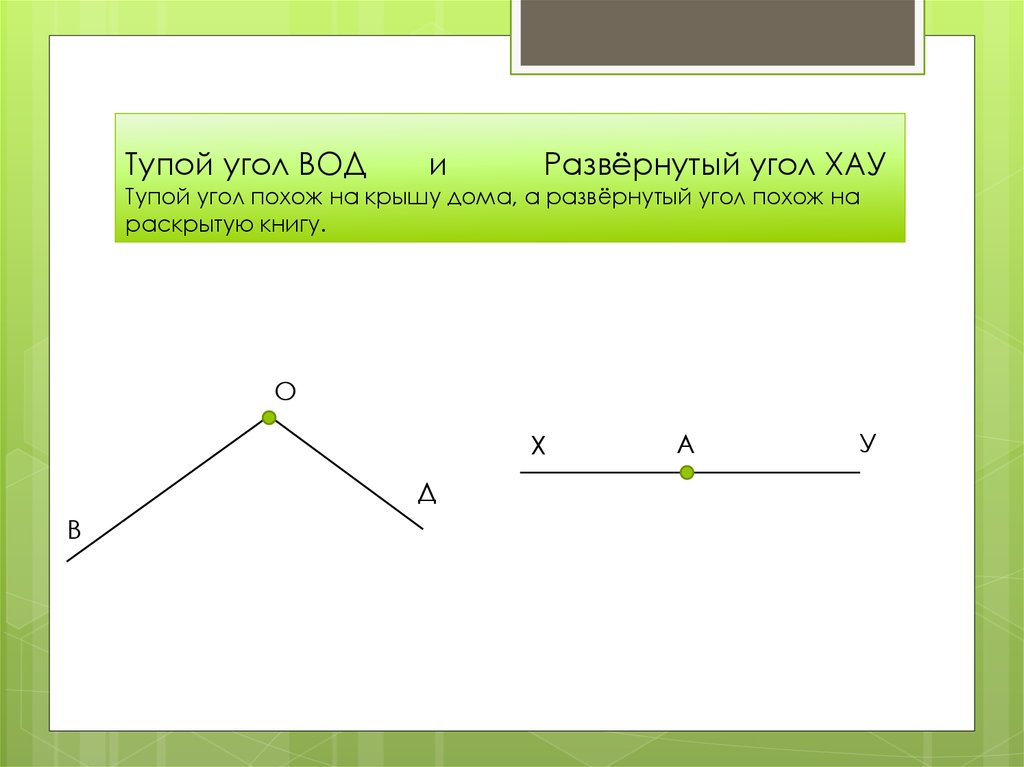
1620. Укажите прямые углы в классной комнате.
а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85;
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК?
1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791: а + 160,961: b, если а = 100, b = 10;
б) 361,62с + 1848: d, если с = 100, d =100.
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
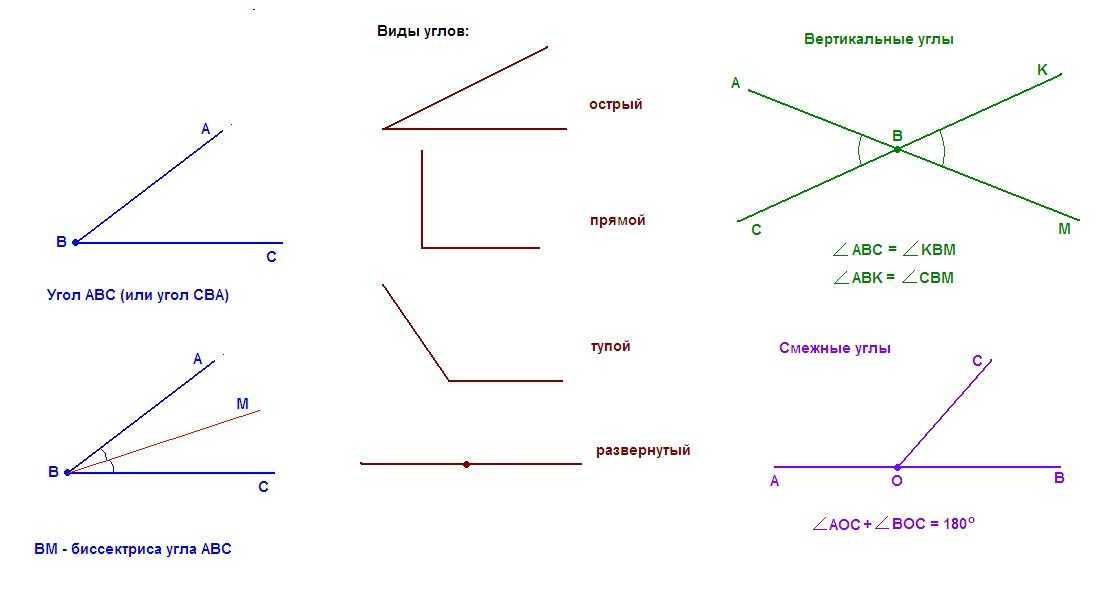
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.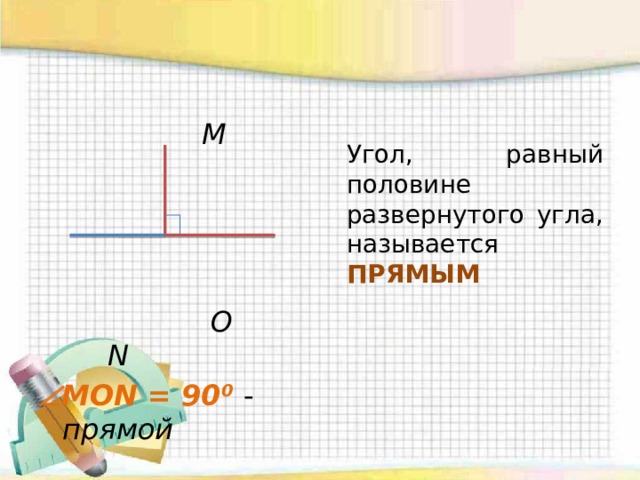
Развернутый и неразвернутый угол
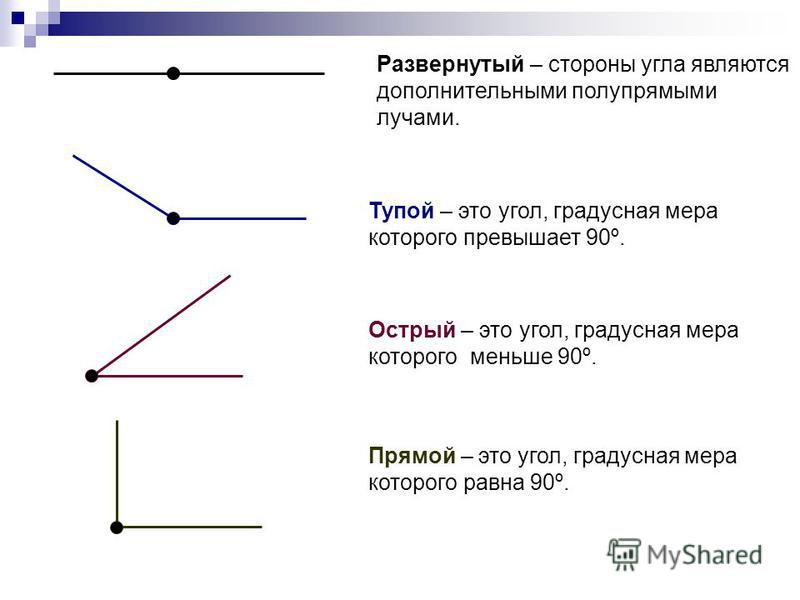
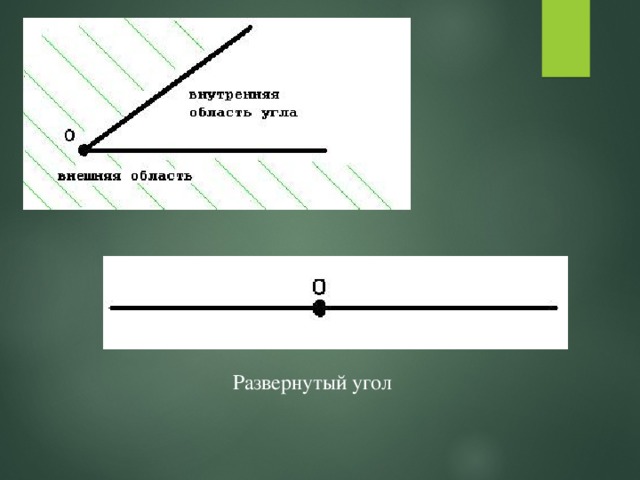
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость.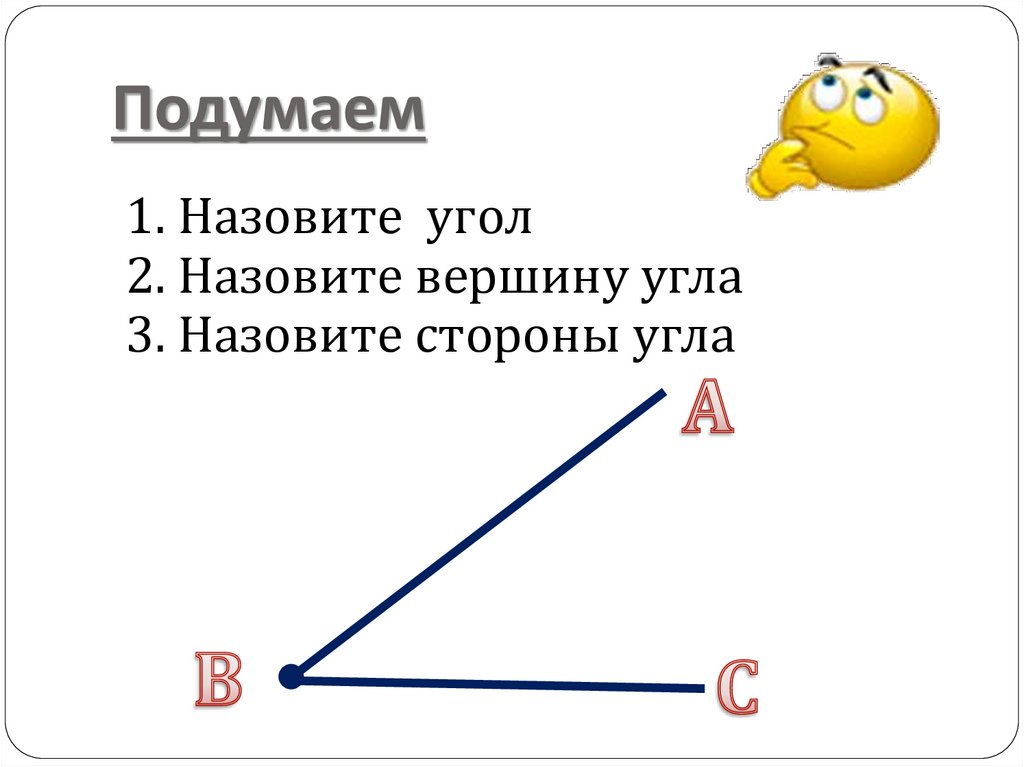 Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.

- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов.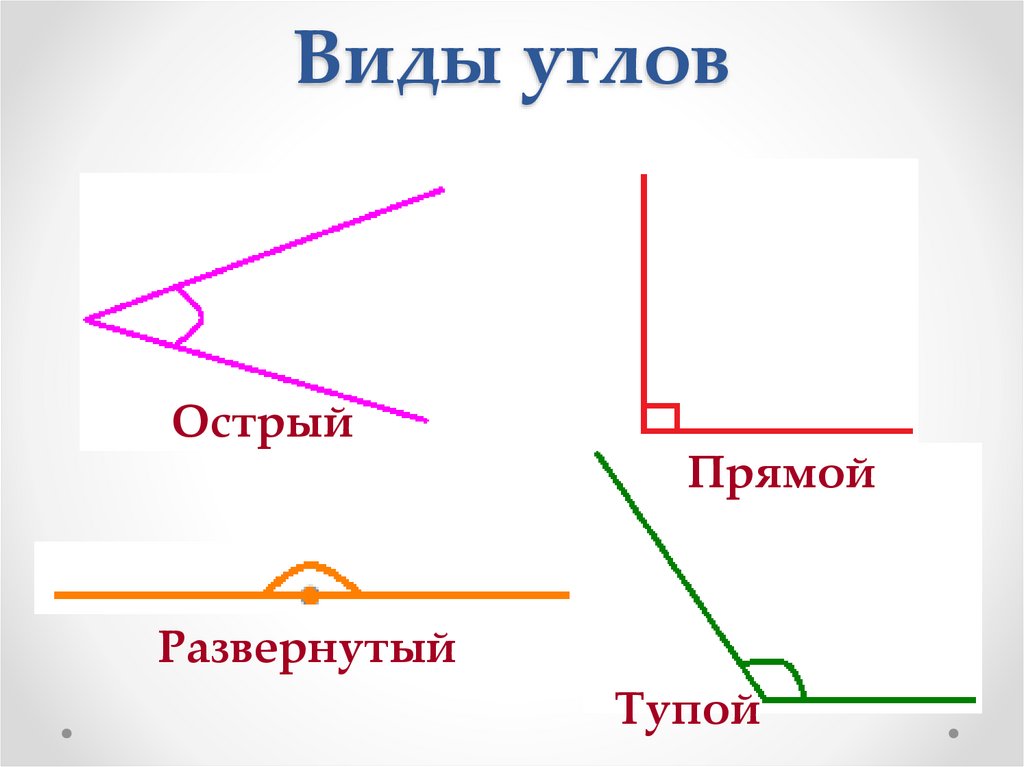 Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.
- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х.
 Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
Угол vs угол: в чем разница?
При использовании в качестве существительных , угол означает фигуру, образованную двумя лучами, исходящими из одной точки (плоский угол) или тремя пересекающимися плоскостями (телесный угол), тогда как угол означает точку, в которой сходятся два линии встречаются.
При использовании в качестве глаголов , угол означает поставить (что-то) под углом, тогда как угол означает загнать (кого-то) в угол или другое замкнутое пространство.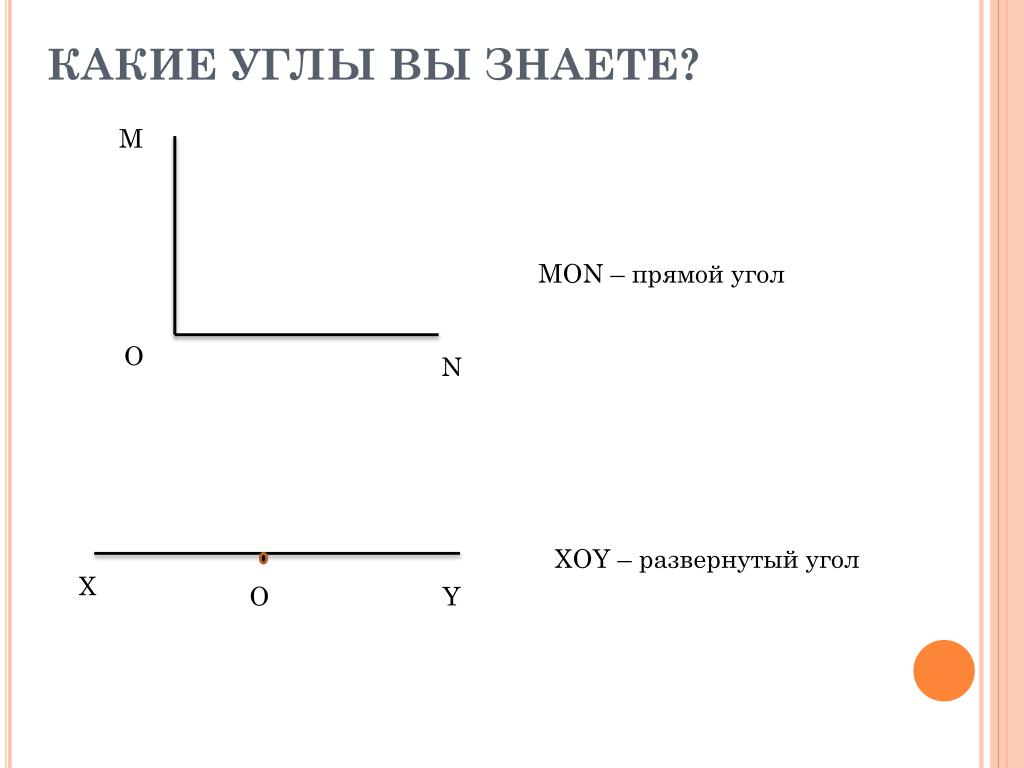
другие определения Угол и Угол
см. ниже.Угол как существительное (геометрия) :
Фигура, образованная двумя лучами, исходящими из одной точки (плоский угол), или тремя пересекающимися плоскостями (телесный угол).
Примеры:
«угол между линиями А и В»
Угол как существительное (геометрия) :
Мера такой фигуры. В случае плоского угла это отношение (или пропорциональное отношению) длины дуги к радиусу сечения круга, пересекаемого двумя лучами с центром в их общей точке. В случае телесного угла это отношение площади поверхности к квадрату радиуса сечения сферы.
Примеры:
«Угол между линиями A и B составляет π/4 радиана или 45 градусов.
 »
»Угол как существительное :
Угол, где пересекаются две стены.
Примеры:
«угол здания»
Угол как существительное :
Изменение направления.
Примеры:
«Лошадь взлетела под углом.»
Угол как существительное :
Точка обзора; способ смотреть на что-л.
Угол как существительное (медиа) :
В центре внимания новости.

Угол как существительное (сленг, профессиональная борьба) :
Сюжетная линия между двумя борцами, показывающая предысторию и подход к вражде.
Угол как существительное (сленг) :
Скрытый мотив; план или способ извлечения выгоды из ситуации, обычно скрытый, часто аморальный
Примеры:
«Его суть в том, что он получает процент, но в основном в торговле.»
Угол как существительное :
Выступающий или острый угол; угловатый фрагмент.

Угол как существительное (астрология) :
Любая из четырех сторон света астрологической карты: Асцендент, Середина Неба, Десцендент и Имум Коэли.
Угол как глагол (переходный, часто в [[пассивном]]) :
Поместить (что-то) под углом.
Примеры:
«Крыша наклонена под углом 15 градусов.»
Угол как глагол (непереходный, неформальный) :
Быстро изменить направление.

Примеры:
«Пятёрка отклонилась от девятки, но не попала в лузу».
Угол как глагол (переходный, неформальный) :
Представлять или аргументировать что-то определенным образом или с определенной точки зрения.
Примеры:
«Как вы хотите это повернуть, когда мы разговариваем с клиентом?»
Угол как глагол (переходный, биток спортивный) :
Мешать (себе или противнику), оставляя биток в пасти лузы таким образом, чтобы окантовка лузы («угол») преграждала путь от битка к прицельному шару.
Примеры:
Угол как глагол (непереходный) :
Пытаться поймать рыбу на крючок и леску.

Угол как глагол (неофициальный) :
(с for) Попытка тонко убедить кого-то предложить желаемую вещь.
Примеры:
«Должно быть, он добивается повышения зарплаты.»
Угол как существительное :
Рыболовный крючок; снасть для ловли рыбы, состоящая из лески, крючка и наживки, с удочкой или без нее.
Угол как существительное :
Точка, где встречаются две сходящиеся линии; угол, внешний или внутренний.
 Пространство в углу между сходящимися линиями или стенами, которые сходятся в точке.
Проекция в пространство угла твердого тела.
Пересечение двух улиц; любая из четырех крайних точек с улицы на этом перекрестке.
Пространство в углу между сходящимися линиями или стенами, которые сходятся в точке.
Проекция в пространство угла твердого тела.
Пересечение двух улиц; любая из четырех крайних точек с улицы на этом перекрестке.Примеры:
«Углы проволочной сетки были усилены небольшими каплями припоя.»
«Угол трубы был весь в паутине.»
«Герберт ушиб голень об угол журнального столика.»
«В винном магазине на углу также продаются лотерейные билеты.»
Угол как существительное :
Ребро или оконечность; самая удаленная от центра часть; следовательно, любая четверть или часть, или направление, в котором она лежит.
Примеры:
«Сияние света в темных уголках разума. Теперь я отправился в путешествие в его угол города.»
Угол как существительное :
Тайное или укромное место; удаленное или труднодоступное место; уголок.

Примеры:
«По выходным Эмили любила находить тихий уголок и свернуться калачиком с хорошей книгой.»
Угол как существительное :
Неловкая ситуация; трудность.
Уголок как существительное (бизнес, финансы) :
Достаточный интерес к продаваемым ценным бумагам или товарам, чтобы позволить стороне, загоняющей в угол, влиять на цены.
Примеры:
«В 1970-х годах частные инвесторы пытались получить свой кусок на рынке серебра, но безуспешно».
Угол как существительное :
Относится к игровому полю.
 Одна из четырех вершин зоны удара. Первая база или третья база. Угловой удар. Угловой защитник. Угол ринга, где боксер отдыхает до и во время боя. Группа людей, помогающих боксеру во время боя.
Одна из четырех вершин зоны удара. Первая база или третья база. Угловой удар. Угловой защитник. Угол ринга, где боксер отдыхает до и во время боя. Группа людей, помогающих боксеру во время боя.Примеры:
«Поле было прямо за углом, низко и снаружи.»
«На поворотах бегуны с одним аутом.»
Угол как существительное :
Место, где люди встречаются с определенной целью.
Примеры:
«Добро пожаловать в наш английский уголок.»
Угол как существительное (устаревшее) :
Очко, набранное в резине в вист.
Угол как глагол (переходный) :
Загнать (кого-либо) в угол или другое замкнутое пространство.

Примеры:
«Кошка загнала сверчка между диваном и телевизионной стойкой.»
Угол как глагол (переходный) :
Чтобы заманить в ловушку в положении большой трудности или безнадежного смущения.
Примеры:
«Репортер загнал политика в угол, указав на лицемерие его позиции по поводу обязательного вынесения приговора в свете собственных действий политика в суде.»
Угол как глагол (переходный) :
Поставить (кого-либо) в неловкое положение.
Уголок как глагол (финансы, бизнес, переходный) :
Получить достаточное владение (акции, товара и т.
 д.), чтобы иметь возможность манипулировать его ценой.
д.), чтобы иметь возможность манипулировать его ценой.Примеры:
«Покупатели пытались завладеть акциями железнодорожной компании, чтобы облегчить их выкуп.»
«Очень трудно загнать рынок нефти в угол, потому что на нем так много игроков.»
Угол как глагол (автомобильный, переходный) :
Чтобы повернуть за угол или объехать кривую.
Примеры:
«Когда водитель серийного автомобиля входил в последний поворот, он потерял управление и развернулся.»
Угол как глагол (автомобильный, непереходный) :
Для обработки при повороте дороги или другом повороте.

Примеры:
«Этот BMW хорошо входит в повороты, но подвеска слишком жесткая.»
Сравните слова:
Сравните с синонимами и родственными словами:
- угол против угла
- угол против отклонения
- угол против мнения
- угол против перспективы
- угол против точки зрения
- угол против наклона
- угол против вида
- угол против точки зрения
Обклеивание лентой скошенных углов — изящное домостроение
Когда наклонный потолок соприкасается с плоским потолком или стеной, образуется внутренний угол , угол которого обычно намного больше 90 градусов, он называется углом со смещением . Важно, чтобы эти углы выглядели прямыми. Придание этим углам красивой прямой центральной линии не должно быть трудным или трудоемким. В дополнение к тому, что эти типы углов видны, они также подвержены растрескиванию из-за структурного движения или оседания.
Важно, чтобы эти углы выглядели прямыми. Придание этим углам красивой прямой центральной линии не должно быть трудным или трудоемким. В дополнение к тому, что эти типы углов видны, они также подвержены растрескиванию из-за структурного движения или оседания.
К счастью, есть несколько лент и бусин , специально предназначенных для таких ситуаций. Один из моих любимых бусин — это виниловый продукт, который приспосабливается к различным углам и имеет гибкий центр, чтобы приспосабливаться к нормальному структурному движению или оседанию. Для установки и отделки требуется немного дополнительной работы, но конечный результат того стоит.
В центр (зону сгиба) этого валика не следует наносить слой шовного герметика. На самом деле, самый центр должен быть после установки абсолютно чистым. Поскольку пломбы для последующей корректировки нет, важно установить ленты как можно более ровно. Начните с заполнения любых провалов в гипсокартоне с помощью шовного герметика. После того, как состав высохнет, используйте обрывок валика, чтобы отметить вдоль ножек ленты на обоих концах прогона, и проведите мелом линию между наборами отметок. Нанесите утвержденный аэрозольный клей на гипсокартон (я наношу два быстрых слоя). Немедленно прижмите ленту к месту, используя меловую линию в качестве ориентира.
После того, как состав высохнет, используйте обрывок валика, чтобы отметить вдоль ножек ленты на обоих концах прогона, и проведите мелом линию между наборами отметок. Нанесите утвержденный аэрозольный клей на гипсокартон (я наношу два быстрых слоя). Немедленно прижмите ленту к месту, используя меловую линию в качестве ориентира.
| WORK SMART: Весь шовный герметик должен быть удален из центра гибких валиков. Возьмите за привычку проверять бусины на каждом этапе процесса наклеивания ленты. |
Этот тип буртика также может быть заделан в шовный герметик. Нанесите состав на гипсокартон и прикатайте валик на место, центрируя его по ходу движения. Визируйте вдоль внутреннего края и при необходимости внесите коррективы. Затем надавите на ножки тейп-ножом. Ножки будут покрыты шовным герметиком и смешаны с гипсокартоном, но гибкий центр должен оставаться свободным от герметика.
Скошенные внутренние углы Виниловый угловой профиль можно приклеить к углам со скошенными углами, а затем покрыть компаундом.
|
Существуют аналогичные изделия, которые можно регулировать под разными углами, но без гибкого растягивающегося центра (они просто шарнирные). Если они виниловые, нанесите их, используя только что упомянутые методы. Если они не виниловые, залейте их компаундом. Используйте эти валики только на углах, которые с меньшей вероятностью треснут из-за смещения конструкции.
Если они виниловые, нанесите их, используя только что упомянутые методы. Если они не виниловые, залейте их компаундом. Используйте эти валики только на углах, которые с меньшей вероятностью треснут из-за смещения конструкции.
Некоторые из этих лент можно использовать как на внутренних, так и на внешних углах. Для внутренних углов установите их, нанеся шовный герметик на гипсокартон и прижав валик на место с помощью строительного ножа. При нанесении финишных слоев компаунда нет необходимости наносить компаунд на центр ленты — достаточно растушевать края. При использовании в качестве внешнего угла лента сгибается, чтобы стать угловой бусиной со слегка выпуклым краем. Эти бусины должны быть обработаны так же, как и любой другой внешний угол. Эти продукты поставляются в рулонах, их можно нарезать по длине и регулировать, чтобы приспособить к широкому диапазону углов.
Также доступны выпуклые буртики для скругления внутренних и внешних углов. Они бывают стандартной длины из металла, винила, металла или пластика с бумажным покрытием. Бусины с закругленными концами крепятся и обрабатываются так же, как и углы под углом 90 градусов. Держите закругленные края как можно более чистыми во время приклеивания и отшлифуйте оставшийся состав, когда он высохнет.
Варианты углового валика: Слева находится закругленный выступ внутри углового валика. В центре находится 90-градусный зауженный конец, а справа — 3/4 дюйма. закругленный наружный угловой выступ.
| Почему углы трескаются? Распространенные причины взлома
Способы предотвращения проблем
|
Техника закругления углов
До того, как стали доступны все эти новые ленты и бусины, варианты были весьма ограничены. Чтобы избежать кривых углов, я использовал обычную бумажную ленту, залитую компаундом. Этот метод не очень силен, и трудно создать прямые законченные линии… но он может работать.
Чтобы избежать кривых углов, я использовал обычную бумажную ленту, залитую компаундом. Этот метод не очень силен, и трудно создать прямые законченные линии… но он может работать.
Я успешно скруглил эти внутренние углы. Это хорошая техника, которую я до сих пор иногда использую на необычно кривых углах, где новые бусины просто не работают. Я также использую эту технику, если работаю в старом доме и пытаюсь соответствовать существующим углам. Подробнее об этом процессе см. рисунок ниже и врезку «Техника закругления углов».
Скругление делает угол прямым, даже если он слегка отклонен, поскольку нет очевидного внутреннего угла. Как и в случае с обычными внутренними углами, закругленные углы можно покрыть тремя слоями шпатлевки. Для первого слоя я рекомендую использовать ленту из стекловолокна в сочетании с закрепляющим составом для швов. Сначала заклейте угол сетчатой лентой. Если между панелями или поврежденными участками есть большие зазоры, наложите дополнительный кусок сетчатой ленты, чтобы закрыть эти участки.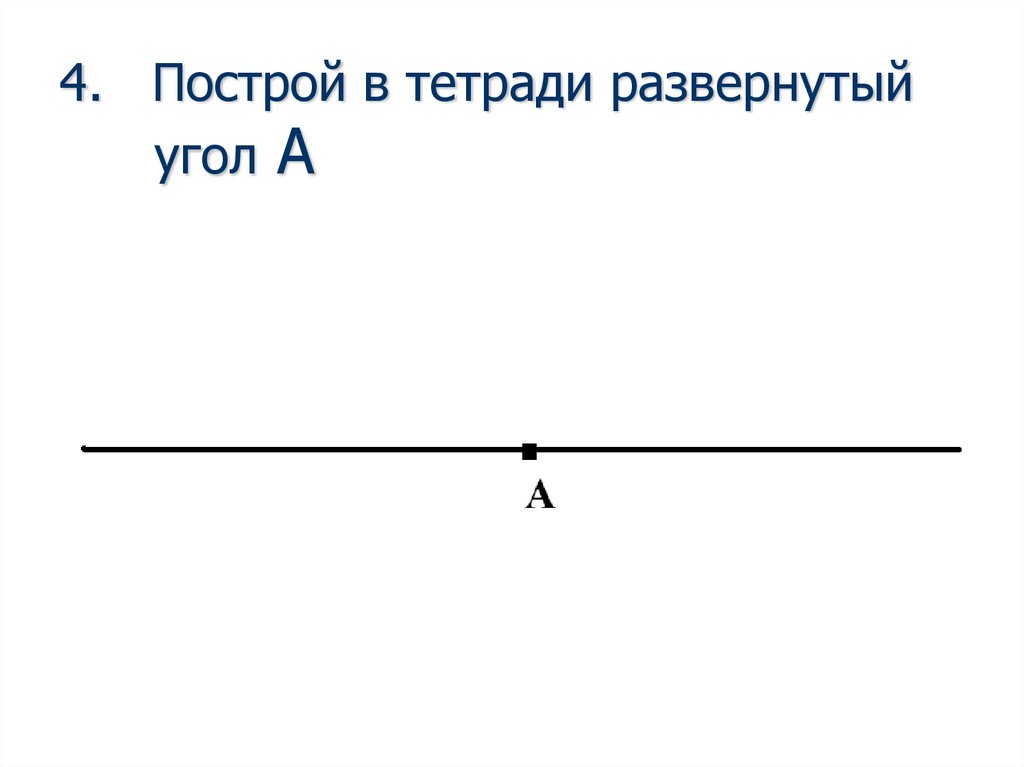 Затем используйте 6-дюймовый. ленточный нож для нанесения тонкого слоя шовного герметика на каждую сторону угла. На этом этапе полностью ленту закрывать не нужно; достаточно слоя толщиной около 1/8 дюйма и шириной 4 или 5 дюймов.
Затем используйте 6-дюймовый. ленточный нож для нанесения тонкого слоя шовного герметика на каждую сторону угла. На этом этапе полностью ленту закрывать не нужно; достаточно слоя толщиной около 1/8 дюйма и шириной 4 или 5 дюймов.
Техника скругления угловВместо того, чтобы использовать валики для обработки скошенных углов, можно также использовать ленту. Этот метод удобен, когда вы пытаетесь сопоставить существующие стыки в старых домах или если угол очень кривой.
|
После того, как вы нанесли состав, протяните нож для тейпирования через угол под углом 90 градусов. После того, как вы прошли угол в одном направлении, в соединении все еще будут пробелы и шероховатые края; чтобы исправить эти области, потяните нож через угол в противоположном направлении.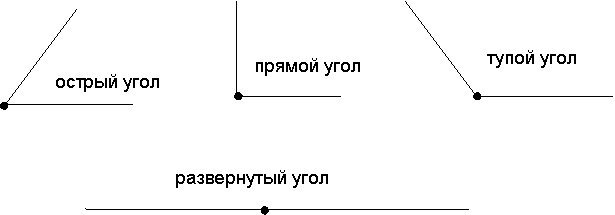 Не торопитесь и не оказывайте слишком большого давления (если вы все делаете правильно, нужно удалить очень мало шовного герметика). Аккуратно проводя ножом по углу, растушуйте края смеси и слегка закруглите центр. К этому моменту лента должна быть полностью покрыта, и нож не должен оставлять больших зазоров или высоких выступов.
Не торопитесь и не оказывайте слишком большого давления (если вы все делаете правильно, нужно удалить очень мало шовного герметика). Аккуратно проводя ножом по углу, растушуйте края смеси и слегка закруглите центр. К этому моменту лента должна быть полностью покрыта, и нож не должен оставлять больших зазоров или высоких выступов.
Для второго слоя на закругленном углу используйте фиксирующий состав, универсальный состав или готовый клейкий состав. Я предпочитаю использовать для этого покрытия закрепляющий состав, потому что в закругленной области угла остается довольно толстый слой состава, что может привести к чрезмерной усадке, если вы используете засохший тип. Усадка может вызвать глубокие трещины, для устранения которых потребуется армирование лентой.
Использование 6-дюймового ножом, нанесите примерно такое же количество состава на каждую сторону угла, как и при нанесении первого слоя. На этом пальто используйте 12-дюймовый. нож с прямой ручкой, чтобы закруглить компаунд (см. нижнее левое фото на следующей странице). Потяните шпатель через угол в одном направлении, а затем в противоположном направлении, как вы это делали для первого слоя. Опять же, очень мало компаунда должно быть удалено, так как угол закруглен, а края сглажены.
нижнее левое фото на следующей странице). Потяните шпатель через угол в одном направлении, а затем в противоположном направлении, как вы это делали для первого слоя. Опять же, очень мало компаунда должно быть удалено, так как угол закруглен, а края сглажены.
| WORK SMART: На закругленном углу сильное скопление состава. Чтобы предотвратить растрескивание, обязательно используйте фиксирующий состав для первых двух слоев. |
Перед нанесением третьего слоя слегка отшлифуйте все высокие следы от шпателя и зачистите края шлифовальной машиной и наждачной бумагой с зернистостью 120 или шлифовальной сеткой (будьте осторожны, чтобы не перешлифовать и не выкопать центральные области). Для третьего слоя используйте топпинг или универсальную готовую смесь. Вы можете нанести шовный герметик с 6-дюймовым. или 12-дюймовый. ножом, но я считаю, что валик работает лучше всего, потому что он легко повторяет изгиб закругленного угла (см.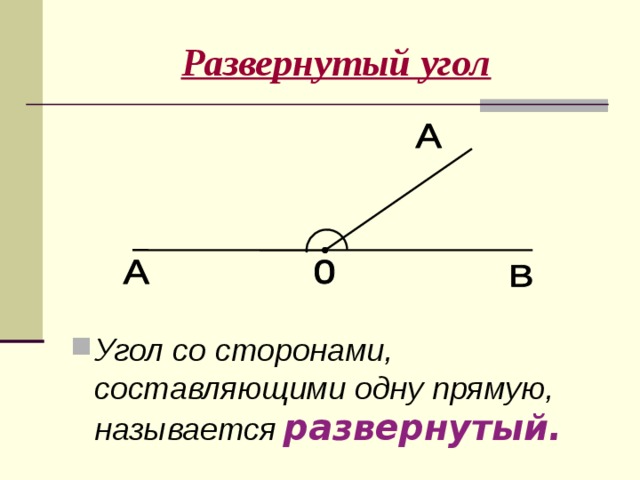


 Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.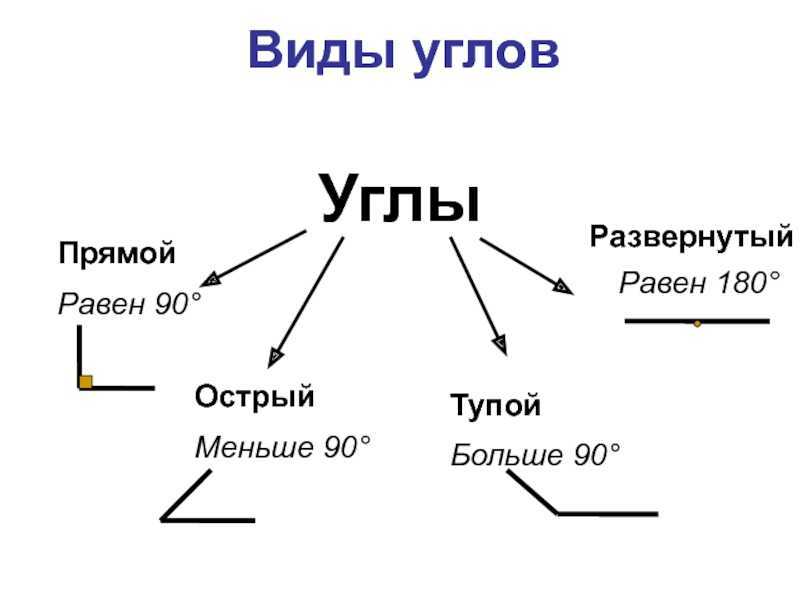 »
»



 Пространство в углу между сходящимися линиями или стенами, которые сходятся в точке.
Проекция в пространство угла твердого тела.
Пересечение двух улиц; любая из четырех крайних точек с улицы на этом перекрестке.
Пространство в углу между сходящимися линиями или стенами, которые сходятся в точке.
Проекция в пространство угла твердого тела.
Пересечение двух улиц; любая из четырех крайних точек с улицы на этом перекрестке.
 Одна из четырех вершин зоны удара. Первая база или третья база. Угловой удар. Угловой защитник. Угол ринга, где боксер отдыхает до и во время боя. Группа людей, помогающих боксеру во время боя.
Одна из четырех вершин зоны удара. Первая база или третья база. Угловой удар. Угловой защитник. Угол ринга, где боксер отдыхает до и во время боя. Группа людей, помогающих боксеру во время боя.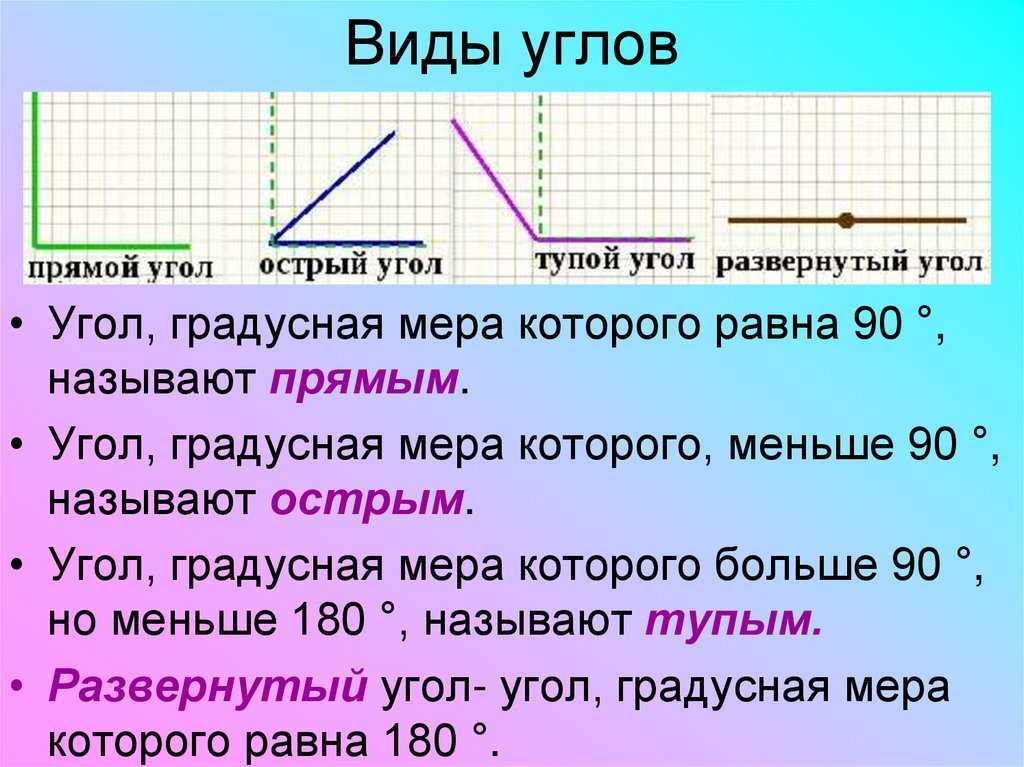
 д.), чтобы иметь возможность манипулировать его ценой.
д.), чтобы иметь возможность манипулировать его ценой.
 При правильном завершении в результате получается красивая прямая складка, обеспечивающая превосходный контроль над расширением.
При правильном завершении в результате получается красивая прямая складка, обеспечивающая превосходный контроль над расширением. Большинству угловых лент не нужно много структурных движений, чтобы треснуть и отсоединиться.
Большинству угловых лент не нужно много структурных движений, чтобы треснуть и отсоединиться. Центр шва должен быть заполнен и слегка закруглен, а края должны быть распушены.
Центр шва должен быть заполнен и слегка закруглен, а края должны быть распушены.