3. Дан неразвернутый угол АВС. Проведите лучи.. Самостоятельные работы. Вариант 5. С-2. 7 класс Зив геометрия ГДЗ. – Рамблер/класс
3. Дан неразвернутый угол АВС. Проведите лучи.. Самостоятельные работы. Вариант 5. С-2. 7 класс Зив геометрия ГДЗ. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
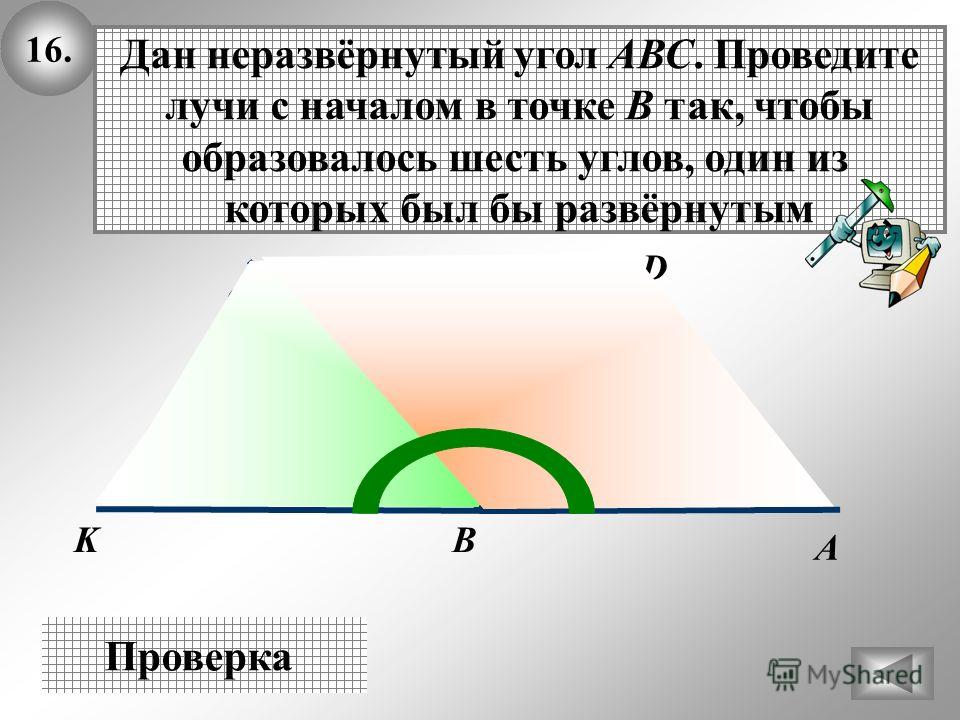
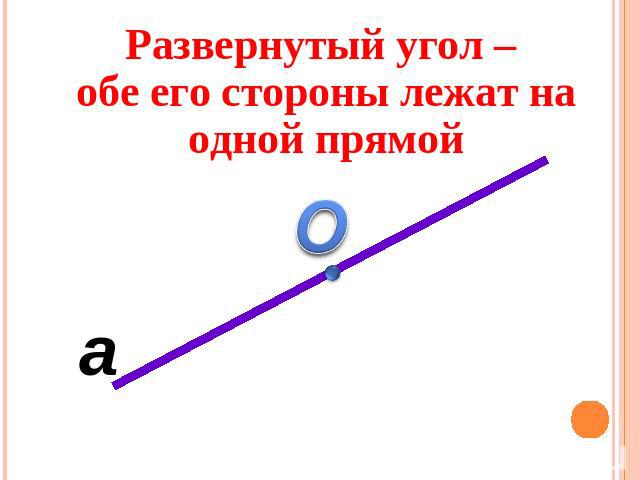
3. Дан неразвернутый угол АВС. Проведите лучи с началом в точке В, чтобы образовались при этом шесть углов, из которых один был бы развернутым.
Дан неразвернутый угол АВС. Проведите лучи с началом в точке В, чтобы образовались при этом шесть углов, из которых один был бы развернутым.
ответы
ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
9. Определите ряд, в котором в обоих словах пропущена одна и та же буква. ЕГЭ-2017 Русский язык Цыбулько И. П. ГДЗ. Вариант 12.
9.
Определите ряд, в котором в обоих словах пропущена одна и та же буква. Выпишите
эти слова, вставив пропущенную букву. (Подробнее…)
ГДЗРусский языкЕГЭЦыбулько И.П.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Зачет № 1по геометрии_7 класс
1. Сколько прямых можно провести через две точки?
2. Объясните, как сравнить два отрезка.
3. Укажите номера верных утверждений.
1) Через любую точку проходит не менее одной прямой.
2) Неразвернутый угол больше развернутого угла. 3) Если угол равен 60, то вертикальный с ним угол равен 120.
1. Сколько общих точек могут иметь две прямые?
2. Луч ОС делит угол АОВ на два угла. Как найти градусную меру угла АОВ, если известны градусные меры углов АОС и СОВ?
3. Укажите номера верных утверждений.
1) Любые две прямые имеют не менее одной общей точки.
2) Если две прямые
перпендикулярны третьей прямой, то эти две прямые перпендикулярны. 3) Если
угол равен 38°, то смежный с ним равен 142°.
3) Если
угол равен 38°, то смежный с ним равен 142°.
1. Объясните, что такое отрезок.
2. Объясните, как сравнить два угла.
3. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120° , то смежный с ним равен 120° . 3) Если угол острый, то его градусная мера меньше 90.
1. Объясните, что такое луч.
2. Точка С делит отрезок АВ на два отрезка. Как найти длину отрезка АВ, если известны длины отрезков АС и СВ?
3. Укажите номера верных утверждений.
1) Через любую точку проходит не менее одной прямой.
2) При пересечении двух прямых образуются два вертикальных угла. 3) Сумма смежных углов равна 180.
1. Какая фигура называется углом?
2. Сформулируйте свойство вертикальных углов.
3. Укажите номера верных утверждений.
1) Больший угол имеет меньшую градусную меру.
2) Смежные углы
равны.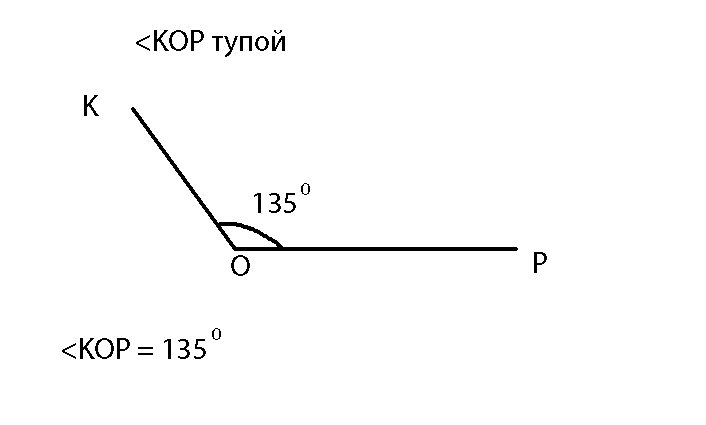 3) Две прямые, перпендикулярные к третьей, не перпендикулярны.
3) Две прямые, перпендикулярные к третьей, не перпендикулярны.
1. Какой угол называется развернутым?
2. Сформулируйте свойство перпендикулярных прямых.
3. Укажите номера верных утверждений. 1) Развернутый угол меньше 180.
2) Через любую точку проходит только две прямые.
3) Вертикальные углы равны. Билет №7
1. Какие фигуры называются равными?
2. Какой угол называется острым? Прямым? Тупым?
3. Укажите номера верных утверждений.
1) Развернутый угол больше 180.
2) Если сумма двух углов равна 180, то они смежные.
3) Теодолит используют для измерения углов.
1. Какая точка называется серединой отрезка?
2. Какие углы называются смежными?
3. Укажите номера верных утверждений. Смежные углы равны 180.
2) Если два угла равны, то они вертикальные.
3) Биссектриса делит угол на два угла.
1. Какой луч называется биссектрисой угла?
2. Объясните,
почему две прямые, перпендикулярные к третьей не пересекаются.
Объясните,
почему две прямые, перпендикулярные к третьей не пересекаются.
3. Укажите номера верных утверждений.
1) Меньший угол имеет большую градусную меру.
2) Через две точки можно провести только одну прямую. 3) Сумма смежных углов равна 180.
1. Что такое градусная мера угла?
2. Сформулируйте свойство смежных углов.
3. Укажите номера верных утверждений.
1) Две прямые, перпендикулярные к третьей, перпендикулярны.
2) Развернутый угол равен 180. 3) Две пересекающиеся прямые образуют прямые углы.
1. Какие прямые называются перпендикулярными?
2. Какой угол называется развернутым?
3. Укажите номера верных утверждений.
1) Теодолит используют для измерения отрезков.
2) Вертикальные углы равны. 3) Острый угол больше 90.
1. Объясните, что такое луч. Как обозначаются лучи?
2. Перечислите
свойства измерения углов.
3. Укажите номера верных утверждений.
1) Если угол равен 50, то смежный с ним угол равен130.
2) Если один из смежных углов равен 90, то второй смежный с ним угол тупой. 3) Через точку можно провести множество прямых.
1. Как обозначаются углы?
2. Как обозначаются лучи?
3. Укажите номера верных утверждений.
1) Биссектриса угла – это луч делящий угол.
2) Если один из смежных углов равен 90, то второй смежный с ним угол равен 90. 3) Две прямые пересекаются в двух точках.
1. Как обозначаются прямые.
2. Объясните, что такое вершина и стороны угла.
3. Укажите номера верных утверждений.
1) Если один из смежных углов равен 90, то второй смежный с ним угол прямой.
2) Луч – это точка, которая разделяет прямую на две части.
Сумма вертикальных углов равна 180
1. Как обозначаются прямые?
2. Какие свойства измерения углов вы знаете?
3. Укажите
номера верных утверждений.
Укажите
номера верных утверждений.
1) Две прямые пересекаются в одной точке.
2) Если один из смежных углов равен 90, то второй смежный с ним угол острый. 3) Вертикальные углы равны.
1. Какие углы называются смежными?
2. Перечислите свойства измерения отрезков.
3. Укажите номера верных утверждений.
1) Если один из смежных углов равен 90, то второй смежный с ним угол тупой.
2) Две прямые не могут иметь двух и более точек пересечения. 3) Если смежные углы равны, то они прямые.
1. Какие углы называются вертикальными?
2. Сформулируйте свойство смежных углов.
3. Укажите номера верных утверждений.
1) Точка делит прямую на два луча.
2) Если один смежный угол равен 60, то второй смежный с ним угол равен 60. 3) Через две точки можно провести только одну прямую.
1. Какими инструментами пользуются для измерения расстояния?
2. Сформулируйте
свойство вертикальных углов.
Сформулируйте
свойство вертикальных углов.
3. Укажите номера верных утверждений.
1) При пересечении двух прямых образуются два вертикальных угла.
2) Угол называется развернутым, если обе его стороны лежат на одной прямой. 3) Сумма смежных углов равна 180.
1. Какие прямые называются перпендикулярными?
2. Сформулируйте свойство смежных углов.
3. Укажите номера верных утверждений.
1) Меньший угол имеет большую градусную меру.
2) Через две точки можно провести только одну прямую. 3) Сумма смежных углов равна 180.
1. Что такое градусная мера угла?
2. Объясните, почему две прямые, перпендикулярные к третьей не пересекаются.
3. Укажите номера верных утверждений.
1) Теодолит используют для измерения отрезков.
2) Вертикальные углы равны. 3) Острый угол больше 90.
1. Какой луч называется биссектрисой угла?
2.
3. Укажите номера верных утверждений.
1) Теодолит используют для измерения отрезков.
2) Вертикальные углы равны. 3) Острый угол больше 90.
1. Объясните, что такое отрезок.
2. Точка С делит отрезок АВ на два отрезка. Как найти длину отрезка АВ, если известны длины отрезков АС и СВ?
3. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120° , то смежный с ним равен 120° .
3) Если угол острый, то его градусная мера меньше 90.
1. Объясните, что такое луч.
2. Объясните, как сравнить два угла.
3. Укажите номера верных утверждений.
1) Через любую точку проходит не менее одной прямой.
2) При пересечении двух прямых образуются два вертикальных угла. 3) Сумма смежных углов равна 180.
1. Какие углы называются смежными?
2. Сформулируйте
свойство смежных углов.
Сформулируйте
свойство смежных углов.
3. Укажите номера верных утверждений.
1) Точка делит прямую на два луча.
2) Если один смежный угол равен 60, то второй смежный с ним угол равен 60. 3) Через две точки можно провести только одну прямую.
1. Как обозначаются прямые?
2. Перечислите свойства измерения отрезков.
3. Укажите номера верных утверждений.
1) Две прямые пересекаются в одной точке.
2) Если один из смежных углов равен 90, то второй смежный с ним угол острый. 3) Вертикальные углы равны.
1. Как обозначаются прямые.
2. Какие свойства измерения углов вы знаете?
3. Укажите номера верных утверждений.
1) Если один из смежных углов равен 90, то второй смежный с ним угол тупой.
2) Две прямые не могут иметь двух и более точек пересечения. 3) Если смежные углы равны, то они прямые.
1. Какие
углы называются вертикальными?
Какие
углы называются вертикальными?
2. Объясните, что такое вершина и стороны угла.
3. Укажите номера верных утверждений.
1) Если один из смежных углов равен 90, то второй смежный с ним угол прямой.
2)Луч – это точка, которая разделяет прямую на две части.
3)Сумма вертикальных углов равна 180
1. Объясните, что такое луч.
2. Объясните, как сравнить два отрезка.
3. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120° , то смежный с ним равен 120° .
3) Если угол острый, то его градусная мера меньше 90.
1. Сколько общих точек могут иметь две прямые?
2. Объясните, как сравнить два угла.
3. Укажите номера верных утверждений.
1) Любые две прямые имеют не менее одной общей точки.
2)
Если две прямые
перпендикулярны третьей прямой, то эти две прямые перпендикулярны. 3) Если
угол равен 38°, то смежный с ним равен 142°.
3) Если
угол равен 38°, то смежный с ним равен 142°.
Билет №30
1. Объясните, что такое отрезок.
2. Луч ОС делит угол АОВ на два угла. Как найти градусную меру угла АОВ, если известны градусные меры углов АОС и СОВ?
3. Укажите номера верных утверждений.
1) Через любую точку проходит не менее одной прямой.
2) Неразвернутый угол больше развернутого угла.
3) Если угол равен 60, то вертикальный с ним угол равен 120.
Билет №31
1. Сколько прямых можно провести через две точки?
2. Точка С делит отрезок АВ на два отрезка. Как найти длину отрезка АВ, если известны длины отрезков АС и СВ?
3. Укажите номера верных утверждений.
1) Через любую точку проходит не менее одной прямой.
2) При пересечении двух прямых образуются два вертикальных угла. 3) Сумма смежных углов равна 180.
Билет №32
1. Как обозначаются
углы?
Как обозначаются
углы?
2. Объясните, что такое вершина и стороны угла.
3. Укажите номера верных утверждений. 1) Если один из смежных углов равен 90, то второй смежный с ним угол прямой.
2) Луч – это точка, которая разделяет прямую на две части.
3) Сумма вертикальных углов равна 180
Билет №33
1. Как обозначаются прямые.
2. Как обозначаются лучи?
3. Укажите номера верных утверждений.
1)Биссектриса угла – это луч делящий угол.
2) Если один из смежных углов равен 90, то второй смежный с ним угол равен 90. 3) Две прямые пересекаются в двух точках.
Билет №34
1. Какой луч называется биссектрисой угла?
2. Сформулируйте свойство смежных углов.
3. Укажите номера верных утверждений.
1)
Теодолит
используют для измерения отрезков.
2) Вертикальные углы равны. 3) Острый угол больше 90.
Билет № 35
1. Что такое градусная мера угла?
2. Какой угол называется развернутым?
3. Укажите номера верных утверждений.
1) Меньший угол имеет большую градусную меру.
2) Через две точки можно провести только одну прямую. 3) Сумма смежных углов равна 180.
Билет №36
1. Какие прямые называются перпендикулярными?
2. Объясните, почему две прямые, перпендикулярные к третьей не пересекаются.
3. Укажите номера верных утверждений.
1) Теодолит используют для измерения отрезков.
2) Вертикальные углы равны. 3) Острый угол больше 90.
Развитие понятий угла путем постепенной абстракции и обобщения
Бейлин, Х.: 1984, «Когнитивная теория и математическое познание: геометрия и пространство», в Б. Голсон и Т.Р. Розенталь (ред.
 ), Приложения теории когнитивного развития Academic Press, Нью-Йорк, стр. 49-93.
), Приложения теории когнитивного развития Academic Press, Нью-Йорк, стр. 49-93.Google Scholar
Боэро П., Дапуэто К., Феррари П., Ферраро Э., Гарути Р., Лемут Э., Паренти Л. и Скали Э.: 1995, «Аспекты отношений математики и культуры», Л. Мейра и Д. Каррахер (ред.), Труды 19-й ежегодной конференции Международной группы психологии математического образования , Ресифи.
Клементс, Д. Х. и Баттиста, М. Т.: 1989, «Изучение геометрических понятий в среде Logo», Journal for Research in Mathematics Education 20, 450-467.
Google Scholar
Клементс, Д.Х., Баттиста, М.Т., Сарама, Дж. и Сваминатан, С.: 1996, «Разработка концепций поворота и измерения поворота в компьютерном учебном блоке», Образовательные исследования по математике 30, 313- 337.
Google Scholar
Close, GS: 1982, Детское понимание угла на этапе первичного/вторичного переноса , Политехнический институт Южного берега, Лондон.

Google Scholar
Кобб, П.: 1994, «Где разум? Конструктивистские и социокультурные взгляды на математическое развитие», Исследователь в области образования 23(7), 13-20.
Google Scholar
Коуп, П., Смит, Х. и Симмонс, М.: 1992, «Заблуждения относительно поворота и угла в LOGO», Journal of Computer Assisted Learning 8, 16-24.
Google Scholar
Damerow, P.: 1996, Абстракция и репрезентация : Очерки культурной эволюции мышления , Kluwer, Dordrecht.
Google Scholar
Дэйви, Г. и Пегг, Дж.: 1991, « Углы на углах : Восприятие студентов », статья, представленная на 14-й ежегодной конференции Исследовательской группы по математическому образованию Австралии, Перт.
Дуэк, Н.: 1998, «Анализ долгосрочного построения концепции угла в поле опыта солнечных теней», в А.
 Оливье и К. Ньюстед (ред.), Труды 20-й ежегодной конференции Международной группы психологии Математическое образование , Стелленбос, Том. 2, стр. 264-271.
Оливье и К. Ньюстед (ред.), Труды 20-й ежегодной конференции Международной группы психологии Математическое образование , Стелленбос, Том. 2, стр. 264-271.Фоксман, Д. и Раддок, Г.: 1984, «Концепции и навыки: линейная симметрия и угол», Математика в школах , март 1984, 9-13.
Фройденталь: 1973, Математика как учебное задание . Ридель, Дордрехт.
Google Scholar
Грино, Дж. Г.: 1983, «Концептуальные сущности», Д. Гентнер и А. Л. Стивенс (ред.), Ментальные модели , Эрлбаум, Хиллсдейл, стр. 227–252.
Google Scholar
Грино, Дж. Г.: 1991, «Смысл числа как знание положения в концептуальной области», Журнал исследований в области математического образования 22, 170-218.
Google Scholar
Horner, C.M.: 1984, Влияние LOGO на решение проблем , локус контроля , отношение к математике и распознаванию углов при обучении детей-инвалидов , неопубликовано Ph.
 D. диссертация, Техасский технический университет.
D. диссертация, Техасский технический университет.Хойлс, К. и Сазерленд, Р.: 1989, LOGO математика в классе , Рутледж, Лондон.
Google Scholar
Келли Г.Н., Келли Дж.Т. и Миллер, Р.Б.: 1986, «Работа с LOGO: развивают ли пяти- и шестиклассники базовое понимание углов и расстояний?», Journal of Computers in Mathematics and Science Teaching 6(2), 23-27.
Google Scholar
Киран, К.: 1986, «ЛОГОС и понятие угла среди детей четвертого и шестого классов», в Л. Бертон и К. Хойлс (ред.), Материалы 10-й Международной конференции по психологии математического образования , Лондон, стр. 99-104.
Krainer, K.: 1989, ‘ Lebendige Geometrie : Ñberlegungen zu einem integriven Verständnis von Geometrieunterricht anhand des Winkelbegriffs ‘[Живая геометрия как пример всеобъемлющего понимания концепции геометрии], Ланг, Франкфурт.

Леви, С.: 1985, «Законные роли аспектов в социальных теориях», в Д. Кантере (ред.), Теория граней , Нью-Йорк: Springer, стр. 60-96.
Google Scholar
Ло, Дж.-Дж., Гэддис, К. и Хендерсон, Д.: 1996, «Основываясь на опыте студентов в курсе геометрии в колледже», Для изучения математики 16(1), 34- 40.
Google Scholar
Матос, М.: 1994, «Когнитивные модели концепции угла», в Дж. П. да Понте и Дж. Ф. Матос (ред.), Материалы 18-й Международной конференции по психологии математического образования , Лиссабон, Vol. 3, стр. 263-270.
Миллер Г.А. и Gildea, PM: 1987, «Как дети учат слова», Scientific American 257(3), 94-99.
Google Scholar
Митчелмор, MC: 1983, «Изучение геометрии детьми: отчет о совместном исследовательском проекте», Карибский журнал образования 10, 179-228.

Google Scholar
Митчелмор, М.К.: 1989, «Развитие детских представлений об угле», в Г. Верно (ред.), Труды 13-й Международной конференции по психологии математического образования , Париж, Том. 2, стр. 304-311.
Митчелмор, М.К.: 1990, «Psychologische und mathematische Schwierigkeiten beim Lernen des Winkelbegriffs» [Психологические и математические трудности в изучении концепции угла], Дидактическая математика 13, 19-37.
Google Scholar
Митчелмор, М.К.: 1992, «Детские концепции перпендикуляров», в В. Гизлин и К. Грэм (ред.), Труды 16-й Международной конференции по психологии математического образования , Дарем, Vol. 2, стр. 120-127.
Митчелмор, MC: 1997, «Неформальные знания детей о ситуациях с физическим углом», Learning and Instruction 7, 1-19.
Google Scholar
Митчелмор, М.
 К.: 1998, «Концепции токарной обработки для юных студентов», Познание и обучение 16, 265-284.
К.: 1998, «Концепции токарной обработки для юных студентов», Познание и обучение 16, 265-284.Google Scholar
Митчелмор, М.К. andWhite, P.: 1996, «Интерпретация маленьких детей ситуаций физического угла», в P.C. Кларксон (ред.), Труды 19-й ежегодной конференции Исследовательской группы по математическому образованию Австралии , Мельбурн, стр. 383-389.
Митчелмор, М.К. и Уайт, П.: 1998a, «Развитие концепций угла: основа для исследования», Mathematics Education Research Journal 10 (3), 4-27.
Google Scholar
Митчелмор, М.К. и Уайт, П.: 1998b, «Распознавание углового сходства между знакомыми физическими ситуациями», в книге А. Оливье и К. Ньюстеда (ред.), Proceedings of the 20 th Международная конференция по психологии математического образования , Stellenbosch, Vol. 3, стр. 271-278.
Нейссер, У.
 : 1991, «Прямое восприятие и другие формы знания», в Р. Р. Хоффман и Д. С. Палермо (ред.), Познание и символические процессы : Прикладные и экологические перспективы , Эрлбаум, Хиллсдейл , стр. 17-30.
: 1991, «Прямое восприятие и другие формы знания», в Р. Р. Хоффман и Д. С. Палермо (ред.), Познание и символические процессы : Прикладные и экологические перспективы , Эрлбаум, Хиллсдейл , стр. 17-30.Google Scholar
Департамент образования Нового Южного Уэльса: 1989, Mathematics K-6 , Сидней.
Носс, Р.: 1987, «Изучение детьми геометрических понятий с помощью LOGO», Journal for Research in Mathematics Education 18, 343-362.
Google Scholar
Noss, R. and Hoyles, C.: 1996, Окна математических значений , Kluwer, Dordrecht.
Google Scholar
Piaget, J.: 1970, Генетическая эпистемология (Э. Дакворт, перевод), Columbia University Press, Нью-Йорк.
Google Scholar
Пиаже, Дж.
 : 1975, «Теория Пиаже», в P.B.Neubauer (ред.), Процесс развития ребенка , Джейсон Аронсон, Нью-Йорк, стр. 164-212.
: 1975, «Теория Пиаже», в P.B.Neubauer (ред.), Процесс развития ребенка , Джейсон Аронсон, Нью-Йорк, стр. 164-212.Google Scholar
Пиаже, Дж. и Инхельдер, Б.: 1946, Представление ребенка о пространстве , Рутледж, Кеган Пол, Лондон.
Google Scholar
Пиаже, Дж., Инхелдер, Б. и Семинска, А.: 1960, Детское представление о геометрии , Рутледж, Кеган Пол, Лондон.
Google Scholar
Roels, G.: 1985, «Het fenomeen hoek» [Феномен угла], Wiskunde en Onderwijs 11, 127-138.
Google Scholar
Рош, Э.: 1977, «Классификация объектов реального мира: происхождение и представления в познании», в П.Н. Джонсон-Лэрд и П.К. Уэйсон (ред.), Thinking : Чтения по когнитивным наукам , Cambridge University Press, стр.
 212-222.
212-222.Scally, SP: 1986, «Клиническое исследование влияния учебной среды LOGO на уровни Ван Хиле учащихся в геометрическом понимании», в Л. Бертон и К. Хойлс (ред.), Proceedings of the 10-я Международная конференция по психологии математического образования , Лондон, стр. 123-128.
Scally, SP: 1987, «Влияние изучения LOGO на понимание геометрических отношений учащимися девятого класса», в J. Bergeron, N. Herscovics and C. Kieran (eds.), Proceedings of the 11th Annual конференция Международной группы психологии математического образования , Монреаль, Vol. 2, стр. 46-52.
Schweiger, F.: 1986, «Winkelbegriff und Winkelmaß» [Концепция угла и измерение угла], Mathematik im Unterricht 11, 1-9.
Google Scholar
Сфард, А.: 1991, «О двойственной природе математических понятий: размышления о процессах и объектах как о разных сторонах одной медали», Образовательные исследования по математике 22, 1-36.

Google Scholar
Скемп, Р.: 1986, Психология обучения математике (2-е изд.), Penguin, Harmondsworth.
Google Scholar
Стрел, Р.: 1983, «Anschauliche Vorstellung und mathematische Theorie beim Winkelbegriff» [Визуализация и математическая теория понятия угла], Mathematica Didactica 6, 129-146.
Google Scholar
Виннер, С.: 1991, «Роль определений в преподавании и изучении математики», в Д. Талле (ред.), Расширенное математическое мышление , Клювер, Дордрехт, стр. 65-81.
Google Scholar
Фон Глазерсфельд, Э.: 1991, «Абстракция, репрезентация и отражение: интерпретация опыта и подход Пиаже», в LP Steffe (ред.), Эпистемологические основы математического опыта , Клювер, Дордрехт , стр. 45-67.
Google Scholar
Выготский, Л.
 С.: 1987, «Мышление и речь», в книге Р.В. Рибера и А.С. Картон (ред.) и Н. Миник (пер.), Собрание сочинений L . С . Выготский : Том . 1 . Проблемы общей психологии , Пленум, Нью-Йорк, стр. 39-285. (Оригинальная работа опубликована в 1934 г.)
С.: 1987, «Мышление и речь», в книге Р.В. Рибера и А.С. Картон (ред.) и Н. Миник (пер.), Собрание сочинений L . С . Выготский : Том . 1 . Проблемы общей психологии , Пленум, Нью-Йорк, стр. 39-285. (Оригинальная работа опубликована в 1934 г.)Google Scholar
Уайт, П. и Митчелмор, М.К.: 1997, «Распознавание абстрактных углов в знакомых физических ситуациях», в Ф. Биддульф и К. Карр (ред.), Труды 20-й ежегодной конференции по математическому образованию Исследовательская группа Австралии , Гамильтон, стр. 577-584.
Уилсон, П.С. и Адамс, В.М.: 1992, «Динамический способ обучения измерению угла и угла», Учитель математики 39 (5), 6-13.
Google Scholar
Скачать ссылки
Развитие закрытия угла и связанные с ним факторы риска: исследование глаз Ханьдань
Сравнительное исследование
. 2022 Февраль; 100 (1): e253-e261.
2022 Февраль; 100 (1): e253-e261.
дои: 10.1111/аос.14887. Epub 2021 7 мая.
Е Чжан 1 , Цин Чжан 2 , Рави Томас 3 4 , Си Чжэнь Ли 5 , Нин Ли Ван 1 2
Принадлежности
- 1 Пекинский глазной центр Тунжэнь, Пекинская ключевая лаборатория офтальмологии и визуальных наук, Пекинская больница Тунжэнь, Столичный медицинский университет, Пекин, Китай.
- 2 Пекинский институт офтальмологии, Пекин, Китай.

- 3 Квинслендский глазной институт, Брисбен, Австралия.
- 4 Университет Квинсленда, Брисбен, Австралия.
- 5 Больница Нанкин Тунжэнь, Цзянсу, Китай.
- PMID: 33960669
- PMCID: PMC9292978
- DOI: 10.1111/аос.14887
Бесплатная статья ЧВК
Сравнительное исследование
Ye Zhang et al.
Акта Офтальмол. 2022 9 фев.0007
2022 9 фев.0007
Бесплатная статья ЧВК
. 2022 Февраль; 100 (1): e253-e261.
дои: 10.1111/аос.14887. Epub 2021 7 мая.
Авторы
Е Чжан 1 , Цин Чжан 2 , Рави Томас 3 4 , Си Чжэнь Ли 5 , Нин Ли Ван 1 2
Принадлежности
- 1 Пекинский глазной центр Тунжэнь, Пекинская ключевая лаборатория офтальмологии и визуальных наук, Пекинская больница Тунжэнь, Столичный медицинский университет, Пекин, Китай.

- 2 Пекинский институт офтальмологии, Пекин, Китай.
- 3 Квинслендский глазной институт, Брисбен, Австралия.
- 4 Университет Квинсленда, Брисбен, Австралия.
- 5 Больница Нанкин Тунжэнь, Цзянсу, Китай.
- PMID: 33960669
- PMCID: ПМС9292978
- DOI: 10.1111/аос.14887
Абстрактный
Цель: Изучить развитие закрытого угла по сравнению с исходным открытым углом и связанные с ним факторы риска у сельского населения Китая с помощью продольного исследования в течение 5-летнего периода.
Методы: Были включены субъекты в возрасте ≥30 лет и старше с двусторонними открытыми углами на исходном уровне исследования Handan Eye Study, которые участвовали в последующем наблюдении и прошли как исходное, так и последующее гониоскопическое обследование. Субъекты с любой формой закрытия угла, глаукомой, инцизионной хирургией глаза или другими состояниями, которые могли повлиять на результаты, были исключены. Развитие закрытия угла определялось как наличие подозрения на первичное закрытие угла (PACS) или первичное закрытие угла (PAC)/первичная закрытоугольная глаукома (PACG) во время наблюдения у нормальных субъектов с исходными двусторонними открытыми углами. Была проведена логистическая регрессия для выявления исходных факторов риска развития закрытия угла.
Результаты: Всего было зарегистрировано 457 пациентов с двусторонними открытыми углами на исходном уровне в возрасте 53,0 (45,5, 58,0) лет.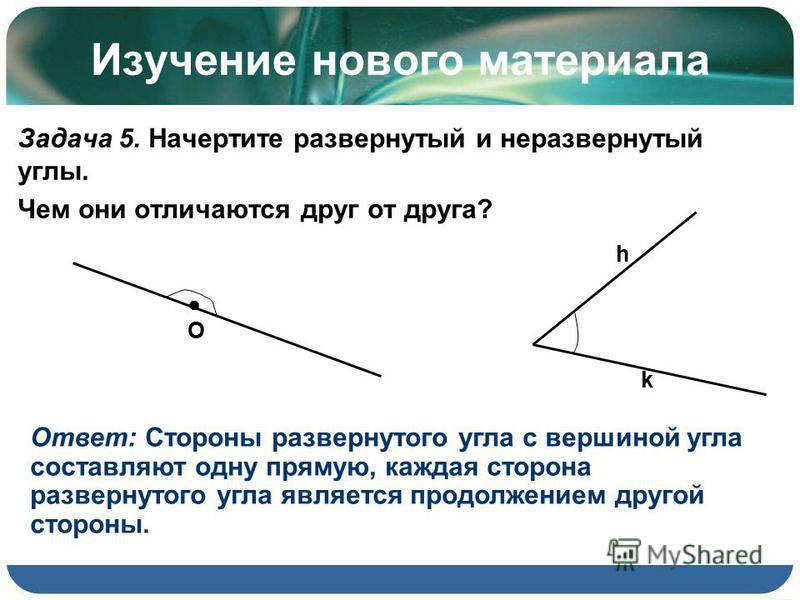 В 94,7% включенных случаев развился PACS, в 5,3% развился PAC, и ни у одного не развился PACG через 5 лет. В логистической регрессии значимыми факторами риска развития закрытия угла были меньшая глубина центральной передней камеры (ACD) (p = 0,002) и более узкая средняя ширина угла (p <0,001).
В 94,7% включенных случаев развился PACS, в 5,3% развился PAC, и ни у одного не развился PACG через 5 лет. В логистической регрессии значимыми факторами риска развития закрытия угла были меньшая глубина центральной передней камеры (ACD) (p = 0,002) и более узкая средняя ширина угла (p <0,001).
Выводы: В этом исследовании сообщается о развитии от исходного открытого угла до закрытия угла после 5-летнего наблюдения. Мы подтверждаем, что средняя ширина угла и центральная ACD были независимыми прогностическими факторами риска развития любой формы закрытия угла.
Ключевые слова: развитие закрытия угла; закрытие первичного угла; первичная закрытоугольная глаукома; подозрение на закрытие первичного угла; факторы риска.
© 2021 Авторы. Acta Ophthalmologica, опубликованная John Wiley & Sons Ltd от имени Acta Ophthalmologica Scandinavica Foundation.
Цифры
Рис. 1
Схема регистрации…
Рис. 1
Схема регистрации предметов
рисунок 1Блок-схема, показывающая зачисление субъектов
Рис. 2
Кривая рабочих характеристик приемника…
Рис. 2
Кривая рабочих характеристик приемника средней ширины угла и центральной передней камеры…
Рис. 2Кривая рабочих характеристик приемника средней ширины угла и глубины центральной передней камеры как комбинированный детерминант развития закрытия первичного угла
См. это изображение и информацию об авторских правах в PMC
это изображение и информацию об авторских правах в PMC
Похожие статьи
Прогрессирование подозреваемого закрытия первичного угла до закрытия первичного угла и сопутствующие факторы риска: исследование глаза Ханьдань.
Чжан И., Томас Р., Чжан Ц., Ли С.З., Ван Н.Л. Чжан И и др. Invest Ophthalmol Vis Sci. 2021 1 июня; 62(7):2. doi: 10.1167/iovs.62.7.2. Invest Ophthalmol Vis Sci. 2021. PMID: 34061952 Бесплатная статья ЧВК.
Десятилетняя частота первичного закрытия угла у пожилых китайцев: исследование глаз Liwan.
Ван Л., Хуан В., Хуан С., Чжан Дж., Го С., Фридман Д.С., Фостер П.Дж., Хе М. Ван Л. и др. Бр Дж Офтальмол. 2019Март; 103 (3): 355-360. doi: 10.1136/bjophthalmol-2017-311808. Эпаб 2018 18 мая.
 Бр Дж Офтальмол. 2019.
PMID: 29777045
Бр Дж Офтальмол. 2019.
PMID: 29777045Глазные биометрические факторы риска прогрессирования первичной болезни закрытия угла: исследование профилактики закрытия угла глаза Чжуншань.
Сюй Б.Я., Фридман Д.С., Фостер П.Дж., Цзян И., Порпорато Н., Пардеши А.А., Цзян И., Муньос Б., Аун Т., Хе М. Сюй Б.И. и др. Офтальмология. 2022 март;129(3): 267-275. doi: 10.1016/j.ophtha.2021.10.003. Epub 2021 8 октября. Офтальмология. 2022. PMID: 34634364 Клиническое испытание.
Детерминанты и характеристики закрытоугольной болезни у пожилых китайцев.
Ko YC, Liu CJ, Hsu WM, Cheng CY, Kuang TM, Chou P. Ко Ю.С. и др. Офтальмологический эпидемиол. 2015 апр; 22(2):109-15. дои: 10.3109/09286586.2015.1012270.
 Офтальмологический эпидемиол. 2015.
PMID: 25777310
Офтальмологический эпидемиол. 2015.
PMID: 25777310Шестилетняя заболеваемость и факторы риска первичной болезни закрытия угла: Сингапурское исследование эпидемиологии глазных болезней.
Тео З.Л., Со З.Д., Там Ю.К., Ю М., Чи М.Л., Тхакур С., Нонгпюр М.Е., Кох В., Вонг Т.И., Аунг Т., Ченг С.И. Тео З.Л. и др. Офтальмология. 2022 июль; 129 (7): 792-802. doi: 10.1016/j.ophtha.2022.03.009. Epub 2022 16 марта. Офтальмология. 2022. PMID: 35306094
Посмотреть все похожие статьи
Цитируется
Ультразвуковая биомикроскопия демонстрирует меньшую толщину цилиарного тела в глазах с закрытым углом.
Chen SY, He N, Yan YJ, Fan X, Wu LL. Чен С.И. и соавт. Int J Офтальмол.
 2022 18 сентября; 15 (9): 1476-1482. doi: 10.18240/ijo.2022.09.10. Электронная коллекция 2022.
Int J Офтальмол. 2022.
PMID: 36124192
Бесплатная статья ЧВК.
2022 18 сентября; 15 (9): 1476-1482. doi: 10.18240/ijo.2022.09.10. Электронная коллекция 2022.
Int J Офтальмол. 2022.
PMID: 36124192
Бесплатная статья ЧВК.Изображения переднего сегмента, полученные с помощью смартфона, для прогнозирования глубины передней камеры методом глубокого обучения: исследование, подтверждающее концепцию.
Qian C, Jiang Y, Soh ZD, Sakthi Selvam G, Xiao S, Tham YC, Xu X, Liu Y, Li J, Zhong H, Cheng CY. Цянь С. и др. Front Med (Лозанна). 2022, 23 июня; 9:912214. doi: 10.3389/fmed.2022.912214. Электронная коллекция 2022. Front Med (Лозанна). 2022. PMID: 35814744 Бесплатная статья ЧВК.
Распределение диаметра роговицы от белого к белому и глубины передней камеры у пациентов с близорукостью в Китае.

Сюй Г, У Г, Ду З, Чжу С, Го И, Ю Х, Ху Ю. Сюй Г и др. Front Med (Лозанна). 2021 18 нояб.;8:732719. doi: 10.3389/fmed.2021.732719. Электронная коллекция 2021. Front Med (Лозанна). 2021. PMID: 34869427 Бесплатная статья ЧВК.
использованная литература
- Alsbirk PH (1992): Анатомические факторы риска при первичной закрытоугольной глаукоме. Десятилетнее последующее исследование, основанное на лимбальной и аксиальной глубинах передней камеры в популяции высокого риска. Int Ophthalmol 16: 265–272. — пабмед
- Кассон Р.Дж., Бейкер М., Эдуссурия К., Сенаратне Т.
 , Сельва Д. и Сеннанаяке С. (2009): Распространенность и детерминанты закрытия угла в центральной части Шри-Ланки: исследование глаза Канди. Офтальмология 116: 1444–1449.
—
пабмед
, Сельва Д. и Сеннанаяке С. (2009): Распространенность и детерминанты закрытия угла в центральной части Шри-Ланки: исследование глаза Канди. Офтальмология 116: 1444–1449.
—
пабмед
- Кассон Р.Дж., Бейкер М., Эдуссурия К., Сенаратне Т.
- Chylack LT Jr, Wolfe JK, Singer DM et al. (1993): Система классификации помутнений хрусталика III. Продольное исследование группы изучения катаракты. Арх Офтальмол 111: 831–836. — пабмед
- Эри Джей Си, Ходж Д.О. и Грей Д.Т. (1997): заболеваемость первичной закрытоугольной глаукомой в округе Олмстед, штат Миннесота.

- Эри Джей Си, Ходж Д.О. и Грей Д.Т. (1997): заболеваемость первичной закрытоугольной глаукомой в округе Олмстед, штат Миннесота.

 ), Приложения теории когнитивного развития Academic Press, Нью-Йорк, стр. 49-93.
), Приложения теории когнитивного развития Academic Press, Нью-Йорк, стр. 49-93.
 Оливье и К. Ньюстед (ред.), Труды 20-й ежегодной конференции Международной группы психологии Математическое образование , Стелленбос, Том. 2, стр. 264-271.
Оливье и К. Ньюстед (ред.), Труды 20-й ежегодной конференции Международной группы психологии Математическое образование , Стелленбос, Том. 2, стр. 264-271. D. диссертация, Техасский технический университет.
D. диссертация, Техасский технический университет.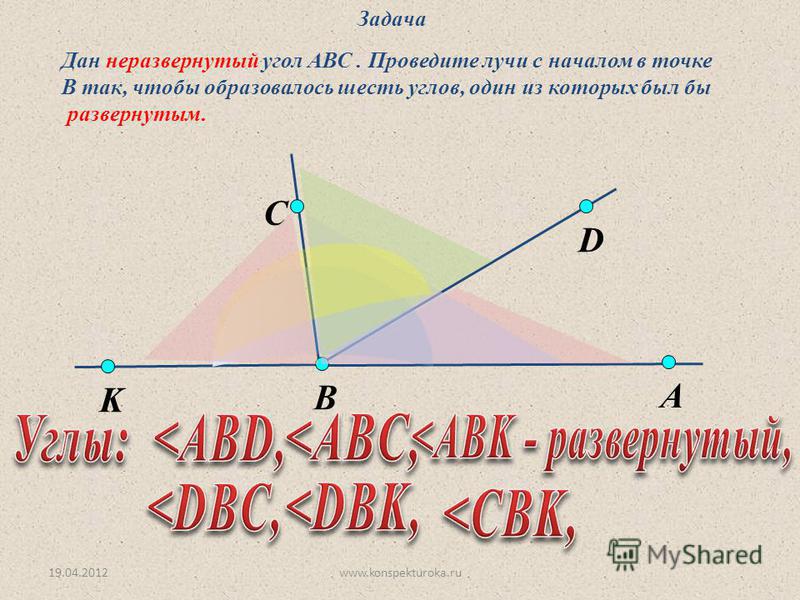

 К.: 1998, «Концепции токарной обработки для юных студентов», Познание и обучение 16, 265-284.
К.: 1998, «Концепции токарной обработки для юных студентов», Познание и обучение 16, 265-284. : 1991, «Прямое восприятие и другие формы знания», в Р. Р. Хоффман и Д. С. Палермо (ред.), Познание и символические процессы : Прикладные и экологические перспективы , Эрлбаум, Хиллсдейл , стр. 17-30.
: 1991, «Прямое восприятие и другие формы знания», в Р. Р. Хоффман и Д. С. Палермо (ред.), Познание и символические процессы : Прикладные и экологические перспективы , Эрлбаум, Хиллсдейл , стр. 17-30.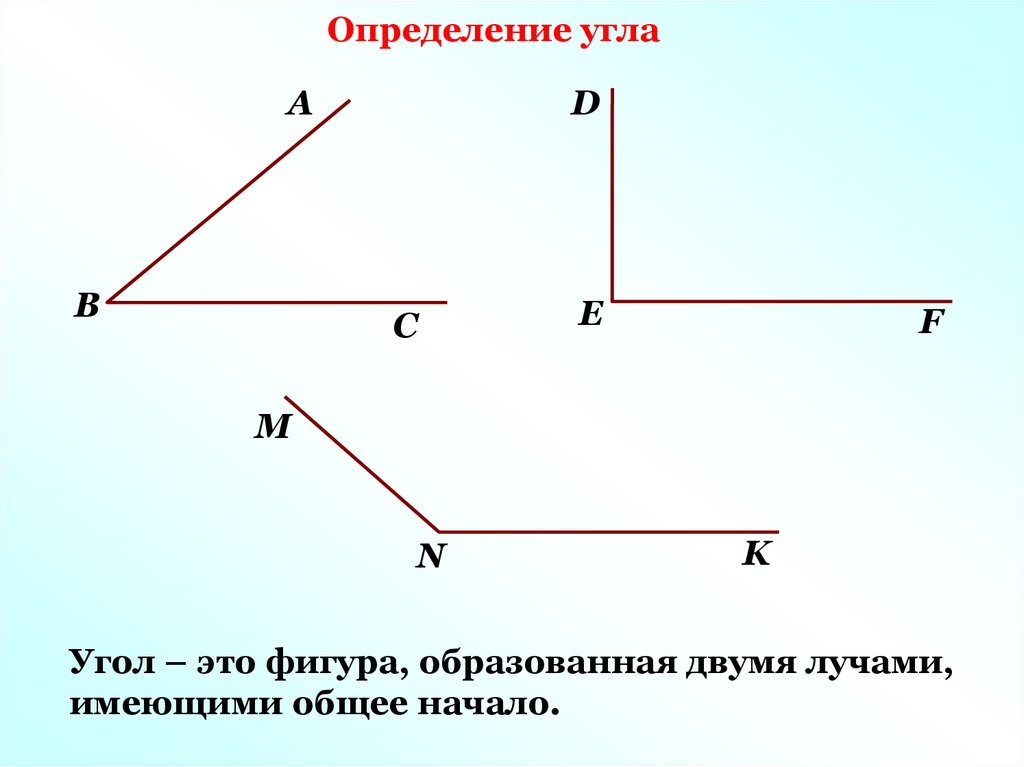 : 1975, «Теория Пиаже», в P.B.Neubauer (ред.), Процесс развития ребенка , Джейсон Аронсон, Нью-Йорк, стр. 164-212.
: 1975, «Теория Пиаже», в P.B.Neubauer (ред.), Процесс развития ребенка , Джейсон Аронсон, Нью-Йорк, стр. 164-212.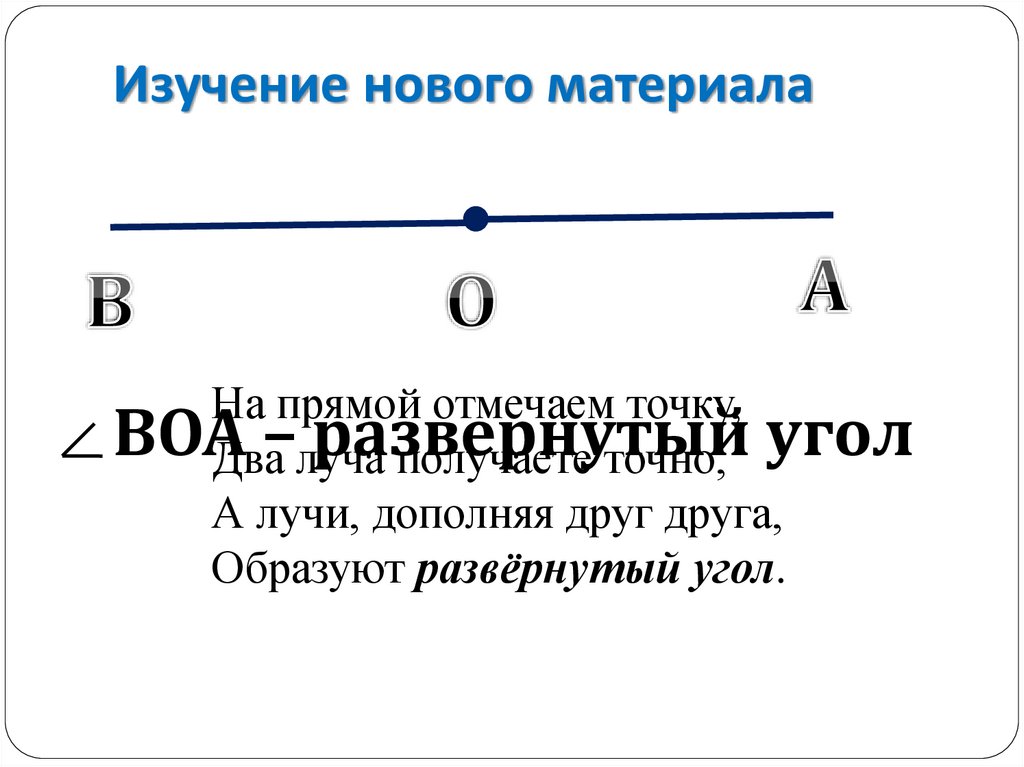 212-222.
212-222.
 С.: 1987, «Мышление и речь», в книге Р.В. Рибера и А.С. Картон (ред.) и Н. Миник (пер.), Собрание сочинений L . С . Выготский : Том . 1 . Проблемы общей психологии , Пленум, Нью-Йорк, стр. 39-285. (Оригинальная работа опубликована в 1934 г.)
С.: 1987, «Мышление и речь», в книге Р.В. Рибера и А.С. Картон (ред.) и Н. Миник (пер.), Собрание сочинений L . С . Выготский : Том . 1 . Проблемы общей психологии , Пленум, Нью-Йорк, стр. 39-285. (Оригинальная работа опубликована в 1934 г.)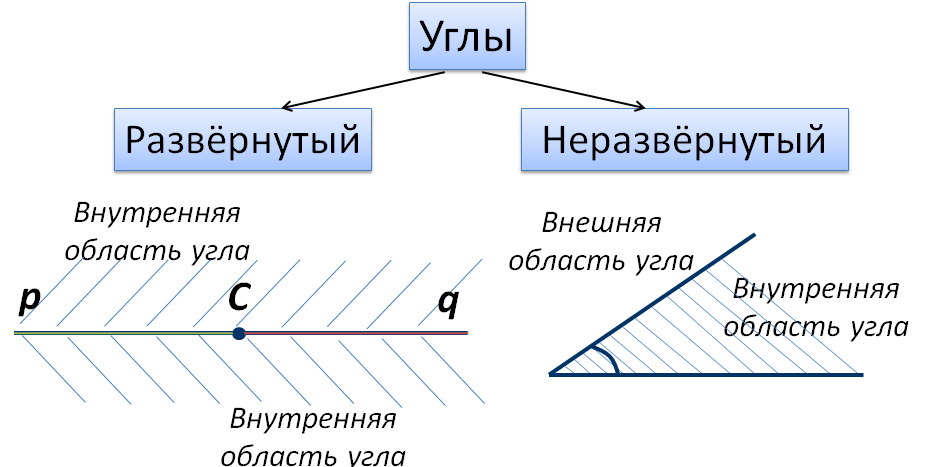

 Бр Дж Офтальмол. 2019.
PMID: 29777045
Бр Дж Офтальмол. 2019.
PMID: 29777045 Офтальмологический эпидемиол. 2015.
PMID: 25777310
Офтальмологический эпидемиол. 2015.
PMID: 25777310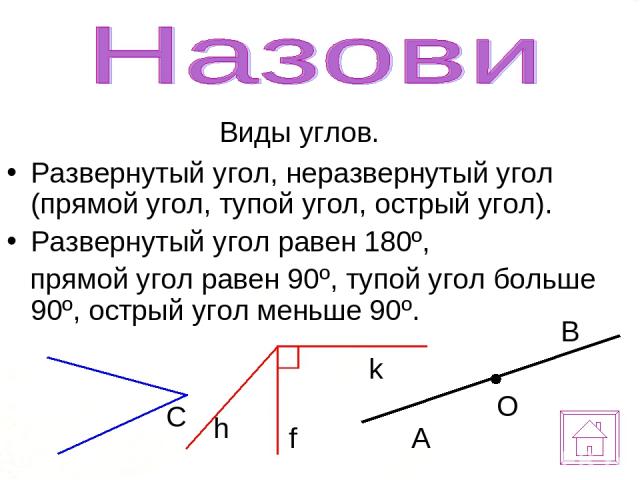 2022 18 сентября; 15 (9): 1476-1482. doi: 10.18240/ijo.2022.09.10. Электронная коллекция 2022.
Int J Офтальмол. 2022.
PMID: 36124192
Бесплатная статья ЧВК.
2022 18 сентября; 15 (9): 1476-1482. doi: 10.18240/ijo.2022.09.10. Электронная коллекция 2022.
Int J Офтальмол. 2022.
PMID: 36124192
Бесплатная статья ЧВК.
 , Сельва Д. и Сеннанаяке С. (2009): Распространенность и детерминанты закрытия угла в центральной части Шри-Ланки: исследование глаза Канди. Офтальмология 116: 1444–1449.
—
пабмед
, Сельва Д. и Сеннанаяке С. (2009): Распространенность и детерминанты закрытия угла в центральной части Шри-Ланки: исследование глаза Канди. Офтальмология 116: 1444–1449.
—
пабмед