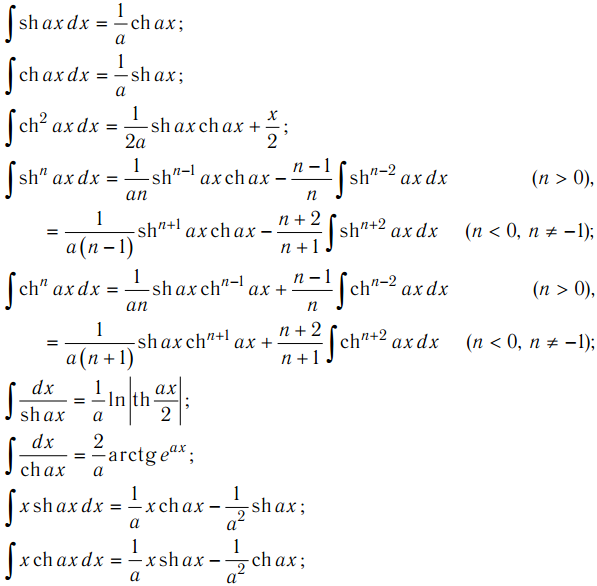Что такое синус гиперболический: Открытая Математика. Функции и Графики. Гиперболические функции

2-1}),\quad x\ge1,\\ \text{arsh}\,x={1\over2}\ln{{1+x}\over{1-x}},\quad ∣x∣\lt1,\\ \text{arcth}\,x={1\over2}\ln{{1+x}\over{1-x}}, \quad ∣x∣\gt1. \end{gathered}arshx=ln(x+x2+1),−∞<x<∞,arshx=ln(x+x2+1),−∞<x<∞,archx=ln(x+x2−1),x≥1,arshx=21ln1−x1+x,∣x∣<1,arcthx=21ln1−x1+x,∣x∣>1.

Рис. 1. Графики гиперболического синуса и гиперболического косинуса.

Редакция математических наук

Дата публикации: 8 ноября 2022 г. в 10:55 (GMT+3)

Содержание

Гиперболические функции свойства графики формулы

Справочные данные по гиперболическим функциям. Определения, графики и свойства гиперболического синуса, косинуса, тангенса и котангенса. Формулы сумм, разностей и произведений. Производные, интегралы, разложения в ряды. Выражения через тригонометрические функции.

Определения гиперболических функций, их области определений и значений

sh x – гиперболический синус: , –∞ < x < +∞; –∞ < y < +∞.
ch x – гиперболический косинус: , –∞ < x < +∞; 1 ≤ y < +∞.
th x – гиперболический тангенс: , –∞ < x < +∞; – 1 < y < +1.
cth x – гиперболический котангенс: , x ≠ 0; y < –1 или y > +1.

Графики гиперболических функций

График гиперболического синуса y = sh x График гиперболического косинуса y = ch x График гиперболического тангенса y = th x График гиперболического котангенса y = cth x

Формулы с гиперболическими функциями

Связь с тригонометрическими функциями

sin iz = i sh z ; cos iz = ch z
sh iz = i sin z ; ch iz = cos z
tg iz = i th z ; ctg iz = – i cth z
th iz = i tg z ; cth iz = – i ctg z
Здесь i – мнимая единица, i² = –1.

Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.

Четность

sh(–x) = – sh x; ch(–x) = ch x.
th(–x) = – th x; cth(–x) = – cth x.

Функция ch(x) – четная. Функции sh(x), th(x), cth(x) – нечетные.

Разность квадратов

ch² x – sh² x = 1.

Формулы суммы и разности аргументов

sh(x &pm; y) = sh x ch y &pm; ch x sh y,
ch(x &pm; y) = ch x ch y &pm; sh x sh y,
,
,

sh 2x = 2 sh x ch x ,
ch 2x = ch² x + sh² x = 2 ch² x – 1 = 1 + 2 sh² x,
.

Формулы произведений гиперболического синуса и косинуса

,
,
,

,
,
.

Формулы суммы и разности гиперболических функций

,
,
,
,
.

Связь гиперболического синуса и косинуса с тангенсом и котангенсом

, ,
, .

Производные

Интегралы от sh x, ch x, th x, cth x

,
,
.

Разложения в ряды

Обратные функции

Ареасинус

При – ∞ < x < ∞ и – ∞ < y < ∞ имеют место формулы:
,
.

Ареакосинус

При 1 ≤ x < ∞ и 0 ≤ y < ∞ имеют место формулы:
,
.

Вторая ветвь ареакосинуса расположена при 1 ≤ x < ∞ и – ∞ < y ≤ 0 :
.

Ареатангенс

При – 1 < x < 1 и – ∞ < y < ∞ имеют место формулы:
,
.

Ареакотангенс

При – ∞ < x < – 1 или 1 < x < ∞ и y ≠ 0 имеют место формулы:
,
.

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

{-х}=0$, что верно именно тогда, когда $x=0$.

Определение 4.11.3 Другие гиперболические функции $ $ \ eqalign {\ tanh x & = {\ sinh x \ over \ cosh x} \ cr \ coth х & = {\ сп х \ над \ зп х} \ кр \sech x &= {1\over\cosh x}\cr \csch x &= {1\over\sinx x}\cr} $$ Область определения $\coth$ и $\csch$ равна $x\neq 0$, а область определения остальные гиперболические функции — это все действительные числа. Графики показаны на рисунке 4.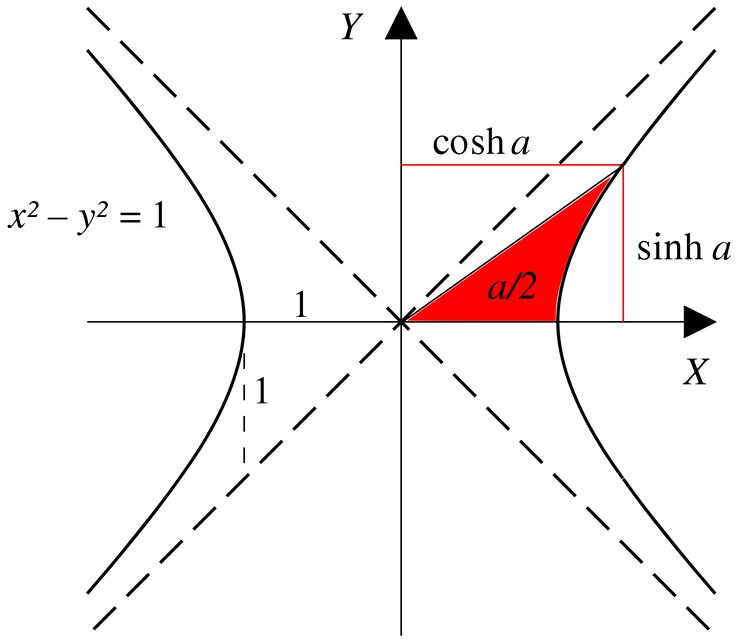

2 x = 1$. 92 t-1}=\pm\sinh t$. Так что для некоторых подходящие $t$, $\cosh t$ и $\sinh t$ — координаты типичного точка на гиперболе. На самом деле получается, что $t$ в два раза больше площадь, показанная на первом графике рисунок 4.11.2. Даже это аналогично тригонометрии; $\cos t$ и $\sin t$ – это координаты типичной точки на единичной окружности, а $t$ дважды площадь, показанная на втором графике рисунка 4.11.2.

Рисунок 4.11.2. Геометрические определения sin, cos, sinh, ch: $t$ в два раза больше заштрихованного площади на каждом рисунке. 9{-x }\over 2} =\cosh x$. $\qed$

Поскольку $\cosh x > 0$, $\sinh x$ возрастает и, следовательно, инъективен, поэтому У $\sinh x$ есть обратный $\arcsinh x$. Кроме того, $\sinh x >

0$, когда $x>0$, поэтому $\cosh x$ инъективен на $[0,\infty)$ и имеет (частичный) обратный, $\arccosh x$. Другие гиперболические функции имеют обратные также, хотя $\arcsech x$ является лишь частично обратным. Мы можем вычислить производные этих функций, поскольку у нас есть другие обратные функции.

2}}$. 92+1})$.)

Пример 4.11.2 Вычислите следующие пределы:

а. $\ds \lim_{x\to \infty} \cosh x$

б. $\ds \lim_{x\to \infty} \sinh x$

в. $\ds \lim_{x\to \infty} \tanh x$

д. $\ds \lim_{x\to \infty } (\cosh x -\sinh x)$

(отвечать)

Пример 4.11.3 Покажите, что диапазон $\tanh x$ равен $(-1,1)$. Что являются диапазонами $\coth$, $\sech$ и $\csch$? (Используйте тот факт, что они являются обратными функциями.) 92 х$. Вычислить производные остальных гиперболических функций.

Пример 4.11.8 Каковы области определения шести обратных гиперболических функции?

Пример 4.11.9 Нарисуйте графики всех шести обратных гиперболических функции.

Гиперболические тригонометрические функции | Brilliant Math & Science Wiki

Одной из ключевых характеристик, которая мотивирует гиперболические тригонометрические функции, является поразительное сходство с тригонометрическими функциями, что видно из формулы Эйлера: 9{\pm a} = \cosh a \pm \sinh a,\]

, что эквивалентно формуле Эйлера для гиперболических функций.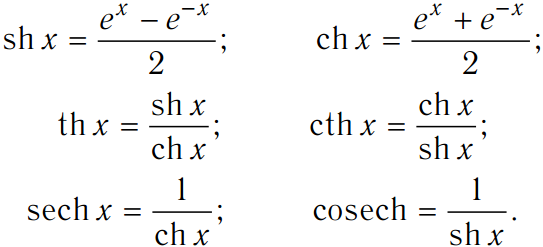 $ _\квадрат$

Билли Тангент наивно полагал, что функция гиперболического косинуса и функция стандартного косинуса одинаковы. Чтобы убедиться, он попробовал одно реальное значение и действительно получил тот же результат.

Какое значение он пробовал?

Если вы считаете, что это сработает для нескольких значений, введите в качестве ответа 99999.
Если вы считаете, что нет значений, для которых это будет работать, введите 88888 в качестве ответа. 9{-x}}{2}\)

$\tanh x = \dfrac{\sinh x}{\cosh x}$

$\coth x =\dfrac{1}{\tanh x}$

$\text{sech}\, x =\dfrac{1}{\cosh x}$

$\text{csch}\, y =\dfrac{1}{\sinx x}$.

Здесь показаны их графические изображения:

Графики шести тригонометрических гиперболических функций

\[ y=\text{sech}\, x\] \[у=\текст{csch}\, х\] \[у=\кош х\] \[y=\танх х\] \[у=\зп х\] \[y=\coth х\]

Какой из следующих гиперболических тригнометрических графиков лучше всего «аппроксимируется» с помощью $y = \frac{1}{x}?$

Параметрические уравнения для единичного круга задаются как

$x = \ cos т$
$у = \sint$.

Когда $t$ идет от $0 \стрелка вправо 2\pi$, $x$ и $y$ вычерчивают единичный круг:

Аналогично, параметрические уравнения для единичной гиперболы имеют вид

\[\sin\] \[\кос\] \[\загар\] \[\кроватка\] \[\сек\] \[\кск\] Ни один из 6 вышеперечисленных Более одного из 6 выше

Чарли Брайанс играл со следующими 6 тригонометрическими функциями:

$\sin$
$\кос$
$\загар$
$\кроватка$
$\сек$
$\кск$.

Он заметил, что для одного из них, если он приравняет его гиперболическому аналогу — $\sinh, \cosh, \tanh, \coth, \text{sech},$ или $\text{csch },$ соответственно — пересекается ровно в четырех точках.

Предполагая, что мы имеем дело только с действительными числами, какую триггерную функцию он выбрал?

Вдохновение: Brian Charlesworth

Часто возникает вопрос, является ли форма висячего моста контактной или параболой.

Теперь, если вы держите кусок веревки или цепь, поддерживаемую с обоих концов, она образует цепную связь \(\big(y =\lambda \cosh \frac{x}{\lambda}\big).\ ) Таким образом, можно сделать вывод, что подвесной мост принимает такую форму.

Однако трос моста отличается от цепи тем, что трос моста выдерживает не только собственный вес, но и вес самого моста. Итак, рассмотрим два примера:

, где вес моста незначителен по сравнению с тросом;
, где вес опорного троса незначителен по сравнению с весом моста.

Найдите форму троса подвесного моста (на фото выше), предполагая, что вес моста пренебрежимо мал по сравнению с весом тросов .

Если это так, то проблема аналогична болтающейся цепи.

Пусть функция ее формы равна $y(x)$, а WLOG определяет, что нижняя точка цепи находится в начале координат.

Определите следующее:

$\mu =$ вес на единицу длины троса

$T=$ натяжение троса.

Определите следующее для заданной точки P:

F = сила вдоль троса, направление которой будет представлять наклон троса в точке P 9{-1}(y’) = \frac{\mu x}{T}.\] $\big($Постоянная интегрирования отсутствует, так как самая нижняя точка троса находится в начале координат, поэтому $y'(0) =0.\big)$

Следовательно, \[y’ = \ sinh \ left (\ frac {\ mu x} {T} \ right) \ подразумевает y = \ frac {T} {\ mu} \ cosh \ left (\ frac {\ mu x} {T }\справа) + С. \] Опять же, нет константы интегрирования, поскольку $y(0) = 0,$, что подразумевает \[y = \frac{T}{\mu} \cosh\left(\frac{\mu x}{T}\right).\] Это можно упростить, установив $\lambda =\frac{T}{\mu}$: \[y=\lambda \cosh \frac{x}{\lambda}.\ _\square\]

Кстати, если вы когда-нибудь предполагали, что кривая оборванной цепи параболическая, вы не одиноки, так как часто говорят, что Галилей также предполагал параболическую форму. Это неудивительно, так как на этом рисунке показано сравнение двух кривых:

Теперь рассмотрим форму подвесного троса, предполагая, что вес троса пренебрежимо мал по сравнению с весом моста. Это немного легче решить, так как вес моста теперь однороден в направлении $x$, тогда как выше он менялся в зависимости от наклона цепи.

Найдите форму троса подвесного моста (на фото выше), считая, что вес троса пренебрежимо мал по сравнению с весом моста .

No related posts.