ОглавлениеОТ РЕДАКТОРА ПЕРЕВОДАГлава 1. ВВЕДЕНИЕ § 1.1. Формулировка задачи распознавания образов § 1.2. Обзор содержания книги по главам Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА § 2.1. Случайные векторы и их распределение 2.1.2. Условные плотности вероятности. 2.1.3. Параметры распределения. 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы. § 2.2. Свойства распределений 2.2.1. Характеристические функции. 2.2.2. Нормальные распределения. 2.2.3. Стохастическая сходимость. § 2.3. Преобразование случайных векторов 2.3.2. Линейное преобразование. 2.3.3. Ортонормированное преобразование. 2.3.4. Декоррелирующее преобразование. 2.3.5. Одновременная диагонализация двух матриц. § 2.4. Свойства собственных значений и собственных векторов 2.  4.2. Положительная определенность. 4.2. Положительная определенность.2.4.3. След матрицы. 2.4.4. Определитель и ранг матрицы. 2.4.5. Обращение матриц. 2.4.6. Теория возмущений. ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ Глава 3. ПРОВЕРКА ГИПОТЕЗ § 3.1. Проверка простых гипотез 3.1.2. Байесовское решающее правило, минимизирующее функцию риска. 3.1.3. Критерий Неймана — Пирсона. 3.1.4. Минимаксный критерий. § 3.2. Вероятность ошибки при проверке гипотез 3.2.2. Независимые случайные величины. 3.2.3. Вероятность ошибки для нормальных случайных векторов X. § 3.3. Верхние границы вероятности ошибки 3.3.2. Выражения для верхних границ в случае нормальных распределений. § 3.4. Другие критерии проверки гипотез 3.4.2. Критерий проверки сложных гипотез. 3.5.1. Последовательный критерий Вальда. 3.5.2. Реализация последовательного критерия Вальда. 3.5.3. Байесовский последовательный критерий. ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ Глава 4.  ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ§ 4.1. Байесовский линейный классификатор § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки. 4.2.2. Обобщенная формула для различных критериев. § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения 4.3.2. Совместная нормировка смеси в случае нормальных распределений. § 4.4. Требуемый выход и среднеквадратичная ошибка решения 4.4.2. Доказательство сходимости для случая линейной разделимости классов. § 4.5. Другие разделяющие функции 4.5.1. Линейные разделяющие функции для бинарных входов. 4.5.2. Кусочно-линейные разделяющие функции. 4.5.3. Обобщенные линейные разделяющие функции. ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ § 5.1. Оценивание неслучайных параметров 5.1.2. Оценки моментов. 5.1.3. Оценка максимального правдоподобия. 5.1.4. Достаточная оценка.  § 5.2. Оценивание случайных параметров 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку. 5.2.4. Выпуклые и симметричные функции штрафа. § 5.3. Интервальное оценивание 5.3.2. Порядковые статистики. 5.3.3. Толерантные пределы для распределений. § 5.4. Оценивание вероятности ошибки 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан. 5.4.3. Метод разбиения выборки. 5.4.4. Метод исключения одного объекта в случае нормальных распределений. ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ § 6.1. Оценка Парзена 6.1.2. Доказательство асимптотической несмещенности и состоятельности. 6.1.3. Равномерная сходимость и оценивание моды. 6.1.4. Обобщение на случай многомерной плотности вероятности. § 6.2. Метод k ближайших соседей 6.2.2. Решающее правило, основанное на методе k ближайших соседей.  6.2.3. Обобщение на случай нескольких классов. 6.2.4. Модифицированное правило k ближайших соседей. § 6.3. Метод гистограмм § 6.4. Разложение по базисным функциям 6.4.2. Плотность вероятности в случае двоичных переменных. ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ § 7.1. Последовательная корректировка линейного классификатора 7.1.1. Линейный классификатор для задач распознавания двух классов. 7.1.2. Доказательство сходимости для случая линейной разделимости классов. 7.1.3. Линейный классификатор для задач распознавания со многими классами. § 7.2. Стохастическая аппроксимация 7.2.1. Задача нахождения корня уравнения регрессии. 7.2.2. Доказательство сходимости метода Роббинса — Монро 7.2.3. Задача поиска максимума функции регрессии. 7.2.4. Обобщение на многомерный случай. 7.2.5. Метед потенциальных функций. 7.2.6. Ускорение сходимости. § 7.3. Последовательное байесовское оценивание ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ Глава 8.  ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ§ 8.1. Дискретное разложение Карунена — Лоева 8.1.2. Проблема нормализации. § 8.2. Другие критерии для случая одного распределения 8.2.2. Энтропия совокупности. § 8.3. Разложение Карунена — Лоева для случайных процессов 8.3.2. Стационарный процесс. § 8.4. Оценивание собственных значений и собственных векторов 8.4.1. Определение размерности. 8.4.2. Оценивание собственных значений и собственных векторов. 8.4.3. Доминирующие собственные значения. ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ § 9.1. Общие свойства разделимости классов § 9.2. Дискриминантный анализ 9.2.2. Выбор признаков, максимизирующих критерий J1 9.  2.3. Выбор признаков, максимизирующих критерий J2 2.3. Выбор признаков, максимизирующих критерий J29.2.4. Выбор признаков, максимизирующих критерий J3 9.2.5. Выбор признаков, максимизирующих критерий J4 9.2.6. Обобщение на случай многих классов. § 9.3. Граница Чернова и расстояние Бхатачария 9.3.2. Выбор признаков для нормальных распределений. 9.3.3. Верхняя граница для распределений, отличных от нормального. 9.3.4. Случай многих классов. § 9.4. Дивергенция ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА 10.1.1. Локальные свойства распределения. 10.1.2. Неитеративный алгоритм. 10.1.3. Итеративный алгоритм. § 10.2. Улучшение разделимости с помощью нелинейного преобразования 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки. 10.2.2. Неитеративный алгоритм. § 10.3. Двумерные отображения 10.3.2. Расстояние до двух фиксированных точек. ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ § 11.  11.1.2. Определение числа классов. § 11.2. Параметрические критерии качества классификации 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего. § 11.3. Иепараметрические критерии качества классификации 11.3.2. Непараметрический алгоритм автоматической классификации. 11.3.3. Асимптотические свойства процедуры. § 11.4. Другие процедуры автоматической классификации 11.4.2. Иерархическая классификация. 11.4.3. Классификация в режиме диалога. ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ ЛИТЕРАТУРА |
Сообщество Экспонента
- вопрос
- 02.05.2023
Другое
Мне нужно сделать интегральную частотно-импульсную систему автоматического управления теплопотреблением помещения. Я никак не могу разобраться как сделать регулятор ичим
Мне нужно сделать интегральную частотно-импульсную систему автоматического управления теплопотреблением помещения.
1 Ответ
- MATLAB
02.05.2023
- вопрос
- 02.05.2023
ПЛИС и СнК, Системы связи, Цифровая обработка сигналов, Другое, Встраиваемые системы
Задача — LDPC декодер внутри FPGA. Первый пришедший в голову вариант — декодер из MATLAB с последующей генерацией HDL. Источник : https://www.mathworks.com/help/wireless-hdl/ref/dvbs2ldpcde…
Задача — LDPC декодер внутри FPGA. Первый пришедший в голову вариант — декодер из MATLAB с последующей генерацией HDL. Источник : https://www.mathworks.com/help/wireless-hdl/ref/dvbs2ldpcde…
- Simulink
- ПЛИС и СнК
- Системы связи
02.05.2023
- вопрос
Системы управления, Электропривод и силовая электроника, Другое, Автоматизация испытаний
Необходимо рассмотреть различные режимы работы энергосистемы в зависимости от загрузки двигателей,но в схеме это просто мощность,активная и реактивная соответсвенно. Так же для этих параметеров рассчи…
Так же для этих параметеров рассчи…
Необходимо рассмотреть различные режимы работы энергосистемы в зависимости от загрузки двигателей,но в схеме это просто мощность,активная и реактивная соответсвенно. Так же для этих параметеров рассчи…
1 Ответ
- Simulink
24.04.2023
- вопрос
- 23.04.2023
ПЛИС и СнК
Здравствуйте! Требуется помощь в написании кода на verilog. Генератор импульсной последовательности с заданными параметрами реализован в виде блок-схемы. Результат этого проектирования, временные диаг…
Здравствуйте! Требуется помощь в написании кода на verilog. Генератор импульсной последовательности с заданными параметрами реализован в виде блок-схемы. Результат этого проектирования, временные диаг…
1 Ответ
- вопрос
- 19.04.2023
Изображения и видео, Цифровая обработка сигналов, Математика и статистика
Вроде как схема у меня получилась но при добавлении зависимости от температуры и старения возникли проблемы кто-нибудь знает как сделать по красоте?
Вроде как схема у меня получилась но при добавлении зависимости от температуры и старения возникли проблемы кто-нибудь знает как сделать по красоте?
- вопрос
- 14.
 04.2023
04.2023
Глубокое и машинное обучение(ИИ), Математика и статистика, Системы управления
Прошу помощи в создании модели газотранспортной системы в Simulink/Simscape. Спасибо
Прошу помощи в создании модели газотранспортной системы в Simulink/Simscape. Спасибо
6 Ответов
- Simulink
- modeling
- газ
14.04.2023
- вопрос
- 12.04.2023
Математика и статистика, Робототехника и беспилотники, Системы связи, Цифровая обработка сигналов
Всем привет. Мне нужно собрать схему FSK-модема для моей научной работы в университете. Требования:1. Модулятор в передатчике должен быть реализован на GMSK или 4-FSK (желательно не брать библиотечный…
Всем привет. Мне нужно собрать схему FSK-модема для моей научной работы в университете.
Требования:1. Модулятор в передатчике должен быть реализован на GMSK или 4-FSK (желательно не брать библиотечный. ..
..
2 Ответа
- вопрос
- 06.04.2023
Цифровая обработка сигналов
Добрый день, уважаемые участники форума! Подскажите, пожалуйста, как можно забрать те данные, по которым был построен график спектра сигнала? Они мне нужны для дальнейшей нормировки в excel.
Добрый день, уважаемые участники форума! Подскажите, пожалуйста, как можно забрать те данные, по которым был построен график спектра сигнала? Они мне нужны для дальнейшей нормировки в excel.
1 Ответ
- вопрос
- 04.04.2023
Цифровая обработка сигналов
End
End
7 Ответов
- вопрос
- 02.04.2023
Другое
Добрый день/вечер! подскажите, пожалуйста, как настроить матлаб чтобы можно было работать с ним удаленно. то есть он развернут на одной ПЭВМ, а мне нужно подключится с другой ПЭВМ, но не к виндоус чер…
Добрый день/вечер! подскажите, пожалуйста, как настроить матлаб чтобы можно было работать с ним удаленно. то есть он развернут на одной ПЭВМ, а мне нужно подключится с другой ПЭВМ, но не к виндоус чер…
то есть он развернут на одной ПЭВМ, а мне нужно подключится с другой ПЭВМ, но не к виндоус чер…
След матрицы
Марко Табога, доктор философии
След квадрата матрица представляет собой сумму своих диагональные входы.
Трассировка имеет несколько свойств, которые используются для доказательства важности приводит к матричной алгебре и ее приложениям.
Содержание
Определение
Примеры
Свойства
След суммы
След скалярного кратного
След линейной комбинации
След транспонирования матрицы
След произведения
900 13
След скаляра
Решенные упражнения
Упражнение 1
Упражнение 2
Определение
Начнем с формального определения.
Определение
Позволять
быть
матрица. Тогда его след, обозначаемый
или
,
это сумма его диагоналей
записей:
Тогда его след, обозначаемый
или
,
это сумма его диагоналей
записей:
Примеры
Ниже приведены некоторые примеры.
Пример Определите матрица Тогда его след
Пример Определите матрица Тогда его след
Свойства
В следующих подразделах сообщается о некоторых полезных свойствах оператора трассировки.
След суммы
След суммы двух матриц равен сумме их следов.
Предложение Позволять и быть двумя матрицы. Затем,
Доказательство
Помните, что сумма двух матриц равна выполняется суммированием каждого элемента одной матрицы с соответствующим элементом другой матрицы (см. лекцию о Добавление матрицы). Как следствие,
След скалярного множителя
Следующее предложение говорит нам, что происходит со следом, когда матрица
умножить на скаляр.
Предложение Позволять быть матрица и скаляр. Затем
Доказательство
Помните, что умножение матрицы скаляром выполняется путем умножения каждого элемента матрицы на заданное скаляр (см. лекцию о Умножение матрицы скаляром). Как следствие,
След линейной комбинации
Два вышеуказанных свойства (след сумм и скалярных кратных) подразумевают, что след линейного комбинация равна линейной комбинации трасс.
Предложение Позволять и быть двумя матрицы и и два скаляра. Затем,
След транспонирования матрицы
Транспонирование матрицы не меняет ее след.
Предложение Позволять быть матрица. Тогда
Доказательство
След матрицы есть сумма ее
диагональные элементы, но транспозиция оставляет диагональные элементы без изменений.
След продукта
Следующее предложение касается следа произведения матриц.
Предложение Позволять быть матрица и ан матрица. Затем
Доказательство
Обратите внимание, что это матрица и является матрица. Тогда где по шагам и мы использовали определение матричного произведения, в частности, те факты, что равно скалярному произведению между -й ряд и -й столбец , и равно скалярному произведению между -й ряд и -й столбец .
След скаляра
Тривиальное, но часто полезное свойство состоит в том, что скаляр равен своему след , потому что скаляр можно рассматривать как матрица, имеющая единственный диагональный элемент, который в свою очередь равен следу.
Это свойство часто используется для записи скалярных произведений в виде следов.
Пример Позволять быть вектор строки и а вектор-столбец. Затем продукт является скаляром, и где на последнем шаге мы использовали предыдущее предложение о следе матрицы продукты. Таким образом, мы смогли записать скаляр как след от матрица .
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Позволять быть матрица определена поНайти его след.
Решение
Суммируя диагональные элементы, мы получить
Упражнение 2
Позволять быть матрица и а вектор. Написать продуктыкак след произведения двух матрицы.
Раствор
С тех пор
это скаляр, у нас есть это
Более того,
является
и
является
.
Следовательно, где
оба
и
являются
.
Как цитировать
Пожалуйста, указывайте как:
Taboga, Marco (2021). «След матрицы», Лекции по матричной алгебре. https://www.statlect.com/matrix-алгебра/trace-of-a-matrix.
След матрицы
Марко Табога, доктор философии
След квадрата матрица представляет собой сумму своих диагональные входы.
Трассировка имеет несколько свойств, которые используются для доказательства важности приводит к матричной алгебре и ее приложениям.
Содержание
Определение
Примеры
Свойства
След суммы 90 003
След скалярного кратного
След линейной комбинации
След транспонирования матрицы
След произведения
След скаляра
Решенные упражнения
Упражнение 1
Упражнение 2
Определение
Начнем с формального определения.
Определение Позволять быть матрица. Тогда его след, обозначаемый или , это сумма его диагоналей записи:
Примеры
Ниже приведены некоторые примеры.
Пример Определите матрица Тогда его след
Пример Определите матрица Тогда его след
Свойства
В следующих подразделах сообщается о некоторых полезных свойствах оператора трассировки.
След суммы
След суммы двух матриц равен сумме их следов.
Предложение Позволять и быть двумя матрицы. Затем,
Доказательство
Помните, что сумма двух матриц равна выполняется суммированием каждого элемента одной матрицы с соответствующим элементом другой матрицы (см. лекцию о Добавление матрицы). Как следствие,
След скалярного множителя
Следующее предложение говорит нам, что происходит со следом, когда матрица
умножить на скаляр.
Предложение Позволять быть матрица и скаляр. Тогда
Доказательство
Помните, что умножение матрицы скаляром выполняется путем умножения каждого элемента матрицы на заданное скаляр (см. лекцию о Умножение матрицы скаляром). Как следствие,
След линейной комбинации
Два вышеуказанных свойства (след сумм и скалярных кратных) подразумевают, что след линейного комбинация равна линейной комбинации трасс.
Предложение Позволять и быть двумя матрицы и и два скаляра. Затем,
След транспонирования матрицы
Транспонирование матрицы не меняет ее след.
Предложение Позволять быть матрица. Затем
Доказательство
След матрицы есть сумма ее
диагональные элементы, но транспозиция оставляет диагональные элементы без изменений.
След продукта
Следующее предложение касается следа произведения матриц.
Предложение Позволять быть матрица и ан матрица. Затем
Доказательство
Обратите внимание, что это матрица и является матрица. Тогда где по шагам и мы использовали определение матричного произведения, в частности, те факты, что равно скалярному произведению между -й ряд и -й столбец , и равно скалярному произведению между -й ряд и -й столбец .
След скаляра
Тривиальное, но часто полезное свойство состоит в том, что скаляр равен своему след , потому что скаляр можно рассматривать как матрица, имеющая единственный диагональный элемент, который в свою очередь равен следу.
Это свойство часто используется для записи скалярных произведений в виде следов.
Пример Позволять быть вектор строки и а вектор-столбец. Затем продукт является скаляром, и где на последнем шаге мы использовали предыдущее предложение о следе матрицы продукты. Таким образом, мы смогли записать скаляр как след от матрица .
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Позволять быть матрица определена поНайти его след.
Решение
Суммируя диагональные элементы, мы получить
Упражнение 2
Позволять быть матрица и а вектор. Написать продуктыкак след произведения двух матрицы.
Раствор
С тех пор
это скаляр, у нас есть это
Более того,
является
и
является
.
Следовательно, где
оба
и
являются
.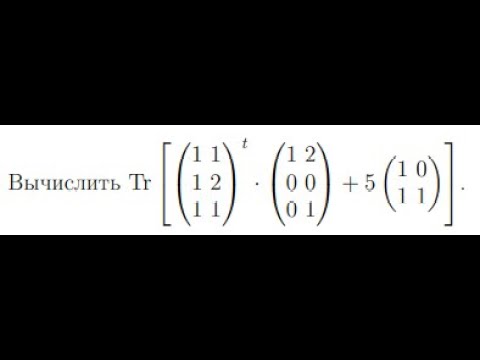


 04.2023
04.2023