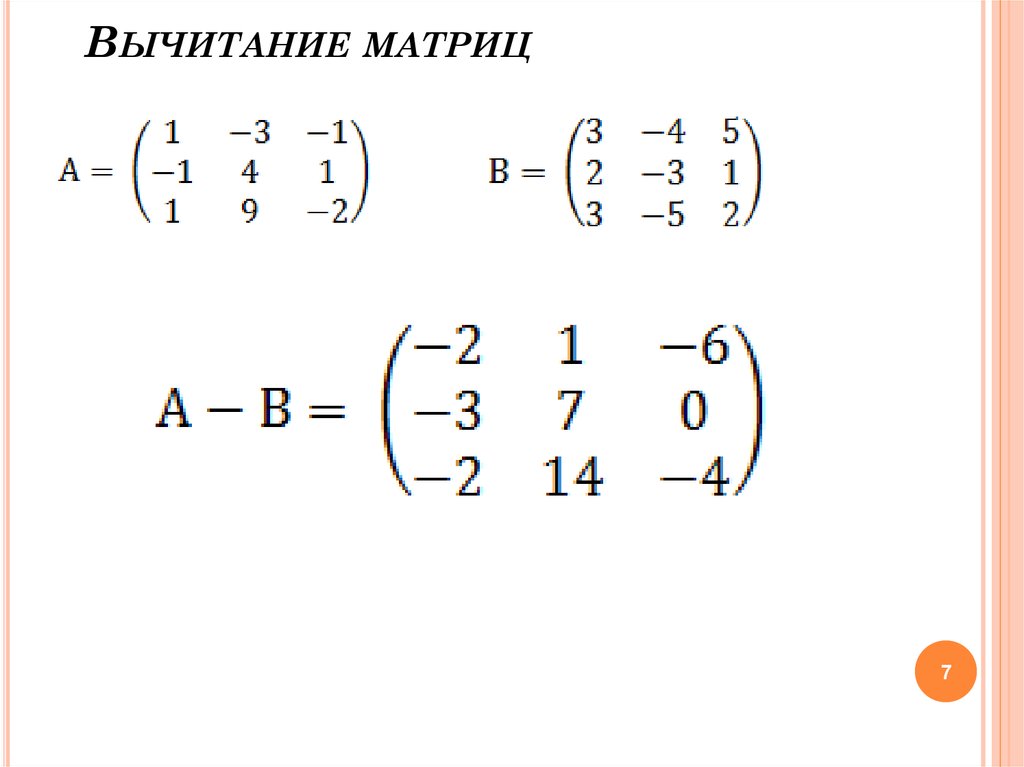Матрицы вычитание: Онлайн калькулятор. Сложение и вычитание матриц

alexxlab / / Разное

1.6. Сложение и вычитание матриц

Складывать и вычитать можно матрицы одного размера. Суммой матриц A=(aij) и B=(bij) размера mn называется матрица C=A+B, элементы которой cij=aij+bij, для i=1,2,…,m; j=1,2,…, n. В частном случае A+0=A.

Аналогично определяется разность двух матриц C=A—B.

Пример

Предположим, что в диапазон ячеек A1:C2 введена матрица A размера 23, а матрица B также размера 23 – в диапазон A4:C5.

1. Табличный курсор установим в левый верхний угол результирующей матрицы , например, в A7.

2. Вводим формулу для вычисления первого элемента результирующей матрицы = A

1+A4

3. Скопируем введенную формулу в остальные ячейки результирующей матрицы A7:C8. В итоге получим:

Аналогично вычисляется разность.

1.7. Умножение матрицы на число

Произведением матрицы на число k называется матрица B=kA, элементы которой bij=kaij, для i=1,2,…,m; j=1,2,…, n.

Пример

Предположим, что в диапазон ячеек A1:C2 введена матрица A размера 23. Найдем матрицу C=3A

1. Табличный курсор установим в левый верхний угол результирующей матрицы , например, в E1.

2. Вводим формулу для вычисления первого элемента результирующей матрицы = 3*A1

3. Скопируем введенную формулу в остальные ячейки результирующей матрицы E1:G3. В итоге получим:

1.8. Умножение матриц

Произведение матриц определено, если число столбцов первой матрицы равно числу строк второй.

Пусть A=(aij)mn, B=(bij)np, тогда размерность произведения AB равна mp. При этом матрица C (размера mp) называется произведением матриц A и B, если каждый ее элемент cij равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B:

, i=1,2,…,m; j=1,2,…, n.

Пример

Предположим, что в диапазон ячеек A1:D3 введена матрица A размера 34, а матрица B размера 42 – в диапазон A5:B8.

1. Выделяем блок ячеек под результирующую матрицу (32). Например, F1:G3

2. Вставляем функцию.

3. В диалоговом окне Мастер функций выбираем категорию Математические и функцию МУМНОЖ.

4. В диалоговом окне МУМНОЖ в поле Массив1 вводим диапазон матрицы A ‑ A1:D3, в поле Массив2 вводим диапазон матрицы B – A5:B8

5. Нажимаем сочетание клавиш CTRL+SHIFT+ENTER. В итоге получим:

2. Решение системы линейных уравнений

Пусть дана система линейных уравнений.

Такая запись называется системой линейных уравнений в нормальной форме.

Эту систему можно записать как AX=B, где

А – матрица коэффициентов при переменных, или матрица системы:

X – матрица-столбец (вектор) неизвестных:

B – матрица-столбец (вектор) свободных членов:

Решение системы методом обратной матрицы будет матрица-столбец X=A-1B

Таким образом, для решения системы необходимо найти обратную матрицу коэффициентов и умножить ее на справа на вектор свободных членов.

Пример

Пусть необходимо решить систему

1. Вводим матрицу A (в данном случае размера 22) в диапазон A1:B2. Вектор B в диапазон D1:D2.

2. Находим обратную матрицу A-1

  • Выделяем блок ячеек под обратную матрицу (22). Например, A4:B5.

  • Вставляем функцию

  • В диалоговом окне Мастер функций выбираем категорию

    Математические и функцию МОБР.

  • В диалоговом окне МОБР в поле Массив вводим диапазон матрицы A ‑ A1:B2

  • Нажимаем сочетание клавиш CTRL+SHIFT+ENTER. В итоге получим:

3. Умножением обратной матрицы A-1 на вектор B найдем вектор X.

  • 1. Выделяем блок ячеек под результирующую матрицу (под вектор X 21). Например, D4:D5

  • Вставляем функцию

  • В диалоговом окне Мастер функций выбираем категорию Математические и функцию МУМНОЖ

  • В диалоговом окне МУМНОЖ в поле Массив1 вводим диапазон матрицы A-1‑ A4:B5, в поле Массив2 вводим диапазон матрицы B – D1:D2

  • Нажимаем сочетание клавиш CTRL+SHIFT+ENTER.

    В итоге получим:

Т.е. x=5, а y=-4

Matrix subtraction within Matlab — MATLAB Answers

whos

Name Size Bytes Class Attributes

E 2×1 16 double

E11 1×1 8 double

E21 1×1 8 double

Er 3×1 24 double

Er11 1×435 3480 double

Er21 1×435 3480 двойной

Er31 1×435 3480 двойной

ErA 3×1 24 double

ErA11 1×434 3472 double

ErA21 1×434 3472 double

ErA31 1×434 3472 double

ErB 3×1 24 double

ErB11 1×434 3472 double

ErB21 1×434 3472 double

ErB31 1×434 3472 double

ErC 3×1 24 двойной

ErC11 1×434 3472 double

ErC21 1×434 3472 double

ErC31 1×434 3472 double

H 2×3 48 double

I 3×3 72 double

InA 2×1 16 double

InA11 1×434 3472 double

InA21 1×434 3472 double

. ..

Вот, кстати, почему вам НЕ НУЖНО создавать такие кучи пронумерованных переменных. Это невероятно плохой стиль программирования, так как вы будете совершать ошибку за ошибкой, вводя неправильное имя переменной. НАУЧИТЕСЬ ИСПОЛЬЗОВАТЬ ВЕКТОРЫ. Лучше научитесь использовать массивы.

Несмотря на это, вы только думаете, что он сделал что-то другое, вероятно, из-за множества разных имен переменных и, возможно, из-за того, что вы используете короткий формат отображения.

format long g

>> x

x =

10869.0885676116

0.228888860503846

-1.088

860864

xt

xt =

10869.05

-0.299999999999384

-1.1

xt — x

ans =

-0,0385676116566174 9Результат будет идентичным. Единственная проблема заключается в том, что иногда, когда вы отображаете вектор в результате, он может отображаться так, что выглядит по-другому, особенно если вы показываете только 4 цифры.

Частая и похожая ошибка, совершаемая новыми пользователями MATLAB, заключается в том, что они будут отображать числа, используя короткий формат, как:

короткий формат

>> x

x =

1. 0e+04 *

1.0869

0.0000

-0.0001

>> xt

xt =

1.0e+04 *

1.0869

-0.0000

-0,0001

, а затем либо пропустят 1.0e+4 вверху, либо решат, что это именно то, что они видят, а затем произведут вычитание вручную.

Извините, но это НЕ ошибки MATLAB. Это ошибка пользователя, с вероятностью 100%. Я даже не буду называть это вероятной ошибкой пользователя, так как это подразумевало бы некую смутную вероятность того, что это не ошибка пользователя. По мере развития навыков работы с MATLAb вы научитесь лучше использовать свои переменные, но вы также научитесь работать медленнее, чтобы более тщательно проверять свою работу.

Matrix Subtraction

arm_status  arm_mat_sub_f16 (const arm_matrix_instance_f16 *pSrcA, const arm_matrix_instance_f16 *pSrcB, arm_matrix_instance_f16 *pDst)
  Floating-point matrix subtraction. Подробнее…
 
arm_status  arm_mat_sub_f32 (const arm_matrix_instance_f32 *pSrcA, const arm_matrix_instance_f32 *pSrc_Binstance_f32 *pSrc_Binstance_matrix_f32 *pSrc_Binstance_matrix_f32 *pSrcB, arm_matrix0137
  Вычитание матрицы с плавающей запятой. More…
 
arm_status  arm_mat_sub_f64 (const arm_matrix_instance_f64 *pSrcA, const arm_matrix_instance_f64 *pSrcB, arm_matrix_instance_f64 *pDst)
  Floating-point matrix subtraction. Подробнее…
 
arm_status  arm_mat_sub_q15 (const arm_matrix_instance_q15 *pSrcA, const arm_matrix_instance_q15 *pSrc_B, arm_matrix) ptrixDst1 *pSrc_B, arm_matrix0137
  Вычитание матрицы Q15. More…
 
arm_status 
arm_mat_sub_q31 (const arm_matrix_instance_q31 *pSrcA, const arm_matrix_instance_q31 *pSrcB, arm_matrix_instance_q31 *pDst)
  Q31 matrix subtraction. Подробнее…
 

Вычтем две матрицы.

Разделение двух матриц 3 x 3

Функции проверяют, чтобы pSrcA , pSrcB и pDst имели одинаковое количество строк и столбцов.

arm_status arm_mat_sub_f16 ( константа arm_matrix_instance_f16 * псркА ,
константа arm_matrix_instance_f16 * pSrcB ,
arm_matrix_instance_f16 *  pDst  
)

Параметры
[in] pSrcA указывает на первую структуру входной матрицы
[in] pSrcB указывает на вторую структуру входной матрицы
[out] pDst указывает на выходную матричную структуру
Возвращает
статус выполнения
  • ARM_MATH_SUCCESS : Операция выполнена успешно
  • ARM_MATH_SIZE_MISMATCH: проверка размера матрицы не удалась

arm_status arm_mat_sub_f32 ( константа arm_matrix_instance_f32 *  псркА ,
константа arm_matrix_instance_f32 *  pSrcB ,
arm_matrix_instance_f32 *  pDst  
)

Параметры
[in] pSrcA points to the first input matrix structure
[in] pSrcB points to the second input matrix structure
[out] pDst points для вывода матричной структуры
Возвращает
статус выполнения
  • ARM_MATH_SUCCESS : Операция выполнена успешно
  • ARM_MATH_SIZE_MISMATCH: проверка размера матрицы не удалась

arm_status arm_mat_sub_f64 ( константа arm_matrix_instance_f64 * псркА ,
 константа arm_matrix_instance_f64 * pSrcB ,
arm_matrix_instance_f64 *  пдст  
)

Параметры
[in] pSrcA points to the first input matrix structure
[in] pSrcB points to the second input matrix structure
[out] pDst points для вывода матричной структуры
Возвращает
статус выполнения
  • ARM_MATH_SUCCESS : Операция выполнена успешно
  • ARM_MATH_SIZE_MISMATCH: проверка размера матрицы не удалась

arm_status arm_mat_sub_q15 ( константа arm_matrix_instance_q15 * псркА ,
константа arm_matrix_instance_q15 *  pSrcB ,
arm_matrix_instance_q15 *  pDst  
)

Параметры
[in] pSrcA указывает на первую структуру входной матрицы
[in] pSrcB указывает на вторую структуру входной матрицы
[out] pDst указывает на структуру выходной матрицы
Возвращает
статус выполнения
  • ARM_MATH_SUCCESS : Операция выполнена успешно
  • ARM_MATH_SIZE_MISMATCH: проверка размера матрицы не удалась
Масштабирование и поведение при переполнении
Функция использует арифметику насыщения.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *