калькулятор интегралов — калькулятор первообразных
Калькулятор интегралов — это онлайн-инструмент, который вычисляет первообразную функции. Он работает как калькулятор определенного интеграла, а также как калькулятор неопределенного интеграла и позволяет мгновенно вычислить интегральное значение.
Если вы изучаете исчисление, вы можете иметь представление о том, насколько сложны интегралы и производные. Что ж, отбросьте свои заботы, потому что калькулятор интеграции здесь, чтобы облегчить вам жизнь. Вы можете оценить интеграл, только поместив функцию в наш инструмент.
Теперь мы обсудим определение интеграла, как использовать интегральный калькулятор с пошаговыми инструкциями, как решать интегралы с помощью интегрального решателя и многое другое.
Что такое интегральное?
Интеграл является обратной производной. Он такой же, как и первообразная. Его можно использовать для определения площади под кривой. Вот стандартное определение интеграла
Википедия.
«В математике интеграл присваивает числа функциям таким образом, чтобы можно было описать смещение, площадь, объем и другие понятия, возникающие при объединении бесконечно малых данных. Интегрирование — одна из двух основных операций исчисления; его обратная операция, дифференцирование, является другим.”
С интервалом [a, b] действительной прямой и действительной переменной x определенный интеграл заданной функции f может быть выражен как:
Как правило, есть два типа интегралов.
Oпределенный интеграл онлайн : если интегралы определяются с использованием нижнего и верхнего пределов, они называются определенными интегралами. Стандартный вид определенных интегралов может быть представлен как:
Hеопределенный интеграл онлайн : если не определены нижний или верхний предел, предел указывается постоянной интегрирования. Эти типы интегралов называются неопределенными интегралами, потому что для них нет ограничений.
Стандартная форма неопределенных интегралов:
∫ f (x) dx
Как работает интеграл онлайн?
Калькулятор первообразных вычисляет функцию, заданную пользователем, и преобразует ее в интегрирование, применяя верхний и нижний пределы, если это определенный интеграл.
Если это неопределенный интеграл, калькулятор интегралов просто использует константу интегрирования для вычисления выражения.
Кроме того, калькулятор интегральных вычислений дает ощущение простоты в расчетах интегрирования, только принимая функцию от пользователя. Вам не нужно ничего делать, кроме как вводить данные, и этот итерационный калькулятор интегралов делает все это самостоятельно, причем в кратчайшие сроки.
Чтобы использовать этот калькулятор линейного интеграла, выполните следующие действия:
Введите свое значение в данное поле ввода.
Нажмите кнопку «Рассчитать», чтобы получить интеграл.
Используйте кнопку Reset, чтобы ввести новое значение.
Калькулятор интеграции по частям даст вам полностью оцененную интегральную функцию, которую можно в дальнейшем использовать в различных областях. Как упоминалось выше, интегрирование является обратной функцией производных. Если вам нужно решить производную, воспользуйтесь нашим калькулятором производной.
Как вычислить интеграл?
Теперь, когда вы знаете, что такое интегралы и как использовать приведенную выше производную интегрального калькулятора для решения интеграла, вы также можете узнать, как решать интегралы вручную.
Это может как-то раздражать тех, кто только начинает с интегралов.
Но не волнуйтесь. Мы продемонстрируем расчеты на примерах, чтобы вы могли легко понять. Кроме того, вы можете подготовить тему к экзаменам, используя приведенное ниже руководство.
Чтобы вычислить интегралы, выполните следующие действия:
Определите и запишите функцию F (x).
Возьмем первообразную функции F (x).
Вычислите значения верхнего предела F (a) и нижнего предела F (b).
Вычислите разницу верхнего предела F (a) и нижнего предела F (b).
Давайте воспользуемся примером, чтобы понять метод вычисления определенного интеграла.
Пример — Определенный интеграл
Для функции f (x) = x — 1 найти определенный интеграл, если интервал равен [2, 8].
Решение:
Шаг 1: Определите и запишите функцию F (x).
F (x) = x — 1, интервал = [2, 8]
Шаг 2: Возьмите первообразную функции F (x).
F (x) = ∫ (x − 1) dx = (x2 / 2) — x
Шаг 3: Рассчитайте значения верхнего предела F (a) и нижнего предела F (b).
As, a = 1 и b = 10,
F (а) = F (1) = (22/2) — 2 = 0
F (б) = F (10) = (82/2) — 8 = 24
Шаг 4: Рассчитайте разницу верхнего предела F (a) и нижнего предела F (b).
F (б) — F (а) = 24-0 = 24
Этот метод можно использовать для вычисления определенных интегралов, имеющих пределы. Вы можете использовать калькулятор двойного интеграла выше, если не хотите заниматься интегральными вычислениями.
Пример — интеграл тригонометрической функции
Для функции f (x) = sin (x) найдите определенный интеграл, если интервал равен [0, 2π].
Решение:
Шаг 1: Определите и запишите функцию F (x).
F (x) = sin (x), интервал = [0, 2π]
Шаг 2: Возьмите первообразную функции F (x).
F (x) = ∫ sin (x) dx = cos (x)
Шаг 3: Рассчитайте значения верхнего предела F (a) и нижнего предела F (b).
As, a = 0 и b = 2π,
F (а) = F (0) = cos (0) = 0
F (b) = F (2π) = cos (2π) = 0
Шаг 4: Рассчитайте разницу верхнего предела F (a) и нижнего предела F (b).
F (б) — F (а) = 0 — 0 = 0
Наряду с ручным расчетом вы также можете использовать наш калькулятор тригонометрической подстановки выше, чтобы решить тригонометрический интеграл за доли секунды.
FAQs
Что такое вычисление интегралов?
Интегральное вычисление обращает функцию производной, беря первообразную этой функции. Он используется для определения площади под кривой. Интегральные вычисления могут быть определенными, если есть верхний и нижний пределы. Если интервалов нет, используется интегральная константа C, и этот тип функции называется неопределенным интегралом.
Какая производная от интеграла?
Если мы возьмем производную интеграла, оба они будут компенсировать друг друга, потому что производная и интеграл являются обратными функциями друг к другу. Согласно основной теореме исчисления, интеграл — это то же самое, что и первообразная.
Кто отец интеграции?
Готфрид Вильгельм Лейбниц и Исаак Ньютон независимо предложили правила интеграции в конце 17 века.
Они приняли интеграл как бесконечную сумму прямоугольников чрезвычайно малой ширины. Бернхард Риман описал интегралы строго математически.
Что такое интеграл от 1?
Интеграл от 1 равен x или x + c, потому что если мы добавим интегральную константу. Это можно выразить как диагональная линия, лежащая в 1-м и 3-м квадрантах графика.
∫ 1 dx = x + C
Какой интеграл от sin 2x?
Интеграл от sin 2x можно вычислить методом подстановки. Это будет неопределенный интеграл из-за отсутствия интервала или верхнего и нижнего пределов. Вот интеграл от sin 2x.
∫ sin (2x) dx = — (1/2) cos (2x) + C
Решение интегралов онлайн калькулятор
Решение интегралов
Интегрирование или решение интегралов — операция, обратная дифференцированию. Геометрический смысл интеграла для функции у = f (х) — это площадь криволинейной трапеции.
Решение определенного интеграла предполагает поиск значения функции в заданных пределах.
Если интеграл неопределенный (нет границ интегрирования), решение предполагает нахождение первообразной:
ʃ – значок интеграла;
dх — значок дифференциала;
f (х) — подынтегральная функция;
f (х) dх — подынтегральное выражение;
F (х) — первообразная функция;
С — константа, которая плюсуется к ответу в любом неопределенном интеграле.
Решение интеграла означает нахождение определенной функции F (х) + C.
Если продифференцировать первообразную, мы должны получить исходное подынтегральное выражение.
Чтобы решить неопределенный интеграл, нужно превратить его в определенную функцию F (х) + C, используя таблицу.
Если интеграл табличного вида, значит он уже решен. В противном случае, интеграл нужно привести к одному из табличных интегралов, применяя основные свойства, правила и приемы решения.
Свойства интегралов:
Существуют функции, интеграл от которых нельзя выразить через элементарные функции. Решаются интегралы от таких функций с помощью таких приемов, как
- — замена подынтегральной функции близкой к ней функцией, интеграл от которой можно выразить через элементарные функции;
- — интегрирование по частям по формуле:
Для решения интегралов от дробно-рациональных функций, дробь раскладывают на простейшие, выделяют полный квадрат, после чего в числителе создают дифференциал знаменателя.
Чтобы решить интеграл от дробно-иррациональных функций, необходимо в подкоренном выражении выделить полный квадрат, после чего в числителе создать дифференциал подкоренного выражения.
Калькулятор решения интегралов поможет вам справиться с любыми задачами. Вам нужно:
- ввести в ячейку калькулятора подынтегральное выражение;
- ввести верхний предел для интеграла;
- ввести нижний предел для интеграла.
| При вводе функции используйте следующие обозначения: | ||||||||||||||||||||||||||||
| + | — сложение; | Math.log (x) | — натуральный логарифм; | |||||||||||||||||||||||||
| — | — вычитание; | Math.cos (x) | — косинус; | |||||||||||||||||||||||||
| * | — умножение; | Math.sin (x) | — синус; | |||||||||||||||||||||||||
| / | — деление; | Math.exp (x) | — экспонента; | |||||||||||||||||||||||||
| Math.sqrt (x) | — квадратный корень; | Math.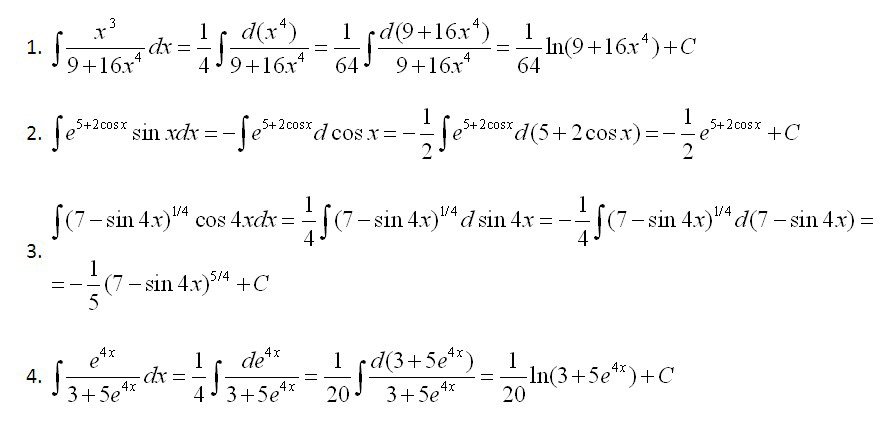 | Функция | Нижняя граница интегрирования | Верхняя граница интегрирования | |||||||||||||||||||||||
|
|
|
Предыдущая Решение линейного уравнения
Следующая Линейные неравенства
Калькулятор определенных интегралов | Расчет определенной интеграции онлайн
Содержание
Получите виджет!
Знакомство с интегральным калькулятором Добавьте этот калькулятор на свой сайт, чтобы пользователи могли выполнять простые расчеты.
Обратная связь
Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам!
Доступно в приложении
Загрузите приложение «Калькулятор потери веса» для своего мобильного телефона.
Гугл игры Магазин приложений
Знакомство с калькулятором определенных интегралов
Вычисление интеграла от многочленов
Включите JavaScript
Вычисление интеграла от многочленов
Калькулятор определенных интегралов — это онлайн-калькулятор, который может вычислять определенные интегралы, помогая пользователям вычислять интегралы онлайн. Интеграл имеет 2 основных типа, включая определенные интерналы и неопределенные интегралы.
Калькулятор определенного интегрирования шаг за шагом вычисляет определенные интегралы и показывает точные результаты.
Калькулятор неопределенной интеграции имеет свою собственную функциональность, и вы также можете использовать его для получения пошаговых результатов.
Если вы хотите вычислить определенный интеграл и неопределенный интеграл в одном месте, калькулятор первообразных с шагами — лучший вариант, который вы можете попробовать.
Связанный: Как вычислять интегралы с помощью дробей?
Формула, используемая Калькулятором определенных интегралов
Калькулятор определенных интегралов с шагами использует приведенную ниже формулу для пошагового отображения результатов. Если F есть неопределенный интеграл для функции f(x) , то формула определенного интегрирования: 9b f(x) dx = F(b) — F(a) {2}$
Важность использования онлайн-калькуляторов для интеграции
Интеграция и дифференцирование являются одними из основных понятий исчисления, и они очень важны с точки зрения обучения и понимание. Онлайн-калькуляторы обеспечивают мгновенный способ вычисления интегралов онлайн.
Эти калькуляторы имеют свои преимущества использования, поскольку пользователь может быстро изучить эти концепции, выполняя вычисления во время выполнения.
Как работает калькулятор определенной интеграции?
Калькулятор определенного интеграла работает онлайн, чтобы решить любое ваше уравнение и показать вам фактический результат вместе с шагами, графиком и т. д. Для расчета результатов он использует соответствующие интегральные правила и формулы.
Вы также можете решать уравнения двойного определенного интегрирования с помощью калькулятора множественных интегралов с шагами. Точно так же вы также можете рассчитать уравнения тройного определенного интегрирования, используя калькулятор тройных интегралов с шагами.
Как найти калькулятор определенных интегралов?
Есть 2 способа найти калькулятор определенной первообразной. Вы можете выполнить поиск в Google, чтобы найти этот калькулятор, или вы можете щелкнуть на этом веб-сайте онлайн-калькулятор определенного интеграла, чтобы использовать его.
Также найдете уникальный метод калькулятора цилиндрических оболочек для расчета объема оболочек вращения. Калькулятор дискового метода с шагами расчета сечения витков. Калькулятор метода шайбы с шагами расчета объема тела вращения.
Как пользоваться Калькулятором определенных интегралов с шагами?
Использование нашего калькулятора определенной интеграции очень просто, так как вам нужно выполнить следующие шаги:
Шаг №. 1: Загрузите пример или введите функцию в основное поле.
Шаг №. 2: Выберите переменную из x, y и z.
Шаг №. 3: Дайте значение верхней границы.
Шаг №. 4: Дайте значение нижней границы.
Шаг №. 5: Проверьте правильность уравнения из предварительного просмотра.
Вперед. 6: Нажмите кнопку «РАССЧИТАТЬ» в этом онлайн-калькуляторе интеграции.
Мы надеемся, что этот пошаговый интегральный калькулятор и статья помогли вам в освоении. Мы предлагаем множество других онлайн-инструментов, таких как калькулятор Фурье и калькулятор Лапласа.
Эти онлайн-инструменты абсолютно бесплатны, и вы можете использовать их для обучения и практики онлайн.
Часто задаваемые вопросы
Как вычислить определенный интеграл?
Определенные интегралы — это определенные формы интегралов, которые включают верхнюю и нижнюю границы. Эти интегралы можно вычислить путем интегрирования, а затем подстановки их граничных значений. Кроме того, вычисление определенного интегрального калькулятора также может помочь в решении таких задач.
Когда использовать u-подстановку определенного интеграла?
В определенных интегралах u-подстановка используется, когда функцию трудно интегрировать напрямую. Методом u-подстановки функцию можно заменить на другую, заменив переменные и переменную интегрирования.
В конечном счете, u-подстановка сложна для решения для студентов, изучающих исчисление, но решатель определенного интеграла облегчает это для всех уровней ученых, изучающих исчисление.
О чем говорит определенный интеграл? 9b f(x) dx {2}$
Таким образом, мы можем найти площадь под кривой, используя интегральный калькулятор с ограничениями или вручную, используя приведенное выше математическое выражение.
Что означает площадь под кривой?
Площадь под кривой означает, сколько места может занимать кривая над осью x. Лучший способ найти площадь под кривой — это калькулятор площади с определенным интегралом, потому что не существует специальной формулы для нахождения площади под кривой.
Так что получайте удовольствие и получайте удовольствие от обучения благодаря интеграции с калькулятором лимитов.
Алан Уокер
Последнее обновление: 4 дня назад
Я математик, технарь и автор контента. Я люблю решать шаблоны различных математических запросов и писать так, чтобы все могли понять. Математика и технология сделали свое дело, и теперь пришло время извлечь из этого пользу.
Калькулятор определенных интегралов | Calculate Definite Integration Online
Введение в калькуляторы Definite Integral
Калькулятор Definite Integration — это онлайн-инструмент для вычислить интегралы с ограничениями онлайн . Это помогает пользователям оценить площадь под кривой.
Определенные интегралы — это противоположные значения функции f(x), заданные для верхних и нижних граничных значений любой независимой переменной x.
Например,
Есть два типа интегралов: один — определенные интегралы, а другой — неопределенные интегралы. Неопределенные интегралы можно рассчитать с помощью онлайн-калькулятора неопределенных интегралов. Но здесь интегральный калькулятор с ограничениями помогает вычислить определенный интеграл онлайн. 9б \;=\; f(b)-f(a) $$
Квадратные скобки традиционно используются для различения двух пределов. Калькулятор определенного интеграла используется для получения точной площади под кривой.
В то время как в неопределенных интегралах, нахождение интегралов также известно как интегрирование или интегрирование f(x). Функция F представляет собой интегрирование f для вещественной константы C. Вот обозначения неопределенных интегралов:
$$ \int f(x) dx \;=\; F(x)+C $$
Здесь следует отметить, что обозначения определенных и неопределенных интегралов почти аналогичны.
2 dx \;=\; \frac{8}{3} $$
Здесь «0» представляет нижний предел, а «2» представляет верхний предел в интегралах с соответствующей осью x. А в определенных интегралах надо найти площадь кривой , для этого разобьем кривую на прямоугольники и затем найдем сумму этих разделенных прямоугольников.
Важность использования решателя определенных интегралов
Калькулятор интегралов с ограничениями вычисляет функцию одной переменной с заданными пределами интегрирования. Этот калькулятор помогает пользователю оценить различные значения интегрирования.
Используя этот онлайн-калькулятор определенных интегралов с шагами, используя этот калькулятор, можно сэкономить много времени. Им не нужно вручную тратить пару часов на подсчет этих сумм.
Калькулятор расчета определенных интегралов также показывает графики, графики, альтернативные формы и другую важную информацию для расширения их математических знаний.
Так же, как интеграл со связанными значениями, наш сайт также предоставляет калькулятор несобственных интегралов для вычисления несобственных интегралов.
Как работает калькулятор определенной интеграции?
Можно быстро получить точные результаты, выполнив следующие шаги в интегральном калькуляторе с границами. Шаги для использования калькулятора определенных интегралов следующие:
- Во-первых, загрузите свой пример/функцию в строку поиска.
- Теперь выберите переменную из координат x, y и z.
- Выберите значение верхнего предела в данном поле.
- Выберите значение нижней границы в предоставленном поле.
- Теперь проверьте правильность ваших значений и уравнения из предварительного просмотра.
- Нажмите кнопку «РАССЧИТАТЬ» на интегральном калькуляторе с границами , чтобы получить пошаговую оценку интегрирования.
Мы также предлагаем калькулятор двойного интегрирования и калькулятор тройного интегрирования для решения интегрирования дважды или трижды.
Преимущества использования калькулятора определенных интегралов
В настоящее время технологии настолько развиты, что студенты получают так много преимуществ.