Трапеция: свойства, признаки, площадь, средняя линия
Т. А. Унегова
Определения:
Трапеция — это называется четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.
Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами трапеции.
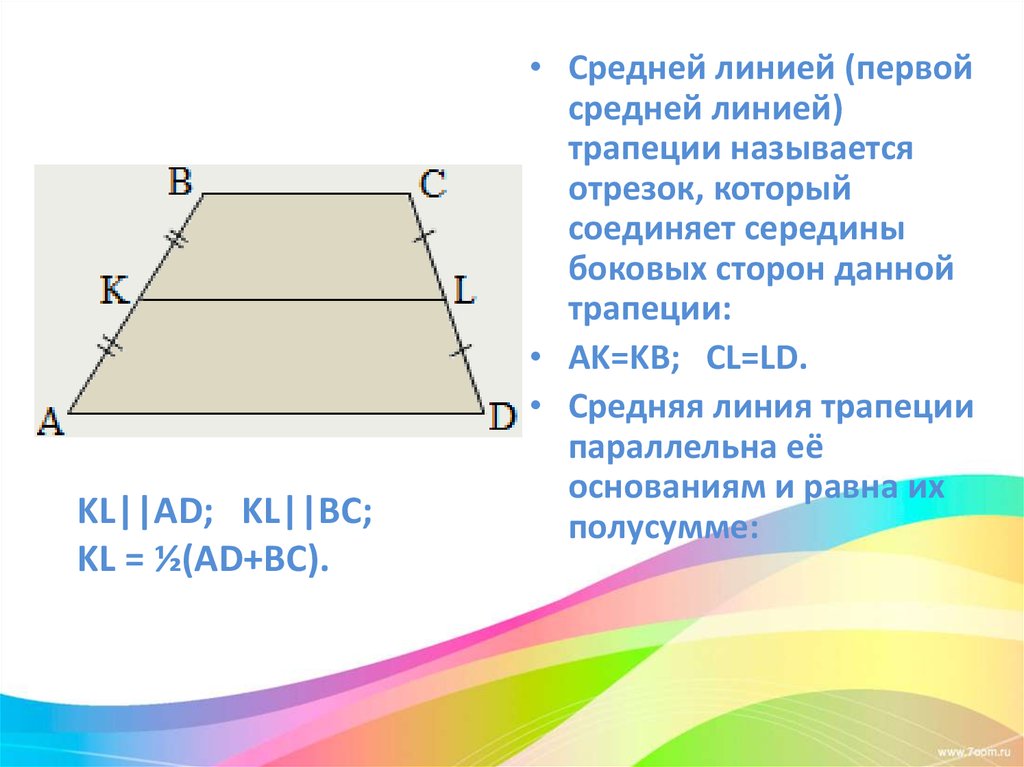
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Если боковые стороны равны, трапеция называется равнобедренной.
Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.
Трапеция называется вписанной в окружность, если каждая ее вершина принадлежит окружности.
Трапеция называется описанной вокруг окружности, если каждая ее сторона касается окружности.
Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Теоремы о средней линии и диагоналях трапеции
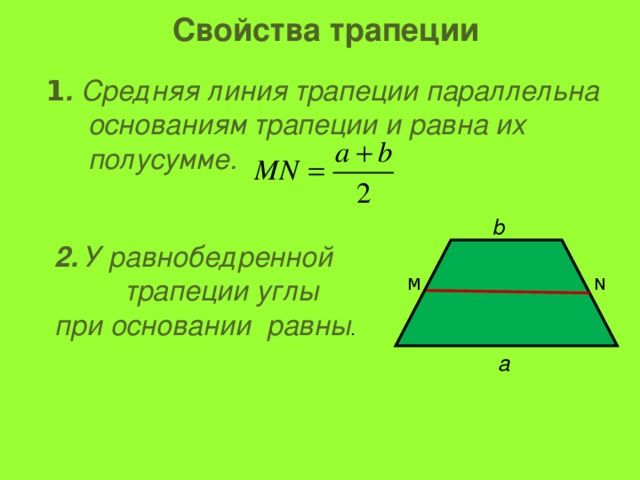
Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме: .
Теорема 2. Диагонали трапеции делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой: .
Теорема 3. Средняя линия треугольника, составленного из диагоналей и суммы оснований трапеции, равна средней линии трапеции: .
Теорема 4. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон — лежат на одной прямой.
Эта теорема называется также «Замечательное свойство трапеции».
Теорема 5. Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.
Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.
Теоремы о площади трапеции
Теорема 6. Площадь трапеции равна произведению полусуммы ее оснований на высоту: .
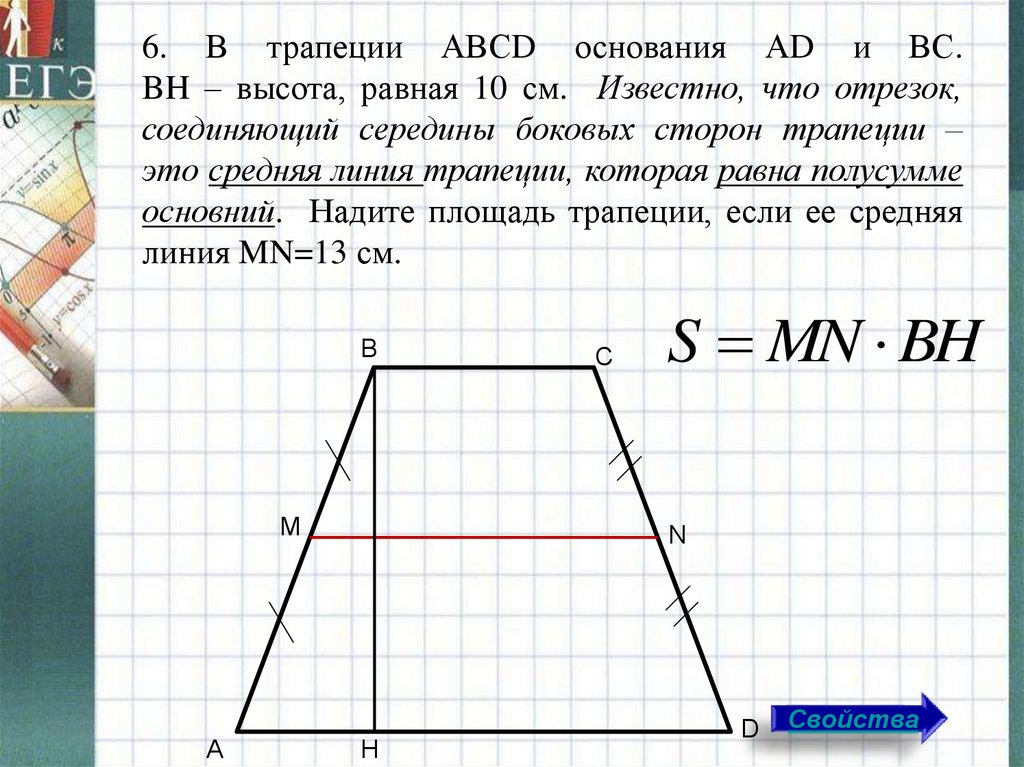
Теорема 7. Площадь трапеции равна произведению ее средней линии на высоту: .
Теорема 8. Площадь трапеции (как и всякого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между ними: , где (Вместо можно брать
Теорема 9. Если в трапецию можно вписать окружность, то (как и для всякого описанного многоугольника) площадь трапеции равна произведению ее полупериметра на радиус вписанной окружности: . Таким образом, .
Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравни эту теорему и теорему 3. )
)
Теоремы о вписанных и описанных трапециях
Теорема 11. Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около нее можно описать окружность.
Теорема 12. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме ее боковых сторон.
Задачи ЕГЭ и ОГЭ по теме: Трапеция
Задача 1.
Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны .
Решение:
Высота трапеции— это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины . Так как сторона квадратной клетки равна , то по теореме Пифагора получаем, что .
Ответ: 2.
Задача 2.
Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол . Найдите площадь трапеции.
Решение:
Углы ABC и BAH — односторонние, их сумма равна , и тогда BAH
Из ABH найдем высоту BH.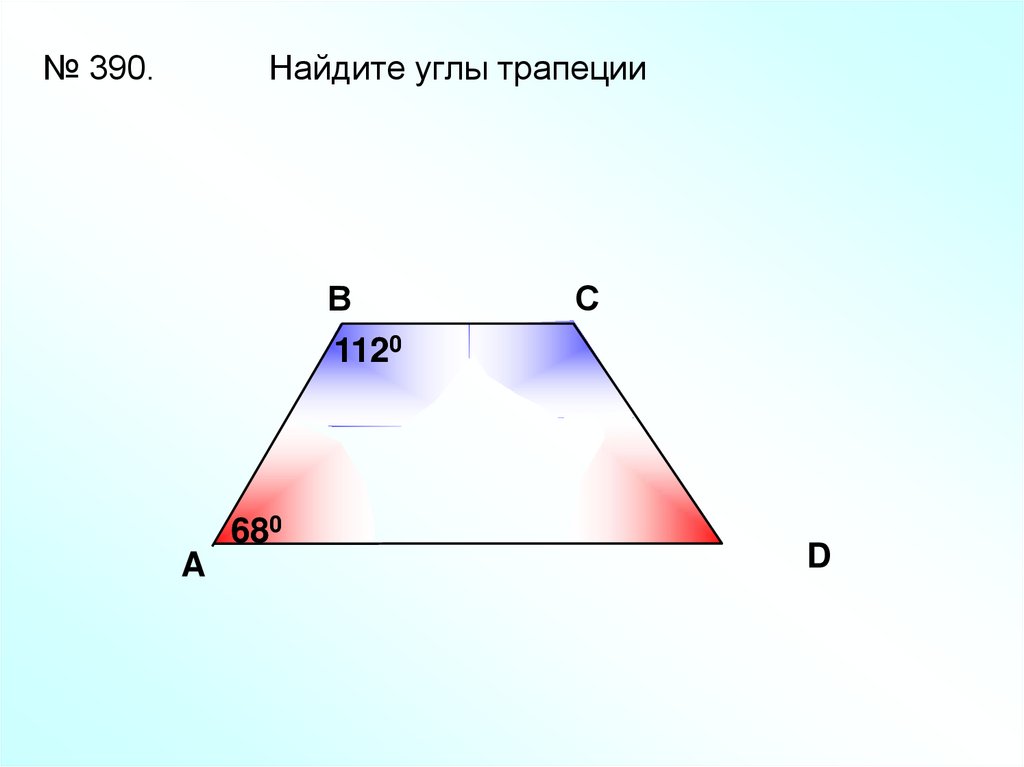 Катет, лежащий против угла в , равен половине гипотенузы. Получаем, что BH = 3,5.
Катет, лежащий против угла в , равен половине гипотенузы. Получаем, что BH = 3,5.
Площадь трапеции равна .
Ответ: 42.
Задача 3.
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.
Решение:
Что можно увидеть на чертеже? Можно сказать, что изображена трапеция ABCD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, ABC и ACD, в которых проведены средние линии.
Напомним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны. Из ACD находим, что
Ответ: 5.
Задача 4.
Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
Решение:
Проведем PQ — среднюю линию трапеции, PQ = 2,5 и . Отсюда получаем, что середина отрезка AC, то есть PM — средняя линия треугольника ABC и PM = 1. Аналогично, NQ = 1.
Аналогично, NQ = 1.
Ответ: 0,5.
Задача 5.
Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
Решение:
Периметр треугольника равен сумме его сторон, то есть
Периметр трапеции равен
Ответ: 23.
Задача 6.
В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует со стороной CD угол . Найдите углы трапеции.
Решение:
Пусть CAD , тогда CAB и BAD , так как трапеция равнобедренная.
Сумма углов , откуда
Итак, , а.
Ответ: .
Задача 7.
В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.
Решение:
В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и Отсюда,
Ответ: 24.
Задача 8.
Тупой угол равнобедренной трапеции равен , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.
Решение:
Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом .
Каждый треугольник равнобедренный, поэтому h = 1,4.
Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее — 4,8. Отсюда площадь трапеции равна .
Ответ: 4,76.
Задача 9.
Площадь трапеции равна 60м а основания 8 м и 12 м. Найдите высоту трапеции.
Решение:
Так как площадь трапеции , то , откуда h = 6.
Ответ: 6.
Задача 10.
В равнобедренной трапеции диагонали перпендикулярны и равны Найдите площадь трапеции.
Решение:
Проведем CE BD и DE — продолжение AD.
Так как BCDE — параллелограмм, то CE = a.
По теореме 10 получим, что .
Ответ:
Задач 11.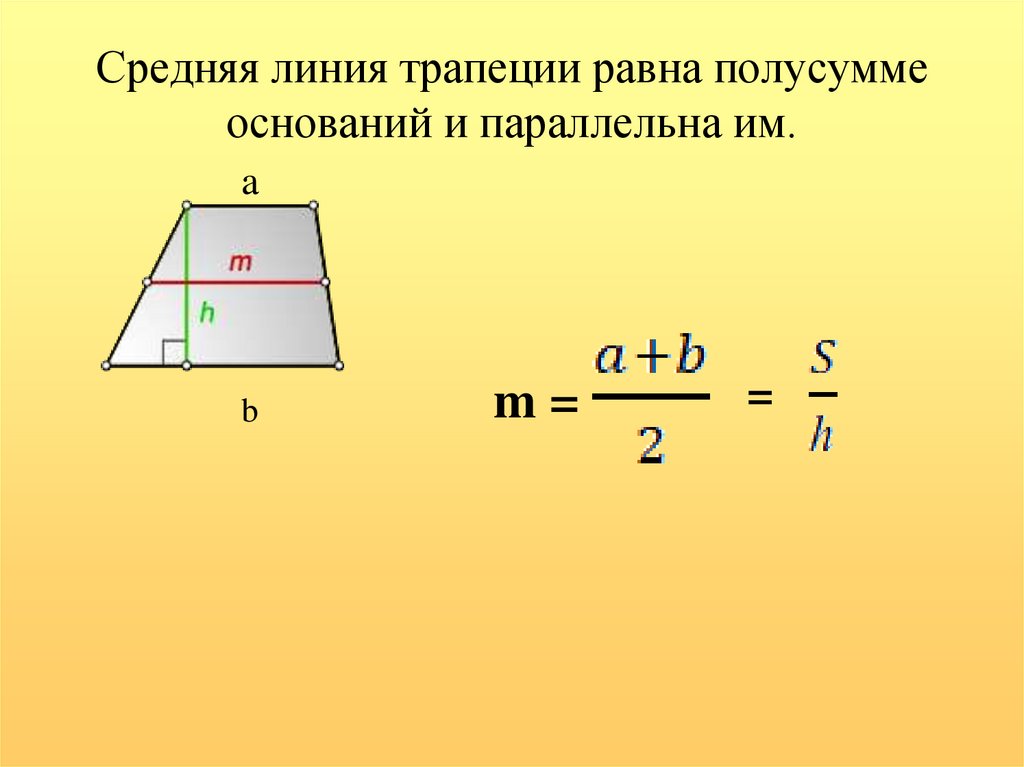
В трапеции ABCD с большим основанием AD диагональ AC перпендикулярна к боковой стороне CD и является биссектрисой угла A.
Найдите AD, если периметр трапеции равен 20, а угол D равен .
Решение:
По условию задачи в прямоугольном ACD
D , следовательно, CAD .
Так как AC — биссектриса, то CAB , откуда DAB , то есть, трапеция равнобедренная. BCA CAD как накрест лежащие, поэтому ABC — равнобедренный.
Обозначим длины боковых сторон ABC буквой x.
Тогда AB = BC = CD = x, и AD = 2x, так как в прямоугольном ACD против угла в лежит катет, равный половине гипотенузы.
Таким образом, периметр трапеции, равный 20, составляет 5x, отсюда
x = 4 и AD = 8.
Ответ: 8.
Задача 12.
В равнобедренной трапеции ABCD с острым углом меньшее основание BC равно 2, а боковая сторона AB равна 10. Продолжения боковых сторон трапеции пересекаются в точке M. Во сколько раз площадь трапеции больше площади треугольника BCM?
Решение:
Нетрудно видеть, что BCM равносторонний и BM = 2, тогда AM = 12 и BCM подобен ADM c коэффициентом .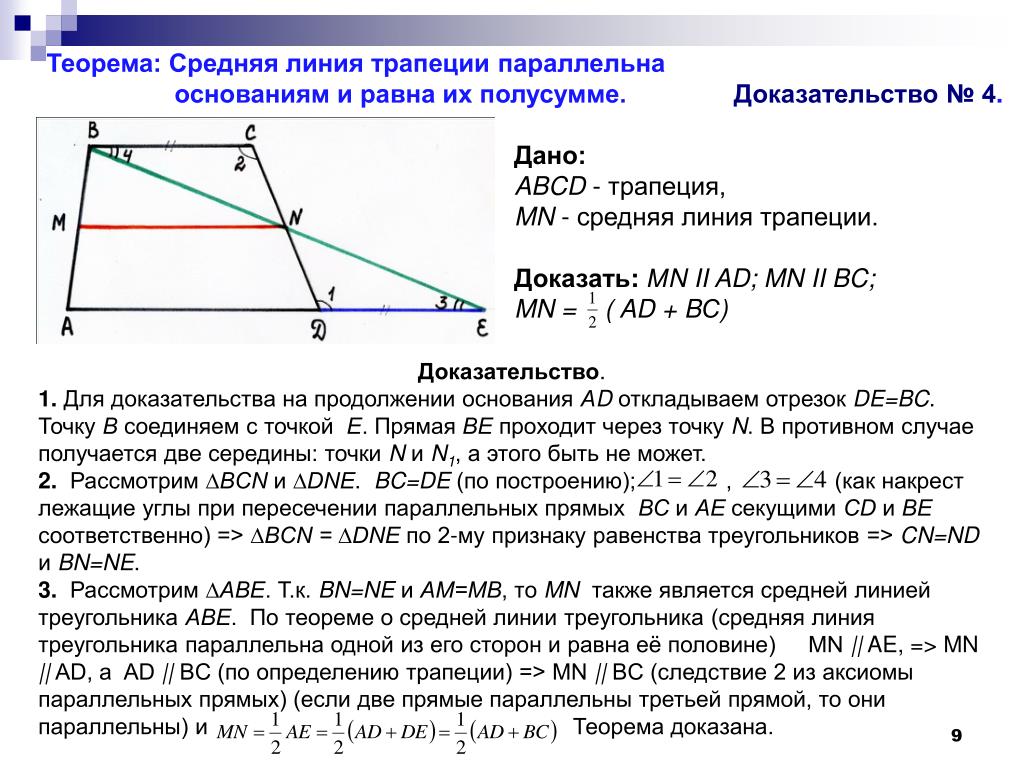
Пусть, , тогда
Площадь трапеции будет равна
Ответ: 35.
Задача 13.
Сумма углов при одном из оснований трапеции равна . Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.
Решение:
Продолжим боковые стороны до пересечения в точке E и отметим точки F и G — середины оснований трапеции.
Так как сумма углов при основании трапеции равна , то , поэтому EF и EG — медианы в прямоугольных треугольниках BEC и AED соответственно.
Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит
Ответ: 2.
Задача 14.
Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.
Решение:
Так как площадь трапеции равна , а высота трапеции равна диаметру вписанной окружности, то есть то , откуда .
Ответ: 1,2.
Задача 15.
Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10.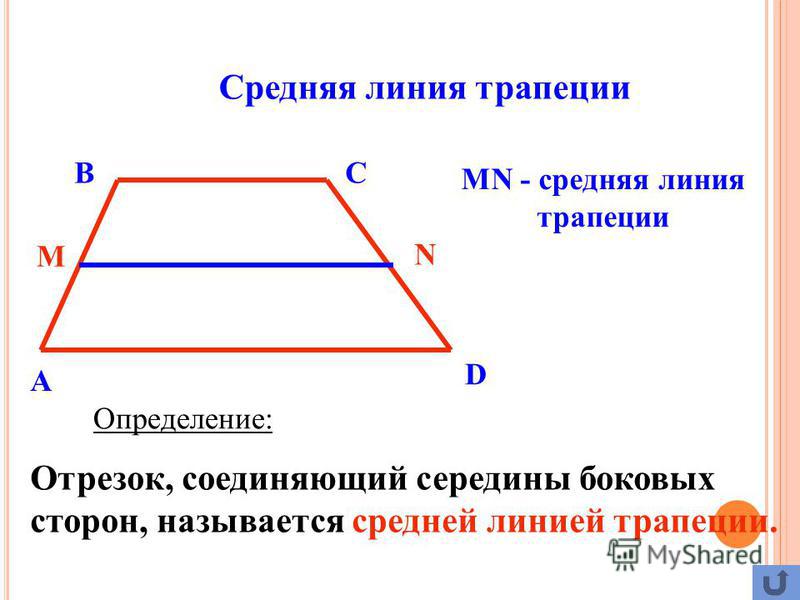 Найдите радиус r вписанной в трапецию окружности.
Найдите радиус r вписанной в трапецию окружности.
Решение:
По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому
откуда
Сторона AB равна диаметру окружности, поэтому .
Ответ: 3.
Задача 16.
Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.
Решение:
Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому
Ответ: 20.
Задача 17.
В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.
Решение:
Так как AD — диаметр окружности, то дуга ABCD равна . Она делится на три равные части по
Вписанный угол D опирается на дугу ABC, которая равна , отсюда и, стало быть,
Ответ: 120.
Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Трапеция и ее свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена: 08.04.2023
определение, как найти, свойства, формулы, задачи
Содержание:
- Средняя линия трапеции – что это?
- Свойства
-
Как вычислить, основные формулы
- Через основания
- Через основание, высоту и углы при нижнем основании
- Через диагонали, высоту и угол между диагоналями
- Примеры задач
Содержание
- Средняя линия трапеции – что это?
- Свойства
-
Как вычислить, основные формулы
- Через основания
- Через основание, высоту и углы при нижнем основании
- Через диагонали, высоту и угол между диагоналями
- Через площадь и высоту
- Примеры задач
Средняя линия трапеции – что это?
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон трапеции.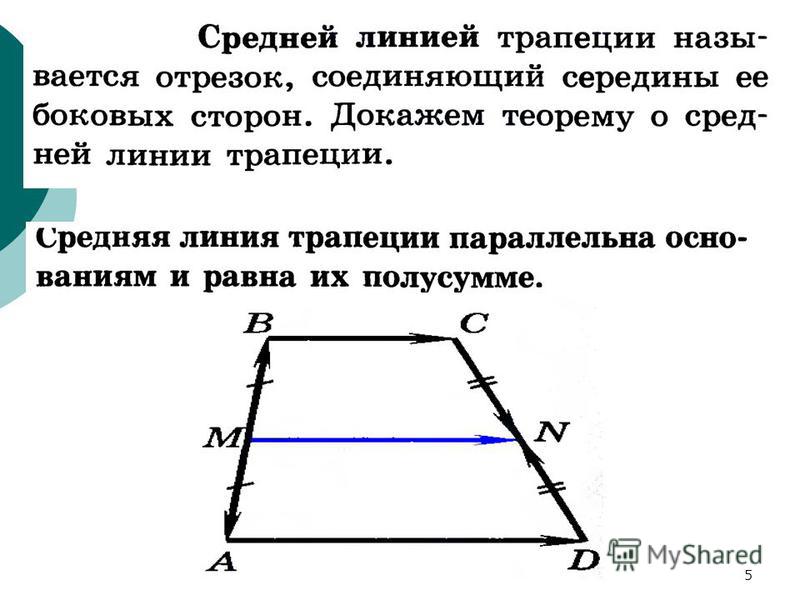
Свойства
- Параллельна обоим основаниям трапеции.
- Вычисляется как половина суммы оснований.
- Разбивает трапецию на две, площади которых соотносятся как \(\frac{S_1}{S_2}=\frac{3\,BC+AD}{BC+3\,AD}\)
Как вычислить, основные формулы
Через основания
Источник: formula.ruГде \(a\) – нижнее основание, \(b\) – верхнее, \(m\) – средняя линия.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Через основание, высоту и углы при нижнем основании
Источник: formula.ru\(m=a-h\times\frac{ctg\alpha+ctg\beta}2\)
\(m=b+h\times\frac{ctg\alpha+ctg\beta}2\)
Где \(a\) – нижнее основание, \(b\) – верхнее, \(m\) – средняя линия, \(h\) – высота, \(\alpha,\beta\) – углы при нижнем основании.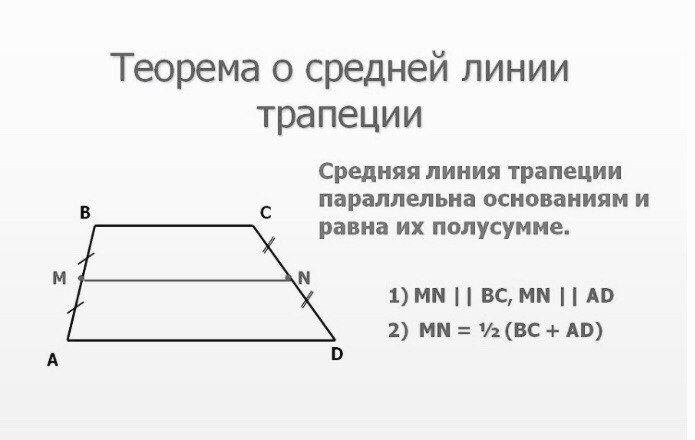 \circ\)
\circ\)
Рассмотрим \(\angle ABH\)
\(BH=\frac12AB=3,5\)
\(S_{ABCD}=\frac{AD+BC}2\times BH=\frac{6+18}2\times3,5=42\)
Ответ: 42
Задача 2
Основания трапеции равны 4 и 10. Чему равен больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей?
Источник: ege-study.ruСредняя линия трапеции ABCD так же является средней линией треугольников ABC и ACD т.к. проходит через середину одной стороны и параллельна основанию. Значит, из треугольника ACD x = 5.
Ответ: 5
Задача 3
ABCD – трапеция, BC = 2, AD = 3, PQ – средняя линия, BD и AC – диагонали. Найти MN.
Источник: ege-study.ru\(PQ=\frac{BC+AD}2=2,5\)
Отрезок MN лежит на средней линии трапеции. Докажем: PM и NQ средние линии треугольников ABC и BCD, значит M и N середины соответственно AC и BD. Из треугольника ABC находим длину PM = 1, из треугольника BCD находим NQ = 1, следовательно MN = 2,5 — 1 — 1 = 0,5
Ответ: 0,5
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.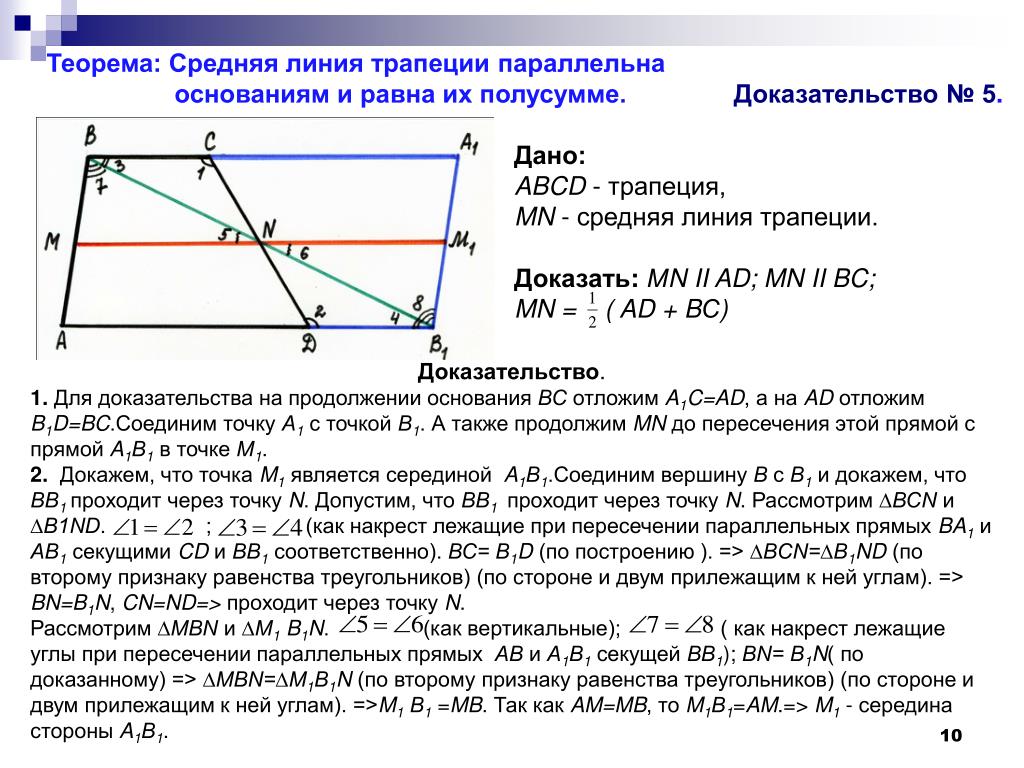
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Средняя часть трапеции | Обзор, теорема и примеры — видео и расшифровка урока
Математические курсы / Большие идеи Math Geometry: онлайн-справка по учебнику Курс / Большие идеи Math Geometry Chapter 7: Четырехугольники и другие многоугольники Глава
Кристиан Киллиан, Стефани Маталоне- Автор Кристиан Киллиан
Кристиан имеет степень бакалавра в области делового администрирования, степень магистра в области медиакоммуникаций и психологии, а также степень доктора философии в области социальной психологии. Они преуспевают в математике и естественных науках и любят объяснять что-то другим. Они также сертифицированы OSHA 30.
Посмотреть биографию - Инструктор Стефани Маталоне
Стефани преподавала естествознание и математику в средней школе и имеет степень магистра среднего образования.
Посмотреть биографию
Научиться определять среднюю часть трапеции и формулировать теорему о средней части трапеции. Узнайте, как найти среднюю часть трапеции с примерами. Обновлено: 03.02.2022
Содержание
- Средняя часть трапеции
- Теорема о средней линии трапеции
- Как найти среднюю часть трапеции
- Краткое содержание урока
Где находится середина трапеции?
Средняя часть трапеции соединяет середины обеих сторон. Неважно, является ли трапеция основной или неправильной.
Что такое теорема о средней части трапеции?
Теорема о средней части трапеции утверждает, что прямая, проходящая через середину стороны трапеции, параллельная обоим основаниям, также проходит через середину другой стороны. Теорема также утверждает, что длина среднего отрезка равна сумме обоих оснований, деленной на 2.
Трапеция представляет собой четырехстороннюю фигуру ( четырехугольник ) только с одним набором параллельных сторон. Параллельные линии идут в одном направлении и всегда находятся на одинаковом расстоянии друг от друга.
Параллельные линии идут в одном направлении и всегда находятся на одинаковом расстоянии друг от друга.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную запись
Трапеции
Вы четырехугольник? У вас есть пара параллельных сторон? У вас есть другая пара сторон, которые не параллельны? Если вы ответили «да» на все эти вопросы, то наши судьи определили, что вы трапеция!
Трапеции — это четырехсторонние фигуры (четырехугольники), у которых пара сторон параллельна, а другая — нет. Параллельность просто означает, что стороны находятся на одинаковом расстоянии друг от друга на всем протяжении, как железнодорожные пути. Начиная с середины, вы можете пройти по ним в любом направлении и убедиться, что расстояние между линиями остается прежним.
В трапеции видно, что линии сверху и снизу трапеции параллельны, а линии по бокам не параллельны.
Произошла ошибка при загрузке этого видео.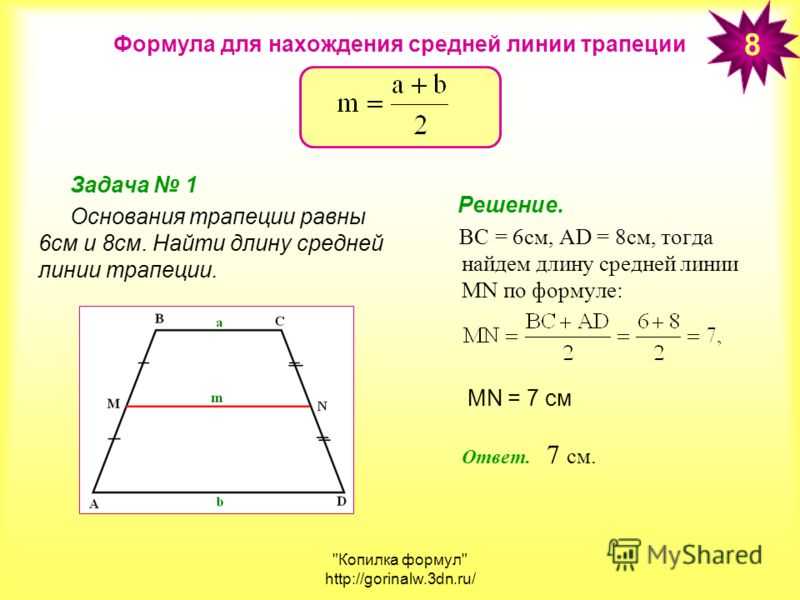
Попробуйте обновить страницу или обратитесь в службу поддержки.
Вы должны создать учетную запись, чтобы продолжить просмотр
Зарегистрируйтесь, чтобы просмотреть этот урок
Вы студент или преподаватель?
Создайте свою учетную запись, чтобы продолжить просмотр
Как участник вы также получите неограниченный доступ к уроки математики, английского языка, науки, истории и многое другое. Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам преуспевать.
Получите неограниченный доступ к более чем 88 000 уроков.
Попробуй это сейчас
Настройка занимает всего несколько минут, и вы можете отменить ее в любое время.
Уже зарегистрированы? Войдите здесь для доступ
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков
и учебные ресурсы‐все
в одном месте.
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Назад
Далее: Воздушные змеи в геометрии: определение и свойства
пройти викторину Смотреть Следующий урок
Повторить
Просто отмечаюсь. Вы все еще смотрите?
Да! Продолжай играть.Ваш следующий урок будет играть в 10 секунд
- 0:04 Трапеции
- 0:46 Средний сегмент
- 1:09 На координатной плоскости
- 1:59 Теорема о средней линии трапеции
- 2:38 Несколько примеров
- 4:12 Итоги урока
Хронология
Автовоспроизведение
Автовоспроизведение
Скорость
Скорость
Теорема о среднем сегменте трапеции делает два утверждения:
- Любая линия, проходящая через середину катетов трапеции, также проходит через середину противоположного катета, если она параллельна основаниям.

- Длина среднего сегмента равна сумме обоих оснований, деленной на 2.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную запись
Чтобы найти середину трапеции, нужно знать длины обоих оснований. Получив их, мы можем ввести их в формулу среднего сегмента трапеции, чтобы вычислить средний сегмент.
Допустим, у нас есть трапеция с длинами оснований 6 и 8. Мы можем использовать эти значения, чтобы найти середину.
- М = 1/2 (b1 + b2), где b1 = 6, а b2 = 8
Заполните базовые длины цифрами 6 и 8.
- M = 1/2 (6 + 8)
Затем сложите 6 и 8, чтобы получить 14.
- М = 1/2 (14)
Разделите 14 на 2, чтобы найти 7.
- М = 7
Средняя часть этой трапеции равна 7.
Средняя часть трапеции — пример
Давайте рассмотрим несколько примеров, где нам нужно найти среднюю часть трапеции.
Пример первый:
Найдите среднюю часть трапеции с длинами оснований 4 и 9.
Для решения этой задачи нам нужно использовать формулу средней части трапеции.
- М = 1/2 (b1 + b2), где b1 = 4 и b2 = 9
Заполните базовые длины 4 и 9.
- М = 1/2 (4 + 9)
Добавьте 4 и 9, чтобы получить 13.
- М = 1/2 (13)
Разделите 13 на 2, чтобы найти 6,5.
- М = 6,5
Средняя линия этой трапеции равна 6,5.
Второй пример:
Найдите среднюю часть трапеции на этом изображении.
Чтобы разблокировать этот урок, вы должны быть участником Study.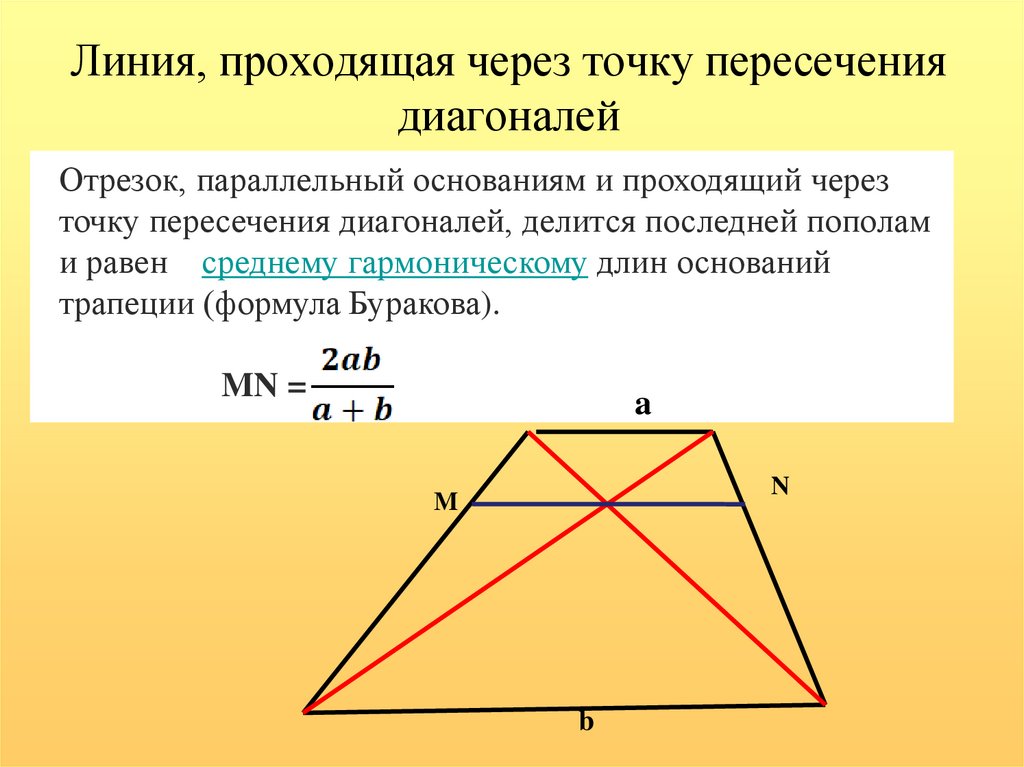 com.
com.
Создайте свою учетную запись
В этом уроке мы рассмотрели средний сегмент трапеции и то, как его найти. Трапеция представляет собой параллелограмм с двумя параллельными основаниями и двумя непараллельными катетами . Средний сегмент проходит через середины обеих ног параллельно обоим основаниям.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свой аккаунт
Средняя часть
Назовем две непараллельные стороны треугольника катетами . Две другие параллельные стороны будут называться основаниями .
Средний сегмент трапеции — это линия, проходящая от середины одной стороны к середине другой стороны. Средний сегмент встречается с каждой ногой в средней точке. Средняя точка находится на равном расстоянии от обоих концов линий ног.
Средний сегмент встречается с каждой ногой в средней точке. Средняя точка находится на равном расстоянии от обоих концов линий ног.
На координатной плоскости
Можно использовать все, что мы узнали, когда у нас есть трапеция на координатной плоскости. Допустим, вам даны следующие четыре балла:
- (0, 0) (5, 0) (1, 4) (5, 4)
Вы можете изобразить их на координатной плоскости, проведя линии между точками, чтобы обнаружить, что они образуют трапецию.
Эта трапеция выглядит немного иначе, чем та, которую мы видели ранее, но вы все равно можете видеть, что основания параллельны, а стороны — нет. Здесь мы можем легко сыграть в средней части.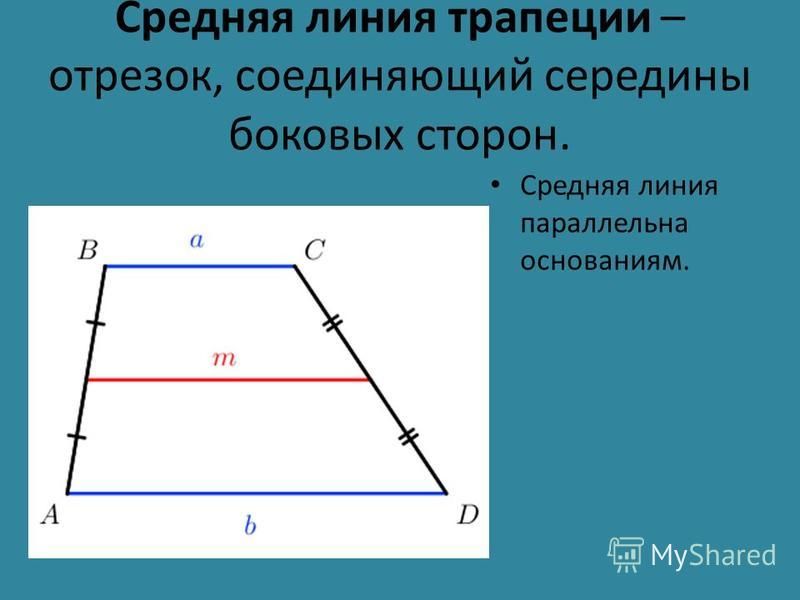 Помните, что средний сегмент должен начинаться в середине каждой ноги.
Помните, что средний сегмент должен начинаться в середине каждой ноги.
Так как обе наши ноги начинаются с 0 на оси y и заканчиваются на 4 на оси y , легко увидеть, что средние точки должны приходиться на 2 на оси y для обеих ног . Затем мы просто проводим нашу линию через середину.
Теорема о среднем сегменте трапеции
Теперь, когда мы поняли некоторые основы трапеций, давайте поговорим о Теорема о среднем сегменте трапеции , которая утверждает, что длина среднего сегмента равна сумме длин оснований, деленной на 2. Другими словами, средний сегмент представляет собой среднюю длину двух оснований.
Итак, допустим, мы смотрим на трапецию, у которой длина основания сверху равна 2, а длина основания снизу равна 4. Чтобы найти длину середины, мы просто сложим длины базы:
- 2 + 4 = 6
Затем разделите сумму на 2:
- 6 / 2 = 3
Таким образом, длина средней части равна 3.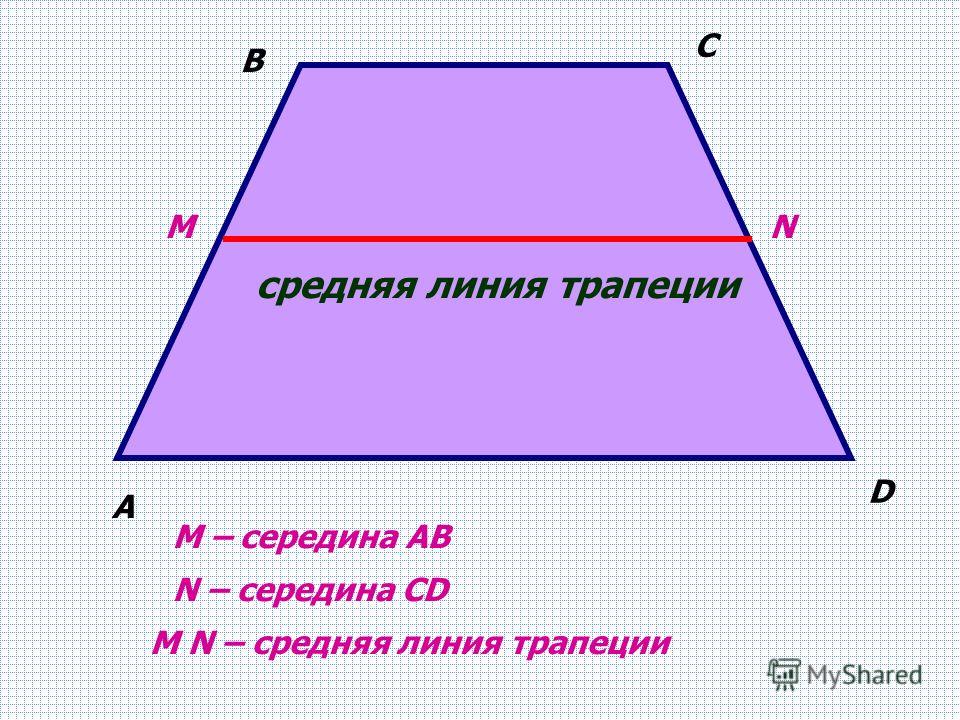
Некоторые примеры
На этот раз длины двух оснований равны 8,975 см и 3,4 см. Какова длина среднего сегмента?
Начните с сложения двух оснований:
- 8,975 см + 3,4 см = 12,375 см
Затем разделить сумму на 2:
- 12,375 см / 2 = 6,1875 см
Легко! Длина среднего сегмента составляет всего 6,1875 см.
Теперь предположим, что вам дали задачу, где вам дали:
- Длина среднего отрезка = 14
- Длина одного из оснований = 16,5
Какой длины другая база? Можем ли мы использовать теорему таким образом? Что ж, давайте посмотрим на пример.
При решении подобных задач проще всего начать с уравнения и заполнить то, что мы знаем:
- Средний сегмент = (основание1 + основание2) / 2
Поскольку мы знаем длину середины сегмента, давайте заполним ее:
- 14 = (основание1 + основание2) / 2
Затем заполним известную нам длину основания:
- 14 = (16,5 + основание2) / 2
Теперь мы будем использовать обратные операции для решения по основанию 2.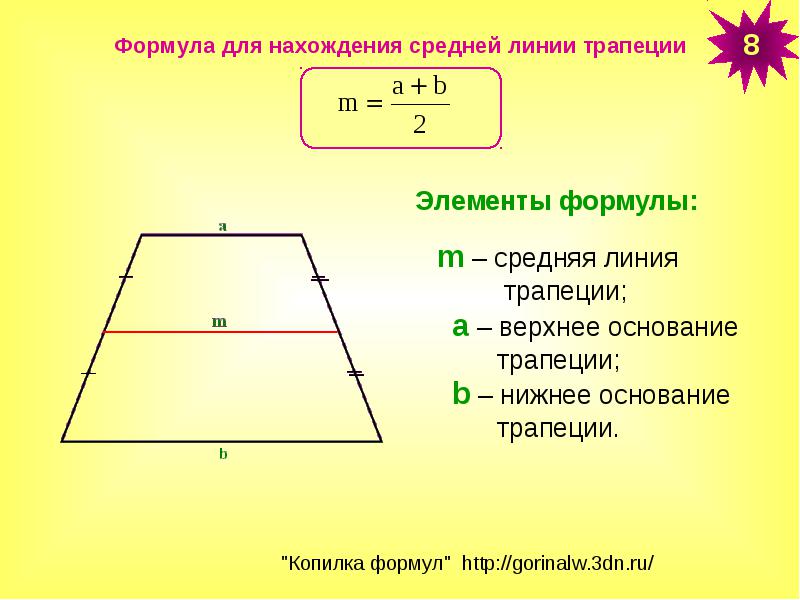 Начните с умножения обеих сторон на 2:
Начните с умножения обеих сторон на 2:
- 28 = 16,5 + основание2
Затем вычтите 16,5 с обеих сторон, чтобы выделить основание2:
- 11,5 = основание2
Таким образом, длина второго основания равна 11,5.
Резюме урока
Хорошо, давайте сделаем небольшой обзор. Как мы узнали, трапеций — это 4-сторонние фигуры (четырехугольники), у которых пара сторон параллельна, а другая пара — нет. У них есть одна пара параллельных сторон, называемая основаниями , и другая пара непараллельных сторон, называемая ножками .
Средний сегмент трапеции проходит через трапецию, начиная с середины каждой стороны, с серединой на равном расстоянии от обоих концов линий ног. Длину среднего отрезка можно рассчитать с помощью теоремы о среднем отрезке трапеции , которая гласит, что длина среднего отрезка равна сумме длин оснований, деленной на 2. Следовательно, ее можно рассчитать, сложив длины каждого основания и деления суммы на 2.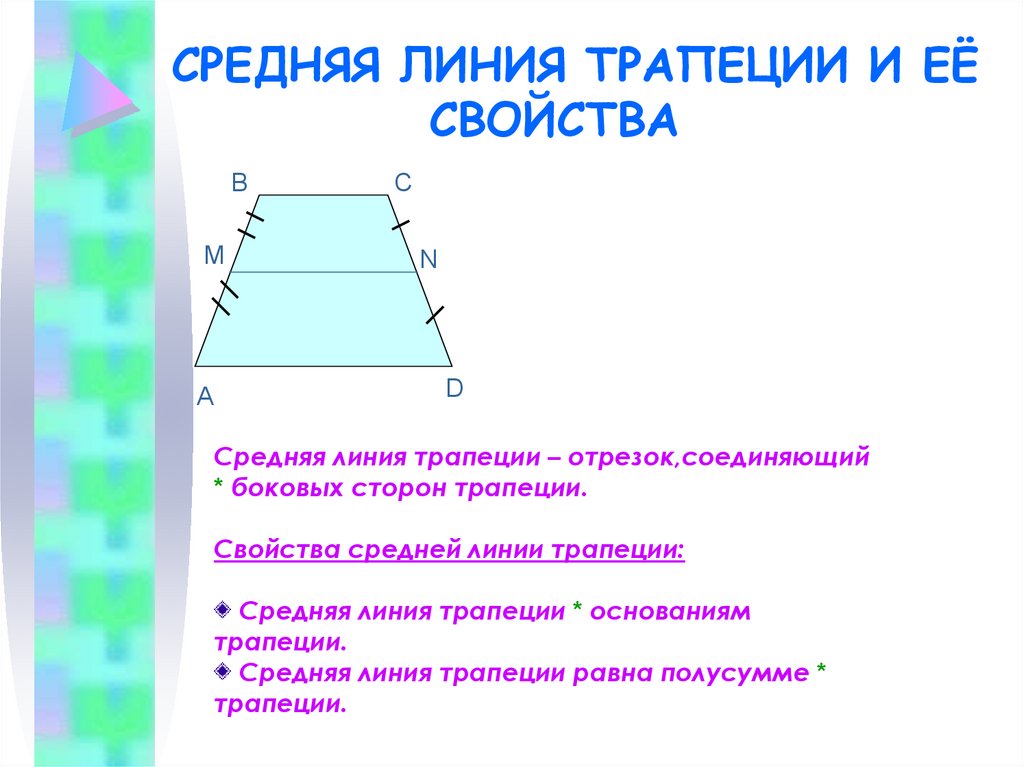
Трапеции
Вы четырехугольник? У вас есть пара параллельных сторон? У вас есть другая пара сторон, которые не параллельны? Если вы ответили «да» на все эти вопросы, то наши судьи определили, что вы трапеция!
Трапеции — это четырехсторонние фигуры (четырехугольники), у которых пара сторон параллельна, а другая — нет. Параллельность просто означает, что стороны находятся на одинаковом расстоянии друг от друга на всем протяжении, как железнодорожные пути. Начиная с середины, вы можете пройти по ним в любом направлении и убедиться, что расстояние между линиями остается прежним.
В трапеции видно, что линии сверху и снизу трапеции параллельны, а линии по бокам не параллельны.
Средняя часть
Назовем две непараллельные стороны треугольника катетами .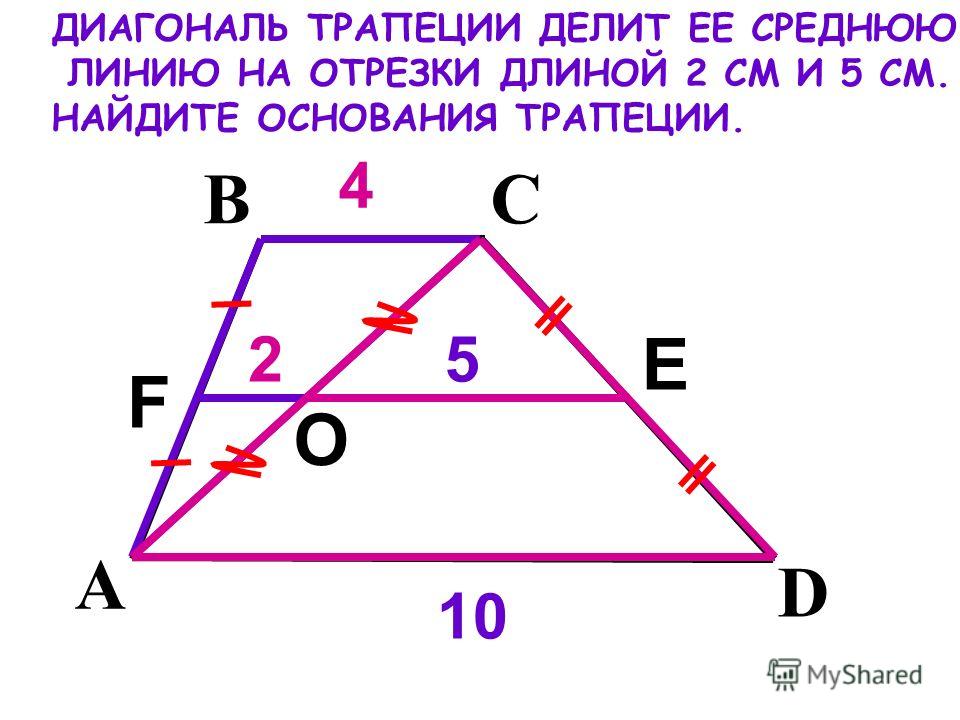 Две другие параллельные стороны будут называться основаниями .
Две другие параллельные стороны будут называться основаниями .
Средний сегмент трапеции — это линия, проходящая от середины одного плеча к середине другого. Средний сегмент встречается с каждой ногой в средней точке. Средняя точка находится на равном расстоянии от обоих концов линий ног.
На координатной плоскости
Можно использовать все, что мы узнали, когда у нас есть трапеция на координатной плоскости. Допустим, вам даны следующие четыре балла:
- (0, 0) (5, 0) (1, 4) (5, 4)
Вы можете изобразить их на координатной плоскости, проведя линии между точками, чтобы обнаружить, что они образуют трапецию.
Эта трапеция выглядит немного иначе, чем та, которую мы видели ранее, но вы все равно можете видеть, что основания параллельны, а стороны — нет.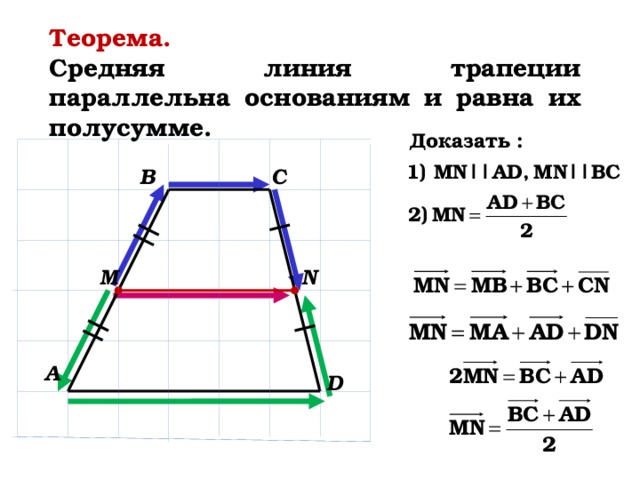 Здесь мы можем легко сыграть в средней части. Помните, что средний сегмент должен начинаться в середине каждой ноги.
Здесь мы можем легко сыграть в средней части. Помните, что средний сегмент должен начинаться в середине каждой ноги.
Так как обе наши ноги начинаются с 0 на оси y и заканчиваются на 4 на оси y , легко увидеть, что средние точки должны приходиться на 2 на оси y для обеих ног . Затем мы просто проводим нашу линию через середину.
Теорема о среднем сегменте трапеции
Теперь, когда мы поняли некоторые основы трапеций, давайте поговорим о Теорема о среднем сегменте трапеции , которая утверждает, что длина среднего сегмента равна сумме длин оснований, деленной на 2. Другими словами, средний сегмент представляет собой среднюю длину двух оснований.
Итак, допустим, мы смотрим на трапецию, у которой длина основания сверху равна 2, а длина основания снизу равна 4. Чтобы найти длину середины, мы просто сложим длины базы:
- 2 + 4 = 6
Затем разделите сумму на 2:
- 6 / 2 = 3
Таким образом, длина средней части равна 3.
Некоторые примеры
На этот раз длины двух оснований равны 8,975 см и 3,4 см. Какова длина среднего сегмента?
Начните с сложения двух оснований:
- 8,975 см + 3,4 см = 12,375 см
Затем разделить сумму на 2:
- 12,375 см / 2 = 6,1875 см
Легко! Длина среднего сегмента составляет всего 6,1875 см.
Теперь предположим, что вам дали задачу, где вам дали:
- Длина среднего отрезка = 14
- Длина одного из оснований = 16,5
Какой длины другая база? Можем ли мы использовать теорему таким образом? Что ж, давайте посмотрим на пример.
При решении подобных задач проще всего начать с уравнения и заполнить то, что мы знаем:
- Средний сегмент = (основание1 + основание2) / 2
Поскольку мы знаем длину середины сегмента, давайте заполним ее:
- 14 = (основание1 + основание2) / 2
Затем заполним известную нам длину основания:
- 14 = (16,5 + основание2) / 2
Теперь мы будем использовать обратные операции для решения по основанию 2. Начните с умножения обеих сторон на 2:
Начните с умножения обеих сторон на 2:
- 28 = 16,5 + основание2
Затем вычтите 16,5 с обеих сторон, чтобы выделить основание2:
- 11,5 = основание2
Таким образом, длина второго основания равна 11,5.
Резюме урока
Хорошо, давайте сделаем небольшой обзор. Как мы узнали, трапеций — это 4-сторонние фигуры (четырехугольники), у которых пара сторон параллельна, а другая пара — нет. У них есть одна пара параллельных сторон, называемая основаниями , и другая пара непараллельных сторон, называемая ножками .
Средний сегмент трапеции проходит через трапецию, начиная с середины каждой стороны, с серединой на равном расстоянии от обоих концов линий ног. Длину среднего отрезка можно рассчитать с помощью теоремы о среднем отрезке трапеции , которая гласит, что длина среднего отрезка равна сумме длин оснований, деленной на 2. Следовательно, ее можно рассчитать, сложив длины каждого основания и деления суммы на 2.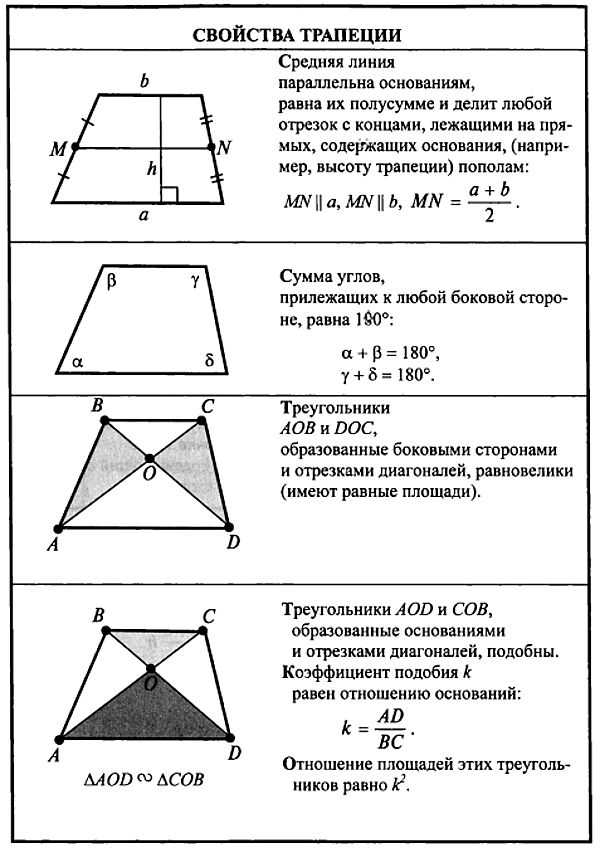
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную запись
Зарегистрируйтесь для просмотра этого урока
Вы студент или преподаватель?
Разблокируйте свое образование
Убедитесь сами, почему 30 миллионов человек используют Study.com
Станьте участником Study.com и начните учиться прямо сейчас.
Стать участником
Уже являетесь участником? Войти
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков и учебные ресурсы‐все в одном месте.
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Спинка
Теорема о среднем сегменте трапеции | Помощь по геометрии
Главная » Четырехугольники » Трапеции » Теорема о середине трапеции
Последнее обновление: Идо Сариг · Этот веб-сайт получает доход от рекламы и использует файлы cookie · Условия использования · Политика конфиденциальности
Сегодня на уроке геометрии мы докажем теорему о середине трапеции, опираясь на ранее доказанную теорема о середине треугольника.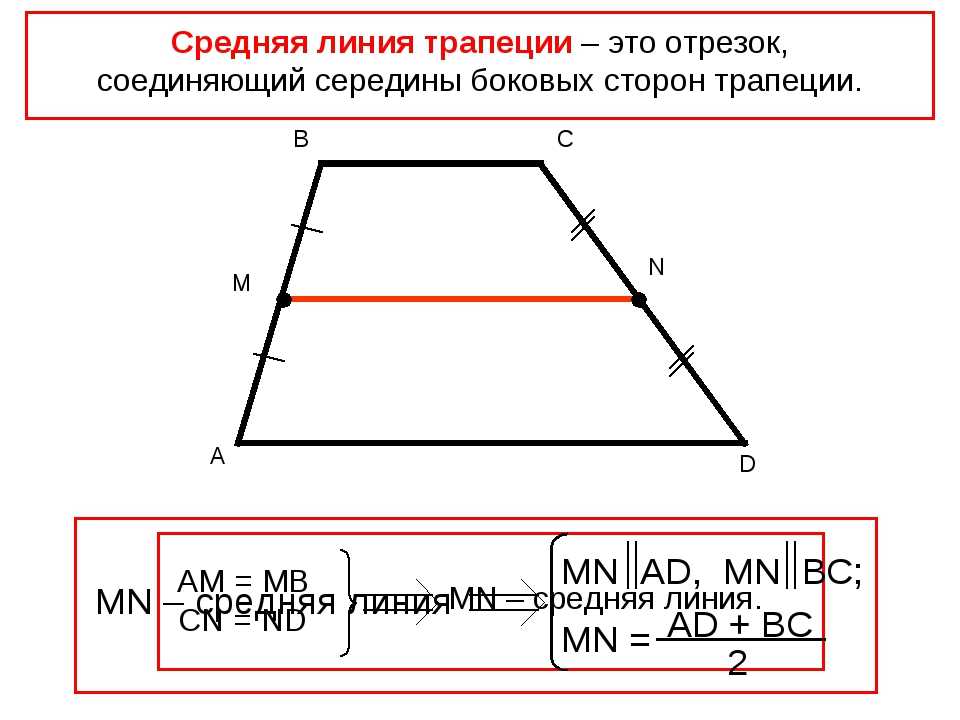
Теорема о средней линии треугольника утверждает, что прямая, соединяющая середины двух сторон треугольника, называемая средней линией, параллельна третьей стороне, а ее длина равна половине длины третьей стороны.
Аналогичная теорема существует и для трапеций: прямая, соединяющая середины двух катетов трапеции, параллельна основаниям, а ее длина равна половине суммы длин оснований.
Задача
ABCD трапеция, AB || CD . EF — линия, соединяющая середины ветвей AD и BC , AE = ED и BF = FC . Докажите, что EF || DC и EF =½( AB + DC )
Стратегия
Поскольку мы имеем дело с серединами сегментов, мы будем использовать то, что мы уже доказали для середины сегментов треугольника. Давайте создадим такие треугольники, проведя линию из вершины A через середину F, пока она не пересечет продолжение основания DC в точке G:
Мы можем легко показать, что ΔABF и ΔGCF конгруэнтны, используя угол-сторона -Угловой постулат.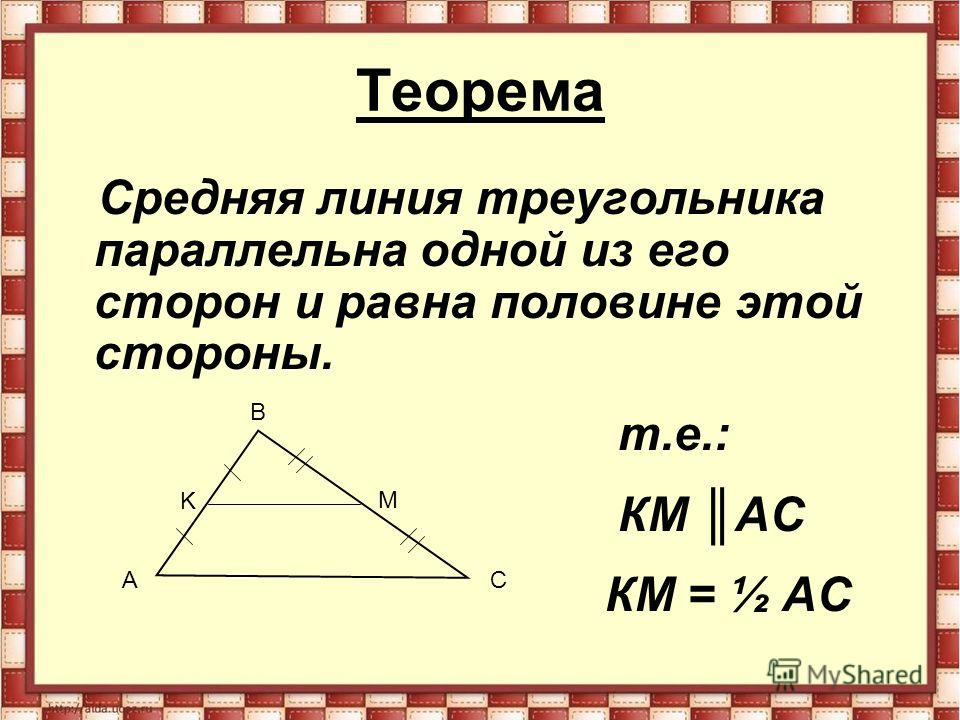 Отсюда мы можем показать, что EF — средняя линия треугольника ΔADG. Таким образом, согласно теореме о середине треугольника, он параллелен DG и равен половине DG .
Отсюда мы можем показать, что EF — средняя линия треугольника ΔADG. Таким образом, согласно теореме о середине треугольника, он параллелен DG и равен половине DG .
Но DG равно DC + CG , и, поскольку ΔABF и ΔGCF конгруэнтны, CG = AB , поэтому 1 90 DC 90 90 89 равно половине 0 8 . 0080 АБ . Другими словами, длина EF есть среднее арифметическое (среднее) длин оснований.
Доказательство
Вот как доказать теорему о середине трапеции:
(1) AB||DG //Дано, ABCD — трапеция
(2) ∠BAF ≅ ∠CGF // Теорема о чередующихся внутренних углах
(3)∠AED ≅ ∠CEF // Вертикальные углы
(4) BF=FC //Дано
(5)ΔABF ≅ ΔGCF // (2), (3), (4), Угол-Сторона-Угол
(6) AF=FG / /(5), соответствующие стороны конгруэнтных треугольников
(7) EF является средней линией //(6), определение средней линии
(8) EF||DG //(7), теорема о средней линии треугольника
(9)EF=½DG //(7), теорема о середине треугольника
(10) DG = DC + CG
(11) CG = AB //(5), соответствующие стороны конгруэнтных треугольников
(12)EF080 + (DC CG ) //(9), (10) , Транзитивность равенства
(13) EF=½ (DC + AB ) //(11), (12) , Транзитивность равенства
Верно и обратное утверждение этой теоремы: прямая, параллельная одному из оснований трапеции и пересекающая середину одного катета, пересекает и середину другого катета, а ее длина равна половине суммы длин оснований.