Стороны треугольника – расчет по формуле, соотношение, уравнение
4.3
Средняя оценка: 4.3
Всего получено оценок: 193.
4.3
Средняя оценка: 4.3
Всего получено оценок: 193.
В математике при рассмотрении треугольника обязательно уделяют много внимание его сторонам. Поскольку данные элементы формируют эту геометрическую фигуру. Стороны треугольника используются для решения многих задач по геометрии.
Определение понятия
Отрезки, соединяющие три точки, которые не лежат на одной прямой, называются сторонами треугольника. Рассматриваемые элементы ограничивают часть плоскости, что называют внутренностью данной геометрической фигуры.
Математики в своих расчетах допускают обобщения, касающиеся сторон геометрических фигур. Так, в вырожденном треугольнике три его отрезка лежат на одной прямой.
Характеристики понятия
Расчет сторон треугольника предполагает определение всех остальных параметров фигуры. Зная длину каждого из этих отрезков можно легко вычислить периметр, площадь и даже углы треугольника.
Значение
Через соотношение сторон треугольника выражают некоторые свойства этой геометрической фигуры:
- Напротив наименьшей стороны треугольника находится его наименьший угол.
- Внешний угол рассматриваемой геометрической фигуры получают, продлевая одну из сторон.
- Напротив равных углов треугольника лежат равные стороны.
- В любом треугольнике одна из сторон всегда больше разности двух других отрезков. А сумма любых двух сторон этой фигуры больше третьей.
Один из признаков равенства двух треугольников является соотношение суммы всех сторон геометрической фигуры. Если эти значения одинаковые, то и треугольники будут равными.
Некоторые свойства треугольника зависят от его типа. Поэтому вначале следует учитывать величину сторон или углов этой фигуры.
Формирование треугольников
Если две стороны рассматриваемой геометрической фигуры будут одинаковыми, то этот треугольник называют равнобедренным.
Когда все отрезки в треугольнике будут равны, то получится равносторонний треугольник.
Рис. 3. Равносторонний треугольник.Любое вычисление удобнее проводить в тех случаях, когда произвольный треугольник можно отнести к определенному типу. Поскольку тогда нахождение требуемого параметра этой геометрической фигуры значительно упростится.
Хотя правильно подобранное тригонометрическое уравнение позволяет решить многие задачи, в которых рассматривается произвольный треугольник.
Что мы узнали?
Три отрезка, которые соединены между собой точками и не принадлежат одной прямой, формируют треугольник. Эти стороны образуют геометрическую плоскость, что используется при определении площади. С помощью данных отрезков можно найти много таких важных характеристик фигуры, как периметр и углы. Соотношение сторон в треугольнике помогает найти его тип. Некоторыми свойствами данной геометрической фигуры можно воспользоваться только, если известны размеры каждой из ее сторон.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 193.
А какая ваша оценка?
Найти стороны треугольника онлайн. Стороны треугольника
В геометрии часто бывают задачи, связанные со сторонами треугольников. Например, часто необходимо найти сторону треугольника, если две другие известны.
Треугольники бывают равнобедренными, равносторонними и неравносторонними. Из всего разнообразия, для первого примера выберем прямоугольный (в таком треугольнике один из углов равен 90°, прилегающие к нему стороны называются катетами, а третья — гипотенузой).
Быстрая навигация по статье
Длина сторон прямоугольного треугольника
Решение задачи следует из теоремы великого математика Пифагора. В ней говорится, что сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы: a²+b²=c²
- Находим квадрат длины катета a;
- Находим квадрат катета b;
- Складываем их между собой;
- Из полученного результата извлекаем корень второй степени.

Пример: a=4, b=3, c=?
- a²=4²=16;
- b² =3²=9;
- 16+9=25;
- √25=5. То есть, длина гипотенузы данного треугольника равна 5.
Если же у треугольника нет прямого угла, то длин двух сторон недостаточно. Для этого необходим третий параметр: это может быть угол, высота площадь треугольника, радиус вписанной в него окружности и т.д..
Если известен периметр
В этом случае задача ещё проще. Периметр (P) представляет собой сумму всех сторон треугольника: P=a+b+c. Таким образом, решив простое математическое уравнение получаем результат.
Пример: P=18, a=7, b=6, c=?
1) Решаем уравнение, перенося все известные параметры в одну сторону от знака равенства:
2) Подставляем вместо них значения и вычисляем третью сторону:
c=18-7-6=5, итого: третья сторона треугольника равна 5.
Если известен угол
Для вычисления третьей стороны треугольника по углу и двум другим сторонам, решение сводится к вычислению тригонометрического уравнения. Зная взаимосвязь сторон треугольника и синуса угла, несложно вычислить третью сторону. Для этого нужно возвести обе стороны в квадрат и сложить их результаты вместе. Затем вычесть из получившегося произведение сторон, умноженное на косинус угла: C=√(a²+b²-a*b*cosα)
Зная взаимосвязь сторон треугольника и синуса угла, несложно вычислить третью сторону. Для этого нужно возвести обе стороны в квадрат и сложить их результаты вместе. Затем вычесть из получившегося произведение сторон, умноженное на косинус угла: C=√(a²+b²-a*b*cosα)
Если известна площадь
В этом случае одной формулой не обойтись.
1) Сначала вычисляем sin γ, выразив его из формулы площади треугольника:
sin γ= 2S/(a*b)
2) По следующей формуле вычисляем косинус того же угла:
sin² α + cos² α=1
cos α=√(1 — sin² α)=√(1- (2S/(a*b))²)
3) И снова воспользуемся теоремой синусов:
C=√((a²+b²)-a*b*cosα)
C=√((a²+b²)-a*b*√(1- (S/(a*b))²))
Подставив в это уравнение значения переменных, получим ответ задачи.
| Введите известные даные треугольника | |
| Сторона а | |
| Сторона b | |
| Сторона c | |
| Угол А в градусах | |
| Угол B в градусах | |
| Угол C в градусах | |
| Медиана на сторону а | |
| Медиана на сторону b | |
| Медиана на сторону c | |
| Высота на сторону a | |
| Высота на сторону b | |
| Высота на сторону c | |
| Координаты вершины А | |
| X Y | |
| Координаты вершины B | |
| X Y | |
| Координаты вершины C | |
| X Y | |
| Площадь треугольника S | |
| Полупериметр сторон треугольника p | |
Представляем Вам калькулятор, который позволял рассчитывать все возможные .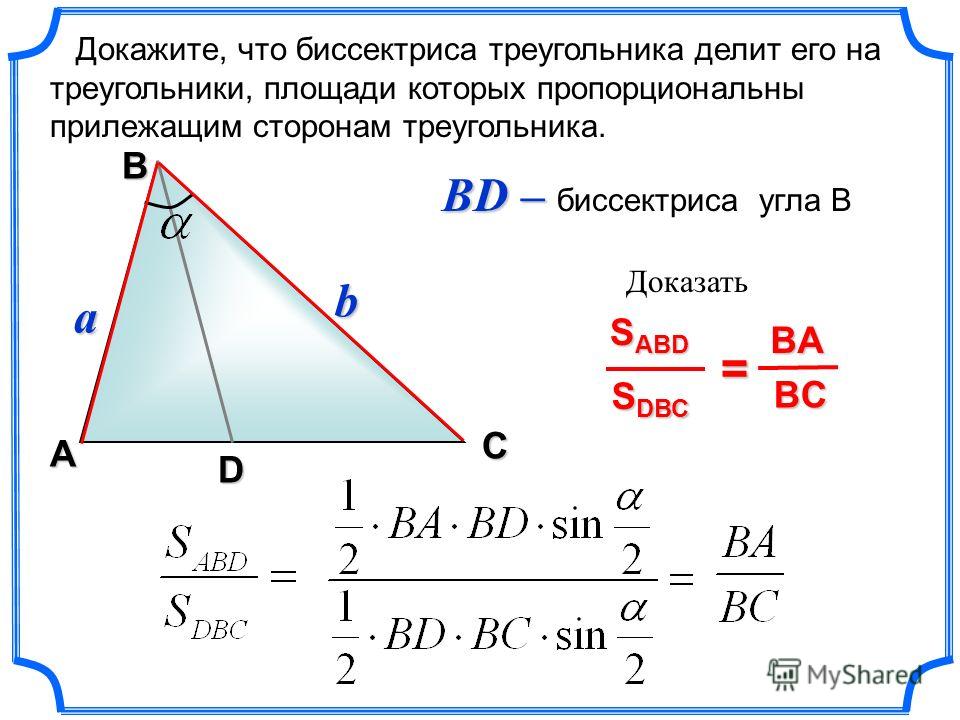
Хотелось бы обратить Ваше внимание именно на то, что это универсальный бот. Он рассчитывает все параметры произвольного треугольника, при произвольно заданных параметрах. Такого бота вы не найдете нигде.
Вам известна сторона и две высоты? или две стороны и медиана? Или биссектриса два угла и основание треугольника?
По любым запросам, мы можем получить правильный расчет параметров треугольника.
Вам нет необходимости искать формулы и делать расчет самостоятельно. За вас уже все сделано.
Создайте запрос и получите точный ответ.
Показан произвольный треугольник. Сразу оговоримся как и что обозначается, дабы в дальнейшем не было путаницы и ошибок в расчетах.
Стороны противоположные любому углу называются так же только маленькой буквой . То есть напротив угла А лежит сторона треугольника а, стороне с противостоит угол С.
ma — это медина, падающая на сторону а, соответственно есть еще медианы mb и mc падающие на соответствующие стороны.
lb — это биссектриса, падающая на сторону b, соответственно есть еще биссектрисы la и lc падающие на соответствующие стороны.
hb — это высота, падающая на сторону b, соответственно есть еще высоты ha и hc падающие на соответствующие стороны.
Ну и второе, помните что треугольником является фигура в которой присутствует фундаментальное правило:
Сумма любых(!) двух сторон должна быть больше третьей .
Поэтому не удивляйтесь если получите ошибку При таких данных треугольника не существует при попытке рассчитатать параметры треугольника со сторонами 3, 3 и 7.
Синтаксис
Для позволяателей XMPP клиентов запрос вот такой treug
Для пользователй сайта, все сделано на этой странице.
Список параметров — параметры которые известны, разделенные точкой с запятой
параметр записываетя как параметр=значение
Например если известна сторона а с значением 10, то так и записываем a=10
Более того, значения могут быть не только в виде вещественного числа, но и например как результат какого то выражения
А вот и сам список парметров которые могут фигурировать в расчетах.
Сторона a
Сторона b
Сторона c
Полупериметр p
Угол А
Угол B
Угол C
Площадь треугольника S
Высота ha на сторону a
Высота hb на сторону b
Высота hc на сторону c
Медиана ma на сторону a
Медиана mb на сторону b
Медиана mc на сторону c
Координаты вершин (xa,ya) (xb,yb) (xc,yc)
Примеры
пишем treug a=8;C=70;ha=2
Параметры треугольника по заданным параметрам
Сторона a = 8
Сторона b = 2.1283555449519
Сторона c = 7.5420719851515
Полупериметр p = 8.8352137650517
Угол А = 2.1882518638666 в градусах 125.37759631119
Угол B = 2.873202966917 в градусах 164.62240368881
Угол C = 1.221730476396 в градусах 70
Площадь треугольника S = 8
Высота ha на сторону a = 2
Высота hb на сторону b = 7.5175409662872
Высота hc на сторону c = 2.
 1214329472723
1214329472723Медиана ma на сторону a = 3.8348889915443
Медиана mb на сторону b = 7.7012304590352
Медиана mc на сторону c = 4.4770789813853
Вот и все, все параметры треугольника.
Вопрос, почему мы сторону назвали а , а не в или с ? Это не влияет на решение. Главное выдержать условие о котором я уже сказал «Стороны противоположные любому углу называются так же, только маленькой буквой .» А далее нарисовать в уме треугольник, и применить к заданному вопросу.
Можно было бы взять вместо а
Например вот такими (xa,ya) =3,4 (xb,yb) =-6,14 (xc,yc)=-6,-3
пишем запрос treug xa=3;ya=4;xb=-6;yb=14;xc=-6;yc=-3
и получаем
Параметры треугольника по заданным параметрам
Сторона a = 17
Сторона b = 11.401754250991
Сторона c = 13.
 453624047073
453624047073Полупериметр p = 20.927689149032
Угол А = 1.4990243938603 в градусах 85.887771155351
Угол B = 0.73281510178655 в градусах 41.987212495819
Угол C = 0.90975315794426 в градусах 52.125016348905
Площадь треугольника S = 76.5
Высота ha на сторону a = 9
Высота hb на сторону b = 13.418987695398
Высота hc на сторону c = 11.372400437582
Медиана ma на сторону a = 9.1241437954466
Медиана mb на сторону b = 14.230249470757
Медиана mc на сторону c = 12.816005617976
Удачных расчетов!!
Определение треугольника
Треугольник — это геометрическая фигура, которая образуется в результате пересечения трех отрезков, концы которых не лежат на одной прямой. У любого треугольника есть три стороны, три вершины и три угла.
Онлайн-калькулятор
Треугольники бывают различных видов. Например, существует равносторонний треугольник (тот, у которого все стороны равны), равнобедренный (в нем равны две стороны) и прямоугольный (в котором один из углов прямой, т.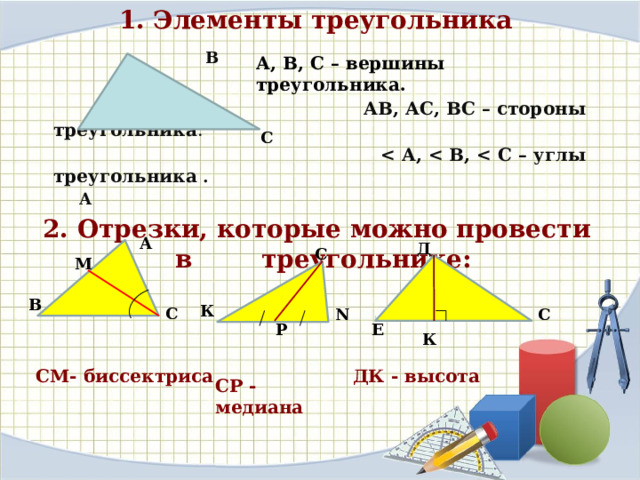 е. равен 90 градусам).
е. равен 90 градусам).
Площадь треугольника можно найти различными способами в зависимости от того, какие элементы фигуры известны по условию задачи, будь то углы, длины, либо же вообще радиусы окружностей, связанных с треугольником. Рассмотрим каждый способ отдельно с примерами.
Формула площади треугольника по основанию и высоте
S = 1 2 ⋅ a ⋅ h S= \frac{1}{2}\cdot a\cdot h S = 2 1 ⋅ a ⋅ h ,
A a
a
— основание треугольника;
h h
h
— высота треугольника, проведенная к данному основанию a.
Пример
Найти площадь треугольника, если известна длина его основания, равная 10 (см.) и высота, проведенная к этому основанию, равная 5 (см.).
Решение
A = 10 a=10
a
=
1
0
h = 5 h=5
h
=
5
Подставляем в формулу для площади и получаем:
S = 1 2 ⋅ 10 ⋅ 5 = 25 S=\frac{1}{2}\cdot10\cdot 5=25
S
=
2
1
⋅
1
0
⋅
5
=
2
5
(см. кв.)
Ответ: 25 (см. кв.)
Формула площади треугольника по длинам всех сторон
S = p ⋅ (p − a) ⋅ (p − b) ⋅ (p − c) S= \sqrt{p\cdot(p-a)\cdot (p-b)\cdot (p-c)} S = p ⋅ (p − a ) ⋅ (p − b ) ⋅ (p − c ) ,
A , b , c a, b, c
a
,
b
,
c
— длины сторон треугольника;
p p
p
— половина суммы всех сторон треугольника (то есть, половина периметра треугольника):
P = 1 2 (a + b + c) p=\frac{1}{2}(a+b+c) p = 2 1 (a + b + c )
Эта формула называется формулой Герона . {\circ})}=50\cdot\frac{1}{2\sqrt{3}}\approx14.4
S
=
2
1
0
2
⋅
sin
(3
0
∘
+
3
0
∘
)
sin
3
0
∘
sin
3
0
∘
=
5
0
⋅
2
3
1
≈
1
4
.
4
(см. кв.)
{\circ})}=50\cdot\frac{1}{2\sqrt{3}}\approx14.4
S
=
2
1
0
2
⋅
sin
(3
0
∘
+
3
0
∘
)
sin
3
0
∘
sin
3
0
∘
=
5
0
⋅
2
3
1
≈
1
4
.
4
(см. кв.)
Ответ: 14.4 (см. кв.)
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = a ⋅ b ⋅ c 4 R S=\frac{a\cdot b\cdot c}{4R} S = 4 R a ⋅ b ⋅ c ,
A , b , c a, b, c
a
,
b
,
c
— стороны треугольника;
R R
R
— радиус описанной окружности вокруг треугольника.
Пример
Числа возьмем из второй нашей задачи и добавим к ним радиус R R R окружности. Пусть он будет равен 10 (см.).
Решение
A = 3 a=3
a
=
3
b = 4 b=4
b
=
4
c = 5 c=5
c
=
5
R = 10 R=10
R
=
1
0
S = 3 ⋅ 4 ⋅ 5 4 ⋅ 10 = 60 40 = 1.5 S=\frac{3\cdot 4\cdot 5}{4\cdot 10}=\frac{60}{40}=1.5 S = 4 ⋅ 1 0 3 ⋅ 4 ⋅ 5 = 4 0 6 0 = 1 . 5 (см. кв.)
Ответ: 1.5 (см.кв.)
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
S = p ⋅ r S=p\cdot r S = p ⋅ r ,
p p p — половина периметра треугольника:
p = a + b + c 2 p=\frac{a+b+c}{2} p = 2 a + b + c ,
a , b , c a, b, c
a
,
b
,
c
— стороны треугольника;
r r
r
— радиус вписанной в треугольник окружности. 2+2bc))/(b+c)=(b√(2c(b+c)))/(b+c)=(a/tanα √(2c(a/tanα +c)))/(a/tanα +c)=(a√(2c(a/tanα +c)))/(a+c tanα)
l_b=√(ac(a+b+c)(a+c-b))/(a+c)=(a√(2c(a+c)))/(a+c)=(a√(2c(a+a/sinα)))/(a+a/sinα)=(a sinα √(2c(a+a/sinα)))/(a sinα+a)
2+2bc))/(b+c)=(b√(2c(b+c)))/(b+c)=(a/tanα √(2c(a/tanα +c)))/(a/tanα +c)=(a√(2c(a/tanα +c)))/(a+c tanα)
l_b=√(ac(a+b+c)(a+c-b))/(a+c)=(a√(2c(a+c)))/(a+c)=(a√(2c(a+a/sinα)))/(a+a/sinα)=(a sinα √(2c(a+a/sinα)))/(a sinα+a)
Средняя линия проходит параллельно одной из сторон треугольника, при этом образуя еще один подобный прямоугольный треугольник с такими же по величине углами, в котором все стороны в два раза меньше, чем у изначального. Исходя из этого, средние линии можно найти по следующим формулам, зная только катет и противолежащий ему угол. (рис.79.7) M_a=a/2 M_b=b/2=a/(2 tanα) M_c=c/2=a/(2 sinα)
Радиус вписанной окружности равен разности катетов и гипотенузы, деленной на два, а чтобы найти радиус описанной окружности, нужно разделить на два гипотенузу. Заменяем второй катет и гипотенузу на отношения катета a к синусу и тангенсу соответственно. (рис. 79.5, 79.6) r=(a+b-c)/2=(a+a/tanα -a/sinα)/2=(a tanα sinα+a sinα-a tanα)/(2 tanα sinα) R=c/2=a/2sinα
В математике при рассмотрении треугольника обязательно уделяют много внимание его сторонам.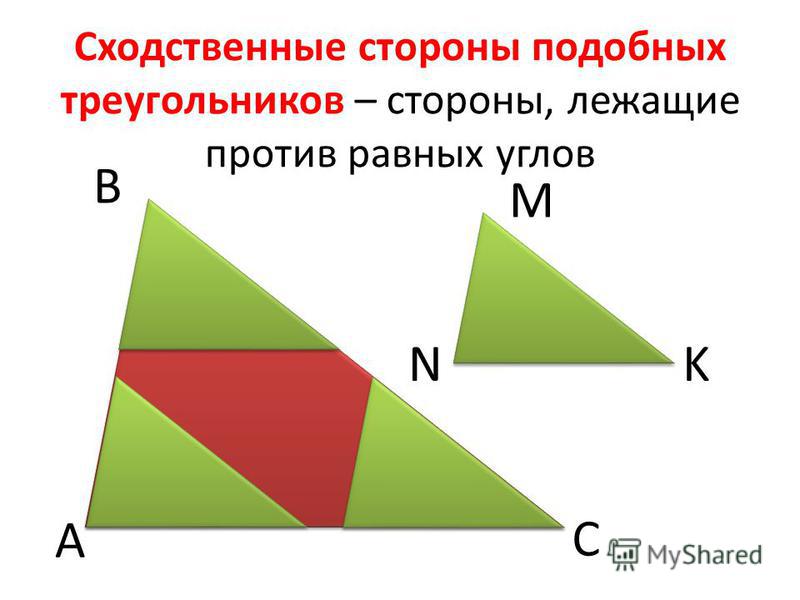 Поскольку данные элементы формируют эту геометрическую фигуру. Стороны треугольника используются для решения многих задач по геометрии.
Поскольку данные элементы формируют эту геометрическую фигуру. Стороны треугольника используются для решения многих задач по геометрии.
Определение понятия
Отрезки, соединяющие три точки, которые не лежат на одной прямой, называются сторонами треугольника. Рассматриваемые элементы ограничивают часть плоскости, что называют внутренностью данной геометрической фигуры.
Математики в своих расчетах допускают обобщения, касающиеся сторон геометрических фигур. Так, в вырожденном треугольнике три его отрезка лежат на одной прямой.
Характеристики понятия
Расчет сторон треугольника предполагает определение всех остальных параметров фигуры. Зная длину каждого из этих отрезков можно легко вычислить периметр, площадь и даже углы треугольника.
Рис. 1. Произвольный треугольник.
Суммировав стороны данной фигуры можно определить периметр.
P=a+b+c, где a, b, c – стороны треугольника
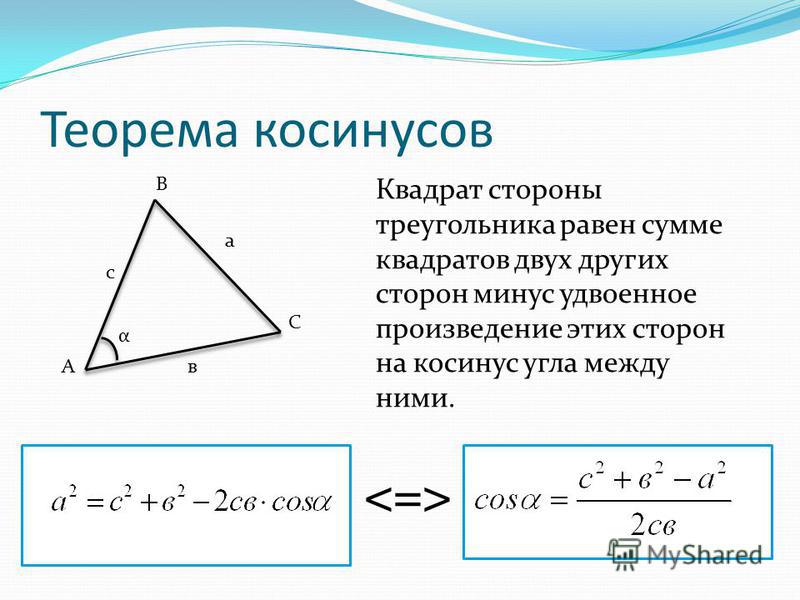
А для нахождения площади треугольника тогда следует использовать формулу Герона. 2}\over{2bc}}$$
2}\over{2bc}}$$
Значение
Через соотношение сторон треугольника выражают некоторые свойства этой геометрической фигуры:
- Напротив наименьшей стороны треугольника находится его наименьший угол.
- Внешний угол рассматриваемой геометрической фигуры получают, продлевая одну из сторон.
- Напротив равных углов треугольника лежат равные стороны.
- В любом треугольнике одна из сторон всегда больше разности двух других отрезков. А сумма любых двух сторон этой фигуры больше третьей.
Один из признаков равенства двух треугольников является соотношение суммы всех сторон геометрической фигуры. Если эти значения одинаковые, то и треугольники будут равными.
Некоторые свойства треугольника зависят от его типа. Поэтому вначале следует учитывать величину сторон или углов этой фигуры.
Формирование треугольников
Если две стороны рассматриваемой геометрической фигуры будут одинаковыми, то этот треугольник называют равнобедренным.
Рис.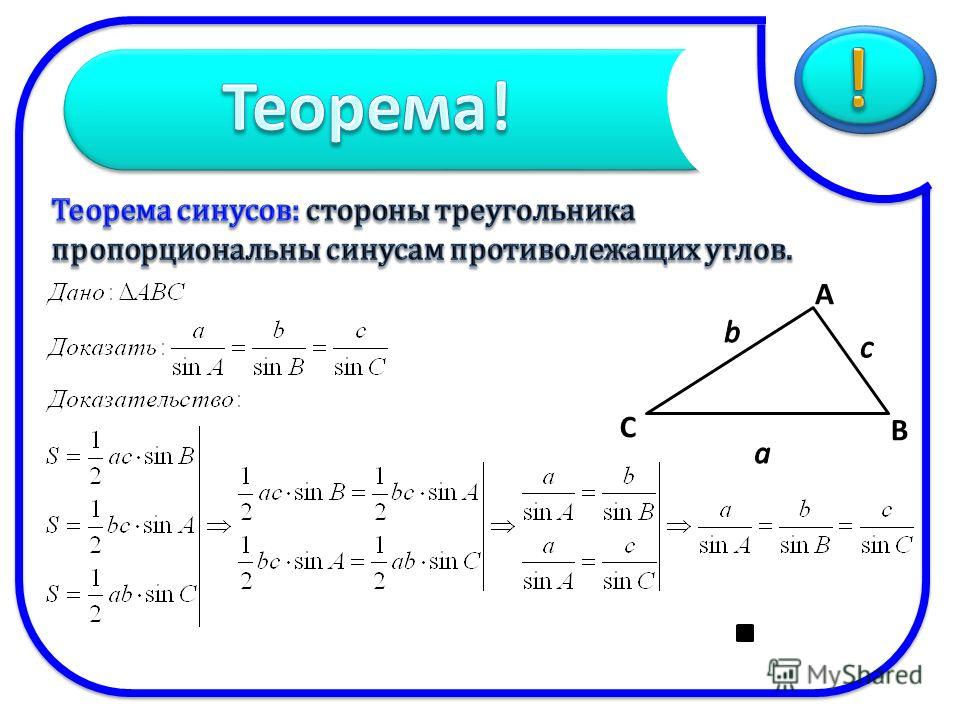 2. Равнобедренный треугольник.
2. Равнобедренный треугольник.
Когда все отрезки в треугольнике будут равны, то получится равносторонний треугольник.
Рис. 3. Равносторонний треугольник.
Любое вычисление удобнее проводить в тех случаях, когда произвольный треугольник можно отнести к определенному типу. Поскольку тогда нахождение требуемого параметра этой геометрической фигуры значительно упростится.
Хотя правильно подобранное тригонометрическое уравнение позволяет решить многие задачи, в которых рассматривается произвольный треугольник.
Что мы узнали?
Три отрезка, которые соединены между собой точками и не принадлежат одной прямой, формируют треугольник. Эти стороны образуют геометрическую плоскость, что используется при определении площади. С помощью данных отрезков можно найти много таких важных характеристик фигуры, как периметр и углы. Соотношение сторон в треугольнике помогает найти его тип. Некоторыми свойствами данной геометрической фигуры можно воспользоваться только, если известны размеры каждой из ее сторон.
Тест по теме
Оценка статьи
Средняя оценка: 4.3 . Всего получено оценок: 132.
6 Правила треугольника Вам необходимо знать
6 Правила треугольника. Вам нужно знать
Jana Russick
март 09, 2021
онлайн -репетиторство
,
Matematics
,
Trigonometry
. нам понять свойства этой формы. Как один из самых центральных элементов тригонометрии, треугольники имеют множество геометрических правил. Среди прочего, они помогают нам отличать прямоугольные треугольники от равносторонних треугольников и равнобедренных треугольников.
Давайте рассмотрим некоторые из наиболее известных тригонометрических правил треугольника.
Правило внутренних углов
Правило внутренних углов гласит, что три угла треугольника должны быть равны 180°. Как вы можете видеть ниже, три угла тупоугольного треугольника ABC в сумме составляют 180°.
Стороны треугольника
Правило сторон треугольника утверждает, что сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. См. Длины сторон остроугольного треугольника ниже. Сумма длин двух самых коротких сторон, 6 и 7, равна 13. Эта длина больше, чем длина самой длинной стороны, 8,9.0005
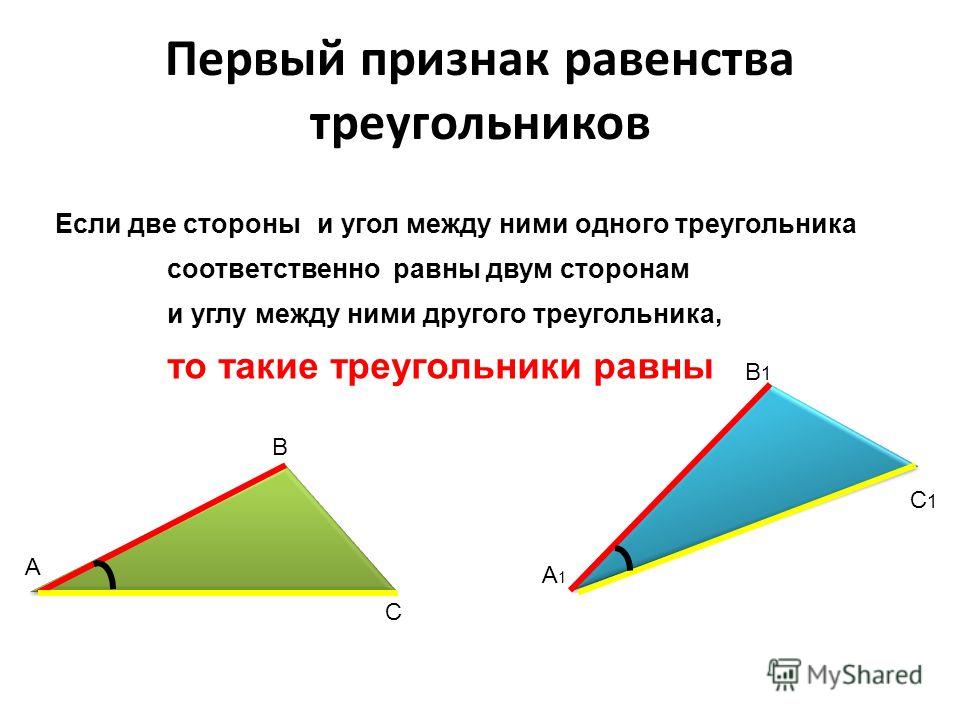
Правила сходства треугольников
Конгруэнтные треугольники — это треугольники, у которых соответствующие стороны и углы равны. В тригонометрической манере равные стороны и равные углы доказываются конгруэнтностью с помощью четырех правил конгруэнтности треугольников. Мы рассмотрим их по очереди.
#1: Правило SSS
Правило стороны-стороны-стороны (SSS) гласит, что когда измерения трех сторон треугольника совпадают с измерениями трех сторон другого треугольника, эти две формы конгруэнтны.
См. прямоугольные треугольники ниже. Стороны треугольника DEF имеют ту же длину, что и треугольник GHI, поэтому они равны.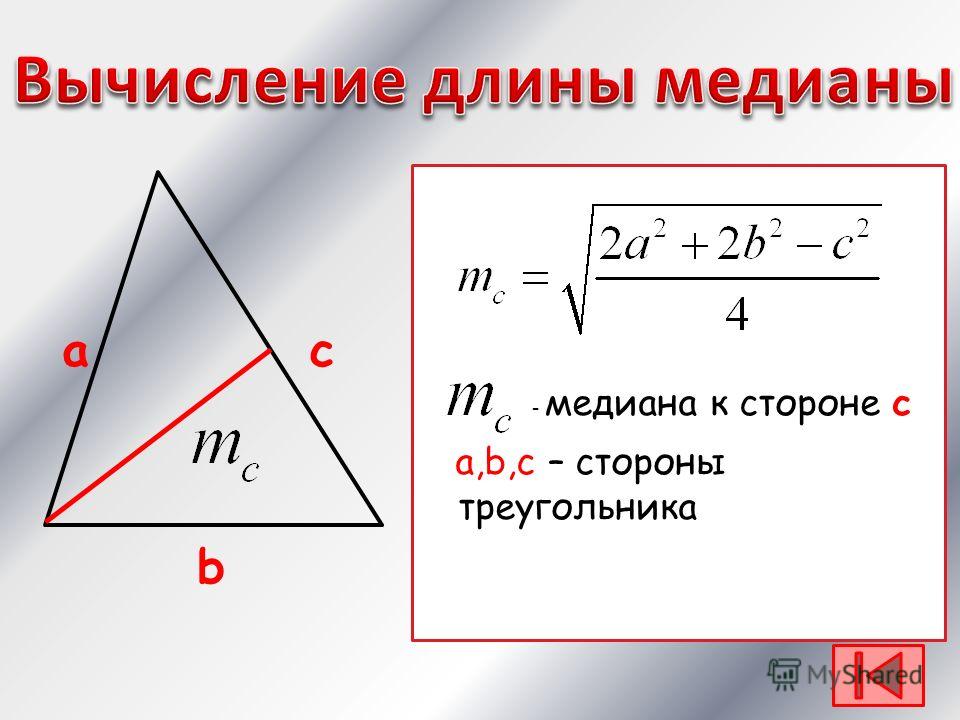
#2: Правило ASA
Правило ASA гласит, что когда два угла и одна сторона треугольника равны стороне другого треугольника, они являются конгруэнтными треугольниками.
См. треугольники JKL и MNO. Углы J и M, K и N (углы, противоположные длине гипотенузы), а также катеты гипотенузы обоих треугольников равны. Следовательно, треугольники JKL и MNO равны.
#3: Правило AAS
Правило угла-угла-стороны (AAS) утверждает, что если два треугольника обладают следующими соответствующими свойствами, они должны быть конгруэнтны:
- Два угла
- Длина одной противоположной стороны без вершин
#4: Правило SAS
Правило SAS гласит, что если прилежащий угол и две прилежащие длины сторон треугольника равны длинам двух прилежащих сторон треугольника, то они конгруэнтны. См. ниже треугольники CDE и FGH. Прямой угол C и угол F, длины d и g и длина гипотенузы c и f равны. Следовательно, треугольник CDE=FGH.
Важность правил треугольника
Расширение ваших знаний о правилах треугольника облегчит изучение других тригонометрических понятий, таких как теорема Пифагора и правила косинуса, тангенса и синуса. Эти знания также помогут вам освоить площадь треугольника и многоугольника.
Дополнительная помощь по домашнему заданию по математике:
- Что такое теорема Пифагора и когда она используется?
- Как найти длину треугольника
- Узнайте, как найти площадь неправильного треугольника
Треугольник
Треугольник — это многоугольник с тремя сторонами и тремя углами.
Три стороны показанного выше треугольника ABC, обозначенные символически как △ABC, являются отрезками AB, BC и AC. Вершина образуется при пересечении двух сторон треугольника. △ABC имеет вершины в точках A, B и C. В каждой вершине образован внутренний угол. Углы A, B и C являются тремя внутренними углами для △ABC.
Отрезок от вершины треугольника до стороны, противоположной вершине, и перпендикулярной противоположной стороне называется высотой.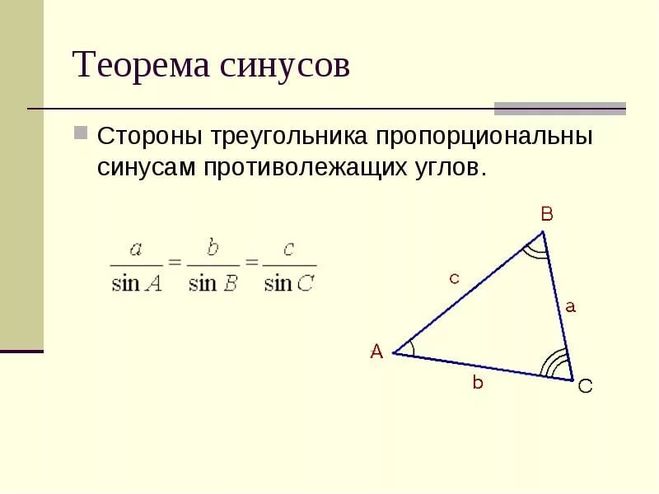 Сторона, перпендикулярная высоте, называется основанием треугольника. В треугольнике ABC ниже отрезок CD является высотой, а сторона AB является основанием.
Сторона, перпендикулярная высоте, называется основанием треугольника. В треугольнике ABC ниже отрезок CD является высотой, а сторона AB является основанием.
Стороны треугольника принято называть по противолежащему углу. Это часто включает использование прописных и строчных букв для обозначения угла и его противоположной стороны. В качестве примера см. △ABC выше. Сторона ВС противоположна углу А, поэтому она обозначена как сторона а.
Сумма углов
Используя свойства параллельных прямых и чередующихся внутренних углов, мы можем показать, что сумма внутренних углов треугольника равна 180°.
- Для △ABC, показанного выше, пусть линия DE, содержащая вершину C, параллельна стороне AB. Поскольку ∠DCE — прямой угол, ∠ECA + ∠DCB + ∠BCA = 180°.
- Кроме того, поскольку DE параллелен AB, это образует два набора конгруэнтных альтернативных внутренних углов, так что ∠ECA≅∠A и ∠DCB≅∠B.
- Подставив углы A и B в наше предыдущее уравнение, ∠A + ∠B + ∠BCA = 180°, где ∠BCA = ∠C.

Внешние углы
Для треугольника внешним углом называется угол, образованный одной стороной треугольника и линией, продолжающейся от другой его стороны. Мера внешнего угла треугольника равна сумме двух удаленных друг от друга внутренних углов.
Для △ABC, показанного выше, ∠CAD — это внешний угол для ∠A, а ∠B и ∠C — два отдаленных внутренних угла. Мы знаем, что ∠CAB + ∠B + ∠C = 180°. Кроме того, ∠CAB и ∠CAD образуют прямой угол, поэтому ∠CAB + ∠CAD = 180°. Поскольку обе суммы равны 180°:
∠CAB + ∠CAD = ∠CAB + ∠B + ∠C
∠CAD = ∠B + ∠C
То же самое можно показать для любого внешнего угла любого треугольника.
Классификация треугольников
Треугольники часто классифицируют по их углам и сторонам, как показано в таблицах ниже.
По углам:
| Тип | Углы | Фигура |
|---|---|---|
| Острая | все внутренние углы < 90° | |
| Тупой | 1 внутренний угол > 90° | |
| Справа | 1 угол = 90° | |
| Равноугольный | каждый внутренний угол = 60° |
По сторонам:
| Тип | Стороны | Фигура |
|---|---|---|
| Масштабность | нет двух равных сторон | |
| Равнобедренный | 2 конгруэнтные стороны | |
| Равносторонний | все стороны равны |
Сравнение сторон и углов
Треугольник может быть образован только тогда, когда сумма любых двух сторон треугольника больше, чем его третья сторона.