Математика во 2 классе. Тема. Угол. Виды углов (прямой, тупой, острый) | План-конспект урока по математике (2 класс) на тему:
Математика во 2 классе.
Тема. Угол. Виды углов (прямой, тупой, острый)
Цель: дать учащимся представление о прямом угле.
Задачи: учить отличать прямой угол от острого и тупого при помощи модели прямого угла; развивать вычислительные навыки, умение складывать и вычитать двузначные числа в столбик (без перехода через десяток).
Планируемые результаты.
Предметные. Научатся отличать прямой угол от острого и тупого при помощи модели прямого угла. Отработают умения складывать и вычитать двузначные числа в столбик с проверкой, решать задачи
УУД. Регулятивные : ставить новые учебные задачи в сотрудничестве с учителем; контролировать свою деятельность по ходу выполнения заданий. Познавательные : ориентироваться в разнообразии способов решения задач; создавать и преобразовывать модели и схемы для решения задач. Коммуникативные : задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнером; осуществлять взаимный контроль.
Личностные результаты. Приобретают навыки сотрудничества в разных ситуациях, умение не создавать конфликтов и находить выходы из спорных ситуаций.
Ход урока
I. Мотивирование к учебным действиям.
II. Каллиграфическая минутка.
10 10 10 10 10
20 20 20 20 20
III. Устный счет.
1. «Цепочка».
2. «Какой пример лишний?»
7 + 7
5 + 9
10 + 4
9 + 7
8 + 6
(Лишними являются примеры 9 + 7, так как его значение равно шестнадцати, значения остальных выражений равны четырнадцати, и пример 10 + 4, так как во всех суммах складываются однозначные числа, а в этой сумме первым слагаемым является двузначное число.)
IV. Изучение нового материала.
1. На доске изображена фигура:
– Знаете ли вы, как называется эта фигура?
– Правильно, она называется углом.
– Это прямой угол.
2. Рассматривают чертежи других углов, изображённых на доске.
– Все ли из этих углов прямые?
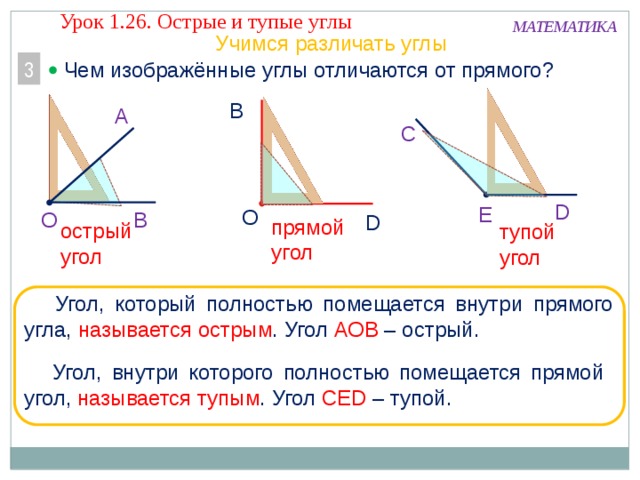
– Кроме прямых, бывают острые и тупые углы.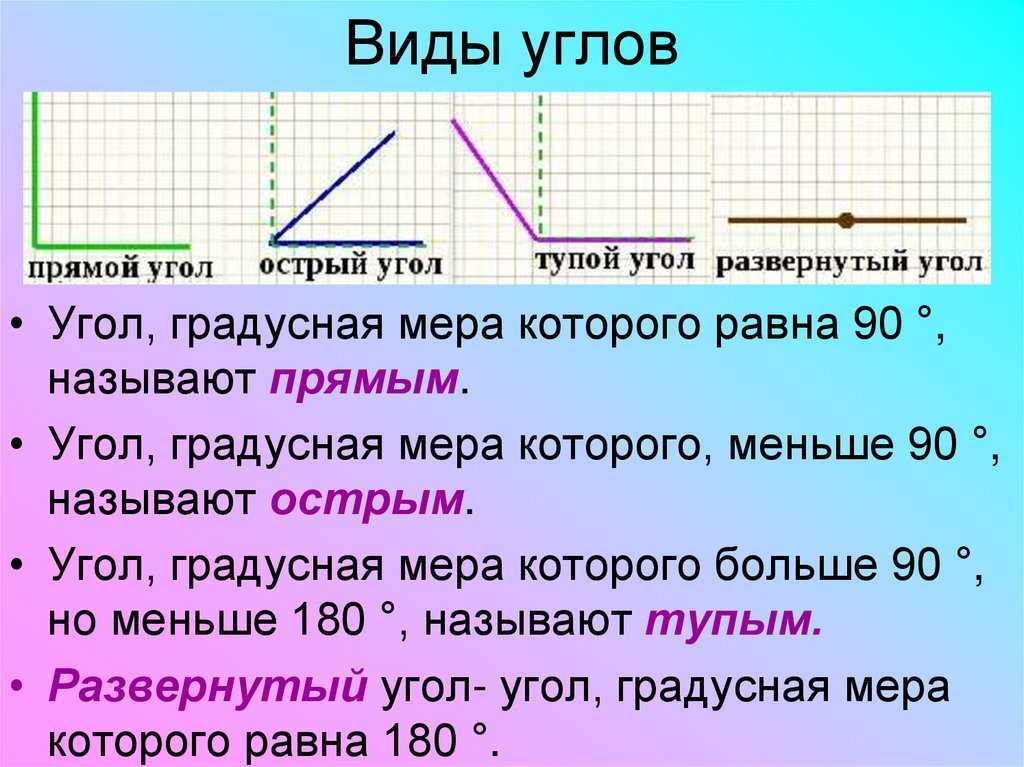
– Это острый угол.
– Это тупой угол.
– Для того чтобы было легче определить, какой угол перед нами, сделаем модель прямого угла. Возьмите лист бумаги и перегните его 2 раза так, как показано на рис. 1 и 2 ваших учебников (с. 8, часть 2).
– Вы получили модель прямого угла.
– При помощи модели прямого угла определите в задании 1, какие углы являются прямыми.
V. Решение выражений.
1. Сложение двузначных чисел в столбик: задание 2 — складывают и вычитают двузначные числа в столбик (без перехода через десяток) с последующей проверкой, также в столбик. Один ученик выполняет работу на доске.
2. Выполняется задание 3 : третий столбик устно (с объяснением), первый и второй столбики – с комментированием
VI. Работа с геометрическим материалом.
– Начертите отрезок, длина которого равна 5 см.
– Ниже начертите отрезок на 2 см короче предыдущего.
– Используя данные отрезки, постройте ломаную линию.
– Замкните ломаную.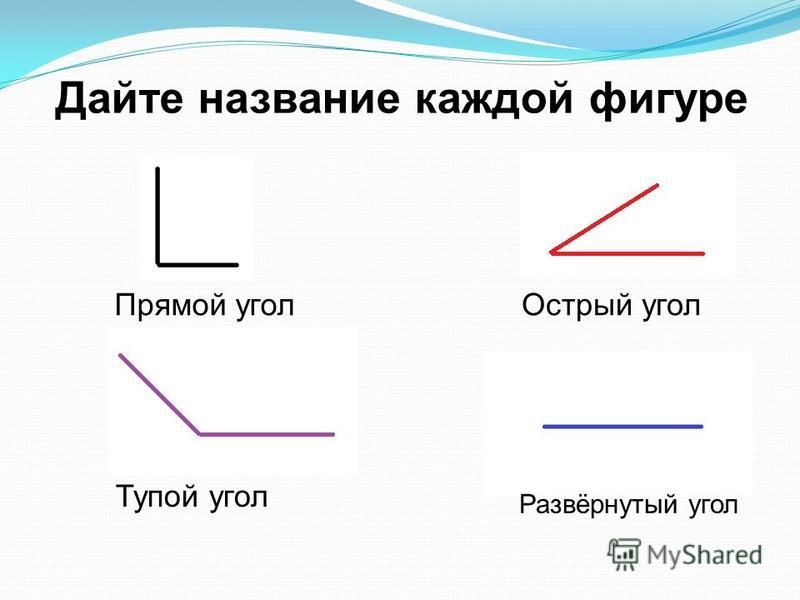
– Какая фигура получилась?
– Найдите периметр полученного треугольника.
VII. Итог урока. Рефлексия.
– Что нового узнали сегодня на уроке?
– Какие открытия сделали?
– Всё ли было понятно?
– Как вы сегодня работали?
– Чью бы работу вам хотелось отметить особенно?
Сколько градусов в остром угле
Сколько градусов прямой, тупой и острый углы?
Сколько градусов прямой угол ?
Сколько градусов тупой угол?
Сколько градусов острый угол ?
Углом в геометрии называют точку, из которой выходят два луча.
В зависимости от того, насколько отличаются направления лучей, определяются характеристики самого угла.
Мера углов меряется в градусах.
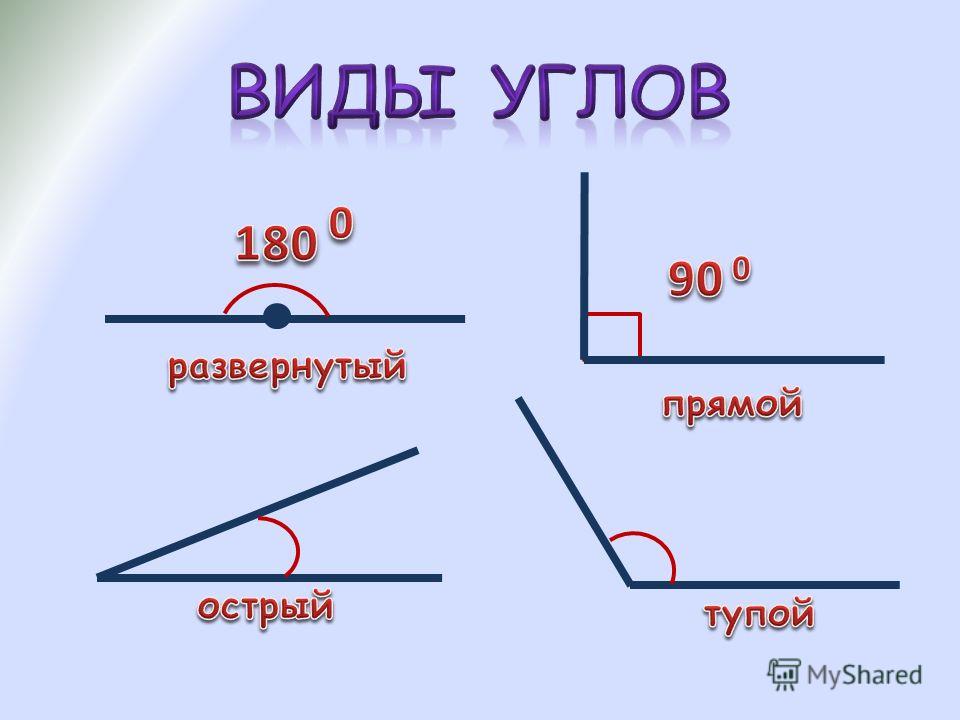
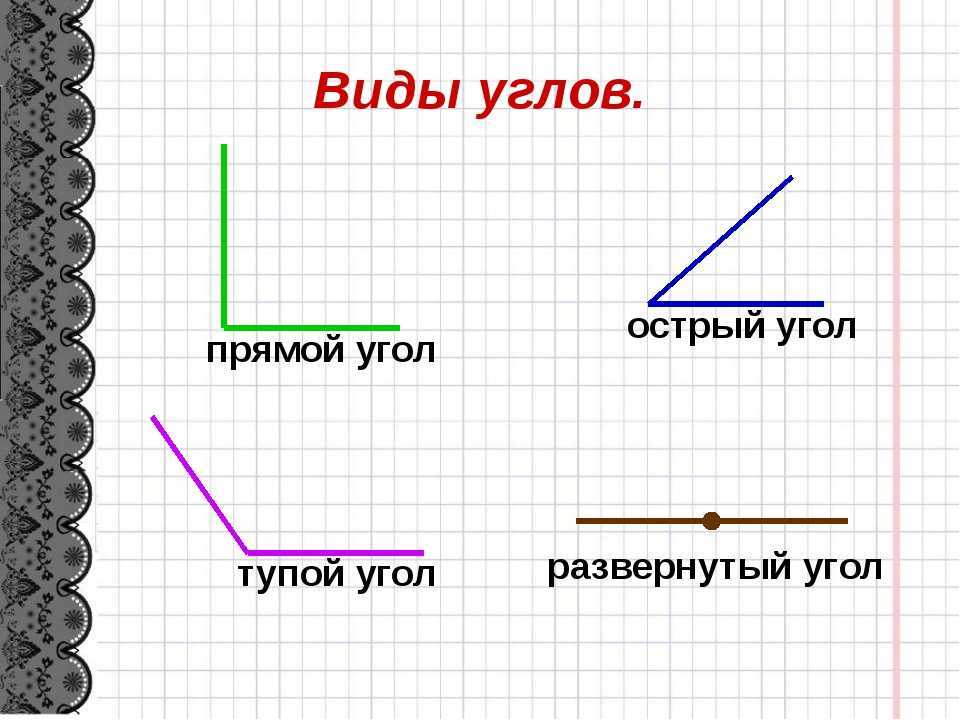
Если лучи угла расходятся один от одного под угол в 90 градусов — это прямой угол.
Если лучи угла расходятся один от одного под угол больше 90 градусов (от 90 до 180 градусов, потому как 180 градусов — это развернутый угол), то угол тупой.
Если лучи угла расходятся меньше чем угол 90 градусов (от 0 до 90 градусов) — угол острый.
Прямой угол собой представляет половину развернутого. А потому как величина развернутого угла в градусах равна 180-ти, то градусная мера прямого угла равна 90°.
Углы, меньшие 90°, называют острыми. Углы же, чья градусная мера превосходит все те же 90 градусов, однако при этом меньше 180°, называют тупыми.
Подобным образом, величина острого угла в градусах может принимать любое значение из диапазона (0; 90), ну а тупого — исходя из этого из диапазона (90; 180).
И только прямой угол из всех обозначенных в вопросе имеет вполне конкретную (не колеблющуюся ни в каких диапазонах) градусную меру — 90.
Какой угол именуется острым, прямым, тупым?
Какой угол в геометрии именуется острым, прямым, тупым? Сколько градусов в остом угле, тупом угле, прямом угле? Как определить острый угол, прямой угол, тупой угол?
Угол грамотный пересечением 2-ух поперечных прямых именуется прямым. Также прямой угол может появиться при делении окружности на ровные 4-ре части (1/4 окружности).
Прямой угол равён 90 градусам.
Когда стороны угла совпадают, подобный угол именуется нулевым
Нулевой угол равён 0 градусам.
Все углы, значения в градусах которых больше нулевого и меньше прямого именуется острыми.
Острый угол — больше 0 градусов и меньше 90 градусов.
Если стороны угла лежат в разных направлениях и создают прямую, подобный угол именуется развернутым и равён он 180 градусам.
Углы, значения в градусах которых больше прямого и меньше развернутого называются тупыми.
Тупой угол — больше 90 градусов и меньше 180 градусов.
Всех их соединяет одно:
острый, прямой и тупой углы — они все рельефные.
Все очень просто. Проведём аналогию с обыкновенными часами. Если одну из стрелок установить таким образом, чтобы она указывала на двенадцать часов, а другою, чтобы указывала на три — то они создают прямой угол в 90 градусов. Если же начать двигать стрелку указывающую на 3 часа в обратном направлении( в двухчасовой метки на циферблате) — то она будет образовывать, одновременно со второй стрелкой, острые углы(менее 90 градусов). Когда же стрелки будут указывать в одну точку — они создают нулевой угол в ноль градусов.А если вернуть вторую стрелку к исходной( трехчасовой отметке) и начать перемещать её вперед по циферблату — то аж до шестичасовой метки она одновременно с первой будут образовывать тупые углы( более 90 градусов). Когда стрелки будут указывать, одна на 12, а остальная на 6 — это будет, говоря иначе, развёрнутый угол в 180 градусов.
Когда же стрелки будут указывать в одну точку — они создают нулевой угол в ноль градусов.А если вернуть вторую стрелку к исходной( трехчасовой отметке) и начать перемещать её вперед по циферблату — то аж до шестичасовой метки она одновременно с первой будут образовывать тупые углы( более 90 градусов). Когда стрелки будут указывать, одна на 12, а остальная на 6 — это будет, говоря иначе, развёрнутый угол в 180 градусов.
Острый угол сколько градусов
Добрый день!
Как понять острый угол сколько градусов равён? Как можно усвоить?
Благодарю!
Усвоить и разобраться очень легко. Начинаем учиться на циферблате обыкновенных часов.
Установим одну стрелку так, что она будет указывать на 12- часов, а остальная будет указывать на 3 часа. В этом положении стрелки создают прямой угол, который равён девяносто град.
Начинаем сдвигать стрелку, которая указывает на 3 часа, против хода часовой стрелки, о есть к двенадцати часам через 2 часа и один час.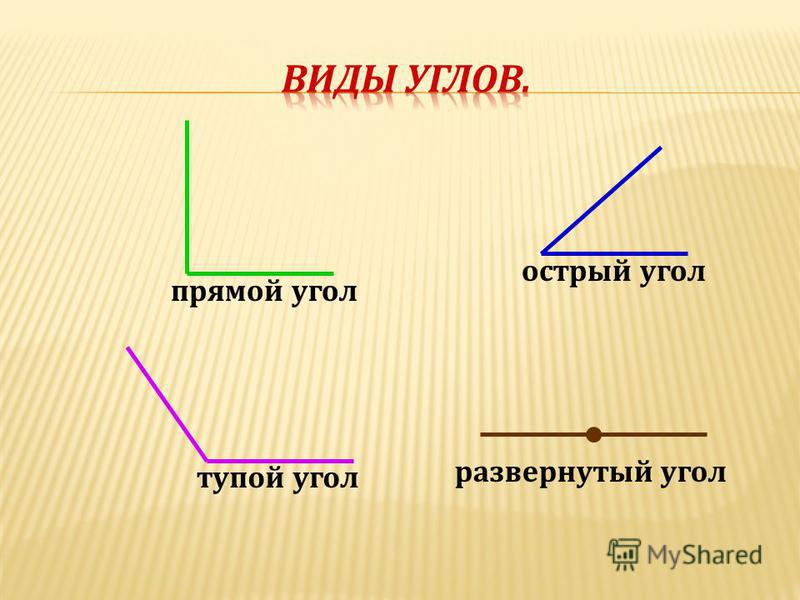 В этом случае две стрелки будут образовывать острый угол, который окажется меньшей 90 град., но больше 0 град.
В этом случае две стрелки будут образовывать острый угол, который окажется меньшей 90 град., но больше 0 град.
Если же стрелки объединить на одной цифре, к примеру, на двенадцати, то стрелки создают угол в ноль град., другими словами нулевой.
Если же первую стрелку оставить на 12-ти часах, а вторую опять уместить на 3 часа и начать двигать по ходу часовой стрелки, другими словами через определения четырех, пяти до 6-ти часов, то полученные углы будут тупыми (больше 90 и меньше 180 градусов).
Когда вторая стрелка будет стоять на 6-ти часах, то подобный угол будет равным 180 градусов, а его называют развернутым.
Полный оборот циферблата равён 360 градусам.
Надеюсь, этот подход поможет Вам хорошо разобраться и усвоить какой из углов каким должен быть и скольким градусам быть равным.
Острый, прямой и тупой углы
тригонометрия — Получение острого угла для тупого угла по закону синусов.
спросил
Изменено 2 года, 7 месяцев назад
Просмотрено 18 тысяч раз
$\begingroup$
Я решал эту задачу снова и снова. Я даже искал учебники о том, как правильно использовать закон синусов. Довольно неловко, что я так сильно борюсь за эту простую тригонометрическую ерунду.
Вот изображение треугольника. Я пытаюсь найти угол $\angle{C}$. Угол $\angle{C}$ обязательно должен быть тупым.
Я продолжаю получать: $$\dfrac{\sin(21.55)}{7.7} = \dfrac{\sin(C)}{16}$$
Я упрощаю и беру $\arcsin\left(16 \ cdot \dfrac{\sin(21.55)}{7.7}\right)$
И я не могу получить тупой угол. Кто-нибудь знает, почему?
- тригонометрия
- треугольники
$\endgroup$
$\begingroup$
9\circ)/7. 7)$ должен дать вам нужный ответ.
7)$ должен дать вам нужный ответ.
$\endgroup$
0
$\begingroup$
Из-за диапазона угловых синусов ваш ответ является дополнением к правильному ответу. Чтобы избежать этой трудности, всегда ищите углы, основанные на длинах сторон в порядке возрастания. Другими словами, если у вас есть выбор, какой угол решать первым, всегда выбирайте угол, противоположный самой короткой из двух имеющихся у вас сторон.
В этой задаче вы вынуждены сначала найти угол C, поэтому вы должны признать, что он тупой, и поэтому ответ, который вы получите, будет дополнением.
$\endgroup$
$\begingroup$
после упрощения вы должны вычесть значение из 180 градусов, так как вы знаете, что угол C должен быть тупым углом, который будет приблизительно равен 180 — 49,76. Значение C равно 130,24 градуса.
Значение C равно 130,24 градуса.
$\endgroup$
$\begingroup$
В треугольнике угол против наибольшей стороны всегда максимален. Итак, сначала решите угол, противоположный двум меньшим сторонам. Затем вычтите сумму этих углов из 180, чтобы получить угол, противоположный самой длинной стороне.
$\endgroup$
$\begingroup$
Причина, по которой вы не можете получить тупой угол, заключается в том, что существует другой треугольник, удовлетворяющий закону синусов, который вы записали, а именно треугольник $\triangle ABC_1$:
Обратите внимание, что треугольник $\triangle ABC_1$ удовлетворяет тому же уравнению:
$$\frac{\sin (21,55)}{7,7} = \frac{\sin (C_1)}{16}.$$
Когда вы решаете уравнение с помощью арксинуса, вы получаете острый угол при вершине $C_1$, который на диаграмме обозначен как $\theta$. Соотношение между $\theta$ и углом при вершине $C$ равно $$\theta + C = 180.$$ Причина: треугольник $\triangle ACC_1$ равнобедренный, поэтому $\angle ACC_1=\angle CC_1A=\theta $. Следовательно, углы $\theta$ и $C$ являются дополнительными.
Соотношение между $\theta$ и углом при вершине $C$ равно $$\theta + C = 180.$$ Причина: треугольник $\triangle ACC_1$ равнобедренный, поэтому $\angle ACC_1=\angle CC_1A=\theta $. Следовательно, углы $\theta$ и $C$ являются дополнительными.
Таким образом, чтобы получить тупой $C$, вы должны вычесть острый $\theta$ из $180$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью GoogleЗарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Тупой угол – Объяснение и примеры
Тупой угол – это угол, превышающий угол в девяносто градусов и меньший, чем прямой.
В градусах тупой угол больше $90$ градусов и меньше $180$ градусов. В радианах тупой угол измеряется больше чем $\frac{\pi}{2}$ радиан и меньше чем $\pi$ радиан.
Прежде чем перейти к этому разделу, обязательно ознакомьтесь с типами углов и их свойствами.
Этот раздел охватывает:
- Что такое тупой угол?
- Определение тупого угла
- Примеры тупого угла
Что такое тупой угол?
Тупой угол больше прямого угла и меньше прямой.
Используя градусы, тупой угол имеет градусную меру больше $90$ и меньше $180$. В радианах его мера находится между $\frac{\pi}{2}$ и $\pi$.
Иногда любой угол больше прямого считается тупым. Углы больше прямых и меньше круга также считаются рефлекторными углами. В этом разделе будет сделано это различие.
Углы больше прямых и меньше круга также считаются рефлекторными углами. В этом разделе будет сделано это различие.
Тупоугольные треугольники
Одной из причин для проведения этого различия является определение тупоугольного треугольника.
Напомним, что существует три типа расположения треугольных углов. Остроугольные треугольники имеют только углы, меньшие прямого угла, а прямоугольные треугольники имеют один прямой угол.
Тупоугольный треугольник — это треугольник, угол которого больше прямого. Поскольку треугольники имеют общий внутренний угол, равный $180$ градусам, они могут иметь не более одного угла больше прямого угла и не иметь углов больше прямого (больше тупого угла).
Это еще одна причина различать тупые углы и рефлекторные углы. То есть рефлекторного треугольника быть не может.
Тупой угол Определение
Тупой угол — это угол, который больше прямого угла и меньше прямого. Он имеет размер от $90$ до $180$ градусов или от $\frac{\pi}{2}$ до $\pi$ радиан.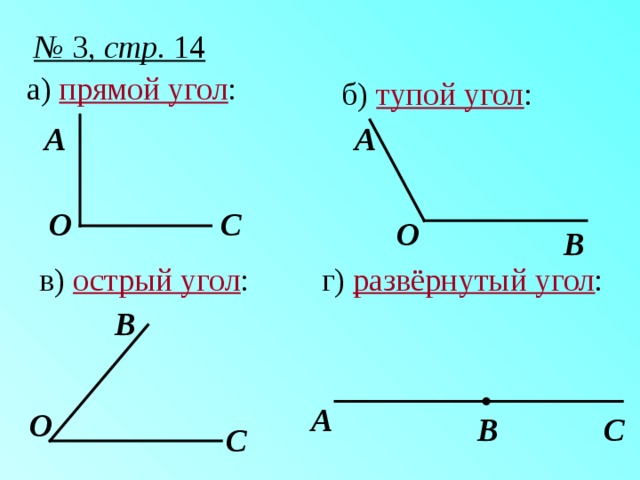
Тупой угол — это любой наибольший угол в тупоугольном треугольнике.
Примеры тупых углов
Так как к тупым углам относятся любые углы, размеры которых превышают $90 $ Степень и менее чем 180 долларов США, примеры включают углы с показателями:
- 90.0001 градусов
- 100 градусов
- 120 градусов
- 145 градусов
- 175 градусов
- 179,99999999999999999999999999999999999999999999999999999999999920 гг. включают любой угол с более чем $\frac{\pi}{2}$ радиан и $\pi$ радиан, они включают:
- $\frac{3}{4}\pi$ радиан
- $\frac{ 3}{5} \pi$ радиан
- $\frac{4}{5} \pi$ радиан
- $\frac{9}{10} \pi$ радианы
Распространенные примеры
В этом разделе рассматриваются распространенные примеры задач на тупые углы и их пошаговые решения.
Пример 1Классифицируйте следующие углы по градусам или радианам.
A. $91$ градусов
B.
 $360-50$ градусов
$360-50$ градусовC. $\frac{99}{100}\pi$
D. $\frac{145}{131}\pi$
Решение
Первая и третья меры угла являются мерами тупого угла. А вот второго и четвертого нет. В частности, оба они являются рефлексивными углами или углами больше прямой линии, но меньше круга.
Основная проверка состоит в том, чтобы определить, находятся ли заданные углы между $90$ и $180$ градусами или между $\frac{\pi}{2}$ радианами.
Ясно, что $91>90$ и $91<180$, так что первый угол действительно тупой. Однако следующий угол равен $310$ градусам. Поскольку $310>180$, этот угол не является тупым. Наоборот, рефлексивно.
Аналогично, $\frac{99}{100}\pi$ меньше $\pi$ и больше $\frac{pi}{2}$. Следовательно, этот угол тупой.
Следующее, однако, равно $\pi$, умноженному на $\frac{145}{131}$. Поскольку $145>131$, эта дробь больше единицы. Следовательно, $\frac{145}{131}\pi$ больше, чем $\pi$. Это делает угол не тупым, а рефлексивным.
Пример 2Пусть в треугольнике $ABC$ два известных угла равны $41$ и $31$ градусам.
 Треугольник тупоугольный? Почему или почему нет?
Треугольник тупоугольный? Почему или почему нет?Решение
Напомним, что внутренний угол треугольника равен $180$ градусам. Следовательно, зная эти две угловые меры, можно определить меру третьего угла.
То есть угол будет равен 180$-(41+31)=180-72=108$. Поскольку $90<108<180$, этот угол тупой. Следовательно, треугольник $ABC$ тупоугольный.
Пример 3Докажите, что угол $ACD$ в фигуре $ACDB$ тупой.
Решение
Прежде всего заметим, что треугольники $ABC$ и $CBD$ являются конгруэнтными равносторонними треугольниками.
Почему?
$AC$ — это радиус окружности с центром $A$, как и $AB$. $AB$ — это также радиус окружности с центром в точке $B$, а $BC$ — еще один радиус этой окружности. Следовательно, $ABC$ равносторонний.
Аналогично, $BC$ и $BD$ — это радиусы одной и той же окружности с центром в $B$. Прямая $BD$ также является радиусом окружности с центром в $E$, как и $DC$. Таким образом, $CB$, $BD$ и $DC$ — это линии одинаковой длины.
 Таким образом, $CBD$ также является равносторонним.
Таким образом, $CBD$ также является равносторонним.Но у двух треугольников общая сторона $CB$. Следовательно, все стороны имеют одинаковую длину.
Следовательно, угол $ACB$ должен быть равен $60$ градусам, как и угол $DCB$.
Поскольку рассматриваемый угол $ACD$ состоит из углов $ACB$ и $DCB$ вместе, мера $ACD$ равна $ACB + DCB = 60 + 60 = 120$ градусов.
Таким образом, поскольку $120$ больше $90$ градусов, но меньше $180$ градусов, угол $ACD$ тупой.
Пример 4Докажите, что внутренние углы любого правильного n-угольника с $n>4$ имеют только тупые углы.
Решение
Эта задача в первую очередь зависит от знания того, что сумма внутренних углов n-угольника равна $180(n-2)$.
Если такой многоугольник является правильным многоугольником, он имеет $n$ равных внутренних углов. Следовательно, каждый внутренний угол имеет меру $\frac{180n-360}{n}$ или $180-\frac{360}{n}$.
Для любого положительного $n$ $180-\frac{360}{n}$ меньше $180$.
 Теперь требуется доказать, что для любого $n>4$ $180-\frac{360}{n}>90$.
Теперь требуется доказать, что для любого $n>4$ $180-\frac{360}{n}>90$.Для этого $\frac{360}{n}$ должно быть меньше $90$. Если он больше или равен 90$, то вычитание его из 180$ дает градусную меру меньше или равную 90$, то есть такие углы либо прямые, либо острые.
Если
$\frac{360}{n} < 90$,
, то:
$360 < 90n$
Деление на $90$ дает:
$4 < n$.
Следовательно, когда $n > 4$, все внутренние углы любого правильного многоугольника лежат в пределах $90$ и $180$ и, следовательно, являются тупыми углами.
Пример 5Два угла составляют окружность. Один из углов тупой. Каков диапазон значений градусов и радианов для второго угла?
Решение
Напомним, что дополнительные углы — это углы, которые при сложении образуют прямую линию. То есть их сумма составляет $180$ градусов или $\pi$ радиан.
Угол, который вместе с тупым углом образует окружность, будет суммой прямой и дополнительного угла к тупому углу.

Если красный угол является заданным тупым углом, то угол, который завершает круг, является фиолетовым прямым углом с синим углом, который является дополнительным к красному углу.
Следовательно, необходимо сначала найти диапазон значений дополнительных углов для тупых углов. Поскольку тупой угол больше 90$, дополнительный угол меньше 180-90$ = 90$.
Аналогично, поскольку тупой угол меньше $180$ градусов, дополнительный угол больше $180-180 = 0$.
Таким образом, дополнительным углом является любой острый угол или любой угол между $0$ и $90$ градусами. В радианах это значение составляет от $0$ до $\frac{\pi}{2}$ радиан.
Но это не тот угол, который нужен для создания круга. Этот угол плюс прямой угол дает необходимый угол. Следовательно, искомым углом будет острый угол плюс прямой угол или угол больше $180$ градусов, но меньше $180+90 = 270$ градусов.
В радианах это угол больше $\pi$ радиан и меньше $\frac{3\pi}{2}$ радиан.
Еще примеры с пояснениями- Докажите, что два тупых угла должны образовывать рефлексивный угол.

- Рассмотрим тупоугольный равнобедренный треугольник. Каковы минимальная и максимальная меры его двух углов при основании? Ответ дайте в радианах и градусах.
- Окружность разделена на три тупых угла. По крайней мере, два угла имеют одинаковую меру. Каков диапазон возможных мер для третьего угла? Ответ дайте в радианах и градусах.
- Докажите, что если внешний угол многоугольника тупой, то этот многоугольник должен быть вогнутым.
- Докажите, что треугольник не может быть одновременно прямоугольным и тупоугольным.
- Рефлексивный угол имеет меру больше прямой, но меньше полной окружности. Поскольку тупые углы должны быть больше прямого угла, два тупых угла вместе должны быть больше двух прямых углов. Но два прямых угла — это прямая. Следовательно, сумма двух тупых углов больше, чем прямой.
Точно так же, поскольку каждый тупой угол должен быть меньше прямой, два тупых угла должны быть меньше двух прямых, что эквивалентно окружности. Следовательно, сумма двух тупых углов больше, чем у прямой, но меньше, чем у окружности, что означает, что это рефлексивный угол.
Следовательно, сумма двух тупых углов больше, чем у прямой, но меньше, чем у окружности, что означает, что это рефлексивный угол. - Диапазон: $0 < \alpha < \frac{180-90}{2} = 45$ градусов или $0 < \alpha < \frac{\pi-\frac{\pi}{2}}{2} = \frac{\pi}{4}$ для некоторого угла $\alpha$.
- Сначала найдите диапазон суммы двух тупых углов. Это было сделано в первой задаче. Следовательно, диапазон больше $180$ градусов и меньше $360$ градусов.
Но третий угол тоже должен быть тупым. То есть она должна быть меньше $180$ градусов, но больше $90$ градусов. Следовательно, сумма двух равных углов должна быть меньше $360-90 = 270$. Таким образом, максимальное значение углов по отдельности меньше $\frac{270}{2} = 135$ градусов.
В радианах это $\frac{\frac{3\pi}{2}}{2} = \frac{3\pi}{4}$. - Вогнутый многоугольник имеет по крайней мере один угол больше, чем прямой. Соответствующий внешний угол для любого угла $\beta$ в многоугольнике будет равен $360-\beta$. Как показано в примере 5, $360$ минус любой тупой угол будет рефлексивным углом, большим, чем прямая линия.


 $360-50$ градусов
$360-50$ градусов Треугольник тупоугольный? Почему или почему нет?
Треугольник тупоугольный? Почему или почему нет? Таким образом, $CBD$ также является равносторонним.
Таким образом, $CBD$ также является равносторонним.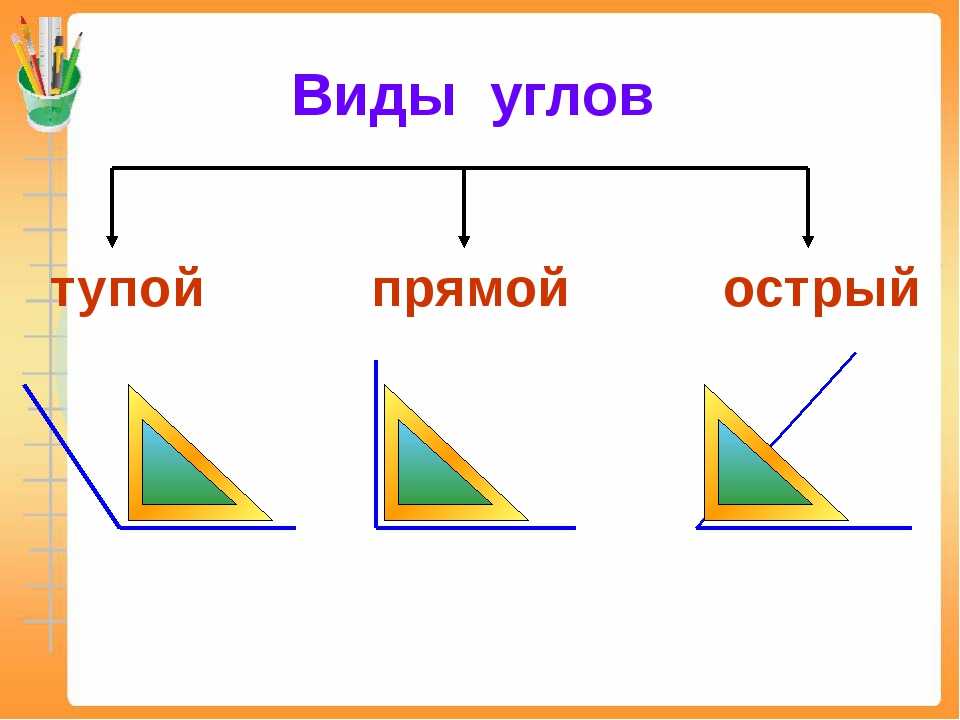 Теперь требуется доказать, что для любого $n>4$ $180-\frac{360}{n}>90$.
Теперь требуется доказать, что для любого $n>4$ $180-\frac{360}{n}>90$.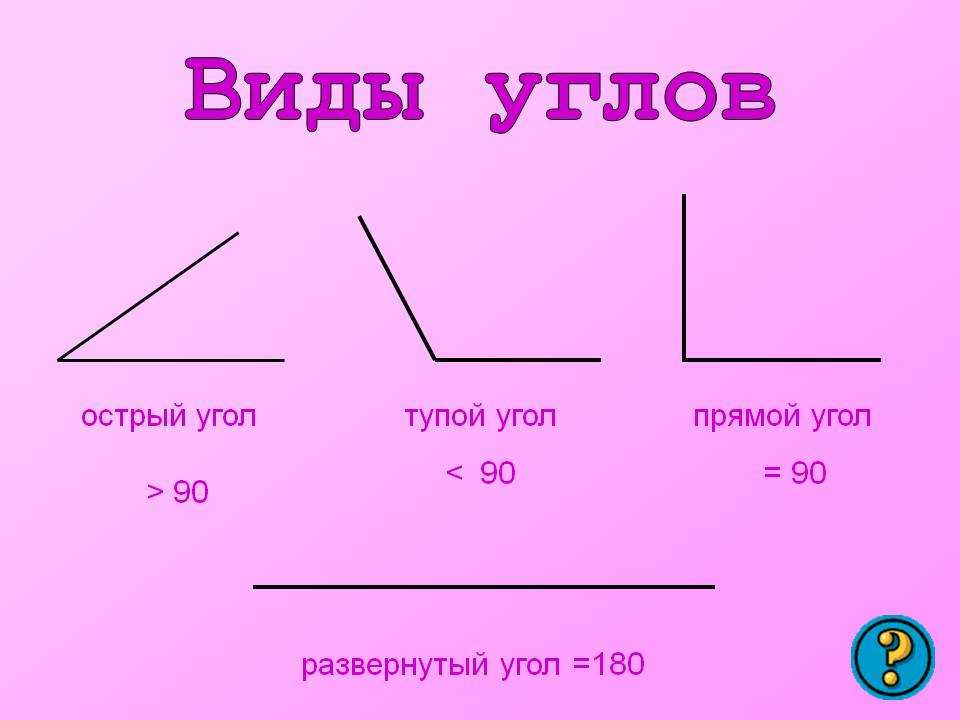
 Следовательно, сумма двух тупых углов больше, чем у прямой, но меньше, чем у окружности, что означает, что это рефлексивный угол.
Следовательно, сумма двух тупых углов больше, чем у прямой, но меньше, чем у окружности, что означает, что это рефлексивный угол.