Синус, косинус, тангенс и котангенс: формулы, таблица
Определение
Тригонометрия — один из видов науки о математике, изучающий функции по тригонометрии с применением их в геометрии.
Начало своего изучения данный научный раздел берет где-то в античной Греции, считается что первыми стали применять такие функции астрономы, а после в землемерии и строительстве. В средние века, большое внимание тригонометрии уделяли учёные Индии и Востока.
В этой статье будут рассмотрены понятия и различные определения тригонометрической науки. А также основные функции которыми являются: синус, косинус, тангенс, котангенс.
В начале стоит поговорить об определениях:
- Угол определяется в двух величинах: градусы и радианы.
- Так как окружность определяется 360 единицами, то 1∘равен 1\360 части окружности.
- Гипотенуза — напротив лежащая сторона относительно прямого угла;
- Катеты — две стороны, отходящие от прямого угла.
Определения основных функций
По началу понятие функций тригонометрии, значением которого был угол, вычислялось через отношение сторон треугольника, который обладает прямым углом.
Определения для острого угла прямоугольника.
- Функция Sin a — Синус угла — отношение напротив лежащего катета к гипотенузе
- Cos a — Косинус угла — отношение стороны треугольника (катета), который прилегает к данному углу и гипотенузы;
- Tg a — Тангенс угла — отношение стороны треугольника который называется катетом и лежит напротив угла к прилежащему углу катету ;
- Ctg a — Котангенс угла — прилежащего катета к противолежащему.
Теорема синусов в формуле:
\[ \frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma} \]
Угол поворота.
Как уже говорилось выше определения, которые мы рассмотрели относятся к острым углам треугольника. Но существует и понятие угол поворота, в котором исчисляемый угол не будет равен значению от 0 градусов до 90. При этом угол поворота может быть любым числом, от +бесконечности и до — бесконечности.
В данной связи можно выдвинуть определение синуса, косинуса, тангенса и котангенса угла любой величины.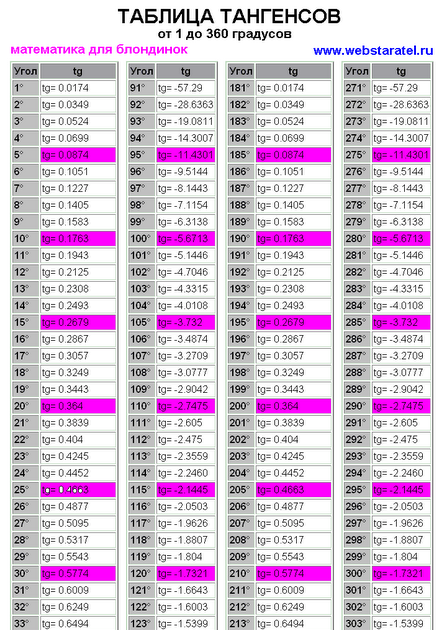 Для этого представим окружность в системе координат с двумя взаимно перпендикулярными осями.
Для этого представим окружность в системе координат с двумя взаимно перпендикулярными осями.
Заданная точка А, имеющая координатные значения 1,0, делает поворот вокруг центра оси на угол α, переходя в точку А1. рассматривая определение через координаты А1(х,у).
Sin угла поворота α, это ордината точки А1(х,у), то есть sinα=у
Косинус α — абсцисса точки А1 (cosα=х)
Tg данного угла — ‘это деление (отношение) ординаты А1 к абсциссе. tgα=у\х
Котангенс поворотного угла α — отношение её абсциссы к ординате, ctgα=х\у
Заметим, что синус и косинус можно выделить для любого угла, а вот тангенс и котангенс нет. И это абсолютно логично, так как при переходе точки в значение ноля для абсциссы, тангенс посчитать невозможно, так как невозможно деление на 0. Тоже самое со значением ординаты равным нулю, котангенс не исчисляется.
Sin и cos можно вычислить для любых углов α. тогда как tg всех кроме α = 90°+180°* k , k ∈ Z ( α = π 2 + π * k , k ∈ Z ) α=90°+180°*k, k∈Z (α=π2+π*k, k∈Z)
Котангенс так же можно вычислить не для всех углов, например для α = 180 ° * k , k ∈ Z ( α = π * k , k ∈ Z , это сделать нельзя.
Отметим, что на практике при решении примеров словосочетание угол поворота опускается из речевого оборота.
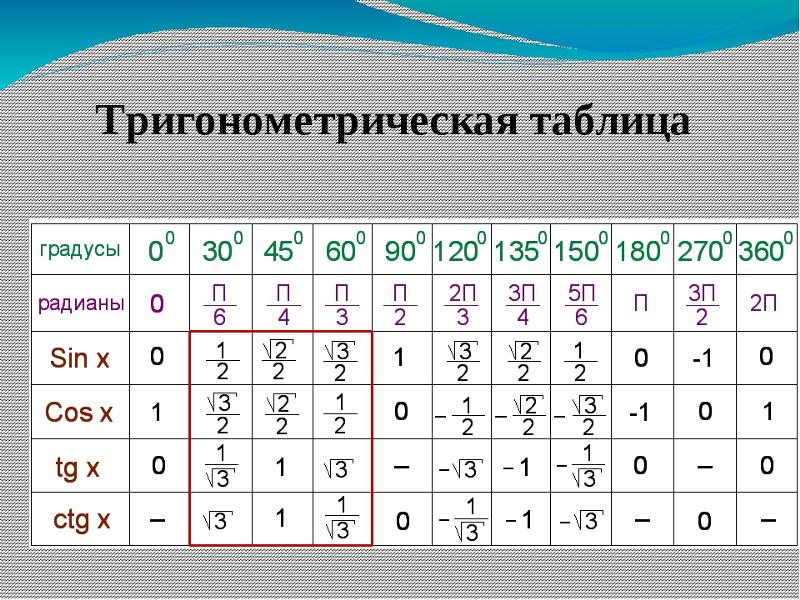
Для удобства существуют таблицы значений часто используемых углов, которые вычисляются в тригонометрических функциях, к примеру, для первой четверти круга:
| 0° | 30° | 45° | 60° | 90° | |
| sin | 0 | 1 2 | √2 2 | √3 2 | 1 |
| cos | 1 | √3 2 | √2 2 | 1 2 | 0 |
| tg | 0 | 1 √3 | 1 | √3 | – |
| ctg | – | √3 | 1 | 1 √3 | 0 |
Вычисление тригонометрических функций числа
В данном пункте рассмотрим случай, когда определение рассматриваемых нами функций тригонометрии, происходит из числового значения, а не угла. Таких подходов два:
Таких подходов два:
- Sin, cos, tg, ctg числа n, является число которое равно sin, сos, tg, ctg n радиан. Где Радиа́н это угол, который соответствует дуге, которая в свою очередь равна длине, её радиуса. Пример: sin числа2k=sin угла2k радиан. Используя формулы можно получить таблицу часто встречаемых углов, которая поможет быстро перевести значения из градусов в радианы и в противоположную сторону.
- На прямоугольной системе координат, в единичной окружности, ставится точка, которой соответствует любое действительное значение числа d. тригонометрические функции можно определить, узнав координаты этой точки.
- Считая начальной точкой А с координатами (1,0). Поэтому для того чтобы найти взаимодействие между точкой на окружности и числом, нужно найти отрицательное и положительное значение числа d, положительным будет значение при движении точки А(1,0) в противоположную сторону движения часовой стрелки и её движение будет равным open t \ t, а отрицательным движение по часовой стрелке.

В связи с этим выделяют следующие функции:
- (sin f = y) Синус числа f- определяется ординатой точки единичной окружности, которая равна числу f;
- (cos f = x) Косинус числа f — абсцисса окружности, которая соответствующая числу f;
- (tg f = y\x=sin f\cos f) тангенс f определяется делением ординаты на абсциссу точки, равной числу f.
Функции аргумента угла и числа
Каждому значению угла а, существует своё значение sin, сos, данного угла, которое ему соответствует. А также углам α, кроме от α = 90 ° + 180 ° * k , k ∈ Z ( α = π 2 + π * k , k ∈ Z ) будет соответствовать определенное значение тангенса. Так же котангенс α, кроме α = 180 ° * k , k ∈ Z ( α = π * k , k ∈ Z ).
Из чего следует что синус а, косинус а, тангенс а, котангенс а — это и есть функции углового аргумента.
Точно также определяются функции числового аргумента. Выбранное любое действительное число, имеет своё соответственное значение функций тригонометрии, все кроме перечисленных исключений.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Определения функций и их связь
Вернемся к единичной окружности в прямоугольной системе координат, где центр окружности и системы координат совпадает. Точку А(1,0) повернём на 90°, и из полученной точки А1 проведём перпендикуляр к абсциссе. В результате получится прямоугольный треугольник, где угол А1 ОН это угол поворота а. длины катета ОН и абсциссы точки А1 также равны. А катет, который находится напротив угла равен ординате точки А1, а длина гипотенузу это единица.
Получается исходя из определения, синус угла а, это отношение катета напротив к гипотенузе.
sin α = A 1 H\ O A 1 = y \1 = y
sin α=A1H\OA1=y\1=y
Из чего следует, что определение sin острого угла, одинаково определению синуса угла поворота а, если а лежит в пределе 0-90°. Точно так же и с вычислением косинуса, тангенса и котангенса.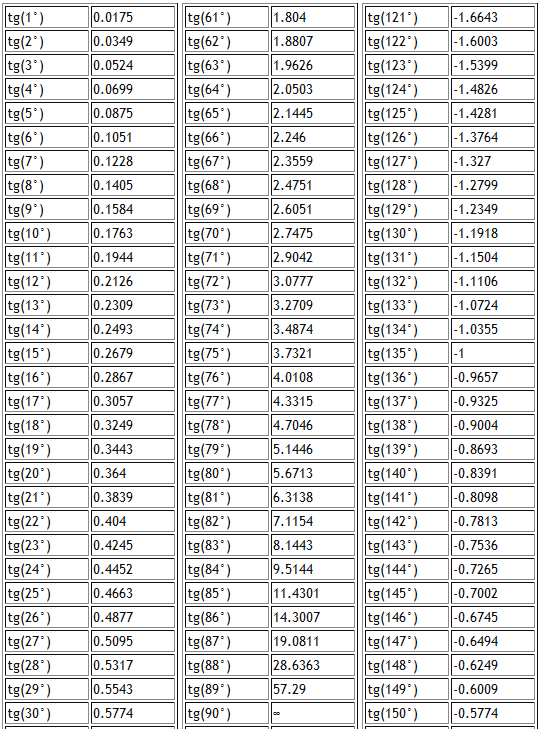
Положительные и отрицательные знаки функций
Знаки sin и cos в изобразительном виде системы координат.| I | II | III | IV | |
| sin | + | + | — | — |
| cos | + | — | — | + |
| tg | + | — | + | — |
| ctg | + | — | + | — |
Знаки тангенса и котангенса на оси
Для того чтобы сделать проверку знаков функций тангенса и котангенса , можно также воспользоваться такой окружностью и её четвертями. Если мы берём угол из третьей четверти и проводим прямую через точку на окружности и начало координат, пока прямая не пересечёт ось тангенсов. Мы увидим что значение tg угла и угла в первой четверти будет положительным. Таким же образом значение из второй четверти и четвёртой отрицательно.
Тождества в тригонометрии
Рассмотрим подробнее тождества функций.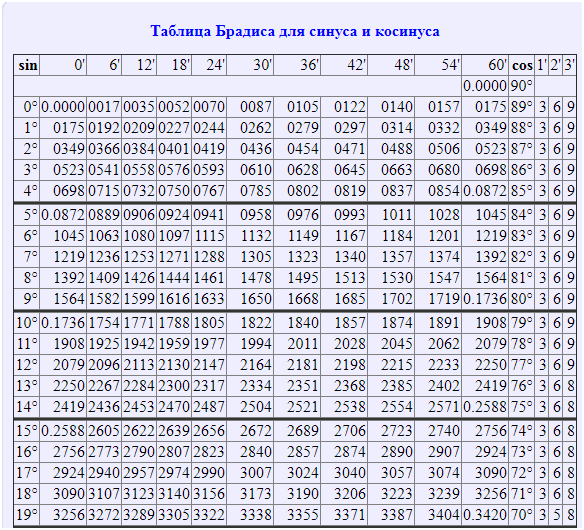 {2} t}, \quad t \neq \pi n, n \in Z
\]
{2} t}, \quad t \neq \pi n, n \in Z
\]
Таблица функций тригонометрии
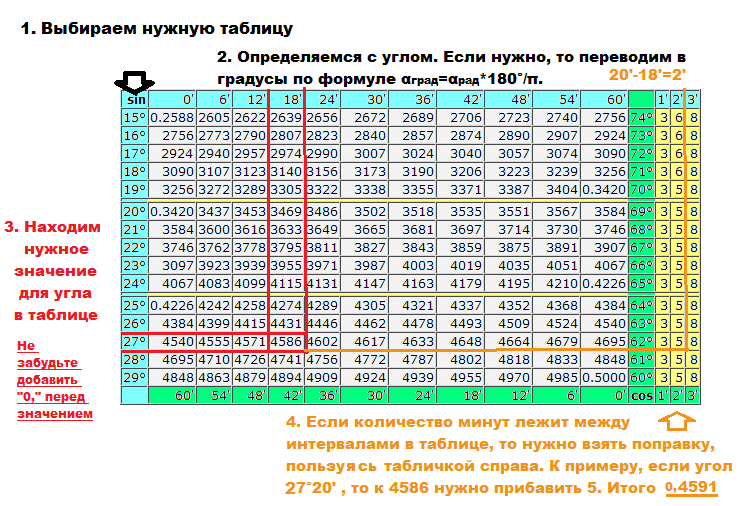
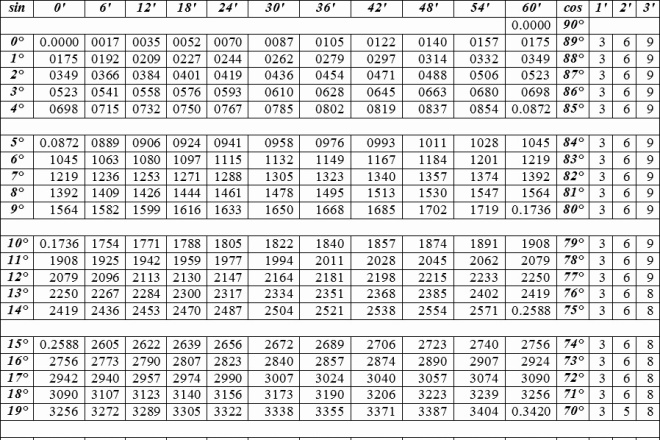
Эта таблица представляет из себя уже посчитанные значения sin, cos, tg, ctg углов от 0до 360 градусов. Такая таблица заменит специальный калькулятор если нужны значения, нужно просто найти нужный угол в таблице.
Области применения тригонометрии
Приведём для примера несколько областей в которых применяются функций:
- В астрономии. Во-первых, как отмечалось выше область астрономии стала первой, где стали применять тригонометрические функции. Именно по этой причине довольно долго этот раздел науки относили к астрономии. Одним из крупных открытий в этой науке при помощи тригонометрических основ стала возможность вычисления наступления темноты, а также составление первых звёздных карт.
- В физике. Мир, который нас окружает построен на колебательных процессах, это такие явления и процессы, которые повторяются через определённый цикл;
- В окружающей нас природе. Например, отражение лучей солнца от различных поверхностей;
- В медицине.
 К примеру, существует такое понятие как формула сердца;
К примеру, существует такое понятие как формула сердца; - В биологии. Биологические ритмы, модель которых строят при помощи тригонометрии;
- В музыке, звуковые ритмы, построение моделей.
- Важную роль тригонометрия играет и для морского флота и авиации;
- В изучении сейсмической активности.
Как мы видим тригонометрия очень важная наука, которая пронизывает практически все сферы нашей жизни.
Tan 10 градусов — Найдите значение Tan 10 градусов
LearnPracticeDownload
Значение tan 10 градусов равно 0,1763269. . . . Тангенс 10 градусов в радианах записывается как тангенс (10° × π/180°), то есть тангенс (π/18) или тангенс (0,174532…). В этой статье мы обсудим методы определения значения тангенса 10 градусов на примерах.
- Tan 10° в десятичном формате: 0,1763269. . .
- Тан (-10 градусов): -0,1763269. . .
- Tan 10° в радианах: tan (π/18) или tan (0,1745329 .
 . .)
. .)
Сколько стоит Тан 10 градусов?
Мы знаем, используя преобразование градусов в радианы, θ в радианах = θ в градусах × (пи/ 180°)
⇒ 10 градусов = 10° × (π/180°) рад = π/18 или 0,1745. . .
∴ тангенс 10° = тангенс (0,1745) = 0,1763269. . .
Объяснение:
Для тангенса 10 градусов угол 10° лежит между 0° и 90° (первый квадрант). Поскольку функция тангенса положительна в первом квадранте, значение тангенса 10° = 0,1763269. . .
Поскольку функция тангенса является периодической функцией, мы можем представить тангенс 10° как тангенс 10 градусов = тангенс (10° + n × 180°), n ∈ Z.
⇒ тангенс 10° = тангенс 190° = тангенс 370° и так далее.
Примечание: Поскольку тангенс является нечетной функцией, значение тангенса (-10°) = -тангенса (10°).
Методы определения значения тангенса 10 градусов
Функция тангенса положительна в 1-м квадранте. Значение тангенса 10° составляет 0,17632. . .. Мы можем найти значение тангенса 10 градусов по:
- Используя единичный круг
- Использование тригонометрических функций
Tan 10 градусов с помощью единичной окружности
Чтобы найти значение tan 10 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 10° с положительной осью x.
- Тангенс 10 градусов равен координате y (0,1736), деленной на координату x (0,9848) точки пересечения (0,9848, 0,1736) единичной окружности и r.
Следовательно, значение тангенса 10° = y/x = 0,1763 (приблизительно).
Тангенс 10° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить тангенс 10° как:
- sin(10°)/cos(10°)
- ± sin 10°/√(1 — sin²(10°))
- ± √(1 — cos²(10°))/cos 10°
- ± 1/√(косек²(10°) — 1)
- ± √(сек²(10°) — 1)
- 1/кровать 10°
Примечание. Поскольку 10° лежит в 1-м квадранте, окончательное значение тангенса 10° будет положительным.
Поскольку 10° лежит в 1-м квадранте, окончательное значение тангенса 10° будет положительным.
Мы можем использовать тригонометрические тождества для представления tan 10° как
- cot(90° — 10°) = cot 80°
- -кроватка(90° + 10°) = -кроватка 100°
- -тангенс (180° — 10°) = -тангенс 170°
☛ Также проверьте:
- загар 12 градусов
- загар 690 градусов
- загар 90 градусов
- загар 210 градусов
- загар 285 градусов
- загар 1260 градусов
Примеры использования Tan 10 градусов
Пример 1: Используя значение tan 10°, найдите: (sec²(10°) — 1).
Решение:
Мы знаем, (sec²(10°) — 1) = (tan²(10°)) = 0,0311
⇒ (сек²(10°) — 1) = 0,0311Пример 2. Найдите значение тангенса 6 (10°)/тангажа 9 (170°).
Решение:
Используя тригонометрические тождества, мы знаем, что tan(10°) = -tan(180° — 10°) = -tan 170°.

⇒ тангенс (10°) = -тангенс (170°)
⇒ Значение 6 тангенса (10°)/9 тангенса (170°) = -6/9 = -2/3Пример 3: Найдите значение (2 sin (5°) cos (5°) sec (10°)). [Подсказка: используйте tan 10° = 0,1763]
Решение:
Используя формулу sin 2a,
2 sin (5°) cos (5°) = sin (2 × 5°) = sin 10°
⇒ 2 sin (5°) cos (5°) сек(10°) = sin 10° сек 10°
= sin 10°/cos 10° = tan 10°
⇒ (2 sin (5°) cos (5°) сек(10°)) = 0,1763
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Tan 10 Degrees
Что такое Tan 10 Degrees?
Тангенс 10 градусов — значение тангенса тригонометрической функции для угла, равного 10 градусам. Значение тангенса 10° составляет 0,1763 (приблизительно).
Значение тангенса 10° составляет 0,1763 (приблизительно).
Каково значение Tan 10 градусов в пересчете на Cos 10°?
Мы знаем, что используя тригонометрические тождества, мы можем записать тангенс 10° как √(1 — cos²(10°))/cos 10°. Здесь значение cos 10° равно 0,984807.
Каково значение Tan 10° в пересчете на Cosec 10°?
Поскольку функция тангенса может быть представлена с помощью функции косеканса, мы можем записать тангенс 10° как 1/√(cosec²(10°) — 1). Значение cosec 10° равно 5,75877.
Как найти значение Тан 10 градусов?
Значение тангенса 10 градусов можно рассчитать, построив угол 10° с осью x и затем найдя координаты соответствующей точки (0,9848, 0,1736) на единичной окружности. Значение tan 10° равно координате y (0,1736), деленной на координату x (0,9848). ∴ тангенс 10° = 0,1763
Как найти тангенс 10° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение тангенса 10° может быть выражено через другие тригонометрические функции следующим образом:
- sin(10°)/cos(10°)
- ± sin 10°/√(1 — sin²(10°))
- ± √(1 — cos²(10°))/cos 10°
- ± 1/√(косек²(10°) — 1)
- ± √(сек²(10°) — 1)
- 1/кровать 10°
☛ Также проверьте: тригонометрическую таблицу
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
Значение, методы поиска, периодичность, таблица и примеры.
 {\circ } = 0\) 9{\circ} \right ) = 0\)
{\circ } = 0\) 9{\circ} \right ) = 0\)Периодичность касательной функции
Период — это продолжительность времени между двумя волнами, тогда как периодическая функция — это функция, значения которой повторяются через равные промежутки времени или периоды.
Поскольку выходные значения тангенса повторяются через равные промежутки времени, \( f\left ( \theta \right ) = \tan \left ( \theta \right )\) является периодической функцией. Любой другой угол с одинаковым значением тангенса для каждого угла существует на полпути вокруг единичной окружности. Следовательно, \(\pi\) является тангенциальным периодом.
Прежде чем график перескочит и снова повторится, мы можем наблюдать один непрерывный цикл из \( \frac{-\pi }{2},\frac{\pi }{2}\).
Trigonometric value table
Tan value table are given below:
| Angle in degrees | \( \tan\theta\) |
| 0 | 0 |
| 30 | \( \frac{1}{\sqrt{3}}\) |
| 45 | 1 9{\circ}\) 0+1 = 1 Если вы хотите хорошо сдать экзамен по математике, то вы попали по адресу. |

 К примеру, существует такое понятие как формула сердца;
К примеру, существует такое понятие как формула сердца;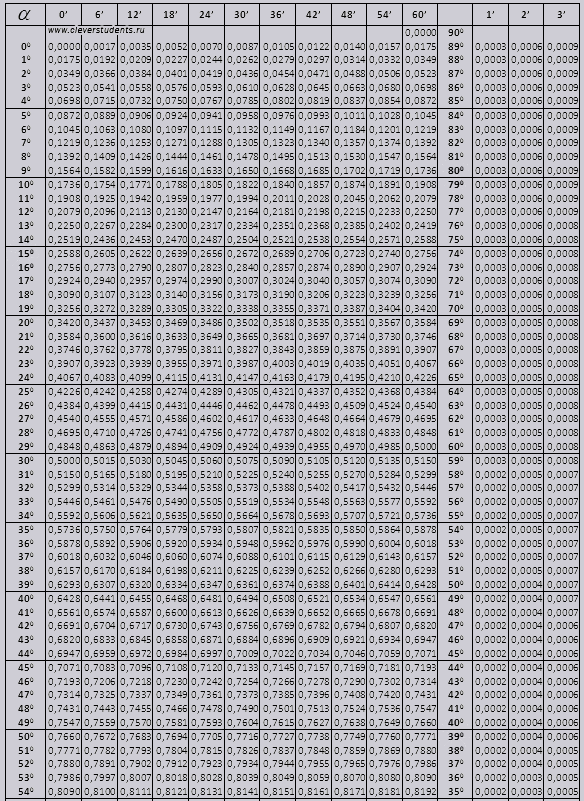 . .)
. .)