Что такое вершина треугольника определение: Что такое вершина треугольника? Ответ на webmath.ru

Значение, Определение, Предложения . Что такое вершина треугольника

• Онлайн-переводчик
• Грамматика
• Видео уроки
• Учебники
• Лексика
• Специалистам
• Английский для туристов
• Рефераты
• Тесты
• Диалоги
• Английские словари
• Статьи
• Биографии
• Обратная связь
• О проекте

Примеры

Значение слова «ВЕРШИНА»

Самый верх, верхняя часть (горы, дерева и т. п.).

Смотреть все значения слова ВЕРШИНА

Значение слова «ТРЕУГОЛЬНИК»

Геометрическая фигура, образованная тремя пересекающимися прямыми, образующими три внутренних угла, а также всякий предмет, устройство такой формы.

Смотреть все значения слова ТРЕУГОЛЬНИК

Предложения с «вершина треугольника»

Другие результаты

Вся Вера Корнильевна была — два треугольника, поставленных вершина на вершину: снизу треугольник пошире, а сверху узкий.

Точки пересечения биссектрисы угла интерьера азу хорды BC, СА, АВ вершин центральной треугольник.

Треугольник Рело-это частный случай, основанный на равностороннем треугольнике, где центр каждой дуги находится на противоположной вершине.

А если вставить все три спички в три вершины треугольника, образуется четырехгранник.

Каждая вершина каждого треугольника либо является общей для еще одного или двух треугольников, либо такой общности не имеет.

Плавник имеет форму треугольника длиной фута в три-четыре с очень тонкой заостренной вершиной и поднимается отвесно над задней частью спины.

Диксон, я хочу, чтобы ты сделал его вершиной треугольника.

Статья Гэддиса Аргоси очертила границы треугольника, назвав его вершинами Майами, Сан-Хуан, Пуэрто-Рико и Бермуды.

В случае прямоугольного треугольника его высота равна длине прямой, проходящей перпендикулярно от гипотенузы до ее вершины под углом 90°.

Обозначая центр треугольника ABC как I, расстояния от центра до вершин в сочетании с длинами сторон треугольника подчиняются уравнению.

Вершиной треугольника Коха является расположение атриовентрикулярного узла.

Рассмотрим единичную сферу с тремя единичными векторами OA, OB и OC, проведенными от начала координат до вершин треугольника.

Графически он часто изображается в виде треугольника с небольшим кругом, прикрепленным к вершине.

Пусть A, B, C-углы в трех вершинах треугольника, а a, b, c-соответствующие длины противоположных сторон.

Барицентрические координаты для точки в треугольнике дают веса, такие что точка является средневзвешенным значением положения вершин треугольника.

Вершинами треугольника являются два дисковых центра и один из двух острых углов vesica piscis.

Стоимость одного треугольника с точки зрения количества необходимых умножений является произведением его вершин.

Для входного размера 3, Если точки являются вершинами острого треугольника, возвращается описанная окружность.

Каждый из трех компонентов, составляющих систему, находится на вершине треугольника, где их соответствующая объемная доля составляет 100%.

Исходные 12 ромбических граней становятся плоскими шестиугольниками, а усеченные вершины-треугольниками.

Там, где вершина общая для двух треугольников, связь может идти в одном или в другом направлении, но для создания избыточной коммуникационной сети достаточно и одного.

Если окружности тех же четырех треугольников напротив вершины P имеют радиусы R1, R2, R3 и R4 соответственно, то четырехугольник является воздушным змеем тогда и только тогда, когда.

Тот же базовый алгоритм может быть применен к треугольным сеткам, которые состоят из Соединенных треугольников с данными, присвоенными вершинам.

Остальные два расположены на третьей вершине обоих равносторонних треугольников, из которых два тела являются первой и второй вершинами.

Они обычно имеют икосаэдрическую симметрию, так что у них есть 6 треугольников в вершине, за исключением 12 вершин, которые имеют 5 треугольников.

Три оцелли расположены треугольником на шаровидной вершине.

---

На данной странице приводится толкование (значение) фразы / выражения «вершина треугольника», а также синонимы, антонимы и предложения, при наличии их в нашей базе данных. Мы стремимся сделать толковый словарь English-Grammar.Biz, в том числе и толкование фразы / выражения «вершина треугольника», максимально корректным и информативным. Если у вас есть предложения или замечания по поводу корректности определения «вершина треугольника», просим написать нам в разделе «Обратная связь».

что это означает, определение, свойства и признаки, правило, доказательство и решения

Что такое треугольник в математике 

Определение 1

Треугольник — геометрическая фигура, образующаяся в случае соединения трех отрезков с тремя точками, которые не лежат на одной прямой.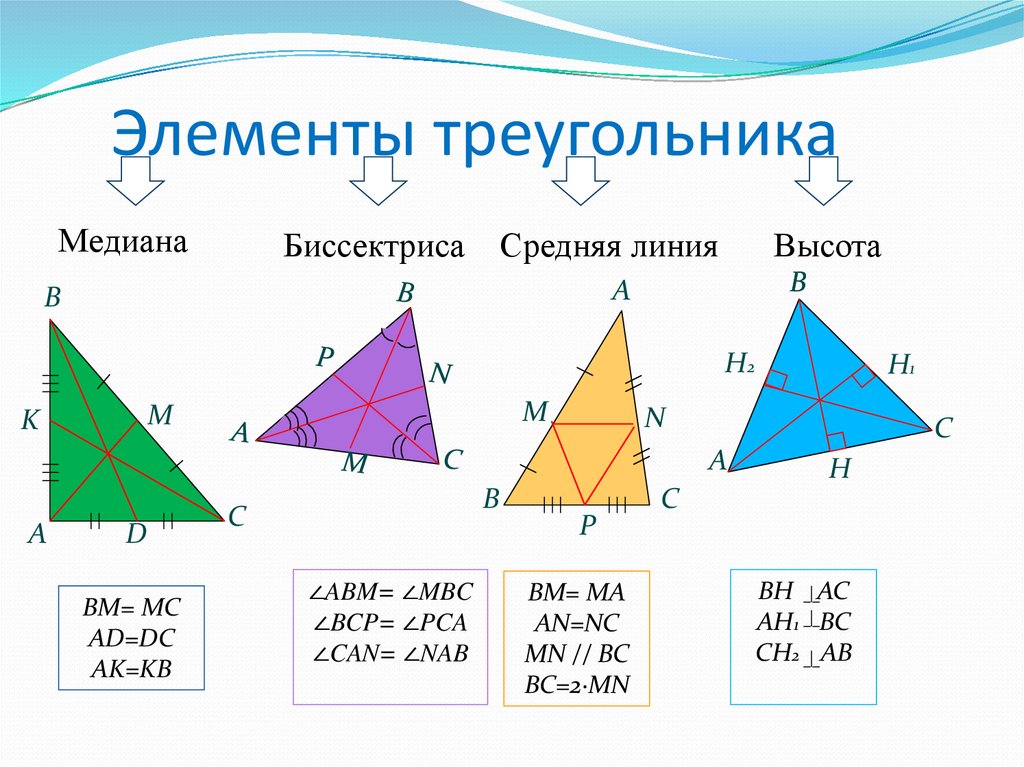 Вершинами треугольника называют три точки, которые соединяются отрезками, а отрезки называют сторонами.

Источник: epmat.ru

На рисунке видно, что угол A является углом, образованным двумя сторонами (AB+AC), он лежит напротив стороны BC. Угол B — угол, который образован сторонами BA+BC, лежит напротив стороны AC. Угол C является углом, который образован сторонами CB+CA, противолежит стороне AB.

Определение 2

Внутренний угол (угол треугольника) — угол, вершина которого соответствует вершине треугольника, его стороны проходят через стороны треугольника. Например, угол ABC — внутренний, как и углы CAB и ACB.

Примечание 1

Буква в середине обозначения угла (например B в угле ABC) — вершина.

Углы и стороны треугольника являются элементами треугольника.

Рассмотрим основные определения для темы «треугольник».

Определение 3

Периметр — сумма всех длин сторон треугольника. Обычно обозначается буквой «P».

Формула 1

Периметр вычисляется по следующей формуле:

P = a + b + c

Периметр равнобедренного треугольника:

P = a + 2b

Периметр равностороннего треугольника:

P = 3a

Попробуем вычислить периметр треугольников:

Примечание 2

Треугольная форма часто встречается в быту. Например, часто ее используют в процессе строительства различных зданий, мостов и тд. В процессе строительства крыш используются стропила треугольной формы.

Как и у всех геометрических фигур, у треугольника есть понятие равенства.

Теорема 1

Два треугольника могут быть названы равными, если возможно их скомбинировать в результате наложения друг на друга, то есть скомбинировать их стороны, вершины, углы.

Пример 1

Возьмем бумажный лист прямоугольной формы, разрежем на две части. У нас получаются прототипы равных треугольников. Можно наложить один на другого и убедиться, что они наложатся друг на друга идеально.

У равных треугольников FAC и F1A1C1 будут скомбинированы стороны, вершины и углы.

Важно запомнить, что в равных треугольниках:

1. Напротив равных сторон соответственно противолежат равные углы.
2. Напротив равных углов соответственно противолежат равные стороны.

То есть, в треугольниках FAC и F1A1C1 напротив сторон AC и A1C1 будут лежать абсолютно равные углы F и F1. Напротив углов C и C1 будут лежать стороны FA и F1A1.

Основные свойства

Основные свойства треугольника:

1. Больший угол всегда лежит напротив большей стороны.
2. Равные углы всегда лежат напротив равных сторон.
3. Совокупность углов в данной фигуре всегда будет равна 180 градусам.
4. В случае, если продлить сторону треугольника (например, сторону AC) и отметить на продленной стороне точку F, то будет образован внешний угол BCF к углу ACB.
5. Внешний угол будет равен совокупности двух внутренних углов, которые не являются смежными ему. То есть, угол BCD = 180 градусов отнять угол ACB; угол BCD = угол A + угол B.
6. Любая сторона фигуры будет меньше совокупности двух других сторон, а также больше разности этих сторон. Пример: AB + BC > AC.

Виды треугольников

По свойствам углов выделяют три вида треугольников:

1. Остроугольный. Все его углы являются острыми.
2. Прямоугольный. Только один угол является прямым (то есть, он равен 90 градусам).
3. Тупоугольный. Один угол является тупым.

Рассмотрим внешний вид данных треугольников:

 

  

Источник: epmat.ru

По свойствам сторон выделяют:

1. Равнобедренный.
2. Равносторонний.
3. Прямоугольный.

Определение 4

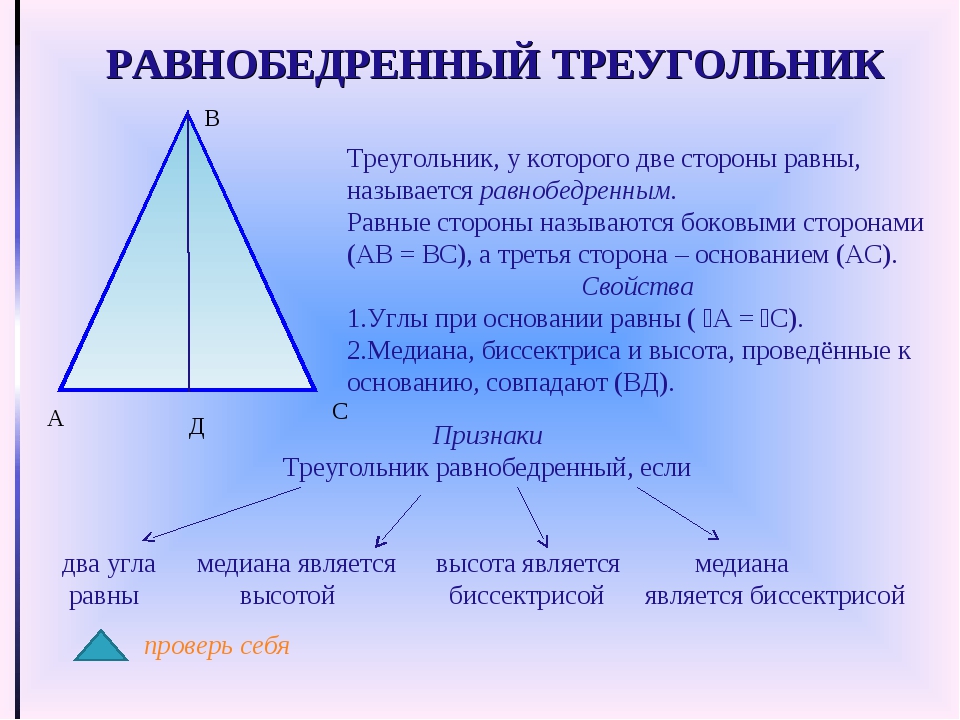
Равнобедренный треугольник — такая фигура, две стороны которой равны. Равные части такой фигуры будут называться боковыми сторонами, а третья сторона будет носить название основания.

И остроугольный, и тупоугольный, и прямоугольный треугольники могут быть равнобедренными.

Посмотрите на рисунки равнобедренных треугольников:

 

  

Источник: epmat.ru

Рассмотрим свойства равнобедренных треугольников:

1. Углы при основании будут всегда равны.
2. Высота, медиана, биссектриса, которые проводятся в равнобедренном треугольнике к основанию, будут совпадать.

Определение 5

Равносторонний треугольник — фигура, стороны и углы которой являются равными.

Как найти площадь данной фигуры?

Формула 2

S=a234

Формула 3

Как найти высоту данной фигуры?

h=a32

Определение 6

Прямоугольный треугольник — фигура, угол которой равен 90 градусам.

Рассмотрим свойства данной фигуры:

1. Совокупность двух острых углов будет равна 90 градусам.
2. Катет, который лежит напротив угла в 30 градусов, будет равен половине гипотенузы.
3. Соответственно, если катет = половина гипотенузы, то этот катет лежит напротив угла в 30 градусов.
4. Медиана, которая проведена из вершины угла прямого, будет равна половине гипотенузы.

Все основные формулы треугольника

Рассмотрим формулы, по которым можно вычислить площадь треугольника:

Формула 4

Формула площади по высоте и стороне.

S=12A×h

Вместо стороны A могут быть и показатели других сторон.

Формула 5

Формула Герона

S=p(p-a)(p-b)(p-c)

В данной формуле полупериметр вычисляется: p=a+b+c2

Формула 6

По двум сторонам, а также углу между этими сторонами — половина произведения двух сторон, умноженная на синус угла между этими сторонами.  

S=12a×b×sinγ

Формула 7

По трем сторонам, а также радиусу описанной окружности:

S=a*b*c4R

Формула 8

По трем сторонам, а также радиусу вписанной окружности. Площадь = произведение полупериметра на радиус вписанной окружности.

S=p*r

Рассмотрим также подобия треугольников.

Определение 7

Подобные треугольники — такие фигуры, в которых соответствующие углы являются равными, а стороны сходственные являются пропорциональными.

Таким образом, треугольник ABC будет подобен MNK. Так угол альфа будет равен углу альфа1, угол бета будет равен углу бета1, угол гамма будет равен углу гамма1. Иначе ABMN будет равно BCNK будет равно ACMK будет равно k.

Коэффициент k = коэффициент подобия.  

Рассмотрим признаки подобия треугольников:

1. Первый признак подобия треугольника. В случае, если два угла треугольника равны соответственно двум углам другого треугольника, то такие треугольники называются подобными.
2. Второй признак подобия фигур. В случае, если три стороны данной фигуры пропорциональны трем сторонам другой фигуры (треугольника), то такие треугольники называют подобными.
3. Третий признак подобия треугольника. В случае, если две стороны треугольника будут пропорциональны двум сторонам другого треугольника, а углы, которые расположены между этими сторонами, являются равными, то такими треугольники называются подобными.

Определение 8

Вписанная окружность — такая окружность, которая касается треугольник со всех трех сторон.

Посмотрите на вписанную окружность:

 

Источник: ru.onlinemschool.com

Основные свойства вписанной окружности:

• Центр вписанной окружности всегда расположен на пересечении биссектрис внутренних углов треугольника.
• В любой треугольник возможно вписать окружность, но только одну.

Угол вершины — определение, твердые формы, парабола, примеры

Угол вершины образуется, когда две линии или лучи встречаются и пересекаются в одной конечной точке или вершине. Этот угол измеряется в градусах и иногда используется как синоним угла лица. В 2D-форме, такой как многоугольник, угол при вершине формируется двумя пересекающимися линиями в углу, а в 3D-фигурах, поскольку линий больше двух, следовательно, возможно множество углов. Давайте узнаем больше об угле вершины, определении вершины, угле вершины в различных формах и решим несколько примеров, чтобы лучше понять концепцию.

1.	Что такое угол вершины?
2.	Угол вершины в твердых фигурах
3.	Угол вершины параболы
4.	Как найти угол вершины?
5.	Часто задаваемые вопросы по Vertex Angle

Что такое угол вершины?

Вершинный угол определяется как угол, образованный двумя линиями или лучами, пересекающимися в одной точке. Эти два луча составляют стороны угла. Другими словами, угол, связанный с данной вершиной, называется углом вершины и измеряется в градусах. Посмотрите на изображение ниже, угол между лучами 1 и лучами 2, исходящими из вершины O, представляет собой угол при вершине, который записывается как ∠AOB. Угол также может быть назван как ∠BOA или только по его вершине, т.е. ∠O. Вершину всегда следует писать посередине, используя три точки для обозначения угла.

Углы, имеющие общую вершину, записываются по-разному. Посмотрите на изображение ниже, мы не можем написать ∠AOB с углом при вершине как O, так как угол используется как для ∠BOC, так и для ∠COA. Следовательно, каждый угол должен быть назван точками на каждой стороне, образующими угол, вместе с вершиной угла.

Определение вершины

Вершина в математике — это точка, в которой встречаются две линии или лучи, образующие угол в этой точке, и обозначается прописными буквами, такими как A, O, P и т. д. Вершина — это вершина во множественном числе.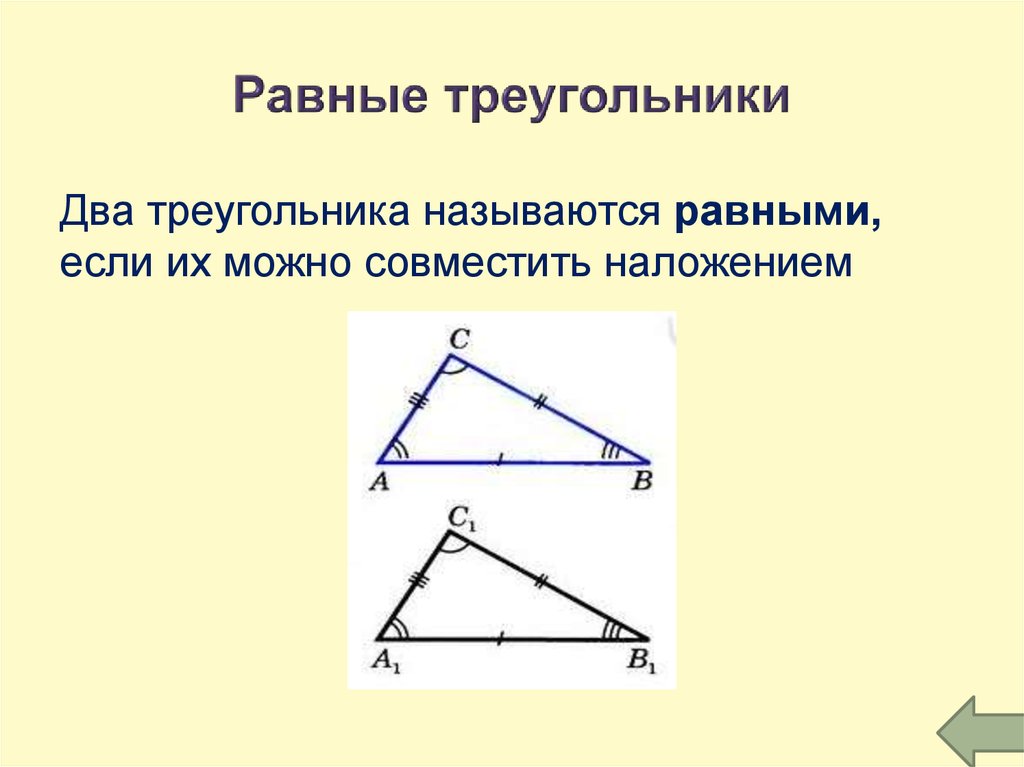 В объемной геометрии, т. е. трехмерной геометрии, такие фигуры, как кубы, прямоугольные параллелепипеды, образуют несколько вершин. В то время как в 2D-формах, таких как многоугольники, образуются только вершины.

Угол вершины в твердотельных фигурах

Не только плоские фигуры, но и твердые формы имеют вершины, которые формируются там, где встречаются ребра. Линии не пересекаются друг с другом, образуя вершину, однако вершину образуют углы или ребра сплошной формы. Например, посмотрите на изображение куба, углы или края фигуры рассматриваются как вершины, составляющие в общей сложности 8 вершин. Вершины иногда также обозначаются как вершина или вершина формы, такой как треугольники и пирамиды. Эта вершина или вершина является верхним углом над основанием основания. Например, посмотрите на изображение тетраэдра, у него 4 вершины.

Чтобы найти вершины твердого тела, мы можем использовать формулу Эйлера, которая задается как:

F + V — E = 2

Где

• F — количество граней
• V обозначает вершины
• E — количество ребер

Угол вершины параболы

Когда мы рисуем квадратное уравнение, мы получаем параболу. Определение вершины параболы — это точка, в которой именно она поворачивается, которая также называется точкой минимума (если она имеет форму «U»). Когда парабола раскрывается вниз, вершина называется точкой максимума (если она имеет форму буквы «U»). форма ‘∩’). Вершина параболы лежит на оси симметрии. Посмотрите на изображение ниже для справки. 92} — 4ac =16\end{array}\]

Координаты вершины.

\[V \equiv \left( { — \frac{b}{{2a}}, -\frac{D}{{4a}}} \right) = \left( { — \frac{1}{ 3},\frac{4}{3}} \right)\]

Обратите внимание, что парабола будет открываться вниз (поскольку \(a\) отрицательно), но вершина имеет положительную y -координату .

Следовательно, вершина параболы находится в точке \(-\dfrac{1}{3} , \dfrac{4}{3}\)

Как найти угол вершины?

Как мы видели, угол, образованный при вершине, называется углом при вершине. Для каждого многоугольника угол при вершине разный и рассчитывается по этим двум формулам.

Формула угла для правильного многоугольника:

Сумма внутренних углов правильного многоугольника

Угол = 180 (n – 2)/n

Где n = количество сторон 92 + k\), где (h, k) — вершина.

Связанные темы:

Ниже перечислены несколько тем, связанных с вершиной угла, посмотрите.

• Формула вершины
• Стандартная форма в вершинную форму
• Графики квадратичных функций
• Смежные углы

Часто задаваемые вопросы по Vertex Angle

Что означает вершина в математике?

Вершина — это точка пересечения ребер или отрезков. Множественное число называется вершинами. Эти вершины различаются по форме, например, треугольник имеет 3 ребра или вершины, а пятиугольник имеет 5 вершин или углов.

Почему угол вершины важен?

Вершина важна, поскольку она определяет высшую или низшую точку, например, высшую точку в равнобедренном треугольнике или минимальную точку в параболе.

Что такое вершина графа?

Вершина — узел графа. Это также точка, которая определяет узел или максимальную или минимальную точку.

Почему угол при вершине равнобедренного треугольника?

Равнобедренный треугольник имеет один угол при вершине и два равных угла при основании. Суммарный угол равен 180,

В чем разница между углом и вершиной?

Угол и вершина считаются одним и тем же, поскольку оба являются ребрами или точками пересечения двух пересекающихся линий.

Что такое вершины в математике?

Обновлено 27 октября 2020 г.

Автор: Jon Zamboni

Вершина — это математическое слово, обозначающее угол. Большинство геометрических фигур, двухмерных или трехмерных, имеют вершины. Например, у квадрата четыре вершины, которые являются его четырьмя углами. Вершина также может относиться к точке угла или графическому представлению уравнения.

TL;DR (слишком длинный; не читал)

В математике и геометрии вершина — вершина во множественном числе — вершины — это точка, в которой пересекаются две прямые линии или ребра.

Вершины отрезков и углов

В геометрии, если два отрезка пересекаются, точка пересечения двух прямых называется вершиной. Это верно, независимо от того, пересекаются ли линии или встречаются в углу. Из-за этого углов также имеют вершины. Угол измеряет отношение двух отрезков, называемых лучами, которые встречаются в определенной точке. Исходя из приведенного выше определения, вы можете видеть, что эта точка также является вершиной.

Вершины двумерных фигур

Двумерная фигура, например треугольник, состоит из двух частей – ребер и вершин. Ребра — это линии, образующие границу фигуры. Каждая точка пересечения двух прямых ребер является вершиной. Треугольник имеет три ребра – три его стороны. Он также имеет три вершины, каждый из которых является углом, где встречаются два ребра.

Из этого определения также видно, что некоторые двумерные фигуры не имеют вершин. Например, круги и овалы состоят из одной грани без углов. Поскольку отдельные ребра не пересекаются, эти фигуры не имеют вершин. Полукруг также не имеет вершин, потому что пересечения на полукруге находятся между кривой линией и прямой линией, а не двумя прямыми линиями.

Вершины трехмерных фигур

Вершины также используются для описания точек в трехмерных объектах. Трехмерные объекты состоят из трех разных частей. Возьмем куб: каждая его плоская сторона называется гранью . Каждая линия, где сходятся две грани, называется ребром. Каждая точка пересечения двух или более ребер является вершиной. У куба шесть квадратных граней, двенадцать прямых ребер и восемь вершин, где сходятся три ребра. Другими словами,

каждый из углов куба является вершиной. Как и двумерные объекты, некоторые трехмерные объекты, такие как сферы, не имеют вершин, поскольку у них нет пересекающихся ребер.