Что значит интеграл: простыми словами об интегрировании функций / Skillbox Media

alexxlab / / Разное

Интегрирование функций с разрывами и несобственные интегралы

До сих пор мы интересовались в первую очередь интегралами непрерывных функций. Именно для такого случая мы доказали формулу Ньютона — Лейбница: непрерывность подынтегральной функции является важным её условием. Что бывает, когда подынтегральная функция терпит разрывы? Мы не сможем дать полный ответ на этот вопрос, но обсудим некоторые важные частные случаи.

27.1Интегрирование функций с конечным числом скачков

27.1.1Скачки интегралу не помеха

Пусть функция f имеет на отрезке [a,b] конечное число (m штук) разрывов в точках z1,…,zm, во всех остальных точках отрезка она непрерывна, и все разрывы являются скачками, то есть в них определены пределы справа и слева. Можно ли посчитать интеграл по [a,b] от такой функции?

Если воспринимать задачу интегрирования геометрически, это не выглядит проблемой. Интеграл — это площадь, а площадь обладает свойством аддитивности — если разрезать фигуру, площадь от которой мы находим, на несколько непересекающихся кусочков, площадь всей фигуры должна равняться сумме площадей этих кусочков.

Соответственно, можно разбить интеграл в сумму интегралов по промежуткам, на которых функция непрерывна (а значит интегрируема), и всё сложить. Именно так мы и сделаем! Но сперва докажем полезную лемму.

Лемма 1. Пусть функции f и g отличаются друг от друга лишь в конечном числе точек z1,…,zm. Тогда их интегралы совпадают (и одновременно существуют или не существуют).

Доказательство. Изменения конечного числа значений не влияет на ограниченность, следовательно, функции f и g либо одновременно неограниченны, либо одновременно ограничены. В первом случае они обе неинтегрируемы и доказывать нечего. Рассмотрим второй случай, пусть обе функции ограничены некоторым числом C>0 (по модулю).

Возьмём произвольное размеченное разбиение P, у которого границами отрезков разбиения являются точки (x0,…,xn) и отмечены точки (x∗1,…,x∗n). Поскольку функции f и g различаются лишь в конечном числе точек, эти точки могут попасть лишь в конечное число отрезков разбиения.

(В худшем случае точка может оказаться общим концом двух отрезков разбиения, значит, число затронутых отрезков не более чем в два раза больше числа точек различия.) Пусть затронуты отрезки с номерами k1,…,kM, M≤2m. Модуль разности между интегральными суммами для функций f и g равен

∣∣ ∣∣M∑i=1f(x∗ki)−g(x∗ki)Δxki∣∣ ∣∣≤M∑i=1|f(x∗ki)−g(x∗ki)|⋅|Δxki|.

∣∣ ∣∣M∑i=1f(x∗ki)−g(x∗ki)Δxki∣∣ ∣∣≤≤M∑i=1|f(x∗ki)−g(x∗ki)|⋅|Δxki|.

Модуль разности между значениями функций f и g не превосходит 2C, поскольку сами значения ограничены по модулю числом C. (Мы используем неравенство |a−b|≤|a|+|b|.) Длина отрезка разбиения |Δxki| не превосходит диаметра разбиения d(P). Всего слагаемых M штук, где M≤2m. Значит разница между двумя интегральными суммами не превосходит (2m)⋅(2C)⋅d(P)=4mC⋅d(P) и стремится к нулю при d(P) стремящемся к нулю. Значит, пределы интегральных сумм совпадают.∎

Теорема 1. Пусть функция f имеет конечное число точек разрывов z1<z2<…<zm на отрезке [a,b] и все разрывы являются скачками, то есть в каждой точке разрыва есть конечные односторонние пределы функции справа и слева. В остальных точках функция непрерывна. Тогда она интегрируема на отрезке [a,b].

Доказательство. Воспользовавшись свойством аддитивности (24.5), разобьем интеграл в сумму интегралов:

∫baf(x)dx=∫z1af(x)dx+∫z2z1f(x)dx+…+∫zmzm−1f(x)dx+∫bzmf(x)dx.(27.1)

∫baf(x)dx=∫z1af(x)dx++∫z2z1f(x)dx+…++∫zmzm−1f(x)dx+∫bzmf(x)dx.(27.1)

Рассмотрим любой из получившихся отрезков интегрирования, обозначим его концы через α и β. Функция f непрерывна на [α,β], за исключением, быть может, концов отрезка. Но в концах существуют односторонние пределы (поскольку все точки разрывов — скачки), и следовательно для вычисления интеграла по [α,β] функцию можно переопределить в α и β, таким образом, чтобы сделать её непрерывной на всём отрезке (как обычно, в концах требуется односторонняя непрерывность). По лемме, значение интегралов от этого не поменяется, равно как и факт интегрируемости. Но функция, непрерывная на отрезке, интегрируема на этом отрезке, и значит все интегралы в правой части равенства (27.

1) существует и функция интегрируема на всём отрезке [a,b].∎

Пример 1. Пусть

sign(x)=⎧⎨⎩1,x>00,x=0−1,x<0

Найдём

F(t):=∫t−2sign(x)dx.

Возможно три варианта: t<0, t=0 или t>0. В первом случае наш интеграл — это площадь прямоугольника высотой 1 и шириной (t−(−2)), взятая со знаком «минус» (потому что значение функции отрицательно), то есть −2−t (см. анимацию на рис. 27.1). При t=0 можно переопределить функцию таким образом, чтобы в точке x=0 она принимала значение (−1) и тем самым сделать её непрерывной на всём отрезке интегрирования. Если же t>0, наш интеграл разбивается в сумму двух интегралов: по отрезку [−2,0] и по отрезку [0,t]. Первый равен −2, второй является площадью прямоугольника с шириной t и высотой 1, то есть t.

Итак,

F(t)=⎧⎨⎩−2−t,t<0;−2,t=0;−2+t,t>0.

Это выражение можно записать короче: F(t)=−2+|t|.

Заметим, что во всех точках t≠0, производная F совпадает с подынтегральной функцией (проверьте!):

F′(t)=sign(t).

Это неудивительно: первая часть формулы Ньютона — Лейбница выполняется для всех точек, в которых подынтегральная функция непрерывна, а разрыв у нас только в нуле. В нуле же функция F не является дифференцируемой, но является непрерывной. Оказывается, так будет всегда.

27.1.2Интеграл с переменным верхним пределом непрерывен

Утверждение 1. Пусть функция f интегрируема на отрезке [a,b]. Тогда функция

F(t)=∫taf(x)dx

непрерывна на отрезке [a,b].

Доказательство. Действительно, для любых точек t,t0∈[a,b]

F(t)−F(t0)=∫taf(x)dx−∫t0af(x)dx=∫tt0f(x)dx.

F(t)−F(t0)=∫taf(x)dx−∫t0af(x)dx==∫tt0f(x)dx.

Иными словами, разность значений F в точках t и t0 равна интегралу от f по отрезку [t0,t].

Поскольку функция под интегралом интегрируема, она ограничена, и значит интеграл по маленькому отрезку от неё будет маленьким. Следовательно, значения функции F в близких точках близки.

Аккуратное доказательство выглядит так. Поскольку функция f ограничена, найдётся такое C, что для всех x∈[a,b]

−C≤f(x)≤C.

Интегрируя эти неравенства по отрезку [t0,t] (будем считать, что t>t0, противоположный случай разбирается аналогично), имеем:

∫tt0(−C)dx≤∫tt0f(x)dx≤∫tt0Cdx.

Считая интегралы в левой и правой части, получаем:

−C(t−t0)dx≤∫tt0f(x)dx≤C(t−t0).

В пределе при t→t0, левая и правая части стремятся к нулю, значит и интеграл посередине стремится к нулю. Но этот интеграл равен разности F(t)−F(t0), следовательно эта разность стремится к нулю, и значит

limt→t0F(t)=F(t0),

то есть F непрерывна в точке t0.∎

Теперь мы можем заключить, что интеграл от кусочно-непрерывной функции f с конечным числом скачков, если рассматривать его как функцию от верхнего предела, является непрерывной функцией, дифференцируемой во всех точках, кроме точек разрывов f; в точках разрывов f у интеграла точки излома и производная не существует (если только эти разрывы не являются устранимыми, устранимые разрывы интеграл «не замечает» в силу леммы).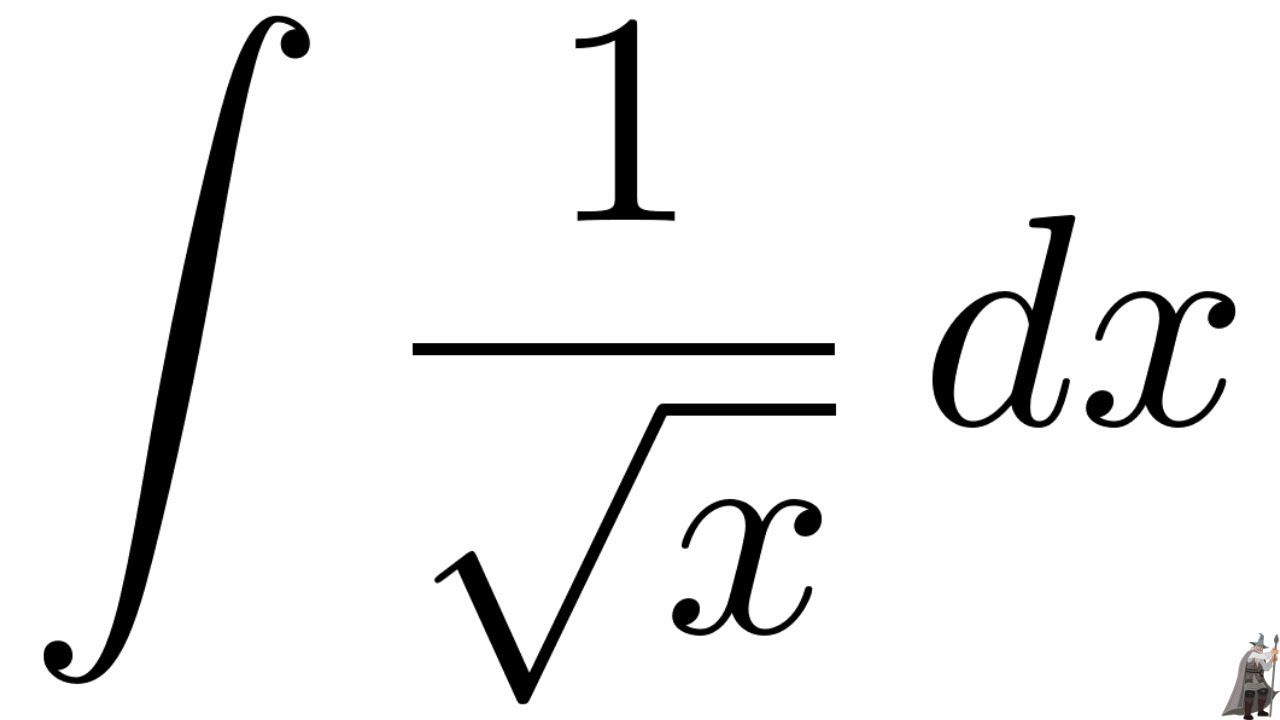

27.2Несобственные интегралы

До сих пор мы рассматривали интегралы, которые отвечали площадям ограниченнух фигур — то есть таких фигур, которые можно поместить в достаточно большой прямоугольник. Действительно, в горизонтальном направлении мы были ограничены отрезком интегрирования, а в вертикальном — ограниченностью подынтегральной функции — мы всегда говорили, что раз функция не является ограниченной, она и не интегрируемая, и даже однажды это доказали.

Однако, можно представить себе фигуру, которая не будет помещаться ни в какой прямоугольник, но тем не менее будет иметь конечную площадь. Как бы нам её найти?

27.2.1Несобственные интегралы с бесконечными пределами интегрирования

Начнём с примера.

Пример 2. Пусть мы хотим найти такой интеграл:

∫+∞11x2dx.(27.2)

Область интегрирования теперь — не отрезок, а бесконечный луч, см. рис. 27.2.

Рис. 27.2: Интеграл по лучу

Использовать обычное определение нельзя — луч нельзя разбить в конечное число отрезков. Теоретически, можно было бы расширить понятие разбиения, разрешив разбиения на бесконечное число отрезков, но тогда в интегральных суммах было бы бесконечное число слагаемых, и надо было думать, как эти суммы определять…

В общем, мы сделаем иначе. Положим по определению, что интеграл (27.2) равен такому пределу:

∫+∞11x2dx:=limt→+∞∫t11x2dx.

То есть мы считаем интеграл до какой-то конечной границы t, для разных t получаем разные значения интеграла, и дальше устремляем t к бесконечности, см. анимацию на рис. 27.3.

Это выглядит логичным: если мы будем всё сильнее увеличивать верхний предел интегрирования t, мы будем захватывать всё большую и большую часть нашей неограниченной фигуры, так что в пределе ничего не останется не захваченным, и значит площадь захваченного куска должна стремиться к площади всей фигуры.

Рис. 27.3: Несобственный интеграл как предел

Попробуем найти, что получится. Заметим, что первообразной 1/x2 является (−1/x). Воспользуемся формулой Ньютона — Лейбница:

limt→+∞∫t11x2dx=limt→+∞(−1x)∣∣∣t1=limt→+∞(−1t−(−11))=1.

limt→+∞∫t11x2dx=limt→+∞(−1x)∣∣∣t1==limt→+∞(−1t−(−11))=1.

Получилось! Искомая площадь равна 1.

Определение 1. Пусть функция f интегрируема на любом отрезке [a,t], t>a. Интеграл

∫+∞af(x)dx

называется несобственным интеграл по бесконечному промежутку. По определению он равен

∫+∞af(x)dx:=limt→+∞∫taf(x)dx.

Всегда ли предел будет существовать? Конечно, нет — легко придумать пример, когда не будет. Скажем,

∫+∞12dx=limt→+∞2(t−1)=+∞.

Но тут история понятная — подынтегральная функция является константой, наша фигура — «бесконечный прямоугольник», неудивительно, что у него бесконечная площадь. Но что если подынтегральная функция стремится к нулю. Может ли быть так, чтобы интеграл по лучу не существовал? Давайте рассмотрим ещё один пример.

Пример 3. Найдём

∫+∞11xdx.

Действуя так же, как и раньше, запишем этот интеграл в виде предела. Напомним, что первообразная 1/x при положительных x — это lnx. Имеем:

∫+∞11xdx:=limt→+∞∫t11xdx=limt→+∞lnx|t1=limt→+∞(lnt−ln1)=+∞.

∫+∞11xdx:=limt→+∞∫t11xdx==limt→+∞lnx|t1==limt→+∞(lnt−ln1)=+∞.

Определение 2. Если предел в определении несобственного интеграла существует, говорят, что интеграл сходится, в противном случае он расходится.

Итак, интеграл по одному и тому же лучу [1,+∞) от функции 1/x2 сходится, а от функции 1/x расходится. Почему так? Казалось бы, они обе стремятся к нулю при x→+∞, и на глаз их графики очень похожи. Однако, мало стремиться к нулю, нужно делать это ещё достаточно быстро. Функция 1/x стремится к нулю медленнее, чем 1/x2, и этого стремления не хватает, чтобы площадь оказалась конечной.

Является ли требование стремления к нулю необходимым для сходимости интеграла? Оказывается, нет.

Упражнение 1. Придумайте пример функции, которая не стремится к нулю при x→+∞, но интеграл от которой по лучу [0,+∞) сходится.

Определение 3. Легко определить интеграл по лучу (−∞,a]:

∫a−∞f(x)dx=limt→−∞∫atf(x)dx.

Интеграл по всей прямой (−∞,∞) определяется так:

∫∞−∞f(x)dx=∫a−∞f(x)dx+∫+∞af(x)dx,

где промежуточную точку a можно выбирать произвольным образом, значение интеграла от этого не изменится (почему?).

27.2.2Признак сравнения

Часто бывает важно даже не найти значение несобственного интеграла, а просто показать, что он сходится. В этом случае полезной оказывается следующая теорема.

Теорема 2. Пусть функции f и g интегрируемы на любом отрезке [a,t], t>a. Пусть также для всякого x≥a

0≤f(x)≤g(x)(27. 3)

и интеграл

∫+∞ag(x)dx(27.4)

сходится. Тогда

∫+∞af(x)dx(27.5)

тоже сходится.

Доказательство. Утверждение выглядит естественным. Фигура, соответствующая интегралу (27.5), содержится внутри фигуры, соответствующей интегралу (27.4). Логично предположить, что если площадь первой конечна, то и второй тоже.

Формальное доказательство выглядит так. Введём обозначения:

G(t):=∫tag(x)dx,F(t):=∫taf(x)dx.

Заметим, что обе функции F и G неубывают на [a,+∞): это следует из того факта, что их производные, равные подынтегральным функциям, неотрицательны. Также интегрируя неравенства (27.3) по отрезку [a,t], имеем:

F(t)=∫taf(t)dt≤∫tag(t)dt=G(t).

По предположению, G(t) имеет предел при t→+∞. Обозначим его через L. Все значения неубывающей функции не превосходят предела: действительно, если для какого-то t0, G(t0)>L, то найдётся такое c>0, что G(t0)>L+c (можно в качестве c взять половину разности G(t0)−L, тогда L+c — середина отрезка [L,G(t0)]), и значит для всех t>t0 выполняется такое же неравенство (в силу неубывания G), а значит предел не меньше L+c, то есть строго больше L — противоречие. Значит для всех t≥a:

F(t)≤G(t)≤L.

Итак, функция F неубывает и ограничена. Можно легко адаптировать теорему Вейерштрасса для функций (сделайте это!) и получить, что существует предел

limt→+∞F(t),

то есть интеграл (27.5) сходится.∎

Пример 4. Докажем, что

∫+∞0e−x2dx

сходится.

Действительно, разобьём этот интеграл в сумму двух:

∫+∞0e−x2dx=∫10e−x2dx+∫+∞1e−x2dx.

С первым слагаемым никаких проблем нет: это обычный (собственный) интеграл Римана, подынтегральная функция непрерывна, значит, интеграл существует. Рассмотрим второе слагаемое. Заметим, что при x≥1, x2≥x и

0≤e−x2≤e−x.

Таким образом, если интеграл

∫+∞1e−xdx

сходится, то и наш интеграл сходится. Но e−x легко проинтегрировать явно: первообразная равна (−e−x). Таким образом,

∫+∞1e−xdx=limt→+∞∫t1e−xdx=limt→+∞(−e−x)|t1=limt→+∞(−e−t−(−e−1))=1e.

∫+∞1e−xdx=limt→+∞∫t1e−xdx==limt→+∞(−e−x)|t1==limt→+∞(−e−t−(−e−1))=1e.

Мы нашли этот интеграл явно, значит, он сходится, и значит наш исходный интеграл тоже сходится.

В том виде, в котором мы его сформулировали, признак сравнения работает только с неотрицательными подынтегральными функциями.

Вопрос 1. Покажите, что условие неотрицательности здесь существенно. Приведите пример функций f и g, для которых условие f(x)≤g(x) выполняется для всех x, ∫+∞0g(x)dx сходится, а интеграл ∫+∞0f(x)dx расходится.

Следующее утверждение позволяет расширить признак сравнения на случай знакопеременных подынтегральных выражений:

Утверждение 2. Если сходится интеграл

∫+∞a|f(x)|dx,

то сходится и интеграл

∫+∞af(x)dx.

Мы не будем сейчас доказывать это утверждение. Однако, из него мгновенно следует, что если существует такая функция g(x), что для всех x, |f(x)|≤g(x) и ∫+∞ag(x)dx сходится, то и ∫+∞af(x)dx тоже сходится.

27.2.3Несобственные интегралы и вертикальные асимптоты

Итак, нам удалось расширить понятие интеграла на случай бесконечных промежутков интегрирования. Может быть, и с неограниченными функциями удастся что-то сделать?

До сих пор мы много раз повторяли мантру «раз функция неограничена, значит, она и не интегрируема» — и даже доказали утверждение на эту тему. Однако, значит ли это, что соответствующие площади на самом деле не определены? Нам уже удалось найти площади некоторых неограниченных фигур, как в примере 2 выше. Может быть, и с площадями под графиками неограниченных функций ситуация может быть аналогичной — и наш реузльтат о неинтегрируемости вызван просто неудачным определением интеграла? Можно ли модифицировать это определение каким-то образом, чтобы хотя бы некоторые неограниченные функции стали интегрируемыми? Давайте попробуем.

Пример 5. Попробуем найти интеграл

∫101√xdx.

Подынтегральная функция стремится к бесконечности при x→0+, и значит не является ограниченной — стало быть интеграл в обычном смысле не определён. Однако, давайте воспользуемся тем же приёмом, которым мы воспользовались для нахождения интеграла по бесконечному промежутку. Положим по определению

∫101√xdx:=limt→0+∫1t1√xdx.

Для всякого t>0 интеграл под знаком предела определён. Более того: его можно найти явно — подынтегральная функция 1/√x может быть записана в виде x−1/2, а все степенные функции мы имеем интегрировать. Первообразная имеет вид 2×1/2=2√x (проверьте дифференцированием!) и значит

∫101√xdx:=limt→0+∫1t1√xdx=limt→0+2√x|1t=limt→0+(2√1−2√t)=2.

∫101√xdx:=limt→0+∫1t1√xdx==limt→0+2√x|1t==limt→0+(2√1−2√t)=2.

Интеграл сошёлся, ура!

Определение 4. Пусть функция f имеет вертикальную асимптоту в точке a и для всякого t∈(a,b) функция f интегрируема по Риману на отрезке [t,b]. Несобственный интеграл

∫baf(x)dx

определяется следующим образом:

∫baf(x)dx:=limt→a+∫btf(x)dx.

Как обычно, предел может существовать (в этом случае говорят, что интеграл сходится), или не существовать (значит, интеграл расходится).

Пример 6. Сходится ли интеграл

∫101x2dx?

Мы уже считали интеграл от этой функции, но по другой области — по бесконечному промежутку [1,+∞) — и он сошёлся. Может быть, и в этот раз нам повезёт?

∫101x2dx=limt→0+∫1t1x2dx=limt→0+(−1x)∣∣∣1t=limt→0+(−11+1t)=+∞.

∫101x2dx=limt→0+∫1t1x2dx==limt→0+(−1x)∣∣∣1t==limt→0+(−11+1t)=+∞.

Увы, этот интеграл расходится.

Почему такая разница с функцией 1/√x? Дело в том, что √x стремится к нулю гораздо медленнее, чем x2, и значит 1/√x стремится к бесконечности гораздо медленнее, чем 1/x2. Поэтому площадь под графиком 1/√x оказывается конечной, а под графиком 1/x2 — бесконечной.

В определении 4 вертикальная асимптота находится на левой границе отрезка интегрирования. Конечно, можно с тем же успехом определить несобственный интеграл для функции с вертикальной асимптотой на правой границе области отрезка интегрирования.

Определение 5. Пусть функция f имеет вертикальную асимптоту в точке b и для всякого t∈(a,b) функция f интегрируема по Риману на отрезке [a,t]. Несобственный интеграл

∫baf(x)dx

определяется следующим образом:

∫baf(x)dx:=limt→b−∫taf(x)dx.

А что если точка бесконечного разрыва попала куда-то внутрь нашего отрезка? Ничего страшного — просто разобьем интеграл на два.

Определение 6. Пусть функция f имеет вертикальную асимптоту в точке c∈(a,b) и интегрируема на любой отрезке [a,t], t<c и на любом отрезке [t,b], t>c. Тогда

∫baf(x)dx:=∫caf(x)dx+∫bcf(x)dx,

где интегралы в правой части — несобственные. Если хотя бы один из этих двух интегралов расходится, интеграл в левой части тоже считается расходящимся.

Пример 7. Что вы можете сказать про интеграл

∫1−11xdx?

Очень хочется сказать, что он равен нулю: ведь это интеграл от нечётной функции по симметричному отрезку, и значит положительная и отрицательные площади должны взаимно уничтожиться. Однако, это не так: по определению,

∫1−11xdx:=∫0−11xdx+∫101xdx,

и оба интеграла в правой части расходятся, значит и исходный интеграл расходится. (Подробнее о том, почему это правильный подход, будет обсуждаться на семинаре.)

27.2.4Несобственные интегралы с несколькими особенностями

Каждое из определений несобственных интегралов, которые мы обсуждали, рассматривает только одну «особенность» — бесконечный разрыв или бесконечную границу интегрирования. Если у интересующего нас интеграла несколько особенностей, его следует разбить в сумму интегралов, у каждого из которых лишь одна особенность, и воспользоваться нашими определениями.

Пример 8. Пусть у функции f бесконечные разрывы в точках 2, 5 и 7, и мы хотим посчитать от неё интеграл по всей числовой прямой. Его следует представить в таком виде:

∫∞−∞f(x)dx=∫1−∞f(x)dx+∫21f(x)dx+∫42f(x)dx+∫54f(x)dx++∫65f(x)dx+∫76f(x)dx∫107f(x)dx+∫+∞10f(x)dx.

∫∞−∞f(x)dx==∫1−∞f(x)dx+∫21f(x)dx++∫42f(x)dx+∫54f(x)dx++∫65f(x)dx+∫76f(x)dx+∫107f(x)dx+∫+∞10f(x)dx.

Каждый из получившихся интегралов — один из несобственных интегралов, которые мы обсуждали. Промежуточные точки 1, 4, 6, 10 выбраны произвольным образом — можно выбрать какие-то другие точки, лежаще на тех же промежутках, от этого ничего не изменилось бы. Если хотя бы один из интегралов в правой части расходится, значит, весь исходный интеграл тоже расходится.

27.3Заключение

Мы вышли за пределы уютного и безопасного мира, в котором все подыинтегральные функции непрерывны. И тут много всего интересного! Во-первых, если функция имеет разрывы типа «скачок», и их конечное число, никаких проблем для интегрирования это не представляет. Правда, интеграл, если думать о нём как о функции от его верхнего предела, будет иметь изломы в точках разрывов подынтегральной функции — но по крайней мере сам останется непрерывным. Случай бесконечных разрывов подынтегральной функции представляет большую опасность: несобственные интегралы, которые мы придумали специально для этого случая, существуют не всегда, иногда они сходится, а иногда расходится. Но тут уж ничего не поделать — площадь под графиком неограниченной функции может быть бесконечной. Мы также обсудили интегралы по бесконечным промежуткам — особенно важный для нас случай, поскольку такие интегралы сплошь и рядом встречаются в теории вероятностей, которую вы будете проходить совсем скоро.

На этом наш краткий экскурс в теорию интегрирования заканчивается. Конечно, мы успели обсудить не всё, но фундамент заложен. Время идти дальше!

← Предыдущая глава Следующая глава →

Интеграл — что это, определение и ответ

Интеграл – это одно из важнейших понятий в математическом анализе. В общем смысле

Интеграл – это сумма всех первообразных функции.

Существуют разные интегралы, которые применяются для вычисления площадей фигур и объёмов тел. В рамках школьного курса начала математического анализа изучают определенный интеграл, он равен площади криволинейной трапеции.

Криволинейной трапеция – это трапеция на координатной плоскости, с вертикальными основаниями \(x = a\) и \(x = b\) (где \(a\) и \(b\) – границы интегрирования), ограниченной сверху графиком функции \(y = f(x)\).

\(S\left( x \right)\) – площадь криволинейной трапеции

Определённый интеграл – это разность первообразных непрерывной неотрицательной функции в крайних точках заданного отрезка. {3}}{3} \right) — \left( 6 + 1 — \frac{1}{3} \right) = — 12 + 4 — \frac{8}{3} — 7 + \frac{1}{3} = — 15\frac{7}{3}\)

Ответ:\(\ — 15\frac{7}{3}\)

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ИНТЕГРАЛА

Определенный интеграла и площадь под графиком функций связаны между собой через понятие приращения, как, например, связана производная и угол наклона касательной. Дело в том, что если мы поделим координатную плоскость под графиком бесконечным количеством вертикальных прямых, расстояние между которыми будет равно \(\Delta x\), при этом \(\Delta x \longrightarrow 0\), тогда мы увидим, что вся площадь под графиком поделилась на бесконечное множество очень-очень узких прямоугольников, с одинаковой шириной \(\Delta x\), но разной высотой.

Две верхние вершины такого прямоугольника будут находиться настолько близко, что сойдутся почти в одной точке. Первообразная функции в этой точке будет равна площади этого прямоугольника. А если мы сложим все такие прямоугольники под функцией, как раз найдем площадь криволинейной трапеции.

Определение

в кембриджском словаре английского языка

Примеры интеграла

интеграла

Портреты умерших составляли неотъемлемую часть процесса скорби.

Из ВРЕМЕНИ