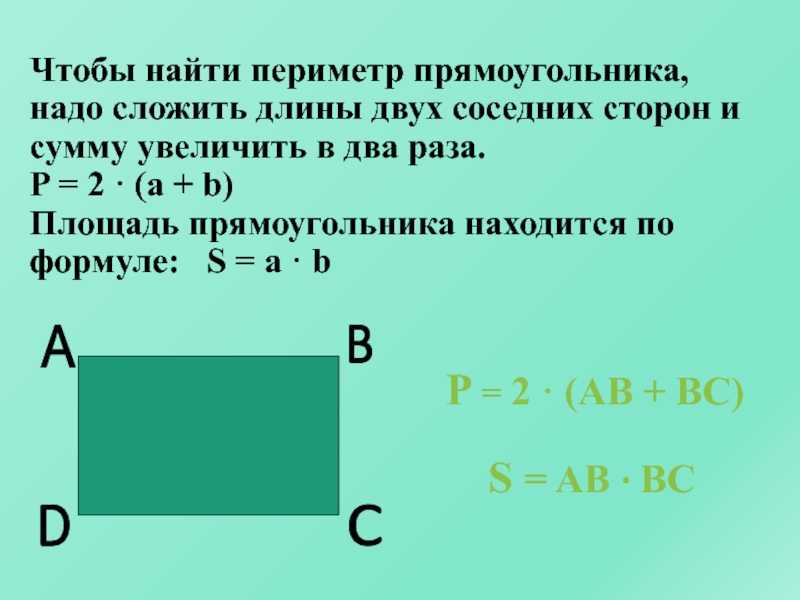
как найти, формула для вычисления, единица измерения
Периметр прямоугольника
Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.
Периметр прямоугольника — это сумма длин всех его ребер.
Основные свойства прямоугольника:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- противоположные стороны фигуры равны и параллельны друг другу;
- сумма всех углов равна 360 градусов;
- диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
- диагонали делят фигуру на два одинаковых прямоугольных треугольника;
- по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
- стороны рассматриваемого четырехугольника также являются его высотами;
- точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
- диагональ этого четырехугольника — это диаметр описанной окружности;
- вокруг него всегда можно описать окружность.
Варианты нахождения периметра прямоугольника
По сторонам
Источник: center-pss.ruЕсли нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:
\(P=2(a+b)\)
где \(a\) и \(b\) — это две соседние стороны фигуры.
По любой стороне и площади
Источник: lifehacker.ruЗная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.
Так как площадь прямоугольника — это произведение двух его смежных сторон \((S=a\times b)\), чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: \(b=\frac Sa\).
Получается, что формула для расчета \(P\) рассматриваемой фигуры будет выглядеть следующим образом:
\(P=2(\frac Sa+a)\)
По любой стороне и диагонали
Источник: lifehacker.
2})=2(3+\sqrt{100-9})=2(3+\sqrt{91})=6+2\sqrt{91}\) см.Ответ: \(6+2\sqrt{91}\) см.
Задачи на нахождение периметра прямоугольника
Урок 20. Решение текстовых задач по математике 1-4 классы
К нам за помощью обратился юный принц. У него много проблем, и все их можно решить, если знать, как найти периметр прямоугольника. А что такое периметр прямоугольника, и как решать задачи на нахождение периметра прямоугольника, рассмотрим на данном уроке.
Конспект урока «Задачи на нахождение периметра прямоугольника»
Сегодня к вам пришёл юный принц. У него возникло много проблем. Давайте его послушаем.
– В моем замке в тронном зале необходимо положить плинтусы на пол. А для этого надо найти
Посмотрите, какая некрасивая ограда вокруг моего сада!
Её тоже надо заменить! И опять необходимо найти периметр
сада.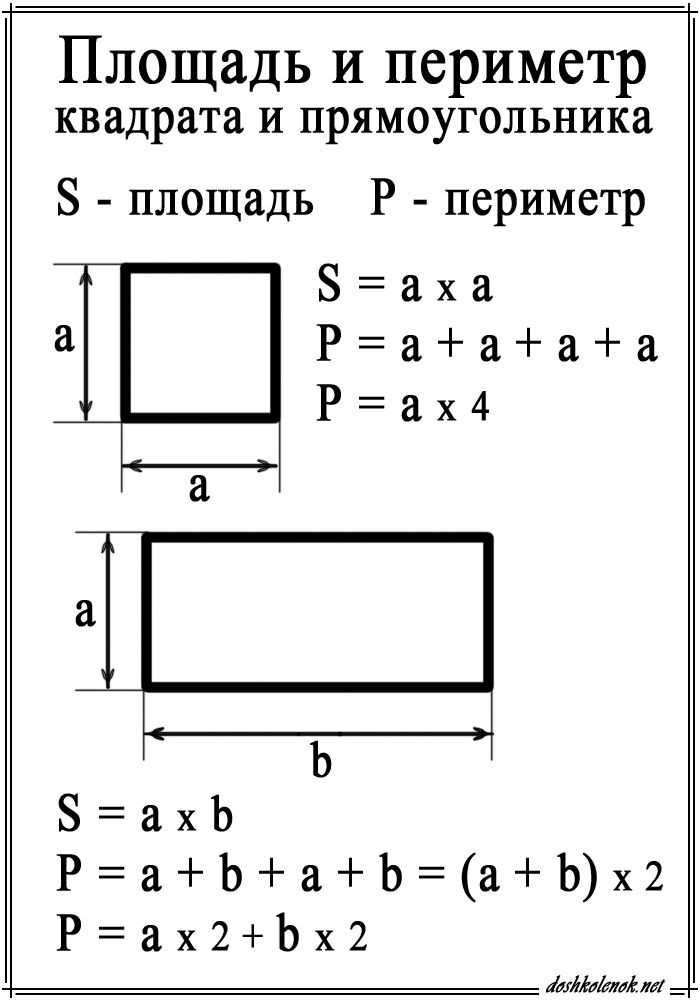
А ещё я хочу сделать своими руками рамку для портрета моей любимой
принцессы.
И опять для этого надо узнать периметр рамки. Но я не умею находить периметр. Помогите, пожалуйста!
– Ну что же, давайте сегодня будем учиться решать задачи на нахождение периметра прямоугольника.
Слово периметр известно уже несколько тысяч лет. Оно возникло в Древней Греции и переводится как «измеряю вокруг». В наше время слово периметр обозначает сумму длин всех сторон той или иной фигуры. Посмотрите на эти фигуры.
Видите, у них контуры? Это и есть периметр фигур.
Давайте рассмотрим 3 фигуры.
Как мы их назовём? Многоугольники. Вот первая фигура. Первый треугольник. Значит у него три угла и три стороны. Чтобы найти периметр мы сложим длины этих сторон друг с другом.
Вторая фигура – четырёхугольник.
Как найти его
периметр? Опять складываем все стороны.
А вот пятиугольник. И вновь складываем все стороны.
Запомнили? Периметр – это сумма длин всех сторон любой фигуры.
Ну что же – начнём учиться находить периметр прямоугольника. Давайте внимательно рассмотрим прямоугольник.
В нем две длинные стороны и две короткие. Длинные так и называются – длина, а у коротких название – ширина. У прямоугольника две длины. Они находятся напротив друг друга, т.е. это –
Допустим, длина прямоугольника – 6 см, а ширина – 4 см.
Как же найти периметр? Мы знаем, что у прямоугольника две длины, значит, длину мы берём 2 раза. Это можно записать так: к 6 прибавить 6, получается 12.
6 + 6 = 12 (см)
Но мы знаем, что сумму одинаковых слагаемых
можно заменить умножением, поэтому мы запишем так: 6 умножаем на 2, равно
12 см.
1) 6 · 2 = 12 (см)
Ширины у прямоугольника тоже две, поэтому мы и 4 умножаем на 2. Равно 8 см.
2) 4 · 2 = 8 (см)
Мы знаем, что периметр – это сумма длин всех сторон. Это значит, что надо сложить все стороны – и длину, взятую два раза, и ширину, тоже удвоенную. Поэтому мы к результату первого действия прибавляем результат второго действия. 3) 12 + 8 = 20 (см)
Это и есть периметр.
Но в математике принято записывать нахождение периметра выражением. И мы объединим все действия в одно выражение. Записываем: 6 · 2, 4 · 2, и между двумя этими действиями ставим знак плюс. Как мы помним, в первом действии ответ 12, во втором – 8, складываем их и получаем ответ 20 см.
6 · 2 + 4 · 2 = 20 (см)
Периметр любого прямоугольника можно найти именно так, поэтому придумали специальную формулу, запомнив которую вы всегда сможете найти его периметр.
Итак, ещё раз рассмотрим прямоугольник.
Его длину
мы обозначим буквой а, а ширину – буквой b. У прямоугольника две длины, поэтому мы а умножаем на 2. Две
ширины – и мы
– Ну вот, теперь я знаю, как находить периметр прямоугольника. Попробую сделать рамку для портрета принцессы. Я уже заготовил 4 куска красивого багета для рамки. Так, беру длинный кусочек, еще один… Пока хотел взять короткие, чтобы сделать ширину рамки, два длинных упали на пол.
А, может быть, есть какой-то другой способ?
– Конечно есть. Мы можем скрепить вместе длину и
ширину. Получился уголок – сумма длины и ширины. Теперь скрепляем оставшиеся
два куска.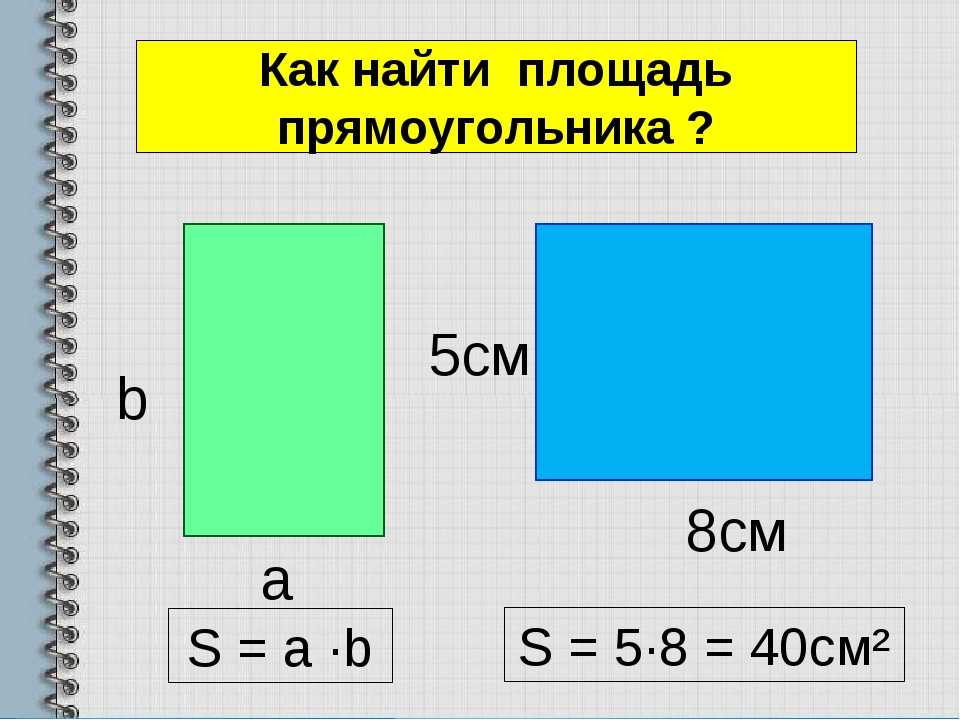
Получается ещё один уголок – тоже сумма длины и ширины. А теперь два эти уголка скрепляем между собой, т.е. мы сумму длины и ширины берём два раза. Вот какая замечательная рамка у нас получилась. И портрет принцессы в ней смотрится замечательно!
А как же это можно записать? Длину рамки вновь обозначим буквой а, а ширину – буквой b. Мы сначала к длине прибавили ширину, т.е. сложили а и b, а потом полученный результат взяли два раза, т.е. умножили на 2.
– Значит, периметр прямоугольника можно найти разными способами?
– Ну, конечно. Вы, принц, можете воспользоваться любым из них. Выбирайте, какой для вас удобнее.
Давайте повторим ещё раз. Итак, можно длину умножить на 2, потом ширину умножить на 2, и результаты этих действий сложить.
А можно сначала сложить длину с шириной, а потом
результат сложения умножить на 2. Только не забудьте умножить на 2, а то у Вас
вместо прямоугольника получится просто угол.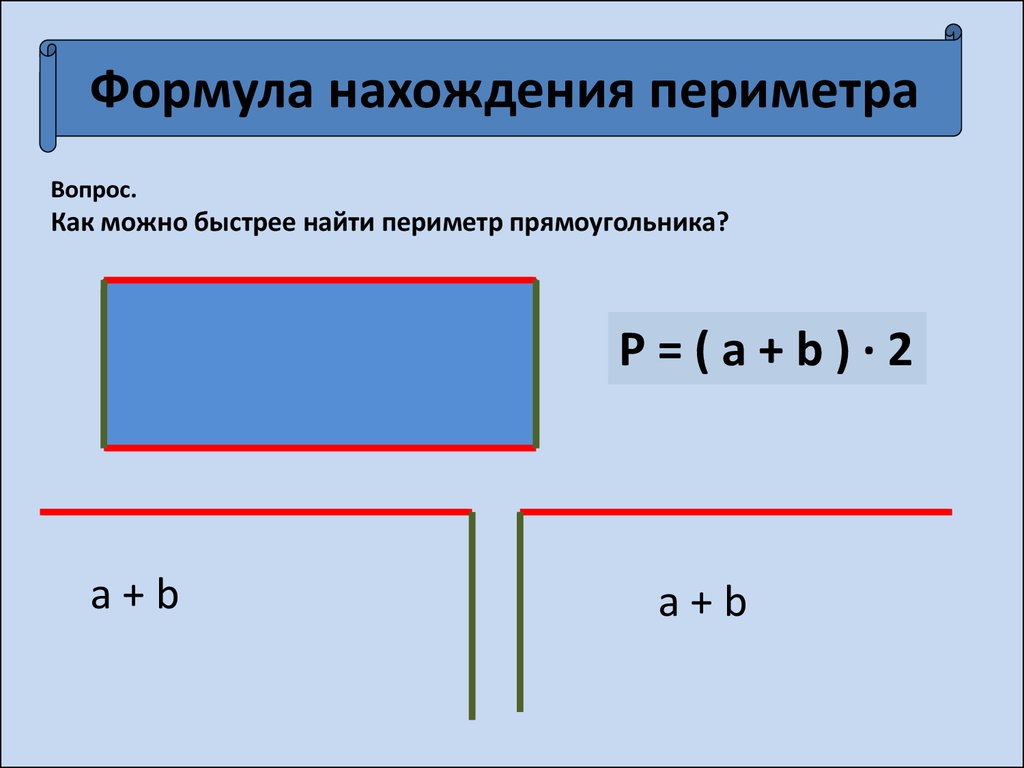
Ну вот, принц и научился находить периметр прямоугольника. У него получилась замечательная рамка для портрета принцессы, он уже сделал плинтуса в зале и очень скоро сделает новую ограду. А вы, ребята запомнили, как находить периметр прямоугольника? Выучите эти формулы и всегда пользуйтесь ими.
Предыдущий урок 19 Составные задачи на разностное и кратное сравнение
Следующий урок 21 Задачи на нахождение четвертого пропорционального (приведение к единице)
Получите полный комплект видеоуроков, тестов и презентаций Решение текстовых задач по математике 1-4 классы
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Периметр прямоугольника — ChiliMath
Периметр прямоугольника равен расстоянию вокруг прямоугольника .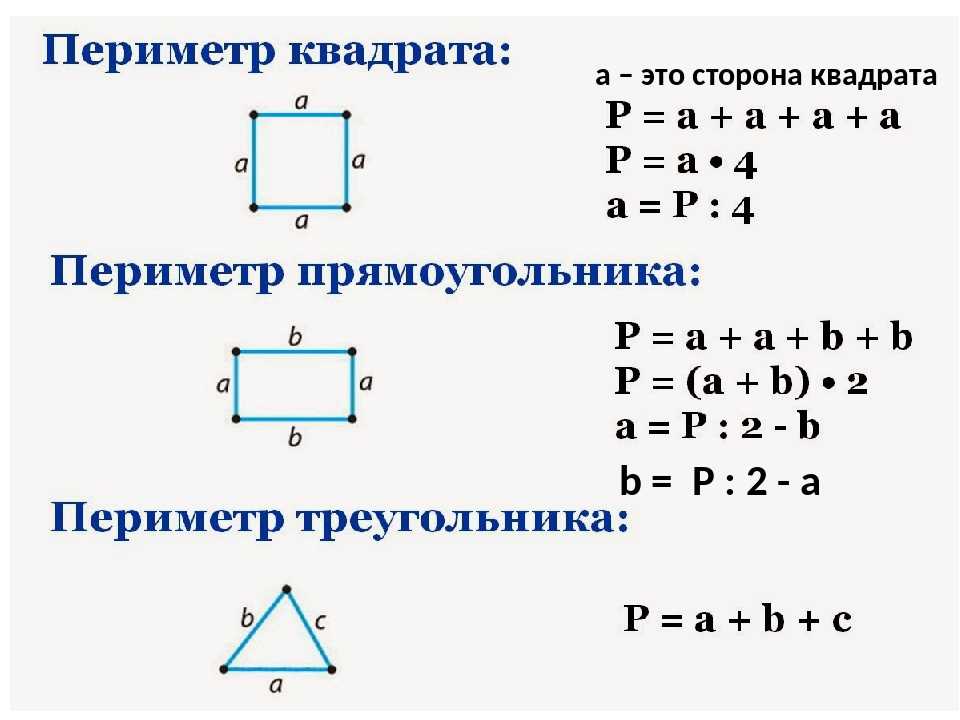
Периметром прямоугольного цветника считается длина забора, окружающего сад. Мы вычисляем периметр прямоугольника, получив сумму всех его сторон.
Как известно, у прямоугольника четыре стороны и четыре прямых угла. Однако по сравнению с квадратом не все его стороны равны. Две пары противоположных сторон прямоугольника имеют равные размеры. То есть длина одной стороны равна длине другой стороны, а ширина одной стороны равна ширине другой стороны.
Примечание. Количество делений указывает на конгруэнтность сторон. Также помните, что длина (l) — самая длинная сторона, а ширина (w) — самая короткая.
Мы находим периметр прямоугольника, складывая все измерения его сторон. Если мы запишем это уравнением, оно будет выглядеть так:
P = l + w + l + w
где P обозначает периметр, l длину и w ширину
Однако, поскольку противоположные стороны прямоугольники конгруэнтны, уравнение можно просто записать как P = 2l + 2w.
Как вы могли заметить, длина и ширина в формуле умножаются на два, а затем складываются вместе, а не записываются дважды.
Примеры нахождения периметра прямоугольника
Нет лучшего способа попрактиковаться в использовании этой формулы и узнать больше о периметре прямоугольника, чем рассмотреть несколько примеров. Хорошо, начнем!
Пример 1 : Найдите периметр прямоугольника.
Прямоугольник выше имеет длина 16 км и ширина 11 км . Несмотря на то, что нам не известны размеры всех четырех сторон, мы знаем, что две другие стороны также имеют размеры 16 км и 11 км соответственно. Как? Потому что противоположные стороны прямоугольника равны. Другими словами, нам нужно знать только длину и ширину, чтобы вычислить периметр прямоугольника.
Теперь воспользуемся формулой для периметра прямоугольника и подставим 16 вместо L и 11 вместо W.
периметр прямоугольника равен 54 км .
Пример 2 : Какой длины прямоугольник ниже, если его периметр равен 154 футам , а его ширина равна 25 футам ?
Иногда возникает проблема, связанная с отсутствием одного из измерений.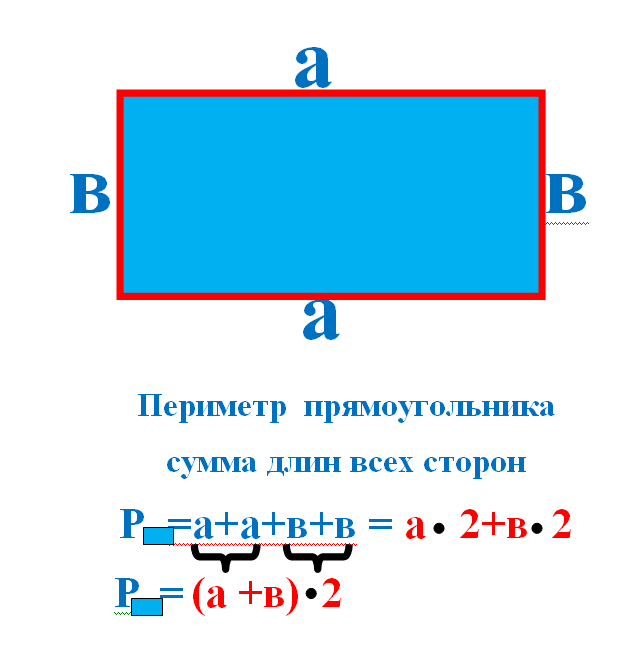
В этой задаче нас просят найти длину прямоугольника, а не вычислять его периметр. Найти недостающую длину или ширину легко, если у вас есть измерение одного из измерений и периметра прямоугольника.
Чтобы найти недостающую длину, все, что нам нужно сделать, это использовать формулу периметра прямоугольника, заменить P на 154 и W на 25, а затем найти L.
Отлично! Длина прямоугольника 52 фута. Однако, прежде чем мы завершим эту задачу, давайте убедимся, что наши длина и ширина действительно дадут нам периметр 154 фута. Снова используя формулу, мы имеем
P = 2L + 2W
154 = 2\влево( {52} \вправо) + 2\влево( {25} \вправо)
154 = 104 + 50
154 = 154
И да, это так! Следовательно, длина прямоугольника равна 52 футам .
Пример 3 : Если длина и ширина прямоугольника ниже уменьшены на 4 дюйма , найдите периметр нового прямоугольника.
В этом примере нас просят уменьшить размеры нашего исходного прямоугольника на 4 дюйма, затем, используя эти новые размеры, мы найдем периметр нового прямоугольника.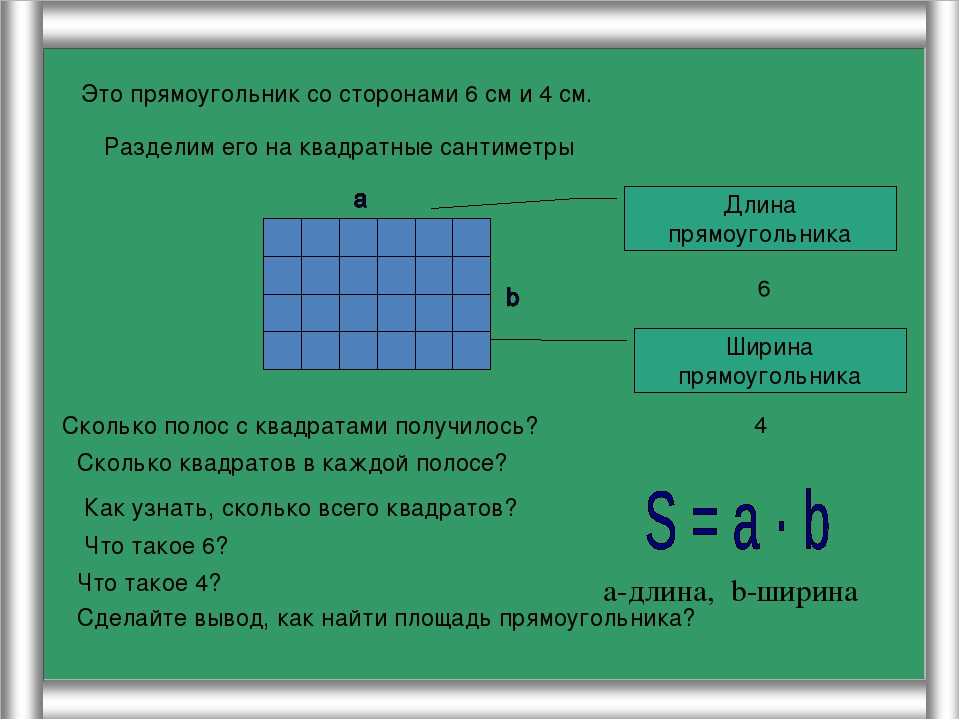
Шаг 1 : Уменьшите длину и ширину исходного (текущего) прямоугольника на 4 дюйма.
- Длина:
L = 37 \ Color {RED} {- 4}
L = 33
- Ширить:
W = 14 \ Color {Red} {-4}
Вт =
W = 10
Мы получили размеры нового прямоугольника. Длина теперь составляет 33 дюйма, а новая ширина — 10 дюймов.
Шаг 2 : Вычислите периметр нового прямоугольника, используя новые длину и ширину.
- Подставьте 33 вместо L и 10 вместо W в формулу периметра прямоугольника.
Вот оно! Периметр для нашего нового прямоугольника равен 86 дюймам .
Пример 4 : длина прямоугольника в раз больше его ширины . Каков периметр прямоугольника с шириной 6,8 см ?
Прежде чем приступать к каким-либо вычислениям, давайте сначала определим и интерпретируем фрагменты информации, данные нам в задаче.
- Ширина (Ш): 6,8\,см
- Длина (Д): Двойная ширина → 6,8\влево(2\вправо) = {13,6\,см}
3 Теперь мы есть наши длина и ширина, мы можем действовать как обычно, чтобы найти периметр прямоугольника.
Периметр прямоугольника равен 40,8 см .
Пример 5: У нашего соседа есть прямоугольный бассейн длиной 36 футов . Если периметр пула составляет 108 футов , какой ширины бассейн?
В этой задаче отсутствует одно из измерений, как и в одном из наших предыдущих примеров. В этом случае измерение ширины бассейна неизвестно. Чтобы получить лучшее представление о проблеме, давайте сначала нарисуем ее, используя предоставленную нам информацию.
Теперь найдем ширину по формуле периметра прямоугольника.
Я оставляю на ваше усмотрение проверить, действительно ли наши длина и ширина дадут нам периметр в 108 футов.
Бассейн нашего соседа 18 футов шириной .
Пример 6 : Саманта хочет поместить рамку вокруг своей фотографии с кошкой. Изображение 14 дюймов на 18 дюймов . Сколько границ нужно Саманте?
Начнем снова с определения доступных нам частей информации.
Вот размеры фотографии Саманты.
Длина :
Д = 18 дюймов.
Ширина :
Вт = 14 дюймов.
Поскольку она хочет обвести прямоугольную картинку рамкой, мы сразу понимаем, что имеем дело с задачей, связанной с периметром прямоугольника. Чтобы узнать, сколько границ ей нужно, нам нужно просто применить формулу для нахождения периметра прямоугольника.
Прекрасно! Саманте нужно 64 дюйма рамки , чтобы обклеить ее фотографию с кошкой.
Вас также может заинтересовать:
Периметр прямоугольника Словесные задачи
Площадь прямоугольника
Периметр квадрата
Площадь прямоугольника — Как рассчитать площадь и периметр прямоугольника?
Геометрия — одна из самых важных тем математики, которая касается различных форм, таких как квадрат, прямоугольник и т.
д. Она также помогает нам понять различные свойства этих фигур. Затем эти фигуры используются для решения задач по различным темам, таким как тригонометрия, алгебра, исчисление и т. д. В этом блоге мы собираемся исследовать форму прямоугольника. Мы будем изучать, как найти площадь прямоугольника и вычислить периметр прямоугольника. Но сначала давайте начнем с некоторых основных понятий.
Что такое прямоугольник?
Прямоугольник – это двухмерная геометрическая фигура, имеющая четыре стороны и четыре вершины или угла. Противоположные стороны прямоугольника имеют одинаковую длину и параллельны друг другу, т. е. все точки равноудалены. Стороны прямоугольника пересекаются друг с другом, образуя прямой угол. Две стороны, которые длиннее, известны как длина прямоугольника, а более короткая сторона — это ширина прямоугольника.
Слово «прямоугольник» происходит от латинского слова «rectangulus», что означает прямой угол. Прямоугольник — одна из самых простых форм для изучения, но вопросы, связанные с прямоугольником в таких понятиях, как тригонометрия и исчисление, могут быть немного сложными.
Следовательно, жизненно важно иметь прочные основы. С помощью онлайн-курсов Cuemath вы можете изучать различные геометрические фигуры с помощью визуальных симуляций, которые позволят вам в будущем решать сложные задачи, связанные с прямоугольниками.
Периметр прямоугольника
Периметр прямоугольника можно определить как сумму всех четырех сторон прямоугольника. Так как противоположные стороны прямоугольника равны, периметр прямоугольника равен удвоенной длине прямоугольника плюс удвоенной ширине прямоугольника.
Предположим, что p — периметр прямоугольника, l — длина, а b — ширина, тогда периметр можно представить в виде уравнения:
P = 2l+2b = 2 (l+b)
Следовательно, уравнение 2 (l+b) представляет периметр, где и b представляет длину и ширину прямоугольника соответственно.
Как найти периметр прямоугольника?
Чтобы найти периметр прямоугольника, нам нужно измерить стороны прямоугольника. После того, как вы измерили все стороны, пришло время сложить их.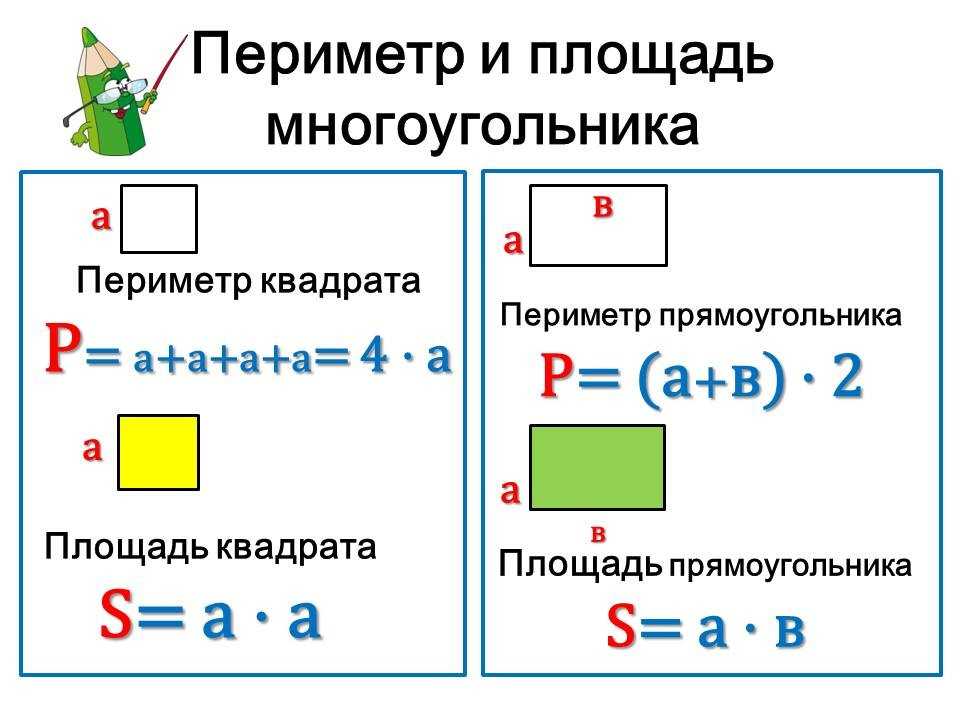
Сложив все стороны, мы получим сумму периметра прямоугольника.
Например, прямоугольник длиной 15 см и шириной 10 см, мы можем применить формулу 2 (l + b), мы получим 2 (15 + 10), т.е. 2 (25) = 50. Следовательно, периметр этого прямоугольника равен 50см.
Площадь прямоугольника
Пространство, занимаемое прямоугольником в 2D-пространстве, называется площадью этого конкретного прямоугольника. Он определяется как произведение длины и ширины прямоугольника. Следовательно, формула площади прямоугольника определяется как A = l*b. Площадь прямоугольника всегда измеряется в квадратных единицах.
Шаги для нахождения площади прямоугольника
Помимо площади прямоугольника, площадь параллелограмма можно вычислить, используя его основание и высоту. Умножьте основание и высоту или используйте площадь калькулятора параллелограмма.
Шаг 1: Прежде чем начать, преобразуйте размеры длины и ширины из данных. У них должны быть одинаковые единицы измерения.