Что значит пропорциональные стороны – 4. — : . 9

📌 ПРОПОРЦИОНАЛЬНЫЙ — это… 🎓 Что такое ПРОПОРЦИОНАЛЬНЫЙ?



ПРОПОРЦИОНАЛЬНЫЙ

ПРОПОРЦИОНАЛЬНЫЙ

(лат. proportionalis — от proportio — отношение, сходство, пропорция). Соразмерный, правомерный.

Словарь иностранных слов, вошедших в состав русского языка.- Чудинов А.Н., 1910.

ПРОПОРЦИОНАЛЬНЫЙ

лат. propotiornalis, от proportio, пропорция. Соразмерный.

Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней.- Михельсон А.Д., 1865.

ПРОПОРЦИОНАЛЬНЫЙ

соразмерный.

Полный словарь иностранных слов, вошедших в употребление в русском языке.- Попов М., 1907.

пропорциона́льный

(лат. proportlona-lis) имеющий правильное соотношение частей с целым, соразмерный, соответственный, находящийся в определенном отношении к какой-л. величине; п-ое деление — деление данной величины на части, пропорциональные заданным числам; прямо п-ые (или п-ые) величины — величины, связанные между собой прямой пропорциональностью, обратно п-ые величины — величины, связанные между собой обратной пропорциональностью; п. налог — налог, взимаемый в соответствии с размером дохода; п-ая избирательная система — система избирательного права в буржуазных странах, при которой голосование за кандидатов производится по партийным спискам, причем каждый список получает количество мест соразмерно (пропорционально) числу поданных за него голосов

ср. мажоритарная избирательная система).

Новый словарь иностранных слов.- by EdwART, , 2009.

пропорциональный

пропорциональная, пропорциональное; пропорционален, пропорциональна, пропорционально [лат. proporcionalis – соразмерный] (книжн.). 1. Обладающий соразмерностью частей. 2. Такой, который с увеличением или уменьшением одной величины соотносительно увеличивается или уменьшается во столько же раз (мат.). Прямо пропорциональные – такие, при которых увеличение (или уменьшение) одного вызывает увеличение (или уменьшение) другого (мат., науч.), обратно пропорциональные величины – такие, при которых увеличение одного вызывает уменьшение другого и наоборот (мат. науч.). Пропорциональное деление (деление данной величины на части, пропорциональные заданным числам). || Находящийся в определенных соотношениях, в определенном количественном соответствии с чем-н. Пропорциональное обложение, пропорциональный налог (обложение всех доходов в одинаковом проценте, независимо от их величины, в противоп. прогрессивному; экон.). Пропорциональные выборы, пропорциональная избирательная система (система, при которой голосуют за списки, и количество избранных из списка соответствует количеству поданных за список голосов; полит.). Пропорциональный циркуль (циркуль, употр. при увеличении или уменьшении чертежей в определенном масштабе; спец.).

Большой словарь иностранных слов.- Издательство «ИДДК», 2007.

пропорциональный

ая, ое, лен, льна (нем. proportional лат. prōportiōnālis соразмерный).
1. мат. О соотношении величин: такой, при котором увеличение одной из них влечет за собой изменение другой во столько же раз. Прямо пропорциональный (возрастающий по мере увеличения другой величины).

Обратно пропорциональный (уменьшающийся по мере увеличения другой величины).
2. Находящийся в определенном количественном соотношении, соответствии с чем-н. Пропорциональное представительство в парламенте.
3. Обладающий правильными пропорциями, соразмерный. Пропорциональное телосложение.
Пропорциональность — свойство пропорционального 1-3.

Толковый словарь иностранных слов Л. П. Крысина.- М: Русский язык, 1998.

.

Синонимы:

• ПРОПОРЦИОНАЛЬНЫЕ ВЕЛИЧИНЫ
• ПРОПОРЦИОНАЛЬНЫЙ НАЛОГ

Смотреть что такое «ПРОПОРЦИОНАЛЬНЫЙ» в других словарях:

• пропорциональный — См. стройный… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. пропорциональный соразмерный, соизмеримый; подходящий, стройный; гармоничный, нормальный, аналогический, рациональный,… …   Словарь синонимов

• ПРОПОРЦИОНАЛЬНЫЙ — ПРОПОРЦИОНАЛЬНЫЙ, пропорциональная, пропорциональное; пропорционален, пропорциональна, пропорционально (лат. proporcionalis соразмерный) (книжн.). 1. Обладающий соразмерностью частей. Пропорциональное телосложение. 2. Такой, который с увеличением …   Толковый словарь Ушакова

• ПРОПОРЦИОНАЛЬНЫЙ — ПРОПОРЦИОНАЛЬНЫЙ, ая, ое; лен, льна. 1. В математике: находящийся в отношениях пропорциональности (во 2 знач.). Пропорциональные величины. 2. Находящийся в определённом количественном соотношении, соответствии с чем н. Пропорциональная… …   Толковый словарь Ожегова

• пропорциональный — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN proportional …   Справочник технического переводчика

• пропорциональный —    1) мат. находящийся в отношениях пропорциональности;    2) находящийся в определенном количественном отношении, соответствии с чем н.;    3) обладающий правильными пропорциями.    ► лат. proportionalis «соразмерный». Заимств., вероятно, из… …   Историко-этимологический словарь латинских заимствований

• Пропорциональный — прил. 1. Обладающий правильными пропорциями [пропорция I 2.]; соразмерный. 2. Находящийся в определенном количественном соотношении с чем либо. отт. Основанный на соблюдении пропорций [пропорция I 2.] между чем либо. 3. Такой, который с… …   Современный толковый словарь русского языка Ефремовой

• пропорциональный — пропорциональный, пропорциональная, пропорциональное, пропорциональные, пропорционального, пропорциональной, пропорционального, пропорциональных, пропорциональному, пропорциональной, пропорциональному, пропорциональным, пропорциональный,… …   Формы слов

• пропорциональный — чему. [У Пушкина] было небольшое лицо и прекрасная, пропорциональная лицу, голова, с негустыми кудрявыми волосами (Гончаров) …   Словарь управления

• пропорциональный — пропорцион альный; кратк. форма лен, льна …   Русский орфографический словарь

• пропорциональный —   соразмерный, находящийся в определенном соотношении с какой нибудь величиной …   Справочный коммерческий словарь

Книги

• Мой прекрасный сад № 03/2019, , «Мой прекрасный сад» – российское издание самого популярного в Европе журнала по декоративному садоводству для садоводов-любителей и владельцев загородных домов, дач и вилл. Центральные темы… Категория: Хобби, Ремесла Серия: Журнал «Мой прекрасный сад» 2019 Издатель: Бурда, Подробнее  Купить за 33.6 руб электронная книга (fb2, fb3, epub, mobi, pdf, html, pdb, lit, doc, rtf, txt)
• Какое питание выбрать для грудничка?, Алексей Мичман, Самый идеальный продукт питания для ребенка от природы – материнское грудное молоко, с которым организм малыша получает все необходимые питательные вещества и элементы, защиту от заболеваний… Категория: Справочники Издатель: Издательские решения, Подробнее  Купить за 6 руб электронная книга (fb2, fb3, epub, mobi, pdf, html, pdb, lit, doc, rtf, txt)

Другие книги по запросу «ПРОПОРЦИОНАЛЬНЫЙ» >>

dic.academic.ru

Что означает слово пропорционально в геометрии и алгебре?

произведение числителя первой дроби и знаменателя второй дроби равно произведению знаменателя первой дроби и числителя второй дроби

в каких то пропорциях. т. е. в пропрции 2 к 3. Первая сторона будет 2 а вторая 3. или первая сторона будет 4 а другая 6. или 12 и 18.

Пропорционально — это соответственно.

соответствено

touch.otvet.mail.ru

📌 Пропорциональность — это… 🎓 Что такое Пропорциональность?

Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.

[1].

Пример

Масса керосина пропорциональна его объёму: 2 л керосина имеют массу 1,6 кг, 5 л имеют массу 4 кг, 7 л имеют массу 5,6 кг. Отношение массы к объёму всегда будет равно плотности:

1,6 / 2 = 0,8;

4 / 5 = 0,8;

5,6 / 7 = 0,8 и т. д.

Коэффициент пропорциональности

Неизменное отношение пропорциональных величин называется коэффициентом пропорциональности. Коэффициент пропорциональности показывает, сколько единиц одной величины приходится на единицу другой^[1].

Символ

Математический символ ‘∝’ используется для указания пропорциональности двух величин. Пример, A ∝ B.

В юникоде для отображения используется символ U+221D.

Прямая пропорциональность

Прямая пропорциональность — функциональная зависимость, при которой некоторая величина зависит от другой величины таким образом, что их отношение остаётся постоянным. Иначе говоря, эти переменные изменяются пропорционально, в равных долях, то есть, если аргумент изменился в два раза в каком-либо направлении, то и функция изменяется тоже в два раза в том же направлении.

Математически прямая пропорциональность записывается в виде формулы:

Графиком прямой пропорциональности является прямая линия, проходящая через начало координат.

Обратная пропорциональность

Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины(аргумента) вызывает пропорциональное уменьшение зависимой величины(функции).

Свойства функции:

См. также

Источники

1. ↑ ^{1 2} М. Я. Выгодский «Справочник по элементарной математике», М., 1974

dic.academic.ru

пропорциональность чисел

1. Число 45 пропорционально числам 4, 5 и 6. Если в задаче есть такие слова «пропорционально числам 4, 5 и 6″, то всегда обозначают одну часть через х. Тогда число 45=4х+5х+6х. Упрощаем: 15х=45, отсюда х=3. Меньшее число содержит 4х, значит, оно равно 4·3=12. 

2. Требуется решить уравнение |4-x|=1,5. Идем от определения модуля числа:  модуль неотрицательного числа равен самому этому числу, модуль отрицательного числа равен числу противоположному. Под знаком модуля могло быть как положительное число, так и отрицательное. Так и запишем:

4-х=1,5 или 4-х=-1,5;

-х=1,5-4;         -х=-1,5-4.

-х=-2,2;           -х=-5,5.

х=2,2;               х=5,5. 

3. Итак, автомобилист, выехавший из пункта А через полчаса после  мотоциклиста, догнал его. Спрашивают, на каком расстоянии от А, если скорость мотоциклиста 48,4 км/ч, а скорость автомобиля больше скорости мотоцикла в

4. Отметим на числовой прямой «пустыми» точками -2 и 3. Решаем неравенство методом интервалов. Проверим знак дроби при х=10, подставив значение 10.  Расставим знаки на промежутках. Так как у нас неравенство больше нуля, то выбираем промежуток знака «+».

5. Упростим данное выражение cos(30°+α)-cos(30°-α), используя формулу разности косинусов двух углов. Получим минус удвоенное произведение синуса полусуммы на синус полуразности: cos(30°+α)-cos(30°-α)=-2sin30°sinα=-sinα.

6. Нам дано однородное линейное уравнение. Решают его делением обеих частей равенства на косинус данного аргумента. В результате получают простейшее уравнение с тангенсом.

7. Известны девятый член (a₉=12)  и разность (d=1,5) арифметической прогрессии.

Требуется найти первый член a₁ данной арифметической прогрессии. Применим формулу n-го члена арифметической прогрессии: a_n=a₁+(n-1)d. Подставим в нее наши данные и получим: a₉=a₁+8d;

12=a₁+8∙1,5;

12+a₁=12 →  a₁=0.

8.  Площадь фигуры, ограниченной данными линиями y=x², y=0, x=2, найдем с помощью определенного интеграла. Искомая площадь будет равна определенному интегралу от нуля до двух функции икс в квадрате по дэ икс. Если вам это понятно — значит, вы представляете себе графики данных линий  и так и должно быть! Если непонятно — строим графики и вспоминаем формулу площади криволинейной трапеции, ограниченной сверху графиком функции y=f(x), а слева и справа — прямыми х=a, x=b.

9. По условию внешний угол при вершине А треугольника АВС в два раза больше одного из несмежных углов треугольника, а по определению, внешний  угол треугольника равен сумме двух внутренних углов, не смежных с ним. Получается, что эти несмежные углы равны между собой. Отсюда следует, что данный треугольник является равнобедренным с вершиной А. И если мы проведем медиану из вершины А, то она будет являться и высотой и биссектрисой.

10. Найдем корень данного уравнения и подставим его значение в выражение (-13х+2)²+х.

11. Дано уравнение (100x)^lgx=x³. Требуется найти сумму его корней. Так как и основание и показатель степени содержат переменную, то решение уравнения начинаем с логарифмирования обеих частей равенства по основанию 10 (у нас ведь десятичный логарифм).

lg(100x)^lgx=lgx³; логарифм степени равен произведению показателя этой степени на логарифм основания:

lgx∙lg(100x)=3lgx. Перенесем 3lgx в левую часть равенства и вынесем lgx за скобки: lgx∙lg(100x)-3lgx =0;

lgx∙(lg(100x)-3)=0. Каждый из множителей может быть равен нулю. Если lgx=0,  то x=10⁰=1.  Если  lg(100x)-3=0, то lg(100x)=3, откуда 100x=10³; 100x=1000; x=10. Сумма квадратов корней: 1²+10²=1+100=101.

12.  Упростим данную систему уравнений, освободившись от знака логарифма во 2-ом уравнении.

log₅(2y+10x+3)=2 → 2y+10x+3=5² → 2y+10x+3=25;  10x+2y=22. Выразим 2х из первого уравнения: 2х=20-3у. Подставим это значение во 2-ое уравнение, имея ввиду, что 10х=5∙2х. Тогда вместо 10x+2y=22 запишем:

5∙(20-3у)+2у=22. Упростим: 100-15у+2у=22 или -13у=-78, откуда у=6. Подставляем это значение в выражение 2х=20-3у. Получаем:

2х=20-3∙6=2. Тогда х=1. Решением системы служит пара значений переменных: (1; 6).

13. Возведем обе части равенства в квадрат. Получаем: x-5=a² → x=a²+5.

14. Область определения функции — это множество таких значений х, при которых выражение в правой части равенства имеет смысл. Так как у нас дробь, то знаменатель ее должен быть отличен от нуля, т.е. x+3x²≠0. Приравняем знаменатель к нулю, решим уравнение, а затем исключим корни этого уравнения.

15. Требуется найти производную сложной функции y=(lnx)². Итак, мы имеем степень, значит, берем производную по формуле производной степени. Далее: основание этой степени — натуральный логарифм, — берем производную  от натурального логарифма и умножаем производную степени на производную натурального логарифма.

16.  Стороны треугольника ВА=14 см и ВС=17 см, а косинус угла В между ними равен (-8/17). Нужно найти площадь треугольника. Мы знаем формулу площади треугольника по двум сторонам и углу между ними: S=(1/2)ac·sinβ. Зная косинус угла В, вычислим синус этого угла, используя основное тригонометрическое тождество sin²β + cos²β=1, и подставим в формулу площади.

17. Дан равносторонний треугольник. Точка, равноудаленная от сторон треугольника на 5 см, от плоскости отстоит на 3 см. Нужно найти площадь этого треугольника.

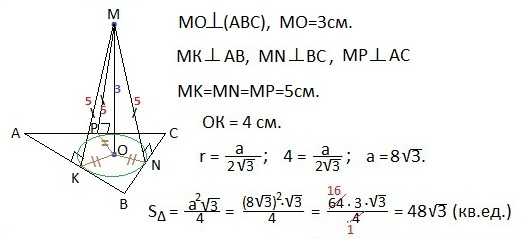
Смотрите видео решение.

18. Основания призмы — правильные треугольники со стороной 6 см. Требуется найти объем призмы, если ее боковое ребро равно Решение. Применяем формулу объема призмы: V=S_осн.∙H, где S_осн. – площадь основания призмы, значит, в нашей задаче, площадь правильного треугольника со стороной 6 см. H – высота призмы, а так как у нас призма  прямая, то в качестве высоты можно взять длину бокового ребра.

19. Чтобы найти координаты точек пересечения окружности x²+y²-10x-6y+9=0 с осью абсцисс, подставим у=0, так как точки, лежащие на оси Ох имеют ординату, равную нулю, и решим получившееся квадратное уравнение х²-10х+9=0. Подбираем корни по теореме Виета: х₁=1, х₂=9. Искомые точки пересечения: (1; 0) и (9; 0).

 20.  Разложим числитель первой дроби по формуле разности кубов двух выражений a³-b³=(a-b)(a²+ab+b²). У нас а⁶-64=(а²)³-4³=(а²-4)(а⁴+4а²+16). В знаменателе первой дроби такое же выражение, как во вторых скобках разложения. Сокращаем. Остается а²-4. Преобразуем вторую дробь. Числитель второй дроби разложим по формуле разности квадратов двух выражений а²-b²=(a-b)(a+b). У нас а⁴-16=(а²)²-4²=(а²-4)(а²+4). Сократим вторую дробь на (а²+4), останется: а²-4. Имеем: а²-4+ а²-4=2а²-8.

21. Чтобы найти значение данного выражения, выразим а из предложенного равенства (из пропорции): 3(a+b)=2(a-2b). Раскрываем скобки: 3a+3b=2a-4b → a=-7b. Теперь подставим вместо а в данное выражение значение (-7b) и упростим.

22. Представим единицу в правой части неравенства в виде логарифма по основанию (2х+1). При потенцировании будем учитывать, что от значения основания логарифма (2х+1) будет зависеть, возрастает функция (если 2х+1>1) или убывает (если 0<2x+1<1). Если функция возрастает, то знак неравенства сохраним, если функция убывает, то знак неравенства поменяем на противоположный. Кроме этого, учтем, что под знаком логарифма могут быть только положительные числа.

23. Упростим предложенное неравенство: sinx+cos2x>1. Есть формула: 1-cos2α=2sin²α. Перепишем данное неравенство в виде:

sinx-(1-cos2x)>0. Применим формулу и получим: sinx-2sin²x>0. Сделаем замену переменной. Пусть sinx=y. Тогда: y-2y²>0 → y(1-2y)>0. Решим полученное неравенство методом интервалов.

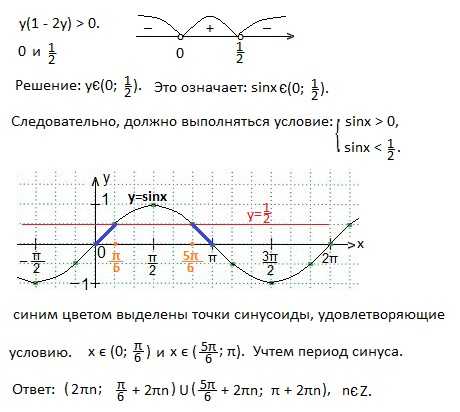
24. Дана функция  f(x)=6x²-4x+1. Известно, что F(x) является первообразной для f(x), причем, F(-1)=2. Требуется найти F(1). Для этого запишем F(x) для данной функции, найдем значение постоянной величины С, а затем искомое значение F(1).

Находим значение С, используя равенство: F(-1)=2.

2=2∙(-1)³-2∙(-1)²-1+С;

2=-2-2-1+C → C=7. Тогда первообразная F(x)=2x³-2x²+x+7. Подставим вместо х число 1 и получим: F(1)=2-2+1+7=8.

25. Пусть в актовом зале х скамеек. Если на каждую скамейку посадить по 5 учеников, то четверо останутся без места, значит, всего 5х+4 учащихся. Если на каждую скамью посадить по 6 детей, то 2 места останутся свободными. Получается 6х-2 учащихся. Но учащихся определенное количество — имеем равенство: 5х+4=6х-2. Отсюда х=6. Следовательно, в зале 6 скамеек, а учеников 5·6+4=34.

test-training.ru

Как понимать слова «пропорционально» «прямо пропорционально»?

Прямо пропорционально&lt;-&gt;обратно пропорционально. Пропорциональность-это соотношение одного к другому. В вашем случае имеется в виду, что чем БОЛЬШЕ шума, тем МЕНЬШЕ реальная стоимость-это обратная пропорциональность. А прямая пропорциональность-это, например, ДАЛЬШЕ в лес-БОЛЬШЕ дров. Прямая пропорциональность-это когда вследствие роста первого показателя возрастает второй. Обратная-когда вследствие роста первого показателя, второй уменьшается или когда вследствие уменьшения первого показателя, второй возрастает.

Слово «пропорционально» означает «зависит». «Обратно пропорционально» означает: с увеличением аргумента функция уменьшается. Соответственно, «Прямо пропорционально» означает, что с увеличением аргумента функция увеличивается.

Это термины вообще-то математические, к разделу «Литература» не имеют никакого отношения. В данном контексте это выражение означает, что у широко рекламируемых товаров настоящая цена гораздо меньше, чем та, по которой его продают.

touch.otvet.mail.ru

Что означает «прямо пропорционален», «обратно пропорционален»??

прямо — увеличивается одно, увеличивается и другое обратно — при увеличении одного, второе умньшается.

чем больше одно, тем болше другое -прямопропорционален чем больше одно, тем меньше другое — обратнопропорционален

прямая зависимость и обратная. например а=В/С а напрямую зависит от b. и обратно от c. тут никак по другому и не скажешь

Пример Урожай прямо пропорционален Погоде: хорошая погода, хороший урожай или наоборот, плохая погода, плоххой урожай Сила электрического удара обратно пропорциональна вероятности выжить после такого удара: чем выше сила удара, тем меньше шансов выжить, чем ниже сила удара, тем больше шансов выжить.. . Как объяснить еще доступней я хз))

неправильный ответ «чем больше одно, тем болше другое» Этого недостаточно Правльно так А прямо пропорционально В если при увеличении В в какое-то чило раз А увеличится в то же чило раз А = к*В Пройденный путь прямо проворционален скорости А обратно пропорционально В если при увеличении В в какое-то чило раз А уменьшится в то же чило раз А = к/В Пример. Затраченное время обратно пропорционально скорости

К ответу Alexey Glazov А если k &lt; 0 ? То в случае прямой пропорциональности увеличение В приведет к уменьшению А ! Пример: А = -5 * В при В = 2, А = — 5 * 2 = -10 увеличиваем В в 3 раза, т. е. В = 6, тогда А = — 5 * 6 = — 30. Результат: А стало в 3 раза меньше, ведь -30 &lt; -10. В случае обратной пропорциональности та же картина. Здесь правильно будет говорить об изменении модулей чисел А и В. Тогда всё будет верно при любых k не равных 0.

Прямо пропорционально, это когда наливают жидкость в два сосуда равномерно. I=U (какое кол-во жидкости в первом сосуде, такое и во втором). Обратно пропорционально, это когда жидкость из полного сосуда переливают в пустой сосуд — ровно на столько, на сколько пустой наполняется, полный опустошается. U\R (чем меньше сопротивление, тем больше сила тока, и наоборот).

Те, кто вот такую ху. ню написал. «В = 2, А = — 5 * 2 = -10 бла бла бла…» Чё вы несёте. Придурки сука! Из-за таких как вы, человек и простого объяснения знать не будет. В школе вечно втирали какую то херню «а+b и всё в квадрате… » Здесь тоже вы. Ботаны не добитые.

touch.otvet.mail.ru

Обратно пропорциональная зависимость | Математика

Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз. Соответственно, при уменьшении одной из них в несколько раз другая увеличивается во столько же раз.

Зависимость между такими величинами — обратно пропорциональная зависимость. Примеры обратной пропорциональной зависимости:

1)  время, затраченное на прохождение определенного пути, и скорость, с которой этот путь был пройден — обратно пропорциональные величины;

2) при одинаковой производительности труда количество рабочих, выполняющих определенную работу, обратно пропорционально  времени выполнения этой работы;

3) количество товара, купленного на определенную сумму денег,  обратно пропорционально его цене.

Чтобы отличить обратно пропорциональную зависимость от прямой, можно использовать пословицу: «Тише едешь — дальше будешь».

Задачи на обратно пропорциональные величины удобно решать с помощью пропорции.

Рассмотрим примеры задач на обратно пропорциональную зависимость.

1) 24 человека за 5 дней пропололи участок. За сколько дней выполнит ту же работу 30 человек, если будут работать с той же производительностью?

(Рассуждаем так:

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы. Значит, это — обратно пропорциональная зависимость.

3. Поэтому вторая стрелка имеет противоположное направление).

Решение:

Пусть за х дней могут прополоть участок 30 человек. Составляем пропорцию (в направлении от начала стрелки к ее концу):

   

Чтобы найти неизвестный крайний член пропорции, надо произведение средних членов разделить на известный крайний член:

   

24 и 30  сокращаем на 6, 5 и 5 — на 5:

   

Значит, 30 человек выполнят эту работу за 4 дня.

Ответ: за 4 дня.

2) Для перевозки груза автомашине грузоподъемностью 7,5 тонн пришлось сделать 12 рейсов. Сколько рейсов понадобится сделать автомашине грузоподъемностью 9 тонн для перевозки этого же груза?

(1. В заполненном столбце ставим стрелку в направлении от большего числа к меньшему.

2. Чем больше грузоподъемность машины, тем меньше рейсов ей нужно сделать, чтобы перевезти груз. Значит, это — обратно пропорциональная зависимость.

3. Поэтому вторая стрелка имеет противоположное направление).

Решение:

Пусть х рейсов потребуется машине грузоподъемностью 9 тонн, чтобы перевезти груз. Составляем пропорцию (от начала стрелки к ее концу):

   

   

   

Значит, понадобится 10 рейсов.

Ответ: 10 рейсов.

www.for6cl.uznateshe.ru