Числовые неравенства и их свойства. Сложение и умножение числовых неравенств 8 класс онлайн-подготовка на Ростелеком
Тема 8: Неравенства
- Видео
- Тренажер
- Теория
Заметили ошибку?
Числовые неравенства и их свойства. Сложение и умножение числовых неравенств.
Мы можем сравнить любые числа а и b и результат сравнения записать в виде равенства или неравенства, используя знаки =, <, >. Для произвольных чисел а и b выполняется одно и только одно из соотношений: a=b, a<b, a>b.
Пример 1. Сравним обыкновенные дроби 58 и 47.
Для этого приведем их к общему знаменателю: 58=3556; 47=3256.
Так как 35>32, то 58>47.
Пример 2. Сравним десятичные дроби 3,6748 и 3,675.
Цифры в разрядах единиц, десятых и сотых совпадают, а в разряде тысячных в первой дроби стоит цифра 4, а во второй – цифра 5. Так как 4<5, то 3,6748<3,675.
Пример 3. Сравним обыкновенную дробь 920 и десятичную дробь 0,45. Обратив дробь 920 в десятичную, получим, что 920=0,45.
Пример 4. Сравним отрицательные числа -15 и -23. Модуль первого числа меньше модуля второго. Значит, первое число больше второго, -15>-23.
В зависимости от вида числа мы использовали тот или иной способ сравнения. Но есть универсальный способ сравнения, который охватывает все случаи.
Число а больше числа b, если разность а-b – положительное число; число а меньше числа b, если разность a-b – отрицательное число. Если разность а-b = 0, то числа а и b равны.
На координатной прямой большее число изображается точкой, лежащей правее, а меньшее – точкой, лежащей левее.
Рассмотрим некоторые свойства числовых неравенств.
-
Если a>b, то b<a, если a<b, то b>a.
Действительно, если разность a-b – положительное число, то разность b-a – отрицательное число, и наоборот.

-
Если a<b и b<c, то а<c.
Докажем, что разность а-с – отрицательное число. Прибавим к этой разности числа b и –b и сгруппируем слагаемые:
а-с = а-с+b-b = (а-b)+(b+c).
По условию а<b и b<c. Поэтому слагаемые а-b и b-c – отрицательные числа. Значит, и их сумма является отрицательным числом. Следовательно, а<c.
-
Если a<b и c – любое число, то а+с<b+c.
Преобразуем разность (а+с)-(b+c) = а-b
По условию а<b, поэтому a-b – отрицательное число. Значит, и разность (а+с)-(b+c) отрицательна. Следовательно, a+c<b+c.
Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство.
-
Если a<b и c – положительное число, то aс<bс. Если a<b и c – отрицательное число, то aс>bc.
Представим разность ас-bc в виде произведения: ас-bc = с(а-b).

Так как a<b, то a-b – отрицательное число. Если с>0, то произведение с(а-b) отрицательно, и, следовательно, ас<bc. Если с<0, то произведение с(а-b) положительно, и, следовательно, ас>bc.
Так как деление можно заменить умножением на число, обратное делителю, то аналогичное свойство справедливо и для деления.
Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство.
Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.
s -
Если а и b – положительные числа и а<b, то 1a>1b.
Разделим обе части неравенства a<b на положительное число ab: aab<bab. Сократив дроби, получим, что 1b<1a, т.е. 1а>1b.
Приведем пример использования рассмотренных свойств неравенств.

Пример 5. Оценим периметр равностороннего треугольника со стороной а мм, если известно, что 54,2<a и a<54,3, и запишем результат в виде двойного неравенства.
54,2·3 < 3a < 54,3·3,
162,6 < 3a < 162,9.
Значит, периметр Р данного треугольника больше 162,6 мм, но меньше 162,9 мм.
Рассмотрим теперь, как выполняется сложение и умножение числовых неравенств.
-
Если a<b и c<d, то a+c<b+d.
Прибавив к обеим частям неравенства a<b число с, получим а+с<b+с. Прибавив к обеим частям неравенства с<d число b, получим b+c<b+d.
То есть а+с<b+с<b+d. Из этого следует, что a+c<b+d.
Если почленно сложить верные неравенства одного знака, то получится верное неравенство.
-
Если a<b и c<d, где а,b,c,d – положительные числа, то ac<bd.

Умножим обе части неравенства a<b на положительное число с, получим ac<bс. Умножив обе части неравенства c<d на положительное число b, получим bc<bd. Получим ac<bс<bd. Следовательно ac<bd.
Если почленно перемножить верные неравенства одного знака, левые и правые части которых – положительные числа, то получится верное неравенство.
Из этой теоремы следует, что
Если числа а и b положительны и a<b, то an<bn, где n – натуральное число.
Доказанные свойства используют для оценки суммы, разности, произведения и частного.
Пример 6. Известно, что 15<x<16 и 2<y<3. Требуется оценить сумму х+у, разность х-у, произведение ху и частное х/у.
Сложим почленно неравенства 15<x<16 и 2<y<3, получим 17<x+y<19.
Оценим разность. Для этого умножим 2<y<3 почленно на (-1).
 Получим -3<-y<-2.
Получим -3<-y<-2.Теперь сложим почленно неравенства 15<x<16 и -3<-y<-2. Получим 12<x-y<14.
Оценим произведение ху. Перемножим почленно неравенства 15<x<16 и 2<y<3. Получим 30<xy<48.
Оценим частное. Для этого сначала запишем неравенство для 1у. Получится 13<1y<12. Теперь перемножим почленно 15<x<16 и 13<1y<12. Получим 5<xy<8.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.числовые равенства и неравенства — FINDOUT.SU
Методика изучения алгебраического материала в начальной школе: числовые равенства и неравенства
Поможем в ✍️ написании учебной работы
Имя
Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой
Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое
Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности
Понятия о равенствах, неравенствах и уравнениях раскрываются во взаимосвязи. Работа над ними ведется с I класса, органически сочетаясь с изучением арифметического материала.
Работа над ними ведется с I класса, органически сочетаясь с изучением арифметического материала.
Числовые равенства и неравенства учащиеся получают в результате сравнения заданных чисел или арифметических выражений. Поэтому знаками «>», «<», «=» соединяются не любые два числа, не любые два выражения, а лишь те, между которыми существуют указанные отношения. Два равных числа или два выражения, имеющие равные значения, соединенные знаком «=», образуют равенство. Если одно число больше (меньше) другого или одно выражение имеет значение больше (меньше), чем другое выражение, то, соединенные соответствующим знаком, они образуют неравенство. Таким образом, первоначально у младших школьников формируются понятия только о верных равенствах и неравенствах.
Ознакомление с равенствами и неравенствами в начальных классах непосредственно связывается с изучением нумерации и арифметических действий.
Сравнение чисел осуществляется сначала на основе сравнения множеств, которое выполняется, как известно, с помощью установления взаимно однозначного соответствии. Этому способу сравнения учат детей в подготовительный период и в начале изучения нумерации чисел первого десятка. Попутно выполняется счет элементов множеств и cpавнение полученных чисел (кругов 7, треугольников 4), кругов больше, чем треугольников, 7 больше, чем 4). В дальнейшем при сравнении чисел учащиеся определяют их место в натуральном ряду: 9 меньше, чем 10, потому что при счёте число 9 называют перед числом 10 и т.д. Установленные отношения записываются с помощью знаков «>», « <», «=», учащиеся упражняются в чтении равенств и неравенств. Впоследствии при изучении нумерации чисел в пределах 100, 1000, нумерации многозначных чисел сравнение чисел ocyществляется на основе сопоставления их по месту в натуральном ряду, либо на основе разложения чисел по десятичному составу и сравнения соответствующих разрядных чисел, начиная с высшего разряда (75>48, так как 7 десятков больше, чем 4 десятка; 75>73, так как десятков поровну, а единиц в первом числе больше, чем во втором).
Этому способу сравнения учат детей в подготовительный период и в начале изучения нумерации чисел первого десятка. Попутно выполняется счет элементов множеств и cpавнение полученных чисел (кругов 7, треугольников 4), кругов больше, чем треугольников, 7 больше, чем 4). В дальнейшем при сравнении чисел учащиеся определяют их место в натуральном ряду: 9 меньше, чем 10, потому что при счёте число 9 называют перед числом 10 и т.д. Установленные отношения записываются с помощью знаков «>», « <», «=», учащиеся упражняются в чтении равенств и неравенств. Впоследствии при изучении нумерации чисел в пределах 100, 1000, нумерации многозначных чисел сравнение чисел ocyществляется на основе сопоставления их по месту в натуральном ряду, либо на основе разложения чисел по десятичному составу и сравнения соответствующих разрядных чисел, начиная с высшего разряда (75>48, так как 7 десятков больше, чем 4 десятка; 75>73, так как десятков поровну, а единиц в первом числе больше, чем во втором).
Сравнение величин сначала выполняется с опорой на сравнение самих предметов по данному свойству, а потом осуществляется на основе сравнения числовых значений величин, для чего заданные величины выражаются в одинаковых единицах измерения. Сравнение величин вызывает трудности у учащихся, поэтому, чтобы научить этой операции, надо систематически в 1-4 классах предлагать разнообразные задания, например:
1) подберите равную величину: 7км 500м =… м, 3080 кг = … т … кг.
2) Подберите числовые значения величин так, чтобы запись была верной: … ч < … мин, … см =… дм … см. и др.
3) Вставьте наименования у величин так, чтобы запись была верной: 35 км =35 000 …. 16 мин >16 …. 17 т 5 ц=17500 …
4) Проверьте, верные или неверные равенства даны, исправьте знак, если равенства неверны: 4 т 8 ц=480 кг, 100 мин =1 ч, 2 м 5 см =250 см.
Подобные задания помогают детям усвоить не только понятия равных и неравных величин, но и отношения единиц измерения.
Переход к cpавнению выражений осуществляется постепенно. Сначала в процессе изучения сложения и вычитания в пределах 10 дети длительное время упражняются в сравнении выражения и числа (числа и выражения). Первые неравенства вида 3+1 >3, 3—1<З полезно получать из равенства (3=3), сопровождая преобразования соответствующими операциями над множествами. Например, на классном наборном полотне и па партах отложено 3 треугольника и 3 круга и записано: 3 = 3. Учитель предлагает детям придвинуть к 3 треугольникам еще 1 треугольник и записать это (3+1—запись под треугольниками). Число кругов не уменьшилось (3). Учащиеся сравнивают число треугольников и кругов и убеждаются, что треугольников больше, чем кругов (4>3), значит, можно записать: 3+1>3 (три плюс один больше, чем три). Аналогичная работа ведется над неравенством 3-1<З (три минус один меньше, чем три).
В дальнейшем выражение и число (число и выражение) учащиеся сравнивают, не прибегая к операциям над множествами; находят значение выражения и сравнивают его с заданным числом, что отражается в записях:
5+3>5 2<7-4 7=4+3
8>5 2<3 7=7
После знакомства с названиями выражений учащиеся читают равенства и неравенства так: сумма чисел 5 и 3 больше, чем число 5; число 2 меньше, чем разность чисел 7 и 4, и т. п.
п.
Опираясь на операции над множествами и сравнение множеств, учащиеся практически усваивают важнейшие свойства равенств и неравенств (если а = b, то b=a; если а>b, то b<а).
Дети видят, что если кругов и треугольников поровну, то можно сказать, что кругов столько, сколько треугольников (3+2=5), а также треугольников столько, сколько кругов (5=3+2). Если же предметов не поровну, то одних больше (3+1>3), а других меньше (3<3+1).
В дальнейшем при изучении действий в пределах 100, 1000 и 1000000 упражнения на сравнение выражения и числа даются на новом числовом материале, и увеличивается количество чисел и знаков действий в выражениях.
Сравнивая неоднократно специально подобранные выражения и числа, например: 17+0 и 17, 19-0 и 19, 7-1 и 7, 0:5 и 0, с+1 и с, с: 1 и с и т. п., учащиеся накапливают наблюдения об особых случаях действий, глубже осознают конкретный смысл действий. Упражнения на сравнение выражений и числа закрепляют умения читать выражения и способствуют формированию вычислительных навыков.
Сравнить выражения — значит, сравнить их значения. Сравнение выражений впервые включается уже в конце изучения сложения и вычитания в пределах 10, а затем при изучении действий во всех концентрах эти задания систематически предлагаются учащимся. Например, надо сравнить суммы: 6+4 и 6+3. Ученик рассуждает так: первая сумма равна 10, вторая — 9, 10 больше, чем 9, значит, сумма чисел 6 и 4 больше, чем сумма чисел 6 и 3. Это рассуждение отражается в записях:
6+4>6+3 7-5<7- 3 4+4=10-2
10>9 2<1 8=8
При изучении действий в других концентрах задания на сравнение выражений усложняются: более сложными становятся выражения, учащимся предлагаются задания вставить в одно из выражений подходящее число так, чтобы получить верные равенства или неравенства; проверить, верные ли равенства (неравенства) даны, неверные исправить, изменить знак отношения или число в одном из выражений; составить из данных выражений верные равенства или верные неравенства. Сами выражения подбираются таким образом, чтобы, сравнивая выражения, учащиеся наблюдали свойства и зависимости между компонентами и результатами действий. Например, после того как установили с помощью вычислений, что сумма 60+40 больше суммы 60+30, учитель предлагает сравнивать соответствующие слагаемые этих сумм, и дети отмечают, что первые слагаемые в этих суммах одинаковые, а второе слагаемое в первой сумме больше, чем во второй. Много раз подмечая эту зависимость, учащиеся приходят к обобщению и затем свои знания используют при сравнении выражений.
Сами выражения подбираются таким образом, чтобы, сравнивая выражения, учащиеся наблюдали свойства и зависимости между компонентами и результатами действий. Например, после того как установили с помощью вычислений, что сумма 60+40 больше суммы 60+30, учитель предлагает сравнивать соответствующие слагаемые этих сумм, и дети отмечают, что первые слагаемые в этих суммах одинаковые, а второе слагаемое в первой сумме больше, чем во второй. Много раз подмечая эту зависимость, учащиеся приходят к обобщению и затем свои знания используют при сравнении выражений.
Таким образом, при изучении всех концентров задания на сравнение чисел и выражений, с одной стороны, способствуют формированию понятий о равенствах и неравенствах, а с другой стороны, усвоению знаний о нумерации и арифметических действиях, а также формированию вычислительных навыков [1].
Свойства истинных числовых равенств — Студопедия
Поделись
КП 28.05.2020,29.05.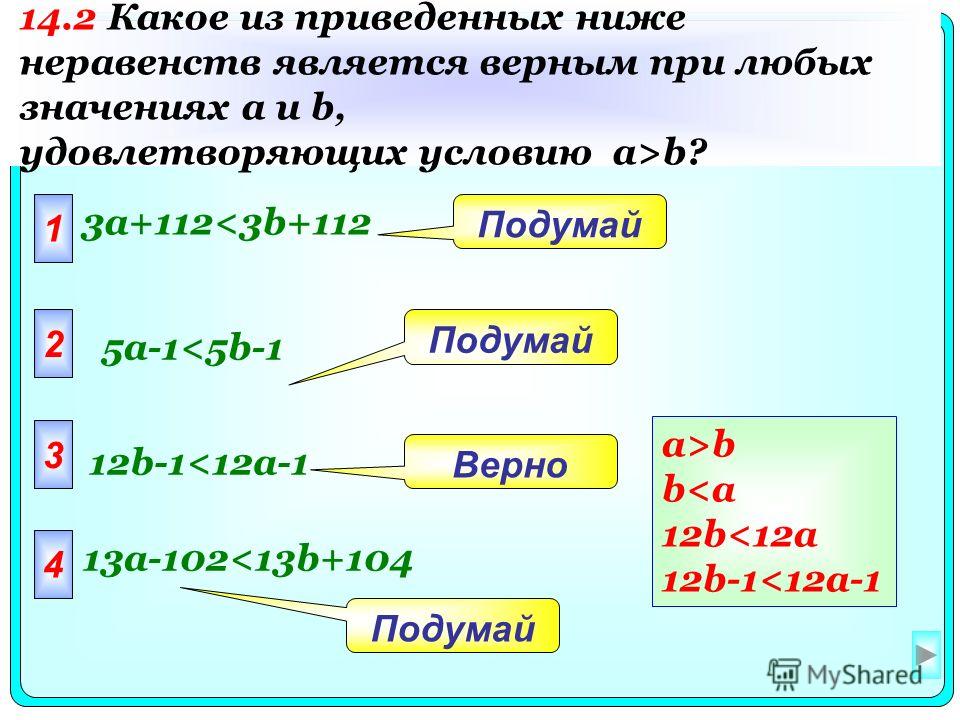 2020
2020
Практическое занятие. «Планирование фрагмента учебного занятия по математике для начальной школы по теме «Равенство. Неравенство».
Цель:планирование учебного процесса по математике, составление конспекта фрагмента урока математики по заданной теме.
Задание 1. Составить фрагмент урока, открытие новых знаний «Равенство. Неравенство», 2 класс» (все этапы, фрагмент на 15 минут).
Конспект урока
| Тема урока | |
| Цель | |
| Задачи |
| Этап урока. Задача этапа | Деятельность учителя | Деятельность обучающихся | Планируемые результаты |
Тема: Понятие числового равенства и неравенства. Основные свойства истинных числовых равенств и неравенств.
Цель: изучение методических особенностей введения понятия числового равенства и неравенства. Основные свойства истинных числовых равенств и неравенств.
Задание 1. Изучите теоретический материал. Составьте тест из 10 вопросов, правильный ответ выделите курсивом. Тест для проверки знаний по теме «Понятие числового равенства и неравенства. Основные свойства истинных числовых равенств и неравенств» студентов.
Числовые равенства и неравенства. Методика изучения числовых равенств и неравенств.
Возьмём два числовых выражения 32-20 и 144 : 12.
Соединим их знаком равенства 32 -20 = 144 : 12 (и), т. к. 12=12
Получим высказывание, которое называется числовым равенством.
Это высказывание истинно.
14 + 4 • 8 = 4 • 9 (л), т. к. 46≠ 36
Определение 1.Два числа или два числовых выражения, соединённые знаком равенства, называются числовым равенством.
Определение 2.Высказывание вида a = b, где а и в числовые выражения, называется числовым равенством.
Символически числовое равенство записывается так: a = b.
Если знаком равенства соединены 2 числовых выражения, значения которых равны, то получится истинное числовое равенство, если не равны, то ложное.
Таким образом, с логической точки зрения числовое равенство — это высказывание, истинное или ложное.
Числовое равенство истинно, если значения числовых выражений, стоящих в левой и правой частях равенства, совпадают.
Свойства истинных числовых равенств
1) Если к обеим частям истинного числового равенства прибавить одно и то же число с, или числовое выражение, имеющее смысл, то получится истинное числовое равенство.
Если a = b (и), то a +c = b + c тоже истинно.
2) Если обе части истинного числового равенства умножить на одно и то же число с, или числовое выражение, имеющее смысл, то получится истинное числовое равенство.
Если a = b (и), то a• c = b•c тоже истинно.
Работа над неравенствами ведется с I класса, органически сочетаясь с изучением арифметического материала. Программа по математике для I-III классов ставит задачу выполнять сравнение чисел, а также сравнение выражений с целью установления отношений «больше», «меньше», «равно»; научить записывать результаты сравнения с помощью знаков и читать полученные неравенства.
Числовые неравенства, учащиеся получают в результате сравнения заданных чисел или арифметических выражений. Поэтому знаками соединяются не любые два числа, не любые два выражения, а лишь те, между которыми существуют указанные отношения. Если одно число больше (меньше) другого или одно выражение имеет значение больше (меньше), чем другое выражение, то, соединенные соответствующим знаком, они образуют неравенство. Таким образом, первоначально у младших школьников формируются понятия только о верных неравенствах.
Если два числовых выражения соединить знаком «>» или «<», то получим числовое неравенство.
Определение. Два числовых выражения, соединённые знаком «>» или «<», образуют числовое неравенство.
Например, если соединить выражение 6 + 2 и 13-7 знаком «>», то получим истинное числовое неравенство 6 + 2 > 13-7.
Однако в процессе работы над уравнениями, выражениями и неравенствами с переменной учащиеся, подставляя различные значения переменной, накапливают наблюдения и убеждаются в том, что равенства и неравенства бывают как верные, так и неверные. Такой подход к раскрытию понятий определяет соответствующую методику работы над равенствами, неравенствами, уравнениями.
Ознакомление с неравенствами в начальных классах непосредственно связывается с изучением нумерации и арифметических действий.
Сравнение осуществляется сначала на основе сравнения множеств, которое выполняется, как известно, с помощью установления взаимно однозначного соответствия. Этому способу сравнения множеств учат детей в подготовительный период и в начале изучения нумерации чисел первого десятка. Попутно выполняется счет элементов множеств и сравнение полученных чисел (кружков 7, треугольников 5, кружков больше, чем треугольников, 7 больше, чем 5). В дальнейшем при сравнении чисел учащиеся опираются на их место в натуральном ряду: 9 меньше, чем 10, потому что при счете число 9 называют перед числом 10; 5 больше, чем 4, потому что при счете число 5 называют после числа 4.
Попутно выполняется счет элементов множеств и сравнение полученных чисел (кружков 7, треугольников 5, кружков больше, чем треугольников, 7 больше, чем 5). В дальнейшем при сравнении чисел учащиеся опираются на их место в натуральном ряду: 9 меньше, чем 10, потому что при счете число 9 называют перед числом 10; 5 больше, чем 4, потому что при счете число 5 называют после числа 4.
Установленные отношения записываются с помощью знаков, учащиеся упражняются в чтении и записи неравенств.
Впоследствии при изучении нумерации чисел в пределах 100, 1000, а также нумерации многозначных чисел сравнение чисел осуществляется либо на основе сопоставления их по месту в натуральном ряду, либо на основе разложения чисел по десятичному составу и сравнения соответствующих разрядных чисел, начиная с высшего разряда (75>48, так как 7 десятков больше, чем 4 десятка; 75>73, так как десятков поровну, а единиц в первом числе больше, чем во втором).
Сравнение величин сначала выполняется с опорой на сравнение самих предметов по данному свойству, а потом осуществляется на основе сравнения числовых значений величин, для чего заданные величины выражаются в одинаковых единицах измерения. Сравнение величин вызывает трудности у учащихся, поэтому, чтобы научить этой операции, надо систематически в I-III классах предлагать разнообразные упражнения, например:
Сравнение величин вызывает трудности у учащихся, поэтому, чтобы научить этой операции, надо систематически в I-III классах предлагать разнообразные упражнения, например:
Подберите равную величину: 7 км 500 м = ? м, 3080 кг= ? т ? кг.
Подберите числовые значения величин так, чтобы запись верной: ? ч<? мин, ? см =? дм ? см, ? т ? ц =? кг;
3) Вставьте наименование у величин так, чтобы запись была верной: 16 мин>16…
Подобные упражнения помогают детям усвоить не только понятия равных и неравных величин, но и отношения единиц измерения.
Переход к сравнению выражений осуществляется постепенно. Сначала в процессе изучения сложения и вычитания в пределах 10 дети длительное время упражняются в сравнении выражения и числа (числа и выражения). Первые неравенства вида 3+1>3, 3-1<3 полезно получать из равенства (3=3), сопровождая преобразования соответствующими операциями над множествами. Например, на классном наборном полотне и на партах отложено 3 треугольника и 3 кружка и записано: 3=3. Учитель предлагает детям придвинуть к 3 треугольникам еще 1 треугольник и записать это (3+1 — запись под треугольниками). Число кружков не уменьшилось (3). Учащиеся сравнивают число треугольников и кружков и убеждаются, что треугольников больше, чем кружков (4>3), значит, можно записать: 3+1>3 (три плюс один больше, чем три). Аналогичная работа ведется над неравенством 3-1<3 (три минус один меньше, чем три).
Учитель предлагает детям придвинуть к 3 треугольникам еще 1 треугольник и записать это (3+1 — запись под треугольниками). Число кружков не уменьшилось (3). Учащиеся сравнивают число треугольников и кружков и убеждаются, что треугольников больше, чем кружков (4>3), значит, можно записать: 3+1>3 (три плюс один больше, чем три). Аналогичная работа ведется над неравенством 3-1<3 (три минус один меньше, чем три).
В дальнейшем выражение и число (число и выражение) учащиеся сравнивают, не прибегая к операциям над множествами; находят значение выражения и сравнивают его с заданным числом, что отражается в записях:
5+3>5 2<7-4 7=4+5
8>5 2<3 7=7
После знакомства с названиями выражений учащиеся читают равенства и неравенства так: сумма чисел 5 и 3 больше, чем число 5; число 2 меньше, чем разность чисел 7 и 4, и т.п.
Опираясь на операции над множествами и сравнение множеств, учащиеся практически усваивают важнейшие свойства равенств и неравенств (если а>b, то b<а).
В дальнейшем при изучении действий в пределах 100, 1000 и 1000000, упражнения на сравнение выражения и числа даются на новом числовом материале и увеличивается количество чисел и знаков действий в выражениях.
Сравнивая неоднократно специально подобранные выражения и числа, например, 17+0 и 17, 19-0 и 19, 7-1 и 7, 0: 5 и 0, с+1 и с, с : 1 и с и т.п., учащиеся накапливают наблюдения об особых случаях действий, глубже осознают конкретный смысл действий. Упражнения на сравнение выражений и числа закрепляют умения читать выражения и способствуют выработке вычислительных навыков.
Сравнить два выражения, значит, сравнить их значения. Сравнение выражений впервые включается уже в конце изучения сложения и вычитания в пределах 10, а затем при изучении действий во всех концентрах эти упражнения систематически предлагаются учащимся. Например, надо сравнить Суммы: 6+4 и 6+3. Ученик рассуждает так: первая сумма равна 10, вторая-9, 10 больше, чем 9, значит, сумма чисел 6 и 4 больше, чем сумма чисел 6 и 3. Это рассуждение отражается в записях:
Это рассуждение отражается в записях:
При изучении действий в других концентрах упражнения на сравнение выражений усложняются: более сложными становятся выражения, учащимся предлагаются задания вставить в одно из выражений подходящее число так, чтобы получить верные равенства или неравенства; проверить, верные ли равенства (неравенства) даны, неверные исправить, изменив знак отношения или число в одном из выражений; составить из данных выражений верные равенства или верные неравенства. Сами выражения подбираются таким образом, чтобы, сравнивая выражения, учащиеся наблюдали свойства и зависимости между компонентами и результатами действий. Например, после того как установили с помощью вычислений, что сумма 60+40 больше суммы 60+30, учитель предлагает сравнивать соответствующие слагаемые этих сумм, и дети отмечают, что первые слагаемые в этих суммах одинаковые, а второе слагаемое в первой сумме больше, чем во второй. Много раз, подмечая эту зависимость, учащиеся приходят к обобщению и затем свои знания используют при сравнении выражений.
Неравенства с переменной вида: х+3<7, 10-х>5, х-4>12, 72: х<36 вводятся во II классе. Заранее ведется соответствующая подготовительная работа: включаются упражнения, в которых переменная обозначается не буквой, а «окошечком» (квадратом), например: ? >0, 6+4> ?, 7+ ? <10 и т.д. Учащимся предлагается подобрать такое число, чтобы получить верную запись. При выполнении таких упражнений учитель должен побуждать детей к подстановке различных чисел; например, в неравенстве ? >0 можно подставить число 1 (1>?), можно 2 (2>?), можно 3 (3>?) и т.д. После того как названо несколько чисел, полезно обобщить наблюдения (например, во втором неравенстве можно подставить любое число, которое меньше 10-от 0 до 9).
Рассматривая во II классе, например, неравенство х+3<10, учащиеся путем подбора находят, при каких значениях буквы х значение суммы х+3 меньше, чем 10. В каждом таком задании дается множество чисел — значений переменной. Ученики подставляют значения буквы в выражение, вычисляют значение выражения и сравнивают его с заданным числом. В результате такой работы выбирают значения переменной, при которых данное неравенство является верным.
В результате такой работы выбирают значения переменной, при которых данное неравенство является верным.
Термины «решить неравенство», «решение неравенства» не вводятся в начальных классах, поскольку во многих случаях ограничиваются подбором только нескольких значений переменной, при которых получается верное неравенство.
Позднее в упражнениях с неравенствами значения переменной не даются, учащиеся сами подбирают их. Такие упражнения, как правило, выполняются под руководством учителя.
Можно ознакомить детей с таким приемом подбора значений переменной в неравенстве. Пусть дано неравенство 7k<70. Сначала устанавливают, при каком значении k данное произведение равно 70 (при k=10). Чтобы произведение было меньше, чем 70, следует множитель брать меньше, чем 10. Учащиеся выполняют подстановку чисел 9, 8 и т.д. до нуля, вычисляют и сравнивают полученные значения выражения с заданным (70) и называют ответ.
Упражнения с неравенствами закрепляют вычислительные навыки, а также помогают усвоению арифметических знаний. Например, подставляя различные числовые значения компонентов, дети накапливают наблюдения об изменении результатов действий в зависимости от изменения одного из компонентов. Здесь уточняются знания детей о конкретном смысле каждого действия (так, подставляя значения вычитаемого, дети убеждаются в том, что вычитаемое не больше уменьшаемого и т.п.). Подбирая значения буквы в неравенствах и равенствах вида: 5+х=5, 5-х=5; 10х=10, учащиеся закрепляют знания особых случаев вычислений. Работая с неравенствами, учащиеся закрепляют представление о переменной и подготавливаются к решению неравенства в IV классе.
Например, подставляя различные числовые значения компонентов, дети накапливают наблюдения об изменении результатов действий в зависимости от изменения одного из компонентов. Здесь уточняются знания детей о конкретном смысле каждого действия (так, подставляя значения вычитаемого, дети убеждаются в том, что вычитаемое не больше уменьшаемого и т.п.). Подбирая значения буквы в неравенствах и равенствах вида: 5+х=5, 5-х=5; 10х=10, учащиеся закрепляют знания особых случаев вычислений. Работая с неравенствами, учащиеся закрепляют представление о переменной и подготавливаются к решению неравенства в IV классе.
.
Значение, расчет, решение, графическое отображение неравенств
В математике уравнения не всегда уравновешиваются с обеих сторон с помощью символа «равно». Иногда речь может идти об отношениях «не равно», например, что-то больше, чем другое или меньше. В математике неравенство относится к отношениям, которые делают неравное сравнение между двумя числами или другими математическими выражениями. Эти математические выражения относятся к алгебре и называются неравенствами.
Эти математические выражения относятся к алгебре и называются неравенствами.
Давайте изучим правила неравенств, а также способы их решения и графического отображения.
| 1. | Что такое неравенство? |
| 2. | Правила неравенств |
| 3. | Решение неравенств |
| 4. | Графические неравенства |
| 5. | Решение полиномиальных неравенств |
| 6. | Решение абсолютных неравенств |
| 7. | Решение рациональных неравенств |
| 8. | Часто задаваемые вопросы о неравенствах |
Что такое неравенство?
Неравенства — это математические выражения, в которых обе стороны не равны. В неравенстве, в отличие от уравнений, мы сравниваем две величины. Знак равенства между ними заменяется знаком меньше (или меньше или равно), больше (или больше или равно) или не равно.
Оливия выбрана в софтболе 12U. Сколько лет Оливии? Вы не знаете, сколько лет Оливии, потому что там не сказано «равный». Но вы знаете, что ее возраст должен быть меньше или равен 12, поэтому его можно записать как Возраст Оливии ≤ 12. Это практический сценарий, связанный с неравенством.
Неравенство Значение
Неравенство означает, что две вещи НЕ равны. Одна из вещей может быть меньше, больше, меньше или равна или больше или равна другим вещам.
- p ≠ q означает, что p не равно q
- p < q означает, что p меньше q
- p > q означает, что p больше q
- p ≤ q означает, что p меньше или равно q
- p ≥ q означает, что p больше или равно q
Существуют различные виды неравенства. Некоторые из важных неравенств:
- Полиномиальные неравенства
- Неравенства абсолютного значения
- Рациональные неравенства
Правила неравенств
Правила неравенств особенные. Вот некоторые из них с примерами неравенств.
Вот некоторые из них с примерами неравенств.
Неравенства Правило 1
Когда неравенства связаны, вы можете перепрыгнуть через среднее неравенство.
- Если p < q и q < d, то p < d
- Если p > q и q > d, то p > d
Пример: Если Огги старше Мии, а Миа старше Черри, то Огги должен быть старше Черри.
Неравенство Правило 2
Перестановка чисел p и q приводит к:
- Если p > q, то q < p
- Если p < q, то q > p
Пример: Огги старше Мии, значит, Мия моложе Огги.
Неравенства Правило 3
Добавление числа d к обеим частям неравенства: Если p < q, то p + d < q + d
Пример: У Огги меньше денег, чем у Мии. Если и Огги, и Миа получат на 5 долларов больше, то у Огги все равно будет меньше денег, чем у Миа.
Аналогично:
- Если p < q, то p − d < q − d
- Если p > q, то p + d > q + d, и
- Если p > q, то p − d > q − d
Таким образом, прибавление и вычитание одного и того же значения как к p, так и к q не изменит неравенство.
Неравенства Правило 4
Если числа p и q умножить на положительное число, неравенство не изменится. Если вы умножаете и p, и q на отрицательное число, неравенство меняется местами: p Вот правила: Положительный пример: оценка Огги, равная 5, ниже, чем оценка Мии, равная 9 (p < q). Если Огги и Миа удвоят свои оценки «×2», оценка Огги все равно будет ниже, чем оценка Миа, 2p < 2q. Если баллы станут минусами, то баллы будут -p > -q. Постановка минусов перед p и q меняет направление неравенства. Принятие обратной величины 1/от p и q изменяет направление неравенства. Квадрат числа всегда больше или равен нулю p 2 ≥ 0. Пример: (4) 2 = 16, (−4) 2 = 16, (0) 2 = 0 Извлечение квадратного корня не изменит неравенство. Если p ≤ q, то √p ≤ √q (при p, q ≥ 0). Пример: Правила неравенств сведены в следующую таблицу. Неравенство Правило 5
Неравенства Правило 6
 Когда p и q оба положительны или оба отрицательны:
Когда p и q оба положительны или оба отрицательны: Неравенства Правило 7
Неравенства Правило 8
р=2, д=7
2 ≤ 7, тогда √2 ≤ √7 Операция, применяемая при решении неравенств Смена знака? Дополнение с обеих сторон № Вычитание с обеих сторон № Умножение или деление обеих частей на положительное число № Умножение или деление обеих частей на отрицательное число Да Замена обеих сторон Да Упростить одну сторону № Решение неравенств
Вот шаги для решения неравенств :
- Шаг — 1: Запишите неравенство в виде уравнения.

- Шаг — 2: Решите уравнение для одного или нескольких значений.
- Шаг — 3: Представьте все значения в числовой строке.
- Шаг – 4: Кроме того, обозначьте все исключенные значения на числовой прямой с помощью незакрашенных кружков.
- Шаг — 5: Определите интервалы.
- Шаг — 6: Берем произвольное число из каждого интервала, подставляем его в неравенство и проверяем, выполняется ли неравенство.
- Шаг — 7: Удовлетворяющие интервалы являются решениями.
Но для решения простых неравенств (линейных) мы обычно применяем алгебраические операции, такие как сложение, вычитание, умножение и деление. Рассмотрим следующий пример:
2x + 3 > 3x + 4
Вычитание 3x и 3 с обеих сторон,
2x — 3x > 4 — 3
-x > 1
Умножение обеих сторон на -1,
23
2 х < -1 Обратите внимание, что мы заменили символ «>» на символ «<». Почему? Это потому, что мы умножили обе части неравенства на отрицательное число. Процесс решения упомянутых выше неравенств работает для простого линейного неравенства. Но чтобы решить любое другое сложное неравенство, мы должны использовать следующий процесс.
Почему? Это потому, что мы умножили обе части неравенства на отрицательное число. Процесс решения упомянутых выше неравенств работает для простого линейного неравенства. Но чтобы решить любое другое сложное неравенство, мы должны использовать следующий процесс.
Применим эту процедуру для решения неравенств разных типов.
Графические неравенства
Пока графически изображая неравенства , мы должны помнить о следующих вещах.
- Если включена конечная точка (т. е. в случае ≤ или ≥), используйте замкнутый кружок.
- Если конечная точка НЕ включена (т. е. в случае < или >), используйте открытый кружок.
- Используйте открытый круг на ∞ или -∞.
- Нарисуйте линию от конечной точки, которая продолжается вправо, если переменная больше числа.
- Нарисуйте линию от конечной точки до левой стороны, если переменная меньше числа.
Запись неравенств в интервальной записи
При записи решения неравенства в интервальной записи мы должны помнить о следующих вещах.
- Если включена конечная точка (т. е. в случае ≤ или ≥), используйте закрывающие скобки ‘[‘ или ‘]’
- Если конечная точка не указана (например, в случае < или >), используйте открытые скобки ‘(‘ или ‘)’
- Всегда используйте открытую квадратную скобку либо на ∞, либо на -∞.
Вот несколько примеров, чтобы понять то же самое:
Неравенство Интервал х < 2 (-∞, 2) х > 2 (2, ∞) х ≤ 2 (-∞, 2] х ≥ 2 [2, ∞) 2 < х ≤ 6 (2, 6]
Графики неравенств с двумя переменными
Для построения графиков неравенств с двумя переменными вам нужно будет построить линию «равно», а затем заштриховать соответствующую область. Есть три шага:
- Напишите уравнение, например, «у» слева, а все остальное справа.

- Постройте линию «y=» (нарисуйте сплошную линию для y≤ или y≥ и пунктирную линию для y< или y>)
- Закрасьте область над линией для «больше чем» (y> или y≥) или под линией для «меньше чем» (y< или y≤).
Давайте рассмотрим пример: Это график линейного неравенства: y ≤ x + 4
Вы можете видеть, что y = x + 4 линия, а заштрихованная область (желтым цветом) находится там, где y меньше или равно x + 4. Давайте теперь посмотрим, как решать различные типы неравенств и как графически отображать решение в каждом случае.
Решение полиномиальных неравенств
Полиномиальные неравенства — это неравенства, которые могут быть выражены полиномом с одной стороны и 0 с другой стороны неравенства. Существуют различные типы полиномиальных неравенств, но наиболее важными из них являются:
- Линейные неравенства
- Квадратные неравенства
Решение линейных неравенств
Линейное неравенство — это неравенство, которое может быть выражено линейным выражением с одной стороны и 0 с другой. Решение линейных неравенств аналогично решению линейных уравнений, но следует соблюдать только правила решения неравенств (которые были объяснены ранее). Давайте посмотрим на некоторые примеры.
Решение линейных неравенств аналогично решению линейных уравнений, но следует соблюдать только правила решения неравенств (которые были объяснены ранее). Давайте посмотрим на некоторые примеры.
Решение одношаговых неравенств
Рассмотрим неравенство 2x < 6 (линейное неравенство с одной переменной). Чтобы решить это, достаточно всего одного шага, который делит обе части на 2. Тогда мы получаем x < 3. Следовательно, решение неравенства x < 3 (или) (-∞, 3).
Решение двухшаговых неравенств
Рассмотрим неравенство -2x + 3 > 6. Чтобы решить его, нам нужно выполнить два шага. Первым шагом является вычитание 3 из обеих сторон, что дает -2x > 3. Затем нам нужно разделить обе части на -2, и в результате x < -3/2 (обратите внимание, что мы изменили знак неравенства). Таким образом, решением неравенства является x < -3/2 (или) (-∞, -3/2).
Решение составных неравенств
Составные неравенства относятся к набору неравенств, между которыми есть «и» или «или». Для решения неравенств в этом случае просто решите каждое неравенство независимо, а затем найдите окончательное решение в соответствии со следующими правилами:
Для решения неравенств в этом случае просто решите каждое неравенство независимо, а затем найдите окончательное решение в соответствии со следующими правилами:
- Окончательное решение является пересечением решений независимых неравенств, если между ними есть «и».
- Окончательное решение — это объединение решений независимых неравенств, если между ними есть «или».
Пример: Решите составное неравенство 2x + 3 < -5 и x + 6 < 3.
Решение:
По первому неравенству:
2x + 3 < -5
2x < -8
x < -4
По второму неравенству,
х + 6 < 3
x < -3
Так как между ними есть «и», мы должны найти пересечение множеств x < -4 и x < -3. В этом случае может помочь числовая линия. Тогда окончательное решение:
х < -3 (или) (-∞, -3).
Решение квадратных неравенств
Квадратное неравенство включает в себя квадратное выражение. Вот процесс решения квадратных неравенств. Процесс поясняется на примере, где мы собираемся решить неравенство x 2 — 4x — 5 ≥ 0.
Процесс поясняется на примере, где мы собираемся решить неравенство x 2 — 4x — 5 ≥ 0.
Мы можем использовать тот же процесс для решения кубических неравенств, биквадратичных неравенств и т. д.
Решение абсолютных неравенств
Неравенство абсолютного значения включает алгебраическое выражение внутри знака абсолютного значения. Вот процесс решения абсолютного неравенства, где процесс объясняется на примере решения абсолютного неравенства |x + 3| ≤ 2. Если вы хотите узнать о различных методах решения абсолютных неравенств, нажмите здесь.
Решение рациональных неравенств
Рациональные неравенства — это неравенства, включающие рациональные выражения (дроби с переменными). Чтобы решить рациональные неравенства (неравенства с дробями), мы просто используем ту же процедуру, что и другие неравенства, но мы должны позаботьтесь об исключенных точках . Например, решая рациональное неравенство (x + 2)/(x — 2) < 3, следует отметить, что рациональное выражение (x + 2)/(x - 2) НЕ определено при x = 2 (положим знаменатель х - 2 = 0 ⇒ х = 2). Пошагово решим это неравенство.
Пошагово решим это неравенство.
- Шаг 5: Интервалы, которые оказались «истинными» в Шаге 4 , являются решениями.
Следовательно, решением рационального неравенства (x + 2)/(x — 2) < 3 является (-∞, 2) U (4, ∞).
Важные примечания о неравенствах:
Вот примечания о неравенствах:
- Если у нас строго меньше или строго больше символа, то мы никогда не получим никакого замкнутого интервала в решении.
- Мы всегда получаем открытые интервалы в символах ∞ или -∞, потому что они НЕ являются числами для включения.
- При решении рациональных неравенств всегда записывать открытые интервалы на исключенных значениях.
- Исключенные значения следует учитывать только в случае рациональных неравенств.
☛ Похожие темы:
- Калькулятор линейных неравенств
- Калькулятор теоремы о неравенстве треугольника
- Калькулятор рациональных неравенств
Часто задаваемые вопросы о неравенствах
Что такое неравенства в математике?
Когда два или более алгебраических выражения сравниваются с использованием символов <, > ≤ или ≥, они образуют неравенство. Они являются математическими выражениями, в которых обе стороны не равны.
Они являются математическими выражениями, в которых обе стороны не равны.
Как решать неравенства на числовой прямой?
Чтобы построить неравенство в математике, например, x>3, на числовой прямой,
- Шаг 1: Нарисуйте кружок над числом (например, 3).
- Шаг 2: Проверьте, включает ли знак равно (≥ или ≤) или нет. Если знак равенства стоит вместе с > или <, то закрасьте кружок, в противном случае оставьте кружок незаполненным.
- Шаг 3: В числовой строке удлините линию от 3 (после ее обведения), чтобы показать, что она больше или равна 3.
Как рассчитать математические неравенства?
Чтобы вычислить неравенства :
- просто составьте уравнение
- решить
- отметьте нули на числовой прямой, чтобы получить интервалы
- проверить интервалы, взяв из него любое число против неравенства.
Объясните процесс решения неравенств графически.

Графическое решение неравенств возможно при наличии системы двух неравенств с двумя переменными. В этом случае мы рассматриваем оба неравенства как два линейных уравнения и изображаем их на графике. Тогда мы получим две строки. Закрасьте верхнюю/нижнюю часть каждой из линий, удовлетворяющих неравенству. Общая часть обеих заштрихованных областей является областью решения.
В чем разница между уравнениями и неравенствами?
Вот различия между уравнениями и неравенствами.
Уравнения Неравенства 1. В уравнениях есть символ «=». 1. Неравенства содержат «>», «<», «≥» или «≤» 2. Количество решений уравнения зависит от степени уравнения. 2. Неравенство может иметь единственное, единственное решение или не иметь решения. Это не зависит от степени. 3. Применяя любую операцию с обеих сторон, уравнение остается верным.
3. Если мы умножим/разделим обе части неравенства на отрицательное число, знак изменится.
Что произойдет, если возвести в квадрат неравенство?
Квадрат числа всегда больше или равен нулю p 2 ≥ 0. Пример: (4) 2 = 16, (−4) 2 = 16, (0) 2 = 0
Каковы шаги для расчета неравенств с дробями?
Вычисление неравенств с дробями так же, как решение любого другого неравенства. Одним из простых способов решения таких неравенств является умножение каждого члена с обеих сторон на LCD всех знаменателей, чтобы все дроби стали целыми числами. Например, чтобы решить (1/2) x + 1 > (3/4) x + 2, умножьте обе части на 4. Тогда мы получим 2x + 4 > 3x + 8 ⇒ -x > 4 ⇒ x < -4.
Как решить неравенство с переменными с обеих сторон?
Когда неравенство имеет переменную с обеих сторон, мы должны попытаться изолировать переменную. Но в этом процессе переворачивайте знак неравенства всякий раз, когда мы делим или умножаем обе части на отрицательное число. Вот пример. 3x — 7 < 5x - 11 ⇒ -2x < -4 ⇒ x > 2.
Вот пример. 3x — 7 < 5x - 11 ⇒ -2x < -4 ⇒ x > 2.
Как найти диапазон неравенства?
Вы можете найти диапазон значений x, решив неравенство, рассматривая его как нормальное линейное уравнение.
Что такое 5 символов неравенства?
5 символов неравенства: меньше (<), больше (>), меньше или равно (≤), больше или равно (≥) и символ неравенства (≠).
Как определить, что это неравенство?
Уравнения и неравенства представляют собой математические предложения, образованные путем связывания двух выражений друг с другом. В уравнении два выражения считаются равными и обозначаются символом =. В то время как в неравенстве два выражения не обязательно равны и обозначаются символами: >, <, ≤ или ≥.
Как построить график решения после решения неравенства?
После решения неравенств мы можем построить график решения, учитывая следующие моменты.
- Используйте незакрашенный кружок рядом с номером, если он не включен, и закрашенный кружок, если он включен.

- Нарисуйте линию справа от числа в случае ‘>’ и слева от числа в случае ‘<'.
Решение неравенств | Начальная алгебра
Результаты обучения
- Описать решения неравенств
- Представление неравенств на числовой прямой
- Представление неравенств с использованием записи интервалов
- Решение одношаговых неравенств
- Использование свойств сложения и умножения для решения алгебраических неравенств и выражения их решений графически и с интервальной записью
- Решение неравенств, содержащих абсолютное значение
- Решение многошаговых неравенств
- Объединение свойств неравенства для выделения переменных, решение алгебраических неравенств и графическое представление их решений
- Упростите и решите алгебраические неравенства, используя распределительное свойство для очистки скобок и дробей
Представление неравенств на числовой прямой
Сначала давайте определимся с некоторыми важными терминами. Неравенство — это математическое утверждение, которое сравнивает два выражения, используя понятия больше или меньше. В этих операторах используются специальные символы. Когда вы читаете неравенство, читайте его слева направо — так же, как читаете текст на странице. В алгебре неравенства используются для описания больших наборов решений. Иногда существует бесконечное количество чисел, удовлетворяющих неравенству, поэтому вместо того, чтобы пытаться перечислить бесконечное количество чисел, мы разработали несколько способов краткого описания очень больших списков.
Неравенство — это математическое утверждение, которое сравнивает два выражения, используя понятия больше или меньше. В этих операторах используются специальные символы. Когда вы читаете неравенство, читайте его слева направо — так же, как читаете текст на странице. В алгебре неравенства используются для описания больших наборов решений. Иногда существует бесконечное количество чисел, удовлетворяющих неравенству, поэтому вместо того, чтобы пытаться перечислить бесконечное количество чисел, мы разработали несколько способов краткого описания очень больших списков.
Первый способ, с которым вы, вероятно, знакомы, — основное неравенство. Например:
- [латекс]{х}\лт{9}[/латекс] указывает список чисел, которые меньше 9. Вы бы предпочли написать [латекс]{х}\лт{9}[/латекс ] или попытаться перечислить все возможные числа меньше 9? (надеюсь, ваш ответ — нет)
- [латекс]-5\le{t}[/латекс] указывает все числа, которые больше или равны [латекс]-5[/латекс].
Обратите внимание, как размещение переменной слева или справа от знака неравенства может измениться независимо от того, ищете ли вы больше или меньше.
Например:
- [латекс]x\lt5[/латекс] означает все действительные числа, которые меньше 5, тогда как;
- [latex]5\lt{x}[/latex] означает, что 5 меньше x, или мы могли бы переписать это с x слева: [latex]x\gt{5}[/latex] обратите внимание, как неравенство по-прежнему указывает то же направление относительно x. Это утверждение представляет все действительные числа, которые больше 5, что легче интерпретировать, чем 5 меньше x.
Второй способ — с графиком с использованием числовой строки:
И третий способ — с интервалом.
В этом разделе мы подробно рассмотрим второй и третий способы. Опять же, этими тремя способами записи решений неравенств являются:
- неравенство
- интервал
- график
Знаки неравенства
В поле ниже показаны символ, значение и пример для каждого знака неравенства. Иногда легко запутаться в неравенствах, просто не забывайте читать их слева направо.
Символ слов Пример [латекс]\neq [/латекс] не равно [латекс]{2}\neq{8}[/латекс], 2 равно , не равному 8 .
[латекс]\gt[/латекс] больше [латекс]{5}\gt{1}[/латекс], 5 больше, чем 1 [латекс]\lt[/латекс] меньше [латекс]{2}\lt{11}[/латекс], 2 меньше, чем 11 [латекс] \geq [/латекс] больше или равно [латекс]{4}\geq{ 4}[/латекс], 4 больше или равно 4 [латекс]\leq [/латекс] меньше или равно [латекс]{7}\leq{9}[/латекс], 7 меньше или равно 9
Неравенство [латекс]х>у[/латекс] можно также записать как [латекс]{у}<{х}[/латекс]. Стороны любого неравенства можно поменять местами, если символ неравенства между ними также перевернут.
Построение графика неравенства
Неравенство также можно изобразить на числовой прямой. Ниже приведены три примера неравенств и их графики. Графики — очень полезный способ визуализации информации, особенно когда эта информация представляет собой бесконечный список чисел!
Графики — очень полезный способ визуализации информации, особенно когда эта информация представляет собой бесконечный список чисел!
[латекс]x\leq -4[/латекс]. Это переводится во все действительные числа на числовой прямой, которые меньше или равны 4.
[латекс]{х}\geq{-3}[/латекс]. Это переводится во все действительные числа на числовой прямой, которые больше или равны -3.
Каждый из этих графиков начинается с круга — открытого или закрытого (заштрихованного) круга. Эту точку часто называют конечной точкой решения. Замкнутый или заштрихованный круг используется для обозначения неравенств больше или равно [латекс] \displaystyle \left(\geq\right) [/latex] или меньше или равно [латекс] \displaystyle \left(\leq\right) [/latex]. Суть является частью решения. Незакрашенный кружок используется для больше (>) или меньше (<). Дело в том, что , а не часть решения.
Затем граф бесконечно расширяется в одном направлении. Это показано линией со стрелкой на конце. Например, обратите внимание, что для графика [латекс] \displaystyle x\geq -3[/латекс], показанного выше, конечная точка равна [латекс]−3[/латекс], представленная замкнутым кругом, поскольку неравенство равно больше или равно [латекс]−3[/латекс]. Синяя линия рисуется справа от числовой строки, потому что значения в этой области больше, чем [латекс]-3[/латекс]. Стрелка в конце указывает, что решения продолжаются бесконечно.
Это показано линией со стрелкой на конце. Например, обратите внимание, что для графика [латекс] \displaystyle x\geq -3[/латекс], показанного выше, конечная точка равна [латекс]−3[/латекс], представленная замкнутым кругом, поскольку неравенство равно больше или равно [латекс]−3[/латекс]. Синяя линия рисуется справа от числовой строки, потому что значения в этой области больше, чем [латекс]-3[/латекс]. Стрелка в конце указывает, что решения продолжаются бесконечно.
Пример
Постройте график неравенства [latex]x\ge 4[/latex]
Показать решение
Пример
Напишите неравенство, описывающее все действительные числа на числовой прямой, которые меньше 2, затем начертите соответствующий график.
Показать решение
youtube.com/embed/E_ZWNVNEvOg?feature=oembed» frameborder=»0″ gesture=»media» allow=»encrypted-media» allowfullscreen=»»> Представление неравенств с помощью интервальной записи
Другой широко используемый и, возможно, самый краткий метод описания неравенств и решений неравенств называется интервальной записью. В соответствии с этим соглашением наборы строятся с помощью скобок или квадратных скобок, каждая из которых имеет свое значение. Решения [latex]x\geq 4[/latex] представлены как [latex]\left[4,\infty \right)[/latex]. Этот метод широко используется и будет присутствовать в других математических курсах, которые вы можете пройти.
Основная концепция, которую следует помнить, заключается в том, что круглые скобки представляют решения, большие или меньшие, чем число, а скобки представляют решения, которые больше или равны или меньше или равны числу. Используйте круглые скобки для обозначения бесконечности или отрицательной бесконечности, поскольку положительная и отрицательная бесконечность не являются числами в обычном смысле этого слова и, следовательно, не могут быть «приравнены». Несколько примеров интервала или набора чисел, в которые попадает решение: [латекс]\влево[-2,6\вправо)[/латекс], или все числа между [латекс]-2[/ латекс] и [латекс]6[/латекс], включая [латекс]-2[/латекс], но не включая [латекс]6[/латекс]; [латекс]\влево(-1,0\вправо)[/латекс], все действительные числа между, но не включая [латекс]-1[/латекс] и [латекс]0[/латекс]; и [latex]\left(-\infty,1\right][/latex], все действительные числа меньше и включая [latex]1[/latex]. В приведенной ниже таблице показаны возможные варианты. Не забывайте читать неравенства слева направо точно так же, как текст.
Несколько примеров интервала или набора чисел, в которые попадает решение: [латекс]\влево[-2,6\вправо)[/латекс], или все числа между [латекс]-2[/ латекс] и [латекс]6[/латекс], включая [латекс]-2[/латекс], но не включая [латекс]6[/латекс]; [латекс]\влево(-1,0\вправо)[/латекс], все действительные числа между, но не включая [латекс]-1[/латекс] и [латекс]0[/латекс]; и [latex]\left(-\infty,1\right][/latex], все действительные числа меньше и включая [latex]1[/latex]. В приведенной ниже таблице показаны возможные варианты. Не забывайте читать неравенства слева направо точно так же, как текст.
В таблице ниже описаны все возможные неравенства, которые могут возникнуть, и способы их записи с использованием интервальной записи, где a и b — действительные числа.
The entries in the third row are: All real numbers greater than a, but not including a; {x| x > a}; (a , infinity). The entries in the fourth row are: All real numbers less than b, but not including b; {x| x < b}; (negative infinity, b). The entries in the fifth row are: All real numbers greater than a, including a; {x| x a}; [a, infinity). The entries in the sixth row are: All real numbers less than b, including b; {x| x b}; (negative infinity, b]. The entries in the seventh row are: All real numbers between a and b, including a; {x| a x < b}; [a, b). The entries in the eighth row are: All real numbers between a and b, including b; {x| a < x b}; (a, b]. The entries in the ninth row are: All real numbers between a and b, including a and b; {x| a x b}; [a, b]. The entries in the tenth row are: all real numbers less than a and greater than b; {x| x < a and x > b}; (negative infinity, a) union (b, infinity). The entries in the eleventh row are: All real numbers; {x| x is all real numbers}; (negative infinity, infinity). «>
«> Неравенство слов Обозначение интервала [латекс] {a}\lt{x}\lt{b}[/латекс] все действительные числа между a и b , кроме a и b [латекс]\влево(а,б\вправо)[/латекс] [латекс]{х}\gt{а}[/латекс] Все действительные числа больше a , но не включая a [латекс]\влево(а,\infty\вправо)[/латекс] [латекс]{x}\lt{b}[/латекс] Все действительные числа меньше b , но не включая b [латекс]\влево(-\infty,b\вправо)[/латекс] [латекс]{х}\ge{а}[/латекс] Все действительные числа больше a , в том числе и [латекс]\влево[а,\infty\вправо)[/латекс] [латекс]{х}\ле{б}[/латекс] Все действительные числа меньше b , включая b [латекс]\влево(-\infty,b\вправо][/латекс] [латекс]{a}\le{x}\lt{b}[/латекс] Все действительные числа между a и b , включая a [латекс]\влево[а,б\вправо)[/латекс] [латекс] {а}\lt{x}\le{b}[/латекс] Все действительные числа между a и b , включая b [латекс]\влево(а,б\вправо][/латекс] [латекс]{a}\le{x}\le{b}[/латекс] Все действительные числа между a и b , включая a и b [латекс]\влево[а,б\вправо][/латекс] [латекс] {x}\lt{a}\text{ или {x}\gt{ b}[/latex] Все действительные числа меньше a или выше b [латекс]\влево(-\infty,a\вправо)\чашка \влево(b,\infty\вправо)[/латекс] Все действительные числа Все действительные числа [латекс]\влево(-\infty,\infty\вправо)[/латекс] Пример
Описать неравенство [latex]x\ge 4[/latex], используя интервальную запись
Показать решение
youtube.com/embed/BKhDzNKjVBc?feature=oembed» frameborder=»0″ gesture=»media» allow=»encrypted-media» allowfullscreen=»»> Пример
Используйте интервальную нотацию для обозначения всех действительных чисел, больших или равных [латекс]-2[/латекс].
Показать решение
Подумайте об этом
В предыдущих примерах вам дали неравенство или его описание словами и попросили нарисовать соответствующий график и написать интервал. В этом примере вам дается интервал и просят написать неравенство и нарисовать график.
Учитывая [латекс]\влево(-\infty,10\вправо)[/латекс], запишите соответствующее неравенство и начертите график.
В поле ниже напишите, что, по вашему мнению, будет проще сначала нарисовать график или сначала написать неравенство.
Показать решение
В следующем видео вы увидите примеры того, как построить график с учетом неравенства в интервальной записи.
И, наконец, последнее видео, в котором показано, как записывать неравенства с помощью графика, с интервальной записью и в виде неравенства.
Решение одношаговых неравенств
Решение неравенств сложением и вычитанием
Большинство неравенств можно решить с помощью обратных операций, как вы это делали для решения уравнений. Это потому, что когда вы добавляете или вычитаете одно и то же значение из обеих частей неравенства, вы сохраняете неравенство. Эти свойства указаны в поле ниже.
Свойства сложения и вычитания неравенства
Если [latex]a>b[/latex], , то [latex]a+c>b+c[/latex].
Если [латекс]а>б[/латекс] , , то [латекс]а-с>б-с[/латекс].
Поскольку неравенства имеют несколько возможных решений, графическое представление решений обеспечивает полезную визуализацию ситуации, как мы видели в предыдущем разделе. В приведенном ниже примере показаны шаги для решения и построения графика неравенства, а также для выражения решения с использованием записи интервалов.
Строка представляет все числа, к которым можно прибавить 3 и получить число меньше 5. Есть много чисел, которые решают это неравенство!
Так же, как вы можете проверить решение уравнения, вы можете проверить решение неравенства. Во-первых, вы проверяете конечную точку, подставляя ее в соответствующее уравнение. Затем вы проверяете правильность неравенства, подставляя любое другое решение, чтобы увидеть, является ли оно одним из решений. Поскольку существует несколько решений, рекомендуется проверить более одного из возможных решений. Это также может помочь вам проверить правильность вашего графика.
В приведенном ниже примере показано, как можно проверить, что [latex]x<2[/latex] является решением для [latex]x+3<5[/latex] .
В следующих примерах показаны задачи на неравенство, включающие операции с отрицательными числами. Также показан график решения неравенства. Не забудьте проверить решение. Это хорошая привычка!
Пример
Найдите a . [latex]a-17>-17[/latex]
Показать решение
Проверить решение [latex]a-17>-17[/latex]
Показать решение
В предыдущих примерах показано, как решить одношаговое неравенство с переменной в левой части. В следующем видеоролике приведены примеры того, как решать однотипные неравенства.
Что бы вы сделали, если бы переменная находилась в правой части неравенства? В следующем примере вы увидите, как справиться с этим сценарием.
Пример
Решите для x : [латекс]4\geq{x}+5[/латекс]
Показать решение
Проверить решение на [latex]4\geq{x}+5[/latex]
Показать решение
youtube.com/embed/RBonYKvTCLU?feature=oembed» frameborder=»0″ gesture=»media» allow=»encrypted-media» allowfullscreen=»»> Решение неравенств с умножением и делением
Решение неравенства с переменной, имеющей коэффициент, отличный от 1, обычно включает умножение или деление. Шаги похожи на решение одношаговых уравнений, включающих умножение или деление, ЗА ИСКЛЮЧЕНИЕМ знака неравенства. Давайте посмотрим, что происходит с неравенством, когда вы умножаете или делите каждую сторону на одно и то же число.
Начнем с истинного утверждения: [латекс]10>5[/латекс]
Попробуем еще раз, начав с того же истинного утверждения: [латекс]10>5[/латекс]
Затем умножьте обе части на одно и то же положительное число: [латекс]10\cdot 2>5\cdot 2[/латекс]
На этот раз умножьте обе части на одно и то же отрицательное число: [латекс]10\cdot-2>5 \\ \,\,\,\,\,\cdot -2\,\cdot-2[/латекс]
20 больше 10, поэтому у вас все еще есть истинное неравенство: [латекс]20>10[/латекс]
Минуточку! [латекс]-20[/латекс] на , а не на больше, чем [латекс]-10[/латекс], поэтому у вас неверное утверждение.
[латекс]−20>−10[/латекс]
При умножении на положительное число оставьте знак неравенства как есть! Вы должны «перевернуть» знак неравенства, чтобы утверждение стало верным: [латекс]−20<−10[/латекс]
Внимание! Когда вы умножаете или делите на отрицательное число, «переворачивайте» знак неравенства. Всякий раз, когда вы умножаете или делите обе части неравенства на отрицательное число, знак неравенства необходимо изменить на противоположный, чтобы сохранить истинное утверждение. Эти правила приведены в рамке ниже.
Свойства умножения и деления неравенства
Начните с Умножить на Окончательное неравенство [латекс]а>б[/латекс] [латекс]с[/латекс] [латекс]ac>bc[/латекс] [латекс]а>б[/латекс] [латекс]-c[/латекс] [латекс]ac
Начать с Разделить на Окончательное неравенство [латекс]а>б[/латекс] [латекс]с[/латекс] [латекс] \displaystyle \frac{a}{c}>\frac{b}{c}[/latex] [латекс]а>б[/латекс] [латекс]-c[/латекс] [латекс] \displaystyle \frac{a}{c}<\frac{b}{c}[/latex]
Помните, что знак меняется только при умножении и делении на отрицательное число . Если вы прибавите или вычтете на отрицательное число, неравенство останется прежним.
Если вы прибавите или вычтете на отрицательное число, неравенство останется прежним.
Не нужно было менять знак неравенства, так как обе части неравенства были поделены на положительное 3. В следующем примере есть деление на отрицательное число, поэтому в решении есть дополнительный шаг !
В следующем видео показаны примеры решения одношаговых неравенств с использованием свойства равенства умножения, где переменная находится в левой части.
Подумайте об этом
Прежде чем читать решение следующего примера, подумайте, какие свойства неравенств вам могут понадобиться для решения неравенства. Чем этот пример отличается от предыдущего? Напишите свои идеи в поле ниже.
Найти x . [latex]-\frac{1}{2}>-12x[/latex]
Показать решение
В следующем видеоролике приведены примеры решения неравенства со свойством умножения на равенство, когда переменная находится в правой части.
Объединение свойств неравенства для решения алгебраических неравенств
Популярная стратегия решения уравнений с выделением переменной также применима к решению неравенств. Складывая, вычитая, умножая и/или деля, вы можете переписать неравенство так, чтобы переменная находилась на одной стороне, а все остальное — на другой. Как и в случае одношаговых неравенств, решения многошаговых неравенств можно изобразить на числовой прямой.
Пример
Решить для x : [латекс]3x–7\ge 41[/латекс]
Показать решение
Проверьте решение.
Показать решение
При решении многошаговых уравнений обратите внимание на ситуации, когда вы умножаете или делите на отрицательное число. В этих случаях необходимо поменять знак неравенства.
В следующем видео вы увидите пример решения линейного неравенства с переменной в левой части неравенства и пример переключения направления неравенства после деления на отрицательное число.
В следующем видео вы увидите пример решения линейного неравенства с переменной в правой части неравенства и пример переключения направления неравенства после деления на отрицательное число.
Упростите и решите алгебраические неравенства, используя распределительное свойство
Как и в случае с уравнениями, распределительное свойство можно применять для упрощения выражений, являющихся частью неравенства. После того, как скобки будут очищены, решение неравенства будет простым.
Подумайте об этом
В следующем примере вам дано неравенство с термином, который выглядит сложным. Если вы сделаете паузу и подумаете, как использовать порядок операций для решения неравенства, надеюсь, это покажется простой задачей. Используйте текстовое поле, чтобы записать то, что вы считаете лучшим первым шагом.
Решите для a. [latex] \displaystyle\frac{{2}{a}-{4}}{{6}}{<2}[/latex]
Показать решение
Проверьте решение.
Показать решение
Резюме
Решение неравенств очень похоже на решение уравнений, за исключением того, что вам нужно поменять местами символы неравенства, когда вы умножаете или делите обе части неравенства на отрицательное число. Существует три способа представления решений неравенств: интервал, график и неравенство. Поскольку обычно существует более одного решения неравенства, при проверке своего ответа вы должны проверить конечную точку и еще одно значение, чтобы проверить направление неравенства.
Поскольку обычно существует более одного решения неравенства, при проверке своего ответа вы должны проверить конечную точку и еще одно значение, чтобы проверить направление неравенства.
Неравенство может иметь несколько ответов. Решения часто изображаются на числовой прямой, чтобы визуализировать все решения. Многошаговые неравенства решаются с использованием тех же процессов, что и для решения уравнений, за одним исключением. Когда вы умножаете или делите обе части неравенства на отрицательное число, вы должны перевернуть знак неравенства. Символы неравенства остаются неизменными всякий раз, когда вы добавляете или вычитаете 90 734 положительных или отрицательных 90 735 чисел с обеих сторон неравенства.
Математические неравенства: значение, примеры и графики
Неравенства представляют собой алгебраические выражения, которые вместо того, чтобы представлять, как обе части уравнения равны друг другу, представляют, как один член меньше, меньше или равен , больше или больше или равно другому.
Этот пример читается как x плюс 1 больше 3.
Обратите внимание, что стрелка символа неравенства указывает на меньшее выражение в неравенстве.
Specifically, the symbols used in inequalities are:
symbol Meaning > greater than < less than greater than or equal меньше или равно
Свойства неравенств
свойства неравенств описаны в Таблице 1:
Таблица 1. Свойства неравенства
, если A, B и C — реальные числа:
Свойство Определение Пример Дополнение Дополнение . Дополнение 0 .
IF, затем , так что Вычитание IF, то , так что Умножение , если и, если и, затем , если0010 и, SO, и, SO Дивизион IF и, если и, затем и, SO,
и, SO,
. Если и , то и , так Сравнение Если и , то и , так
900 Основные типы неравенств, которые вы можете найти:
Линейные неравенства
Линейные неравенства — это неравенства, в которых максимальный показатель степени в переменных равен степени 1.
Квадратные неравенства
Если максимальный показатель степени в неравенстве равен степени 2, такое неравенство называется квадратным.
Решение неравенств
Чтобы решить неравенства, вам придется выполнить различные шаги в зависимости от того, являются ли они линейными или квадратичными.
Решение линейных неравенств
Чтобы решить линейные неравенства, вы можете манипулировать ими, чтобы найти решение так же, как и уравнение, имея в виду следующие дополнительные правила:
Решением неравенства является множество всех вещественных неравенство верное. Следовательно, любое значение x, удовлетворяющее неравенству, является решением для x.
Символы> (больше) и <(меньше) исключают конкретное значение как часть решения. Символы (больше или равно) и (меньше или равно) включить конкретное значение как часть решения, а не исключить его.
Решение неравенства может быть представлено на числовой прямой, используя пустой кружок для обозначения того, что значение x не является частью решения , и замкнутый кружок , если значение x является частью решения .
Если умножить или разделить неравенство на отрицательное число , то нужно поменять местами символ неравенства . Лучший способ понять, зачем вам это нужно, — посмотреть пример.
Лучший способ понять, зачем вам это нужно, — посмотреть пример.
Вы знаете, что 4 > 2, но если умножить это неравенство на -1
Тогда получится -4 > -2, что неверно
Чтобы неравенство оставалось верным, нужно обратить символ , например:
-4 <-2 ✔ что верно
Это потому, что в случае отрицательных чисел, чем ближе число к нулю, тем оно больше.
Вы можете видеть -4 и -2, представленные на числовой прямой следующим образом:
Числа на числовой прямой, Marilu García De Taylor — StudySmarter Originals
Если у вас есть дробь в неравенстве, где x находится в знаменателя (т.е. ), вам нужно помнить, что x может быть как положительным, так и отрицательным. Следовательно, нельзя умножать обе части неравенства на x; вместо этого умножьте на так, чтобы неравенство продолжало оставаться верным.
Примеры решения линейных неравенств
1) x — 5> 8 выделить x и скомбинировать одинаковые члены
x> 8 + 5
x> 13
Используя обозначить , решение равно {x: x: x> 8 > 13}, которое можно прочитать как набор значений x, для которых x больше 13.
2) 2x + 2 <16 изолировать x и объединить подобные элементы
2x <16 -2
2x <14
х <7
Установите обозначение: {x: x <7}
3) 5 — x <19
— x <19 - 5
— x <14 Не забудьте изменить символ, так как вы делите на -1
x> -14
Задайте нотацию: {x:x> -14}
4) Если вам нужно найти множество значений, для которых два неравенства верны вместе, вы можете использовать числовую прямую чтобы увидеть решение более ЯСНО.
Решением будут значения, удовлетворяющие обоим уравнениям одновременно. Например:
Решение линейных неравенств с использованием числовой прямой, Marilu García De Taylor — StudySmarter Originals
Установить запись: {x: 4 Если нет перекрытия , то неравенства будут написано отдельно.
Решение линейных неравенств с использованием числовой прямой — без перекрытия, Марилу Гарсия Де Тейлор — StudySmarter Originals
Задайте обозначение: {x: x <4} ∪ {x: x> 5}
Решение квадратных неравенств
Чтобы решить квадратные неравенства, вам необходимо выполнить следующие шаги 3 :3 9. Переставьте члены
Переставьте члены
в левую часть неравенства так, чтобы в другой части был только ноль.
Перед решением квадратного неравенства вам может понадобиться раскрыть скобки и объединить одинаковые члены.
2. Решить квадратное уравнение на найти критические значения . Для этого можно разложить на множители, дополнить квадрат или воспользоваться формулой квадрата.
3. Нарисуйте график квадратичной функции. График квадратичной функции ( ) представляет собой параболу, пересекающую ось абсцисс в критических значениях. Если коэффициент при (а) отрицательный, то парабола будет перевернутой.
4. По графику найти требуемый набор значений .
Примеры решения квадратных неравенств
- Найдите множество значений x, для которых
разложите на множители, чтобы найти критические значения
(x — 2) (x + 3) = 0
критических значения : x = 2 и x = -3
Вы можете использовать таблицу, чтобы увидеть, где график будет положительным или отрицательным.
x <-3 -3 x> 2 (x — 2) — — + (x + 3) — + + (x — 2) (x + 3) + — +
Вы можете прочитать информацию в таблице следующим образом: Если x <-3, (x - 2) отрицательное, (x + 3) отрицательное и (x - 2) (x + 3) положительное, а то же самое для других столбцов. Последняя строка (x - 2) (x + 3) говорит вам, где график будет положительным или отрицательным.
Теперь вы можете нарисовать график:
График решения квадратных неравенств, Марилу Гарсиа Де Тейлор — StudySmarter Originals
Решением задачи являются значения x, где кривая выше оси x . Это происходит, когда x <-3 или x> 2. В системе обозначений: {x: x <-3} ∪ {x: x> 2}
График решения квадратных неравенств — кривая над осью x, Марилу Гарсия Де Тейлор — StudySmarter Originals
График решения квадратных неравенств — кривая под осью X, Марилу Гарсия Де Тейлор — StudySmarter Originals
Как изобразить неравенство графически?
Вам может понадобиться представить решение неравенства графически, рассмотрев графики, к которым они относятся.
В этом случае применяются следующие правила:
Значения x, для которых кривая y = f (x) на ниже кривой y = g (x), удовлетворяют неравенству f (x)
Значения x, для которых кривая y = f (x) на выше кривой y = g (x) удовлетворяют неравенству f (x) > g (x)
Примеры графического представления неравенств
Учитывая уравнения y = 3x + 10, и , найти решение неравенства
Приравняйте уравнения друг к другу, чтобы найти точки пересечения и критические значения:
разложите на множители, чтобы найти критические значения
Критические значения равны x = -2 и x = 5
Подставьте критические значения, чтобы найти точки пересечения :
Когда x = -2, A = (- 2, 4)
Когда x = 5, B = (5, 25)
Представление неравенств графически — точки пересечения, Марилу Гарсиа Де Тейлор — StudySmarter Originals
Решением являются значения x, для которых график 3x + 10 находится выше графика . Это происходит, когда -2
Это происходит, когда -2 Представление областей неравенствами
Иногда, когда вы работаете с неравенствами, вас попросят найти и закрасить область, которая одновременно удовлетворяет линейному и квадратному неравенствам.
Наилучший способ решить этот тип задач — изобразить все неравенства графически, чтобы найти область, в которой выполняются все неравенства, обращая особое внимание на следующие рекомендации:
Если неравенства содержат символы < или > , то кривая не входит в область и ее нужно изобразить пунктирной линией .
Если неравенства содержат символы или , то кривая включается в область и должна быть представлена сплошной линией .
Пример представления областей неравенствами
Закрасьте область, удовлетворяющую неравенствам:
и
В неравенстве y + x <5 используется символ <, поэтому его график представлен пунктирной линией. В неравенстве используется символ, поэтому оно представлено сплошной линией.
В неравенстве используется символ, поэтому оно представлено сплошной линией.
Область, в которой выполняются оба неравенства одновременно, закрашена синим цветом.
Графическое представление регионов в неравенствах, Марилу Гарсия Де Тейлор — StudySmarter Originals
Математика неравенств — основные выводы чем, меньше или равно, больше или больше или равно другому.
С неравенствами можно работать так же, как и с уравнениями, но необходимо учитывать несколько дополнительных правил.
При умножении или делении неравенства на отрицательное число необходимо перевернуть символ, чтобы неравенство оставалось верным.
Решением неравенства является множество всех действительных чисел, которые делают неравенство верным.
Вы можете использовать числовую прямую для одновременного представления двух или более неравенств, чтобы более четко увидеть значения, которые удовлетворяют всем неравенствам одновременно.
 Почему? Это потому, что мы умножили обе части неравенства на отрицательное число. Процесс решения упомянутых выше неравенств работает для простого линейного неравенства. Но чтобы решить любое другое сложное неравенство, мы должны использовать следующий процесс.
Почему? Это потому, что мы умножили обе части неравенства на отрицательное число. Процесс решения упомянутых выше неравенств работает для простого линейного неравенства. Но чтобы решить любое другое сложное неравенство, мы должны использовать следующий процесс.

 Решение линейных неравенств аналогично решению линейных уравнений, но следует соблюдать только правила решения неравенств (которые были объяснены ранее). Давайте посмотрим на некоторые примеры.
Решение линейных неравенств аналогично решению линейных уравнений, но следует соблюдать только правила решения неравенств (которые были объяснены ранее). Давайте посмотрим на некоторые примеры. Для решения неравенств в этом случае просто решите каждое неравенство независимо, а затем найдите окончательное решение в соответствии со следующими правилами:
Для решения неравенств в этом случае просто решите каждое неравенство независимо, а затем найдите окончательное решение в соответствии со следующими правилами:2x + 3 < -5
2x < -8
x < -4
х + 6 < 3
x < -3
 Процесс поясняется на примере, где мы собираемся решить неравенство x 2 — 4x — 5 ≥ 0.
Процесс поясняется на примере, где мы собираемся решить неравенство x 2 — 4x — 5 ≥ 0. Пошагово решим это неравенство.
Пошагово решим это неравенство.Следовательно, решением рационального неравенства (x + 2)/(x — 2) < 3 является (-∞, 2) U (4, ∞).
 Они являются математическими выражениями, в которых обе стороны не равны.
Они являются математическими выражениями, в которых обе стороны не равны.
 Вот пример. 3x — 7 < 5x - 11 ⇒ -2x < -4 ⇒ x > 2.
Вот пример. 3x — 7 < 5x - 11 ⇒ -2x < -4 ⇒ x > 2.
- Представление неравенств на числовой прямой
- Представление неравенств с использованием записи интервалов
- Использование свойств сложения и умножения для решения алгебраических неравенств и выражения их решений графически и с интервальной записью
- Решение неравенств, содержащих абсолютное значение
- Объединение свойств неравенства для выделения переменных, решение алгебраических неравенств и графическое представление их решений
- Упростите и решите алгебраические неравенства, используя распределительное свойство для очистки скобок и дробей
 Неравенство — это математическое утверждение, которое сравнивает два выражения, используя понятия больше или меньше. В этих операторах используются специальные символы. Когда вы читаете неравенство, читайте его слева направо — так же, как читаете текст на странице. В алгебре неравенства используются для описания больших наборов решений. Иногда существует бесконечное количество чисел, удовлетворяющих неравенству, поэтому вместо того, чтобы пытаться перечислить бесконечное количество чисел, мы разработали несколько способов краткого описания очень больших списков.
Неравенство — это математическое утверждение, которое сравнивает два выражения, используя понятия больше или меньше. В этих операторах используются специальные символы. Когда вы читаете неравенство, читайте его слева направо — так же, как читаете текст на странице. В алгебре неравенства используются для описания больших наборов решений. Иногда существует бесконечное количество чисел, удовлетворяющих неравенству, поэтому вместо того, чтобы пытаться перечислить бесконечное количество чисел, мы разработали несколько способов краткого описания очень больших списков.

 Графики — очень полезный способ визуализации информации, особенно когда эта информация представляет собой бесконечный список чисел!
Графики — очень полезный способ визуализации информации, особенно когда эта информация представляет собой бесконечный список чисел! Это показано линией со стрелкой на конце. Например, обратите внимание, что для графика [латекс] \displaystyle x\geq -3[/латекс], показанного выше, конечная точка равна [латекс]−3[/латекс], представленная замкнутым кругом, поскольку неравенство равно больше или равно [латекс]−3[/латекс]. Синяя линия рисуется справа от числовой строки, потому что значения в этой области больше, чем [латекс]-3[/латекс]. Стрелка в конце указывает, что решения продолжаются бесконечно.
Это показано линией со стрелкой на конце. Например, обратите внимание, что для графика [латекс] \displaystyle x\geq -3[/латекс], показанного выше, конечная точка равна [латекс]−3[/латекс], представленная замкнутым кругом, поскольку неравенство равно больше или равно [латекс]−3[/латекс]. Синяя линия рисуется справа от числовой строки, потому что значения в этой области больше, чем [латекс]-3[/латекс]. Стрелка в конце указывает, что решения продолжаются бесконечно. Несколько примеров интервала или набора чисел, в которые попадает решение: [латекс]\влево[-2,6\вправо)[/латекс], или все числа между [латекс]-2[/ латекс] и [латекс]6[/латекс], включая [латекс]-2[/латекс], но не включая [латекс]6[/латекс]; [латекс]\влево(-1,0\вправо)[/латекс], все действительные числа между, но не включая [латекс]-1[/латекс] и [латекс]0[/латекс]; и [latex]\left(-\infty,1\right][/latex], все действительные числа меньше и включая [latex]1[/latex]. В приведенной ниже таблице показаны возможные варианты. Не забывайте читать неравенства слева направо точно так же, как текст.
Несколько примеров интервала или набора чисел, в которые попадает решение: [латекс]\влево[-2,6\вправо)[/латекс], или все числа между [латекс]-2[/ латекс] и [латекс]6[/латекс], включая [латекс]-2[/латекс], но не включая [латекс]6[/латекс]; [латекс]\влево(-1,0\вправо)[/латекс], все действительные числа между, но не включая [латекс]-1[/латекс] и [латекс]0[/латекс]; и [latex]\left(-\infty,1\right][/latex], все действительные числа меньше и включая [latex]1[/latex]. В приведенной ниже таблице показаны возможные варианты. Не забывайте читать неравенства слева направо точно так же, как текст.


[латекс]10>5[/латекс]
[латекс]10>5[/латекс]
[латекс]10\cdot 2>5\cdot 2[/латекс]
[латекс]10\cdot-2>5 \\ \,\,\,\,\,\cdot -2\,\cdot-2[/латекс]
[латекс]20>10[/латекс]

[латекс]−20>−10[/латекс]
[латекс]−20<−10[/латекс]
 Если вы прибавите или вычтете на отрицательное число, неравенство останется прежним.
Если вы прибавите или вычтете на отрицательное число, неравенство останется прежним.


 Поскольку обычно существует более одного решения неравенства, при проверке своего ответа вы должны проверить конечную точку и еще одно значение, чтобы проверить направление неравенства.
Поскольку обычно существует более одного решения неравенства, при проверке своего ответа вы должны проверить конечную точку и еще одно значение, чтобы проверить направление неравенства.

и, SO,
и, SO,

Решением неравенства является множество всех вещественных неравенство верное. Следовательно, любое значение x, удовлетворяющее неравенству, является решением для x.
Символы> (больше) и <(меньше) исключают конкретное значение как часть решения. Символы (больше или равно) и (меньше или равно) включить конкретное значение как часть решения, а не исключить его.
Решение неравенства может быть представлено на числовой прямой, используя пустой кружок для обозначения того, что значение x не является частью решения , и замкнутый кружок , если значение x является частью решения .
Если умножить или разделить неравенство на отрицательное число , то нужно поменять местами символ неравенства .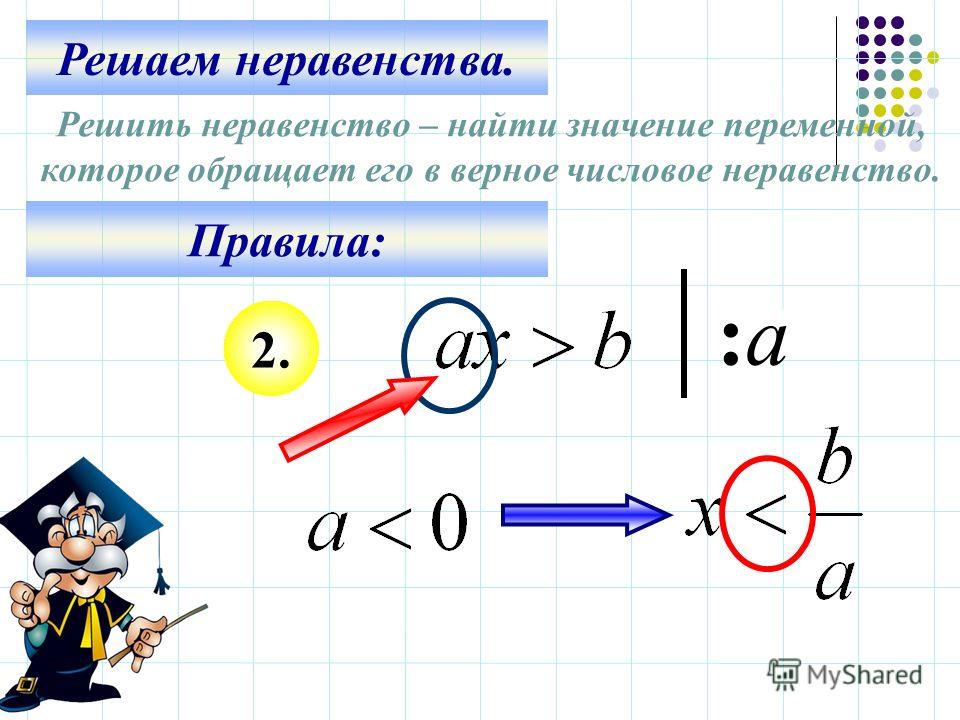 Лучший способ понять, зачем вам это нужно, — посмотреть пример.
Лучший способ понять, зачем вам это нужно, — посмотреть пример.
Если у вас есть дробь в неравенстве, где x находится в знаменателя (т.е. ), вам нужно помнить, что x может быть как положительным, так и отрицательным. Следовательно, нельзя умножать обе части неравенства на x; вместо этого умножьте на так, чтобы неравенство продолжало оставаться верным.

Если нет перекрытия , то неравенства будут написано отдельно.
Решение линейных неравенств с использованием числовой прямой — без перекрытия, Марилу Гарсия Де Тейлор — StudySmarter Originals
Задайте обозначение: {x: x <4} ∪ {x: x> 5}
Решение квадратных неравенств
3 9. Переставьте члены
Переставьте члены
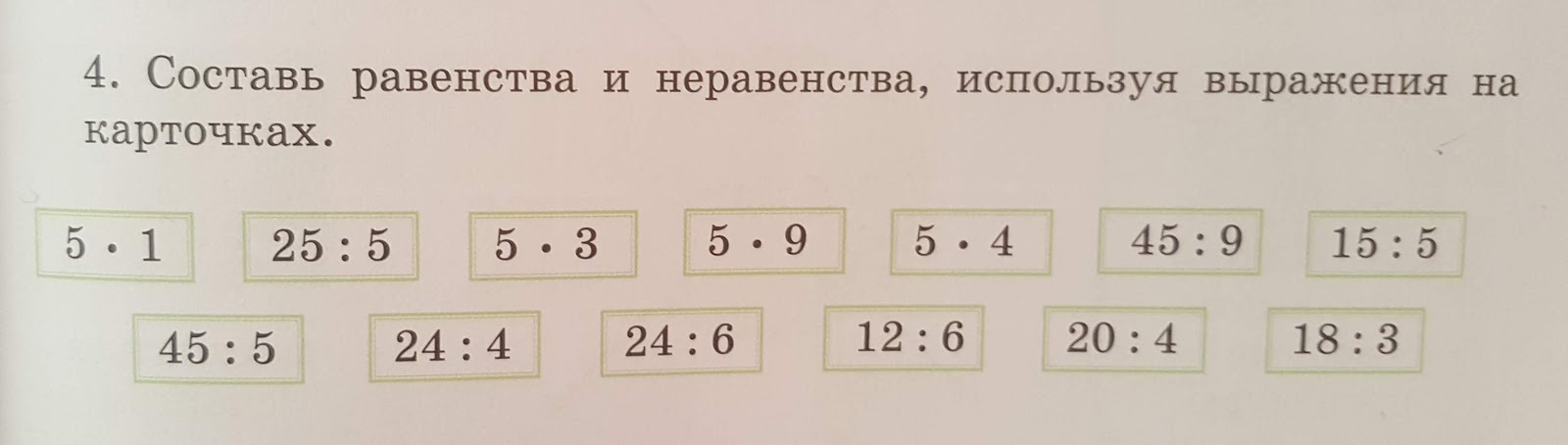

Значения x, для которых кривая y = f (x) на ниже кривой y = g (x), удовлетворяют неравенству f (x)
Значения x, для которых кривая y = f (x) на выше кривой y = g (x) удовлетворяют неравенству f (x) > g (x)
 Это происходит, когда -2
Это происходит, когда -2 Представление областей неравенствами
Иногда, когда вы работаете с неравенствами, вас попросят найти и закрасить область, которая одновременно удовлетворяет линейному и квадратному неравенствам.
Наилучший способ решить этот тип задач — изобразить все неравенства графически, чтобы найти область, в которой выполняются все неравенства, обращая особое внимание на следующие рекомендации:
Если неравенства содержат символы < или > , то кривая не входит в область и ее нужно изобразить пунктирной линией .
Если неравенства содержат символы или , то кривая включается в область и должна быть представлена сплошной линией .
Пример представления областей неравенствами
Закрасьте область, удовлетворяющую неравенствам:
и
В неравенстве y + x <5 используется символ <, поэтому его график представлен пунктирной линией. В неравенстве используется символ, поэтому оно представлено сплошной линией.
В неравенстве используется символ, поэтому оно представлено сплошной линией.
Область, в которой выполняются оба неравенства одновременно, закрашена синим цветом.
Графическое представление регионов в неравенствах, Марилу Гарсия Де Тейлор — StudySmarter Originals
Математика неравенств — основные выводы чем, меньше или равно, больше или больше или равно другому.
С неравенствами можно работать так же, как и с уравнениями, но необходимо учитывать несколько дополнительных правил.
При умножении или делении неравенства на отрицательное число необходимо перевернуть символ, чтобы неравенство оставалось верным.
Решением неравенства является множество всех действительных чисел, которые делают неравенство верным.
Вы можете использовать числовую прямую для одновременного представления двух или более неравенств, чтобы более четко увидеть значения, которые удовлетворяют всем неравенствам одновременно.





 Получим -3<-y<-2.
Получим -3<-y<-2.

 «>
«>