Как решить квадратное уравнение через дискриминант: § Дискриминант. Решение квадратных уравнений через дискриминант

Квадратное уравнение с чётным вторым коэффициентом

Если в квадратном уравнении ax² + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D₁ = k² − ac, а корни по формулам и .

Примеры

Решим квадратное уравнение x² + 6x − 16 = 0. В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k.

Любое четное число n можно представить в виде произведения числа 2 и числа k, то есть 2k.

n = 2k

Например, число 10 можно представить как 2 × 5.

10 = 2 × 5

В этом произведении k = 5.

---

Число 12 можно представить как 2 × 6.

12 = 2 × 6

В этом произведении k = 6.

---

Число −14 можно представить как 2 × (−7)

В этом произведении k = −7.

Как видим, сомножитель 2 не меняется. Меняется только сомножитель k.

В уравнении x² + 6x − 16 = 0 вторым коэффициентом является число 6. Это число можно представить как 2 × 3. В этом произведении k = 3. Теперь можно воспользоваться формулами для чётного коэффициента.

Найдем дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = 3² − 1 × (−16) = 9 + 16 = 25

Теперь вычислим корни по формулам: и .

Значит корнями уравнения x² + 6x − 16 = 0 являются числа 2 и −8.

В отличие от стандартной формулы для вычисления дискриминанта (D=b² − 4ac), в формуле D₁ = k² − ac не нужно выполнять умножение числа 4 на ac.

И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.

---

Пример 2. Решить квадратное уравнение 5x² − 6x + 1=0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3). То есть k = −3. Найдём дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = (−3)² − 5 × 1 = 9 − 5 = 4

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

---

Пример 3. Решить квадратное уравнение x² − 10x − 24 = 0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5). То есть k = −5. Найдём дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = (−5)² − 1 × (−24) = 25 + 24 = 49

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Обычно для определения числа k поступают так: делят второй коэффициент на 2.

Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2k. Чтобы из этого равенства выразить сомножитель k, нужно произведение b разделить на сомножитель 2

Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2

---

Пример 5. Решить квадратное уравнение

Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k. Получается, что

Найдём дискриминант по формуле D₁ = k² − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.

В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .

Вычислим второй корень уравнения:

---

Вывод формул

Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.

Рассмотрим квадратное уравнение ax² + bx + c = 0. Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k

b = 2k

Заменим в уравнении ax² + bx + c = 0 коэффициент b на выражение 2k

ax² + 2kx + c = 0

Теперь вычислим дискриминант по ранее известной формуле:

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac

Вынесем в получившемся выражении за скобки общий множитель 4

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac = 4(k² − ac)

Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k² − ac.

В выражении 4(k² − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k² − ac. Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.

То есть выражение k² − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D₁

D₁ = k² − ac

Теперь посмотрим как выводятся формулы и .

В нашем уравнении ax² + bx + c = 0 коэффициент b заменён на выражение 2k. Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k. Также на забываем, что D у нас равно выражению 4(k² − ac)

Но ранее было сказано, что выражение k² − ac обозначается через D₁. Тогда в наших преобразованиях следует сделать и эту замену:

Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:

Теперь в получившемся выражении вынесем за скобки общий множитель 2

Сократим получившуюся дробь на 2

Аналогично вывóдится формула для вычисления второго корня:

Задания для самостоятельного решения

Задание 1. Решить уравнение:

Решение:

Ответ: 1; 0,6

Показать решение

Задание 2. Решить уравнение:

Решение:

Ответ:

Показать решение

Задание 3. Решить уравнение:

Решение:

Ответ: 1; −1,4

Показать решение

Задание 4. Решить уравнение:

Решение:

Ответ:

Показать решение

Задание 5. Решить уравнение:

Решение:

Ответ:

Показать решение

Задание 6. Решить уравнение:

Решение:

Ответ:

Показать решение

Задание 7. Решить уравнение:

Решение:

Ответ

:

Показать решение

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Квадратное уравнение где дискриминант равен нулю. Решение квадратных уравнений с помощью дискриминанта

Дискриминант, как и квадратные уравнения начинают изучать в курсе алгебры в 8 классе. Решить квадратное уравнение можно через дискриминант и с помощью теоремы Виета. Методика изучения квадратных уравнений, как и формулы дискриминанта достаточно неудачно прививается школьникам, как и многое в настоящем образовании. 2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D) :
D>0 – уравнение имеет 2 различных действительных корня;

D=0 — уравнение имеет 1 корень (2 совпадающих корня):
D Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра. .

Общая формула для нахождения корней квадратного уравнения :

Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле

Вторая способ нахождения корней — это Теорема Виета.

Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)

Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни

До 4 уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6, следовательно корнями могут быть значения (1, 6) и (2, 3) или пары с противоположным знаком. Сумма корней равна 7 (коэффициент при переменной с противоположным знаком).

Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».

Давайте попробуем разобраться,

что описывает дискриминант?

В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox

Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0) ,

или парабола ветвями вниз (a

Вершина параболы лежит посередине между корнями

Физический смысл дискриминанта:

Если дискриминант больше нуля (D>0) парабола имеет две точки пересечения с осью Ox .
Если дискриминант равен нулю (D=0) то парабола в вершине касается оси абсцисс.
И последний случай, когда дискриминант меньше нуля (D

Неполные квадратные уравнения

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Виды квадратных уравнений

Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.

Говоря математическим языком, квадратное уравнение — это уравнение вида:

Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:

Здесь а =1; b = 3; c = -4

Здесь а =2; b = -0,5; c = 2,2

Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

В этих квадратных уравнениях слева присутствует

полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.

Такие квадратные уравнения называются полными.

А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:

5х 2 -25 = 0,

2х 2 -6х=0,

-х 2 +4х=0

И т. п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:

2х 2 =0,

-0,3х 2 =0

Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.

Кстати, почему а не может быть равно нулю? А вы подставьте вместо

а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а , b и c .

Формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем

со своими знаками! Например, в уравнении:

а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок

резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения .

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .

Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно.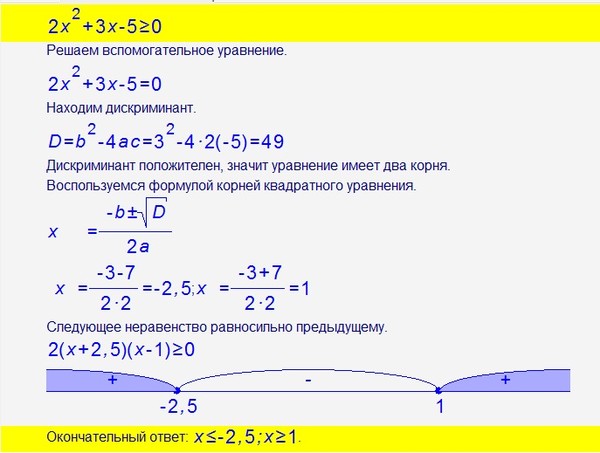

В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1 — то, что меньше, а х 2 — то, что больше.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х 1 = -3 , х 2 = 3 .

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

Дискриминант. Формула дискриминанта.

Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:

Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:

D = b 2 — 4ac

И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)

Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.

Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Теперь можно и порешать.)

Решить уравнения:

8х 2 — 6x + 1 = 0

х 2 + 3x + 8 = 0

х 2 — 4x + 4 = 0

(х+1) 2 + x + 1 = (x+1)(x+2)

Ответы (в беспорядке):

х 1 = 0
х 2 = 5

х 1,2 = 2

х 1 = 2
х 2 = -0,5

х — любое число

х 1 = -3
х 2 = 3

решений нет

х 1 = 0,25
х 2 = 0,5

Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.

Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

В данной статье мы рассмотрим решение неполных квадратных уравнений.

Но сначала повторим какие уравнения называются квадратными. Уравнение вида ах 2 + bх + с = 0, где х – переменная, а коэффициенты а, b и с некоторые числа, причем а ≠ 0, называется квадратным . Как мы видим коэффициент при х 2 не равен нулю, а следовательно коэффициенты при х или свободный член могут равняться нулю, в этом случае мы и получаем неполное квадратное уравнение.

Неполные квадратные уравнения бывают трех видов :

1) Если b = 0, с ≠ 0, то ах 2 + с = 0;

2) Если b ≠ 0, с = 0, то ах 2 + bх = 0;

3) Если b= 0, с = 0, то ах 2 = 0.

• Давайте разберемся как решаются уравнения вида ах 2 + с = 0.

Чтобы решить уравнение перенесем свободный член с в правую часть уравнения, получим

ах 2 = ‒с. Так как а ≠ 0, то разделим обе части уравнения на а, тогда х 2 = ‒с/а.

Если ‒с/а > 0 , то уравнение имеет два корня

x = ±√(–c/a) .

Если же ‒c/a

Давайте попробуем разобраться на примерах, как решать такие уравнения.

Пример 1 . Решите уравнение 2х 2 ‒ 32 = 0.

Ответ: х 1 = ‒ 4, х 2 = 4.

Пример 2 . Решите уравнение 2х 2 + 8 = 0.

Ответ: уравнение решений не имеет.

• Разберемся как же решаются уравнения вида ах 2 + bх = 0.

Чтобы решить уравнение ах 2 + bх = 0, разложим его на множители, то есть вынесем за скобки х, получим х(ах + b) = 0. Произведение равно нулю, если хотя бы один из множителей равен нулю. Тогда или х = 0, или ах + b = 0. Решая уравнение ах + b = 0, получим ах = ‒ b, откуда х = ‒ b/a. Уравнение вида ах 2 + bх = 0, всегда имеет два корня х 1 = 0 и х 2 = ‒ b/a. Посмотрите как выглядит на схеме решение уравнений этого вида.

Закрепим наши знания на конкретном примере.

Пример 3 . Решить уравнение 3х 2 ‒ 12х = 0.

х(3х ‒ 12) = 0

х= 0 или 3х – 12 = 0

Ответ: х 1 = 0, х 2 = 4.

• Уравнения третьего вида ах 2 = 0 решаются очень просто.

Если ах 2 = 0, то х 2 = 0. Уравнение имеет два равных корня х 1 = 0, х 2 = 0.

Для наглядности рассмотрим схему.

Убедимся при решении примера 4, что уравнения этого вида решаются очень просто.

Пример 4. Решить уравнение 7х 2 = 0.

Ответ: х 1, 2 = 0.

Не всегда сразу понятно какой вид неполного квадратного уравнения нам предстоит решить. Рассмотрим следующий пример.

Пример 5. Решить уравнение

Умножим обе части уравнения на общий знаменатель, то есть на 30

Сократим

5(5х 2 + 9) – 6(4х 2 – 9) = 90.

Раскроем скобки

25х 2 + 45 – 24х 2 + 54 = 90.

Приведем подобные

Перенесем 99 из левой части уравнения в правую, изменив знак на противоположный

Ответ: корней нет.

Мы разобрали как решаются неполные квадратные уравнения. Надеюсь, теперь у вас не будет сложностей с подобными заданиями. Будьте внимательны при определении вида неполного квадратного уравнения, тогда у вас все получится.

Если у вас появились вопросы по данной теме, записывайтесь на мои уроки , мы вместе решим возникшие проблемы.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Рассмотрим задачу. Основание прямоугольника больше высоты на 10 см., а его площадь равна 24 см². Найти высоту прямоугольника. Пусть х сантиметров — высота прямоугольника, тогда его основание равно (х +10) см. Площадь этого прямоугольника равна х (х + 10) см². По условию задачи х (х + 10) = 24. Раскрывая скобки и перенося число 24 с противоположным знаком в левую часть уравнения, получаем: х ² + 10х -24 = 0. При решении этой задачи было получено уравнение, которое называют квадратным.

Квадратным уравнением называется уравнение вида

ax ²+bx +c= 0

где a, b, c — заданные числа, причем а ≠ 0, а х — неизвестное.

Коэффициенты a, b, c квадратного уравнения обычно называют так: a — первым или старшим коэффициентом, b — вторым коэффициентом, c — свободным членом. Например в нашей задаче старший коэффициент равен 1, второй коэффициент 10, свободный член -24. Решение многих задач математики и физики сводится к решению квадратных уравнений.

Решение квадратных уравнений

Полные квадратные уравнения. Первым делом надо заданное уравнение привести к стандартному виду ax ²+ bx + c = 0. Вернемся к нашей задаче, в которой уравнение может быть записано как х (х + 10) = 24 приведем его к стандартному виду, раскроем скобки х ² + 10х — 24 = 0, решим это уравнение с помощью формулы корней квадратного уравнения общего вида.

Выражение под знаком корня в этой формуле называется дискриминант D = b ² — 4ac

Если D>0, то квадратное уравнение имеет два различных корня, которые можно найти по формуле корней квадратного уравнения.

Если D=0, то квадратное уравнение имеет один корень.

Если D

Подставим значения в нашу формулу а = 1, b = 10, c = -24.

получаем D>0, следовательно у нас получится два корня.

Рассмотрим пример где D=0, при этом условии должен получится один корень.

25x ² — 30x + 9 = 0

Рассмотрим пример где D

2x ² + 3x + 4 = 0

Число, стоящее под знаком корня (дискриминант) отрицательное, ответ запишем так: уравнение не имеет действительных корней.

Решение неполных квадратных уравнений

Квадратное уравнение ax ² + bx + c = 0 называют неполным, если хотя бы один из коэффициентов b или c равен нулю. Неполное квадратное уравнение, есть уравнение одного из следующих видов:

ax ² = 0,

ax ² + c = 0, c ≠ 0,

ax ² + bx = 0, b ≠ 0.

Рассмотрим несколько примеров, решим уравнение

Разделив обе части уравнения на 5, получим уравнение х ² = 0, в ответе будет один корень х = 0.

Рассмотрим уравнение вида

3х ² — 27 = 0

Разделив обе части на 3, получим уравнение х ² — 9 = 0, или его можно записать х ² = 9, в ответе будет два корня х = 3 и х = -3.

Рассмотрим уравнение вида

2х ² + 7 = 0

Разделив обе части на 2, получим уравнение х ² = -7/2. Это уравнение действительных корней не имеет, так как х ² ≥ 0 для любого действительного числа х .

Рассмотрим уравнение вида

3х ² + 5х = 0

Разложив левую часть уравнения на множители, получим х (3х + 5) = 0, в ответе будет два корня х = 0, х =-5/3.

Самое главное при решении квадратных уравнений, привести квадратное уравнение к стандартному виду, выучить наизусть формулу корней квадратного уравнения общего вида и не запутаться в знаках.

Библиографическое описание: Гасанов А. Р., Курамшин А. А., Ельков А. А., Шильненков Н. В., Уланов Д. Д., Шмелева О. В. Способы решения квадратных уравнений // Юный ученый. — 2016. — №6.1. — С. 17-20..03.2019).



Наш проект посвящен способам решения квадратных уравнений. Цель проекта: научиться решать квадратные уравнения способами, не входящими в школьную программу. Задача: найти все возможные способы решения квадратных уравнений и научиться их использовать самим и познакомить одноклассников с этими способами.

Что же такое «квадратные уравнения»?

Квадратное уравнение — уравнение вида ax 2 + bx + c = 0 , где a , b , c — некоторые числа (a ≠ 0 ), x — неизвестное.

Числа a, b,c называются коэффициентами квадратного уравнения.

• a называется первым коэффициентом;
• b называется вторым коэффициентом;
• c — свободным членом.

А кто же первый «изобрёл» квадратные уравнения?

Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Найденные древние вавилонские глиняные таблички, датированные где-то между 1800 и 1600 годами до н.э., являются самыми ранними свидетельствами об изучении квадратных уравнений. На этих же табличках изложены методы решения некоторых типов квадратных уравнений.

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Вавилонские математики примерно с IV века до н.э. использовали метод дополнения квадрата для решения уравнений с положительными корнями. Около 300 года до н.э. Эвклид придумал более общий геометрический метод решения. Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был индийский ученый Брахмагупта (Индия, VII столетие нашей эры).

Брахмагупта изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ax2 + bх = с, а>0

В этом уравнении коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корням», т. е. ах2 = bх.

2) «Квадраты равны числу», т. е. ах2 = с.

3) «Корни равны числу», т. е. ах2 = с.

4) «Квадраты и числа равны корням», т. е. ах2 + с = bх.

5) «Квадраты и корни равны числу», т. е. ах2 + bх =с.

6) «Корни и числа равны квадратам», т. е. bх + с == ах2.

Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи . Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.

Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья,Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Рассмотрим несколько способов решения квадратных уравнений.

Стандартные способы решения квадратных уравнений из школьной программы:

1. Разложение левой части уравнения на множители.
2. Метод выделения полного квадрата.
3. Решение квадратных уравнений по формуле.
4. Графическое решение квадратного уравнения.
5. Решение уравнений с использованием теоремы Виета.

Остановимся подробнее на решение приведенных и не приведенных квадратных уравнений по теореме Виета.

Напомним, что для решения приведенных квадратных уравнений достаточно найти два числа такие, произведение которых равно свободному члену, а сумма — второму коэффициенту с противоположным знаком.

Пример. x 2 -5x+6=0

Нужно найти числа, произведение которых равно 6, а сумма 5. Такими числами будут 3 и 2.

Ответ: x 1 =2, x 2 =3.

Но можно использовать этот способ и для уравнений с первым коэффициентом не равным единице.

Пример. 3x 2 +2x-5=0

Берём первый коэффициент и умножаем его на свободный член: x 2 +2x-15=0

Корнями этого уравнения будут числа, произведение которых равно — 15, а сумма равна — 2. Эти числа — 5 и 3. Чтобы найти корни исходного уравнения, полученные корни делим на первый коэффициент.

Ответ: x 1 =-5/3, x 2 =1

6. Решение уравнений способом «переброски».

Рассмотрим квадратное уравнение ах 2 + bх + с = 0, где а≠0.

Умножая обе его части на а, получаем уравнение а 2 х 2 + аbх + ас = 0.

Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у 2 + by + ас = 0, равносильному данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.

Окончательно получаем х 1 = у 1 /а и х 2 = у 2 /а.

При этом способе коэффициент a умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Пример. 2х 2 — 11х + 15 = 0.

«Перебросим» коэффициент 2 к свободному члену и сделав замену получим уравнение у 2 — 11у + 30 = 0.

Согласно обратной теореме Виета

у 1 = 5, х 1 = 5/2, х 1 =2,5 ;у 2 = 6, x 2 = 6/2, x 2 = 3.

Ответ: х 1 =2,5; х 2 = 3.

7. Свойства коэффициентов квадратного уравнения.

Пусть дано квадратное уравнение ах 2 + bх + с = 0, а ≠ 0.

1. Если a+ b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х 1 = 1.

2. Если а — b + с = 0, или b = а + с, то х 1 = — 1.

Пример. 345х 2 — 137х — 208 = 0.

Так как а + b + с = 0 (345 — 137 — 208 = 0), то х 1 = 1, х 2 = -208/345.

Ответ: х 1 =1; х 2 = -208/345 .

Пример. 132х 2 + 247х + 115 = 0

Т.к. a-b+с = 0 (132 — 247 +115=0), то х 1 = — 1, х 2 = — 115/132

Ответ: х 1 = — 1; х 2 =- 115/132

Существуют и другие свойства коэффициентов квадратного уравнения. но ихиспользование более сложное.

8. Решение квадратных уравнений с помощью номограммы.

Рис 1. Номограмма

Это старый и в настоящее время забытый способ решения квадратных уравнений, помещенный на с.83 сборника: Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.

Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.

Криволинейная шкала номограммы построена по формулам (рис. 1):

Полагая ОС = р, ED = q, ОЕ = а (все в см), из рис. 1 подобия треугольников САН и CDF получим пропорцию

откуда после подстановок и упрощений вытекает уравнение z 2 + pz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.

Рис. 2 Решение квадратных уравнения с помощью номограммы

Примеры.

1) Для уравнения z 2 — 9z + 8 = 0 номограмма дает корни z 1 = 8,0 и z 2 = 1,0

Ответ:8,0; 1,0.

2) Решим с помощью номограммы уравнение

2z 2 — 9z + 2 = 0.

Разделим коэффициенты этого уравнения на 2, получим уравнение z 2 — 4,5z + 1 = 0.

Номограмма дает корни z 1 = 4 и z 2 = 0,5.

Ответ: 4; 0,5.

9. Геометрический способ решения квадратных уравнений.

Пример. х 2 + 10х = 39.

В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».

Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5x. Полученную фигуру дополняют затем до нового квадрата АВСD, достраивая в углах четыре равных квадрата, сторона каждого из них 2,5, а площадь 6,25

Рис. 3 Графический способ решения уравнения х 2 + 10х = 39

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4∙2,5x = 10х) и четырех пристроенных квадратов (6,25∙ 4 = 25) , т.е. S = х 2 + 10х = 25. Заменяя х 2 + 10х числом 39, получим что S = 39+ 25 = 64, откуда следует, что сторона квадрата АВСD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

10. Решение уравнений с использованием теоремы Безу.

Теорема Безу. Остаток от деления многочлена P(x) на двучлен x — α равен P(α) (т.е. значению P(x) при x = α).

Если число α является корнем многочлена P(x), то этот многочлен делится на x -α без остатка.

Пример. х²-4х+3=0

Р(x)= х²-4х+3, α: ±1,±3, α =1, 1-4+3=0. Разделим Р(x) на (х-1):(х²-4х+3)/(х-1)=х-3

х²-4х+3=(х-1)(х-3), (х-1)(х-3)=0

х-1=0; х=1, или х-3=0, х=3; Ответ: х 1 =2, х 2 =3.

Вывод: Умение быстро и рационально решать квадратные уравнения просто необходимо для решения более сложных уравнений, например, дробно-рациональных уравнений, уравнений высших степеней, биквадратных уравнений, а в старшей школе тригонометрических, показательных и логарифмических уравнений. Изучив все найденные способы решения квадратных уравнений, мы можем посоветовать одноклассникам, кроме стандартных способов, решение способом переброски (6) и решение уравнений по свойству коэффициентов (7), так как они являются более доступными для понимания.

Литература:

1. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
2. Алгебра 8 класс: учебник для 8 кл. общеобразоват. учреждений Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. под ред. С. А. Теляковского 15-е изд., дораб. — М.: Просвещение, 2015
3. https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
4. Глейзер Г. И. История математики в школе. Пособие для учителей. / Под ред. В.Н. Молодшего. — М.: Просвещение, 1964.

Формула когда дискриминант равен 1. Решение квадратных уравнений с помощью дискриминанта

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x 2 − 8x + 12 = 0;
2. 5x 2 + 3x + 7 = 0;
3. x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

1. x 2 − 2x − 3 = 0;
2. 15 − 2x − x 2 = 0;
3. x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x 2 + 9x = 0;
2. x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x 2 − 7x = 0;
2. 5x 2 + 30 = 0;
3. 4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Прежде чем мы узнаем, как найти дискриминант квадратного уравнения вида ax2+bx+c=0 и как найти корни данного уравнения, нам необходимо вспомнить определение квадратного уравнения. Уравнение, которое имеет вид ax 2 + bx + c = 0 (где a,b и c — любые числа, также надо помнить, что a ≠ 0) является квадратным. Все квадратные уравнения мы разделим на три разряда:

1. те, у которых нет корней;
2. имеется один корень в уравнении;
3. есть два корня.

Для того чтобы определить количество корней в уравнении нам необходим дискриминант.

Как найти дискриминант. Формула

Нам дано: ax 2 + bx + c = 0.

Формула дискриминанта: D = b 2 — 4ac .

Как найти корни дискриминанта

По знаку дискриминанта определяется количество корней:

1. D = 0, у уравнения один корень;
2. D > 0, у уравнения два корня.

Корни у квадратного уравнения находятся по следующей формуле:

X1= -b + √D/2а; X2= -b + √D/2a.

Если D = 0, то Вы можете смело использовать любую из представленных формул. У Вас получится одинаковый ответ в любом случае. А если получается так, что D > 0, то тогда Вам не придется ничего считать, так как корней уравнение не имеет.

Надо сказать, что находить дискриминант — это не так уж сложно, если знать формулы и внимательно осуществлять подсчеты. Иногда возникают ошибки при подстановке отрицательных чисел в формулу (нужно помнить, что минус на минус дает плюс). Будьте внимательны, и все получится!

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Виды квадратных уравнений

Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.

Говоря математическим языком, квадратное уравнение — это уравнение вида:

Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:

Здесь а =1; b = 3; c = -4

Здесь а =2; b = -0,5; c = 2,2

Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.

Такие квадратные уравнения называются полными.

А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:

5х 2 -25 = 0,

2х 2 -6х=0,

-х 2 +4х=0

И т. п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:

2х 2 =0,

-0,3х 2 =0

Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.

Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а , b и c .

Формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня называется дискриминант .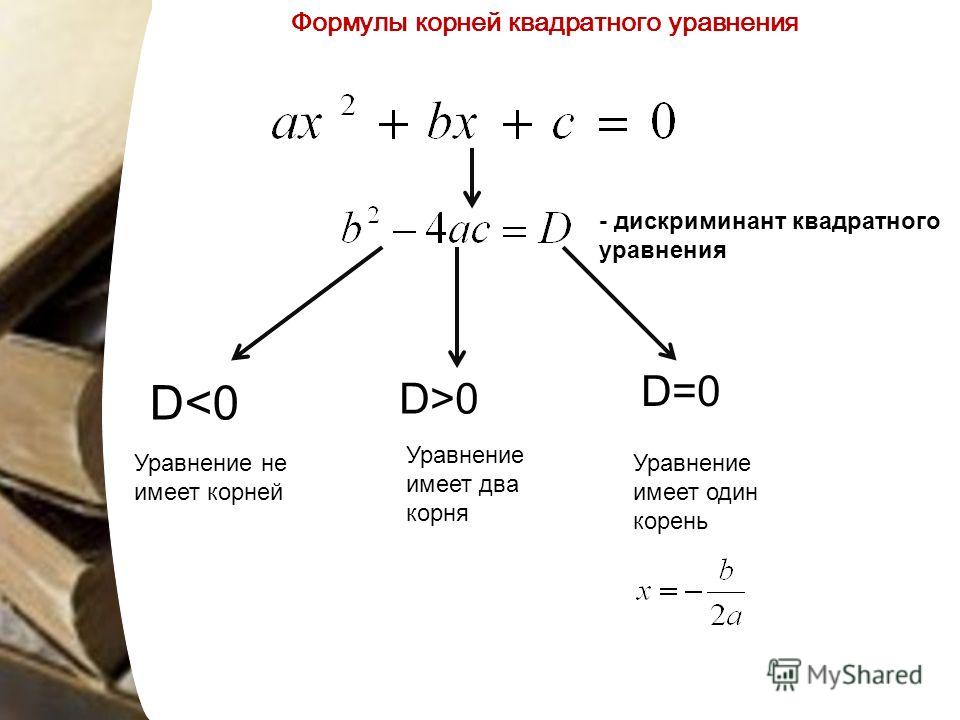 Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:

а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения .

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .

Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1 — то, что меньше, а х 2 — то, что больше.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х 1 = -3 , х 2 = 3 .

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

Дискриминант. Формула дискриминанта.

Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:

Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:

D = b 2 — 4ac

И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)

Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.

Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Теперь можно и порешать.)

Решить уравнения:

8х 2 — 6x + 1 = 0

х 2 + 3x + 8 = 0

х 2 — 4x + 4 = 0

(х+1) 2 + x + 1 = (x+1)(x+2)

Ответы (в беспорядке):

х 1 = 0
х 2 = 5

х 1,2 = 2

х 1 = 2
х 2 = -0,5

х — любое число

х 1 = -3
х 2 = 3

решений нет

х 1 = 0,25
х 2 = 0,5

Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. 2
D1>0, значит, уравнение имеет 2 корня
x1,2= k +/ квадратный корень из D1)/a
x1= (-(-12) +9)/3=21/3=7
x2= (-(-12) -9)/3=3/3=1

Оценили на сколько легче решение?;)
Спасибо за внимание, желаю Вам успехов в учебе =)

• В нашем случае в уравнениях D и D1 были >0 и мы получили по 2 корня. Если бы было D=0 и D1=0, то мы получили бы по одному корню, а если бы было D
• Через корень дискриминанта (D1) можно решать только те уравнения, в которых член b четный(!)

Использование дискриминанта и его понимание – легко

В вашем браузере деактивирован JavaScript.

Чтобы получить доступ ко всем функциям нашего веб-сайта,
активируйте JavaScript для вашего браузера.

Попробуйте 30 дней бесплатно

Узнайте, почему более 1,2 МИЛЛИОНА студентов выбирают диван-репетитор!

org/BreadcrumbList»>
• Математика
• Алгебра 1
• Квадратные уравнения/функции
• Использование и понимание дискриминанта

Рейтинг

Ø 5,0 / 2 балла

Вы должны войти в систему, чтобы иметь возможность дать оценку.

Вау, спасибо!
Пожалуйста, оцените нас и в Google! Мы с нетерпением ждем этого!

Перейти в Google

Авторы

Крис Регер

Основы по теме

Использование и понимание дискриминанта

Квадратное уравнение стандартной формы ax² + bx + c = 0 можно решить различными способами. К ним относятся разложение на множители, завершение квадрата, построение графика и использование квадратичной формулы. Нахождение корней или решений квадратного уравнения с помощью квадратной формулы часто является наиболее удобным способом. Решения квадратного уравнения можно определить по следующей квадратной формуле: x = [-b ± √(b²-4ac)] / 2a. Мы можем предсказать количество решений квадратного уравнения, оценив дискриминант, заданный b²-4ac, или подкоренное выражение в квадратной формуле. Значение дискриминанта определяет характер и количество решений квадратного уравнения.

Если b²-4ac положителен, будет два различных реальных решения.

Например, квадратное уравнение x² — 7x + 12 = 0 имеет два различных действительных решения, поскольку b²-4ac = (-7)² — 4(1)(12) = 49 — 48 = 1 положительно.

Если b²-4ac равно нулю, будет одно отличное действительное решение.

Например, квадратное уравнение 4x² — 4x + 1 = 0 имеет единственное действительное решение, поскольку b²-4ac = (-4)² — 4(4)(1) = 16 — 16 = 0.

Если b2 -4ac отрицательно, реальных решений нет.

Например, квадратное уравнение 5x² + 2x + 3 = 0 не имеет действительных решений, поскольку b2-4ac = (2)² — 4(5)(3) = 4 — 60 = -56 отрицательно.

Решение квадратных уравнений с вещественными коэффициентами, имеющих комплексные решения.

CCSS.MATH.CONTENT.HSN.CN.C.7

Стенограмма

Использование и понимание дискриминанта

«Здравствуйте! Снова настало время вашей любимой викторины СТЕНА СЛАВЫ!» «Первая участница сегодняшнего шоу — Тереза! Надеюсь, вы готовы сыграть в СТЕНУ СЛАВЫ!» Прежде чем мы начнем сегодняшнюю игру, давайте быстро повторим наши правила игры. Тереза, ты сейчас увидишь сегодняшнюю стену. На стене 5 потайных дверей, над каждой из которых написано уравнение . Во время игры вы сможете открыть 3 из этих дверей. За каждую выбранную вами дверь вы получите приз, равный количеству решений уравнения. Если каждая дверь, которую вы выберете, откроет приз, вы вернетесь на шоу завтра, чтобы получить шанс выиграть еще больший приз!

Понимание дискриминанта

Секрет этой игры заключается в том, что понимает и использует дискриминант . Если Тереза ​​сможет понять, как использовать этот инструмент, у нее может быть шанс выиграть все призы и вернуться завтра! Давайте взглянем на сегодняшнюю СТЕНУ СЛАВЫ! уравнений , которые мы имеем сегодня:
Уравнение 1: х-квадрат минус 10х плюс 34.
Уравнение 2: 3 х-квадрат минус 4х плюс 10.
Уравнение 3: х-квадрат минус 3х плюс 5.
Уравнение 4: х-квадрат плюс 2 корень 2х плюс 2.
Уравнение 5: х-квадрат плюс 6х минус 16.

При первом выборе Тереза ​​выбирает дверь номер 4. Помните, мы сказали, что можем использовать дискриминант , чтобы быстро определить, выиграла ли Тереза ​​один из наших замечательных призов . Дискриминант получается из квадратичной формулы , и его формула представляет собой b-квадрат минус 4ac, где a, b и c относятся к коэффициентам и константе квадратного уравнения в стандартной форме .

Когда дискриминант положителен на , наше уравнение будет иметь 2 решений ; когда дискриминант равен 0 , наше уравнение имеет 1 решение , а когда наш дискриминант отрицательный , наше уравнение не будет иметь решений . Давайте посмотрим на уравнение , которое только что выбрала Тереза. В уравнении, которое только что выбрала Тереза, «а» равно 1, «b» равно удвоенному квадратному корню из 2, а «с» равно 2.

Вычислим дискриминант ! Величина, умноженная на 2 квадратного корня из 2 в квадрате, будет равна 8. 8 минус 8 будет равно 0. Поскольку дискриминант равен 0, это уравнение будет иметь 1 решение. Тереза, ты только что выиграла 1 совершенно нового единорога! Разве она не выглядит счастливой?! Это самое хорошее начало, о котором вы можете мечтать!

Второй пример

Вторым выбором Тереза ​​выбирает пятое уравнение. Давайте посмотрим поближе! В этом уравнении «а» равно 1, «b» равно 6, а «с» равно минус 16. Вычислим дискриминант! Подставляя наши значения, мы получаем 6 в квадрате минус 4 умножить на 1 умножить на минус 16.
Используя PEMDAS , мы получаем 36 плюс 64, что равно 100. Ничего себе! Посмотри на это! Тереза ​​только что выиграла пару фигурок Позитрона и Негатрона! 2 приза за уравнение с 2 решениями! У Терезы пока все хорошо! Если она сможет выбрать дверь с еще одним призом, ее снова пригласят на завтрашнее шоу и она получит шанс выиграть главный приз!

И в своем окончательном выборе Тереза ​​выбирает уравнение на двери номер 2! Давайте посмотрим на ее уравнение! В этом уравнении «а» равно 3, «б» равно минус 4, а «с» равно 10. Вычислим дискриминант! Подключаем наш принимает значение , мы получаем минус 4 в квадрате минус 4 умножить на 3 умножить на 10. Вычислив наше математическое , мы получим 16 минус 120, что равно отрицательному 104. Как вы думаете, что это значит? Не только из-за того, сколько решений имеет наше уравнение, но и из-за шансов Терезы вернуться завтра?

Итог

Помните, когда наш дискриминант на больше, чем 0 , это означает, что наше уравнение будет иметь 2 решений . Когда наш дискриминант равен равно 0 наше уравнение будет иметь 1 решение . И когда наш дискриминант равен отрицательному , наше уравнение не будет иметь реальных решений .

Ну что, ребята! Это также означает, что приза нет! Хотя Тереза ​​будет разочарована, по крайней мере, у нее есть фигурки и новый Единорог! Хотя этот Единорог выглядит немного подозрительно. .. И волосы хозяина тоже выглядят немного подозрительно!

Использование и понимание дискриминанта. Упражнение 92-4(1)(2)$

Используя PEMDAS, она находит, что дискриминант равен $0$.

Она знает, что если дискриминант положительный, уравнение имеет два решения. Если он равен нулю, уравнение имеет одно решение. Если оно отрицательное, уравнение не имеет решений.

Поскольку дискриминант равен нулю, Тереза ​​видит, что это уравнение имеет одно решение, и она должна получить один приз, открыв эту дверь.

Найдите дискриминанты.

2-4ac$.

Решение

Все уравнения над дверями представляют собой стандартные квадратные уравнения. Поэтому Джон может использовать дискриминант, чтобы проверить, сколько решений имеет каждое уравнение.

Если дискриминант положительный, уравнение имеет два решения. Если он равен нулю, уравнение имеет одно решение. Если оно отрицательное, уравнение не имеет решений. Поэтому Джон должен найти уравнение, определитель которого положителен.

Джон решает вычислить определитель каждого квадратного уравнения. Он начинает с уравнения: 92 — 4(2)(3) = 12$

Определитель этого уравнения положителен. Следовательно, это правильная дверь.

Объясните, что говорит вам дискриминант, равный $100$.

Подсказки

Квадратное уравнение может иметь ноль, одно или два решения.

Если дискриминант равен нулю, уравнение имеет одно решение.

Если дискриминант отрицательный, уравнение не имеет решений.

Решение

Дискриминант полезен, потому что он показывает количество решений или корней квадратного уравнения. Если дискриминант положительный, уравнение имеет два решения. Если он равен нулю, уравнение имеет одно решение. Если оно отрицательное, уравнение не имеет решений.

В этом случае дискриминант равен $100$ и положителен. Следовательно, это уравнение имеет два решения.

Вычислить дискриминант.

Подсказки

В расчетах обращайте особое внимание на знаки.

Помните, что вы можете определить, сколько решений имеет уравнение, сравнив дискриминант с нулем.

Помните, что квадратное уравнение может иметь только $0$, $1$ или $2$ решений.

Решение 92 + 5x -3 = 0$ она находит, что дискриминант равен 109$. Следовательно, уравнение имеет $2$ решений.

Еще видео по теме Квадратные уравнения / функции

Что такое квадратичные функции?

Графики квадратичных функций

ФОЛЬГИРОВАНИЕ и пояснение к ФОЛЬГЕ

Решение квадратных уравнений путем извлечения квадратных корней

Решение квадратных уравнений методом факторинга

Факторинг с группировкой

Решение квадратных уравнений с использованием квадратичной формулы

Решение квадратных уравнений путем заполнения квадрата

Нахождение значения, которое завершает квадрат

Использование и понимание дискриминанта

Word задачи с квадратными уравнениями

Компания

• Наша команда
• Цены
• Вакансии

Платформа

Как это работает

• Обучающие видео
• Упражнения
• Диван-герой
• Рабочие листы
• Чат

Справка

• Часто задаваемые вопросы
• Дайте нам отзыв

Юридический

• Условия
• Право на отзыв
• Политика конфиденциальности
• Свяжитесь с нами
• Не продавать мою личную информацию

Есть вопросы? Свяжитесь с нами!

help@sofatutor. com

• дивантутор.com
• диван-репетитор.ch
• диван-репетитор.ат
• дивантутор.com
• ru.sofatutor.co.uk

Есть вопросы? Свяжитесь с нами!

[email protected]

Руководство по решению квадратных уравнений и приложений

9.4 Рекомендации по решению квадратных уравнений и приложения

Цели обучения

1. Используйте дискриминант для определения количества и типа решений любого квадратного уравнения.
2. Разработайте общую стратегию решения квадратных уравнений.
3. Решайте приложения, включающие квадратные уравнения.

Дискриминант

Если задано квадратное уравнение в стандартной форме, ax2+bx+c=0, где a , b и c — действительные числа, а a≠0, то решения можно вычислить, используя квадратичная формула:

Решения рациональны, иррациональны или нереальны. Мы можем определить тип и количество решений, изучая дискриминант Выражение внутри радикала квадратичной формулы, b2-4ac., выражение внутри радикала, b2-4ac. Если значение этого выражения отрицательное, то уравнение не имеет действительных решений. Если дискриминант положительный, то у нас есть два действительных решения. И если дискриминант равен 0, то у нас есть одно действительное решение.

 

Пример 1: Определить тип и количество решений: x2−10x+30=0.

Решение: Начнем с идентификации a , b и c . Здесь

Подставляем эти значения в дискриминант и упрощаем.

Так как дискриминант отрицателен, мы заключаем, что реальных решений нет.

Ответ: Нет действительного решения

 

Если мы воспользуемся квадратичной формулой из предыдущего примера, мы обнаружим, что отрицательное подкоренное число останавливает процесс упрощения и показывает, что действительного решения нет.

Примечание

Мы будем изучать квадратные уравнения без действительных решений по мере нашего продвижения в изучении алгебры.

 

Пример 2: Определите тип и количество решений: 7×2−10x+1=0.

Решение: Здесь

Подставляем эти значения в дискриминант:

Поскольку дискриминант положительный, мы можем заключить, что существует два действительных решения.

Ответ: Два действительных решения

 

Если мы воспользуемся квадратичной формулой из предыдущего примера, мы обнаружим, что положительное подкоренное в квадратной формуле приводит к двум действительным решениям.

Два действительных решения: 5−327 и 5+327. Обратите внимание, что эти решения иррациональны; мы можем приблизить значения на калькуляторе.

 

Пример 3: Определите тип и количество решений: 2×2−7x−4=0.

Решение: В этом примере

Подставьте эти значения в дискриминант и упростите.

Поскольку дискриминант положителен, мы заключаем, что существует два действительных решения. Кроме того, поскольку дискриминант представляет собой полный квадрат, мы получаем два рациональных решения.

Ответ: Два действительных решения

 

Мы могли бы решить предыдущее квадратное уравнение, используя квадратную формулу следующим образом:

Обратите внимание, что если дискриминант представляет собой полный квадрат, то мы могли бы разложить исходное уравнение на множители.

Учитывая особое условие, когда дискриминант равен 0, мы получаем только одно решение, двойной корень.

 

Пример 4: Определите тип и количество решений: 9×2−6x+1=0.

Решение: Здесь a=9, b=−6 и c=1, и мы имеем

Поскольку дискриминант равен 0, мы заключаем, что существует только одно действительное решение, двойной корень.

Ответ: Одно действительное решение

 

Поскольку 0 — полный квадрат, мы можем решить приведенное выше уравнение, разложив его на множители.

Здесь 1/3 — решение, встречающееся дважды; это двойной корень.

Таким образом, если задано любое квадратное уравнение в стандартной форме, ax2+bx+c=0, где a , b и c — действительные числа, а a≠0, то мы имеем следующее:

Положительный дискриминант :	b2−4ac>0	Два действительных решения
Нулевой дискриминант :	b2−4ac=0	Одно реальное решение
Отрицательный дискриминант :	b2−4ac<0	Нет реального решения

Как мы увидим, заранее зная количество и тип решений, мы можем определить, какой метод лучше всего подходит для решения квадратного уравнения.

 

Попробуйте это! Определить количество и тип решений: 3×2−5x+4=0.

Ответ: Реального решения нет

Видеорешение

(нажмите, чтобы посмотреть видео)

Общие рекомендации по решению квадратных уравнений

Используйте коэффициенты квадратного уравнения, чтобы решить, какой метод наиболее подходит для его решения. Хотя квадратичная формула работает всегда, иногда это не самый эффективный метод. Для любого квадратного уравнения в стандартной форме, ax2+bx+c=0, общие рекомендации по определению метода его решения следующие:

1. Если c = 0, то следует вынести GCF и решить факторингом.
2. Если b = 0, то решить путем извлечения корней.

3. Если a , b и c отличны от нуля, то определите значение дискриминанта b2−4ac:

   1. Если дискриминант является полным квадратом, то решить с помощью факторизации.

   2. Если дискриминант не является полным квадратом, то решить по квадратичной формуле.

      • Если дискриминант положительный, мы получаем два действительных решения.
      • Если дискриминант отрицательный, то действительного решения нет.

 

Пример 5: Решите: 15×2−5x=0.

Решение: В данном случае c = 0, и мы можем решить, выделив GCF.

Ответ: Решения равны 0 и 1/3.

 

Пример 6: Решите: 3×2−5=0.

Решение: В этом случае b = 0 и мы можем решить путем извлечения корней.

Ответ: Решения равны ±153.

 

Пример 7: Решите: 9×2−6x−7=0.

Решение: Начните с идентификации a , b и c как коэффициенты каждого члена. Здесь

Подставим эти значения в дискриминант и упростим.

Поскольку дискриминант положительный, а не полный квадрат, используйте квадратичную формулу и ожидайте два действительных решения.

Ответ: Решения 1±223.

 

Пример 8: Решите: 4x(x−2)=−7.

Решение: Начните с переписывания квадратного уравнения в стандартной форме.

Здесь

Подставьте эти значения в дискриминант и упростите.

Поскольку дискриминант отрицателен, решения не являются действительными числами.

Ответ: Реального решения нет

 

Пример 9: Решите: (3x+5)(3x+7)=6x+10.

Решение: Начните с переписывания квадратного уравнения в стандартной форме.

Подставляем в дискриминант a = 9, b = 30 и c = 25.

Поскольку дискриминант равен 0, решите факторингом и ожидайте одно действительное решение, двойной корень.

Ответ: Решение равно −5/3.

 

Попробуйте! Решите: 5×2+2x−7=2x−3.

Ответ: ±255

Решение для видео

(нажмите, чтобы посмотреть видео)

Приложения, использующие квадратные уравнения

В этом разделе алгебраические установки обычно состоят из квадратного уравнения, решения которого могут не быть целыми числами.

 

Пример 10: Высота треугольника на 2 дюйма меньше, чем удвоенная длина его основания. Если общая площадь треугольника 11 квадратных дюймов, то найти длины основания и высоты. Ответы округлить до сотых.

Решение:

Используйте формулу A=12bh и тот факт, что площадь равна 11 квадратных дюймов, чтобы составить алгебраическое уравнение.

Чтобы переписать это квадратное уравнение в стандартной форме, сначала распределите 12x.

Используйте коэффициенты a = 1, b = −1 и c = −11, чтобы определить тип решения.

Поскольку дискриминант положительный, ожидайте два действительных решения.

В этой задаче игнорируйте отрицательное решение и рассматривайте только положительное решение.

Обратно подставить, чтобы найти высоту.

Ответ: Размер основания 1+352≈3,85 дюйма, а высота -1+35≈5,71 дюйма.

 

Пример 11: Сумма квадратов двух последовательных натуральных чисел равна 481. Найдите эти числа.

Решение:

Алгебраическая установка следующая:

Перепишите квадратное уравнение в стандартной форме.

Когда коэффициенты большие, иногда проще использовать квадратичную формулу вместо того, чтобы пытаться разложить ее на множители. В этом случае a=1, b=1 и c=-240. Подставляем в квадратную формулу и упрощаем.

Так как задача требует положительных целых чисел, не принимайте во внимание отрицательное решение и выберите n = 15.

Ответ: Положительные целые числа равны 15 и 16. квадратное уравнение в стандартной форме с использованием дискриминанта b2−4ac. Если дискриминант отрицателен, то решения недействительны. Если дискриминант положительный, то решения действительны. Если дискриминант равен 0, то есть только одно решение — двойной корень.

Выберите подходящий метод решения квадратного уравнения на основе значения его дискриминанта. Хотя квадратичная формула решает любое квадратное уравнение, это может быть не самый эффективный метод.

При решении задач используйте ключевые слова и фразы, чтобы составить алгебраическое уравнение, моделирующее задачу. В этом разделе установка обычно включает квадратное уравнение.

Тематические упражнения

Часть A: Использование дискриминанта

Вычислите дискриминант и используйте его для определения количества и типа решений. Не решить.

1. x2+2x+3=0

2. x2−2x−3=0

3. 3×2−1x−2=0

4. 3×2−1x+2=0

5. 9y2 +2=0

6. 9y2−2=0

7. 5×2+x=0

8. 5×2−x=0

9. 12×2−2x+52=0

10. 12×2−x− 12=0

11. −x2−2x+4=0

12. −x2−4x+2=0

13. 4t2−20t+25=0

14. 9t2−6t+1=0

Часть B: Решение

Выберите подходящий метод для решения следующего.

15. x2−2x−3=0

16. x2+2x+3=0

17. 3×2−x−2=0

18. 3×2−x+2=0

19. 9y 9y +2=0

20. 9y2−2=0

21. 5×2+x=0

22. 5×2−x=0

23. 12×2−2x+52=0

24. 12×2−x 12=0

25. −x2−2x+4=0

26. −x2−4x+2=0

27. 4t2−20t+25=0

28. 9t2−6t+1=0

29. y2−4y−1=0

30. y2−6y−3=0

31. 25×2+1=0

32. 36×2+4=0

33 5t2−4=0

34. 2t2−9=0

35. 12×2−94x+1=0

36. 3×2+12x−16=0

37. 36y2=2y 2=5

3.

−10y

39. x(x−6)=−29

40. x(x−4)=−16

41. 4y(y+1)=5

42. 2y(y+2) =3

43. −3×2=2x+1

44. 3×2+4x=−2

45. 6(x+1)2=11x+7

46. 2(x+2)2=7x +11

47. 9t2=4(3t−1)

48. 5t(5t−6)=−9

49. (x+1)(x+7)=3

50. (x−5) (x+7)=14

Часть C: Приложения

Составьте алгебраическое уравнение и используйте его для решения следующего.

Задачи с числами

51. Положительное действительное число на 2 меньше другого. Если к квадрату меньшего прибавить в 4 раза больше, получится 49. Найдите числа.

52. Положительное действительное число больше другого на 1. Если из квадрата большего вычесть удвоенное меньшее, получится 4. Найдите числа.

53. Положительное действительное число на 6 меньше другого. Если сумма квадратов двух чисел равна 38, то найдите числа.

54. Положительное действительное число на 1 больше, чем в два раза. Если 4 раза меньшее число вычесть из квадрата большего, то получится 21. Найдите числа.

Задачи по геометрии

Округлите ответы до сотых.

55. Площадь прямоугольника 60 квадратных дюймов. Если длина в 3 раза больше ширины, то найдите размеры прямоугольника.

56. Площадь прямоугольника 6 квадратных футов. Найдите размеры прямоугольника, если его длина на 2 м больше ширины.

57. Площадь прямоугольника 27 квадратных метров. Если длина на 6 м меньше ширины в 3 раза, то найдите размеры прямоугольника.

58. Площадь треугольника 48 квадратных дюймов. Если основание в 2 раза больше высоты, то найдите длину основания.

59. Площадь треугольника 14 квадратных футов. Если основание на 4 фута больше высоты в 2 раза, то найдите длину основания и высоту.

60. Площадь треугольника 8 квадратных метров. Если основание на 4 метра меньше высоты, то найти длину основания и высоту.

61. Периметр прямоугольника равен 54 сантиметрам, а площадь 180 квадратных сантиметров. Найдите размеры прямоугольника.

62. Периметр прямоугольника 50 дюймов, а площадь 126 квадратных дюймов. Найдите размеры прямоугольника.

63. Джордж успешно ухаживает за садом размером 6 на 8 метров. В следующем сезоне он планирует удвоить площадь посадки, увеличив ширину и высоту на одинаковую величину. На сколько он должен увеличить длину и ширину?

64. Вокруг сада размером 6 на 8 футов должна быть построена ровная кирпичная ограда. Если общая площадь сада, включая бордюр, должна быть 100 квадратных футов, то найдите ширину кирпичного бордюра.

Теорема Пифагора

65. Если стороны квадрата 106 единиц, то найдите длину диагонали.

66. Если диагональ квадрата равна 310 единицам, найдите длину каждой стороны.

67. Диагональ прямоугольника равна 63 дюймам. Найдите размеры прямоугольника, если его ширина на 4 см меньше длины.

68. Диагональ прямоугольника равна 23 дюймам. Найдите размеры прямоугольника, если его ширина на 2 см меньше длины.

69. Вершина 20-футовой лестницы, прислоненной к зданию, достигает высоты 18 футов. На каком расстоянии основание лестницы от стены? Округлите до сотых.

70. Для безопасного использования лестницы основание должно располагаться примерно на 1/4 длины лестницы от стены. Если безопасно использовать 20-футовую лестницу, то какой высоты по отношению к зданию будет достигать вершина лестницы? Округлите до сотых.

71. Диагональ телевизионного монитора составляет 32 дюйма. Если монитор имеет соотношение сторон 3:2, то определите его длину и ширину. Округлите до сотых.

72. Диагональ телевизионного монитора составляет 52 дюйма. Если монитор имеет соотношение сторон 16:9, то определите его длину и ширину. Округлите до сотых.

Бизнес-задачи

73. Прибыль в долларах от работы сборочной линии, ежедневно производящей униформу на заказ, определяется функцией P(t)=−40t2+960t−4000, где t представляет количество часов работы линии.

а. Рассчитайте прибыль от работы конвейера по 10 часов в день.

б. Рассчитайте количество часов, в течение которых сборочная линия должна работать, чтобы обеспечить безубыточность. Округлите до ближайшей десятой доли часа.

74. Прибыль в долларах, полученная от производства и продажи x нестандартных ламп, определяется функцией P(x)=−10×2+800x−12 000.

а. Рассчитайте прибыль от производства и продажи 35 ламп.

б. Подсчитайте количество ламп, которые необходимо продать, чтобы получить прибыль в размере 3000 долларов.

75. Если $1,200 вложены на счет с годовой процентной ставкой r , то сумма A на счете в конце 2-х лет определяется по формуле A=1,200(1+r) 2. Если по истечении 2 лет сумма на счете составит 1335,63 доллара, то какова будет процентная ставка?

76. Предприятие-производитель определило, что ежедневная выручка, Р , в тысячах долларов зависит от числа, n , паллет продукта, реализуемого по формуле R=12n−0,6n2. Определите количество палитр, которые необходимо продать, чтобы поддерживать доход на уровне 60 000 долларов в день.

Проблемы со снарядами

77. Высота снаряда, запущенного вверх со скоростью 32 фута/сек с высоты 128 футов, определяется функцией h(t)=−16t2+32t+128.

а. Какова высота снаряда через 1/2 секунды?

б. Через какое время после запуска снаряд достигнет высоты 128 футов?

78. Высота снаряда, запущенного вверх со скоростью 16 футов в секунду с высоты 192 фута, определяется функцией h(t)=−16t2+16t+192.

а. Какова высота снаряда через 3/2 секунды?

б. Через какое время снаряд достигнет 128 футов?

79. Высота объекта, падающего с крыши 144-футового здания, определяется как h(t)=−16t2+144. Сколько времени потребуется, чтобы достичь точки на полпути к земле?

80. Высота снаряда, выпущенного прямо в воздух на скорости 80 футов/сек от земли, определяется выражением h(t)=−16t2+80t. Через какое время снаряд достигнет 95 футов?

Часть D: Дискуссионная доска

81. Обсудите стратегию постоянного использования квадратной формулы для решения квадратных уравнений.

82. Перечислите все известные нам методы решения квадратных уравнений. Обсудите плюсы и минусы каждого.

Ответы

1: −8, нет вещественных решений

3: 25, два действительных решения

5: −72, нет действительных решений

7: 1, два действительных решения

9: −1, нет действительных решений раствор

11:20, два действительных решения

13:0, одно действительное решение

15: −1, 3

17: −2/3, 1

19: Нет действительного решения

21: −1/5 , 0

23: действительного решения нет

25: −1±5

27: 5/2

29: 2±5

31: действительного решения нет

33: ±254

1 33: ±255 9000 3

2, 4

37: 0, 1/18

39: нет действительного решения

41: −1±62

43: нет действительного решения

45: −1/2, 1/3

47: 2/3

49: −4±23

51: 35 и 35−2

53: 3+10 и −3+10

55: Длина: 13,42 дюйма; ширина: 4,47 дюйма

57: длина: 6,48 метра; ширина: 4,16 метра

59: высота: 2,87 фута; база: 9,74 фута

61: длина: 15 см; ширина: 12 сантиметров

63: 2,85 метра

65: 203 шт.

67: длина: 2+52 дюйма; ширина: −2+52 дюйма

69: 219≈8,72 фута

71: длина: 26,63 дюйма; ширина: 17,75 дюйма

73: а. 1600 долларов США; б. 5,4 часа и 18,6 часа

75: 5,5%

77: а. 140 футов; б. 0 секунд и 2 секунды

79: 2,12 секунды

7.3 Классификация квадратных уравнений – Промежуточная алгебра

Цели обучения

• Квадратные уравнения с комплексными решениями
  • Используйте квадратную формулу для решения квадратных уравнений с комплексными решениями
  • Соедините комплексные решения с графиком квадратичной функции, не пересекающей ось x.
• Дискриминант
  • Определите дискриминант и используйте его для классификации решений квадратных уравнений

В этом уроке мы объединим концепции решения квадратных уравнений и комплексных чисел для обработки квадратных уравнений, не имеющих действительных решений. Вы также узнаете о полезном свойстве квадратной формулы, которое может помочь вам узнать, имеет ли квадратное уравнение действительные или комплексные решения.

Заполняя квадрат или используя квадратную формулу, мы видели три разных результата для квадратных уравнений: обычно было два решения из-за «плюс-минус» природы квадратного корня, но иногда было только одно решение, потому что мы заканчивали с «плюс-минус ноль», и иногда у нас не было реальных решений, потому что нам нужен был квадратный корень из отрицательного числа. Теперь мы узнали, что можно извлечь квадратный корень из отрицательного числа, используя мнимые числа. Наличие этих новых знаний позволяет нам исследовать результат, когда не существует реальных решений. Рассмотрим это уравнение: 92+3x+6=0\)

Используя квадратную формулу для решения этого уравнения, мы сначала идентифицируем \(a\), \(b\) и \(c\).

\(a = 2,b = 3,c = 6\)

Мы можем подставить \(a\), \(b\) и \(c\) в квадратичную формулу и упростить, чтобы получить следующее результат:

\(\displaystyle x=-\frac{3}{4}+\frac{\sqrt{-39}}{4}, \;\;\;\;\; x=-\frac{ 3}{4}-\frac{\sqrt{-39}}{4}\)

До этого момента мы бы сказали, что \(\sqrt{-39}\) не определено для действительных чисел и установлено, что это уравнение не имеет решений. Но теперь, когда мы определили квадратный корень из отрицательного числа, мы также можем определить решение этого уравнения следующим образом.

\(x=-\frac{3}{4}+\frac{\sqrt{39}}{4}i, x=-\frac{3}{4}-\frac{\sqrt{39} {4}i\)

В этом разделе мы будем практиковаться в упрощении и записи решений сложных квадратных уравнений. Затем мы представим метод классификации того, будет ли решение(я) квадратного уравнения комплексным, и сколько будет решений.

В нашем первом примере мы рассмотрим процесс решения квадратного уравнения с комплексными решениями. Обратите внимание, что мы будем упрощать комплексные числа, поэтому, если вам нужен обзор того, как преобразовать квадратный корень из отрицательного числа в мнимое число, сейчас самое подходящее время. 9{2}+х+2=0\).

Показать ответ

В следующем видео показан еще один пример использования формулы квадратного уравнения для поиска решений квадратного уравнения, имеющего комплексные решения. {2}-4ac\) называется 9{2}-4ac<0\), то число под радикалом будет отрицательным. Поскольку вы не можете найти квадратный корень из отрицательного числа, используя действительные числа, реальных решений нет. Однако вы можете использовать мнимые числа. Тогда у вас будет два сложных решения: одно путем добавления мнимого квадратного корня, а другое путем его вычитания.

В таблице ниже значения дискриминанта соотносятся с решениями квадратного уравнения.

No related posts.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт