Калькулятор с дробями десятичными и обыкновенными: Онлайн сервис для вычислений обыкновенной и десятичной дробями, сложение, вычитание, умножение и деление десятичной и обыкновенной дробей.

Как считать дроби на калькуляторе / Бери и делай

По умолчанию большинство калькуляторов работает только с десятичными дробями. Например, вместо 1/2 калькулятор оперирует числом 0,5. И тем не менее есть пара способов посчитать дроби на обычном калькуляторе, а затем перевести их из десятичных в обыкновенные. Также существуют специальные калькуляторы, которые умеют выполнять действия с простыми дробями, но и здесь есть подводные камни.

«Бери и Делай» объясняет, как с помощью разных калькуляторов складывать, вычитать, умножать и делить дроби.

Как считать дроби с помощью научного калькулятора

Такой калькулятор предназначен для инженерных и научных расчетов, поэтому его возможности гораздо шире, чем у обычных. У такого калькулятора может быть два поля: в одном отражаются введенные значения, а в другом — результат.

На таком калькуляторе в числе прочего есть кнопка, которая позволяет вводить в него число в виде обыкновенной дроби.

Как это сделать? Допустим, вам нужно записать число ³/₄.

1. Включаете калькулятор. Нажимаете на цифру 3, которая должна быть в числителе.
2. Нажимаете на кнопку, которая меняет формат записи числа, позволяя записать обыкновенную дробь. Она находится в левом верхнем углу и обозначается символами a^b/_c или двумя прямоугольниками, один из которых закрашен, а второй нет. В строке записи введенных значений появляется символ, похожий на ˩.
3. Нажимаете на цифру 4, которая должна быть в знаменателе.
4. Таким образом в калькулятор вводится число ³/₄ в виде обыкновенной дроби для дальнейших расчетов.

Допустим, мы хотим узнать результат простого действия и сложить 1³/₄ и ³/₈. Начнем с записи смешанной дроби, а затем перейдем к действию сложения.

Шаг № 1. Нажимаете на калькуляторе цифру 1.

Шаг № 2. Затем нажимаете на кнопку, которая позволяет менять формат записи числа и вводить число в виде обыкновенной дроби. В данном случае это нужно сделать уже на этом этапе, чтобы калькулятор распознал это число как смешанную дробь.

Шаг № 3. Нажимаете на цифру 3.

Шаг № 4. Снова нажимаете на кнопку, которая позволяет вводить число в виде обыкновенной дроби. Затем нажимаете на цифру 4. Смешанная дробь введена!

Шаг № 5. Теперь нажимаете на кнопку действия сложения и добавляете вторую дробь, записывая ее аналогичным образом.

Шаг № 6. В конце нажимаете на кнопку равенства, чтобы получить результат. Калькулятор в данном случае отображает результат в виде смешанной дроби. Таким же образом вы можете выполнять другие действия с дробями.

Обратите внимание, что формат записи такого числа в результате аналогичен тому, который был при вводе обыкновенных дробей в калькулятор.

У таких калькуляторов есть свои особенности:

• Если при вычислениях вы смешиваете дробные и десятичные значения, то результат будет отображаться в виде десятичной дроби, что заметно на картинке выше.
• Дроби в результатах вычислений на калькуляторе всегда отображаются после их приведения к несократимым дробям.

Как считать дроби с помощью обычного калькулятора

У обычного калькулятора нет кнопки для записи дроби, но есть другие функции, которые облегчают работу.

Допустим, вы получили результат выражения, работая с десятичными дробями, но это число теперь нужно записать в виде обыкновенной дроби. Как перевести десятичную дробь в обыкновенную?

1. Введите в калькулятор десятичную дробь. В нашем примере это 0,7143. Нажмите на кнопку действия умножения.
2. Чтобы превратить десятичную дробь в обыкновенную, выберите число, которое будет стоять в знаменателе обыкновенной дроби, которая получится в результате. Допустим, это 7. Умножьте на него десятичную дробь.
3. Число, полученное в результате этого умножения, округляете до целого и записываете в числитель. В данном случае это 5. А число 7, соответственно, записываете в знаменателе.

Таким образом получается, что число 0,7143 можно представить в виде обыкновенной дроби 5/7:

У этого способа есть свой минус: существует риск столкнуться с погрешностью при вычислениях, поэтому конечный результат нужно проверять. Просто разделите числитель на знаменатель: чем ниже погрешность, тем ближе результат будет к первоначальной десятичной дроби, а значит, полученную ранее простую дробь можно использовать для дальнейших расчетов.

Может быть и обратная ситуация: у вас есть обыкновенные дроби, но вы хотите перевести их в десятичные, чтобы затем выполнять действия над ними с помощью обычного калькулятора. Как в таком случае перевести обыкновенную дробь в десятичную? Возьмем дробь ⁷/₄ и превратим ее в десятичную.

1. Вбиваете в калькулятор число 7, стоящее на месте числителя. Выбираете действие деления.
2. В качестве делителя вбиваете 4 (знаменатель дроби).
3. Нажимаете на знак равенства. В результате получаете десятичную дробь. Таким образом, вы перевели число ⁷/₄ в десятичную дробь 1,75.

Важно: обыкновенная дробь после перевода в десятичную может превратиться в бесконечную периодическую дробь. В таком случае ее можно округлить.

Как выполнять действия с дробями, используя кнопки памяти (MR, M-, M+) на калькуляторе

На некоторых моделях калькуляторов есть кнопки памяти, которые позволяют сохранять в памяти устройства определенное число, а также выполнять с ним действия сложения или вычитания. Эти функции можно использовать при работе с дробями. Например, посмотрим, как с их помощью можно сложить числа ¹/₄ и ³/₈.

Шаг № 1. Сначала введите дробь ¹/₄. Нажмите на калькуляторе цифру 1, затем на кнопку действия деления.

Шаг № 2. Введите цифру 4 и нажмите на кнопку M+. Если при нажатии кнопки М+ результат деления не отобразился на дисплее, начните с начала и перед нажатием кнопки M+ здесь и далее, в шаге № 5, нажмите на кнопку «=».

Шаг № 3. На экране калькулятора отражается результат действия деления этих чисел, и он же записывается в память калькулятора.

Шаг № 4. Теперь введите вторую дробь аналогичным образом. Сначала нажимаете на калькуляторе цифру 3, затем на кнопку действия деления.

Шаг № 5. Далее введите цифру 8 и нажмите на кнопку M+.

Шаг № 6. На экране калькулятора отражается результат действия деления этих чисел, который тоже сохраняется в памяти калькулятора.

Шаг № 7. Теперь нажмите на кнопку MR: калькулятор отобразит сумму чисел, которые вы сохранили в его памяти. Так вы получите результат сложения дробей. При желании эту десятичную дробь можно записать в виде обыкновенной, как это делалось выше. Для этого выполните действие умножения.

Шаг № 8. В качестве множителя можно выбрать любое число. В ряде случаев удобнее, если оно совпадает с числом, которое находилось в знаменателе одной из дробей. В нашем примере это 8.

Шаг № 9. В результате умножения получаете число 5, которое записываете на место числителя. Получается, ¹/₄ + ³/₈ =_⁵/8.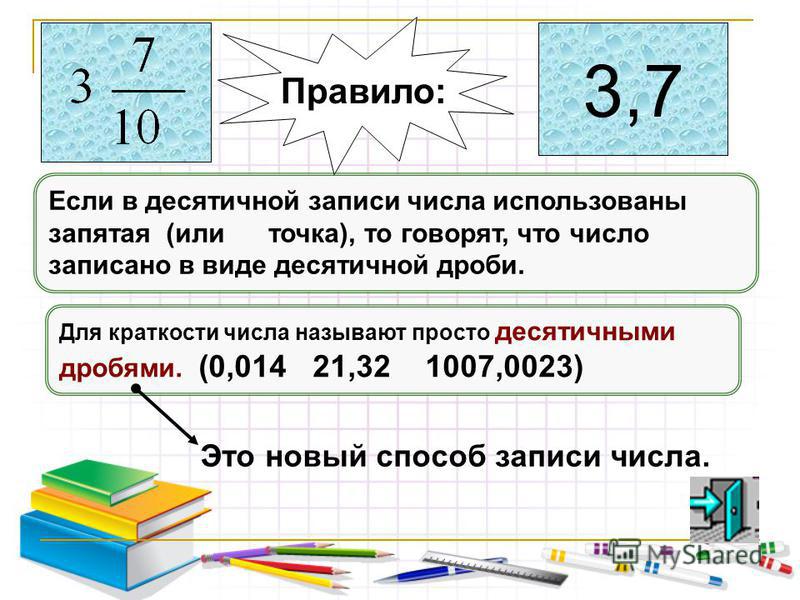

Так, используя кнопки памяти, мы сложили две обыкновенные дроби, а затем перевели результат из десятичной дроби в обыкновенную. Аналогичным образом можно использовать кнопку M-, позволяющую вычитать из одной дроби другую.

Из дробной в десятичную. Перевод дроби в понятное число. Перевод конечных десятичных дробей в обыкновенные дроби

Большое количество учащихся, и не только, задаются вопросом, как перевести дробь в число. Чтобы это сделать, имеется несколько достаточно простых и понятных способов. Выбор конкретного способа зависит от предпочтений решающего.

В первую очередь нужно знать, как дроби записываются. А записываются они следующим образом:

1. Обыкновенная. Пишется с числителем и знаменателем через наклонную или столбиком (1/2).
2. Десятичная. Пишется через запятую (1,0, 2,5 и так далее).

Перед тем как приступить к решению, нужно знать, что такое неправильная дробь, ведь она встречается достаточно часто. Она имеет числитель больше знаменателя, например, 15/6. Неправильную дробь также можно решать такими способами, без каких-либо усилий и затрат времени.

Смешанное число — это когда в результате выходит целое число и дробная часть, к примеру 52/3.

Любое натуральное число можно записать дробью с совершенно разными натуральными знаменателями, например:1= 2/2=3/3 = и т.д.

Перевести можно еще и с помощью калькулятора, но не все они имеют такую функцию. Существует специальный инженерный калькулятор, где есть такая функция, но не всегда есть возможность его использовать, особенно в школе. Поэтому лучше разобраться в данной теме.

Первым делом стоит обратить внимание на то, какая дробь. Если ее можно с легкостью множить до 10 на одинаковые с числителем значения, то можно воспользоваться первым способом. Например: обыкновенная ½ умножаете в числителе и знаменателе на 5 и получаете 5/10, которое можно записать как 0,5.

Данное правило основано на том, что десятичная всегда имеет в знаменателе круглое значение, такое как 10,100,1000 и так далее.

Из этого выходит, что если множить числитель и знаменатель, то нужно добиваться получения в знаменателе именно такого значения в результате умножения, независимо от того, что выходит в числителе.

Стоит помнить, что некоторые дроби нельзя перевести, для этого необходимо перед началом решения проверить ее.

Например: 1,3333, где цифра 3 повторяется до бесконечности, причем калькулятор тоже не избавит от нее. Решением такой проблемы может быть только округление таким образом, чтобы получилось целое число, если это возможно. Если такой возможности не имеется, то следует вернуться в начало примера и проверить правильность решения задачи, возможно, была допущена ошибка.

Рисунок 1-3. Перевод дробей путем умножения.

Рассмотрим для закрепления описанной информации следующий пример перевода:

1. Например, необходимо перевести 6/20 в десятичную. Первым делом ее следует проверить, как показано на рисунке 1.
2. Только после того как убедились, что можно разложить, как в данном случае на 2 и 5, нужно приступать к самому переводу.
3. Наиболее простым вариантом будет умножить знаменатель, получив результат 100, является 5, так как 20х5=100.
4. Следуя примеру на рисунке 2, в итоге получится 0,3.

Можно закрепить результат и еще раз все просмотреть по рисунку 3. Для того чтобы полностью разобраться в теме и больше не прибегать к изучению этого материала. Эти знания помогут не только ребенку, но и взрослому человеку.

Перевод путем деления

Второй вариант перевода дробей является немного сложней, но более популярным. Таким методом в основном пользуются в школах учителя для объяснения. В целом, он намного проще объясняется и быстрее понимается.

Стоит помнить, что для правильного преобразования простой дроби необходимо ее числитель поделить на знаменатель. Ведь если задуматься, то решение это и есть процесс деления.

Для того чтобы понять это простое правило, нужно рассмотреть следующий пример решения:

1. Возьмем 78/200, которую нужно перевести в десятичную. Для этого следует 78 разделить на 200, то есть числитель на знаменатель.
2. Но перед тем как начать, стоит провести проверку, как показано на рисунке 4.
3. После того как убедились, что ее можно решить, следует приступать к процессу. Для этого стоит разделить числитель на знаменатель в столбик или уголком, как показано на рисунке 5. В начальных классах школ учат такому делению, и трудностей с этим не должно возникнуть.

На рисунке 6 показаны примеры наиболее распространенных примеров, их просто можно запомнить, чтобы при необходимости не тратить время для решения. Ведь в школе на каждую контрольную или самостоятельную работы дается мало времени для решения, поэтому не стоит тратить его на то, что можно выучить и просто помнить.

Перевод процентов

Переводить проценты в десятичное число тоже достаточно легко. Этому начинают учить в 5 классе, а в некоторых школах еще раньше. Но если ваш ребенок на уроке математики не понял эту тему, можно наглядно ему еще раз объяснить. Для начала следует выучить определения понятия, что такое процент.

Процент — это одна сотая часть от какого-либо числа, другими словами, абсолютная произвольная. Например, от 100 это будет 1 и так далее.

На рисунке 7 показан наглядный пример перевода процентов.

Чтобы перевести процент, надо всего лишь убрать значок %, а затем разделить его на 100.

Еще 1 пример показан на рисунке 8.

Если надо провести обратную «конвертацию», необходимо все сделать с точностью до наоборот. Другими словами, число необходимо умножить на сто и после приписать значок процентов.

А для того чтобы обычную перевести в проценты, также можно использовать этот пример. Только изначально следует перевести дробь в число и только потом в проценты.

Исходя из описанного выше, можно легко понять принцип перевода. С помощью этих способов можно ребенку объяснять тему, если он ее не понял или не присутствовал на уроке в момент ее прохождения.

И никогда не будет необходимости нанимать репетитора, чтобы он объяснил ребенку, как перевести дробь в число или процент.

Материалов по дробям и изучать последовательно. Ниже для вас подробная информация с примерами и пояснениями.

1. Смешанное число в обыкновенную дробь. Запишем в общем виде число:

Запоминаем простое правило – целую часть умножаем на знаменатель и прибавляем числитель, то есть:

Примеры:

2. Наоборот, обыкновенную дробь в смешанное число. *Конечно, это возможно сделать только с неправильной дробью (когда числитель больше знаменателя).

При «небольших» числах никаких действий, в общем, и не нужно делать, результат «видно» сразу, например, дроби:

*Подробнее:

15:13 = 1 остаток 2

4:3 = 1 остаток 1

9:5 = 1 остаток 4

А вот если числа будут более, то без вычислений не обойтись. Здесь всё просто – делим уголком числитель на знаменатель до тех пор пока остаток не получится менее делителя. Схема деления:

Например:

*Числитель у нас – это делимое, знаменатель – это делитель.

Получаем целую часть (неполное частное) и остаток. Записываем – целое, затем дробь (в числителе остаток, а знаменатель оставляем тот же):

3. Десятичную переводим в обыкновенную.

Частично в первом пункте, где рассказывали про десятичные дроби мы уже коснулись этого. Как слышим так и записываем. Например — 0,3; 0,45; 0,008; 4,38; 10,00015

Первые три дроби у нас без целой части. А четвёртая и пятая её имеют, переведём их в обыкновенные, это делать уже умеем:

*Мы видим, что дроби можно ещё и сократить, например 45/100 =9/20, 38/100=19/50 и другие, но мы здесь делать этого не будем. По сокращению вас ожидает отдельный пункт ниже, где подробно всё разберём.

4. Обыкновенную переводим в десятичную.

Тут не всё так просто. По каким-то дробям сразу видно и ясно, что с ней сделать, чтобы она стала десятичной, например:

Используем наше замечательное основное свойство дроби – умножаем числитель и знаменатель соответственно на 5, 25, 2, 5, 4, 2, получим:

Если имеется целая часть, то тоже ничего сложного:

Умножаем дробную часть соответственно на 2, 25, 2 и 5, получим:

А есть такие, по которым без опыта и не определить, что их можно перевести в десятичные, например:

На какие числа умножать числитель и знаменатель?

Тут опять на помощь приходит проверенный способ – деление уголком, способ универсальный, им для перевода обыкновенной дроби в десятичную можно пользоваться всегда:

Так вы сможете всегда определить переводится ли дробь в десятичную.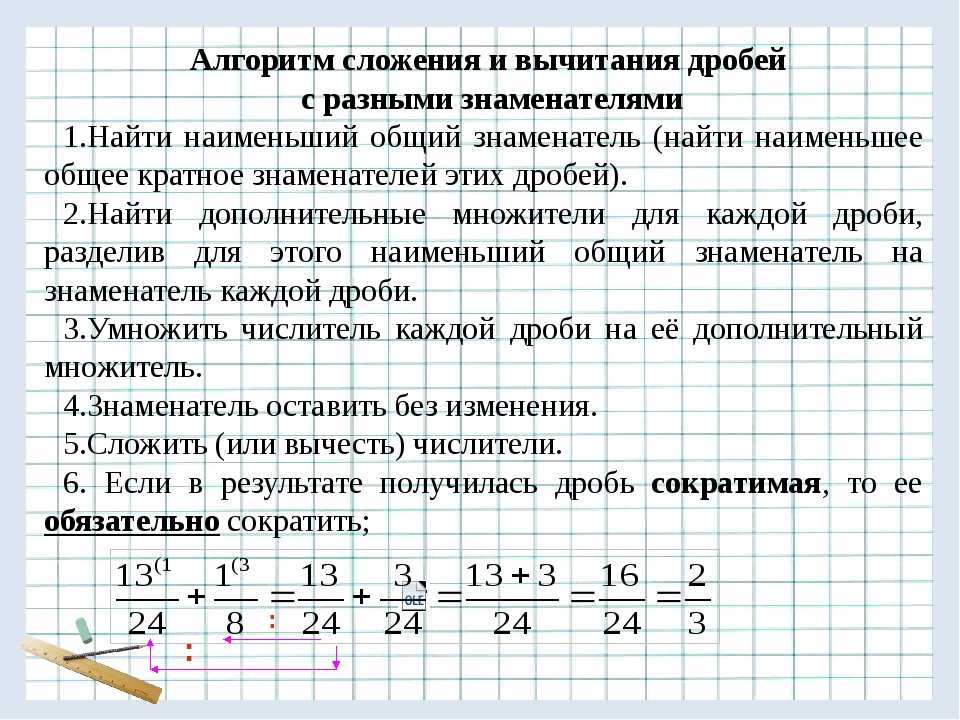 Дело в том, что не каждую обыкновенную дробь можно перевести в десятичную, например такие как 1/9, 3/7, 7/26 не переводятся. А что же тогда получается за дробь при делении 1 на 9, 3 на 7, 5 на 11? Отвечаю – бесконечная десятичная (говорили о них в пункте 1). Разделим:

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

В этой статье мы разберем, как осуществляется перевод обыкновенных дробей в десятичные дроби , а также рассмотрим обратный процесс – перевод десятичных дробей в обыкновенные дроби. Здесь мы озвучим правила обращения дробей и приведем подробные решения характерных примеров.

Навигация по странице.

Перевод обыкновенных дробей в десятичные дроби

Обозначим последовательность, в которой мы будем разбираться с переводом обыкновенных дробей в десятичные дроби .

Сначала мы рассмотрим, как обыкновенные дроби со знаменателями 10, 100, 1 000, … представить в виде десятичных дробей . Это объясняется тем, что десятичные дроби по сути являются компактной формой записи обыкновенных дробей со знаменателями 10, 100, … .

После этого мы пойдем дальше и покажем, как любую обыкновенную дробь (не только со знаменателями 10, 100, … ) записать в виде десятичной дроби. При таком обращении обыкновенных дробей получаются как конечные десятичные дроби, так и бесконечные периодические десятичные дроби.

Теперь обо всем по порядку.

Перевод обыкновенных дробей со знаменателями 10, 100, … в десятичные дроби

Некоторые правильные обыкновенные дроби перед переводом в десятичные дроби нуждаются в «предварительной подготовке». Это касается обыкновенных дробей, количество цифр в числителе которых меньше, чем количество нулей в знаменателе. Например, обыкновенную дробь 2/100 нужно предварительно подготовить к переводу в десятичную дробь, а дробь 9/10 в подготовке не нуждается.

«Предварительная подготовка» правильных обыкновенных дробей к переводу в десятичные дроби заключается в дописывании слева в числителе такого количества нулей, чтобы там общее количество цифр стало равно количеству нулей в знаменателе. Например, дробь после дописывания нулей будет иметь вид .

После подготовки правильной обыкновенной дроби можно приступать к ее обращению в десятичную дробь.

Дадим правило перевода правильной обыкновенной дроби со знаменателем 10, или 100, или 1 000, … в десятичную дробь . Оно состоит из трех шагов:

• записываем 0 ;
• после него ставим десятичную запятую;
• записываем число из числителя (вместе с дописанными нулями, если мы их дописывали).

Рассмотрим применение этого правила при решении примеров.

Пример.

Переведите правильную обыкновенную дробь 37/100 в десятичную.

Решение.

В знаменателе находится число 100 , в записи которого два нуля. В числителе находится число 37 , в его записи две цифры, следовательно, эта дробь не нуждается в подготовке к переводу в десятичную дробь.

Теперь записываем 0 , ставим десятичную запятую, и записываем число 37 из числителя, при этом получаем десятичную дробь 0,37 .

Ответ:

0,37 .

Для закрепления навыков перевода правильных обыкновенных дробей с числителями 10, 100, … в десятичные дроби разберем решение еще одного примера.

Пример.

Запишите правильную дробь 107/10 000 000 в виде десятичной дроби.

Решение.

Количество цифр в числителе равно 3 , а количество нулей в знаменателе равно 7 , поэтому данная обыкновенная дробь нуждается в подготовке к переводу в десятичную. Нам нужно дописать 7-3=4 нуля слева в числителе, чтобы общее количество цифр там стало равно количеству нулей в знаменателе. Получаем .

Осталось составить нужную десятичную дробь. Для этого, во-первых, записываем 0 , во-вторых, ставим запятую, в-третьих, записываем число из числителя вместе с нулями 0000107 , в итоге имеем десятичную дробь 0,0000107 .

Ответ:

0,0000107 .

Неправильные обыкновенные дроби не нуждаются в подготовке при переводе в десятичные дроби. Следует придерживаться следующего правила перевода неправильных обыкновенных дробей со знаменателями 10, 100, … в десятичные дроби :

• записываем число из числителя;
• отделяем десятичной запятой столько цифр справа, сколько нулей в знаменателе исходной дроби.

Разберем применение этого правила при решении примера.

Пример.

Переведите неправильную обыкновенную дробь 56 888 038 009/100 000 в десятичную дробь.

Решение.

Во-первых, записываем число из числителя 56888038009, во-вторых, отделяем десятичной запятой 5 цифр справа, так как в знаменателе исходной дроби 5 нулей. В итоге имеем десятичную дробь 568 880,38009 .

Ответ:

568 880,38009 .

Для обращения в десятичную дробь смешанного числа , знаменателем дробной части которого является число 10 , или 100 , или 1 000, … , можно выполнить перевод смешанного числа в неправильную обыкновенную дробь, после чего полученную дробь обратить в десятичную дробь. Но можно пользоваться и следующим правилом перевода смешанных чисел со знаменателем дробной части 10, или 100, или 1 000, … в десятичные дроби :

• при необходимости выполняем «предварительную подготовку» дробной части исходного смешанного числа, дописав необходимое количество нулей слева в числителе;
• записываем целую часть исходного смешанного числа;
• ставим десятичную запятую;
• записываем число из числителя вместе с дописанными нулями.

Рассмотрим пример, при решении которого выполним все необходимые шаги для представления смешанного числа в виде десятичной дроби.

Пример.

Переведите смешанное число в десятичную дробь.

Решение.

В знаменателе дробной части 4 нуля, в числителе же находится число 17 , состоящее из 2 цифр, поэтому, нам нужно дописать два нуля слева в числителе, чтобы там число знаков стало равно числу нулей в знаменателе. Выполнив это, в числителе окажется 0017 .

Теперь записываем целую часть исходного числа, то есть, число 23 , ставим десятичную запятую, после которой записываем число из числителя вместе с дописанными нулями, то есть, 0017 , при этом получаем искомую десятичную дробь 23,0017 .

Запишем все решение кратко: .

Несомненно, можно было сначала представить смешанное число в виде неправильной дроби, после чего перевести ее в десятичную дробь. При таком подходе решение выглядит так: .

Ответ:

23,0017 .

Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби

В десятичную дробь можно перевести не только обыкновенные дроби со знаменателями 10, 100, … , но обыкновенные дроби с другими знаменателями. Сейчас мы разберемся, как это делается.

В некоторых случаях исходная обыкновенная дробь легко приводится к одному из знаменателей 10 , или 100 , или 1 000, … (смотрите приведение обыкновенной дроби к новому знаменателю), после чего не составляет труда полученную дробь представить в виде десятичной дроби. Например, очевидно, что дробь 2/5 можно привести к дроби со знаменателем 10 , для этого нужно числитель и знаменатель умножить на 2 , что даст дробь 4/10 , которая по правилам, разобранным в предыдущем пункте, легко переводится в десятичную дробь 0,4 .

В остальных случаях приходится использовать другой способ перевода обыкновенной дроби в десятичную, к рассмотрению которого мы и переходим.

Для обращения обыкновенной дроби в десятичную дробь выполняется деление числителя дроби на знаменатель, числитель предварительно заменяется равной ему десятичной дробью с любым количеством нулей после десятичной запятой (об этом мы говорили в разделе равные и неравные десятичные дроби). При этом деление выполняется так же, как деление столбиком натуральных чисел , а в частном ставится десятичная запятая, когда заканчивается деление целой части делимого. Все это станет понятно из решений примеров, приведенных ниже примеров.

Пример.

Переведите обыкновенную дробь 621/4 в десятичную дробь.

Решение.

Число в числителе 621 представим в виде десятичной дроби, добавив десятичную запятую и несколько нулей после нее. Для начала допишем 2 цифры 0 , позже, при необходимости, мы всегда можем добавить еще нулей. Итак, имеем 621,00 .

Теперь выполним деление столбиком числа 621,000 на 4 . Первые три шага ничем не отличаются от деления столбиком натуральных чисел, после них приходим к следующей картине:

Так мы добрались до десятичной запятой в делимом, а остаток при этом отличен от нуля. В этом случае в частном ставим десятичную запятую, и продолжаем деление столбиком, не обращая внимания на запятые:

На этом деление закончено, а в результате мы получили десятичную дробь 155,25 , которая соответствует исходной обыкновенной дроби.

Ответ:

155,25 .

Для закрепления материала рассмотрим решение еще одного примера.

Пример.

Переведите обыкновенную дробь 21/800 в десятичную дробь.

Решение.

Для перевода данной обыкновенной дроби в десятичную, выполним деление столбиком десятичной дроби 21,000… на 800 . Нам после первого же шага придется поставить десятичную запятую в частном, после чего продолжить деление:

Наконец-то мы получили остаток 0 , на этом перевод обыкновенной дроби 21/400 в десятичную дробь закончен, и мы пришли к десятичной дроби 0,02625 .

Ответ:

0,02625 .

Может случиться, что при делении числителя на знаменатель обыкновенной дроби мы так и не получим в остатке 0 . В этих случаях деление можно продолжать сколь угодно долго. Однако, начиная с некоторого шага, остатки начитают периодически повторяться, при этом повторяются и цифры в частном. Это означает, что исходная обыкновенная дробь переводится в бесконечную периодическую десятичную дробь .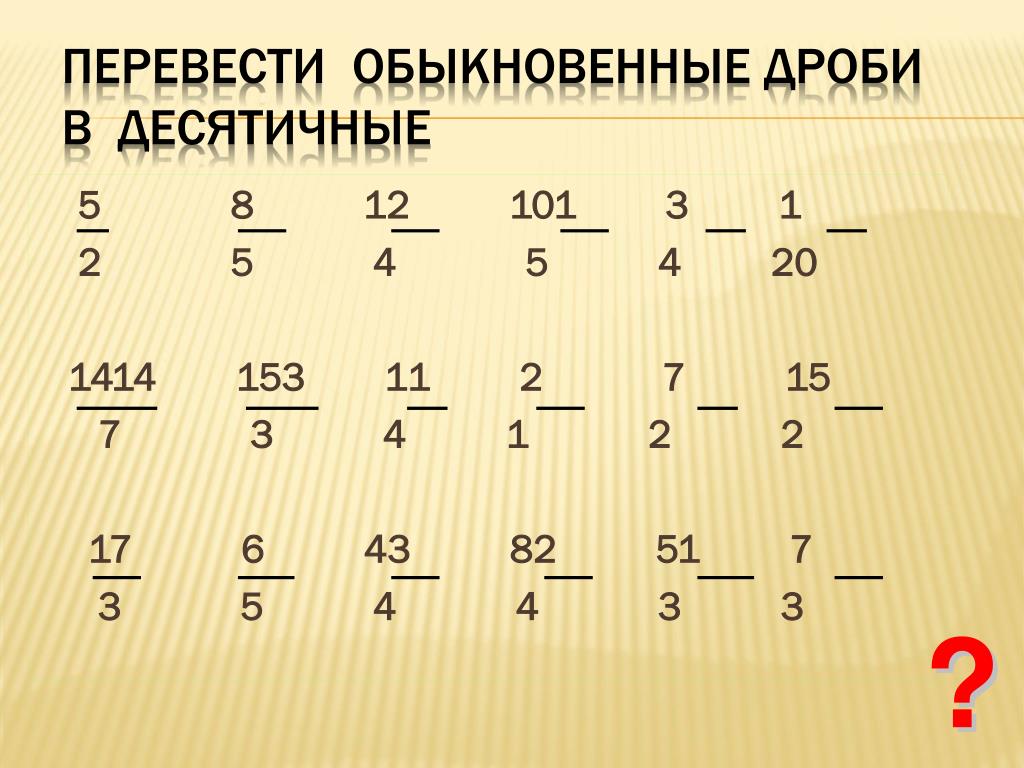 Покажем это на примере.

Пример.

Запишите обыкновенную дробь 19/44 в виде десятичной дроби.

Решение.

Для перевода обыкновенной дроби в десятичную выполним деление столбиком:

Уже сейчас видно, что при делении начали повторяться остатки 8 и 36 , при этом в частном повторяются цифры 1 и 8 . Таким образом, исходная обыкновенная дробь 19/44 переводится в периодическую десятичную дробь 0,43181818…=0,43(18) .

Ответ:

0,43(18) .

В заключение этого пункта разберемся, какие обыкновенные дроби можно перевести в конечные десятичные дроби, а какие – только в периодические.

Пусть перед нами находится несократимая обыкновенная дробь (если дробь сократимая, то предварительно выполняем сокращение дроби), и нам нужно выяснить, в какую десятичную дробь ее можно перевести – в конечную или периодическую.

Понятно, что если обыкновенную дробь можно привести к одному из знаменателей 10, 100, 1 000, … , то полученную дробь легко перевести в конечную десятичную дробь по правилам, разобранным в предыдущем пункте. Но к знаменателям 10, 100, 1 000 и т.д. приводятся далеко не все обыкновенные дроби. К таким знаменателям можно привести лишь дроби, знаменатели которых являются хотя бы одного из чисел 10, 100, … А какие числа могут быть делителями 10, 100, … ? Ответить на этот вопрос нам позволят чисел 10, 100, … , а они таковы: 10=2·5 , 100=2·2·5·5 , 1 000=2·2·2·5·5·5, … . Отсюда следует, что делителями 10, 100, 1 000 и т.д. могут быть лишь числа, разложения которых на простые множители содержат лишь числа 2 и (или) 5 .

Теперь мы можем сделать общий вывод о переводе обыкновенных дробей в десятичные дроби:

• если в разложении знаменателя на простые множители присутствуют лишь числа 2 и (или) 5 , то эту дробь можно перевести в конечную десятичную дробь;
• если кроме двое и пятерок в разложении знаменателя присутствуют другие простые числа, то эта дробь переводится к бесконечную десятичную периодическую дробь.

Пример.

Не выполняя перевод обыкновенных дробей в десятичные, скажите, какие из дробей 47/20 , 7/12 , 21/56 , 31/17 можно перевести в конечную десятичную дробь, а какие — только в периодическую.

Решение.

Разложение на простые множители знаменателя дроби 47/20 имеет вид 20=2·2·5 . В этом разложении присутствуют лишь двойки и пятерки, поэтому эта дробь может быть приведена к одному из знаменателей 10, 100, 1 000, … (в этом примере к знаменателю 100 ), следовательно, может быть переведена в конечную десятичную дробь.

Разложение на простые множители знаменателя дроби 7/12 имеет вид 12=2·2·3 . Так как оно содержит простой множитель 3 , отличный от 2 и 5 , то эта дробь не может быть представлена в виде конечной десятичной дроби, но может быть переведена в периодическую десятичную дробь.

Дробь 21/56 – сократимая, после сокращения она принимает вид 3/8 . Разложение знаменателя на простые множители содержит три множителя, равных 2 , следовательно, обыкновенная дробь 3/8 , а значит и равная ей дробь 21/56 , может быть переведена в конечную десятичную дробь.

Наконец, разложение знаменателя дроби 31/17 представляет собой само 17 , следовательно, эту дробь нельзя обратить в конечную десятичную дробь, но можно обратить в бесконечную периодическую.

Ответ:

47/20 и 21/56 можно перевести в конечную десятичную дробь, а 7/12 и 31/17 — только в периодическую.

Обыкновенные дроби не переводятся в бесконечные непериодические десятичные дроби

Информация предыдущего пункта порождает вопрос: «Может ли при делении числителя дроби на знаменатель получиться бесконечная непериодическая дробь»?

Ответ: нет. При переводе обыкновенной дроби может получиться либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь. Поясним, почему это так.

Из теоремы о делимости с остатком ясно, что остаток всегда меньше делителя, то есть, если мы выполняем деление некоторого целого числа на целое число q , то остатком может быть лишь одно из чисел 0, 1, 2, …, q−1 . Отсюда следует, что после завершения деления столбиком целой части числителя обыкновенной дроби на знаменатель q , не более чем через q шагов возникнет одна из двух следующих ситуаций:

• либо мы получим остаток 0 , на этом деление закончится, и мы получим конечную десятичную дробь;
• либо мы получим остаток, который уже появлялся ранее, после этого остатки начнут повторяться как в предыдущем примере (так как при делении равных чисел на q получаются равные остатки, что следует из уже упомянутой теоремы о делимости), так будет получена бесконечная периодическая десятичная дробь.

Других вариантов быть не может, следовательно, при обращении обыкновенной дроби в десятичную дробь не может получиться бесконечная непериодическая десятичная дробь.

Из приведенных в этом пункте рассуждений также следует, что длина периода десятичной дроби всегда меньше, чем значение знаменателя соответствующей обыкновенной дроби.

Перевод десятичных дробей в обыкновенные дроби

Теперь разберемся, как перевести десятичную дробь в обыкновенную. Начнем с перевода конечных десятичных дробей в обыкновенные дроби. После этого рассмотрим метод обращения бесконечных периодических десятичных дробей. В заключение скажем о невозможности перевода бесконечных непериодических десятичных дробей в обыкновенные дроби.

Перевод конечных десятичных дробей в обыкновенные дроби

Получить обыкновенную дробь, которая записана в виде конечной десятичной дроби, достаточно просто. Правило перевода конечной десятичной дроби в обыкновенную дробь состоит из трех шагов:

• во-первых, записать данную десятичную дробь в числитель, предварительно отбросив десятичную запятую и все нули слева, если они есть;
• во-вторых, в знаменатель записать единицу и к ней дописать столько нулей, сколько цифр находится после запятой в исходной десятичной дроби;
• в-третьих, при необходимости выполнить сокращение полученной дроби.

Рассмотрим решения примеров.

Пример.

Обратите десятичную дробь 3,025 в обыкновенную дробь.

Решение.

Если в исходной десятичной дроби убрать десятичную запятую, то мы получим число 3 025 . В нем нет нулей слева, которые бы мы отбросили. Итак, в числитель искомой дроби записываем 3 025 .

В знаменатель записываем цифру 1 и справа к ней дописываем 3 нуля, так как в исходной десятичной дроби после запятой находятся 3 цифры.

Так мы получили обыкновенную дробь 3 025/1 000 . Эту дробь можно сократить на 25 , получаем .

Ответ:

.

Пример.

Выполните перевод десятичной дроби 0,0017 в обыкновенную дробь.

Решение.

Без десятичной запятой исходная десятичная дробь имеет вид 00017 , отбросив нули слева получаем число 17 , которое и является числителем искомой обыкновенной дроби.

В знаменатель записываем единицу с четырьмя нулями, так как в исходной десятичной дроби после запятой 4 цифры.

В итоге имеем обыкновенную дробь 17/10 000 . Эта дробь несократима, и перевод десятичной дроби в обыкновенную закончен.

Ответ:

.

Когда целая часть исходной конечной десятичной дроби отлична от нуля, то ее можно сразу перевести в смешанное число, минуя обыкновенную дробь. Дадим правило перевода конечной десятичной дроби в смешанное число :

• число до десятичной запятой надо записать как целую часть искомого смешанного числа;
• в числитель дробной части нужно записать число, полученное из дробной части исходной десятичной дроби после отбрасывания в ней всех нулей слева;
• в знаменателе дробной части нужно записать цифру 1 , к которой справа дописать столько нулей, сколько цифр находится в записи исходной десятичной дроби после запятой;
• при необходимости выполнить сокращение дробной части полученного смешанного числа.

Рассмотрим пример перевода десятичной дроби в смешанное число.

Пример.

Представьте десятичную дробь 152,06005 в виде смешанного числа

Дробь представляет собой число, которое состоит из одной или нескольких долей единицы. В математике существует три вида дробей: обыкновенные, смешанные и десятичные.

• 
  Обыкновенные дроби

Обыкновенная дробь записывается как соотношение, в котором в числителе отражается, сколько взято частей от числа, а знаменатель показывает, на сколько частей разделена единица. Если числитель меньше знаменателя, то перед нами правильная дробь.Например: ½, 3/5, 8/9.

Если числитель равен знаменателю или больше его, то мы имеем дело с неправильной дробью. Например: 5/5, 9/4, 5/2 При делении числителя может получиться конечное число. Например, 40/8 = 5. Следовательно, любое целое число может быть записано в виде обыкновенной неправильной дроби или ряда таких дробей. Рассмотрим записи одного и того же числа в виде ряда различных .

• Смешанные дроби

В общем виде смешанная дробь может быть представлена формулой:

Таким образом, смешанная дробь записывается как целое число и обыкновенная правильная дробь, а под такой записью понимают сумму целого и его дробной части.

• Десятичные дроби

Десятичная дробь – это особая разновидность дроби, у которой знаменатель может быть представлен как степень числа 10. Существуют бесконечные и конечные десятичные дроби. При записи этой разновидности дроби сначала указывается целая часть, затем через разделитель (точку или запятую) фиксируется дробная часть.

Запись дробной части всегда определяется ее размерностью. Десятичная запись выглядит следующим образом:

Правила перевода между различными видами дробей

• Перевод смешанной дроби в обыкновенную

Смешанную дробь можно перевести только в неправильную. Для перевода необходимо целую часть привести и тому же знаменателю, что и дробную. В общем виде это будет выглядеть следующим образом:
Рассмотрим использование этого правила на конкретных примерах:

• Перевод обыкновенной дроби в смешанную

Неправильную обыкновенную дробь можно превратить в смешанную путем простого деления, в результате которого находится целая часть и остаток (дробная часть).

Для примера переведем дробь 439/31 в смешанную:
​​

• Перевод обыкновенной дроби

В некоторых случаях перевести дробь в десятичную достаточно просто. В этом случае применяется основное свойство дроби, числитель и знаменатель умножаются на одно и то же числу, для того, чтобы привести делитель к степени числа 10.

Например:

В некоторых случаях может понадобиться найти частное путем деления уголком или с помощью калькулятора. А некоторые дроби невозможно привести к конечной десятичной дроби. Например, дробь 1/3 при делении никогда не даст конечный результат.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Дроби в старших классах не сильно досаждают. До поры до времени. Пока не столкнётесь со степенями с рациональными показателями да логарифмами. А вот там…. Давишь, давишь калькулятор, а он все полное табло каких-то циферок кажет. Приходится головой думать, как в третьем классе.

Давайте уже разберёмся с дробями, наконец! Ну сколько можно в них путаться!? Тем более, это всё просто и логично. Итак, какие бывают дроби?

Виды дробей. Преобразования.

Дроби бывают трёх видов.

1. Обыкновенные дроби , например:

Иногда вместо горизонтальной чёрточки ставят наклонную черту: 1/2, 3/4, 19/5, ну, и так далее. Здесь мы часто будем таким написанием пользоваться. Верхнее число называется числителем , нижнее — знаменателем. Если вы постоянно путаете эти названия (бывает…), скажите себе с выражением фразу: «Ззззз апомни! Ззззз наменатель — вниззззз у!» Глядишь, всё и ззззапомнится.)

Чёрточка, что горизонтальная, что наклонная, означает деление верхнего числа (числителя) на нижнее (знаменатель). И всё! Вместо чёрточки вполне можно поставить знак деления — две точки.

Когда деление возможно нацело, это надо делать.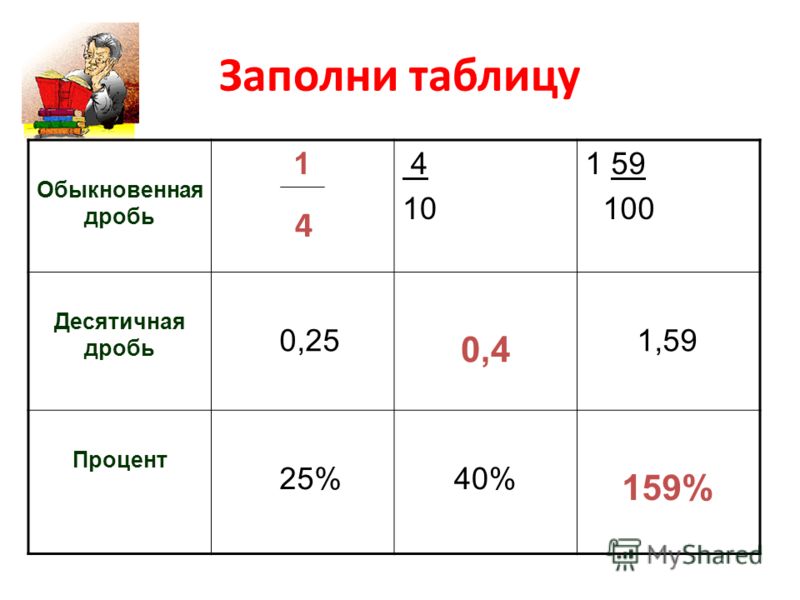 Так, вместо дроби «32/8» гораздо приятнее написать число «4». Т.е. 32 просто поделить на 8.

32/8 = 32: 8 = 4

Я уж и не говорю про дробь «4/1». Которая тоже просто «4». А если уж не делится нацело, так и оставляем, в виде дроби. Иногда приходится обратную операцию проделывать. Делать из целого числа дробь. Но об этом далее.

2. Десятичные дроби , например:

Именно в таком виде нужно будет записывать ответы на задания «В».

3. Смешанные числа , например:

Смешанные числа практически не используются в старших классах. Для того, чтобы с ними работать, их всяко надо переводить в обыкновенные дроби. Но это точно надо уметь делать! А то попадётся такое число в задачке и зависните… На пустом месте. Но мы-то вспомним эту процедуру! Чуть ниже.

Наиболее универсальны обыкновенные дроби . С них и начнём. Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями !

Основное свойство дроби.

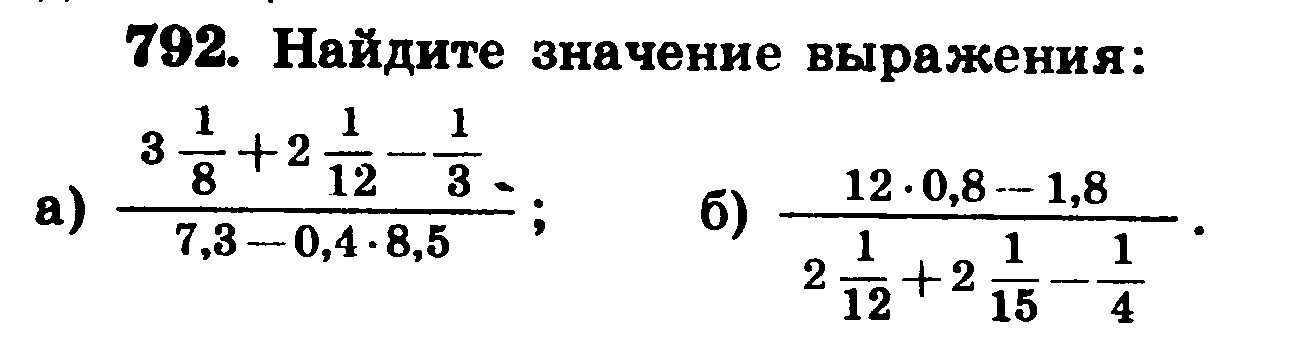
Итак, поехали! Для начала я вас удивлю. Всё многообразие преобразований дробей обеспечивается одним-единственным свойством! Оно так и называется, основное свойство дроби . Запоминайте: если числитель и знаменатель дроби умножить (разделить) на одно и то же число, дробь не изменится. Т.е:

Понятно, что писать можно дальше, до посинения. Синусы и логарифмы пусть вас не смущают, с ними дальше разберёмся. Главное понять, что все эти разнообразные выражения есть одна и та же дробь . 2/3.

А оно нам надо, все эти превращения? Ещё как! Сейчас сами увидите. Для начала употребим основное свойство дроби для сокращения дробей . Казалось бы, вещь элементарная. Делим числитель и знаменатель на одно и то же число и все дела! Ошибиться невозможно! Но… человек — существо творческое. Ошибиться везде может! Особенно, если приходится сокращать не дробь типа 5/10, а дробное выражение со всякими буковками.

Как правильно и быстро сокращать дроби, не делая лишней работы, можно прочитать в особом Разделе 555 .

Нормальный ученик не заморачивается делением числителя и знаменателя на одно и то же число (или выражение)! Он просто зачеркивает всё одинаковое сверху и снизу! Здесь-то и таится типичная ошибка, ляп, если хотите.

Например, надо упростить выражение:

Тут и думать нечего, зачеркиваем букву «а» сверху и двойку снизу! Получаем:

Все правильно. Но реально вы поделили весь числитель и весь знаменатель на «а». Если вы привыкли просто зачеркивать, то, впопыхах, можете зачеркнуть «а» в выражении

и получить снова

Что будет категорически неверно. Потому что здесь весь числитель на «а» уже не делится ! Эту дробь сократить нельзя. Кстати, такое сокращение – это, гм… серьезный вызов преподавателю. Такого не прощают! Запомнили? При сокращении делить надо весь числитель и весь знаменатель!

Сокращение дробей сильно облегчает жизнь. Получится где-нибудь у вас дробь, к примеру 375/1000. И как теперь с ней дальше работать? Без калькулятора? Умножать, скажем, складывать, в квадрат возводить!? А если не полениться, да аккуратненько сократить на пять, да ещё на пять, да ещё. .. пока сокращается, короче. Получим 3/8! Куда приятнее, правда?

Основное свойство дроби позволяет переводить обыкновенные дроби в десятичные и наоборот без калькулятора ! Это важно на ЕГЭ, верно?

Как переводить дроби из одного вида в другой.

С десятичными дробями всё просто. Как слышится, так и пишется! Скажем, 0,25. Это ноль целых, двадцать пять сотых. Так и пишем: 25/100. Сокращаем (делим числитель и знаменатель на 25), получаем обычную дробь: 1/4. Всё. Бывает, и не сокращается ничего. Типа 0,3. Это три десятых, т.е. 3/10.

А если целых — не ноль? Ничего страшного. Записываем всю дробь без всяких запятых в числитель, а в знаменатель — то, что слышится. Например: 3,17. Это три целых, семнадцать сотых. Пишем в числитель 317, а в знаменатель 100. Получаем 317/100. Ничего не сокращается, значит всё. Это ответ. Элементарно, Ватсон! Из всего сказанного полезный вывод: любую десятичную дробь можно превратить в обыкновенную .

А вот обратное преобразование, обыкновенной в десятичную, некоторые без калькулятора не могут сделать.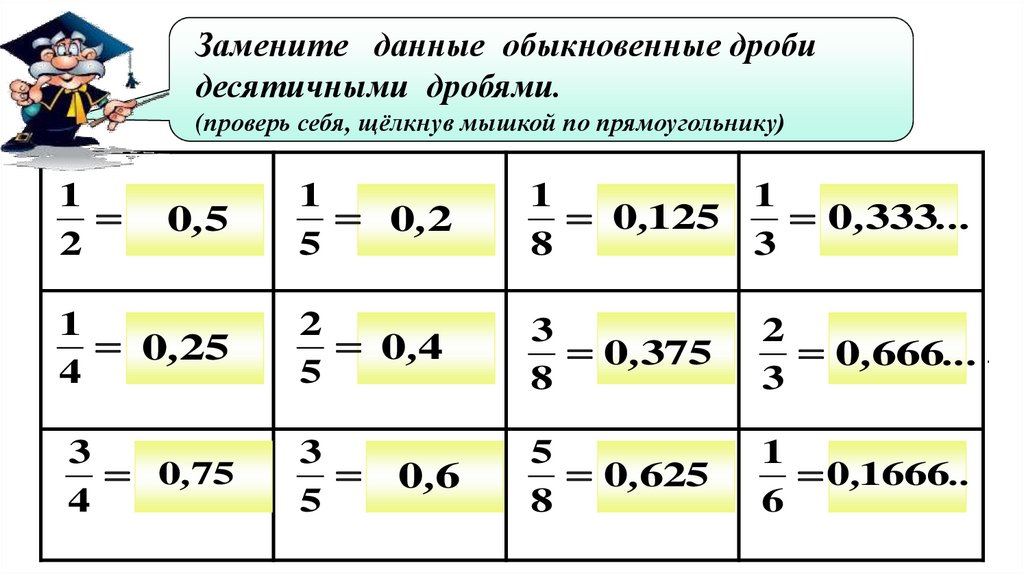 А надо! Как вы ответ записывать будете на ЕГЭ!? Внимательно читаем и осваиваем этот процесс.

Десятичная дробь чем характерна? У неё в знаменателе всегда стоит 10, или 100, или 1000, или 10000 и так далее. Если ваша обычная дробь имеет такой знаменатель, проблем нет. Например, 4/10 = 0,4. Или 7/100 = 0,07. Или 12/10 = 1,2. А если в ответе на задание раздела «В» получилось 1/2? Что в ответ писать будем? Там десятичные требуются…

Вспоминаем основное свойство дроби ! Математика благосклонно позволяет умножать числитель и знаменатель на одно и то же число. На любое, между прочим! Кроме нуля, разумеется. Вот и применим это свойство себе на пользу! На что можно умножить знаменатель, т.е. 2 чтобы он стал 10, или 100, или 1000 (поменьше лучше, конечно…)? На 5, очевидно. Смело умножаем знаменатель (это нам надо) на 5. Но, тогда и числитель надо умножить тоже на 5. Это уже математика требует! Получим 1/2 = 1х5/2х5 = 5/10 = 0,5. Вот и всё.

Однако, знаменатели всякие попадаются.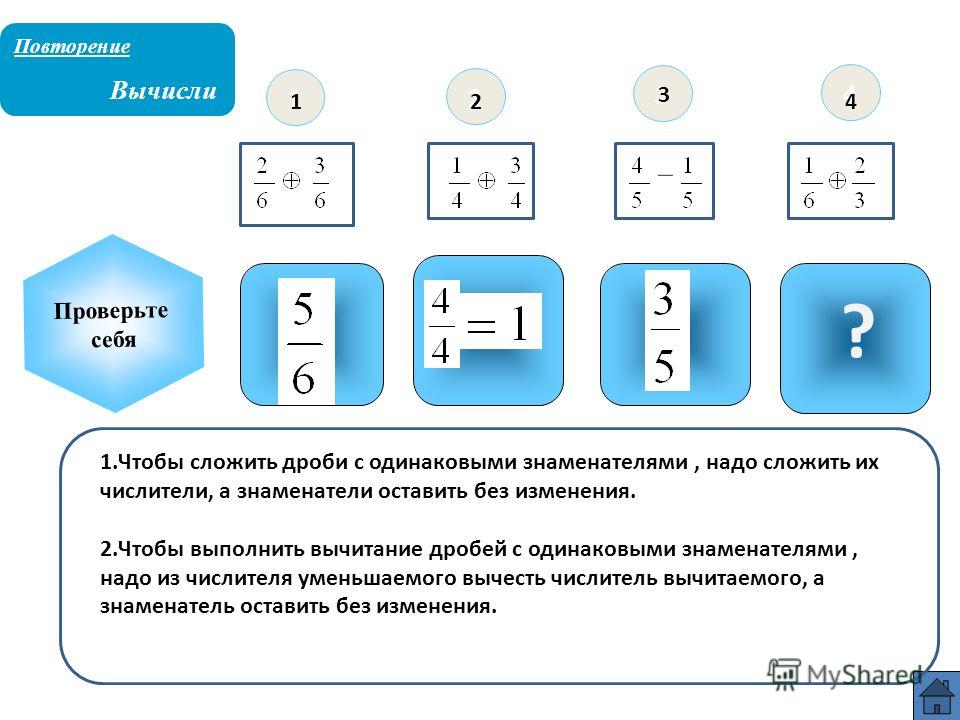 Попадётся, например дробь 3/16. Попробуй, сообрази тут, на что 16 умножить, чтоб 100 получилось, или 1000… Не получается? Тогда можно просто разделить 3 на 16. За отсутствием калькулятора делить придётся уголком, на бумажке, как в младших классах учили. Получим 0,1875.

А бывают и совсем скверные знаменатели. Например, дробь 1/3 ну никак не превратишь в хорошую десятичную. И на калькуляторе, и на бумажке, мы получим 0,3333333… Это значит, что 1/3 в точную десятичную дробь не переводится . Так же, как и 1/7, 5/6 и так далее. Много их, непереводимых. Отсюда ещё один полезный вывод. Не каждая обыкновенная дробь переводится в десятичную !

Кстати, это полезная информация для самопроверки. В разделе «В» в ответ надо десятичную дробь записывать. А у вас получилось, например, 4/3. Эта дробь не переводится в десятичную. Это означает, что где-то вы ошиблись по дороге! Вернитесь, проверьте решение.

Итак, с обыкновенными и десятичными дробями разобрались. Осталось разобраться со смешанными числами. Для работы с ними их всяко нужно перевести в обыкновенные дроби. Как это сделать? Можно поймать шестиклассника и спросить у него. Но не всегда шестиклассник окажется под руками… Придётся самим. Это несложно. Надо знаменатель дробной части умножить на целую часть и прибавить числитель дробной части. Это будет числитель обычной дроби. А знаменатель? Знаменатель останется тем же самым. Звучит сложно, но на деле всё элементарно. Смотрим пример.

Пусть в задачке вы с ужасом увидели число:

Спокойно, без паники соображаем. Целая часть — это 1. Единица. Дробная часть — 3/7. Стало быть, знаменатель дробной части — 7. Этот знаменатель и будет знаменателем обыкновенной дроби. Считаем числитель. 7 умножаем на 1 (целая часть) и прибавляем 3 (числитель дробной части). Получим 10. Это будет числитель обыкновенной дроби. Вот и всё. Еще проще это выглядит в математической записи:

Ясненько? Тогда закрепите успех! Переведите в обыкновенные дроби. У вас должно получится 10/7, 7/2, 23/10 и 21/4.

Обратная операция — перевод неправильной дроби в смешанное число — в старших классах редко требуется. Ну если уж… И если Вы — не в старших классах — можете заглянуть в особый Раздел 555 . Там же, кстати, и про неправильные дроби узнаете.

Ну вот, практически и всё. Вы вспомнили виды дробей и поняли, как переводить их из одного вида в другой. Остаётся вопрос: зачем это делать? Где и когда применять эти глубокие познания?

Отвечаю. Любой пример сам подсказывает необходимые действия. Если в примере смешались в кучу обыкновенные дроби, десятичные, да ещё и смешанные числа, переводим всё в обыкновенные дроби. Это всегда можно сделать . Ну а если написано, что-нибудь типа 0,8 + 0,3, то так и считаем, безо всякого перевода. Зачем нам лишняя работа? Мы выбираем тот путь решения, который удобен нам !

Если в задании сплошь десятичные дроби, но гм… злые какие-то, перейдите к обыкновенным, попробуйте! Глядишь, всё и наладится. Например, придется в квадрат возводить число 0,125. Не так-то просто, если от калькулятора не отвыкли! Мало того, что числа перемножать столбиком надо, так ещё думай, куда запятую вставить! В уме точно не получится! А если перейти к обыкновенной дроби?

0,125 = 125/1000. Сокращаем на 5 (это для начала). Получаем 25/200. Ещё раз на 5. Получаем 5/40. О, ещё сокращается! Снова на 5! Получаем 1/8. Легко возводим в квадрат (в уме!) и получаем 1/64. Всё!

Подведём итоги этого урока.

1. Дроби бывают трёх видов. Обыкновенные, десятичные и смешанные числа.

2. Десятичные дроби и смешанные числа всегда можно перевести в обыкновенные дроби. Обратный перевод не всегда возможен.

3. Выбор вида дробей для работы с заданием зависит от этого самого задания. При наличии разных видов дробей в одном задании, самое надёжное — перейти к обыкновенным дробям.

Теперь можно потренироваться. Для начала переведите эти десятичные дроби в обыкновенные:

3,8; 0,75; 0,15; 1,4; 0,725; 0,012

Должны получиться вот такие ответы (в беспорядке!):

На этом и завершим. В этом уроке мы освежили в памяти ключевые моменты по дробям. Бывает, правда, что освежать особо нечего…) Если уж кто совсем крепко забыл, или ещё не освоил… Тем можно пройти в особый Раздел 555 . Там все основы подробненько расписаны. Многие вдруг всё понимать начинают. И решают дроби с лёту).

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Как считать дроби на калькуляторе

По умолчанию большинство калькуляторов работает только с десятичными дробями. Например, вместо 1/2 калькулятор оперирует числом 0,5. И тем не менее есть пара способов посчитать дроби на обычном калькуляторе, а затем перевести их из десятичных в обыкновенные. Также существуют специальные калькуляторы, которые умеют выполнять действия с простыми дробями, но и здесь есть подводные камни.

«Бери и Делай» объясняет, как с помощью разных калькуляторов складывать, вычитать, умножать и делить дроби.

Как считать дроби с помощью научного калькулятора

Такой калькулятор предназначен для инженерных и научных расчетов, поэтому его возможности гораздо шире, чем у обычных. У такого калькулятора может быть два поля: в одном отражаются введенные значения, а в другом — результат. На таком калькуляторе в числе прочего есть кнопка, которая позволяет вводить в него число в виде обыкновенной дроби. Как это сделать? Допустим, вам нужно записать число 3/4.

1. Включаете калькулятор. Нажимаете на цифру 3, которая должна быть в числителе.
2. Нажимаете на кнопку, которая меняет формат записи числа, позволяя записать обыкновенную дробь. Она находится в левом верхнем углу и обозначается символами ab/c или двумя прямоугольниками, один из которых закрашен, а второй нет. В строке записи введенных значений появляется символ, похожий на ˩.
3. Нажимаете на цифру 4, которая должна быть в знаменателе.
4. Таким образом в калькулятор вводится число 3/4 в виде обыкновенной дроби для дальнейших расчетов.

Допустим, мы хотим узнать результат простого действия и сложить 13/4 и 3/8. Начнем с записи смешанной дроби, а затем перейдем к действию сложения.

Шаг № 1. Нажимаете на калькуляторе цифру 1. Шаг № 2. Затем нажимаете на кнопку, которая позволяет менять формат записи числа и вводить число в виде обыкновенной дроби. В данном случае это нужно сделать уже на этом этапе, чтобы калькулятор распознал это число как смешанную дробь.

Шаг № 3. Нажимаете на цифру 3. Шаг № 4. Снова нажимаете на кнопку, которая позволяет вводить число в виде обыкновенной дроби. Затем нажимаете на цифру 4. Смешанная дробь введена!

Шаг № 5. Теперь нажимаете на кнопку действия сложения и добавляете вторую дробь, записывая ее аналогичным образом. Шаг № 6. В конце нажимаете на кнопку равенства, чтобы получить результат. Калькулятор в данном случае отображает результат в виде смешанной дроби. Таким же образом вы можете выполнять другие действия с дробями. Обратите внимание, что формат записи такого числа в результате аналогичен тому, который был при вводе обыкновенных дробей в калькулятор.

У таких калькуляторов есть свои особенности:

• Если при вычислениях вы смешиваете дробные и десятичные значения, то результат будет отображаться в виде десятичной дроби, что заметно на картинке выше.
• Дроби в результатах вычислений на калькуляторе всегда отображаются после их приведения к несократимым дробям.

Как считать дроби с помощью обычного калькулятора

У обычного калькулятора нет кнопки для записи дроби, но есть другие функции, которые облегчают работу. Допустим, вы получили результат выражения, работая с десятичными дробями, но это число теперь нужно записать в виде обыкновенной дроби. Как перевести десятичную дробь в обыкновенную?

1. Введите в калькулятор десятичную дробь. В нашем примере это 0,7143. Нажмите на кнопку действия умножения.
2. Чтобы превратить десятичную дробь в обыкновенную, выберите число, которое будет стоять в знаменателе обыкновенной дроби, которая получится в результате. Допустим, это 7. Умножьте на него десятичную дробь.
3. Число, полученное в результате этого умножения, округляете до целого и записываете в числитель. В данном случае это 5. А число 7, соответственно, записываете в знаменателе.

Таким образом получается, что число 0,7143 можно представить в виде обыкновенной дроби 5/7:

У этого способа есть свой минус: существует риск столкнуться с погрешностью при вычислениях, поэтому конечный результат нужно проверять. Просто разделите числитель на знаменатель: чем ниже погрешность, тем ближе результат будет к первоначальной десятичной дроби, а значит, полученную ранее простую дробь можно использовать для дальнейших расчетов. Может быть и обратная ситуация: у вас есть обыкновенные дроби, но вы хотите перевести их в десятичные, чтобы затем выполнять действия над ними с помощью обычного калькулятора. Как в таком случае перевести обыкновенную дробь в десятичную? Возьмем дробь 7/4 и превратим ее в десятичную.

1. Вбиваете в калькулятор число 7, стоящее на месте числителя. Выбираете действие деления.
2. В качестве делителя вбиваете 4 (знаменатель дроби).
3. Нажимаете на знак равенства. В результате получаете десятичную дробь. Таким образом, вы перевели число 7/4 в десятичную дробь 1,75.

Важно: обыкновенная дробь после перевода в десятичную может превратиться в бесконечную периодическую дробь. В таком случае ее можно округлить.

Как выполнять действия с дробями, используя кнопки памяти (MR, M-, M+) на калькуляторе

На некоторых моделях калькуляторов есть кнопки памяти, которые позволяют сохранять в памяти устройства определенное число, а также выполнять с ним действия сложения или вычитания. Эти функции можно использовать при работе с дробями. Например, посмотрим, как с их помощью можно сложить числа 1/4 и 3/8.

Шаг № 1. Сначала введите дробь 1/4. Нажмите на калькуляторе цифру 1, затем на кнопку действия деления. Шаг № 2. Введите цифру 4 и нажмите на кнопку M+. Если при нажатии кнопки М+ результат деления не отобразился на дисплее, начните с начала и перед нажатием кнопки M+ здесь и далее, в шаге № 5, нажмите на кнопку «=». Шаг № 3. На экране калькулятора отражается результат действия деления этих чисел, и он же записывается в память калькулятора. Шаг № 4. Теперь введите вторую дробь аналогичным образом. Сначала нажимаете на калькуляторе цифру 3, затем на кнопку действия деления. Шаг № 5. Далее введите цифру 8 и нажмите на кнопку M+. Шаг № 6. На экране калькулятора отражается результат действия деления этих чисел, который тоже сохраняется в памяти калькулятора. Шаг № 7. Теперь нажмите на кнопку MR: калькулятор отобразит сумму чисел, которые вы сохранили в его памяти. Так вы получите результат сложения дробей. При желании эту десятичную дробь можно записать в виде обыкновенной, как это делалось выше. Для этого выполните действие умножения. Шаг № 8. В качестве множителя можно выбрать любое число. В ряде случаев удобнее, если оно совпадает с числом, которое находилось в знаменателе одной из дробей. В нашем примере это 8. Шаг № 9. В результате умножения получаете число 5, которое записываете на место числителя. Получается, 1/4 + 3/8 =5/8. Так, используя кнопки памяти, мы сложили две обыкновенные дроби, а затем перевели результат из десятичной дроби в обыкновенную. Аналогичным образом можно использовать кнопку M-, позволяющую вычитать из одной дроби другую.

Калькулятор десятичной дроби (двунаправленный)

Используйте этот калькулятор десятичной дроби , если вы хотите преобразовать десятичное число в дробную форму. Выполнение этого вручную иногда может быть сложным, особенно если вы еще не знакомы с процессом преобразования. С помощью этого калькулятора вы можете удобно конвертировать эти значения из десятичной дроби в дробь и наоборот.

Как пользоваться калькулятором десятичной дроби

Довольно легко вычислить десятичный эквивалент дроби или наоборот для хорошо знакомых нам чисел. Скажем, для десятичного числа 1,5 это очень распространенное десятичное число, и мы можем быстро сказать, что это дробная форма как 1 1/2.

Однако для десятичных чисел, которые не так распространены, например 5,87, 6,348 и т. д., у нас могут возникнуть сомнения, как преобразовать их в дроби. Вот почему этот калькулятор создан, чтобы устранить эту проблему, и дает вам выбор, хотите ли вы использовать его или выполнить расчет самостоятельно.

Вот пошаговое руководство по использованию калькулятора десятичной дроби:

• 1. В поле ввода Decimal введите десятичное число, которое вы хотите преобразовать в дробь. Поэтому, если вы хотите конвертировать 0,375, введите это число в это поле.
• 2. Нажмите кнопку Вычислить , и полученная дробь будет отображаться рядом или под ней в зависимости от вашего экрана. Наибольший общий знаменатель также отображается там, если вы хотите выполнить это вычисление вручную, чтобы проверить правильность результата.
• 3. С другой стороны, если вы хотите преобразовать дробь в десятичную, вы можете нажать кнопку Поменять местами . Он будет менять режим преобразования каждый раз, когда нажимает эту кнопку.

Как преобразовать десятичное число в дробное

Это простые шаги о том, как преобразовать десятичное число в дробное число.

Допустим, у нас есть десятичное число 0,75, и мы хотим преобразовать его в дробь, вот как это делается:

• 1. Игнорируйте все число, в этом примере, поскольку целое число равно нулю (0), мы можем продолжить. Мы игнорируем целое число, потому что оно не является частью преобразования, вы можете просто добавить его позже, когда мы вычислим дробь.
• 2. Далее подсчитывается, сколько десятичных знаков после запятой. Для 0,75 это 2 знака после запятой. Таким образом, чтобы сделать 0,75 целым числом в качестве числителя, вам нужно умножить его на 10 в степени 2, так как есть 2 десятичных знака. Результат 10 ² равен 100. Таким образом, 0,75 x 100 равно 75. Затем сделайте 100 в качестве знаменателя.
• 3. Пока имеем вот это: 75 100. Пришло время найти Наибольший Общий Делитель. Наибольшее число, которое может разделить числитель и знаменатель на точное число. В данном случае это 25.
• 4. Итак, давайте разделим оба числа на 25. Сделав это, мы получим десятичный эквивалент дроби 0,75: 3 4.

Существует также особый случай преобразования повторяющихся десятичных чисел, таких как 0,333, 0,1666, 0,8333 и т. д. Вы можете проверить, как вычислять повторяющиеся десятичные дроби.

Общие эквиваленты десятичной дроби

Это одни из наиболее распространенных десятичных значений с формой эквивалентной дроби.

Decimal	Fraction
0.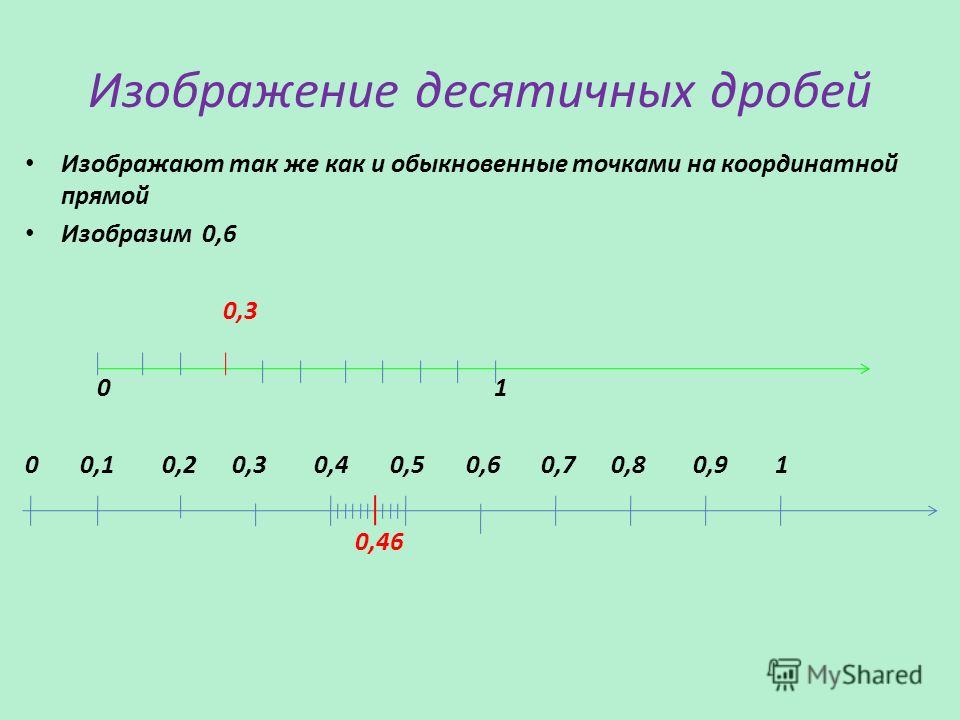 5	1/2
0.33	1/3
0.66	2/3
0.25	1/4
0.75	3/4
0.2	1/5
0.4	2/5
0.6	3/5
0.8	4/5
0.166	1/6
0. 833	5/6
0.125	1/8
0.375	3/8
0.625	5/8
0.875	7/8
0.11	1/9
0.22	2/9
0.0833	1/12
0.4166	5/12
0.5833	7/12
0. 83	10/12
0.916	11/12

Open Textbooks | Siyavula

Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.

Математика

• • Читать онлайн

  • Учебники

    • Английский

      • • 7A PDF (CC-BY-ND)
        • 7B PDF (CC-BY-ND)

    • Африкаанс

      • • 7A PDF (CC-BY-ND)
        • 7B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • 8A PDF (CC-BY-ND)
        • 8B PDF (CC-BY-ND)

    • Африкаанс

      • • 8A PDF (CC-BY-ND)
        • 8B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • 9A PDF (CC-BY-ND)
        • 9B PDF (CC-BY-ND)

    • Африкаанс

      • • 9A PDF (CC-BY-ND)
        • 9B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)

Наука

• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителя

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 7А

        • PDF (CC-BY-ND)

      • Класс 7Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 7А

        • PDF (CC-BY-ND)

      • Граад 7Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 8А

        • PDF (CC-BY-ND)

      • Класс 8Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 8А

        • PDF (CC-BY-ND)

      • Граад 8Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 9А

        • PDF (CC-BY-ND)

      • Класс 9Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 9А

        • PDF (CC-BY-ND)

      • Граад 9Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 4А

        • PDF (CC-BY-ND)

      • Класс 4Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 4А

        • PDF (CC-BY-ND)

      • Граад 4Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 5А

        • PDF (CC-BY-ND)

      • Класс 5Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 5А

        • PDF (CC-BY-ND)

      • Граад 5Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителя

    • Английский

      • Класс 6А

        • PDF (CC-BY-ND)

      • Класс 6Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 6А

        • PDF (CC-BY-ND)

      • Граад 6Б

        • PDF (CC-BY-ND)

Лицензирование наших книг

Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.

Узнайте здесь больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (версии без торговой марки)

Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.

Калькулятор десятичной дроби ✔️ ConvertBinary.com

Преобразование любого десятичного числа в дробь.

Оцените этот калькулятор

[Всего: 1 Среднее: 5]

Как использовать калькулятор преобразования десятичных дробей в дроби?

Необходимое время: 1 минута.

1. Введите десятичное число

   Введите десятичное число в первое поле.

2. Нажмите кнопку «Рассчитать».

   Нажмите кнопку «Рассчитать» под числовым полем.

3. Просмотр результатов

   Результаты появятся в поле Вывод.

4. Копировать или сохранить

   При желании вы можете скопировать вывод в буфер обмена или сохранить его как файл на вашем устройстве.

Calculator features

🔢 Result Format:	Reduced fraction or Mixed number
⚡ Speed ​​ of Computation:	Instant!
➡️ Calculator Output:	Display, Copy, Save
🎯 Calculator Accuracy:	100%
📋 Definitions and Formulas :	Available

What is a Десятичное число?

В математике десятичная цифра обозначает нецелое число; другими словами, число, которое показывает десятичную точку, за которой следуют цифры, представляющие дробную часть.

Десятичные числа равны альтернативный способ выражения дробей , в котором цифры слева от десятичной точки представляют собой целое число или целое число, а цифры справа от десятичной точки представляют собой десятичные дроби.

Примеры десятичных чисел:

0,1 , что равно 1/10

2,5 , что равно 2 + 1/2

Как преобразовать десятичную дробь в дробь

4 дробь состоит в том, чтобы найти два целых числа (один числитель и один знаменатель), которые мы можем разделить сами по себе, чтобы получить начальное значение.

Это общий процесс преобразования десятичной дроби в дробь:

1. Запишите десятичную дробь в качестве числителя (верхнее число дроби) и 1 в качестве знаменателя (нижнее число дроби, также известное как как десятое место ).
2. Умножить числитель и знаменатель на 10 столько раз, сколько знаков после запятой (цифр после запятой)
3. Упростить/уменьшить дробь: переписать дробь в простейшей форме:
   1. Найдите наибольший общий делитель (НОД) между числителем и знаменателем
   2. Разделите числитель и знаменатель на НОД

Пример:

Преобразуем 4,125 в дробь. Запишите дробь в виде 4 0,125 / 1

Теперь умножьте числитель и знаменатель на 10 3 раза (поскольку 0,125 имеет 3 десятичных знака): 4 125 / 1000

НОД между 125 и 1000 равен 125, поэтому разделите как числитель, так и знаменатель дроби 125/1000 на 125, чтобы упростить дробь до 4 1/8

Как преобразовать отрицательное десятичное число в дробь

Если десятичное число отрицательное, процесс такой же, но перед дробью будет стоять знак минус.

Пример: преобразуем -2,5 в дробь. Запишите дробь в виде -2 5/10

НОД между 5 и 10 равен 5, поэтому разделите числитель и знаменатель дроби -5/10 на 5, чтобы упростить дробь до -2 1/2

Как для преобразования повторяющихся десятичных чисел в дроби

Вы можете столкнуться с повторяющимися десятичными цифрами, такими как 0,3333333… (что часто представляется как 0,3, где черта над десятичной цифрой 3 означает, что она повторяется).

В этом случае преобразование включает в себя решение уравнений:

1. Пусть десятичное число будет «x» в уравнении
2. Подсчитайте количество повторяющихся десятичных цифр, и пусть будет «y»
3. Умножьте обе части уравнения на 10 ^y
4. Вычесть исходное уравнение из полученного уравнения
5. Решить x
6. Упростить дробь

Пример: преобразуем 0,13 в дробь.

Уравнение будет x = 0,13

Умножьте обе части на 10 ¹ (поскольку имеется один повторяющийся десятичный знак): 10x = 1,3

Теперь вычтите исходное уравнение из полученного уравнения: (10x – x) = (1,3 – 0,13)

Результат: 9x = 1,2

Решите уравнение: x = 1,2 / 9

Умножьте числитель и знаменатель на степени 10, чтобы исключить десятичные разряды в числителе: 12 / 90

Упростите дробь, найдя НОД для обоих 12 и 90 (что равно 6) и разделите оба значения на 6.

The result is 2/15

Common Decimals to Fraction conversion table

Decimal	Fraction
0.00001	1/100000
0.0001	1/10000
0.001	1/1000
0.01	1/100
0.08333333	1/12
0.0 09	1/11
0. 1	1/10
0.11111111	1/9
0.125	1/8
0.14285714	1/7
0.16666667	1/6
0.2	1/5
0.22222222	2/9
0.25	1/4
0.28571429	2/7
0.3	3/10
0.33333333	1/3
0.375	3/8
0.4	2/5
0.42857143	3/7
0.44444444	4/9
0.5	1/2
0.55555555	5/9
0.57142858	4/7
0.6	3/5
0.625	5/8
0.66666667	2/3
0. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт