ГДЗ учебник по математике 4 класс Петерсон. Часть 1. 15 урок Номер 2
- Учебники
- 4 класс
- Математика 👍
- Петерсон
- №2
авторы: Петерсон.
издательство: «Фгос» 2013 год
Раздел:
- Предыдущее
- Следующее
Литературная викторина.
а) Расположи ответы примеров в порядке убывания, сопоставив их соответствующим буквам, и ты узнаешь, кто из поэтов написал о русском языке такие строки:
Язык, великолепный наш язык.
Речное и степное в нем раздолье, В нем клекоты орла и волчий рык, Напев и звон, и ладан богомолья.
В нем воркованье голубя весной,
Взлет жаворонка к солнцу − выше, выше.
Березовая роща. Свет сквозной.
Небесный дождь, просыпанный по крыше.
б) Кто автор этих стихов?
Когда не ладятся дела, Мне помогает похвала.
Вот, например, такой пример:
Я не сумел решить пример,
Но вдруг сказал мне педагог:
− А ты способный, ты бы мог…
Нажал на ручку я слегка,
Чтоб лучше шли чернила,
И за минуту до звонка
Мня вдруг осенило,
И без особого труда
Я сладил с цифрами тогда.
Не может быть двух мнений:
Во мне родился гений!
С.Маршак − 245112
А.Барто − 342514
С.Баруздин − 312514
С.Михалков − 342124
К.Чуковский − 342511
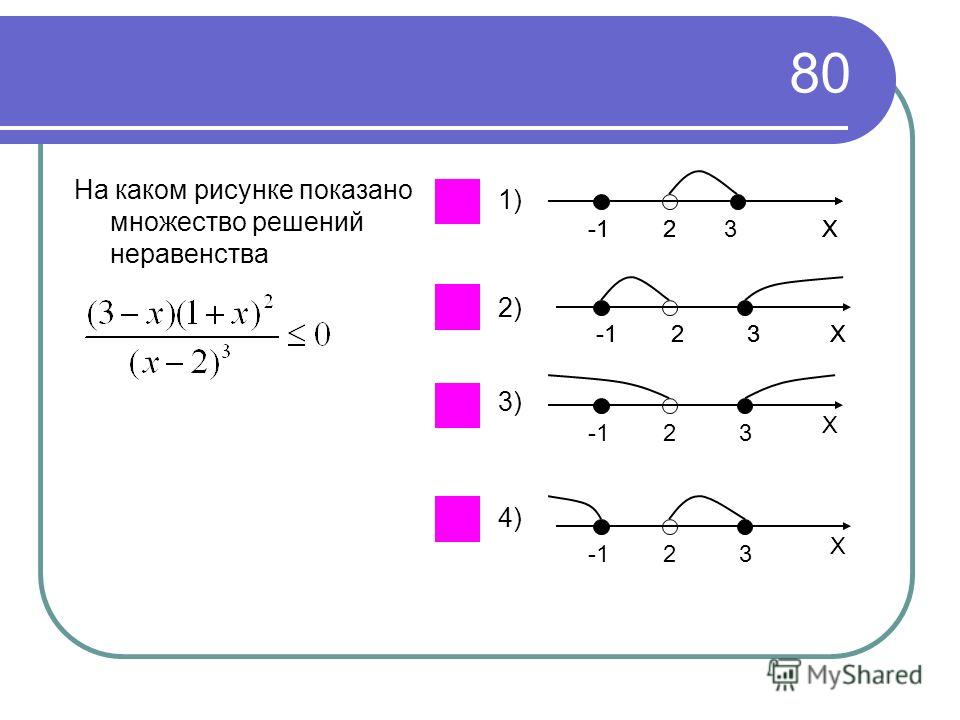
Чтобы проверить правильность ответа, найди множество решений каждого неравенства и последовательно запиши соответствующие номера из верхней строчки в пустые клетки. В результате должно получиться число, записанное около автора стихов.
reshalka.com
Решение а
Решим примеры и найдем автора строк:
(ь): 69861 : 73 = 957
0¯698610657¯00¯41600365¯000¯511000511¯00000073957¯
(т): 23040 : 64 = 360
0¯230400192¯00¯38400384¯00000¯0000000¯00000064360¯
(л): 174087 : 87 = 2001
0¯1740870174¯0000¯000000¯00000¯8000000¯00000¯870000087¯0000000872001¯
(м): 72471 : 119 = 609
0¯724710714¯00¯10700000¯00¯1071001071¯000000119609¯
(а): 940800 : 196 = 4800
0¯9408000784¯0¯156801568¯00000¯0000000¯000000¯00000000¯00000001964800¯
(н): 299520 : 780 = 384
0¯29952002340¯00¯6552006240¯000¯31200003120¯0000000780384¯
(о): 199920 : 490 = 408
0¯19992001960¯000¯392000000¯000¯39200003920¯0000000490408¯
(б): 1888380 : 234 = 8070
0¯188838001872¯000¯163000000¯000¯16380001638¯0000000¯000000000¯000000002348070¯
Ответ: Бальмонт
Решение б
Найдем автора стихотворения:
А. Барто − 342514 − автор стихотворения.
Барто − 342514 − автор стихотворения.
Ответ: А.Барто.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
ГДЗ Математика 4 класс Петерсон
Подробные решения по математике за 4 класс авторы Петерсон
Для полноценного и эффективного освоения математики необходимы регулярные практические занятия. Рекомендуется практиковаться каждый день, применяя полученные теоретические знания на уроке. Для выполнения этой задачи вам потребуются эффективные и интересные пособия. А для ускорения и улучшения работы пригодится гдз по математике 4 класс Петерсон, сборник в трех частях. Этот ресурс можно назвать одним из самых актуальных и полезных источников с точки зрения специалистов и самих школьников, а также их родителей, особенно если подходить к подготовке с ним максимально эффективно. Сборник содержит верные решения к заданиям по всем темам этого учебного года. С ним любой ребенок сможет без труда самостоятельно проверить правильность своих ответов, а в случае выявления ошибок своевременно обратиться к книгам и восполнить пробелы в знаниях.
С ним любой ребенок сможет без труда самостоятельно проверить правильность своих ответов, а в случае выявления ошибок своевременно обратиться к книгам и восполнить пробелы в знаниях.
Для кого предназначен решебник по математике?
Среди тех, кто использует быстрые ответы к учебнику по математике 4 класс Петерсон, следующие категории пользователей:
- родители четвероклассников стремятся проверить правильность поставленных учителем задач, не углубляясь слишком сильно в программу курса, при этом хочется быть уверенным в результате;
- преподаватели, которым необходимо быстро проверить большое количество представленных рабочих тетрадей, не рискуя качеством своей работы;
- дети, занимающиеся в профильных кружках по математике, для которых данный предмет является основной специальностью, что позволяет глубже и полнее понимать интересующие их темы и разделы, которые были изучены;
- четвероклассники, интересующиеся этой наукой, желающие в будущем глубоко овладеть ею, а возможно, даже сделать ее основой своей будущей профессии;
- школьники, которые занимаются математикой в рамках школьной программы, и им непросто усваивать науку, но готовы разбираться во всех тонкостях и нюансах, осваивать новые знания.

Какими достоинствами обладает онлайн гдз по математике для 4 класса автора Петерсон?
Хотя многие специалисты и родители школьников по-прежнему неоднозначно оценивают эффективность решебника, указывая на то, что ученики хотят переписать готовый ответ, а не размышлять над этим самостоятельно, среди тех, кто ценит полезность, появляется все больше и больше сторонников этого ресурса. Их аргументы:
- возможность пользоваться ресурсом круглосуточно, в любой день недели;
- экономия семейного бюджета, так как этот материал является действенной альтернативой или серьезным дополнением к образовательной помощи, платным кружкам;
- значимость информации, ее соответствие требованиям положений об образовательных стандартах, в том числе – и оформление решений;
- быстрый поиск ответа на самое сложное задание, ознакомление с алгоритмом решения и использование полученной информации в дальнейшей учебе, для решения аналогичных задач;
- грамотный поиск, чтобы быстро найти и использовать желаемый результат.

Обратившись один раз за помощью к решебникам, нельзя не убедиться в том, насколько полезной для обучения является собранная в них информация. С готовыми ответами еуроки ГДЗ любой ребенок сможет справиться с итоговыми контрольными по самым сложным темам и показать хороший результат.
Проверка решений | Brilliant Math & Science Wiki
Содержание
- Проверка решений путем замены
- Перестановка уравнений
- Практика Проблемы
Чтобы убедиться, что определенные значения являются решениями данного уравнения, мы просто подставляем их и проверяем. Это очень похоже на метод проб и ошибок.
(2,3),(3,5),(4,4),(6,3),(10,0)(2,3),(3,5),(4,4),(6) , 3), (10, 0)(2,3),(3,5),(4,4),(6,3),(10,0)
Сколько из приведенных выше пар целых чисел являются решениями уравнения 2x+3y=20? 2x + 3y = 20 ?2x+3y=20?
(A) 1\ \ 1 1
(B) 2\ \ 2 2
(C) 3\ \ 3 3
(D) 4\ \ 4 4
(E) 5\ \ 5 5Правильный ответ: B
Решение:
Пробуем каждую из пар целых чисел:
Для (2,3)(2, 3)(2,3) имеем 2×2+3×3=4+9=13≠20 2 х 2 + 3 х 3 = 4 + 9 = 13 \neq 20 2×2+3×3=4+9=13=20.

Для (3,5)(3, 5)(3,5) имеем 2×3+3×5=6+15=21≠20 2 х 3 + 3 х 5 = 6 + 15 = 21 \neq 20 2×3+3×5=6+15=21=20.
Для (4,4)(4, 4)(4,4) имеем 2×4+3×4=8+12=20 2 х 4 + 3 х 4 = 8 + 12 = 20 2× 4+3×4=8+12=20. Это решение.
Для (6,3)(6,3)(6,3) имеем 2×6+3×3=12+9=21≠20 2 х 6 + 3 х 3 = 12 + 9 = 21 \neq 20 2×6+3×3=12+9=21=20.Для (10,0)(10, 0)(10,0) имеем 2×10+3×0=20+0=20 2 \times 10 + 3 \times 0 = 20 + 0 = 20 2× 10+3×0=20+0=20. Это решение. Таким образом, 2 пары являются решениями.
Неверный выбор:
(A) , (C) , (D) и (E)
См. решение, почему эти варианты неверны.
Решите следующую задачу и проверьте решение:
x+4=18x+4=18x+4=18
Математические уравнения гибки: даже простые можно переписать несколькими способами.
3x−4=53x-4=53x−4=5
Эту задачу можно переписать, чтобы изолировать член с переменной, добавив 4 к каждой части уравнения.
3x−4=53x-4=53x−4=53x−4+4=5+43x-4+4=5+43x−4+4=5+4
3x=93x=93x=9
Уравнение можно также обнулить, переместив все члены в одну сторону уравнения.
3x−4=53x-4=53x−4=53x−4−5=5−53x-4-5=5-53x−4−5=5−5
3x-9=03x-9=03x-9=0
Любая операция, примененная к одной части уравнения, должна быть выполнена и с другой стороны. Таким образом, стороны остаются равными, даже если они выглядят по-разному. Преобразование уравнения — полезный навык для решения задач, а также для проверки решений. Значение для xxx, найденное с помощью любого из приведенных выше уравнений, можно подставить обратно в другие уравнения, чтобы проверить правильность решения.
3x=93x=93x=9 можно решить делением.
3x÷3=9÷33x\div3=9\div33x÷3=9÷3
х=3х=3х=3
Затем подставьте ответ обратно в исходную форму уравнения: 3x−4=53x-4=53x−4=5
3(3)−4=53(3)-4=53(3)−4=5
9−4=59-4=59−4=5
5=55=55=5
Решение проверено.
2 + топор + b = 0. х2+ах+b=0.Каково значение a+b a+b a+b?
Цитировать как: Проверка решений. Brilliant.org . Извлекаются из https://brilliant.org/wiki/verify-solutions/
Вопросы и ответы по анализу измерений – Дхананджай Паркар
Q1: Дайте определение термину «Измерение»
Ответ: Термин «измерение» используется для обозначения физическая природа величины и тип единицы, используемой для ее определения. С математической точки зрения размерность физической величины — это степень, в которую должны быть возведены фундаментальные величины.
напр. Измерение скорости = перемещение / время = [L]/[T] = [M 0 ][L 1 ][T -1 ]Q2: Что такое размерные константы?
Ответ: Константы, обладающие измерениями, называются размерными константами. Например. Планковская постоянная.Q3: Что такое размерные переменные?
Ответ: Те физические величины, которые обладают размерностью, но не имеют фиксированного значения, называются размерными переменными.Например. Перемещение, сила, скорость и т. д.
Q4: Что такое безразмерные величины?
Ответ: Физические величины, не обладающие размерностью, называются безразмерными величинами. Например. Угол, удельный вес, деформация. В общем случае физическая величина, представляющая собой отношение двух величин одинаковой размерности, будет безразмерной.Q5: Определить принцип однородности размеров. На каком принципе он основан?
Ответ: Принцип однородности размерностей утверждает, что уравнение правильно с размерной точки зрения, если размерности различных членов по обе стороны уравнения одинаковы.
Этот принцип основан на том факте, что сложить можно только две величины одной размерности, и полученная величина также будет иметь одну и ту же размерность., т.е. в уравнении X + Y = Z верно, если размеры X, Y и Z одинаковы. Q6: Кто ввел анализ измерений
Ответ: Фурье (Жозеф Фурье – французский математик)Q7: Перечислите основные измерения.

Ответ:
- Длина – L
- Время – Т
- Масса — М
- Температура – K или θ
- Ток – А
Q8: Каковы виды использования (приложения) многомерного анализа?
Ответ: Применение размерного анализа:
Преобразование физической величины из одной системы единиц в другую.
Для проверки размерной правильности данного уравнения. Установите связь между различными физическими величинами в уравнении.
Q9 (NCERT): Книга с множеством опечаток содержит четыре разные формулы для смещения y частицы, совершающей определенное периодическое движение:
(а) y = a sin 2π t/T
(b) y = a sin vt
(c) y = (a/T) sin t/a
(d) y = (a 2) (sin 2πt / T + cos 2πt / T )(a = максимальное перемещение частицы, v = скорость частицы. T = время -период
движения).Исключите неправильные формулы на основании размерности.
Ответ:
Дано,
Размер а = перемещение = [M 0 L 1 T 0 ]
Размерность v (скорость) = расстояние/время = [M 0 L 1 T -1 ]
Размерность периода t = или [M 0 L0 T 1 ] Тригонометрическая функция синус является отношением, поэтому она должна быть безразмерной.
(a) y = a sin 2π t/T ( правильно ✓ )
Размеры RHS = [L 1 ] sin([T].[T -1 ] ) = [M 0 Л 1 T 0 ] = LHS (уравнение верное).(b) y = a sin vt (неправильно ✗)
RHS = [L 1 ] sin([LT -1 ] [T 1 ]) = [L 1 ] sin([L ]) = неправильно, так как тригонометрическая функция должна быть безразмерной.(c) y = (a/T) sin t/a (неверно ✗)
RHS = [L 1 ] sin([T].[L -1 ] ) = [L 1 ] sin([TL -1 ] ) = неправильно, функция синуса должна быть безразмерной.
(г) y = (a 2) (sin 2πt / T + cos 2πt / T ) ( правильно ✓ )
RHS = [L 1 ] ( sin([T].[T -1 ] + cos([T].[T -1 ] ) = [L 1 ] ( sin(M 0 L 1 T 0 ) + cos(M 0 L 1 T 0 )) )
= [L 1 ) )
= [L 1 правильноQ10(NCERT): известное соотношение в физике связывает «движущуюся массу» m с «массой покоя» mo частицы через ее скорость v и скорость света с (это соотношение впервые возникло как следствие специальной теории относительности Альберта Эйнштейна). Мальчик почти правильно помнит соотношение, но забывает, куда поставить константу с. Он пишет
Answer:
Dimension of m (mass) = [M 1 L 0 T 0 ]
Dimension of m 0 (mass) = [M 1 L 0 T 0 ]
Размер V (скорость) = [M 0 L 1 T -1 ]∴ размер V 2 = [M 0 L 2 = [M 0 L 2 = [M 0 L 2 = [M 0 L 2 = [M 0 L 2 = [M 0 L 2 = [M 0 L 2 = [M 0 L 2
Размер c (скорость) = [M 0 L 1 T -1 ]
Применяя принцип однородности размеров, [LHS] = [RHS] = [M 1 L 0 T 0 ]
⇒ Уравнение (1- v 2 ) ½ должно быть безразмерным, что возможно, если мы имеем выражения вида:
(1 – v 4 /c 2 ) Уравнение после размещения ‘c’Q11: Проверьте правильность размеров следующего уравнения для расчета смещения
(a) x = x0 + ut + (1/2) at 2
где x — водоизмещение в данный момент времени t
xo — смещение в момент времени t = 0
u — скорость в момент времени t = 0
a представляет собой ускорение.
(b) p = (ρgh) ½
, где P — давление,
ρ — плотность
G, является гравийной АККАЛЕРС.Ответ:
(a) x = x0 + ut + (1/2) at 2
Применяя принцип однородности, все подвыражения уравнения должны иметь одинаковую размерность и быть равными [LHS]
Размерность x = [M 0 L 1 T 0 ]Размеры подвыражений [RHS] должны быть [M 0 L 1 T 0 ⇒ размерность 0 ] . ) = [M 0 L 1 T 0 ] = [LHS]
Размерность ut = скорость x время = [M 0 L 1 T -1 ] [M 0 L 0 T 1 ] = [M 0 L 1 T 0134 0134 0134] = ] = ]. в 2 = ускорение x (время) 2 = [M 0 L 1 T -2 ] [M 0 L 0 T -2 ; L 1 T 0 ] = [LHS]
∴ Размерность уравнения верна.
(б) P = (ρgh) ½
Размеры LHS, т. е. давление [P] = [M 1 L -1 T -2 ]
Размеры ρ = масса/объем = [M 1 L T 0 ]
Размеры g (ускорение) = [M 0 L 1 T -2 ]
Размеры h (высота) = [M 0 L 1 T ]
Размеры RHS = [(ρgh) ½ ] = ([M 1 L -3 T 0 ]. [M 0 L 1 T -2 ]. ½
= [M ½ L -½ T -1 ] ≠ [LHS]Q.12 (NCERT): Человек, быстро идущий под дождем на скорости v, должен наклонить зонт вперед, создавая угол θ с вертикалью. Студент выводит следующее соотношение между θ и v : tan θ = v и проверяет, что отношение имеет правильный предел: при v → 0, θ → 0, как и ожидалось. (Мы предполагаем, что нет сильного ветра и что дождь падает вертикально для неподвижного человека).
Как вы думаете, может ли это соотношение быть правильным? Если нет, угадайте правильное отношение.
Ответ: Дано, v = tanθ
Размерность LHS = [v] = [M 0 L 1 T -1 ]
Размерность RHS = [tanθ] = [M 0 L 0 T 0 ] (тригонометрические отношения безразмерны)Так как [левая сторона] ≠ [правая сторона]. Уравнение неправильно по размерам.
Чтобы размерность уравнения была правильной, LHS также должен быть безразмерным. Это может быть возможно, если учесть скорость дождя (V r ), и уравнение примет вид:
tan θ = v/V rQ.13: Закон Гука утверждает, что сила F в пружине, растянутой на длину x, определяется выражением F = −kx.
Согласно второму закону Ньютона F = ma, где m — масса, а a — ускорение.
Рассчитайте размер жесткости k.Ответ: Дано, F = -kx
⇒ k = – F/xF = ma, размерность силы:
[F] = ma = [M 1 L 0 T 0 ].[M 0 L 1 T -2 ] = [M 1 L 1 T -2 ]
Следовательно, размер жесткости пружины (k) равен:
[k] = [F]/[x] = [M 1 L 1 T -2 ].[M 0 L -1 T 0 ] = [M 1 1 3 4 0 L T -2 ] или [MT -2 ] ….. (ответ)Q.14: Вычислите размерную формулу электрического сопротивления (R).
Ответ: По закону Ома
V = IR или R = V/I
Поскольку выполненная работа = QV , где Q — заряд
⇒ R = W/QI = W/I 2 t (I = Q/t)
Размеры работы [W] = [M 1 L 2 T -2 ]
∴Размер R = [R] = [M 1 L 2 T -2 -3 901] ][A -3 T 1 ] = [M 1 L 2 T -3 A -2 ] … (ответ)Q.
15: Калория – это единица теплоты или энергии, равная примерно 4,2 Дж где 1J = 1 кг м 2 s –2 . Предположим, мы используем систему единиц, в которой единица массы равна α кг, единица длины равна β м, единица времени равна γ с. Покажите, что калория имеет величину 4,2 α –1 β –2 γ 2
Ответ: Учитывая формулу преобразования единиц измерения,
n 1 U 1 = N 1 U 2
N 1 [M 1 A L 1 3333. M 2 a L 2 b T 2 c ]
Приведено здесь: 1 кал = 4,2 Дж = 4,2 кг м 3 1 1 .n 1 = 4,2, M 1 = 1 кг, L 1 = 1 м, T 1 = 1 сек
и
n 2 = ?, М 2 = α кг, л 2 = βм, Т 2 = γ секРазмерная формула энергии = [M 3 9013 3 L ]
⇒ a = 1, b = 1 и c = -2 Подставив эти значения в приведенное выше уравнение,n 2 = n 1 [M 1 /M 2 ] a 1 /L 2 ] b [T 1 /T 2 ] c
= n 1 3 [M0322 1 /M 2 ] 1 [L 1 /L 2 ] 2 [T 1 /T 2 ]] 4 /T 2 ]] 4 (2 2 /T 2 ].
γ 2 … (ответ) γ 2 … (ответ) γ 2 … (ответ) Z 2 … (ответ)] 1 [1M/βM] 2 [1sec/γ Sec] -2 = 4,2 α –1 β –2 γ 2 … (ответ)
Z 2 … кинетическая энергия K вращающегося тела зависит от его момента инерции I и его угловой скорости ω. Учитывая соотношение K = kI a ω b где k — безразмерная константа.
Найдите a и b. Момент инерции сферы относительно ее диаметра равен (2/5)Mr 2Ответ:
Размеры кинетической энергии K = [M 1 L 2 T -2 90] момента инерции (I) = [ (2/5)Mr 2 ] = [ML 2 T 0 ]
Размеры угловой скорости ω = [θ/t] = [M 0 L 0 T -1 ]
Applying principle of homogeneity in dimensions in the equation K = kI a ω b[M 1 L 2 T -2 ] = k ( [ML 2 T 0 ]) a ([M 0 L 0 T -1 ]) b
[M 1 L 2 T — 2 ] = k [M a L 2a T -b ]
⇒ a = 1 и b = 2
⇒ K = kIω 2 … (ответ)Q.
17: Каковы ограничения размерного анализа?
Ответ: Ограничения размерного анализа:Он не может определить значение безразмерных констант.
Мы не можем использовать этот метод для уравнений, содержащих экспоненциальные и тригонометрические функции.
Его нельзя применять к уравнению, включающему более трех физических величин.
Это тоже не решение, т. е. оно может проверить только правильность уравнения в размерности или нет. Но нельзя сказать, что уравнение абсолютно правильное.
Q.18: Переведите 1 ньютон в дину, используя метод измерений.
Ответ: Размеры силы = [M 1 L 1 T -2 ]
, учитывая преобразование размерной единицы, т.е. N 1 [M 1 322 1 [M 1 33322 1 [M 1 9 33322 1 [M 1 33322 1 [M 1 33322 1 [M 1 33322 1 .T 1 C ] = N 2 [M 2 A L 2 B T 2 C ] T 2 C ] .
в системе SI, M 1 = 1 кг, L 1 = 1M и T 1 = 1S
в системе CGS, M 2 = 1G, L 2 = 1CM и T 2 2 = 1S и T 2 2 2 = 1C.Подставляя значения в формулу преобразования,
n 2 = n 1 (1 кг/1 г) 1 .(1 м/1 см) 1 (1 с/1 с) -4 9013,( 10 3 /1г)(10 2 см) = 10 5 дин …(ответ)Q.19: Центростремительная сила (F), действующая на частицу (равномерно движущуюся по окружности), зависит от массы (m) частицы, ее скорости (v) и радиуса (r) окружности. Выведите размерную формулу для силы (F).
4. R. DIMENTS DIMENTS DIMENTS) каждой величины в уравнении,
Ответ: дано, F ∝ M A .V B .R C
∴ F = KM A .V B .R C (где Kontaint)[M 1 L 1 T -2 ] = [M 1 L 0 T 0 ] a . [М 0 Л 1 Т -1 ] б . [M 0 L 1 T 0 ] c = [M a L b+cT +cT -b ]
b = -2
8 Q. 201298 : Если в качестве основных единиц выбраны скорость света c, гравитационная постоянная G и постоянная Планка h, найдите значение грамма, а см и секунды в новых единицах массы, длины и времени соответственно.
⇒ a= 1, b = 2, c = -1
∴ F = km 1 .v 2 .r -1 = kmv 2 /r
(Take c = 3 x 10 10 cm/sec, G = 6.67 x 10 8 dyn cm 2 /gram 2 and h = 6.6 x 10 -27 erg sec)
Answer: Given,
c = 3 x 10 10 cm/sec
G = 6.67 x 10 8 dyn cm 2 /г 2
ч = 6,6 x 10 -27 эрг сек
Нанесение соответствующих размеров,
Формула измерения для c = [M 0 L 1 T -1 ] = 3 x 10 10 см/сек … (I)
Dimensions of G = [M -1 L 3 T -2 ] = 6.67 x 10 8 dyn cm 2 /gm 2 …(II)
Dimensions of h = [M 1 L 2 T -1 ] = 6,6 x 10 -27 эрг с …(III)(Примечание. Применяя закон тяготения Ньютона, вы можете найти размеры G, т.е. G = Fr 2 /(мМ)
3 ]. -3 T 2 ]
Аналогично, постоянная Планка (h) = энергия / частота)
Чтобы получить M, умножьте eqn-I и III и разделить на уравнение-II,
⇒ [M 0 L 1 T -1 ].[M 1 L 2 T -1 L ].[M 1
= ( 3 x 10 10 см/сек).( 6,6 x 10 -27 эрг сек)/ 6,67 x 10 8 Dyn CM 2 /GM2
⇒ [M 2 ] = 2,968 x 10 -9
⇒ [M] = 0,5448 x 10 -4 GM
или 1GM = [M] /0,54444444444448333333333333. GM
или 1GM = [M] /0.544444444444444444444444444833.33333333333333333333333333333333333 гг. -4 = 1,835 x 10 -4 Блок массыДо длины [L], EQN.-II X. [M -1 L 3 T -2 ].[M 1 L 2 T -1 ].[M 0 L -3 T 3 ]
= (6,67 x 10 8 дин см 2 /гм 2 ).( 6,6 x 10 -27 эрг см 9 1/(3 x 10 эрг 9 с) 1/(3 x 10 34 эрг см 9 1 с)/(3 x 10 34 эрг см 9 1 с) 3⇒ [L 2 ] = 1,6304 x 10 -65 СМ 2
⇒ [L] = 0,4038 x 10 -3 2 .]/ 0,4038 x 10 -32 = 2,47 x 10 -32 единица длины
В уравнении-I, [M 0 L 1 T -1 ] = 3 x 10 10 см/сек
⇒ [T] = [L] ÷ 3 x 10 10 см/сек 3 x 8 T ≥ 0 0. 10 -32 cm ÷ 3 x 10 10 cm/s = 0.1345 x 10 -42 s
or 1s = [T]/0.1345 x 10 -42 s = 7.42 x 10 42 единица времениВопрос 21. Студент, проводя эксперимент, обнаружил, что скорость объекта меняется со временем, и это можно выразить уравнением:
v = Xt 2 + Yt +Z .
Если единицы измерения v и t выражены в единицах СИ, определите единицы измерения констант X, Y и Z в данном уравнении.Ответ: Дано, v = Xt 2 + Yt +Z
Размерности скорости v = [M 0 L 1 T -1 ]
тот же размер.
[v] = [Xt 2 ] + [Yt] + [Z]
∴ [v] = [Xt 2 ]
⇒ [X] = [v] /[t 2 ] = [M 0 L 1 T -1 ] / [M 0 L 0 T 2 ] = [M 0 L 1 T -3 -3 -3 ).Аналогично, [v] = [Yt]
⇒ [Y] = [v] / [t] = [M 0 L 1 T -1 ]/ [M 0 L 0 T -1 ] = [М 0 Л 1 T -2 ] …(ii)Аналогично, [v]= [Z]
[Z] = [M 0 L 1 T -1 8 iii) 9 1 8 9 134 0 … 0 ] ⇒ Unit of X = m-s -3
⇒ Unit of Y = m-s -2
⇒ Unit of Z = m-s -1Q.22 : Выразите емкость через размерность фундаментальных величин, т. е. массу (M), длину (L), время (T) и ампер (A)
Ответ: Емкость (C) определяется как способность электрического тела накапливать электрический заряд.

∴ Емкость (C) = Общий заряд (q) / разность потенциалов между двумя пластинами (В)
= Кулон/Вольт
∵ Вольт = Проделанная работа (Вт)/Заряд (q) = Джоуль/Кулон
⇒ Емкость (C) = Заряд(q) 2 / Работа(Вт)
∵ Заряд (q) = Ток (I) × Время(t)
Размерность [q] = [AT] ———– Размер работы
= Сила × расстояние = [MLT -2 ][L] = [ML 2 T -2 ] ——— (II)Подстановка значений I и II,
[C] = ([AT]) 2 / [ ML 2 T -2 ] = [M -1 L -2 T 2+2 A 2 ] = [M 34] = [M 34.134] = . 2 T 4 A 2 ]Величины, имеющие одинаковые физические формулы01:30 :
а. импульс и импульс.
б. усилие, тяга.
в. работа, энергия, крутящий момент, момент силы, энергия
d.




 Например. Перемещение, сила, скорость и т. д.
Например. Перемещение, сила, скорость и т. д.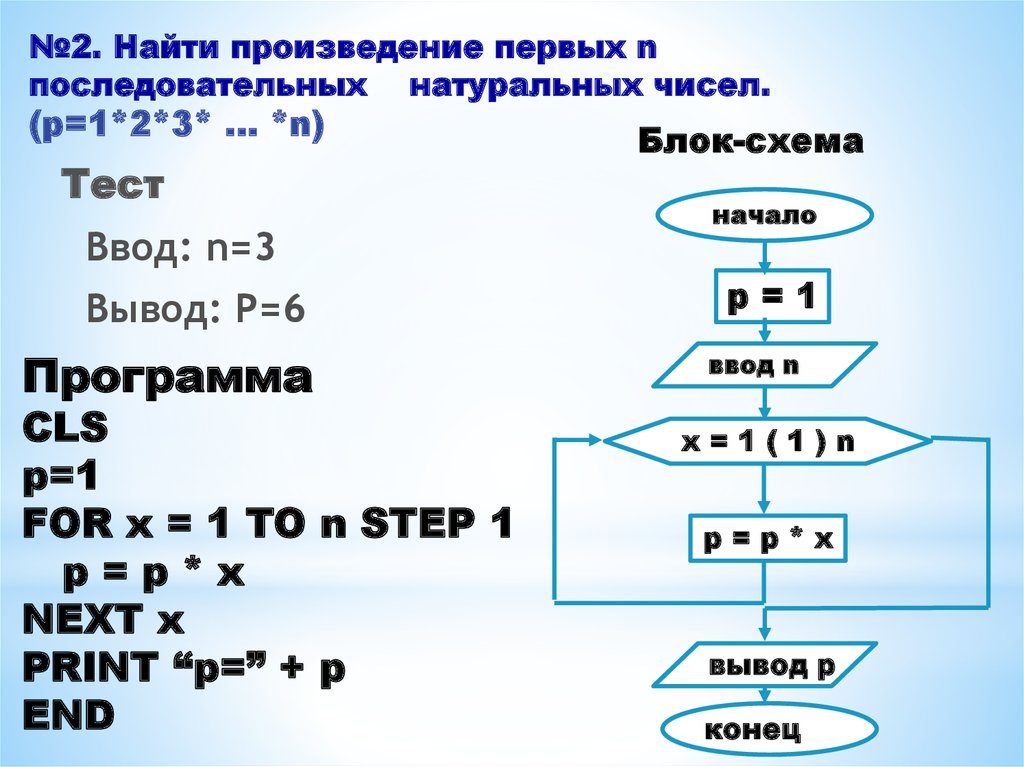
 Исключите неправильные формулы на основании размерности.
Исключите неправильные формулы на основании размерности.  [L -1 ] ) = [L 1 ] sin([TL -1 ] ) = неправильно, функция синуса должна быть безразмерной.
[L -1 ] ) = [L 1 ] sin([TL -1 ] ) = неправильно, функция синуса должна быть безразмерной.

 Как вы думаете, может ли это соотношение быть правильным? Если нет, угадайте правильное отношение.
Как вы думаете, может ли это соотношение быть правильным? Если нет, угадайте правильное отношение.  [M 0 L 1 T -2 ] = [M 1 L 1 T -2 ]
[M 0 L 1 T -2 ] = [M 1 L 1 T -2 ]  15: Калория – это единица теплоты или энергии, равная примерно 4,2 Дж где 1J = 1 кг м 2 s –2 . Предположим, мы используем систему единиц, в которой единица массы равна α кг, единица длины равна β м, единица времени равна γ с. Покажите, что калория имеет величину 4,2 α –1 β –2 γ 2
15: Калория – это единица теплоты или энергии, равная примерно 4,2 Дж где 1J = 1 кг м 2 s –2 . Предположим, мы используем систему единиц, в которой единица массы равна α кг, единица длины равна β м, единица времени равна γ с. Покажите, что калория имеет величину 4,2 α –1 β –2 γ 2  ] 1 [1M/βM] 2 [1sec/γ Sec] -2 = 4,2 α –1 β –2 γ 2 … (ответ)
] 1 [1M/βM] 2 [1sec/γ Sec] -2 = 4,2 α –1 β –2 γ 2 … (ответ) 17: Каковы ограничения размерного анализа?
17: Каковы ограничения размерного анализа?  T 1 C ] = N 2 [M 2 A L 2 B T 2 C ] T 2 C ] .
T 1 C ] = N 2 [M 2 A L 2 B T 2 C ] T 2 C ] . 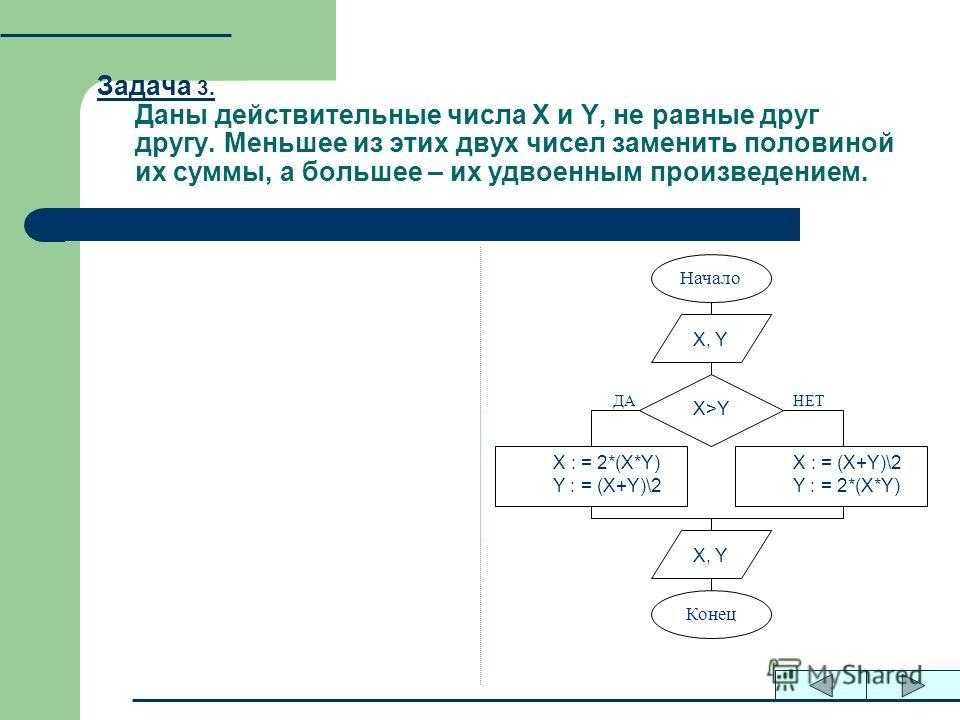 R C
R C  6 x 10 -27 erg sec)
6 x 10 -27 erg sec)  [M 1 L 2 T -1 L ].[M 1
[M 1 L 2 T -1 L ].[M 1 ]/ 0,4038 x 10 -32 = 2,47 x 10 -32 единица длины
]/ 0,4038 x 10 -32 = 2,47 x 10 -32 единица длины