Cos 1 2 на окружности: cos 1 2 на окружности

10 класс. Алгебра. Тригонометрические уравнения. Арккосинус и арксинус. — Арккосинус и решение уравнения cost = a.

Комментарии преподавателя

Арк­ко­си­нус и ре­ше­ние урав­не­ния cost=a

Мы знаем, что такое арк­ко­си­нус, и те­перь с его по­мо­щью смо­жем ре­шить урав­не­ние  при всех до­пу­сти­мых зна­че­ни­ях , т.е. при .

При­мер 1. Ре­шить урав­не­ние 

Ре­ше­ние.

 зна­чит, урав­не­ние имеет ре­ше­ние. Мы по­лу­чим бес­чис­лен­ное мно­же­ство ре­ше­ний, т.к. функ­ция пе­ри­о­дич­на.

За­да­на абс­цис­са точки еди­нич­ной окруж­но­сти. Через эту точку про­ве­дем пер­пен­ди­ку­ляр к линии ко­си­ну­сов и по­лу­чим две точки пе­ре­се­че­ния с окруж­но­стью (рис. 1).

Точке  со­от­вет­ству­ет мно­же­ство дей­стви­тель­ных чисел 

Точке  со­от­вет­ству­ет мно­же­ство 

Про­ил­лю­стри­ру­ем на гра­фи­ке:

На про­ме­жут­ке  функ­ция мо­но­тон­но убы­ва­ет, и    до­сти­га­ет­ся толь­ко при одном зна­че­нии ар­гу­мен­та  Функ­ция  чёт­ная, её гра­фик сим­мет­ри­чен от­но­си­тель­но оси  зна­чит, вто­рая точка имеет абс­цис­су  С уче­том пе­ри­о­да  

Ответ: 

 

Решим урав­не­ние  в общем виде, при 

Ре­ше­ние:

Абс­цис­су  имеют две точки окруж­но­сти –  (рис. 3).

Они и толь­ко они про­ек­ти­ру­ют­ся на линию ко­си­ну­сов в точку с ко­ор­ди­на­той  Каж­дой точке со­от­вет­ству­ет опре­де­лен­ное мно­же­ство дей­стви­тель­ных чисел.

Ответ: 

Рас­смот­рим част­ные слу­чаи три­го­но­мет­ри­че­ских урав­не­ний вида 

1. 

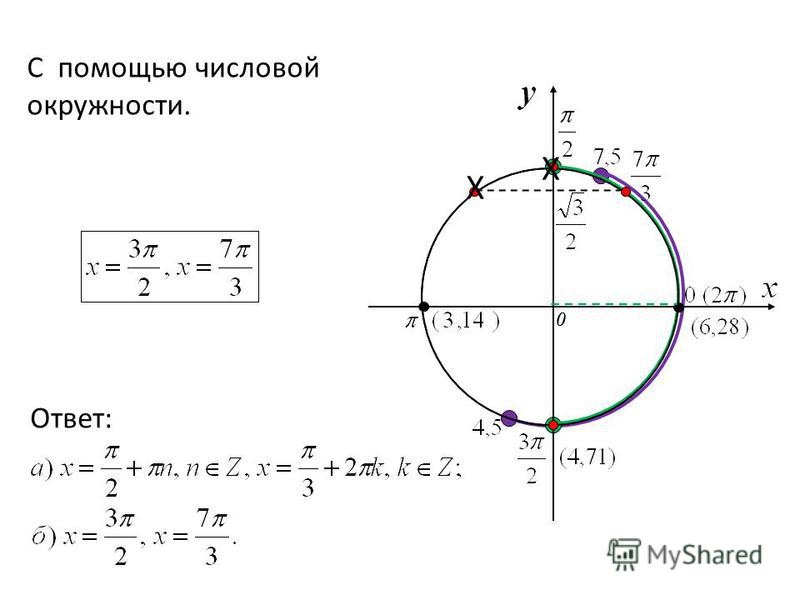
Решим с по­мо­щью чис­ло­вой окруж­но­сти и про­ил­лю­стри­ру­ем на гра­фи­ке:

А как по­лу­чить ре­ше­ние с по­мо­щью общей фор­му­лы?

2. 

3. 

При­мер 2. Ре­шить урав­не­ние и про­ил­лю­стри­ро­вать ре­ше­ние на чис­ло­вой окруж­но­сти и на гра­фи­ке:

a) 

b) 

Ре­ше­ние:

a) 

От­ме­тим точку  на оси . Про­ве­дём пер­пен­ди­ку­ляр, по­лу­чим две точки пе­ре­се­че­ния с чис­ло­вой окруж­но­стью:  (рис. 7).

Про­ил­лю­стри­ру­ем ре­ше­ние на гра­фи­ке.

На про­ме­жут­ке  функ­ция  мо­но­тон­но убы­ва­ет, зна­чит, на дан­ном про­ме­жут­ке есть толь­ко одно ре­ше­ние  

 Ко­си­нус чёт­ная функ­ция, гра­фик сим­мет­ри­чен от­но­си­тель­но оси , зна­чит, точка  тоже яв­ля­ет­ся ре­ше­ни­ем.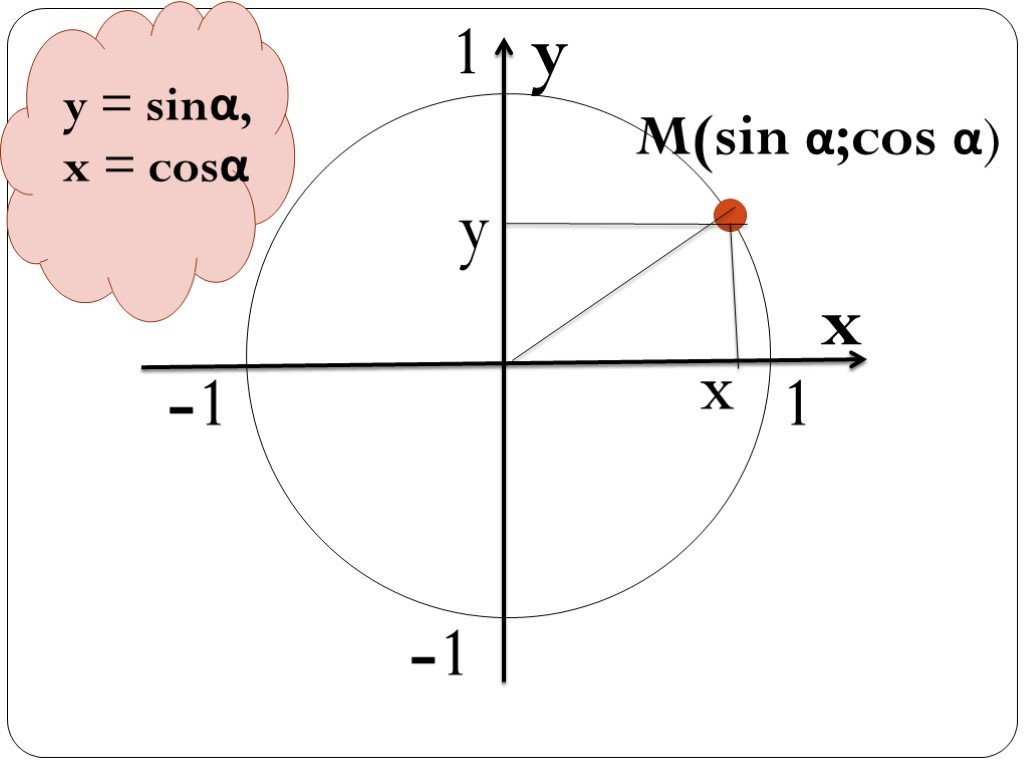

Ответ: 

b) 

Абс­цис­су  имеют две точки –  Им со­от­вет­ству­ет мно­же­ство дей­стви­тель­ных чисел  

Про­ил­лю­стри­ру­ем ре­ше­ние на гра­фи­ке.

На от­рез­ке  функ­ция мо­но­тон­но убы­ва­ет и при­ни­ма­ет зна­че­ние  толь­ко  в одной точке 

Ко­си­нус – чёт­ная функ­ция, гра­фик сим­мет­ри­чен от­но­си­тель­но оси , зна­чит, точка  также яв­ля­ет­ся ре­ше­ни­ем урав­не­ния.

Ответ: 

Рас­смот­рим более слож­ное три­го­но­мет­ри­че­ское урав­не­ние.

При­мер 3. Ре­шить урав­не­ние 

Ре­ше­ние:

Осу­ще­ствим за­ме­ну пе­ре­мен­ной, обо­зна­чим 

Те­перь вер­нем­ся к ста­рой пе­ре­мен­ной:

Ответ: 

Мы на­учи­лись ре­шать урав­не­ния вида  при любом до­пу­сти­мом  Мы ис­поль­зо­ва­ли по­ня­тие арк­ко­си­ну­са. На сле­ду­ю­щем уроке мы по­зна­ко­мим­ся с по­ня­ти­ем арк­си­ну­са.

ИСТОЧНИК

http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-uravneniyab/arkkosinus-i-reshenie-uravneniya-cos-t-a

http://www. youtube.com/watch?v=4A_4BjsglRo

http://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.pdf

http://vklasse.org/10-klass/reshebniki/algebra/ag-mordkovich-2009-zadachnik

http://uslide.ru/images/20/26205/736/img11.jpg

http://mypresentation.ru/documents/c999f5a1a34bf46e02d0b3bbdcf9e1d7/img11.jpg

 

Тригонометрические уравнения — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1.

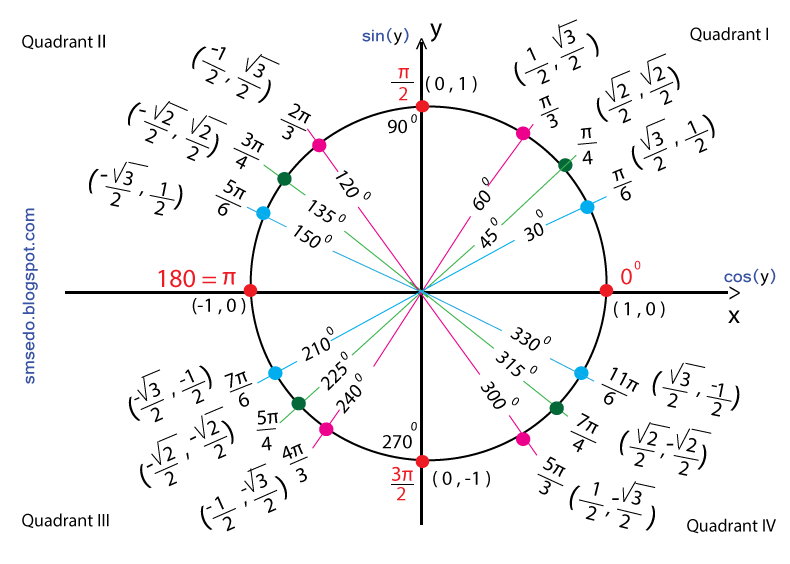Тригонометрические уравненияsin x=a,cos x=a,tg x=a,ctg x=a
Преподаватель: Кадирова А.М.
http://aida.ucoz.ru

2. С помощью тригонометрической окружности найти все значения из промежутка [-2π; 2π] для следующих выражений

arcsin 0,
arcsin

3. Верно ли равенство

1
а ) arccos ;
2 3
3 11
г ) arcsin
;
2
6
2
б ) arcsin(
) ;
2
4
2
3
д) arccos(
)
.
2
4
3
в ) arccos(
) ;
2
6
е)arctg 3
3
.

4. Имеет ли смысл выражение:

7. Определение.

• Уравнения вида f(x) = а, где а – данное
число, а f(x) – одна из тригонометрических
функций,
называются
простейшими
тригонометрическими уравнениями.

8. Решение простейших тригонометрических уравнений.

Чтобы успешно решать простейшие
тригонометрические уравнения нужно
1) уметь отмечать точки на числовой
окружности;
2) уметь определять значения синуса, косинуса,
тангенса и котангенса для точек числовой
окружности;
3) знать свойства основных
тригонометрических функций;
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и уметь отмечать их
на числовой окружности.
06.10.2020
9

10. 1. Найти координаты точки М, лежащей на единичной окружности и соответствующей числу

3
3
2
3
2
1
2
3

11. 2. Дана точка М с абсциссой ½. Найдите ординату этой точки; укажите три угла поворота, в результате которых начальная точка

(1;0) переходит в точку М
М
3
2
7
2
3
3
3
1
2
5
2
3
3

12. 3. Дана точка М с абсциссой -½. Найдите ординату этой точки; укажите три угла поворота, в результате которых начальная точка

(1;0) переходит в точку М
М
3
2
1
2
2
3
2
8
2
3
3
2
26
8
3
3

13. Решите уравнение

2
cos x
2
4
х
2
2
4
х
4
2 п, п Z
4
2 п, п Z

14. Решите уравнение

5
6
3
2
5
6
3
cos x
2
5
х
2 п, п Z
6
5
х
2 п, п Z
6
Арккосинусом числа а
называют такое число
из промежутка
[0;π ], косинус
у
π-arccos
a
1
arccos
а
которого равен а
х
π
-а
0
а
-1
arccos (-a)= π -arccos a
0
y
Решим при помощи
числовой окружности
уравнение cos х = a.
1)
1
а 1
1
1
x
Нет точек пересечения с
окружностью.
Уравнение не имеет решений.
1
y
Решим при помощи
числовой окружности
уравнение cos х = a.
2)
1
а 1
1
0
cos х = 1
х = 2πk
1
0
cos х = -1
х = π+2πk
к Z
1
Частные
решения
x
y
Решим при помощи
числовой окружности
уравнение cos х = a.
3) а
x
=0
2
1 2
1
0
1
x
n n Z
2
Частное
решение
Решим при помощи
числовой окружности
уравнение cos х = a.
4)
y
1
а 1
arccos а
Корни, симметричные
относительно Оx
1
могут быть записаны:
а
x
arccos a 2 k
х
arccos a 2 k
или
х = ± arccos a+2πk
1
-arccos а
1
Общее решение

20. Уравнение cos х = a называется простейшим тригонометрическим уравнением

Решается с помощью единичной окружности
х
1. Проверить условие | a | ≤ 1
y
1
a
0
-1
1
x
2. 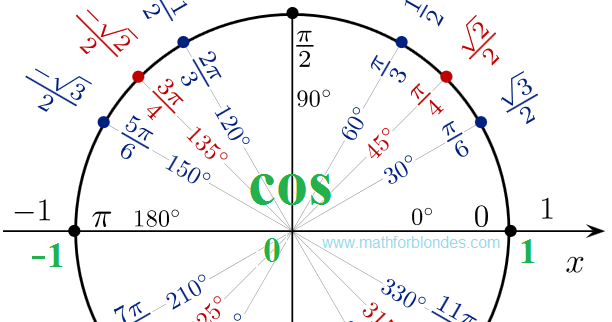Отметить точку а на оси
абсцисс (линии косинусов)
3. Провести перпендикуляр
из этой точки к окружности
4. Отметить точки
пересечения перпендикуляра
с окружностью.
5. Полученные числа–
решения уравнения cosх = a.
6. Записать общее решение
уравнения.
-х1
х х1 2 n
n Z

21. Уравнение cos t = a

a) при -1< t < 1 имеет две серии корней
t1 = arсcos a + 2πk, k ϵ Z
t 2 = — arсcos a + 2πm, m ϵ Z.
Эти серии можно записать так
t = ± arсcos a + 2πn, n ϵ Z ;
• б) при а = 1 имеет одну серию решений
t = 2πn, n ϵ Z ;
• в) при а = -1 имеет одну серию решений
t = π + 2πn, n ϵ Z ;
• г) при а = 0 имеет две серии корней
t1 =
+ 2πk, k ϵ Z
t 2 = — + 2πm, m ϵ Z. Обе серии можно записать в одну серию
t=
+ πn, n ϵ Z.
д) при а > 1 и a < -1 уравнение не имеет корней.

22. Решите уравнение

1) cos х =
1
2
2) cos х = —
1
2

23. Решите уравнение

3) cos 4x = 1
4x = 2πn, n ϵ Z
4)

24.

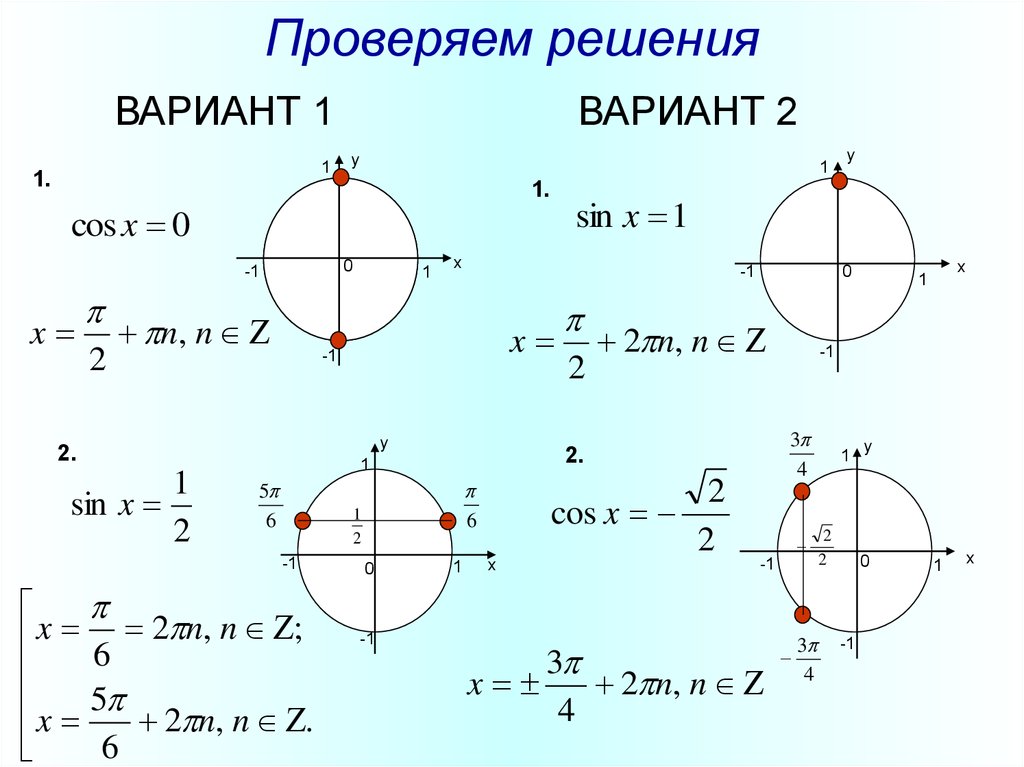Решите уравнение.
Решите уравнение
5)

25. Уравнение sin t = a

Уравнение
a)
sin t = a
при -1< t < 1 имеет две серии корней
t1 = arсsin a + 2πn, n ϵ Z
t 2 = π — arсsin a + 2πn, n ϵ Z.
Эти серии можно записать так
t = ( -1)k arсsin a + πk, k ϵ Z ;
б) при а = 1 имеет одну серию решений
t=
+ 2πn, n ϵ Z
в) при а = -1 имеет одну серию решений
t= + 2πn, n ϵ Z;
г) при а = 0 имеет две серии корней
t1 = 2πk, k ϵ Z,
t2 = π + 2πm, m ϵ Z.
Обе серии можно записать в одну серию
t = πn, n ϵ Z ;
д) при а > 1 и a < -1 уравнение не имеет корней.

26. Решите уравнение

,,
1) sin х =
x = ( -1)k
+ πk,
kϵ Z.

27. Решите уравнение

(;
Решите
,,;
2) sin х = —
x = ( -1)k ( —
уравнение
2
2
+ πk, k ϵ Z
x = ( -1)k+1
+ πk, k ϵ Z

28. Уравнение tg t = a

при любом а ϵ R имеет одну серию решений
х = аrctg a + πn, nϵ Z.

29.

Уравнение ctg t = aпри любом а ϵ R имеет одну серию решений
х = аrcctg a + πn, nϵ Z.

30. Подводим итоги

Значение а
cos x = a
sin x = a
tg x = a
ctg x = a
|a|>1
Ø
Ø
x=arctg a +πn
x=arcctg a +πn
|a|<1
x=±arccos a+2πn
x=(-1)ⁿarcsin a+πn
x=arctg a +πn
x=arcctg a +πn
a=1
x=2πn
x=π/2+2πn
x=π/4+πn
x=π/4+πn
a = -1
x=π+2πn
x=-π/2+2πn
x=-π/4+πn
x=3π/4+πn
a=0
x=π/2+πn
x=πn
x=πn
x=π/2+πn
Продолжите фразу :
Сегодня на уроке я повторил …
Сегодня на уроке я узнал …
Сегодня на уроке я научился
…

English     Русский Правила

cos(theta)=-1/2 Перечислите 6 конкретных решений.

Тригонометрия

Криста П.

спросил 08.07.19

Подписаться І 1

Подробнее

Отчет

3 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Лиз З. ответил 07/09/19

Репетитор

4.7 (28)

Триг крут!

Смотрите таких репетиторов

Смотрите таких репетиторов

Проверьте свой круг юнитов. (Погуглите «единичный круг», если у вас его нет, и свяжитесь с видеочатом, если вы не понимаете, откуда он взялся.) Координаты (x, y) для каждого угла — это косинус и синус этого угол.

Вы увидите это на 120 ^o , или 2π/3 и 240 ^o , или 4π/3, координата x равна -1/2. Это два угла, с которых вы начинаете. В градусах прибавьте или вычтите число, кратное 360 ^или , к любому из них, чтобы получить другой ответ, так как это проведет вас по кругу еще раз/с. Например, поскольку 120 ^o работает, то (120+360)= 480 ^o , (120+360+360) = 840 ^{4 и (1,6- 4) = -240 о .}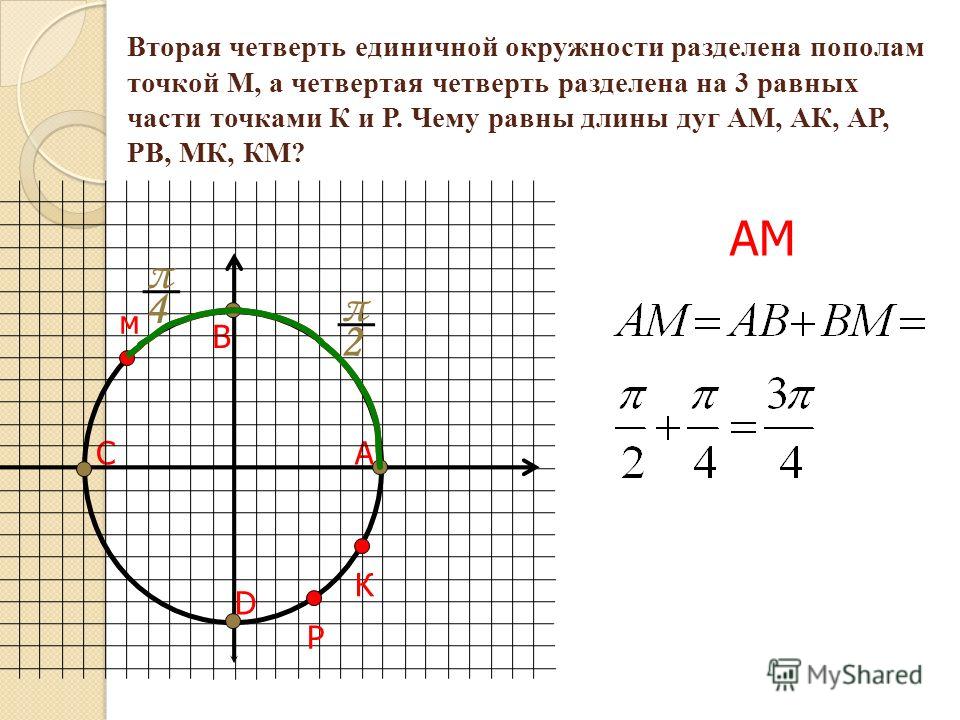

Вы можете сделать то же самое с радианами: вместо сложения или вычитания кратных 360

o прибавьте или вычтите кратное 2π. Поскольку исходные углы измеряются в третях числа пи, преобразуйте 2π в дробь с 3 в знаменателе: 2π = 6π/3. Вот еще три решения в дополнение к 4π/3: (4π/3 — 6π/3)= -2π/3 , (4π/3 -6π/3 — 6π/3)= -8π/3 и (4π/3 +6π/3)= 10π/3 . Вы можете сколько угодно раз прибавлять или вычитать 2π из 4π/3 или 2π/3, чтобы получить бесконечное количество ответов.

Надеюсь, это поможет! Если вы все еще в замешательстве или не совсем уверены, почему или как работает единичный круг, ПОЖАЛУЙСТА, свяжитесь с нами! Это действительно фундаментально для всего в тригонометрии !

Удачной учебы!

Лиз

Голосовать за 0 голос против

Подробнее

Отчет

Уильям В.

ответил 07/09/19

Репетитор

5,0 (838)

Опытный репетитор и инженер на пенсии

См. таких репетиторов

Смотрите таких репетиторов

Чтобы определить, какой угол соответствует косинусу -1/2, посмотрите на единичный круг. Помните, что косинус связан со значением x. Косинус равен -1/2, когда угол равен 120° и 240° (или в радианах (2π)/3 и (4π)/3). Это единственные значения, проходящие по единичному кругу один раз, когда косинус равен -1/2. Так как ваш вопрос ищет 6 ответов, это означает, что вы должны пройти по кругу больше раз.

Добавьте к каждому ответу 360° или 2π радиан, и вы получите 480° и 600° (или 8π/3 и 10π/3).

Добавьте к каждому из этих ответов еще 360° или 2π радиан, и вы получите 840° и 960° (или 14π/3 и 16π/3).

Обратите внимание, что правильных ответов много. Я мог бы вычесть 360° или 2π радиан, чтобы получить правильные ответы (или мог добавить или вычесть любое число, кратное 360° или 2π радианам).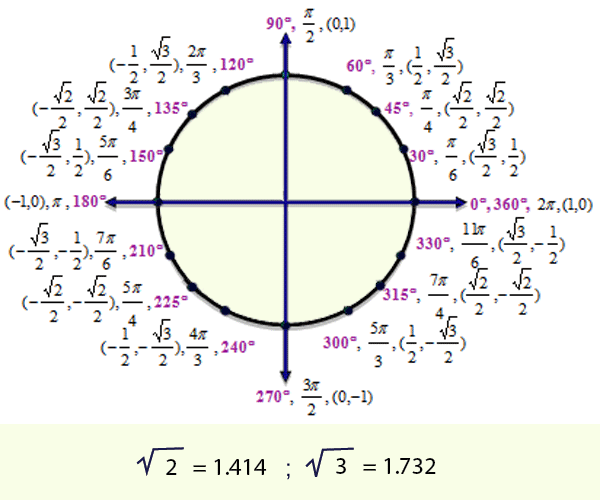

Голосовать за 0 голос против

Подробнее

Отчет

Виктория В. ответил 08.07.19

Репетитор

5,0 (402)

Более 15 лет опыта преподавания тригонометрии

См. таких репетиторов

Смотрите таких репетиторов

Смотрите видео

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

Quizlet-Trig-идентичность-Google Suce

Allebildervideosbüchermapsnewshopping

Sucoptionen

Триг-карты-Quizlet

Quizlet.com ›Trig-идентификаторы-флир-карты

4444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444 40002.com› trig-eduic0003

(38)

Взаимные тождества, тождества Пифагора, частные тождества, тождества кофункций, тождества четных и нечетных, формулы сумм-разностей, двойной угол . .. › Математика › Геометрия › Тригонометрия

Bewertung 4,5

(10)

Изучайте с помощью Quizlet и запоминайте карточки, содержащие такие термины, как csc x=, sec x=, cot x= и другие. … триггерные личности. 4,5 (10 отзывов) …

Ähnliche Fragen

Каковы 12 тригонометрических тождеств?

Какие 6 личностей?

Каковы 10 тригонометрических тождеств?

Карточки Trig Identities — Quizlet

quizlet.com › Математика › Исчисление

Изучайте с Quizlet и запоминайте карточки, содержащие такие термины, как взаимные тождества, пифагорейские тождества, частные тождества и другие.

Карточки Calculus II Trig Identities — Quizlet

quizlet.com › Математика › Исчисление

Bewertung 4,8

(4)

Исчисление II Триггерные тождества. 4.8 (4 отзыва). Карточки · Изучай · Тест · Подбери. Срок. 1 / 38. производная от tan(x). Нажмите на карту, чтобы перевернуть 👆. Определение.

Карточки Trig Identities — Quizlet

quizlet.com › Trig-identities-flash-cards

Обложки: частные личности; взаимные тождества; четно-нечетные тождества; тождества периодичности; кофункциональные тождества; пифагорейские тождества; сумма углов…

Флэш-карточки с триггерами — Quizlet

quizlet.com › триг-тождества-флэш-карточки

Изучайте с помощью Quizlet и запоминайте карточки, содержащие такие термины, как фундаментальные тождества триггеров, взаимные тождества, частные тождества и другие.

Тригонометрические тождества Флэш-карточки — Quizlet

quizlet.com › Математика › Геометрия › Тригонометрия

Изучайте с помощью Quizlet и запоминайте карточки, содержащие такие термины, как взаимные тождества, частные тождества, пифагорейские тождества и другие.

Карточки Trig Identities — Quizlet

quizlet.

No related posts.