Механическая работа — определение, формула, виды, свойства
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
| Механическая работа А = FScosα A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] α — угол между векторами силы и перемещения [°] |
Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости.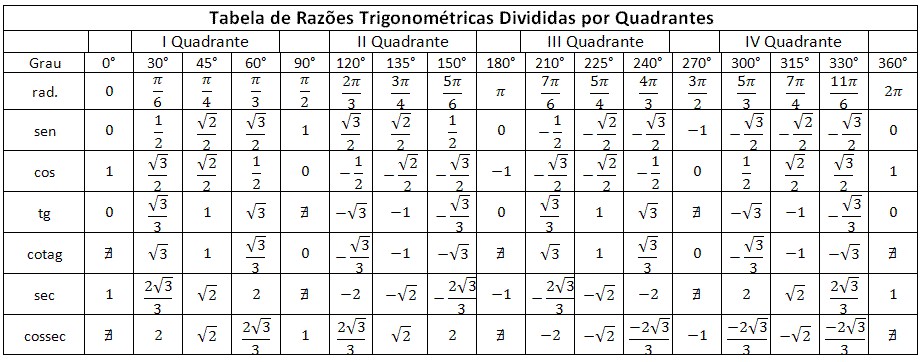
Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Для совершения работы необходимы два условия:
- чтобы на тело действовала сила,
- чтобы происходило перемещение тела.
Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Запомнить!
Работа равна нулю, если:
- при приложенной силе перемещение отсутствует;
- сила не приложена и тело перемещается по инерции;
- угол между векторами силы и перемещения равен 90°.
Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
Потенциальная энергия Еп = mgh m — масса тела [кг] g — ускорение свободного падения [м/с2] h — высота [м] На планете Земля g ≈ 9,8 м/с2 |
Затраченная работа в нашем примере — это механическая работа Сизифа.
Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
За счет чего происходит процесс?
Ради какого результата?
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).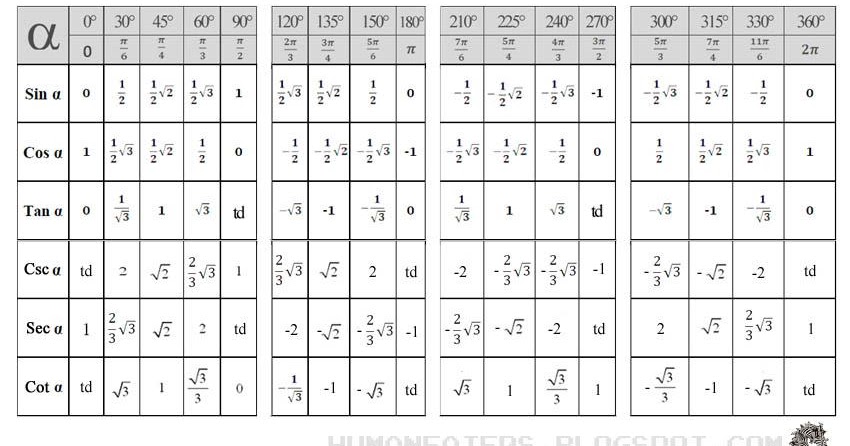
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность N = A/t N — мощность [Вт] A — механическая работа [Дж] t — время [с] |
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.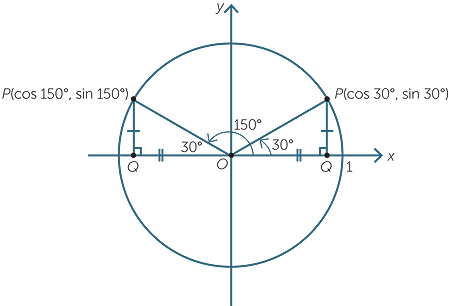
Также для мощности справедлива другая формула:
Мощность N = Fv N — мощность [Вт] F — приложенная сила [Н] v — скорость [м/с] |
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
Мощность N = FvcosαN — мощность [Вт] F — приложенная сила [Н] v — скорость [м/с] α — угол между векторами силы и скорости [°] |
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой.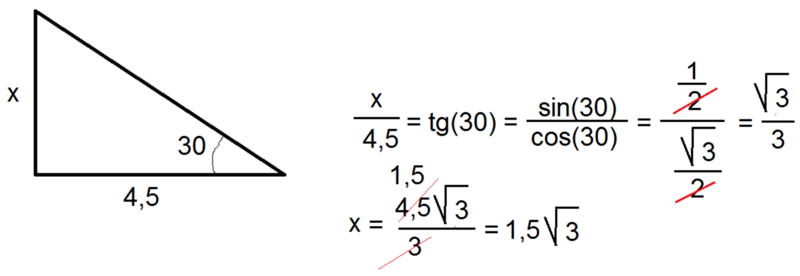
Запишитесь и участвуйте в розыгрыше 8 уроков
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
Выталкивающая сила.
Сила вязкого трения.
Сила тяжести.
Ни одна из перечисленных сил.
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью.
Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости.
Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости vx тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.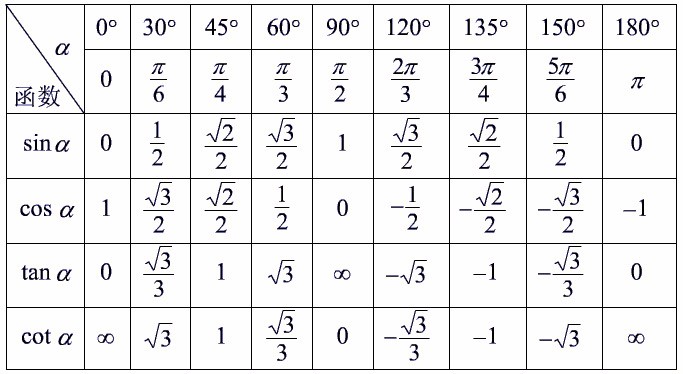
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
Синус, косинус, тангенс углов от 0° до 180° — ГЕОМЕТРИЯ — Уроки для 9 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
УРОК № 1
Тема. Синус, косинус, тангенс углов от 0° до 180°
Цель урока: формирование понятий синуса, косинуса, тангенса углов от 0° до 180°. Формирование умений находить тригонометрические функции тупых углов.
Тип урока: комбинированный.
Наглядность и оборудование: таблица «Соотношение между сторонами и углами треугольника» [13].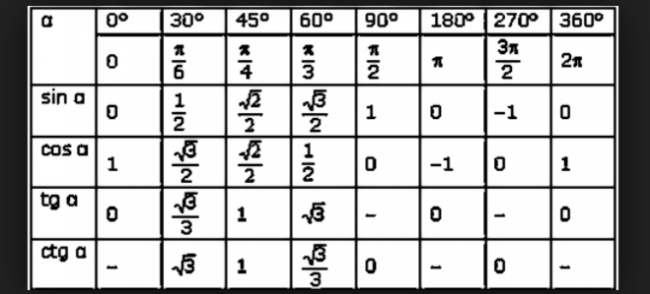
Требования к уровню подготовки учащихся: объясняют, что такое синус, косинус, тангенс углов от 0° до 180°.
Ход урока
И. Организационный этап
Вступительное слово учителя. Мы продолжаем изучение геометрии. В девятом классе вы ознакомитесь с новыми разделами геометрии: решения произвольных треугольников; правильные многоугольники; декартовы координаты на плоскости; геометрические преобразования; векторы на плоскости; начальные сведения из стереометрии. Впереди вас ждут новые теоремы о свойствах геометрических фигур, интересные задачи.
Желаю вам преодолеть препятствия, которые встанут на вашем пути лабиринтами геометрии. Пусть изучение геометрии принесет вам радость от полученных побед.
II. Актуализация опорных знаний
Фронтальная беседа
Для повторения сведений о тригонометрические функции острых углов прямоугольного треугольника можно использовать таблицу из пособия [13].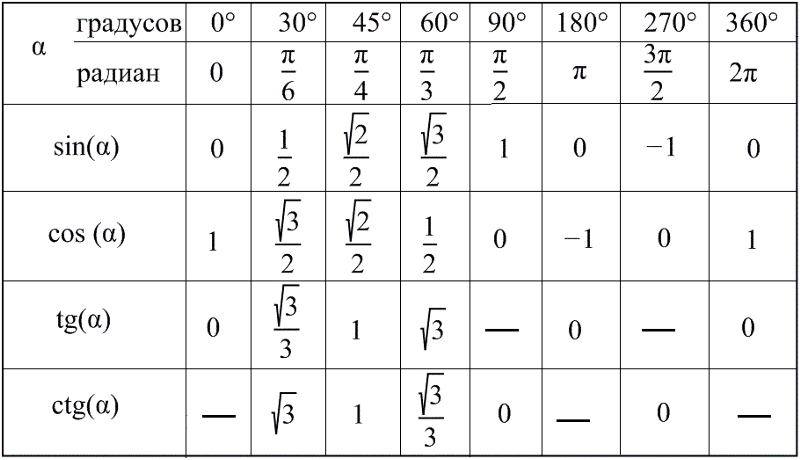
1. Сформулируйте определение синуса, косинуса, тангенса острого угла прямоугольного треугольника.
2. Найдите по рис. 1 sinα, cosα, tgα, cosβ, sinβ, tgβ.
3. Как связаны sinα и cosα, если α — острый угол прямоугольного треугольника?
4. Упростите выражение:
а) 1 + sin2α + cos2α;
б) 2cos2α + sin2α — 1.
5. Какой зависимостью связаны sinα, cosα, tgα?
6. Найдите tgα, если:
а) sinα = , cosα = ;
б) sinα = , cosα = .
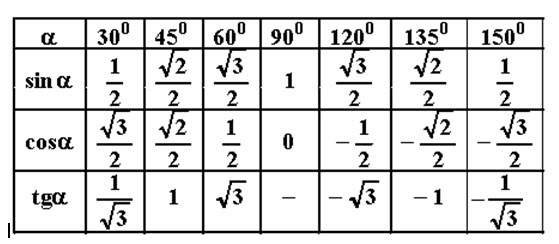
7. Укажите значение выражений:
а) sin 30°, cos 30°, tg 30°;
б) sin 45°, cos 45°, tg 45°;
в) sin 60°, cos 60°, tg 60°.
III. Поэтапное восприятие и осознание нового материала
Определение синуса, косинуса и тангенса углов от 0° до 180°
Изучение нового материала можно провести так. Построим окружность с центром в начале координат и радиусом 1 (рис. 2). Такой круг называется единичным.
Построим острый угол а, который образует радиус ОА этого круга с положительным направлением оси Ох. Пусть точка А имеет координаты (х; у). Тогда для прямоугольного треугольника АОВ имеем:
sinα = = = в;
cosα = = = x;
tgα = = .
Таким образом: синусом угла α есть ордината точки единичной окружности, причем радиус ОА образует с положительным направлением оси Ох угол α. Косинусом угла α является абсцисса точки единичной окружности, причем радиус ОА образует с положительным направлением оси Ох угол α. Тангенсом угла α есть отношение ординаты точки А до абсциссы этой точки, причем радиус ОАутворює с положительным направлением оси Ох угол α.
Нахождение значений синуса, косинуса и тангенса тупых углов
Пользуясь предоставленными определениями, дадим определение для любого угла α, 0° α 180°.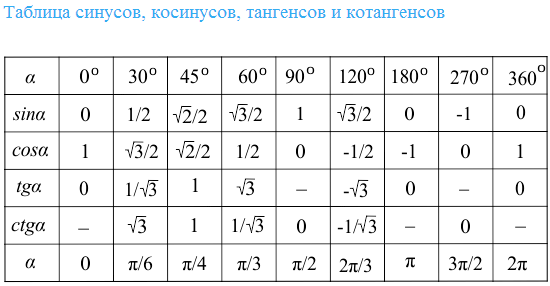
Тогда sin 0° = 0, cos 0° = 1, tg 0° = 0; sin 180° = 0, cos 180° = -l, tg 180° = 0.
Если угол α — тупой (0° α 90°), то ордината точки А (рис. 3) положительная (т.е. sin α > 0), абсцисса — отрицательная (то есть cosα 0), и отношение ординаты к абсциссы — отрицательное (т.е. tgα 0).
Следовательно, косинус, тангенс тупого угла отрицательные.
Если α — тупой угол (рис. 4), то cos α = ОС = — OD = -cos (180°- α),
sinα = AC = AD = sin (180° — α), тогда tg α = = — = -tg(180° — α).
Итак, чтобы найти синус тупого угла, достаточно найти синус смежного угла; чтобы найти косинус, тангенс тупого угла, надо найти число, противоположное косинуса, тангенса смежного угла.
Например, sin 120° = sin (180° — 120°) = sin 60° = ,
cos 150o = — cos (180° — 150°) = — cos 30° = — ,
tg 135° = -tg (180° — 135°) = — tg 45° = — 1.
Если учащиеся класса имеют недостаточную математическую подготовку, то можно упростить объяснение.
Достаточно сказать, что синус тупого угла равна синуса смежного угла, а косинус и тангенс тупого угла равны числу, противоположном косинуса и тангенса смежного угла.
Синус 0° равна 0, синус 180° равен 0, синус 90 градусов равен 1, а косинус 0° равна 1, косинус 180° равен -1, косинус 90 градусов равен 0; тогда тангенс 0° и 180° равны 0, а тангенс 90° не существует.
IV. Закрепление и осмысление нового материала
Выполнение упражнений
1. Вычислите синус, косинус и тангенс угла:
а) 120°; б) 135°; в) 150°.
2. Пользуясь калькулятором (таблицами), найдите:
a) sin 100°, sin 132°, sin 175°;
б) cos 95°, cos 127°, cos l70°;
в) tg 93°, tg 129°, tg 172°.
V. Домашнее задание
1. Изучить определение синуса, косинуса, тангенса углов от 0° до 180°.
2. Пользуясь калькулятором (таблицами), вычислить:
a) sin 105°, sin 140°, sin 165°;
б) cos 100°, cos 130°, cos 160°;
в) tg 103°, tg 131°, tg 163°.
VI. Подведение итогов урока
Задача класса
1. Дайте определение синуса, косинуса, тангенса углов от 0° до 180°.
2. Пользуясь рис. 5, найдите:
а) sin α; б) cos α; в) tg α.
| Содержание | Вперед |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Найти точное значение sin 150 градусов
Тригонометрия — это дисциплина математики, изучающая отношения между длинами сторон и углами прямоугольного треугольника. Тригонометрические функции, также известные как гониометрические функции, угловые функции или круговые функции, — это функции, которые устанавливают связь между углом и отношением двух сторон прямоугольного треугольника. Шесть основных тригонометрических функций — это синус, косинус, тангенс, котангенс, секанс и косеканс.
Углы, определяемые соотношениями тригонометрических функций, известны как тригонометрические углы. Тригонометрические углы представляют собой тригонометрические функции. Значение угла может быть где угодно между 0-360°.
Как показано на приведенном выше рисунке в прямоугольном треугольнике:
- Гипотенуза: Сторона, противоположная прямому углу, является гипотенузой, Это самая длинная сторона в прямоугольном треугольнике и напротив до угла 90°.
- Основание: Сторона, на которой лежит угол С, называется основанием.
- Перпендикуляр: Это сторона, противоположная рассматриваемому углу C.
Тригонометрические функции
Тригонометрия имеет 6 основных тригонометрических функций: синус, косинус, тангенс, косеканс, секанс и котангенс. Теперь давайте рассмотрим тригонометрические функции. Шесть тригонометрических функций следующие:
синус: Он определяется как отношение перпендикуляра к гипотенузе и представляется как sin θ
косинус: Определяется как отношение основания к гипотенузе и представляется как косинус θ
тангенс: Определяется как отношение синуса к косинусу угла. Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как tan θ
косеканс: Это величина, обратная sin θ, и представляется как cosec θ.
секанс: Это величина, обратная cos θ, обозначается как sec θ.
Котангенс: Это величина, обратная тангенсу θ, обозначается как cot θ.
Тригонометрические идентичности комплементарных и дополнительных углов
- Комплементарные углы: Пара углов, чья сумма равна 909 ° . Тождества дополнительных углов
sin (90° – θ) = cos θ
cos (90° – θ) = sin θ
tan (90° – θ) = cot θ
cot (90° – θ) = tan θ
сек (90° – θ) = cosec θ
cosec (90° – θ) = sec θ
Тождества дополнительных углов
sin (180° – θ) = sin θ
cos (180° – θ) = – cos θ
– θ) = – tan θcot (180° – θ) = – cot θ
сек (180° – θ) = – сек θ
cosec (180° – θ) = – cosec θ
Найти точное значение sin 150 градусов.
Решение:
Здесь грех положителен только в 1-м и 2-м квадранте.
150° лежит во 2-м квадранте.
Следовательно
sin (180° – θ) = sin θ
sin (150°) = sin (180° – 30°)
sin (150°) = sin (30°) ° 5
) = 1/2Таким образом, точное значение sin 150° равно 1/2
Аналогичные вопросы
Вопрос 1: Найдите значение sin 135°.