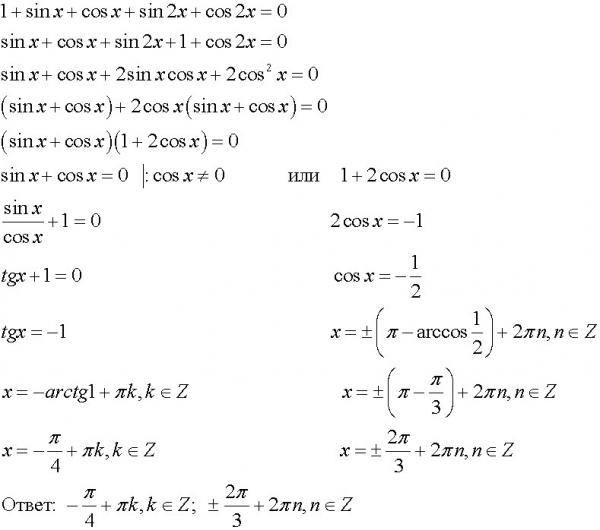Решите уравнение $\\cos 2x = 0$.
Ответ
Проверено
216,6 тыс.+ просмотров
Подсказка: В этом вопросе нам нужно найти общее решение cos2x = 0. Для этого воспользуемся общей формой cosx, согласно которой if $\ cos\theta=\cos\alpha$, тогда $\theta=2n\pi\pm\alpha$. Здесь мы сначала найдем значение $\alpha$ такое, что $\cos\alpha=0$ и приравняем его к cos2x, чтобы найти значение 2x через найденное $\alpha$. Затем мы разделим на 2, чтобы получить окончательное решение.
Полное пошаговое решение
Здесь нам дано уравнение вида cos2x = 0. Нам нужно найти значение x. Поскольку не дается интервал, поэтому нам нужно найти значение x в целом (в терминах n, где n = 0, 1, 2. … …)
Как мы знаем, общая форма Cosx утверждает, что если $\cos \theta =\cos \alpha $, то $\theta =2n\pi \pm \alpha $, где n = 0, 1, 2 . . . .
Итак, найдем такие значения $\alpha $, что $\cos \alpha =0$.
Из известных значений функции косинуса мы знаем, что $\cos \dfrac{\pi }{2}=0$. Следовательно, $\alpha =\dfrac{\pi }{2}$. Получаем:
$\cos 2x=\cos \dfrac{\pi }{2}$ откуда следует, что $2x=2n\pi \pm \dfrac{\pi }{2}$, где n = 0, 1, 2 . . . . .
Мы нашли значение 2x, но нам нужно значение x, поэтому, разделив обе части на 2, мы получим:
$\dfrac{2x}{2}=\dfrac{2n\pi \pm \dfrac{\pi } {2}}{2}$, где n = 0, 1, 2. . . . . .
Сокращая 2 в левой части уравнения и разделяя члены в правой части уравнения, мы получаем:
$x=\dfrac{2n\pi }{2}\pm \dfrac{\pi }{4}$ где п = 0, 1, 2. . . . . . . . .
$\Rightarrow x=n\pi \pm \dfrac{\pi }{4}$, где n = 0, 1, 2. . . . . . . . .
Теперь, взяв $\pi $ из обоих членов в правой части уравнения, мы получим:
$x=\left( n\pm \dfrac{1}{4} \right)\pi $, где n = 0 , 1, 2. . . . . . . .
Следовательно, это требуемое решение cos2x = 0.
Примечание: Студенты должны отметить, что мы должны начать принимать значения с n = 0.
Они могут проверить свой ответ, подставив значение n и проверив, что cos2x = 0. Например, для n = 1 имеем $x=\left( 1\pm \dfrac{1}{4} \right)\pi \Rightarrow x=\dfrac{3}{4}\pi ,\ dfrac{5}{4}\pi $. Cos2x становится $\cos 2\left(\dfrac{3}{4}\pi \right)\text{ и }\cos 2\left(\dfrac{5}{4}\pi \right)$.
Теперь $\cos \dfrac{3}{2}\pi =\cos \left( \pi +\dfrac{\pi }{2} \right)=\cos \dfrac{\pi }{2}= 0$.
Кроме того, $\cos \dfrac{5}{2}\pi =\cos \left( 2\pi +\dfrac{\pi }{2} \right)=\cos \dfrac{\pi }{2} =0$
Не забудьте взять как положительные, так и отрицательные знаки в общем виде значения функции косинуса. Студенты должны знать общие решения всех тригонометрических функций для решения этих сумм.
Недавно обновленные страницы
Если ab и c единичные векторы, то левое ab2 правое+bc2+ca2 математика класса 12 JEE_Main
Стержень AB длиной 4 единицы движется горизонтально, когда математика класса 11 JEE_Main
Оценить значение intlimits0pi cos 3xdx A 0 B 1 математика класса 12 JEE_Main
Что из следующего верно 1 nleft S cup T right класс 10 математики JEE_Main
Какова площадь треугольника с вершинами? ca2 класс 12 математика JEE_Main
Стержень AB длиной 4 единицы перемещается горизонтально, когда математика класса 11 JEE_Main
Оценить значение intlimits0pi cos 3xdx A 0 B 1 математика класса 12 JEE_Main
Что из следующего является правильным 1 nleft S cup T right класс 10 математики JEE_Main
Какова площадь треугольника с вершинами Aleft класс 11 математика JEE_Main
KCN легко реагирует с образованием цианида с A Этиловый спирт класса 12 химический JEE_Main
Актуальные сомнения
2sinxcosx-sin(2x)cos(2x)=0.
Упростите левую часть выражения, чтобы каждое слагаемое включало только 2x, факторизируйте левую часть так, чтобы она могла быть… значок-вопрос
Спросите репетитораНачать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяСсылайтесь на эту страницу следующим образом:
«2sinxcosx-sin(2x)cos(2x)=0. Упростите левую часть выражения, чтобы каждый член включал только 2x, факторизируйте левую часть, чтобы ее можно было решить. Кроме того, как только я получу факторизованное уравнение, как бы Я решаю это? Большое спасибо! Будем признательны за любую помощь!» eNotes Editorial , 18 февраля 2013 г., https://www.enotes.com/homework-help/2sinxcosx-sin-2x-cos-2x-0-simplify-left-side-385167. По состоянию на 8 ноября 2022 г.
Ответы экспертов
Решить `2sinxcosx-sin(2x)cos(2x)=0`
Использовать тождество триггера `sin(2x)=2sinxcosx` :
2sinxcosx-sin(2x)cos(2x)=0
sin(2x)-sin(2x)cos(2x)=0
sin(2x)(1-cos(2x))=0
Таким образом, по свойству нулевого произведения либо sin(2x)=0, либо 1- cos(2x)=0
(a) sin(2x)=0 Синус равен 0 при `x=+-kpi`, где k — целое число.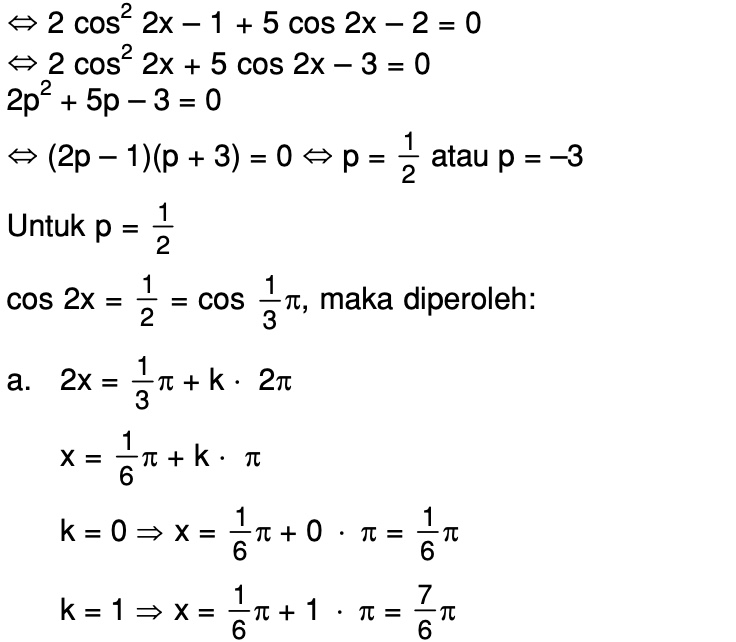
Итак, sin(2x)=0 ==> `x=pi/2+-kpi/2` 9(-1)(0)==>2x=0+-kpi ==> x=0+-kpi/2`, что эквивалентно **
(b) 1-cos(2x)=0 ==>cos (2x)=1…
См.
Этот ответ сейчас
Начните 48-часовую бесплатную пробную версию , чтобы разблокировать этот и тысячи других ответов. Наслаждайтесь eNotes без рекламы и отмените подписку в любое время.
Уже зарегистрирован? Войдите здесь. 9(-1)(1) ==>2x=0+-2pi ==>x=0+-pi`
———————- ———————————————————-
Решения для 2sinxcosx- sin(2x)cos(2x)=0 являются `x=0+-kpi/2`
—————————- ————————————-
** Обратите внимание, что целые числа, кратные `пи` кратно `pi/2` **
График y=2sinxcosx-sin(2x)cos(2x):
svg» sscr=»-9.4,9.4,-2,2,1.57,1,1,1.57,1,300,200,func,2sin(x)cos(x)-sin(2x)cos(2x),null,0,0,,,black,1,none»/>
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 ответов воспитателя
математика
Последний ответ опубликован 07 октября 2013 г. в 20:13:27.
Как определить, является ли это уравнение линейной или нелинейной функцией?
84 Ответы воспитателя
Математика
Последний ответ опубликован 14 ноября 2011 г. в 5:49:28.
Решите для b2:A= 1/2h (b1+b2)
1 Ответ учителя
Математика
Последний ответ опубликован 3 октября 2011 г.