Уравнение касательной к нормали к графику функции – ?

9. Уравнения касательной и нормали.

Рассмотрим кривую, уравнение которой имеет вид

Уравнение касательной к данной кривой в точке имеет вид:

(34)

Нормалью к кривой в данной точке называется прямая, проходящая через данную точку, перпендикулярную к касательной в этой точке.

Уравнение нормали к данной кривой в точке имеет вид:

(35)

_{Длина отрезка касательной, заключенного между точкой касания и осью абсцисс называется длиной касательной, проекция этого отрезка на ось абсцисс называется подкасательной.}

_{Длина отрезка нормали, заключенного между точкой касания и осью абсцисс называется длиной нормали,проекция этого отрезка на ось абсцисс называется}

_{поднормалью.}

Пример 17

Написать уравнения касательной и нормали к кривой в точке, абсцисса которой равна.

Решение:

Найдем значение функции в точке :

Найдем производную заданной функции в точке

Уравнение касательной найдем по формуле (34):

Уравнение нормали найдем по формуле (35):

Ответ: Уравнение касательной :

Уравнение нормали :.

Пример 18

Написать уравнения касательной и нормали, длины касательной и подкасательной, длины нормали и поднормали для эллипса

в точке , для которой.

Решение:

Найдем как производную функции, заданной параметрически по формуле (10):

Найдем координаты точки касания : и значение производной в точке касания :

Уравнение касательной найдем по формуле (34):

Найдем координаты точкипересечения касательной с осью:

Длина касательной равна длине отрезка :

Согласно определению, подкасательная равна

Где угол – угол между касательной и осью. Поэтому,- угловой коэффициент касательной, равный

Таким образом, подкасательная равна

Уравнение нормали найдем по формуле (35):

Найдем координатыточкипересечения нормали с осью:

Длина нормали равна длине отрезка :

Согласно определению, поднормаль равна

Где угол – угол между нормалью и осью. Поэтому,- угловой коэффициент нормали, равный

Поэтому, поднормаль равна:

Ответ: Уравнение касательной :

Уравнение нормали :

Длина касательной ; подкасательная;

Длина нормали ; поднормаль

Задания 7. Написать уравнения касательной и нормали:

1. К параболе в точке, абсцисса которой

.

2. К окружности в точках пересечения её с осью абсцисс

.

3. К циклоиде в точке, для которой

.

4. В каких точках кривой касательная параллельна:

а) оси Оx; б) прямой

.

10. Промежутки монотонности функции. Экстремумы функции.

Условие монотонности функции:

Для того, чтобы дифференцируемая на функцияне возрастала, необходимо и достаточно, чтобы во всех точках, принадлежащихее производная была неположительна .

(36)

Для того, чтобы дифференцируемая на функцияне убывала, необходимо и достаточно, чтобы во всех точках, принадлежащихее производная была неотрицательна.

(37)

Промежутки, на которых производная функции сохраняет определенный знак, называются промежутками монотонности функции

Пример 19

Найти промежутки монотонности функции .

Решение:

Найдем производную функции .

Найдем промежутки знакопостоянства полученной производной. Для этого

разложим полученный квадратный трехчлен на множители:

.

Исследуем знак полученного выражения, используя метод интервалов.

Таким образом, получаем согласно (36), (37),что заданная функция возрастает на и убывает на.

Ответ: Заданная функция возрастает наи убывает на.

_{Определение} Функция имеет в точкелокальный максимум (минимум), если существует такая окрестность точки , что для всехвыполняется условие

().

Локальный минимум или максимум функции называетсялокальным экстремумом.

Необходимое условие существования экстремума.

Пусть функция определена в некоторой окрестности точки. Если функцияимеет в точкеэкстремумом, то производнаяв точкелибо равна нулю, либо не существует.

Точка называетсякритической точкой функции , если производнаяв точкелибо равна нулю, либо не существует.

Достаточные условия наличия экстремума в критической точке .

Пусть точка является критической.

Первое достаточное условие экстремума:

Пусть функция непрерывна в некоторой окрестноститочкии дифференцируема в каждой точке.

Точка является локальным максимумом, если при переходе через

производная функции меняет знак с плюса на минус.

Точка является локальным минимумом, если при переходе через

производная функции меняет знак с минуса на плюс.

Пример 20

Найти экстремумы функции .

Решение:

Найдем производную заданной функции

Приравнивая в полученной производной к нулю числитель и знаменатель, найдем критические точки:

Исследуем знак производной, используя метод интервалов.

Из рисунка видно, что при переходе через точку производная меняет знак с плюса на минус. Следовательно, в точке- локальный максимум.

При переходе через точку производная меняет знак с минуса на плюс.

Следовательно, в точке — локальный минимум.

При переходе через точку производная не меняет знак. Следовательно, критическая точкане является экстремумом заданной функции.

Ответ: — локальный максимум, — локальный минимум.

Второе достаточное условие экстремума:

Если первые производные функциив точкеравны нулю, а-ная производная функциив точкеотлична от нуля, то точкаявляется экстремумом функции, причем,

если

, (38)

то -локальный минимум

если

, (39)

то -локальный максимум.

Пример 21

Найти экстремумы функции, пользуясь второй производной .

Решение:

ОДЗ: .

Найдем первую производную заданной функции

Найдем критические точки функции:

Точку мы не рассматриваем, так как функция определена только в левой окрестности.

Найдем вторую производную

Находим

Таким образом, на основании (39) делаем вывод о том, что при — локальный максимум.

Ответ: — локальный максимум.

Задания 8.

Исследовать на возростание и убывание функции:

Исследовать на экстремумы функции:

studfiles.net

Как найти уравнение нормали к графику функции в заданной точке

Как найти уравнение нормали к графику функции в заданной точке?

На данном уроке мы узнаем, как найти уравнение нормали к

графику функции в точкеи разберём многочисленные примеры, которые касаются этой задачи. Для качественного усвоения  материала нужно пониматьгеометрический смысл производной и уметь их находить хотя бы на уровне следующих статей:

Как найти производную? Производная сложной функции и Простейшие задачи с производными.

Перечисленные уроки позволят «чайникам» быстро сориентироваться в теме и поднять свои навыки дифференцирования практически с полного нуля. По существу, сейчас последует развёрнутое продолжение параграфа об уравнении касательной 3-й статьи из вышеприведенного списка. Почему продолжение? Уравнение нормали тесно связано с уравнением касательной. Помимо прочего я рассмотрю задачи о том, как построить уравнения этих линий в ситуациях, когда функция задана неявно либо параметрически.

Но сначала освежим воспоминания: если функция

дифференцируема в точке (т.е. если существуетконечная производная ), то уравнение касательной к графику функции в точкеможно найти по следующей формуле:

Это самый распространенный случай, с которым мы уже столкнулись на уроке Простейшие задачи с производными. Однако дело этим не ограничивается: если в точке существует бесконечная производная:, то касательная будет параллельна осии её уравнение примет вид. Дежурный пример: функцияс производной, которая обращается в бесконечность вблизикритической точки . Соответствующая касательная выразится уравнением:(ось ординат).

Если же производной не существует(например, производной от в точке), то, разумеется, не существует и общей касательной.

Как различать последние два случая, я расскажу чуть позже, а пока что вернёмся в основное русло сегодняшнего урока:

Что такое нормаль? Нормалью к графику функции в точкеназывается

прямая, проходящая через данную точку перпендикулярно касательной к графику функции в этой точке (понятно, что касательная должна существовать). Если совсем коротко, нормаль – это перпендикулярная к касательной прямая, проходящая через точку касания.

Как найти уравнение нормали? Из курса аналитической геометрии напрашивается очень простой алгоритм: находим уравнение касательной и представляем его в общем виде . Далее «снимаем»нормальный вектор и составляем уравнение нормали по точкеи направляющему вектору.

Этот способ применять можно, но в математическом анализе принято пользоваться готовой формулой, основанной на взаимосвязи угловых коэффициентов перпендикулярных прямых. Если существует конечная и отличная от нуля производная , то уравнение нормали к графику функциив точкевыражается следующим уравнением:

Особые случаи, когда равна нулю либо бесконечности мы обязательно рассмотрим, но сначала «обычные» примеры:

Пример 1

Составить уравнения касательной и нормали к графику кривой в точке, абсцисса которой равна.

В практических заданиях часто требуется найти и касательную тоже. Впрочем, это очень только нА руку – лучше будет «набита рука» =)

Решение: Первая часть задания хорошо знакома, уравнение касательной составим по формуле:

В данном случае:

Найдём производную: Здесь на первом шагевынесли константу за знак производной, на втором – использовали правило дифференцирования сложной функции.

Теперь вычислим производную в точке :

Получено конечное число и это радует. Подставим ив формулу:

Перебросим наверх левой части, раскроем скобки и представим уравнение касательной вобщем виде: Вторая часть задания ничуть не сложнее. Уравнение нормали составим по формуле:Избавляемся оттрёхэтажности дроби и доводим уравнение до ума: – искомое уравнение.

Ответ:

Здесь можно выполнить частичную проверку. Во-первых, координаты точки должны удовлетворять каждому уравнению:

– верное равенство.

– верное равенство.

И, во-вторых, векторы нормали должны быть ортогональны. Это элементарно проверяется с помощьюскалярного произведения: , что и требовалось проверить.

Как вариант, вместо нормальных векторов можно использовать направляющие векторы прямых.

! Данная проверка оказывается бесполезной, если неверно найдена производная и/или производная в точке. Это «слабое звено» задания – будьте предельно внимательны!

Чертежа по условию не требовалось, но полноты картины ради: 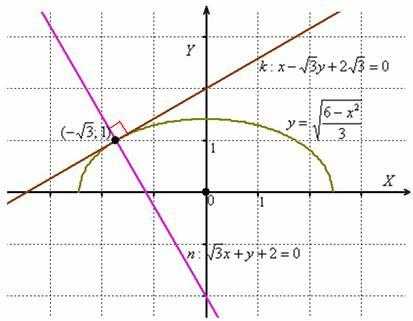Забавно, но фактически получилась и полная проверка, поскольку чертёж выполнен достаточно точно =) Кстати, функциязадаёт верхнюю дугуэллипса.

Следующая задача для самостоятельного решения:

Пример 2

Составить уравнения касательной и нормали к графику функции в точке.

Примерный образец чистового оформления задания в конце урока.

Теперь разберём два особых случая:

1) Если производная в точке равна нулю:, то уравнение касательной упростится:То есть, касательная будет параллельна оси.

Соответственно, нормаль будет проходить через точку параллельно оси, а значит её уравнение примет вид.

2) Если производная в точке существует, но бесконечна:, то, как отмечалось в самом начале статьи, касательная станет вертикальной:. И поскольку нормаль проходит через точкупараллельно оси, то её уравнение выразится «зеркальным» образом:

Всё просто:

Пример 3

Составить уравнения касательной и нормали к параболе в точке. Сделать чертёж.

Требование выполнить чертёж я не добавлял – так было сформулировано задание в оригинале. Хотя это редкость.

Решение: составим уравнение касательной . В данном случае

Казалось бы, расчёты пустяковые, а в знаках запутаться более чем реально:

Таким образом:

Поскольку касательная параллельна оси (Случай №1), то нормаль, проходящая через ту же точку , будет параллельна оси ординат:

Чертёж – это, конечно же, дополнительные хлопоты, но зато добротная проверка аналитического решения: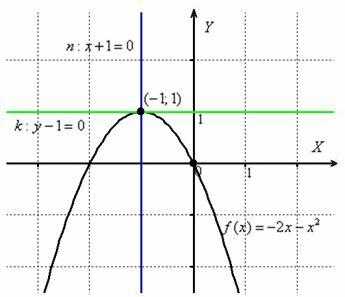

Ответ: ,

В школьном курсе математики распространено упрощённое определение касательной, которое формулируется примерно так: «Касательная к графику функции – это прямая, имеющая с данным графиком единственную общую точку». Как видите, в общем случае это утверждение некорректно. Согласно геометрическому смыслу производной, касательной является именно зелёная, а не синяя прямая.

Следующий пример посвящён тому же Случаю №1, когда :

Пример 4

Написать уравнение касательной и нормали к кривой в точке.

Краткое решение и ответ в конце урока

Случай №2, в котором на практике встречается редко, поэтому начинающие могут особо не волноваться и с лёгким сердцем пропустить пятый пример. Информация, выделенная курсивом, предназначена для читателей с высоким уровнем подготовки, которые хорошо разобрались сопределениями производной и касательной, а также имеют опыт нахождения производной по определению:

Пример 5

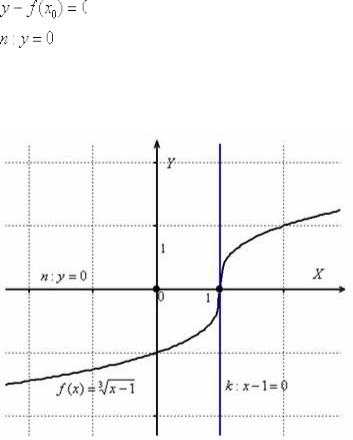
Найти уравнения касательной и нормали к графику функции в точке

Решение: в критической точке знаменатель производнойобращается в ноль, и поэтому здесь нужно вычислить односторонние производныес помощью определения производной (см. конец статьиПроизводная по определению): Обе производные бесконечны, следовательно, в точке существует общая вертикальная касательная: Ну, и очевидно, что нормалью является ось абсцисс. Формально по формуле: Для лучшего понимания задачи приведу чертёж: 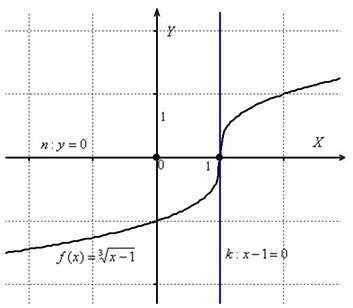Ответ:

Я рад, что вы не ушли бороздить просторы Интернета, потому что всё самое интересное только начинается! Чтобы осилить материал следующего параграфа, нужно уметь находить производную от неявно заданной функции:

Как найти уравнение касательной и уравнение нормали, если функция задана неявно?

Формулы касательной и нормали остаются прежними, но меняется техника решения:

Пример 6

Найти уравнения касательной и нормали к кривой в точке.

Решение: судя по уравнению, это какая-то линия 3-го порядка, какая именно – нас сейчас совершенно не интересует.

В уравнении присутствует зловред , и поэтому перспектива выразить функция вявном виде выглядит весьма туманной.

Но этого и не требуется! Есть куда более остроумное решение. Уравнение касательной составим по той же формуле .

Из условия известны значения , кстати, не помешает убедиться, что они действительно удовлетворяют предложенному уравнению:Получено верное равенство, значит, с точкойвсё в порядке.

Осталось вычислить . Сначала по стандартной схеме найдёмпроизводную от функции, заданной неявно:

Перепишем результат с более подходящим для нашей задачи обозначением:

На 2-м шаге в найденное выражение производной подставим :

Вот так-то!

Осталось аккуратно разобраться с уравнением:

Составим уравнение нормали:

Ответ:

Готово! А поначалу представлялось всё непросто. Хотя производная здесь, конечно,  – место уязвимое. Миниатюра для самостоятельного решения:

Пример 7

Найти уравнение нормали к линии в точке

Хватит уже вымучивать касательную =)

В данном случае легко выяснить, что это окружность центром в точкерадиусаи даже выразить нужную функцию. Но зачем?! Ведь найти производную отнеявно заданной функции на порядок легче! Она тут чуть ли не самая примитивная.

Краткое решение и ответ в конце урока.

Как найти уравнение касательной и уравнение нормали, если функция задана параметрически?

Ещё проще. Но для этого нужно потренироваться в нахождении производной от параметрически заданной функции. А так – почти халява:

Пример 8

Составить уравнения касательной и нормали к циклоиде , проведенные в точке, для которой.

Чертёж циклоиды можно найти на странице S и V, если линия задана параметрически (так получилось, что эта статья была создана раньше). Там даже изображена точка касания.

Решение: абсцисса и ордината точки касания рассчитываются непосредственно из параметрических уравнений кривой:

Найдём 1-ую производную от параметрически заданной функции:

И вычислим её значение при  :

Уравнение касательной составим по обычной формуле с поправкой на несколько другие обозначения:

Уравнение нормали:

Ответ:

В заключение предлагаю познакомиться с ещё одной интересной линией:

Пример 9

Составить уравнение нормали к полукубической параболе , проведенной в точке, для которой.

Это пример для самостоятельного решения. Напоминаю, что графики параметрически заданных функций можно построить, например, с помощью моего расчётного геометрического макета.

Ну а наш урок подошёл к концу, и я надеюсь, что изложенный материал прошёл для вас не по касательной, а нормально =)

Спасибо за внимание и успехов!

Решения и ответы:

Пример 2: Решение: уравнение касательной составим по формуле: В данном случае: Таким образом: Уравнение нормали составим по формуле : Ответ:

Пример 4: Решение: уравнение касательной составим по формуле: В данной задаче: Таким образом: В точке касательная параллельна оси, поэтому соответствующее уравнение нормали: Ответ:

Пример 7: Решение: в данной задаче: . Найдём производную: Или: Подставим в выражение производной : Искомое уравнение нормали: Ответ:

Пример 9: Решение: в данном случае: Найдём производную и вычислим её значение при : Уравнение нормали: Ответ:

Взято с сайта http://www.mathprofi.ru

studfiles.net

Уравнения касательной и нормали к графику функции — Мегаобучалка

Раздел 8. Дифференциальное исчисление функций одной переменной.

1. Производная функции, её геометрический и физический смысл

2. Уравнения касательной и нормали к графику функции.

3. Таблица производных.

4. Основные правила дифференцирования.

5. Связь непрерывности и дифференцируемости.

6. Дифференциал функции.

7. Формула приближённых вычислений значений функций с помощью дифференциала.

8. Основные теоремы дифференциального исчисления

9. Формула Тейлора.

10. Исследование функции с помощью первой производной.

11. Исследование функции с помощью второй производной.

12. Пример полного исследования функции.

Производная функции, её геометрический и физический смысл.

 

Рассмотрим функцию , дадим аргументу приращение получим новое значение функции В результате функция получит приращение ( х).

Определение. Производной функции в произвольной точке называется предел отношения приращения функции в этой точке к приращению аргумента при

Производная функции в точке обозначается Итак, по определению

Пример 1. Найти производную функции

Решение. По определению

= = =

=

 

Если аргумент интерпретировать как время t движения материальной точки, а путь, пройденный этой точкой изменяется по закону , то отношение означает среднюю скорость точки на временном промежутке Тогда означает мгновенную скорость точки в любой момент времени – в этом состоит физический смысл производной.

Поскольку все процессы в природе находятся в движении, в развитии, а характеристикой всякого движения является скорость, то ясно, какое значение в изучении реальных процессов принадлежит производной функции.

Мы часто пользуемся графиками функций, поэтому рассмотрим геометрический смысл производной.

 

 

В

A

Рис. 1

 

 

Рассмотрим график функции (рис.1) Возьмём некоторую точку , вычислим и покажем на рисунке значение производной в точке . Дадим аргументу приращение , получим новое значение аргумента и вычислим новое значение функции Имеем две точки на графике: Проведём секущую , тем самым получится В этом треугольнике

тогда .

При точка , оставаясь на кривой, стремится к точке ; секущая становится в пределе касательной к графику функции в точке Тангенс угла наклона секущей становится тангенсом угла наклона касательной.

Геометрический смысл производной функции в точке — это тангенс угла наклона касательной к графику функции в этой точке к положительному направлению оси (рис.2)

 

A

0

 

Рис.2.

Уравнения касательной и нормали к графику функции.

 

Рассмотрим функцию и напишем уравнение касательной к графику этой функции в некоторой точке где ( см.рис.2)

Воспользуемся уравнением прямой с угловым коэффициентом и опорной точкой: у — =k(x — Исходя из геометрического смысла производной Обозначим это число следовательно, уравнение касательной имеет вид: .

Нормалью к кривой в точке называется прямая, перпендикулярная касательной к кривой в этой точке. Условие перпендикулярности двух прямых состоит в том, что произведение их угловых коэффициентов равно – 1. Получаем окончательный вывод:

— уравнение касательной,

— уравнение нормали к графику функции в точке , где .

Пример 2. Написать уравнения касательной и нормали к графику функции в точке

Решение. Воспользуемся уравнениями касательной и нормали — осталось найти ( (0). Так как (x)= =cosx, то (0)=cos0=1. Получаем: , т.е. биссектриса I-III координатных углов, является касательной графика синуса в начале координат; — уравнение нормали.

Таблица производных.

 

Первым непременным условием освоения техники дифференцирования является знание таблицы производных, т.е. производных всех основных элементарных функций. Приводим доказательства.

 

а) – показательная функция.

Частный случай

 

 

Отметим замечательное свойство показательной функции — она при дифференцировании не меняется. Это свойство является причиной огромного значения этой функции в теоретических исследованиях и практических приложениях.

 

б) — логарифмическая функция.

частный случай

 

в) -степенная функция.

 

 

г)

 

 

Остальные табличные производные доказываются аналогично. Приводим теперь таблицу производных:

 

1) ;

2) ; ) ;

3) ; ;

4)

5) ;

6) ;

7) ;

8) ;

9) ;

10) :

11) .

megaobuchalka.ru

13. Определение производной и ее геометрический смысл. Уравнение касательной и нормали к графику функции в данной точке.

Определение: производной функции y=f(x) в точке x₀ называется предел отношения приращения функции Δу к приращению аргумента Δх, когда приращение аргумента стремиться к нулю Δх→0

f^’(x) = lim_Δх→0Δу/Δх= lim_Δх→0f(x₀+Δx)-f(x₀)/Δx. Производная в т.х₀-это число. Если т.х₀ меняется, мы получаем функцию f^’(x), которая также называется производной функцией. Нахождение производной-дифференцирование. Производные обозначаются у’ или f^’(x), dy/dx.

Δу/Δх=tg угла наклона секущей к оси ОХ (т.е. её угловому коэффициенту).Если Δх→0, то секущая стремиться к касательной к графику в точке х, поэтому её угловой коэффиц.стремиться к угловом.коэффиц.касательной,т.е. получаем, что углов.коэффиц.касательной-производная. Значение производной в точке х₀ равно тангенсу угла наклона касательной к графику функции.

Определение: нормалью к плоской кривой γ в т.М₀ называется перпендикуляр к касательной к кривой γ в этой точке. Угловые коэффициенты двух перпендикулярных прямых связаны соотношение к₂=-1/к₁. Отсюда получаем уравнение нормали к графику f(x) в точке х₀:

n:у-у₀=1/ f^’(x₀)(х-х₀)

14. Доказать, что дифференцируемая функция непрерывна.

Теорема: если существует() f^’(x₀), то фун-ия у= f(x) непрерывна в точке x₀.

Док-во: пусть существ. f^’(x₀)= lim_Δx→0Δy/Δx. Тогда Δy/Δx= f^’(x₀)+α, где α=α(х)-б.м. в точке x_{0 =>} Δy= f^’(x₀)Δх+α* Δх или lim_Δx→0Δy=0, это значит, что у= f(x) непрерывна в точке x₀.

15.Производная суммы и произведения функций.

Пусть u=u(x) и v=v(x)- функции, определенные в некоторой окрестности точки х и имеют производные в этой точке. Обозначим Δ u=u(x+Δх)- u(x) и Δ v=v(x+Δх)- v(х) приращения этих функций, соответствующие приращению Δх. Эти формулы можно записать в виде u(x+Δх)=u+Δu и v(x+Δх)=v+Δv

Теорема: производная суммы (разности) равна сумме (разности) производных: (u+v)’= u’+ v’

Производная произведения (uv)’= u’v+ u v’, в частности, постоянную можно выносить за знак производной: (Сv)’= Сv’

Док-во: пусть у=u(x)+v(x),тогда приращение суммы равно сумме приращений, Δ у=(u(x+Δх)+v(x+Δх)-(u(x)+ v(х))= Δu+Δ v и => у’= lim_Δx→0Δy/Δx= lim_Δx→0 Δu+Δ v /Δх== lim_Δx→0 (Δu/Δх+Δ v /Δх)= lim_Δx→0 Δu/Δх+ lim_Δx→0Δ v /Δх= u’+ v’

пусть у=u(x)*v(x),тогда приращение произведения равно Δ у=(u(x+Δх)*v(x+Δх)-u(x)*v(х)=(u+Δ u)(v+Δv)- uv=Δuv+uΔv+ΔuΔvи=>у’=lim_Δx→0Δy/Δx=lim_Δx→0Δuv+uΔv+ΔuΔv/Δх==lim_Δx→0(Δu/Δх*v+u*Δv/Δх+Δu/Δx*Δv)= u’v+uv’.

Пусть u(x)=const. применяя2 получаем (Сv)’= C’v+Сv’, т.к. С’=0

16.Производная частного. Производная функций у=tgx, y=ctgx.

Производная частного: (u/v)’= u’v-uv’/v²

Док-во: пусть у=: u(х)/v(х), тогда приращение частного равно Δу= u(х+Δх)/v(х+Δх)- u(х)/v(х)=u+Δu/v+Δv-u/v=(u+Δu)v-u(v+Δv)/(v+Δv)v=Δuv-uΔv/(v+Δv)v и следовательно, y’=lim_Δx→0 Δy/Δx= lim_Δx→0 Δuv-uΔv/Δx*1/(v+Δv)v== lim_Δx→0 Δu/Δx*v-u*Δv/Δx/(v+Δv)v=u’v-uv’/v²

у=tgx, y’=( tgx’)=(sinx/cosx)’= cosxcosx—sinx(-sinx)/cos²x=1/cos²x

y=ctgx, y’=( ctgx’)=(cosx/sinx)’=-sinxsinx— cosxcosx/ sin²x =-1/sin²x

studfiles.net

Как найти уравнение нормали к графику функции в заданной точке?

На данном уроке мы узнаем, как найти уравнение нормали к графику функции в точкеи разберём многочисленные

примеры, которые касаются этой задачи. Для качественного усвоения материала нужно понимать геометрический смысл производной и

уметь их находить хотя бы на уровне следующих статей:

Как найти производную? Производная сложной функции

и

Простейшие задачи с производными.

Перечисленные уроки позволят «чайникам» быстро сориентироваться в теме и поднять свои навыки дифференцирования практически с полного нуля. По существу, сейчас последует развёрнутое продолжение параграфа об уравнении касательной 3-йстатьи из вышеприведенного списка. Почему продолжение? Уравнение нормали тесно связано с уравнением касательной. Помимо прочего я рассмотрю задачи о том, как построить уравнения этих линий в ситуациях, когда функциязадана неявно либопараметрически.

Но сначала освежим воспоминания: если функция дифференцируема в точке(т.е. если существуетконечная производная), то уравнение касательной к графику функции в точкеможно найти по следующей формуле:

Это самый распространенный случай, с которым мы уже столкнулись на уроке Простейшие задачи с производными. Однако дело этим не

ограничивается: если в точке существует бесконечная производная:, то касательная будет параллельна осии её уравнение примет вид. Дежурный пример: функцияс

производной , которая обращается в бесконечность

вблизи критической точки . Соответствующая касательная выразится уравнением:

(ось ординат).

Если же производной не существует(например, производной от в точке ), то, разумеется, не существует иобщей касательной.

Как различать последние два случая, я расскажу чуть позже, а пока что вернёмся в основное русло сегодняшнего урока:

Что такое нормаль?Нормалью к графику функциив точкеназываетсяпрямая, проходящая через данную точку перпендикулярно касательной к графику функции в этой точке

(понятно, что касательная должна существовать). Если совсем коротко, нормаль – это перпендикулярная к касательной прямая, проходящая через точку касания.

Как найти уравнение нормали? Из курса аналитической геометрии напрашивается очень простой алгоритм: находим

уравнение касательной и представляем его в общем виде

. Далее «снимаем»нормальный вектор и составляем уравнение нормали по точкеи направляющему вектору.

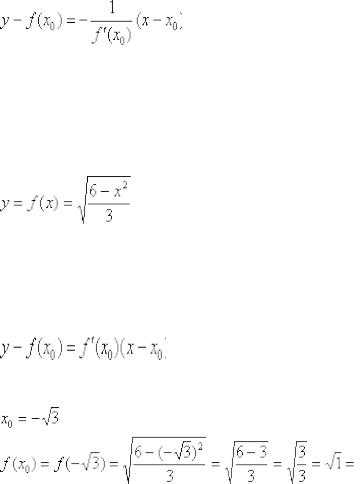
Этот способ применять можно, но в математическом анализе принято пользоваться готовой формулой, основанной на взаимосвязи угловых коэффициентов перпендикулярных прямых. Если

существует конечнаяи отличная от нуляпроизводная , то уравнение нормали к графику функции в точке выражается следующим уравнением:

Особые случаи, когда равна нулю либо бесконечности мы обязательно рассмотрим, но сначала «обычные» примеры:

Пример 1 Составить уравнения касательной и нормали к графику кривой

в точке, абсцисса которой равна .

В практических заданиях часто требуется найти и касательную тоже. Впрочем, это очень только нА руку – лучше будет «набита рука» =)

Решение: Первая часть задания хорошо знакома, уравнение касательной составим по формуле:

В данном случае:

Найдём производную:

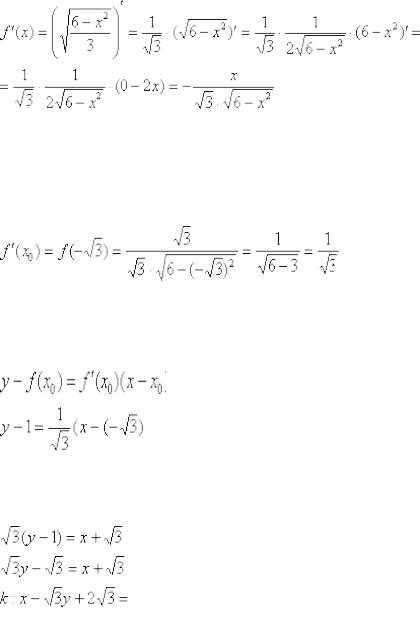
Здесь на первом шаге вынесли константу за знак производной, на втором – использовали правило дифференцирования сложной функции.

Теперь вычислим производную в точке :

Получено конечное число и это радует. Подставимив формулу

:

Перебросим наверх левой части, раскроем скобки и представим уравнение касательной вобщем виде:

Вторая часть задания ничуть не сложнее. Уравнение нормали составим по формуле:

Избавляемся от трёхэтажности дроби и доводим уравнение до ума:

– искомое уравнение.

Ответ:

Здесь можно выполнить частичную проверку. Во-первых,координаты точкидолжны удовлетворять каждому уравнению:

– верное равенство.

– верное равенство.

И, во-вторых,векторы нормали должны быть

ортогональны. Это элементарно проверяется с помощью скалярного произведения:

, что и требовалось проверить.

Как вариант, вместо нормальных векторов можно использовать

направляющие векторы прямых.

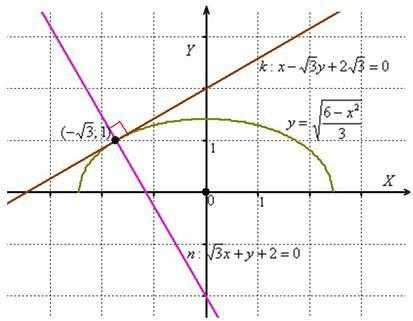
! Данная проверка оказывается бесполезной, если неверно найдена производнаяи/или производная в точке. Это «слабое звено» задания – будьте предельно внимательны!

Чертежа по условию не требовалось, но полноты картины ради:

Забавно, но фактически получилась и полная проверка, поскольку чертёж выполнен достаточно точно =) Кстати, функция

задаёт верхнюю дугуэллипса. Следующая задача для самостоятельного решения:

Пример 2 Составить уравнения касательной и нормали к графику функции

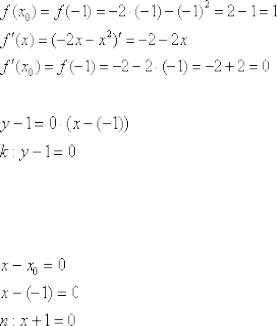
В данном случае

Казалось бы, расчёты пустяковые, а в знаках запутаться более чем реально:

Таким образом:

Поскольку касательная параллельна оси (Случай №1), то нормаль, проходящая через ту же точку, будет параллельна оси ординат:

Чертёж – это, конечно же, дополнительные хлопоты, но зато добротная проверка аналитического решения:

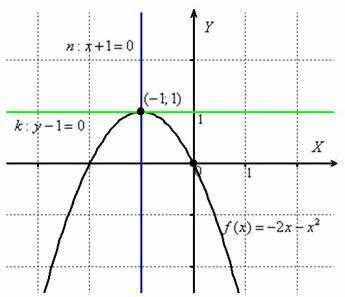
Ответ: ,

В школьном курсе математики распространено упрощённое определение касательной, которое формулируется примерно так:

«Касательная к графику функции – это прямая, имеющая с данным графиком единственную общую точку». Как видите, в общем случае это утверждение некорректно. Согласно геометрическому смыслу производной, касательной является именно зелёная, а не синяя прямая.

Следующий пример посвящён тому же Случаю №1, когда :Пример 4

Написать уравнение касательной и нормали к кривой в точке.

Краткое решение и ответ в конце урока

существует общая вертикальная касательная:

Ну, и очевидно, что нормалью является ось абсцисс. Формально по формуле:

Для лучшего понимания задачи приведу чертёж:

Ответ:

Я рад, что вы не ушли бороздить просторы Интернета, потому что всё самое интересное только начинается! Чтобы осилить материал следующего параграфа, нужно уметь находить производную от неявно заданной функции:

studfiles.net

Как найти уравнение касательной и уравнение нормали, если функция задана неявно?

Формулы касательной и нормали остаются прежними, но меняется техника решения:

Пример 6

Найти уравнения касательной и нормали к кривой в точке.

Решение: судя по уравнению, этокакая-толиния 3-го порядка, какая именно – нас сейчас совершенно не интересует.

В уравнении присутствует зловред , и поэтому перспектива выразить функция вявном виде выглядит весьма туманной.

Но этого и не требуется! Есть куда более остроумное решение. Уравнение касательной составим по той же формуле

.

Из условия известны значения , кстати, не помешает убедиться, что они действительно удовлетворяют предложенному уравнению:

Получено верное равенство, значит, с точкой всё в порядке.

Осталось вычислить . Сначала по стандартной схеме найдёмпроизводную от функции, заданной неявно:

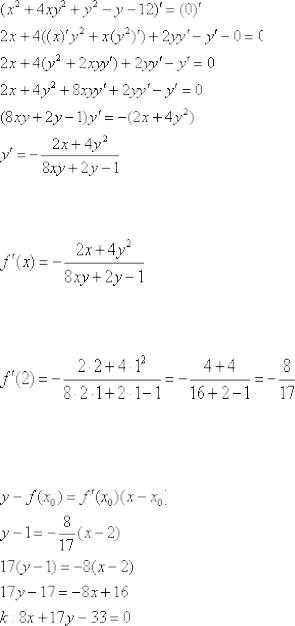
Перепишем результат с более подходящим для нашей задачи обозначением:

На 2-мшаге в найденное выражение производной подставим:

Вот так-то!

Осталось аккуратно разобраться с уравнением:

Составим уравнение нормали:

Ответ:

Готово! А поначалу представлялось всё непросто. Хотя производная здесь, конечно, – место уязвимое. Миниатюра для самостоятельного решения:

Пример 7

Найти уравнение нормали к линии в точке

Хватит уже вымучивать касательную =)

В данном случае легко выяснить, что это окружность центром в точкерадиусаи даже выразить нужную функцию. Но зачем?! Ведь найти производную отнеявно

заданной функции на порядок легче! Она тут чуть ли не самая примитивная.

Краткое решение и ответ в конце урока.

Как найти уравнение касательной и уравнение нормали, если функция задана параметрически?

Ещё проще. Но для этого нужно потренироваться в нахождении

производной от параметрически заданной функции. А так – почти халява:

Пример 8

Составить уравнения касательной и нормали к циклоиде , проведенные в точке, для которой.

Чертёж циклоиды можно найти на странице S и V, если линия задана параметрически (так получилось, что эта статья была создана раньше). Там даже изображена точка касания.

Решение: абсцисса и ордината точки касания рассчитываются непосредственно из параметрических уравнений кривой:

Найдём 1-уюпроизводную от параметрически заданной функции:

И вычислим её значение при :

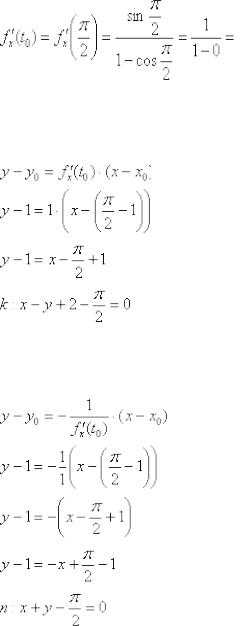
Уравнение касательной составим по обычной формуле с поправкой на несколько другие обозначения:

Уравнение нормали:

Ответ:В заключение предлагаю познакомиться с ещё одной интересной

линией: Пример 9

Составить уравнение нормали к полукубической параболе , проведенной в точке, для которой.

Это пример для самостоятельного решения. Напоминаю, что графики параметрически заданных функций можно построить, например, с помощью моего расчётного геометрического макета.

Ну а наш урок подошёл к концу, и я надеюсь, что изложенный материал прошёл для вас не по касательной, а нормально =)

Спасибо за внимание и успехов!

Решения и ответы:

Пример 2: Решение: уравнение касательной составим по формуле:

В данном случае:

Таким образом:

Уравнение нормали составим по формуле :

Ответ:

Пример 4: Решение: уравнение касательной составим по формуле:

В данной задаче:

Таким образом:

В точке касательная параллельна оси, поэтому соответствующее уравнение нормали:

Ответ:

Пример 7: Решение: в данной задаче:. Найдём производную:

Или:

Подставим в выражение производной :

Искомое уравнение нормали:

Ответ:Пример 9:Решение: в данном случае:

Найдём производную и вычислим её значение при :

Уравнение нормали:

Ответ:

studfiles.net

Как составить уравнения касательной и нормали к графику функции? ≪ ∀ x, y, z

.

при и .
при .
при .

Касательная к графику функции в точке с абсциссой задается уравнением

В нашем случае , и , следовательно , то есть .

Можно было рассуждать проще. Касательная проходит через точку . В точке производная , касательная горизонтальная и задается уравнением .

Найдем уравнение нормали к касательной, заданной уравнением , в точке .

Для этого воспользуемся следующими двумя утверждениями.

1. Пусть прямая задана уравнением (это общее уравнение прямой)

.Тогда вектор является направляющим вектором ее нормали.

2. Прямая с направляющим вектором , проходящая через точку , имеет уравнение (каноническое уравнение прямой)

.В нашем случае общее уравнение касательной и вектор является направляющим вектором ее нормали. Следовательно, уравнение нормалито есть , или . Как и ожидалось, нормаль есть вертикальная прямая, проходящая через точку .

Возможно, предполагается более простой путь. А именно, с помощью следующего утверждения.

Нормаль к графику функции в точке с абсциссой задается уравнением

,и уравнением.

forany.xyz