Cos 3 2 пи: Mathway | Популярные задачи

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значение tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение
sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Мэтуэй | Популярные задачи

92
1 Найти точное значение грех(30)
2 Найти точное значение грех(45)
3 Найти точное значение грех(30 градусов)
4 Найти точное значение грех(60 градусов)
5 Найти точное значение загар (30 градусов)
6 Найти точное значение угловой синус(-1)
7		 Найти точное значение грех(пи/6)
8 Найти точное значение cos(pi/4)
9 Найти точное значение грех(45 градусов)
10 Найти точное значение грех(пи/3)
11 Найти точное значение арктан(-1)
12 Найти точное значение cos(45 градусов)
13 Найти точное значение cos(30 градусов)
14 Найти точное значение желтовато-коричневый(60)
15 Найти точное значение csc(45 градусов)
16 Найти точное значение загар (60 градусов)
17 Найти точное значение сек(30 градусов)
18 Найти точное значение cos(60 градусов)
19 Найти точное значение cos(150)
20 Найти точное значение грех(60)
21 Найти точное значение cos(pi/2)
22 Найти точное значение загар (45 градусов)
23 Найти точное значение arctan(- квадратный корень из 3)
24 Найти точное значение csc(60 градусов)
25 Найти точное значение сек(45 градусов)
26 Найти точное значение csc(30 градусов)
27 Найти точное значение грех(0)
28 Найти точное значение грех(120)
29 Найти точное значение соз(90)
30 Преобразовать из радианов в градусы пи/3
31 Найти точное значение желтовато-коричневый(30)
32
35 Преобразовать из радианов в градусы пи/6
36 Найти точное значение детская кроватка(30 градусов)
37 Найти точное значение арккос(-1)
38 Найти точное значение арктан(0)
39 Найти точное значение детская кроватка(60 градусов)
40 Преобразование градусов в радианы 30
41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3)
43 Найти точное значение sin((3pi)/4)
44 Найти точное значение тан(пи/2)
45 Найти точное значение грех(300)
46 Найти точное значение соз(30)
47 Найти точное значение соз(60)
48 Найти точное значение соз(0)
49 Найти точное значение соз(135)
50 Найти точное значение cos((5pi)/3)
51 Найти точное значение cos(210)
52 Найти точное значение сек(60 градусов)
53 Найти точное значение грех(300 градусов)
54 Преобразование градусов в радианы 135
55 Преобразование градусов в радианы 150
56 Преобразовать из радианов в градусы (5 дюймов)/6
57 Преобразовать из радианов в градусы (5 дюймов)/3
58 Преобразование градусов в радианы 89 градусов
59 Преобразование градусов в радианы 60
60 Найти точное значение грех(135 градусов)
61 Найти точное значение грех(150)
62 Найти точное значение грех(240 градусов)
63 Найти точное значение детская кроватка(45 градусов)
64 Преобразовать из радианов в градусы (5 дюймов)/4
65 Найти точное значение грех(225)
66 Найти точное значение грех(240)
67 Найти точное значение cos(150 градусов)
68 Найти точное значение желтовато-коричневый(45)
69 Оценить грех(30 градусов)
70 Найти точное значение сек(0)
71 Найти точное значение cos((5pi)/6)
72 Найти точное значение КСК(30)
73 Найти точное значение arcsin(( квадратный корень из 2)/2)
74 Найти точное значение загар((5pi)/3)
75 Найти точное значение желтовато-коричневый(0)
76 Оценить грех(60 градусов)
77 Найти точное значение arctan(-( квадратный корень из 3)/3)
78 Преобразовать из радианов в градусы (3 пи)/4 
79 Найти точное значение sin((7pi)/4)
80 Найти точное значение угловой синус(-1/2)
81 Найти точное значение sin((4pi)/3)
82 Найти точное значение КСК(45)
83 Упростить арктан(квадратный корень из 3)
84 Найти точное значение грех(135)
85 Найти точное значение грех(105)
86 Найти точное значение грех(150 градусов)
87 Найти точное значение sin((2pi)/3)
88 Найти точное значение загар((2pi)/3)
89 Преобразовать из радианов в градусы пи/4
90 Найти точное значение грех(пи/2)
91 Найти точное значение сек(45)
92 Найти точное значение cos((5pi)/4)
93 Найти точное значение cos((7pi)/6)
94 Найти точное значение угловой синус(0)
95 Найти точное значение грех(120 градусов)
96 Найти точное значение желтовато-коричневый ((7pi)/6)
97 Найти точное значение соз(270)
98 Найти точное значение sin((7pi)/6)
99 Найти точное значение arcsin(-( квадратный корень из 2)/2)
100 Преобразование градусов в радианы 88 градусов

Предварительное вычисление алгебры — Решение $5+2\cos(3\theta-\frac{\pi}{4})=6$ с $-\pi\leq\theta

Уже показано много решений, которые прекрасно работают.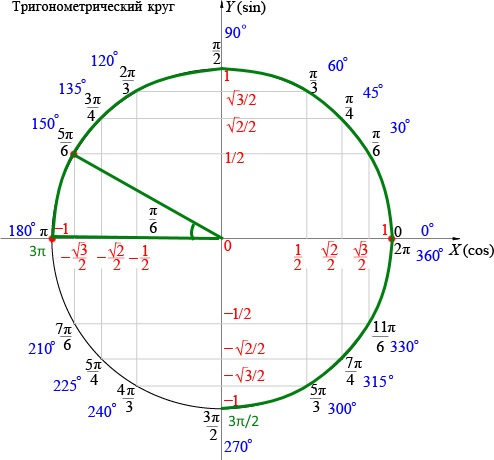 Поэтому я попробую что-то немного другое, используя единичный круг для визуализации.

Чтобы решить $\cos(\alpha) = \frac12$ с помощью единичной окружности, мы проводим вертикальную линию в точке $x = \frac12$ и пересекаем окружность в двух точках:

Каждая точка находится в конкретный угол. Как обычно, существует бесконечно много углов для каждой точки в зависимости от того, движетесь ли вы против часовой стрелки или по часовой стрелке и сколько раз вы проходите по кругу, прежде чем остановиться, но репрезентативные углы $$ \alpha_A = \frac\pi3, \quad \alpha_B = -\frac\pi3. $$

Но, конечно, мы не пытаемся решить $\cos(\alpha) = \frac12$; нам нужно решить $\cos\left(3\theta — \frac\pi4\right) = \frac12$. Но давайте просто сконцентрируемся на части $3\theta$, а $\frac\pi4$ займемся позже.

Если бы мы пытались найти $\phi$ в $\cos(3\phi) = \frac12$, одно решение — просто взять $\frac13$ одного из решений $\cos(\alpha) = \frac12$. То есть вместо определения точки $A$ под углом $\alpha_A = \frac\pi3,$ мы отождествляем точку $A_1$ под углом $\phi_{A1} = \frac13 \alpha_A = \frac13\left(\frac\pi3\right) = \frac\pi9,$ как показано ниже.

Итак, $\cos(3\phi_{A1}) = \cos\left(3\times\frac\pi9\right) = \cos\left(\frac\pi3\right) = \frac12$ по желанию.

Но мы должны помнить, что $A$ также может быть достигнута такими углами, как $\frac\pi3 + 2\pi,$ $\frac\pi3 — 2\pi,$ и так далее. И обратите внимание, что вам нужно всего лишь добавить $\frac{2\pi}3$ к $\phi$, чтобы добавить от $2\pi$ до $3\phi.$ То есть

\begin{align} 3\left(\frac\pi9 + \frac{2\pi}3\right) &= \frac\pi3 + 2\pi, \\ 3\влево(\фракция\pi9- \frac{2\pi}3\right) &= \frac\pi3 — 2\pi. \\ \end{align}

Под углами $\frac\pi9 + \frac{2\pi}3$ и $\frac\pi9 — \frac{2\pi}3$ у нас есть еще две точки, $A_2$ и $A_3$:

Мы также можем попробовать такие углы, как $\frac\pi9 + \frac{4\pi}3$ и $\frac\pi9 — \frac{4\pi}3$, так как $3\times\frac{4\pi}3 = 4\pi,$ но обратите внимание, что $\frac\pi9 + \frac{4\pi}3$ определяет ту же точку, что и $\frac\pi9 — \frac{2\pi}3$, так что это ничего не добавит к диаграмме.

Так же, как мы сделали для точки $A$, мы можем сделать для точки $B$: одно решение для $\cos(3\phi) = \frac12$ $\phi_{B1} = \frac13 \alpha_B = \frac13\left(-\frac\pi3\right) = -\frac\pi9,$ поставив точку $B_1$ на рисунке ниже; и снова мы получаем решения, добавляя или вычитая $\frac{2\pi}3,$ дающие точки $B_2$ и $B_3. $

Итак, это шесть точек на единичной окружности, углы которых решают $\cos(3\phi) = \frac12.$ Есть и другие углы, которые решают уравнение, но каждый из них приземляется в одной из этих шести точек, поэтому эти шесть точек представляют все решения. Давайте покажем их все вместе:

Сейчас самое время вспомнить, что на самом деле мы пытаемся решить $\cos\left(3\theta — \frac\pi4\right) = \frac12$ и не $\cos(3\phi) = \frac12$. Полезно переписать исходное уравнение в виде $$\cos\left(3\left(\theta — \frac\pi{12}\right)\right) = \frac12,$$ потому что это говорит нам о том, что для каждого решения для $\theta$ нам просто нужно добавить $\frac\pi{12}$ на одно из решений для $\phi$ (чтобы вернуться к $\phi$ после вычитания $\frac\pi{12}$). То есть все решения поворачиваются против часовой стрелки на угол $\frac\pi{12}$.

Это все точки, которые можно определить по углу $\theta$, где $\cos\left(3\theta — \frac\pi4\right) = \frac12$. Нам просто нужно определить углы для каждого из них, такие что $-\pi \leq \theta < \pi. $ Мы можем восстановить углы, следуя шагам построения этих шести точек, то есть отождествляя углы $\frac\pi9$ и $\frac\pi9$, получая из каждого из них три угла (исходный угол и угол плюс-минус $\frac{2\pi}3$), и добавление $\frac\pi{12}$ к каждому углу:

\begin{align} \theta_{A1} &= \frac\pi9 + \frac\pi{12} & \theta_{B1} &= -\frac\pi9 + \frac\pi{12} \\ \theta_{A2} &= \frac\pi9 + \frac{2\pi}3 + \frac\pi{12} & \theta_{B2} &= -\frac\pi9 + \frac{2\pi}3 + \frac\pi{12} \\ \theta_{A3} &= \frac\pi9 — \frac{2\pi}3 + \frac\pi{12} & \theta_{B3} &= -\frac\pi9 — \frac{2\pi}3 + \frac\pi{12}. \end{align}

Теперь (чтобы сделать ответ более кратким) мы просто хотим выяснить, что представляет собой каждый из этих углов в более простых терминах, найдя общий знаменатель для всех дробей и объединив их. Например, $$\frac\pi9+ \frac\pi{12} = \frac{7\pi}{36}.$$ К счастью, оказывается, что все углы в списке оказываются между $-\pi$ и $\pi,$, но если бы некоторые из них вышли за пределы этого диапазона, нам нужно было бы просто добавить или вычесть кратные $2\pi$, чтобы вернуть их в желаемый диапазон.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *