Площадь прямоугольника и квадрата – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
Площадь – часть плоскости, заключенной внутри замкнутой геометрической фигуры. Площадь фигуры выражается положительным числом. За единицу площади принимается площадь квадрата со стороной, равной единице длины.
Две фигуры называют равными, если одну из них можно так наложить на другую, что эти фигуры совпадут. Площади равных фигур равны.
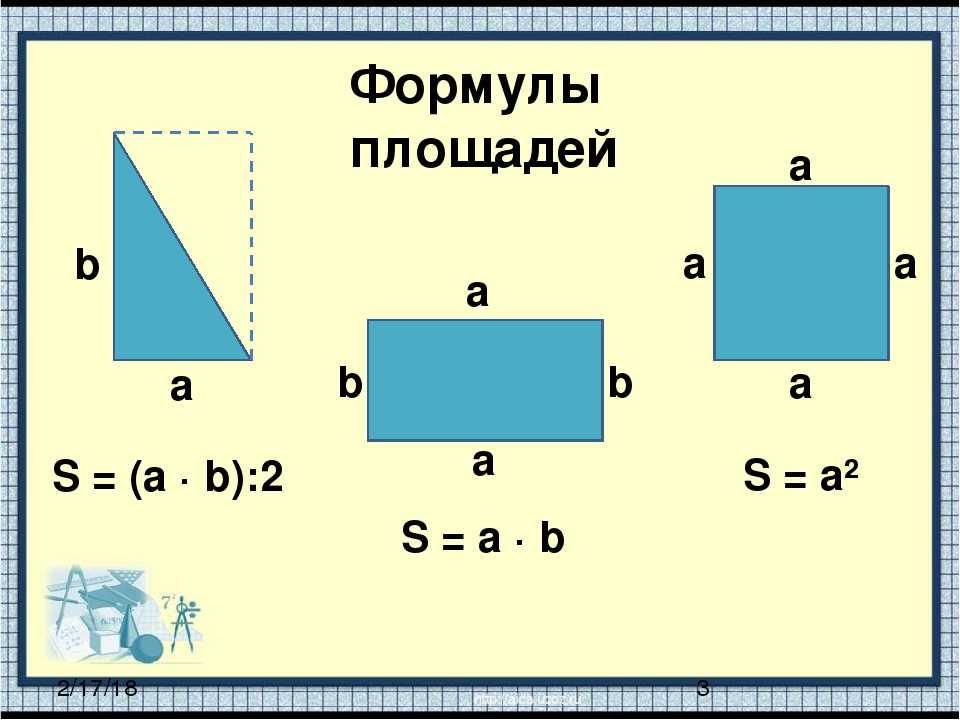
Формулы площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон: \(S=a\times b\).
- Площадь прямоугольника равна половине произведения его диагоналей на синус угла между ними: \(S=\frac{1}{2}d_1d_2sin\alpha=\frac{1}{2}d^2sin\alpha\).
 2\).
2\).
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Сообщить об ошибке
Обязательные
Математическая грамотность
Грамотность чтения
История Казахстана
Предметы по профилю
Биология
Химия
Английский язык
Французский язык
География
Немецкий язык
Информатика
Основы права
Русская литература
Математика
Физика
Русский язык
Всемирная история
Укажите предмет *
Скопируйте и вставьте вопрос задания *
Опишите подробнее найденную ошибку в задании *
Прикрепите скриншот
Объем файла не должен превышать 1МБ
Казахский
Русский
Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market
2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами
Площадь. Формулы площади прямоугольника и квадрата
В этом уроке рассмотрим такие понятия как площадь фигуры и формулы нахождения площади прямоугольника и квадрата. Давайте начертим квадрат со стороной 1 см.
Соответственно можем сделать вывод, что если какую – либо фигуру можно разбить на несколько таких квадратов, например, р квадратов, то ее площадь равна р см2.
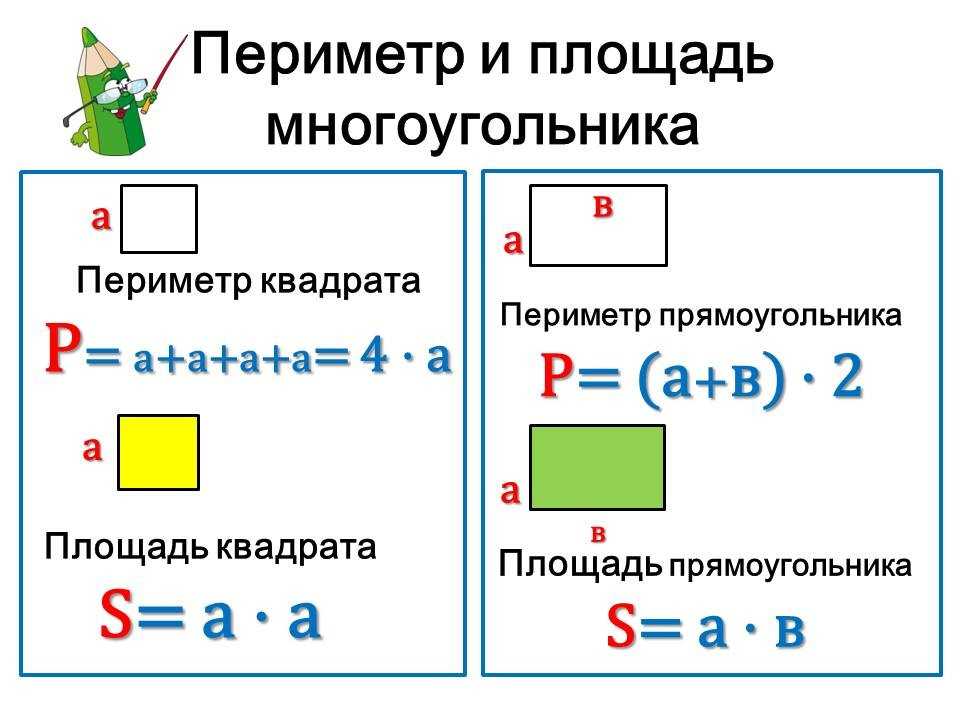
Значит площадь такого прямоугольника равна 20 см2. Таким образом, получили правило: Чтобы найти площадь прямоугольника, надо умножить его длину на ширину. Это правило можно записать в виде формулы. Для этого обозначим площадь прямоугольника буквой S, кстати площади всех фигур принято обозначать этой буквой, длину прямоугольника буквой a, ширину – буквой b. Получаем формулу площади прямоугольника: S равно а умножить на b (S = аb). Теперь давайте рассмотрим следующую фигуру – квадрат, это тоже прямоугольник, но у него все стороны равны. Так как квадрат является прямоугольником, то воспользуемся формулой площади прямоугольника (S = аb). Начертим квадрат со стороной 5 см и найдем его площадь.
Давайте рассмотрим две фигуры:
Это легко проверить, если выполнить наложение, т.е. одну фигуру наложить на другую. Если они полностью совместятся или совпадут, то они равные. Таким образом, сформулируем правило: Две фигуры называются равными, если они совпадут при наложении. А как вы думаете, равны ли их площади и периметры? Конечно, да! Площади равных фигур равны. Например, прямоугольник со сторонами 16 и 4 см имеет площадь 64 см2 и квадрат со стороной 8 см тоже имеет площадь 64 см2, но эти фигуры не равны между собой. Давайте построим прямоугольник ABCD со сторонами 7 см и 4 см.
Если сложить все эти части, получим 8 + 16 + 4 = 28. Т.е. сумма площадей всех частей также равна 28 см2. Итак, можно сделать вывод, что площадь всей фигуры равна сумме площадей ее частей. Таким образом, на этом уроке мы рассмотрели такие понятия как площадь фигуры и формулы нахождения площади прямоугольника и квадрата. |
формул площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.

Онлайн-калькуляторы. Площадь геометрических фигур
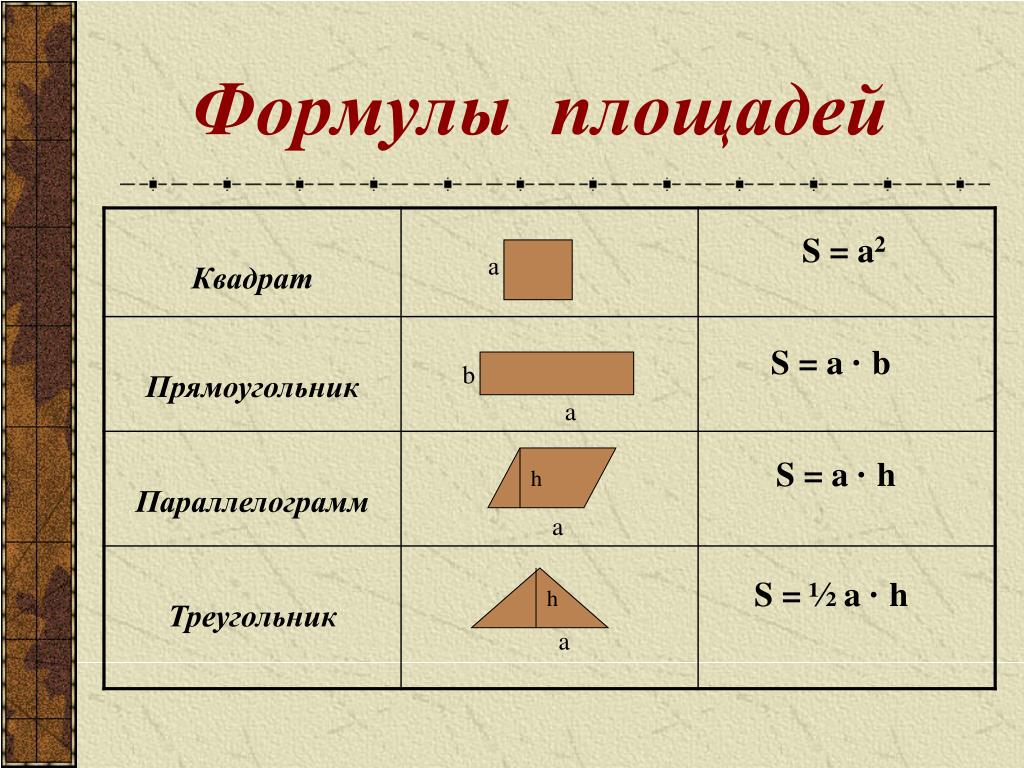
Формулы площади треугольника
Площадь треугольника, если известны основание и высота
Площадь треугольника равна половине произведения основания на высоту.
А = 1 а · ч 2 Площадь треугольника, если известны длины всех трех его сторон
Формула Герона
А = √s(s-a)(s-b)(s-c)
Площадь треугольника, если известны две стороны и угол между ними
Площадь треугольника равна половине произведения двух сторон и синуса угла между этими сторонами.
A = 1 a · b · sin γ 2 A = 1 a · c · sin β 2
29А = 1 б · в · sin α 2 4
Площадь треугольника, если известны три стороны и радиус описанной окружности
А = а · б · с 4R Площадь треугольника, если известны полупериметр и внутренний радиус
Площадь треугольника равна полупериметру, умноженному на внутренний радиус.

где А — площадь треугольника,А = с · г
a, b, c — длины сторон BC,AC,AB соответственно,
h — высота, длина высоты,
α, β, γ — углы,
r — длина по радиусу,
R — длина окружности,s = a + b + c — полупериметр, или половина периметра треугольника. 2
Вы можете использовать онлайн калькулятор для расчета площади треугольника
Площадь квадрата формулы
Площадь квадрата, если известна длина стороны
Площадь квадрата равна квадрату стороны.
А = а 2
Площадь квадрата, если известна длина диагонали
Площадь квадрата равна половине диагонали в квадрате.
9А = 1 d 2 2 03 где А — площадь квадрата,
а — длина стороны,
Вы можете использовать онлайн-калькулятор для расчета площади квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух сторон (высоты и ширины)
A = a · b
где А — площадь прямоугольника,
a, b — длины сторон (высота и ширина прямоугольника).
Вы можете использовать онлайн-калькулятор для расчета площади прямоугольника.
Формулы площади параллелограмма
Площадь параллелограмма, если известны сторона и высота
Площадь параллелограмма равна произведению стороны на высоту.
А = а · ч
Площадь параллелограмма, если известны две стороны и угол между ними
Площадь параллелограмма равна произведению двух сторон и синусу угла между этими сторонами.
А = а · б · sin α
где А — площадь параллелограмма,
а, б — длины сторон,
h — высота, длина высоты,
α — мера угла между сторонами.
Вы можете использовать онлайн-калькулятор для расчета площади параллелограмма.
Формулы площади ромба
Площадь ромба, если известны сторона и высота
Площадь ромба равна произведению стороны на высоту.
А = а · ч
Площадь ромба, если известны длина стороны и угол между ними
Площадь ромба равна произведению квадрата стороны и синуса угла между сторонами ромба.
А = а 2 · sin α
Площадь ромба, если известны длины его диагоналей
Площадь ромба равна половине произведения длин его диагоналей.
где А — площадь ромба,A = 1 D 1 · D 2 2
а — длина стороны,
h — высота, длина высоты,
α — мера угла между сторонами ромба,
d 1 , d 2 — длины диагоналей.
Вы можете использовать онлайн-калькулятор для вычисления площади ромба.
Area of a trapezium formulas
Heron’s formula for a trapezium
A = a + b √(s-a)(s-b)(s-a-c)(s-a-d) |а — б| Площадь трапеции, если известны длина двух оснований и высота
Площадь трапеции равна произведению высоты на полусумму двух оснований
где А — площадь трапеции,А = 1 (a + b) · ч 2
a, b — длина 2-х оснований, т. е. параллельных сторон,
c, d — длина катетов (боковых сторон),s = a + b + c + d — полупериметр, или половина периметра трапеции. 
2
Вы можете использовать онлайн-калькулятор для расчета площади трапеции.
Формулы площади четырехугольника
Площадь четырехугольника, зная длину его диагоналей и угол между ними
Площадь четырехугольника равна произведению его диагоналей и синуса угла между ними диагонали
A = 1 d 1 d 2 sin α 2
где А — площадь четырехугольника,
d 1 , d 2 — длина диагоналей,
α — угол между диагоналями.Площадь четырехугольника, если известны длина его периметра и радиус внутри
Площадь четырехугольника равна периметру, умноженному на радиус
A = s · r
Площадь четырехугольника, если известны длины его сторон и величина противоположных углов
A = √(s — a)(s — b)(s — c)(s — d) — abcd cos 2 θ
где А — площадь четырехугольника,
A, B, C, D — Длина сторон,
15S = A + B + C + D — полупериметр Quadrangle, 2 2 2 2 2 2 α + β — половина суммы двух противоположных углов четырехугольника. 
2
Формулы площади круга
Площадь круга, если известен его радиус
Площадь круга равна произведению квадрата радиуса на число пи.
А = πr 2
Площадь круга, если нам известен его диаметр
Площадь круга равна четверти произведения квадрата диаметра и пи.
29 где А — площадь круга,А = 1 π d 2 4 4
r — длина радиуса,
d — длина диаметра.
Вы можете использовать онлайн-калькулятор для расчета площади круга.
Площадь эллипса формулы
Площадь эллипса равна произведению длин большой и малой полуосей на число пи.
А = π · а · б
где А — площадь эллипса,
а — длина большой полуоси,
б — длина малой полуоси,
Вы можете использовать онлайн-калькулятор для вычисления площади эллипса.
Формулы геометрии Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Круг, диск, сегмент, сектор. Формулы и свойства Эллипс. Формулы и свойства эллипса Цилиндр. Формулы и свойства цилиндра Конус. Формулы, характеристики и свойства конуса Область. Формулы площади Периметр. Формулы периметра Объем. Формулы объема Формулы площади поверхности
Все таблицы и формулы
Площадь квадрата | Определение, примеры и формулы
Площадь квадрата — важное понятие в геометрии. Это позволяет нам лучше понять свойства квадрата, а также открывает широкий спектр приложений и задач, связанных с квадратами. В прошлом мы узнали, что квадраты — это четырехугольники с равными сторонами, поэтому пришло время установить правила нахождения площади квадрата.
Существуют различные способы вычисления площади квадрата, например: 1) подсчет одноэлементных квадратов, составляющих больший квадрат, 2) использование сторон квадрата и 3) использование диагоналей квадрата. В этой статье рассматриваются все эти методы и разбираются формулы для каждого из них.
В этой статье рассматриваются все эти методы и разбираются формулы для каждого из них.
В этом обсуждении рассматриваются основы квадрата и его площади, важные измерения и формулы, которые мы можем использовать для нахождения его площади, а также текстовые задачи на площади квадратов. К концу этого обсуждения мы хотим, чтобы вы чувствовали себя уверенно, имея дело с площадью квадрата.
Какова площадь квадрата?
Площадь квадрата представляет собой площадь, покрываемую данной поверхностью, заключенной в квадратную область. Напомним, что квадрат — это четырехсторонняя фигура с четырьмя одинаковыми сторонами. Квадраты также имеют параллельные противоположные стороны и углы, образующие прямоугольные треугольники. Площадь квадрата определяется как произведение его длины и ширины и измеряется в единицах, возведенных в квадрат.
Изображения ниже являются примерами поверхностей квадратной формы. Мера области, покрывающей эти поверхности, представляет их площади.
Для каждой поверхности мы можем определить ее площадь, подсчитав меньшие квадраты внутри, размеры квадрата или даже его диагонали — в зависимости от того, что задано. Это приводит к широкому кругу приложений и задач, которые мы наконец можем решить, узнав о площади квадрата.
Площадь квадрата
92. Более быстрый способ подсчета квадратов — умножение количества квадратов в каждой строке и в каждом столбце. Расширив это, чтобы найти площадь квадрата, просто умножьте размеры квадрата. Это приводит к более быстрому способу нахождения площадей квадратов по длинам их сторон.Формула площади квадрата с использованием его стороны
Теперь, когда мы разобрались с идеей площади квадрата, давайте установим для нее общую формулу. Поскольку квадраты имеют четыре равные стороны, длина и ширина квадрата всегда будут равны. Это означает, что при заданной длине стороны квадрата его площадь равна произведению длины стороны на себя или квадрату длины стороны. 92\end{align}
Формулу легко применять, поэтому попробуйте ее и поработайте над задачами, которые мы подготовили для вас, чтобы привыкнуть к процессу.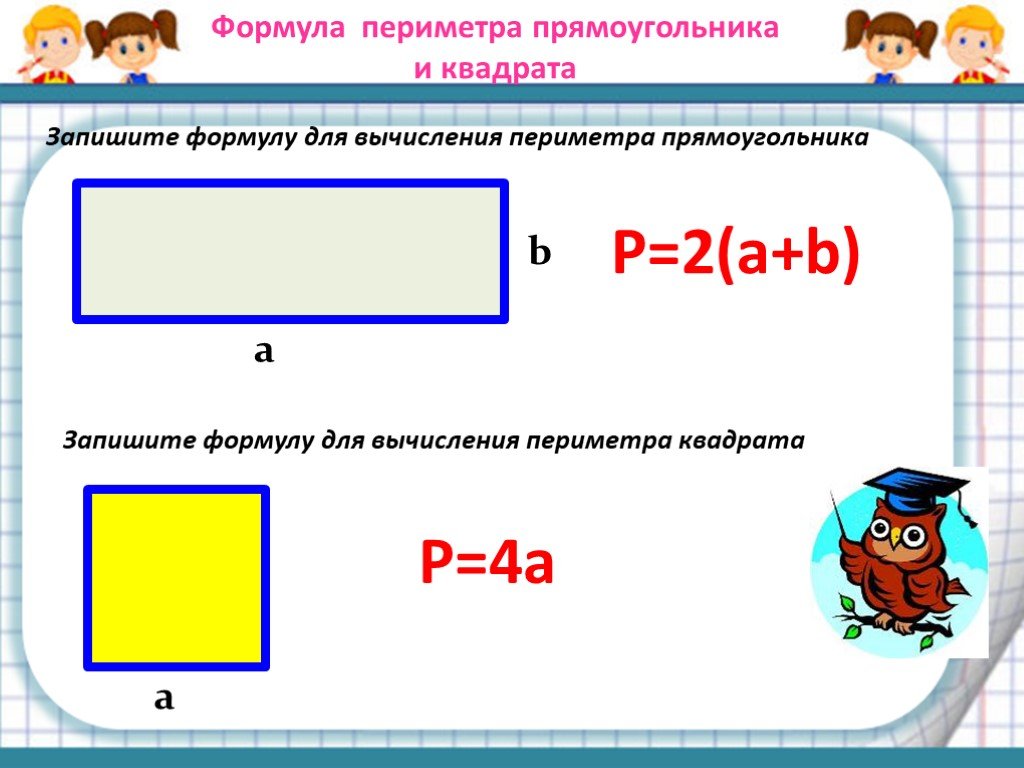 Давайте теперь посмотрим, что произойдет, если вместо этого нам дана диагональ квадрата. Это требует понимания радикальных чисел и теоремы Пифагора, поэтому, если это еще не обсуждалось, перейдите к следующему разделу, чтобы попробовать разные примеры!
Давайте теперь посмотрим, что произойдет, если вместо этого нам дана диагональ квадрата. Это требует понимания радикальных чисел и теоремы Пифагора, поэтому, если это еще не обсуждалось, перейдите к следующему разделу, чтобы попробовать разные примеры!
Формула площади квадрата с использованием его диагонали
92}\конец{выровнено}Это просто означает, что мы можем найти площадь квадрата, возведя длину его диагонали в квадрат и разделив результат на 2. В следующем разделе мы узнаем, как решить, какой подход будет лучше, в зависимости от заданных размеров и фигур. .
Как найти площадь квадрата?
Подводя итог тому, что мы узнали, мы можем найти площадь квадрата тремя способами:
- Подсчитав единичные квадраты, составляющие больший квадрат, а затем умножив количество квадратов на 1 квадратную единицу. 92 .
Задача 4
Теперь давайте посмотрим, что произойдет, если вместо этого нам будет задан периметр квадрата. Предположим, что квадратное поле имеет периметр 60 ярдов.


 2\).
2\).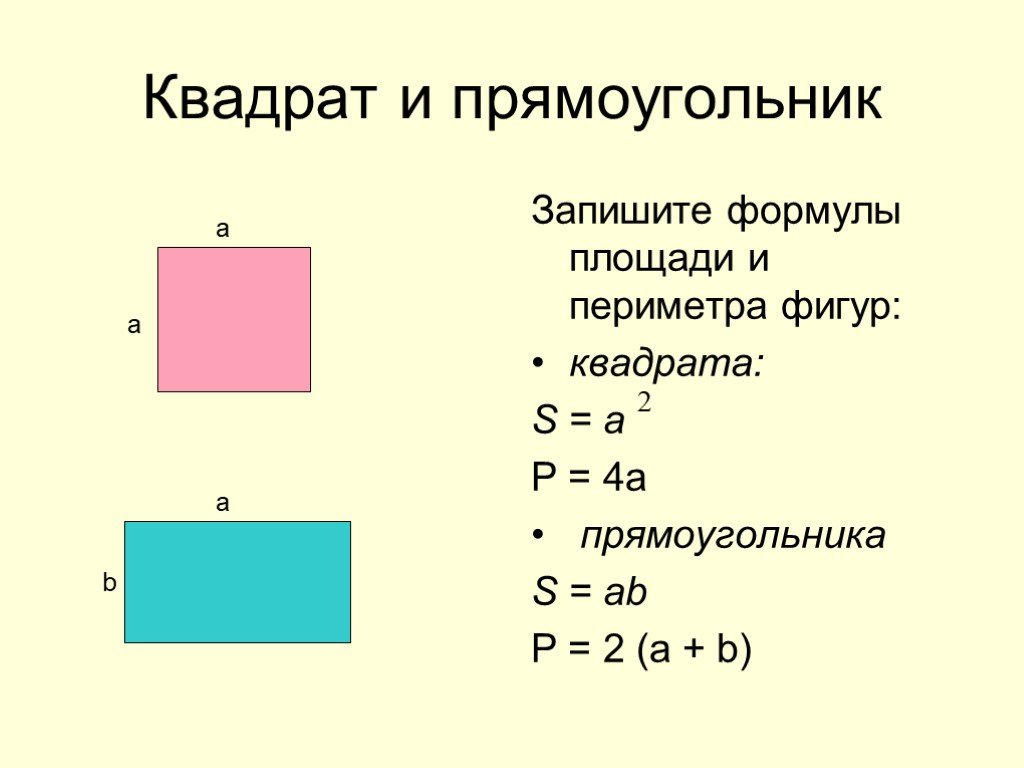
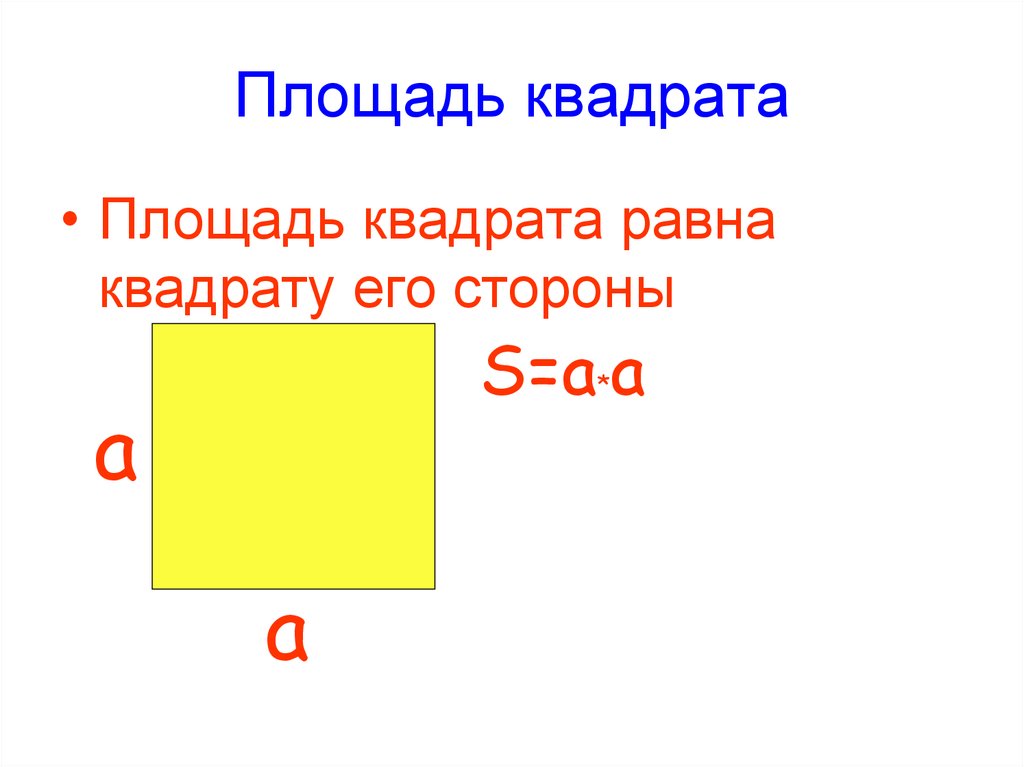 Но в случае квадрата b будет равно а, т.е. площадь равна а умножить на а, или принято записывать а в квадрате, значит: (S = а2). Получили еще одну формулу – формулу площади квадрата.
Но в случае квадрата b будет равно а, т.е. площадь равна а умножить на а, или принято записывать а в квадрате, значит: (S = а2). Получили еще одну формулу – формулу площади квадрата.  Периметры равных фигур равны. Но не всегда выполняется наоборот.
Периметры равных фигур равны. Но не всегда выполняется наоборот.