| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.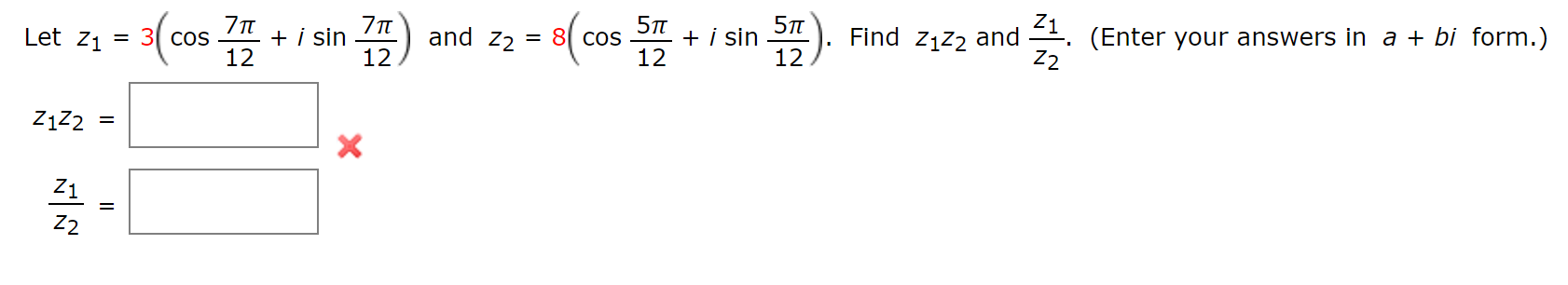 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | cos(150 град. ) | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Как изобразить стандартное положение на графике? – Обзоры Вики
com/embed/Ndnsds-E_Lc» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Точно так же, какой луч является калькулятором на стороне терминала? Исходное положение луча называется начальной стороной и конечное положение луча называется его конечной стороной. Если разница между двумя углами кратна 360 градусам, то эти два угла будут сотерминальными друг другу.
Что такое стандартная позиция? Определение стандартного положения
: положение угла с вершиной в начале прямоугольной системы координат и его начальная сторона совпадает с положительной осью абсцисс.
Что является опорным углом для угла? Что понимается под опорным углом? В математике опорный угол определяется как острый угол и он измеряет менее 90 градусов. Это всегда наименьший угол, и он составляет конечную сторону угла с осью x.
Во-вторых, в каком квадранте лежат 470 градусов? Примеры тригонометрии
Угол находится в третий квадрант.
Каково стандартное положение 60 градусов?
Угол 60 градусов в стандартном положении имел бы начальная сторона все еще находится на положительной оси x (указывая на 3). Угол, равный 60 градусам, можно получить, повернув сторону терминала против часовой стрелки от 3 до 1 на часах, как показано ниже.
тогда какой опорный угол для 390? С 30° находится в первом квадранте, опорный угол равен 30°.
540 градусов — это квадрант? Угол между вторым и третьим квадрантом.
Как мне узнать, есть ли у меня SOH CAH TOA?
SOHCAHTOA — это мнемоническое устройство, помогающее запомнить, какое соотношение соответствует какой функции.
- SOH = Синус противоположен гипотенузе.
- CAH = косинус смежен с гипотенузой.
- TOA = Касательная противоположна соседнему.
Что такое стандартная должность? Углы измеряются в градусах. Один полный оборот измеряется как 360°. … Угол с его начальной стороной на оси x считается стандартным.
Какой угол 45 градусов?
Угол 45 градусов — это ровно половина угла в 90 градусов, образованного двумя лучами. Это острый угол, и два угла, равные 45 градусам, образуют прямой угол золото имеет угол 90 градусов. Мы знаем, что угол образуется, когда два луча встречаются в вершине.
Сколько стоит угол 60 градусов? Угол 60 градусов является острым углом, потому что он меньше 90 градусов. 60° в радианах π / 3 а мера каждого угла равностороннего треугольника равна 60°. Поэтому его также называют треугольником с углом 60 градусов.
Каково точное значение cos390?
Значение cos 390 градусов в десятичном виде равно 0.866025403. . .. Cos 390 градусов также можно выразить с помощью эквивалента заданного угла (390 градусов) в радианах (6.80678 . . .) ⇒ 390 градусов = 390° × (π/180°) рад = 13π/6 или 6.8067 . . . ∴ cos 390 ° = cos (6.8067) = √ 3/2 или 0.8660254. . .
Что такое опорный угол 300?
360 — 300 = 60 градусов. Базовый угол для 300 составляет 60 градусов.
Как найти точное значение sin 390? Sin 390 градусов — это значение тригонометрической функции синуса для угла, равного 390 градусам. Значение sin 390° равно 1/2 или 0.5.
1080 это квадрантный угол? Угол между четвертым и первым квадрантом.
Как найти квадранты?
Если и x, и y положительны, то точка лежит в первый квадрант. Если x отрицательно, а y положительно, то точка лежит во втором квадранте. Если и x, и y отрицательны, то точка лежит в третьем квадранте. Если x положительный, а y отрицательный, то точка лежит в четвертом квадранте.
Минус 180 это квадрантный угол? Квадранты и углы квадрантов
Углы от 0° до 90° находятся в первом квадранте. Углы между 90∘ и 180∘ находятся в второй квадрант. Углы между 180° и 270° находятся в третьем квадранте. Углы между 270° и 360° находятся в четвертом квадранте.
Sohcahtoa только для прямоугольных треугольников?
В: Сохчатоа только для прямоугольных треугольников? А: Да, это относится только к прямоугольным треугольникам. Если у нас есть наклонный треугольник, мы не можем предположить, что эти триггерные отношения будут работать. … A: У прямоугольного треугольника гипотенуза всегда противоположна углу 90 градусов и является самой длинной стороной.
Если у нас есть наклонный треугольник, мы не можем предположить, что эти триггерные отношения будут работать. … A: У прямоугольного треугольника гипотенуза всегда противоположна углу 90 градусов и является самой длинной стороной.
Как решить задачу Сохкахтоа?
Где находится в стандартном положении? Стандартное положение: угол находится в стандартном положении, если его вершина находится в начале координат и один луч находится на положительной оси x. Луч на оси X называется начальной стороной, а другой луч называется конечной стороной.
Как выглядит в стандартном положении?
Угол в стандартном положении имеет его вершина в начале координатной плоскости.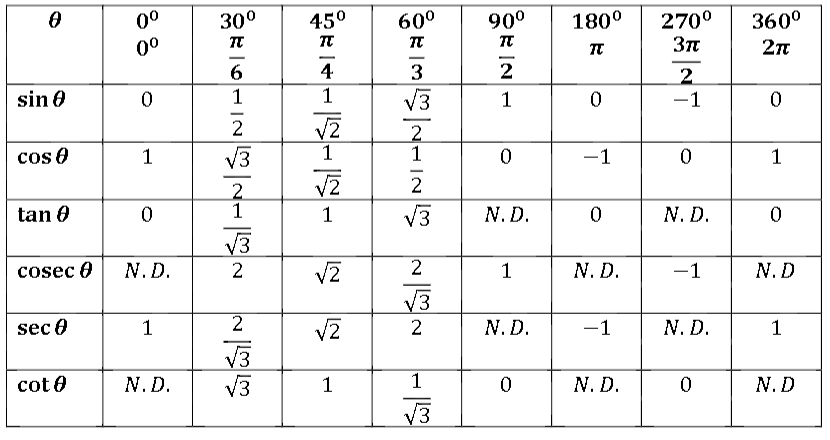 Его начальный луч (начальная сторона) лежит вдоль положительной оси абсцисс. Его конечный луч (конечная сторона) движется против часовой стрелки от начальной стороны. … Длина лучей, образующих угол, не имеет ничего общего с размером угла.
Его начальный луч (начальная сторона) лежит вдоль положительной оси абсцисс. Его конечный луч (конечная сторона) движется против часовой стрелки от начальной стороны. … Длина лучей, образующих угол, не имеет ничего общего с размером угла.
Как выглядит угол 90 градусов? Угол 90 градусов является прямым углом и ровно половина прямого угла. … Прямоугольник и квадрат — это основные геометрические фигуры, у которых все четыре угла равны 90 градусам. Если две прямые пересекаются друг с другом и угол между ними равен 90 градусов, то прямые называются перпендикулярными.
Как выглядит угол 30 градусов?
Какой угол 90 градусов?
Углы, составляющие 90 градусов (θ = 90 °), равны прямые углы. Углы, которые составляют 180 градусов (θ = 180 °), известны как прямые углы. Углы между 180 и 360 градусами (180° < θ < 360°) называются рефлекторными углами.
Светодиодные прожекторы Volpe, Uniel и Shine
Главная » Каталог товаров » Светильники » Светодиодные прожекторы Volpe, Uniel и Shine
Светодиодные прожекторы Uniel, Volpe, ASD (LLT) и Shine — это мощный свет и низкое энергопотребление.
Светодиодные (LED) прожекторы марок Uniel, Volpe, ASD (LLT) и Shine предназначены для освещения территории, зданий и объектов, баннеров, вывесок и рекламных плакатов. По сравнению с аналогичными по мощности света галогенными прожекторами потребление электроэнергии у светодиодных прожекторов Uniel, Volpe, ASD (LLT) и Shine в 10-12 раз меньше, а распределение света — лучше. Предлагаемый ассортимент светодиодных прожекторов состоит из трех основных групп: LED-прожекторы с углом пучка света 30 градусов, 60 градусов и 120°.
Прожекторы с углом 30° предназначены для освещения удаленных объектов: их световой пучок имеет малую площадь освещения, но зато обладает большой дальностью и высокой освещенностью на небольших расстояниях.
LED-прожекторы с углом 60° можно назвать универсальным решением. У них меньшая дальность «стрельбы» пучка и интенсивность света по сравнению с прожекторами 30°, но большая площадь освещения. Такие прожекторы можно использовать практически для любых целей. Идеально подходят для освещения подъездных путей, придомовых дворов, периметров территорий, а также фасадов зданий и объектов.
Светодиодный одночиповый (COB) прожектор с углом рассеивания 120 градусов обеспечивает «заливающий свет». Он обладает небольшой дальностью пучка, но может осветить большую площадь. По распределению света такой прожектор наиболее близок к прожектору с галогеновой лампой. Идеально подходит для освещения вывесок, баннеров, биллбордов, рекламных щитов, общего освещения территорий, фасадов и ворот.
LED-прожекторы, изготовленные по технологии SMD (surface mounted device), имеют угол рассеивания 100°. Они могут использоваться, как в виде источника акцентного, так и заливающего освещения. Использование технологии SMD позволяет добиться равномерности освещения и отсутствие ослепления.
Линейный светодиодный прожектор Volpe ULF-Q552 IP65 SILVER для архитектурной подсветки | |
| Влагозащищенные уличные линейные прожекторы Volpe ULF-Q552 используются в основном для архитектурной подсветки зданий. Угол рассеивания светового пучка составляет 45º. Светильник имеет степень защиты IP65. Корус выполнен из алюминия, рассеиватель — закаленное стекло. Рабочая температура — от -20º до +50ºС. Цветности — 2700К (WW) и 4000К (NW). Рабочее напряжение — от 85 до 230 В. Cos φ=0,85. Ra≥80%. 30000 часов срок службы. Гарантия — 2 года. Модельный ряд состоит из 4 моделей мощностью 9 и 18 Вт, цветностью 2700К (WW) и 4000К (NW):
Цвет корпуса — серебристый. |
Светодиодные SMD и одночиповые (COB) прожекторы Volpe, Uniel и Shine
Светодиодный SMD прожектор Volpe ULF-Q507 DW IP65 175-265B BLACK мощностью 10, 20, 30, 50 и 70 Вт | |
Светодиодные прожекторы Volpe ULF-Q507 предназначены для замены галогеновых прожекторов, по сравнению с которыми они в 10 раз экономичнее и имеют большой срок службы. Корпус выполнен из металла, окрашен в черный цвет, литой алюминиевый радиатор. Степень защиты — IP65. Угол рассеивания светового пучка составляет 120º. Рабочая температура — от -25º до +45ºС. Цветность — 6500К (DW). Рабочее напряжение — от 175 до 265 В. Cos φ=0,8. Ra≥80%. 30000 часов срок службы. Гарантия — 12 месяцев. Модельный ряд состоит из 5 моделей разной мощности:
| |
Светодиодный COB прожектор Uniel ULF-S01 DW IP65 мощностью 10, 20, 30 и 50Вт. | |
Светодиодные прожекторы Uniel ULF-S01 DW выпускаются мощностью 10, 20, 30 и 50 Вт и могут собой заменить галогенные прожекторы мощностью 100, 200, 300 и 500 Вт соответственно. По сравнению с галогенными прожекторами Uniel ULF-S01 экономичнее в 10 раз и имеют срок службы почти в 30 раз больше! Корпус с радиатором прожектора Uniel ULF-S01 DW изготовлен из литого алюминия, окрашен в серый цвет. Степень защиты — IP65. Угол рассеивания светового пучка составляет 120º. Рабочая температура — от -25º до +45ºС. Цветность — 6500К (DW). Рабочее напряжение — от 110 до 240 В. Cos φ=0,9. Ra≥80%. 30000 часов срок службы. Гарантия — 24 месяца. Модельный ряд состоит из 4 моделей разной мощности:
| |
Светодиодный прожектор Shine SMD 10W 100° 172555 | |
Светодиодный прожектор Shine SMD 10W 100° (172555) имеет световой поток 850 лм, что эквивалентно галогенному прожектору мощностью 100Вт. Светодиодный прожектор Shine SMD 10W 120° выпускается со цветовой температурой света 6000К. На плате используется 18 светодиодов. Срок службы LED-прожектора Shine 10W составляет 40000 часов. Гарантия — 3 года. | |
Светодиодный прожектор Shine COB 10W 120° 188555 | |
LED-прожектор Shine COB 10W 120° имеет световой поток 850 лм, поэтому его можно считать аналогом галогенного прожектора с лампой мощностью 75—100 Вт. Светодиодный прожектор Shine COB 10W 120° выпускается со цветовой температурой света 6000К. Срок службы LED-прожектора Shine 10W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 110 х 125 х 80 мм. Вес — 0,43 кг. Источником света в светодиодном прожекторе Shine COB 10W 120° является светодиод Epistar CABLV38. Гарантия — 3 года. | |
Светодиодный прожектор Shine SMD 20W 100° 172560 | |
Светодиодный прожектор Shine SMD 20W 100° (172560) имеет световой поток 1700 лм, что эквивалентно галогенному прожектору мощностью 200Вт. Срок службы LED-прожектора Shine 20W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры — 114х95х85 мм. Вес — 0,49 кг. Гарантия — 3 года. | |
Светодиодный прожектор Shine COB 20W 120° 188560 | |
Светодиодный прожектор Shine COB 20W 120° имеет световой поток 1700 лм, поэтому его можно считать аналогом галогенного прожектора с лампой мощностью 150—200 Вт. LED-прожектор Shine COB 20W 120° выпускается со цветовой температурой света 6000К. Срок службы LED-прожектора Shine 20W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 180 х 160 х 100 мм. Вес — 1,1 кг. Источником света в светодиодном прожекторе Shine COB 20W 120° является светодиод Epistar CABLV38. Гарантия — 3 года. | |
Светодиодный прожектор Shine SMD 30W 100° 172565 | |
Светодиодный прожектор Shine SMD 30W 100° (172565) имеет световой поток 2550 лм, что эквивалентно галогенному прожектору мощностью 300Вт. Светодиодный прожектор Shine SMD 30W 120° выпускается со цветовой температурой света 6000К. На плате используется 60 светодиодов. Срок службы LED-прожектора Shine 30W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры — 180х154х110 мм. Вес — 1,14 кг. Гарантия — 3 года. | |
Светодиодный прожектор Shine COB 30W 120° 188565 | |
LED-прожектор Shine COB 30W 120° имеет световой поток 2550 лм, поэтому его можно считать аналогом галогенного прожектора с лампой мощностью 300 Вт. Светодиодный прожектор Shine COB 30W 120° выпускается со цветовой температурой света 6000К. Срок службы LED-прожектора Shine 30W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 220 х 195 х 125 мм. Вес — 2,2 кг. Источником света в светодиодном прожекторе Shine COB 30W 120° является светодиод Epistar CABLV38. Гарантия — 3 года. | |
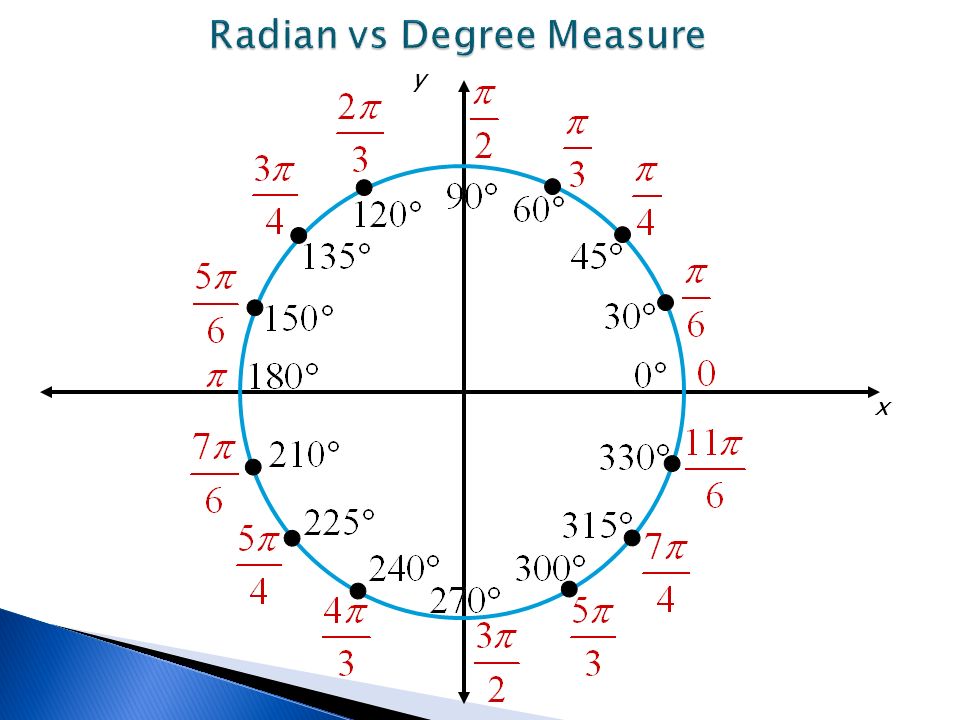
Светодиодный прожектор Shine SMD 50W 100° 172566 | |
Светодиодный прожектор Shine SMD 50W 100° (172566) имеет световой поток 4250 лм, что эквивалентно галогенному прожектору мощностью 500Вт. Светодиодный прожектор Shine SMD 50W 120° выпускается со цветовой температурой света 6000К. На плате используется 96 светодиодов. Срок службы LED-прожектора Shine 50W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры — 225х183х123 мм. Вес — 1,85. Гарантия — 3 года. | |
Светодиодный прожектор Shine COB 50W 120° | |
Светодиодный прожектор Shine COB 50W 120° имеет световой поток 4250 лм, поэтому его можно считать аналогом галогенного прожектора с лампой мощностью 500 Вт. Срок службы LED-прожектора Shine 50W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 285 х 235 х 128 мм. Вес — 2,55 кг. Источником света в светодиодном прожекторе Shine COB 50W 120° является светодиод Epistar. Гарантия — 3 года. | |
Светодиодный прожектор Shine COB 70W 120° 188550 | |
LED-прожектор Shine COB 70W 120° имеет световой поток 5600 лм — аналог галогенного прожектора с лампой мощностью 700 Вт. Светодиодный прожектор Shine COB 70W 120° выпускается со цветовой температурой света 6000К. Срок службы LED-прожектора Shine 70W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 290 х 390 х 103 мм. Вес — 4,9 кг. Источником света в светодиодном прожекторе Shine COB 70W 120° является 1 COB светодиод (chip-on-board — чип на плате). Гарантия — 3 года. | |
Прожектор светодиодный Uniel 100W ULF-S04-100W SMD IP65 100º | |
Светодиодный прожектор Uniel 100W ULF-S04-100W IP65 имеет светодиоды, изготовленные по технологии SMD. Световой поток LED-прожектора Uniel ULF-S04-100W составляет 8500 лм — поэтому он может быть использован в качестве современной и экономичной замены галогенного прожектора 1 кВт! Выпускаются светодиодные прожекторы Uniel серии ULF-S04 в двух цветовых температурах: 4000К (NW) и 6500К (DW). Срок службы Uniel 100W ULF-S04-100W составляет 50000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 286x236x144 мм. Цвет корпуса — серый. Рабочее напряжение LED-прожектора Uniel S04 — 85-265В. | |
Светодиодный прожектор Shine COB 100W 120° 188569 | |
LED-прожектор Shine COB 100W 120° имеет световой поток 8000 лм, поэтому он может заменить галогенный прожектор 1000 Вт. Срок службы LED-прожектора Shine 100W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 290 х 405 х 100 мм. Вес — 5,5 кг. Источником света в светодиодном прожекторе Shine COB 70W 120° является 1 COB светодиод (chip-on-board — чип на плате). Гарантия — 3 года. | |
Светодиодный прожектор Shine COB 150W 120° 188507 | |
LED-прожектор Shine COB 150W 120° имеет световой поток 12000 лм, поэтому он может заменить галогенный прожектор 1,5 кВт. Светодиодный прожектор Shine COB 150W 120° выпускается со цветовой температурой света 6000К. Срок службы LED-прожектора Shine 150W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры — 325х425х190 мм. Вес — 8,9кг. Источником света в светодиодном прожекторе Shine COB 150W 120° является 3 COB светодиод (chip-on-board — чип на плате). Гарантия — 3 года. | |
Светодиодные (LED) прожекторы Shine 30° и 60°
Светодиодный прожектор Shine 6W 30°/60° 170553 | |
LED-прожектор Shine 6W является аналогом галогенового прожектора 75 Вт (световой поток составляет 500 лм). Светодиодные прожекторы Shine 6W выпускаются с углом рассеивания светового пучка 30° и 60° и цветовой температурой света 6000К. Конструктивной особенностью прожекторов является наличие у каждого светодиода индивидуальной линзы, оптика которой рассчитана так, чтобы световое пятно прожектора было круглой формы и имело равномерное светораспределение. Срок службы LED-прожектора Shine 6W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 140 х 125 х 72 мм. Вес — 0,77 кг. Источниками света светодиодного прожектора Shine 6W являются светодиоды Epistar CABLV38. Гарантия — 3 года. | |
Светодиодный прожектор Shine 8W 30°/60° 171554 | |
Светодиодный (LED) прожектор Shine 8W с углами рассеивания 30° и 60° может заменить галогеновый прожектор мощностью 100 Вт, потому что световой поток такого прожектора составляет 700 лм. Цветовая температура света составляет 6000К. Каждый светодиод снабжен индивидуальной линзой, оптика которой рассчитана так, чтобы световое пятно прожектора было круглой формы и имело равномерное светораспределение. Срок службы LED-прожектора Shine 8W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 140 х 125 х 72 мм. Вес — 0,78 кг. Источниками света в прожекторе Shine 8W являются светодиоды Epistar CABLV38. Гарантия — 3 года. | |
Светодиодный прожектор Shine 12W 30°/60° 170556 | |
LED-прожектор Shine 12W по своему световому потоку 1000 лм равен галогеновому прожектору 150 Вт. Конструктивной особенностью прожекторов является наличие у каждого светодиода индивидуальной линзы, оптика которой рассчитана так, чтобы световое пятно прожектора было круглой формы и имело равномерное светораспределение. Срок службы светодиодного прожектора Shine 12W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 185 х 175 х 82 мм. Вес — 1,3 кг. Источниками света светодиодного прожектора Shine 12W служат светодиоды Epistar CABLV38. Гарантия — 3 года. | |
Светодиодный прожектор Shine 18W 30°/60° 171557 | |
Экономичная замена галогеновому прожектору с лампой 200 Вт — это светодиодный (LED) прожектор Shine 18W со световым потоком 1500 лм. Угол рассеивания прожектора составляет 30° или 60°. Цветовая температура света — 6000К. Срок службы LED-прожектора Shine 18W — 40000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 185 х 175 х 82 мм. Вес — 1,4 кг. Источниками света в прожекторе Shine 18W служат светодиоды Epistar CABLV38. Гарантия на прожектор Shine 18W составляет 3 года.
| |
Светодиодный прожектор Shine 24W 30°/60° 170558 | |
LED-прожектор Shine 24W по своему световому потоку 1000 лм равен галогеновому прожектору 300 Вт. Светодиодный прожектор Shine 24W может иметь угол рассеивания света 30° и 60°. Цветовая температура света 6000К. Конструктивной особенностью прожекторов является наличие у каждого светодиода индивидуальной линзы, оптика которой рассчитана так, чтобы световое пятно прожектора было круглой формы и имело равномерное светораспределение. Срок службы светодиодного прожектора Shine 24W составляет 40000 часов. Степень защиты — IP65. Габаритные размеры (с креплением) — 270 х 250 х 118 мм. Вес — 3,2 кг. Источниками света светодиодного прожектора Shine 24W служат светодиоды Epistar CABLV38. Гарантия — 3 года. | |
Светодиодный прожектор Shine 40W 30°/60° 171559 | |
LED-прожектор Shine 40W является полным аналогом галогенового прожектора 500 Вт (световой поток составляет 3400 лм). Светодиодные прожекторы Shine 40W выпускаются с углом рассеивания светового пучка 30° и 60° и цветовой температурой света 6000К. Конструктивной особенностью прожекторов является наличие у каждого светодиода индивидуальной линзы, оптика которой рассчитана так, чтобы световое пятно прожектора было круглой формы и имело равномерное светораспределение. Срок службы LED-прожектора Shine 40W составляет 40000 часов. Источниками света светодиодного прожектора Shine 40W являются светодиоды Epistar CABLV38. Гарантия — 3 года. | |
Cos-b
www.roscosmos.ru/media/img/2020/June/rgb_final_annotated_fig1.png
Может быть я ошибаюсь, но такое чувство, что знаковое событие во внеатмосферной астрономии, произошедшее 10 июня, прошло практически незамеченным. Речь про то, что космический флагман нашей и немецкой астрономии телескоп Спектр-РГ завершил первое полное сканирование всего неба.
Попробую это исправить. Для этого постараюсь объяснить в двух
словах чем отличаются разные телескопы, чем важен для мировой науки
этот аппарат и описать особенности его работы. Тем более, что судя
по тем публикациям прошедшим публикациям, порой авторы не понимают,
что означает фраза о его рекордной точности, относя ее вообще ко
всем телескопам подобного диапазона.
Дело в том, что орбитальные телескопы уже достаточно давно
разбираются на два типа: обзорные и детальные. Первые,
предназначены для поиска новых объектов на небесной сфере,
желательно с составлением полной карты неба. Вторые, уже нужны для
детального изучения выявленных новых источников с выяснением их
физической природы и дополнительных характеристик.
Для первых, допустимо использовать широкоугольные оптические системы, для вторых системы, с как можно меньшим углом. Кроме зоны осмотра, это часто задает ограничения времени наблюдения. Самым близким аналогом является выдержка в фотографии. Чем более широкий угол объектива, тем меньше выдержка для получения одного снимка и наоборот. Ниже это будет показано на примере.
Перед пуском вторых, должны идти первые станции. Именно это позволит ученым управляющим первыми аппаратами, как сказал мне один астрофизик, рассказывая про Спектр-РГ: Перестать тыкаться наудачу, как слепые котята.
Лучше всего это можно показать на примере реальных телескопов.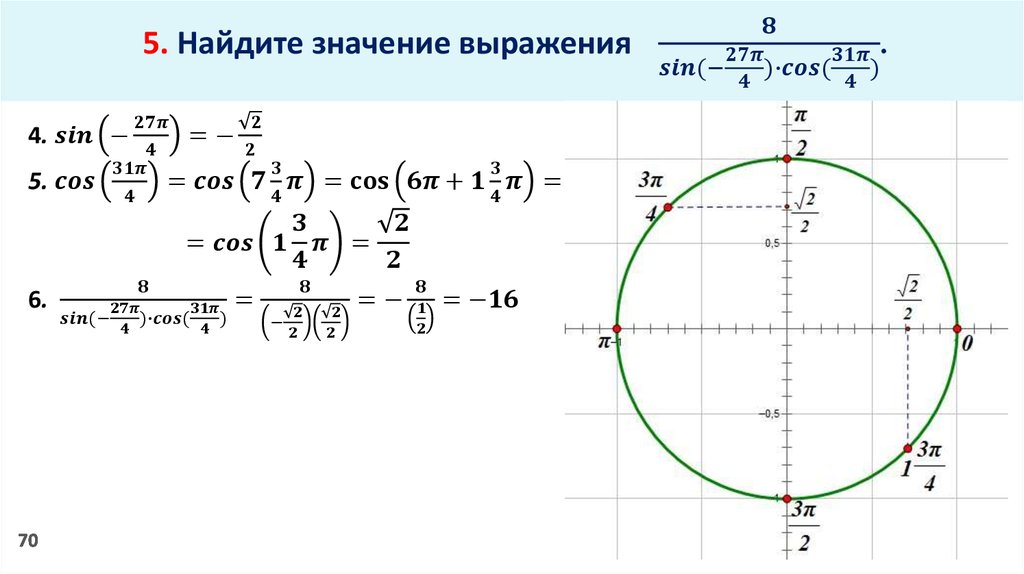 Например, первым обзорным аппаратом в диапазоне жесткого
гамма-излучения был COS-B, запущенный в 1975 году. Он имел поле
зрения порядка 30х30 градусов, то есть для полного перекрытия
небесной сферы ему нужно было сделать 50 наблюдений. Из-за
специфики его орбиты ожидалось, что он построит карту неба в гамма
лучах за 4 года, а в реальности за 6 лет работы только около
половины всего неба. Но и это был очень весомый результат.
Например, первым обзорным аппаратом в диапазоне жесткого
гамма-излучения был COS-B, запущенный в 1975 году. Он имел поле
зрения порядка 30х30 градусов, то есть для полного перекрытия
небесной сферы ему нужно было сделать 50 наблюдений. Из-за
специфики его орбиты ожидалось, что он построит карту неба в гамма
лучах за 4 года, а в реальности за 6 лет работы только около
половины всего неба. Но и это был очень весомый результат.
Для примера детальной станции можно взять НЕАО-2 Эйнштейн изучавшей в 1978-1981 годах мягкий рентгеновский диапазон. Ее поле зрения было порядка 1 градуса, разрешение до 2 угловых секунд, а чувствительность датчиков требовало выдержки около 104 секунд (2.7 часа).
Если бы от этого телескопа потребовали составить карту всего неба,
ему бы понадобилось для этого порядка 100 лет. За время своей
работы он просмотрел только 3% неба, но, с качественной точки
зрения, это были очень важные 3%. Он изучил почти всех
представителей классов рентгеновских источников и даже открыл
новые.
И он бы не смог это сделать, если бы ученые не знали заранее, куда смотреть, благодаря пусть и менее детальным картам всего неба, полученным обзорными телескопами.
Так как обзор всего неба это качественный результат, повторять его другим аппаратам с тем же результатом обычно не имеет смысла. В отличии от детальных станций. Последних желательно иметь, как можно больше, пусть и с равным разрешением. Это позволит быстрее изучить открытые районы.
В обзорных системах, для каждой следующей карты желательно повышать разрешение на порядки, что весьма не просто. И проблема даже не в том, что нужно переварить на порядок больший трафик аппарата.
С технической точки зрения обзорный аппарат нужно делать
стабилизированным вращением, чтобы за один виток он снимал узкую
полосу на небе. И после каждого оборота новую. Именно эта схема и
была реализована для Спектра-РГ. Он был впервые для наших аппаратов
выведен в точку Лагранжа, после чего занял постоянную ориентацию на
Солнце и начал сканировать небо.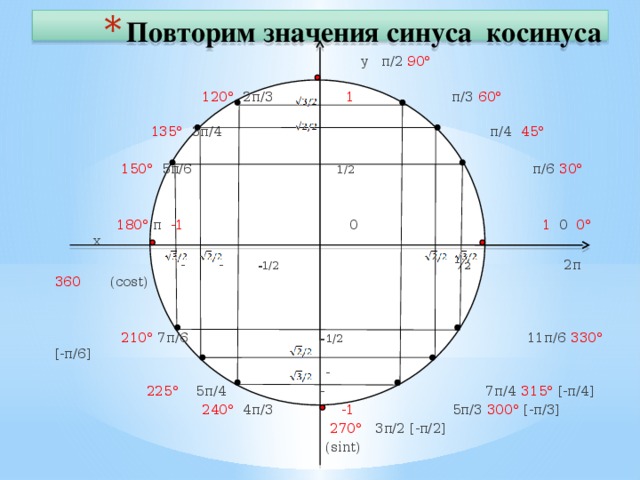 Это хорошо видно на схеме из
Вестника НПО им Лавочкина.
Это хорошо видно на схеме из
Вестника НПО им Лавочкина.
Полный период обращения аппарата вокруг своей оси составляет порядка 4 часов. За эти часы благодаря движения Земли, плоскость вращения аппарата изменилась приблизительно на 0.17 градуса и в поле зрения телескопов попали новые области неба.
Выглядит просто, но каждая следующая карта, дается со все большим трудом. Видно, что время сканирования, передачи и параметров сканирующей системы должны быть жестко синхронизированы.
Но чем более узкое поле зрения, тем быстрее проходит объект через
него. Скажем, при угле зрения 10х10 градусов, объект из плоскости
эклиптики будет в поле зрения 105 секунд (почти сутки),
а при угле 1х1 градус, максимально возможная выдержка падает в сто
раз до 103 секунд (16 минут). Требования к приемникам
возросли в 100 раз, а линейное разрешение всего в 10 раз. А если
потребуем сделать следующий шаг, что максимально возможная выдержка
снизиться до считанных минут. А при такой выдержке даже в
оптическом диапазоне могут быть проблемы, не говоря о
рентгеновском.
В результате, если изначально на обзорных аппаратах были достаточно простые приемники, то на том же Спектре-РГ применены сложнейшие телескопы косого падения некоторые элементы которых буквально могут изготовить всего несколько предприятий в мире. И не факт, что когда все научные открытия Спектра-РГ будут изучены детальными телескопами, создание следующей обзорной станции будет упираться только в финансовые проблемы, а не встретит сложные технические и научные ограничения.
Сравнение одного участка неба с разных телескопов.
АРТ-П/Гранат(детальный), ART-XC/Спектр-РГ (обзорный), NuSTAR
(детальный)
Впрочем, до этого еще далеко. Первая обзорная карта неба в рентгеновском диапазоне построена, за следующие несколько лет станция ее дополнительно уточнит, просканирует небо несколько раз. После чего на десятилетия затянутся изучение новых объектов, как по данным Спектра-РГ, так и при помощи более детальных станций.
Угол равный примерно 57 17 45. Углы на плоскости и их измерение.
 Значения тригонометрических функций при α=45°
Значения тригонометрических функций при α=45°Примечание : см. также таблицу значений тригонометрических функций других углов .
Табличные значения синуса 45, косинуса 45 и тангенса 45 градусов указаны . Далее по тексту следует пояснение метода и правильности вычисления этих значений для произвольного прямоугольного треугольника.
45 градусов — это π/4 радиан . Формулы для значений косинуса, синуса и тангенса пи/4 радиан указаны ниже (хотя они и тождественны).
То есть, например, tg π/4 = tg 45 градусов
Как самостоятельно вычислить значения sin cos tg 45 градусов?
Построим и рассмотрим прямоугольный треугольник АВС у которого угол ∠ В = 45°. На основании соотношения его сторон, вычислим значения тригонометрических функций в прямоугольном треугольнике для угла 45 градусов. Поскольку треугольник прямоугольный, то значения функций синуса, косинуса и тангенса будут равны соотношению его соответствующих сторон.
Поскольку значение функций синуса, косинуса и тангенса зависят исключительно от градусной меры угла (или значения, выраженного в радианах), то найденные нами соотношения и будут значениями функции синуса 45, косинуса 45 и тангенса 45 градусов.
Согласно свойствам прямоугольного треугольника, угол С — прямой и равен 90 градусам. Угол B мы изначально построили с градусной мерой 45 градусов. Найдем значение угла А. Так как сумма углов треугольника равна 180 градусам, то
∠ А + ∠ В + ∠ С = 180°
Угол C прямой и равен 90 градусам, угол B мы изначально определили как 45 градусов, таким образом:
∠ А = 180° —∠ С — ∠ В = 180° — 90° — 45° = 45°
Поскольку у данного треугольника два угла равны между собой, то треугольник АВС – прямоугольный, и, одновременно, равнобедренный , в котором оба катета равны между собой: AC = BC.
Допустим, что длина сторон равна некому числу АС = ВС = а. Зная длины катетов, вычислим длину гипотенузы.
По теореме Пифагора: АВ 2 =АС 2 +ВС 2
Заменим длины AC и BC на переменную а, тогда получим:
АВ 2 = а 2 + а 2 = 2а 2 ,
тогда АВ=а√ 2.
В результате мы выразили длины всех сторон прямоугольного треугольника с углом 45 градусов через переменную а.
Согласно свойств тригонометрических функций в прямоугольном треугольнике соотношение соответствующих сторон треугольника будет равным значению соответствующих функций . Таким образом для угла α = 45 градусов:
sin α = BC / AB (согласно определению синуса для прямоугольного треугольника — это отношение противолежащего катета к гипотенузе, BC — катет, AB — гипотенуза)
cos α = AC / AB (согласно определению косинуса — это отношение прилежащего катета к гипотенузе, AC — катет, AB — гипотенуза)
tg α = BC / AC (аналогично, тангенс для угла α будет равен отношению противолежащего катета к прилежащему)
Вместо обозначений сторон подставим значения их длин через переменную а.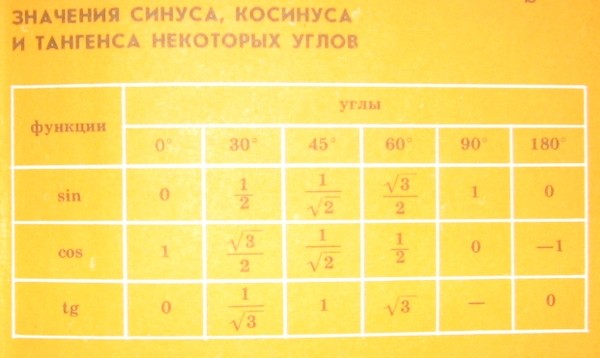
Исходя из этого (см. таблицу значений sin 45, cos 45, tg 45 ) получаем:
Табличные значения sin 45, cos 45, tg 45 (то есть значение синуса 45, косинуса 45 и тангенса 45 градусов можно вычислить как соотношение соответствующих сторон данного треугольника), подставим вычисленные выше значения длин сторон в формулы и получим результат на картинке ниже.
Табличные значения: синус 45, косинус 45 и тангенс 45 градусов
Таким образом:
- тангенс 45 градусов равен единице
- синус 45 градусов равен косинусу 45 градусов и равен корню из двух пополам (то же самое, что и единица, деленная на корень из двух)
Как видно из вычислений, приведенных выше, для вычисления значений соответствующей тригонометрической функции важны не длины сторон треугольника, а их соотношение, которое всегда одно и то же для одинаковых углов, независимо от размеров конкретного треугольника.
Синус, косинус и тангенс угла π/4 радиан
В задачах, предлагаемых для решения в старших классах и на ЗНО/ЕГЭ вместо градусной меры угла часто встречается указание на его величину, измеренную в радианах.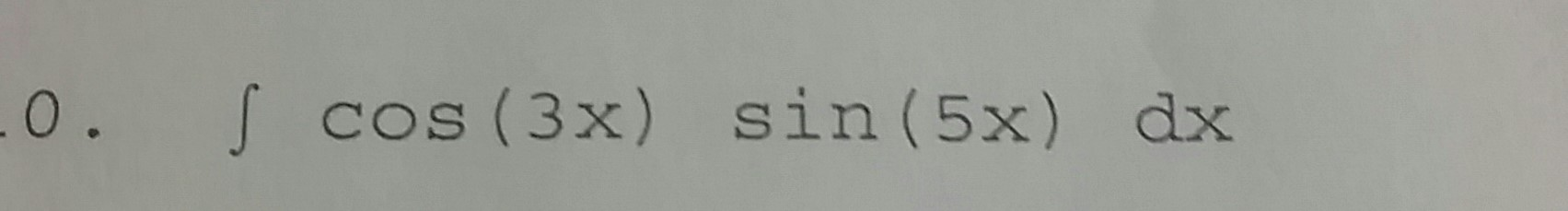 Мера угла, выраженная в радианах, базируется на числе пи, которое выражает зависимость длины окружности от ее диаметра.
Мера угла, выраженная в радианах, базируется на числе пи, которое выражает зависимость длины окружности от ее диаметра.
Для простоты понимания, рекомендую запомнить простой принцип перевода градусов в радианы . Диаметр окружности охватывает дугу, равную 180 градусам. Таким образом, пи радиан будет равно 180 градусам. Откуда легко пересчитать любую градусную меру угла в радианы и обратно.
Учтем, что угол 45 градусов, выраженный в радианах , равен (180 / 45 = 4) π/4 (пи на четыре). Поэтому найденные нами значения верны для той же самой градусной меры угла, выраженной в радианах:
- тангенс π/4 (пи на четыре) равен единице
- синус π/4 (пи на четыре) градусов равен косинусу π/4 градусов и равен корню из двух пополам
Угол: ° π rad =
Преобразовать в: радианы градусы 0 — 360° 0 — 2π положительное отрицательное Вычислять
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами .
На картинке видны 4 разных угла, образованных пересечением прямых AB и CD
Обычно углы измеряются в градусах, что обозначается как °.
Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°).
Таким образом, градус — это $\frac{1}{360}$ круга.
Углы больше 360 градусов
Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.
Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.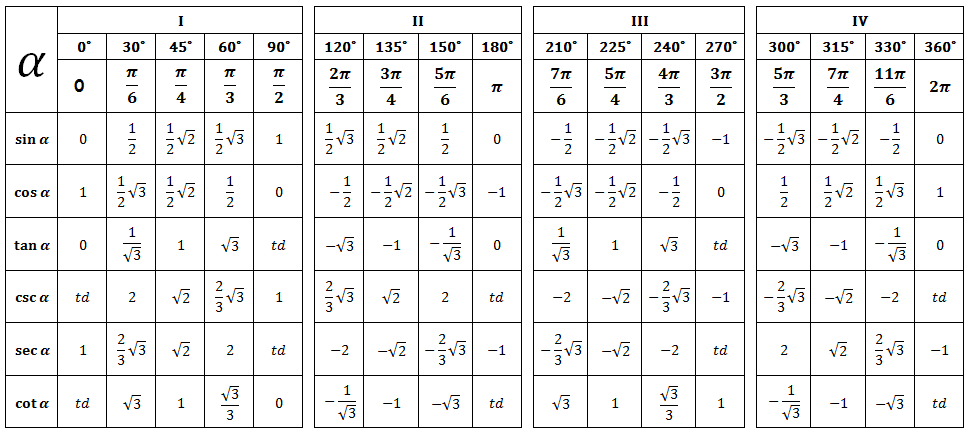 {\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
{\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
Объект описал $2\frac{7}{9}$ кругов
Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.
В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.
Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)
Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360.
Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.
Пример 3
1. Найти соответствующий положительный угол
Найти соответствующий положительный угол
a) -35°
b) -60°
c) -180°
d) — 670°
2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°
2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°
Радиан
Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга. {\circ}$
{\circ}$
c) 1 рад = 57,3°
$2,4 = \frac{2,4 \times 57,3}{1} = 137,52$
Отрицаетльные углы и углы больше, чем $2\pi$ радиан
Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2\pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2\pi$.
Пример 5
1. Преобразовать $-\frac{3}{4}\pi$ и $-\frac{5}{7}\pi$ в позитивные углы в радианах.
Решение
Прибавляем к углу $2\pi$
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4}\pi$
$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2}{7}\pi$
Когда объект вращается на угол больший, чем $2\pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2\pi$, результат равен или меньше, но как можно ближе к данному числу.
Пример 6
1. Найти количество кругов пройденных объектом при данных углах
a) $-10\pi$
b) $9\pi$
c) $\frac{7}{2}\pi$
Решение
a) $-10\pi = 5(-2\pi)$;
$-2\pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.
b) $9\pi = 4(2\pi) + \pi$, $\pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки
c) $\frac{7}{2}\pi=3,5\pi=2\pi+1,5\pi$, $1,5\pi$ равно три четверти цикла $(\frac{1,5\pi}{2\pi}=\frac{3}{4})$
объект прошел один и три четверти цикла против часовой стрелки
УГЛЫ НА ПЛОСКОСТИ И ИХ ИЗМЕРЕНИЕ. Фигура на плоскости, образованная двумя лучами, исходящими из одной точки O , называется углом. Лучи OA и OB называются сторонами угла, а точка O вершиной. Угол со сторонами OA и OB обозначается Р AOB.
Углы сравнивают, складывают, измеряют. Они равны, если их можно совместить перемещением. Два угла называются смежными (рис. 1), если у них общие вершина и одна сторона, а две другие образуют прямую. Вообще, углы, имеющие общую вершину и одну общую сторону, называются прилежащими (рис. 2). Углы называются вертикальными (рис. 3), если стороны одного являются продолжениями за вершину сторон другого. Вертикальные углы равны между собой. Угол, у которого стороны образуют прямую, называется развернутым (рис. 4). Угол, равный своему смежному, называется прямым. Угол меньший прямого – острый, больший прямого, но меньший развернутого – тупой.
Вертикальные углы равны между собой. Угол, у которого стороны образуют прямую, называется развернутым (рис. 4). Угол, равный своему смежному, называется прямым. Угол меньший прямого – острый, больший прямого, но меньший развернутого – тупой.
При пересечении двух прямых, лежащих в одной плоскости, третьей прямой образуются углы (рис. 5). 1 и 5, 2 и 6, 4 и 8, 3 и 7 называются соответственными; 2 и 5, 3 и 8 – внутренними односторонними; 1 и 6, 4 и 7 – внешними односторонними; 3 и 5, 2 и 8 – внутренними накрест лежащими; 1 и 7, 4 и 6 – внешними накрест лежащими.
Если луч OC проходит внутри угла AOB (рис. 6), то, по определению, считают, что угол AOC , как и угол COB , меньше угла AOB и что угол AOB равен сумме углов AOC и COB. Взяв за единицу измерения какой-либо конкретный угол, определяют величину любого угла, т.е. находят, сколько раз укладывается в нем данный единичный угол. При измерении угла исходят из двух его свойств, аналогичных свойствам длины отрезка: 1) величины равных углов равны, 2) величина суммы двух углов равна сумме их величин.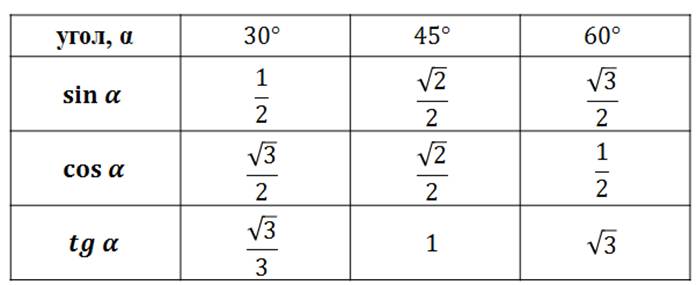
Если рассмотреть углы, вершиной которых является центр окружности, а сторонами – радиусы, то можно отметить, что равные углы высекают на окружности равные дуги, и сумме углов будет соответствовать сумма стягиваемых ими дуг. Поэтому величина угла пропорциональна длине высекаемой им дуги, и единицы измерения можно задавать, указывая, какую часть окружности составляет соответствующая дуга.
Обычно пользуются двумя системами измерения углов: градусной и радианной .
В градусной системе за единицу измерения принимают дугу размером в 1/360 окружности (обозначают °
). Градус делится на 60 минут (обозначают «), минута на 60 секунд (обозначают «»). Шестидесятиричность измерений напоминает о Вавилоне, но был в истории еще один градус. Во времена Великой французской революции (1793) во Франции вместе с десятичной (метрической) системой мер была введена сотенная (центезимальная) система измерения углов. В ней прямой угол делится на 100 градусов («градов»), градус на 100 минут, минута на 100 секунд. Эта система наиболее часто применяется в геодезических измерениях.
Эта система наиболее часто применяется в геодезических измерениях.
Математики предпочитают пользоваться радианной мерой – за единицу измерения принимается угол, под которым видна из центра окружности ее дуга, равная радиусу. Величина такого угла и есть радиан. Она не зависит от радиуса окружности и от положения дуги на окружности. Т.к. полуокружность видна из центра под углом 180° , а ее длина равна 241 радиусам, то радиан в 241 раз меньше, чем угол 180° , т.е. один радиан равен 180° /241 :
1 радиан » 57,2958° » 57° 17″45″»
И в радианной и в градусной системе угол измеряется единицей угла. То, что наименование в одном случае (для градуса) проставляется, а в другом (для радиана) подразумевается, не играет никакой роли.
Радианная мера, выражающаяся отношением длины дуги, описанной произвольным радиусом из центра и заключенной между сторонами угла, к радиусу этой дуги, не зависит от выбора единицы длины. Так же не зависит и градусная мера, т. к. она тоже является отношением двух длин, а именно длины дуги, описанной из вершины угла и заключенной между ее сторонами, к длине дуги равной 1/360 части окружности того же радиуса.
к. она тоже является отношением двух длин, а именно длины дуги, описанной из вершины угла и заключенной между ее сторонами, к длине дуги равной 1/360 части окружности того же радиуса.
Таким образом, никакой принципиальной разницы между градусной и радианной мерой угла нет, однако введение радианной меры позволяет придать многим формулам более простой вид.
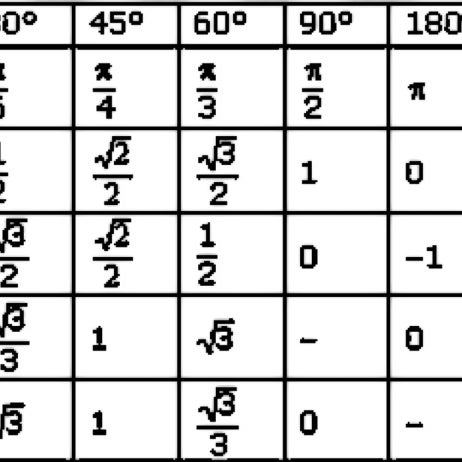
Соотношение градусной и радианной мер наиболее часто встречающихся углов приведено в следующей таблице
Прямой угол содержит в себе 90° или 241 /2 радиан. Острый лежит в пределах от 0 до 90° или от 0 до 241 /2 радиан, тупой – от 90 до 180° или от 241 /2 до 241 . Прямые линии, образующие прямой угол, называются перпендикулярными одна другой.
Часто важно указать, в каком направлении измеряется угол. Если рассматривать в качестве меры угла поворот вокруг вершины О , переводящий луч OA в положение OB, то положительной мера угла считается, если поворот происходит против часовой стрелки, в противном случае угол считается отрицательным . Таким образом, угол может иметь своей величиной любое действительное число. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.
Таким образом, угол может иметь своей величиной любое действительное число. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.
Под углом между двумя кривыми, выходящими из общей точки, в которой каждая из кривых имеет определенную касательную, понимают угол, образованный этими касательными. Понятие угла обобщается и на различные объекты в пространстве (двугранные, телесные и многогранные углы.
Cos 390 градусов — Найдите значение Cos 390 градусов
LearnPracticeDownload
Значение cos 390 градусов равно 0,8660254. . . . Cos 390 градусов в радианах записывается как cos (390° × π/180°), то есть cos (13π/6) или cos (6,806784…). В этой статье мы обсудим способы нахождения значения cos 390 градусов на примерах.
- Cos 390°: 0,8660254. . .
- Cos 390° в дробях: √3/2
- Cos (-390 градусов): 0,8660254.
 . .
. . - Cos 390° в радианах: cos (13π/6) или cos (6,8067840 . . .)
Каково значение Cos 390 градусов?
Значение cos 390 градусов в десятичной системе равно 0,866025403. . .. Cos 390 градусов также можно выразить с помощью эквивалента заданного угла (390 градусов) в радианах (6,80678 . . .)
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (pi/ 180°)
⇒ 390 градусов = 390° × (π/180°) рад = 13π/6 или 6,8067. . .
∴ cos 390 ° = cos (6,8067) = √ 3/2 или 0,8660254. . .
Объяснение:
Для cos 390° угол 390° > 360°. Учитывая периодическое свойство функции косинуса, мы можем представить ее как cos(390° mod 360°) = cos(30°). Угол 390°, котерминальный углу 30°, расположен в Первом квадранте (квадрант I).
Поскольку функция косинуса положительна в 1-м квадранте, значение косинуса 390 градусов = √3/2 или 0,8660254. . .
Точно так же cos 390 ° также можно записать как cos 390 градусов = (390 ° + n × 360 °), n ∈ Z.
⇒ cos 390° = cos 750° = cos 1110° и так далее.
Примечание: Поскольку косинус — четная функция, значение cos(-390°) = cos(390°).
Методы определения значения Cos 390 градусов
Функция косинуса положительна в 1-м квадранте. Значение cos 390° составляет 0,86602. . .. Мы можем найти значение cos 390 градусов по:
- Используя Unit Circle
- Использование тригонометрических функций
Косинус 390 градусов с использованием единичной окружности
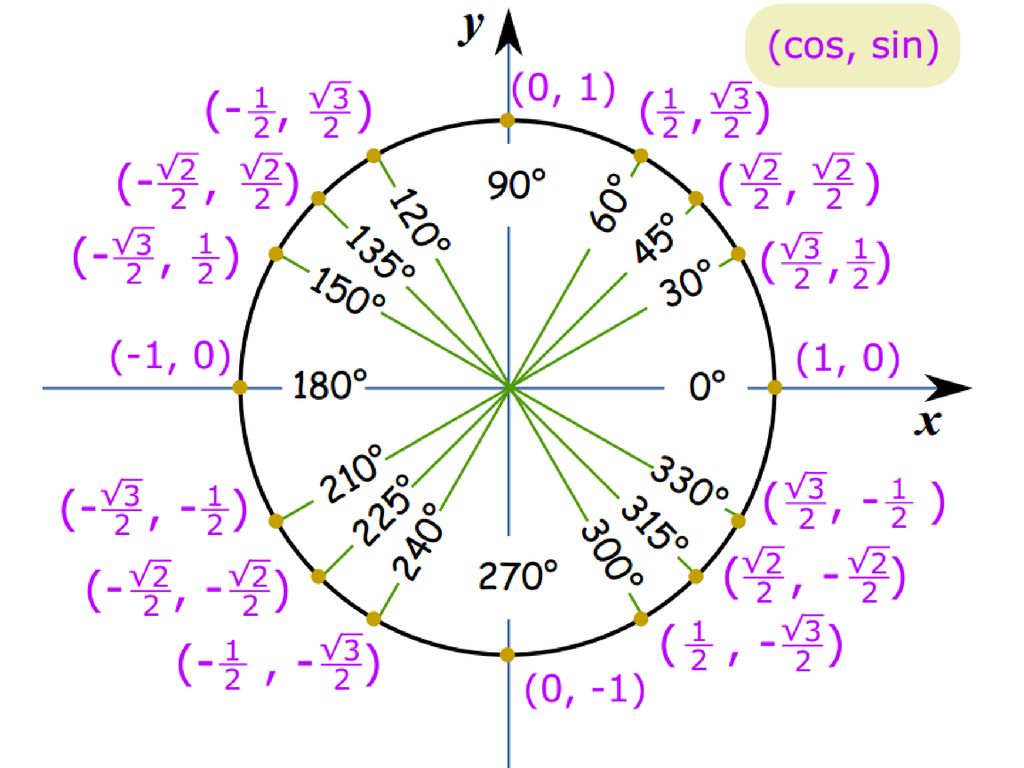
Чтобы найти значение косинуса 390 градусов с помощью единичной окружности, представьте 390° в виде (1 × 360°) + 30° [∵ 390°>360°] ∵ косинус периодическая функция, cos 390° = cos 30°.
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 30° или 390° с положительной осью x.
- Cos 390 градусов равен x-координате (0,866) точки пересечения (0,866, 0,5) единичной окружности и r.
Следовательно, значение cos 390° = x = 0,866 (приблизительно)
Cos 390° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cos 390 градусов как:
- ± √(1-sin² (390°))
- ± 1/√(1 + tan²(390°))
- ± кроватка 390°/√(1 + кроватка²(390°))
- ±√(косек²(390°) — 1)/косек 390°
- 1/сек 390°
Примечание. Поскольку 390° лежит в 1-м квадранте, окончательное значение cos 390° будет положительным.
Поскольку 390° лежит в 1-м квадранте, окончательное значение cos 390° будет положительным.
Мы можем использовать тригонометрические тождества для представления cos 390° как
- -cos(180° — 390°) = -cos(-210°)
- -cos(180° + 390°) = -cos 570°
- sin(90° + 390°) = sin 480°
- sin(90° — 390°) = sin(-300°)
☛ Также проверьте:
- cos 45 градусов
- потому что 3 градуса
- потому что 75 градусов
- потому что 26 градусов
- соз 38 градусов
- потому что 145 градусов
Примеры использования Cos 390 градусов
Пример 1: Найдите значение cos 390°, если sec 390° равно 1,1547.
Решение:
Так как cos 390° = 1/сек 390°
⇒ cos 390° = 1/1,1547 = 0,866Пример 2: Найдите значение (cos² 195° — sin² 195°).
 [Подсказка: используйте cos 390° = 0,866]
[Подсказка: используйте cos 390° = 0,866] Решение:
Используя формулу cos 2a,
(cos² 195° — sin² 195°) = cos(2 × 195°) = cos 390°
∵ косинус 390° = 0,866
⇒ (cos² 195° — sin² 195°) = 0,866Пример 3. Найдите значение 2 cos(390°)/3 sin(-300°).
Решение:
Используя тригонометрические тождества, мы знаем, что cos(390°) = sin(90° — 390°) = sin(-300°).
⇒ потому что (390°) = sin(-300°)
⇒ Значение 2 cos(390°)/3 sin(-300°) = 2/3
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о Cos 390 Degrees
Что такое Cos 390 Degrees?
Кос 390 градусов — значение тригонометрической функции косинуса для угла, равного 390 градусам. Значение cos 390° равно √3/2 или 0,866 (приблизительно)
Значение cos 390° равно √3/2 или 0,866 (приблизительно)
Как найти Cos 390° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение cos 390° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-sin²(390°))
- ± 1/√(1 + tan²(390°))
- ± кроватка 390°/√(1 + кроватка²(390°))
- ± √(косек²(390°) — 1)/косек 390°
- 1/сек 390°
☛ Также проверьте: таблицу тригонометрии
Каково значение Cos 390 градусов в пересчете на Sin 390°?
Используя тригонометрические тождества, мы можем записать cos 390° через sin 390° как cos(390°) = √(1 — sin²(390°)). Здесь значение sin 390° равно 0,5.
Каково точное значение cos 390 градусов?
Точное значение для cos 390 градусов может быть задано с точностью до 8 знаков после запятой как 0,86602540 и √3/2 в дроби.
Как найти значение Cos 390 градусов?
Значение cos 390 градусов можно рассчитать, построив угол 390° с осью x и затем найдя координаты соответствующей точки (0,866, 0,5) на единичной окружности. Значение cos 390° равно координате x (0,866). ∴ cos 390° = 0,866.
Значение cos 390° равно координате x (0,866). ∴ cos 390° = 0,866.
Скачать БЕСПЛАТНО учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
| 1 | Найдите точное значение | грех(30) | |
| 2 | Найдите точное значение | грех(45) | |
| 3 | Найдите точное значение | грех(30 градусов) | |
| 4 | Найдите точное значение | грех(60 градусов) | |
| 5 | Найдите точное значение | загар (30 градусов) | |
| 6 | Найдите точное значение | угловой синус (-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найдите точное значение | cos(pi/4) | |
| 9 | Найдите точное значение | грех(45 градусов) | |
| 10 | Найдите точное значение | грех(пи/3) | |
| 11 | Найдите точное значение | арктический(-1) | |
| 12 | Найдите точное значение | cos(45 градусов) | |
| 13 | Найдите точное значение | cos(30 градусов) | |
| 14 | Найдите точное значение | желтовато-коричневый(60) | |
| 15 | Найдите точное значение | csc(45 градусов) | |
| 16 | Найдите точное значение | загар (60 градусов) | |
| 17 | Найдите точное значение | сек (30 градусов) | |
| 18 | Найдите точное значение | cos(60 градусов) | |
| 19 | Найдите точное значение | соз(150) | |
| 20 | Найдите точное значение | грех(60) | |
| 21 | Найдите точное значение | cos(pi/2) | |
| 22 | Найдите точное значение | загар (45 градусов) | |
| 23 | Найдите точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найдите точное значение | csc(60 градусов) | |
| 25 | Найдите точное значение | сек (45 градусов) | |
| 26 | Найдите точное значение | csc(30 градусов) | |
| 27 | Найдите точное значение | грех(0) | |
| 28 | Найдите точное значение | грех(120) | |
| 29 | Найдите точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найдите точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найдите точное значение | детская кроватка(30 градусов) | |
| 37 | Найдите точное значение | арккос(-1) | |
| 38 | Найдите точное значение | арктический(0) | |
| 39 | Найдите точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найдите точное значение | sin((5pi)/3) | |
| 43 | Найдите точное значение | sin((3pi)/4) | |
| 44 | Найдите точное значение | желтовато-коричневый (pi/2) | |
| 45 | Найдите точное значение | грех(300) | |
| 46 | Найдите точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найдите точное значение | соз(0) | |
| 49 | Найдите точное значение | соз(135) | |
| 50 | Найдите точное значение | cos((5pi)/3) | |
| 51 | Найдите точное значение | соз(210) | |
| 52 | Найдите точное значение | сек (60 градусов) | |
| 53 | Найдите точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найдите точное значение | грех(135 градусов) | |
| 61 | Найдите точное значение | грех(150) | |
| 62 | Найдите точное значение | грех(240 градусов) | |
| 63 | Найдите точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найдите точное значение | грех(225) | |
| 66 | Найдите точное значение | грех(240) | |
| 67 | Найдите точное значение | cos(150 градусов) | |
| 68 | Найдите точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найдите точное значение | сек(0) | |
| 71 | Найдите точное значение | cos((5pi)/6) | |
| 72 | Найдите точное значение | КСК(30) | |
| 73 | Найдите точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найдите точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найдите точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найдите точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт. )/4 )/4 | |
| 79 | Найдите точное значение | sin((7pi)/4) | |
| 80 | Найдите точное значение | угловой синус(-1/2) | |
| 81 | Найдите точное значение | грех((4pi)/3) | |
| 82 | Найдите точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найдите точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найдите точное значение | грех(150 градусов) | |
| 87 | Найдите точное значение | грех((2pi)/3) | |
| 88 | Найдите точное значение | желтовато-коричневый ((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найдите точное значение | грех(пи/2) | |
| 91 | Найдите точное значение | сек(45) | |
| 92 | Найдите точное значение | cos((5pi)/4) | |
| 93 | Найдите точное значение | cos((7pi)/6) | |
| 94 | Найдите точное значение | угловой синус(0) | |
| 95 | Найдите точное значение | грех(120 градусов) | |
| 96 | Найдите точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найдите точное значение | соз(270) | |
| 98 | Найдите точное значение | sin((7pi)/6) | |
| 99 | Найдите точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Докажите, что 1.
 грех 420 потому что 390°+ cos (-300°) sin (-330°) 1 ?
грех 420 потому что 390°+ cos (-300°) sin (-330°) 1 ?Шолр
| Поделиться этим вопросом |
3 ответа
шрейтяги12 класс |
Sin420=sin60
Cos 390=cos 30
Cos (-300)=cos (60)
Sin(-330)=sin30
При вводе,
(root3/2)²+(1/2)²=1
| 0 | Поделитесь этим ответом |
Друба Дей11 класс |
| 0 | Поделитесь этим ответом |
Эмбер Мишра11 класс |
но мы должны доказать 1 не 1/2
| 0 | Поделитесь этим ответом |
Похожие вопросы
График V-I для хорошего проводника дает угол 420 с осью V. Здесь V обозначает напряжение
и I обозначает ток. Тогда сопротивление
дирижер будет
(а) грех 420
(с) загар 42
(б) косинус 42°
(г) раскладушка 42°
…
9{2}=\frac{1-\cos\theta}{1+\cos\theta}
1+sin 6 — 0056 ) » 1-cos®
1+sin@+cos® ) 1+cos®
… Здесь V обозначает напряжение
и I обозначает ток. Тогда сопротивление
дирижер будет
(а) грех 420
(с) загар 42
(б) косинус 42°
(г) раскладушка 42°
…
9{2}=\frac{1-\cos\theta}{1+\cos\theta}
1+sin 6 — 0056 ) » 1-cos®
1+sin@+cos® ) 1+cos®
… |
\begin{align} \text { 7. } & \text { (i) } \frac { 1 + \cos \theta + \sin \theta } { 1 + \cos \theta — \sin \theta } = \frac { 1 + \sin \theta } { \cos \theta } \\ \left( \text { ii) } \frac { \sin \theta + 1 — \cos \theta } { \cos \theta — 1 + \sin \ тета } \ справа. & = \ frac { 1 + \ sin \ theta } { \ cos \ theta } \ end {align}
… } & \text { (i) } \frac { 1 + \cos \theta + \sin \theta } { 1 + \cos \theta — \sin \theta } = \frac { 1 + \sin \theta } { \cos \theta } \\ \left( \text { ii) } \frac { \sin \theta + 1 — \cos \theta } { \cos \theta — 1 + \sin \ тета } \ справа. & = \ frac { 1 + \ sin \ theta } { \ cos \ theta } \ end {align}
… |
1 22 ¸ 1. грех? (2р + 5) 4. грех (2г+1)
2. грех 3х, потому что 4х
с. грех х потому что х
3. cos 2x cos 4x cos 6x
6, грех х грех 2х грех 3х
… грех (2г+1)
2. грех 3х, потому что 4х
с. грех х потому что х
3. cos 2x cos 4x cos 6x
6, грех х грех 2х грех 3х
… |
cos α cos β cos α sin β -sin α Докажи это грех потому что β 0 1 sin α cos β sin α sin β потому что α . .. .. |
27 ( \frac \sin A 1 %2B \cos A %2B \frac 1 %2B \cos A \sin A ) ( \frac \sin A 1 — \cos A — \frac 1 — \cos A \sin A ) … |
\frac { \operatorname {cos} \theta} { 1 — \operatorname {sin} \theta} + \frac { \operatorname {sin} \theta} {1 — \operatorname {cos} \theta} + 1 = \frac { \operatorname {sin} \theta \cdot \operatorname {cos} \theta} { (1 — \operatorname {sin} \theta) (1 — \operatorname {cos} \theta)} . .. .. |
Значение sin A -sin B cos B — cos A cos A + cos B sin A + sin B 1 1С … |
cosA 1 — sin A 1-coS A грех А, потому что А (1-sinA) (1-cos A) грех А 27.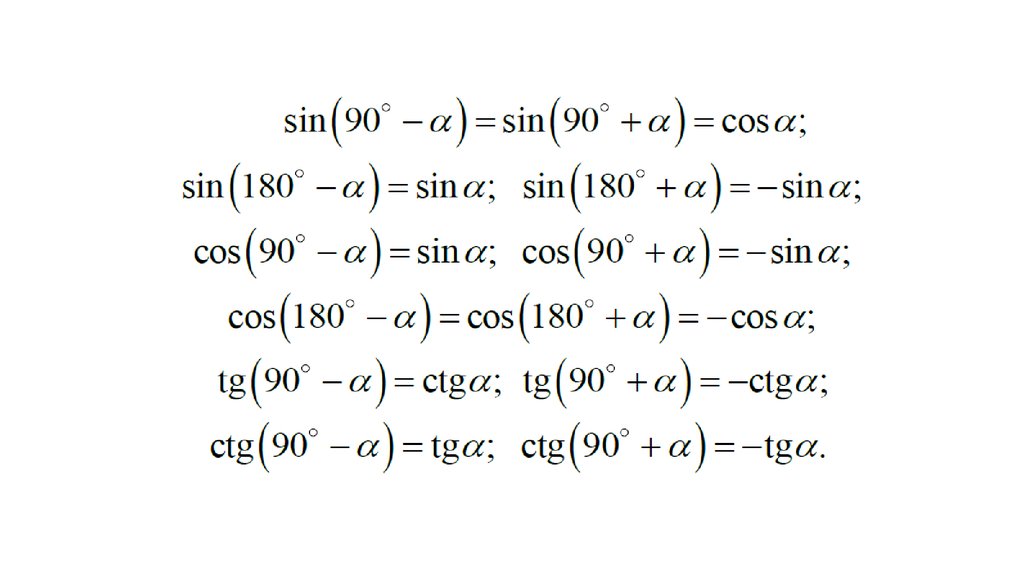 Докажите, что 1-sinA
1-cosA
28. Ifx-rsin A cos C. vrsinA sin and7-rcOSA nrovo the
… Докажите, что 1-sinA
1-cosA
28. Ifx-rsin A cos C. vrsinA sin and7-rcOSA nrovo the
… |
Sholr — крупнейшая в Индии платформа для обмена знаниями. Отправляйте свои вопросы на Эксперты.
Спросите
Copyright Scholr 2018 ©
मन में है सवाल?
घर
पूछें
2.
 3.9: Тригонометрические функции углов больше 360 градусов
3.9: Тригонометрические функции углов больше 360 градусов- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14465
На основе котерминальных и опорных углов.
Находясь в местном парке развлечений с друзьями, вы катаетесь на картинге. Вы объезжаете круговую трассу на телегах три с половиной раза, а затем останавливаетесь на «пит-стопе» для отдыха. Ожидая, пока ваш Go Kart заправится топливом, вы разговариваете с друзьями о поездке. Вы знаете, что один из способов измерения того, как далеко что-то прошло по кругу (или связанных с ним триггерных значений), заключается в использовании углов. Однако вы прошли более одного полного круга по трассе.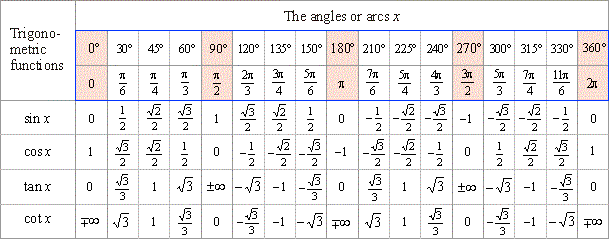 9{\circ}\).
9{\circ}\).
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 1.20.
Дополнительные ресурсы
Интерактивный элемент
Видео: Единичный круг
Практика: Тригонометрические функции углов больше 360 градусов
Эта страница под названием 2.3.9: Тригонометрические функции углов больше 360 градусов распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, который был отредактирован в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- CK12
- Лицензия
- СК-12
- Программа ООР или издатель
- СК-12
- Теги
- источник@https://www.
 ck12.org/c/trigonometry
ck12.org/c/trigonometry
- источник@https://www.
Точные значения тригонометрических функций
Найдите точные значения тригонометрических функций, не используя калькулятор. Представлены вопросы с решениями и ответами. Тригонометрические тождества и формулы на этом сайте могут быть использованы для решения приведенных ниже вопросов.
| Предположим, что мы хотим найти точное значение f(x), где f — любая из шести тригонометрических функций синуса, косинуса, тангенса, котангенса, секанса и косеканса. Чтобы найти точное значение f(x), мы предлагаем следующие шаги: 1 — Если угол x отрицательный, мы сначала используем формулу для отрицательных углов, такую как sin (- x) = — sin (x), cos (- x) = cos (x) и так далее.  2 — Затем мы находим конечную сторону рассматриваемого угла напрямую или с помощью положительного котерминального угла t, который дает знак тригонометрической функции. 3 — Находим относительный угол Tr к рассматриваемому углу и используем тот факт, что f(x) = + или — f(Tr). Знак + или — определяется с использованием квадранта, найденного на шаге 2. Если рассматриваемый угол или его котерминальный угол находятся в квадранте 1, этот последний шаг не требуется. Вопрос 1Найдите точное значение sin (- Pi / 3). Ответ на вопрос 1:
Вопрос 2Найдите точное значение cos (- 390 o ). Решение вопроса 2:
Вопрос 3Найдите точное значение секунды (3 Пи / 4). Ответ на вопрос 3:
Вопрос 4Найдите точную стоимость детской кроватки ( 840 o ).  Ответ на вопрос 4:
Вопрос 5Найдите точное значение csc (- 7 Pi/4). 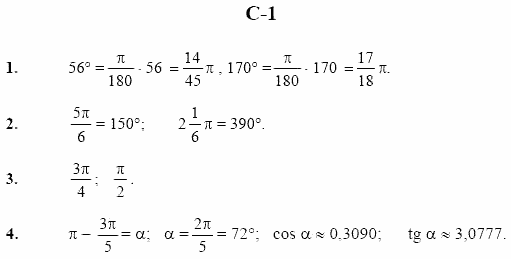 Решение вопроса 5:
Вопрос 6Найдите точное значение кроватки (121 Пи / 3).  Ответ на вопрос 6:
Вопрос 7Найдите точное значение секунды (- 3810 o ). Ответ на вопрос 7:
 |
report this ad
Prove that sin 600circ cos 390circ +cos 480circ sin class 11 maths CBSE
Answer
Verified
231.3k+ views
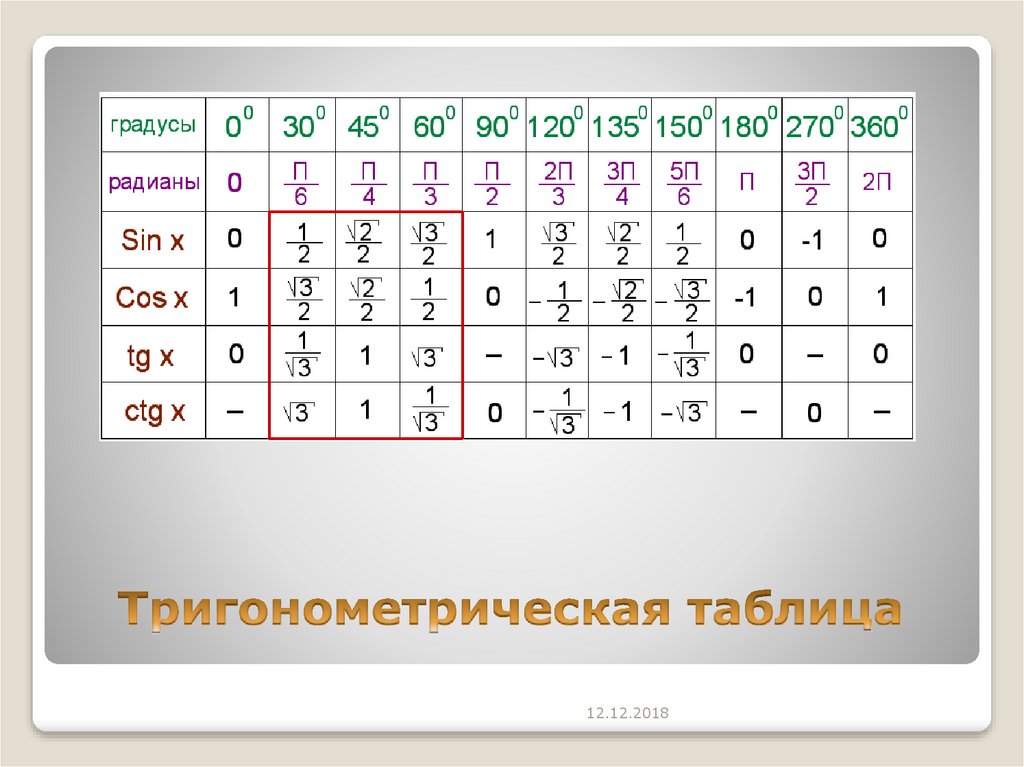
Hint: For solving this problem, first converting the angle given in постановка задачи в диапазоне от 0 до 90 градусов с использованием подходящих тригонометрических свойств. Теперь мы используем тригонометрическую таблицу значений, чтобы доказать эквивалентность обеих сторон.
Полный пошаговый ответ:
Некоторые важные тригонометрические формулы, используемые при решении этой задачи:
\[\begin{align}
& \sin \left( 360-\theta \right)=- \sin \theta \\
& \cos \left( 360+\theta \right)=\cos \theta \\
& \cos \left( 180-\theta \right)=-\cos \theta \\
& \sin \left( 180-\theta \right)=\sin \theta \\
\end{align}\]
Конкретное значение функций sin и cos можно проиллюстрировать следующим образом: 9\circ $
Теперь, подставляя значения из приведенной выше таблицы, получаем
$\begin{align}
& \Rightarrow -\dfrac{\sqrt{3}}{2}\times \dfrac{\sqrt{3 }}{2}-\dfrac{1}{2}\times \dfrac{1}{2} \\
& \Rightarrow -\dfrac{3}{4}-\dfrac{1}{4} \\
& \Rightarrow \dfrac{-4}{4}=-1 \\
\end{align}$
Следовательно, мы доказали эквивалентность обеих частей, рассмотрев выражение левой части.

 2/a, если loga b = -3
2/a, если loga b = -3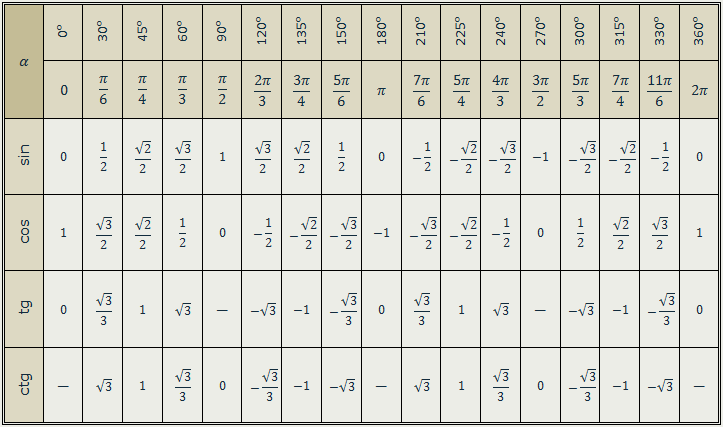 05.17
05.17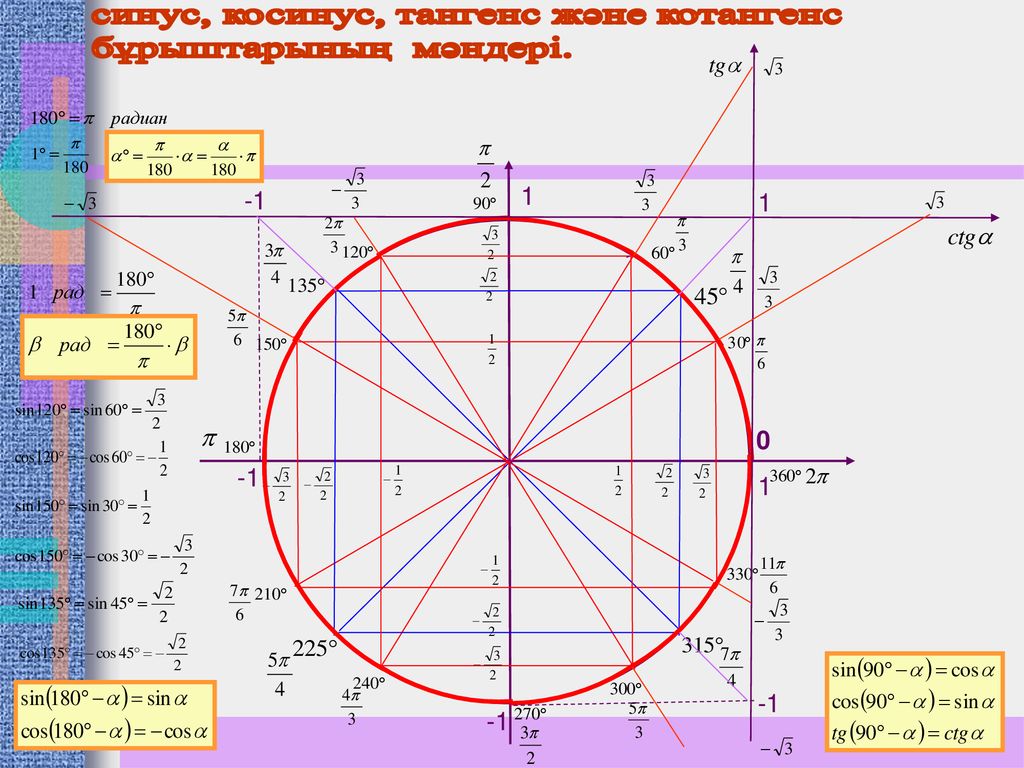 Световой поток — 720лм, габаритные размеры — 505×51×42 мм, вес — 0,65 кг, цветовая температура — 4000К
Световой поток — 720лм, габаритные размеры — 505×51×42 мм, вес — 0,65 кг, цветовая температура — 4000К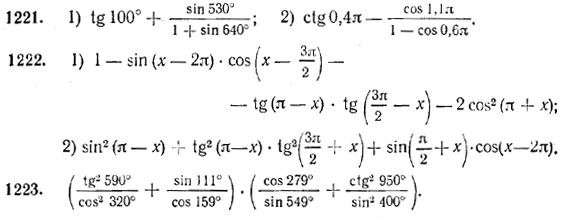 Степень защиты — IP65. Габаритные размеры — 114х95х85 мм. Вес — 0,47 кг.
Степень защиты — IP65. Габаритные размеры — 114х95х85 мм. Вес — 0,47 кг. Светодиодный прожектор Shine SMD 20W 120° выпускается со цветовой температурой света 6000К. На плате используется 36 светодиодов.
Светодиодный прожектор Shine SMD 20W 120° выпускается со цветовой температурой света 6000К. На плате используется 36 светодиодов.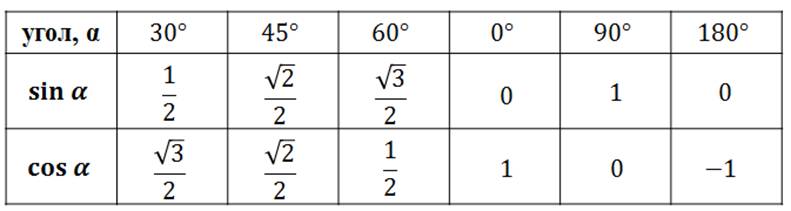

 LED-прожектор Shine COB 50W 120° выпускается со цветовой температурой света 6000К.
LED-прожектор Shine COB 50W 120° выпускается со цветовой температурой света 6000К.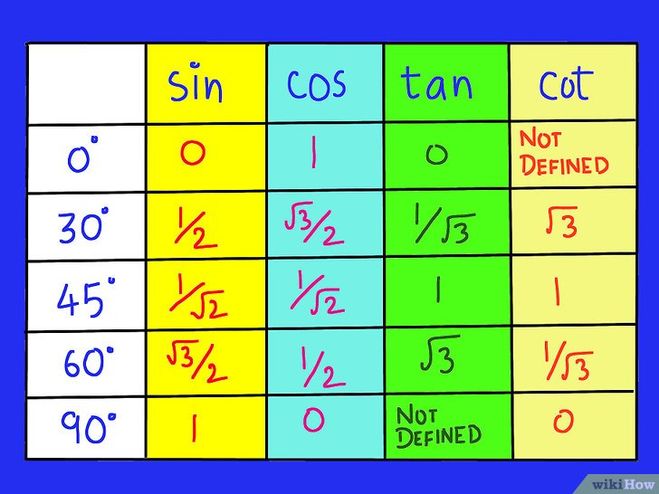
 Светодиодный прожектор Shine COB 100W 120° выпускается со цветовой температурой света 6000К.
Светодиодный прожектор Shine COB 100W 120° выпускается со цветовой температурой света 6000К.

 Светодиодный прожектор Shine 12W может иметь угол рассеивания света 30° и 60°. Цветовая температура света 6000К.
Светодиодный прожектор Shine 12W может иметь угол рассеивания света 30° и 60°. Цветовая температура света 6000К. Каждый светодиод снабжен индивидуальной линзой, оптика которой рассчитана так, чтобы световое пятно прожектора было круглой формы и имело равномерное светораспределение.
Каждый светодиод снабжен индивидуальной линзой, оптика которой рассчитана так, чтобы световое пятно прожектора было круглой формы и имело равномерное светораспределение.
 Степень защиты — IP65. Габаритные размеры (с креплением) — 270 х 250 х 118 мм. Вес — 3,2 кг.
Степень защиты — IP65. Габаритные размеры (с креплением) — 270 х 250 х 118 мм. Вес — 3,2 кг.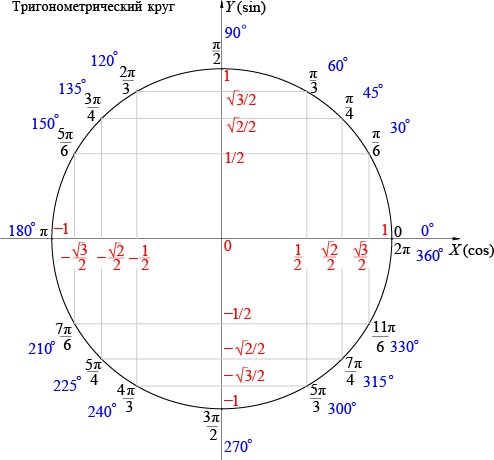 . .
. . [Подсказка: используйте cos 390° = 0,866]
[Подсказка: используйте cos 390° = 0,866]  ck12.org/c/trigonometry
ck12.org/c/trigonometry sin (- Pi / 3) оценивается непосредственно следующим образом
sin (- Pi / 3) оценивается непосредственно следующим образом 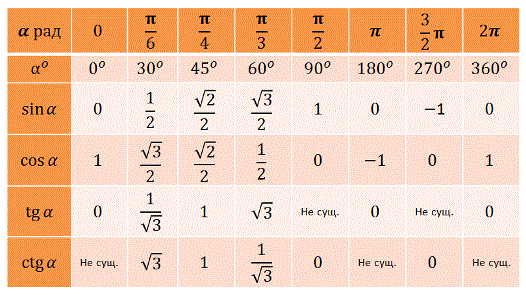
 Следовательно
Следовательно