2+n-72)=1/(n+9)Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
04.16
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .
.. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
Высота правильной треугольной пирамиды равно…
задумали число,увеличили его на 1/7…
Решите задачу. На координатной прямой отмечены точки А(2) и В(10). Найдите координату точки М, расположенной вне отрезка АВ, если известно, что: а) АМ : АВ = 3 : 1; б) АМ : МВ = 1 : 3.
геометрическая прогрессия bn задана условиями b1=-6. bn+1=2bn .Найдите b6
Пользуйтесь нашим приложением
[tex] \sin( x ) \cos( x)
15.04.2019 09:13, qwerty06151
Всего ответов: 1
Посмотреть ответы
Похожие вопросы:
Алгебра, 27.02.2019 16:20
.(Андрей собирает модель самолёта. за 6 часов он выполнил 2/3 всей работы. сколько ещё времени нужно андрею чтобы собрать модель полностью?).
Ответов: 3
Открыть
Алгебра, 28.
2 -6у+13) 3)пусть x1 и x2 — корни уравнения x(2x-3)=1. найдите (в степени -1*)
Ответов: 2
Открыть
Алгебра, 28.02.2019 10:20
Вбассейн проведены четыре трубы. через первые две трубы вода втекает в бассейн, через две другие вытекает. если работают все четыре трубы одновременно, то бассейн наполняется за 2,5 часа. если работают первая, вторая и третья
трубы, то бассейн наполняется за 1,5 часа. если работают первая, третья и четвертая трубы, то бассейн наполняется за 15 часов. найти время за которое наполнит бассейн только первая и третья трубы.
Ответов: 4
Открыть
Алгебра, 28.02.2019 11:00
Спортсмен прыгает с трамплина в воду: сначала трамплин подбрасывает его вверх на 1 метр, затем он летит вниз на 6 метров и, выныривая, поднимается на 2 метра до поверхности. на какой высоте над водой находится трамплин
Ответов: 4
Открыть
Алгебра, 28.02.2019 15:20
Какие из чисел -2, -1, 0, 2, 3 являются корнями многочлена x в кубе минус 3x в квадрате минус 4x плюс 12?
Ответов: 3
Открыть
Алгебра, 28.
2+5x )-x(x-5)=0
Ответов: 2
Открыть
Алгебра, 02.03.2019 22:30
Найдите значение выражения .3 квадратный корень из 2 * на 4 квадратный корень из 10 * квадратный корень из 5
Ответов: 2
Открыть
Алгебра, 03.03.2019 00:20
Напишите уравнение касательной к графику функции y=ln(15-7x) в точке x=2.
Ответов: 4
Открыть
Вопросы по другим предметам:
Английский язык, 12.07.2019 23:10
Как прочитать стих на буквами handy pandy, jack-a-dandy, loves plum cake and sugar candy. he buys some at the grocer’s shop and out he comes, hop, hop, hop!…
Физика, 12.07.2019 20:38
Какое соотношение выражает закон фарадея для электролиза…
Математика, 12.07.2019 23:10
Как делить столбиком например 312/39…
Геометрия, 12.07.2019 23:10
Концы отрезка ab удалены от плоскости альфа на расстояние a и b. найти расстояние от середины ab до плоскости альфа; если данный отрезок а)не пересекает альфа б)пересекает альфа с.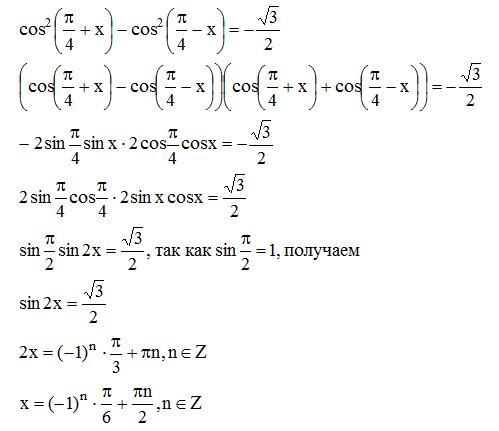
..
Обществознание, 12.07.2019 23:10
Достаточно ли того, чтобы человек в жизни действовал в соответствии со своими желаниями? ответ 1.нет, так это противоречит закону…
Английский язык, 12.07.2019 23:10
Complete the text . use the verbs in past simple . what name can you give to the text . last summer victor ( decide ) 1 to take up water polo. he ( to think) 2 the game ( be) 3 eas…
Биология, 12.07.2019 23:10
Выберите из предложенных терминов лишний и обоснуйте свой выбор чиж медведь ящерица сосна медуза яблоня олень лиса сова ландыш…
Математика, 12.07.2019 23:10
Дробные выражения: 0,68*3/4 3,212: 4/5 5/6*24,6 0,121: 11/12 43,75*2/35 13/21*8,4 5,6: 3 целых 1/2 10 целых 2/3*6,3 2 целых 3/20*4,2…
Українська мова, 12.07.2019 23:10
Составить предложения с словосочетаниями: не розквітлі на сонці кульбаби, не вмитий дощем сад, ніким не порушувана тиша )…
Математика, 12.07.2019 23:10
Алпай, бякир и джейхун играли во дворе в футбол.
один из них случайно попал мячом в окно и разбил стекло. алпай сказал: «стекло разбил не я».бякир: «стекло разбил джейхун».затем вы…
Еще вопросы по предмету: Алгебра Другие вопросы
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | угловой синус(-1) | ||
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Видео с вопросами: Нахождение общего решения тригонометрического уравнения cos (3𝑥) = sin (𝑥/4)
Расшифровка видео
Найдите общее решение
уравнение cos трех 𝑥 равен греху 𝑥 над четырьмя.
Нам даны тригонометрические уравнение cos три 𝑥 равно sin 𝑥 больше четырех и попросили найти общее решение. Поэтому мы хотим решить эту проблему для всех возможные 𝑥-значения, удовлетворяющие данному уравнению. Теперь мы можем попробовать использовать некоторые тригонометрические тождества, чтобы переписать нашу левую часть, что мы можем сделать, если напишем три 𝑥 как два 𝑥 плюс 𝑥. Затем мы могли бы попробовать использовать сумму тождество для cos 𝐴 плюс 𝐵, которое говорит нам, что cos 𝐴 плюс 𝐵 равно cos 𝐴 cos 𝐵 минус sin 𝐴 sin 𝐵 и с 𝐴 равно двум 𝑥 и 𝐵 равно 𝑥 дает cos два 𝑥 умножить на cos 𝑥 минус грех два 𝑥 умножить на грех 𝑥 равно грех 𝑥 больше четырех.
Мы пытаемся добраться до левого и
правые части в аналогичные формы, поэтому мы могли бы попробовать использовать двойной угол
тождества для cos two 𝐴 и sin two 𝐴.
Это дает, например, cos
в квадрате 𝑥 минус квадрат греха 𝑥 умножить на cos 𝑥 минус два греха в квадрате 𝑥 умножить на cos 𝑥
равно греху 𝑥 больше четырех. Затем с помощью пифагорейского
тождество cos в квадрате 𝐴 плюс sin в квадрате 𝐴 равно единице дает cos 𝑥 умножить на
четыре кос в квадрате 𝑥 минус три равно греху 𝑥 больше четырех.
Мы уменьшили аргумент
косинусов слева просто 𝑥, но справа у нас все еще есть грех 𝑥
более четырех. И как-то не манипулируя
аргумент 𝑥 больше четырех превращается всего в 𝑥, теперь мы ближе к поиску решений для
𝑥. Итак, наш метод использования обычного
тригонометрические тождества, похоже, здесь не работают. Итак, давайте попробуем взглянуть на это с
другой угол. Если вместо этого рассматривать часть
графики функций косинуса и синуса, мы видим, например, что cos нуля
равно греху 𝜋 на два, что равно единице.
cos 𝜋 на два равно sin 𝜋,
что равно нулю. Точно так же cos отрицательного 𝜋 на
два равно грех нуля равно нулю. И потому что отрицательный 𝜋 равен греху
отрицательного 𝜋 на два равно отрицательному единице и так далее.
На самом деле схема здесь такая cos угла 𝜃 равен греху 𝜋 на два плюс-минус 𝜃. Так, например, если 𝜃 равно 𝜋, взяв положительный вариант, мы имеем cos 𝜋, равный греху 𝜋 на два плюс 𝜋, что является грехом три 𝜋 на два. А грех троих 𝜋 на двоих есть отрицательный, который совпадает с cos 𝜋. Аналогично, для отрицательного варианта у нас есть cos 𝜋, равный греху 𝜋 на два минус 𝜋. Это грех отрицательного 𝜋 by два, что снова является отрицательным. И это работает для любого угла 𝜃.
Так что освободим немного места и
применяя это к левой части нашего уравнения, потому что три 𝑥, так что 𝜃
равно трем 𝑥, у нас есть cos трех 𝑥, равный sin 𝜋 на два плюс-минус три
𝑥.
И это должно равняться правой руке
сторона нашего исходного уравнения; это грех 𝑥 больше четырех. Итак, теперь у нас есть грех 𝜋 на два
плюс-минус три 𝑥 равно греху 𝑥 больше четырех, и все в
условия синусов. Давайте теперь назовем 𝜋 на два плюс или
минус три 𝑥 𝐴 и 𝑥 больше четырех 𝐵, так что наше уравнение sin 𝐴 равно
грех 𝐵.
Мы можем изменить это, чтобы дать грех
𝐴 минус грех 𝐵 равно нулю. И если мы сможем решить это уравнение,
мы должны быть в состоянии найти наше общее решение для 𝑥. Для этого вспомним сумму и
разностное тригонометрическое тождество. Это говорит нам о том, что в два раза
Кос 𝐴 плюс 𝐵 больше двух, умноженный на грех 𝐴 минус 𝐵 больше двух, равен
грех 𝐴 минус грех 𝐵. Теперь в нашем случае грех 𝐴 минус грех
𝐵 равно нулю, и в нашей идентичности есть два способа, которыми это может
происходить.
Либо потому что 𝐴 плюс 𝐵 больше двух должно
быть равным нулю, или грех 𝐴 минус 𝐵 больше двух должен быть равен нулю.
Принимая первый из них, из-за 𝐴 плюс 𝐵 больше двух равно нулю, если мы снова посмотрим на график косинуса мы видим, что cos 𝜃 равно нулю, когда 𝜃 равно 𝜋 больше двух плюс 𝑛𝜋, где 𝑛 — целое число. В нашем случае это означает, что 𝐴 плюс 𝐵 больше двух должно равняться 𝜋 больше двух плюс 𝑛𝜋. А если умножить на два, это дает 𝐴 плюс 𝐵 равно 𝜋 плюс два 𝑛𝜋. Освободив немного места, мы можем подставим наши выражения вместо 𝐴 и 𝐵. Теперь вычтем 𝜋 более двух из с обеих сторон, у нас есть положительные или отрицательные три 𝑥 плюс 𝑥 больше четырех равно 𝜋 плюс два 𝑛𝜋 минус 𝜋 больше двух.
Теперь ставим нашу левую сторону
над общим знаменателем четырех и немного упростив нашу правую часть, то
умножая обе части на четыре, мы имеем две возможности в левой части:
либо взять первое положительное 12𝑥 плюс 𝑥, поэтому 13𝑥 равно двум 𝜋 плюс
восемь 𝑛𝜋, или с минусом 12𝑥 плюс 𝑥 получаем минус 11𝑥 равно двум 𝜋
плюс восемь 𝑛𝜋.
Итак, расчищая немного места,
деление обеих частей на 13 в нашем первом решении дает нам 𝑥, равное двум 𝜋 больше 13
плюс восемь 𝑛𝜋 больше 13. Далее, разделив наше второе уравнение
на минус 11 мы имеем 𝑥, равное двум 𝜋 на минус 11 плюс восемь 𝑛𝜋 на
отрицательное 11. А так как 𝑛 — любое целое число,
положительный или отрицательный, мы можем переписать это как отрицательное два 𝜋 больше 11 плюс восемь 𝑛𝜋
более 11,
Общее решение проблемы уравнение потому что три 𝑥 равно sin 𝑥 больше четырех, поэтому 𝑥 равно двум 𝜋 больше 13 плюс восемь 𝑛𝜋 больше 13, а 𝑥 равно минус два 𝜋 больше 11 плюс восемь 𝑛𝜋 больше 11, где 𝑛 — целое число.
Теперь вы можете вспомнить, что были
два возможных направления, по которым мы могли бы следовать из нашего тригонометрического тождества греха
𝐴 минус грех 𝐵. Мы могли бы также попытаться решить
грех 𝐴 минус 𝐵 больше двух равно нулю.
Но на самом деле это дает нам ровно
тот же набор решений, который мы нашли, решая cos 𝐴 плюс 𝐵 над двумя, равен
ноль, поэтому наше решение завершено.
Решения NCERT для математики 11 класса, глава 3, тригонометрические функции
Получить бесплатно Решения NCERT для математики 11 класса, глава 3, тригонометрические функции Ex 3.1, Ex 3.2, Ex 3.3, Ex 3.4 и различные упражнения PDF на хинди и английском языке Medium. Тригонометрические функции Класс 11 Математика Решения NCERT чрезвычайно полезны при выполнении домашних заданий. Тригонометрические функции Все упражнения Решения NCERT по математике для 11 класса были подготовлены опытными учителями LearnCBSE.in.
Математические тригонометрические функции класса 11 Решения NCERT на английском языке Medium и языке хинди Medium
- Тригонометрические функции класса 11 Ex 3.1
- Тригонометрические функции Класс 11 Ex 3.2
- Тригонометрические функции Класс 11 Ex 3.
3 - Тригонометрические функции Класс 11 Ex 3.4
- Тригонометрические функции Класс 11 Разное упражнение
- त्रिकोणमितीय फलन प्रश्नावली 3.1 का हल हिंदी म ू94
- त्रिकोणमितीय फलन प्रश्नावली 3.2 का हल हिंदी म ।
- त्रिकोणमितीय फलन प्रश्नावली 3.3 का हल हिंदी म ू 904ी
- त्रिकोणमितीय फलन प्रश्नावली 3.4 का हल हिंदी म ।94म
- त्रिकोणमितीय फलन विविध प्रश्नावली क मल हिद2
- Тригонометрические формулы
- Тригонометрические функции Класс 11 Примечания
- Образец NCERT, класс 11, математика, глава 3, тригонометрические функции
- Шпаргалка по триггерам
- Основные вопросы тригонометрии JEE за предыдущий год
3 Скачать бесплатно Решения NCERT для 11 класса по математике Глава 3 Тригонометрические функции Примеры 3.1, Примеры 3.2, Примеры 3.3, Примеры 3.4 и Разное упражнение PDF на хинди Medium, а также на английском языке для студентов CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate и UP Board, которые используют книги NCERT на основе обновленной программы CBSE для сессии 2019-20.
| Название раздела | Название темы |
| 3.1 | Введение |
| 3.2 | Уголки |
| 3,3 | Тригонометрические функции |
| 3,4 | Тригонометрические функции суммы и разности двух углов |
| 3,5 | Тригонометрические уравнения |
| 3,6 | Резюме |
Решения NCERT для 11 класса по математике Глава 3 Упражнение 3.1
Упр. 3.1 Класс 11 Математика Вопрос 1:
Найдите радианы, соответствующие следующим градусным мерам:
(i) 25°
(ii) – 47° 30′
(iii) 240°
(iv) 520°
ANS:
EX 3.1 класс 11 Математика 2:
ANS:
(I) \ FRAC as while as whip rak rac as wis rak as his.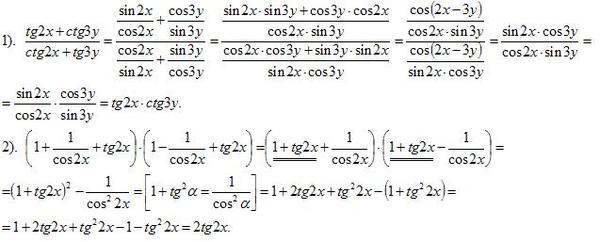
радиан = 180°
∴ \(\frac{11}{16}\) radain = \(\frac{180}{\pi} \times \frac{11}{16}\) × степень
= \(\frac{45 \times 11}{\pi \times 4}\) градус
= \(\frac{45 \times 11 \times 7}{22 \times 4}\) градус
= \(\frac{315}{8}\) градус
= 39 \(\frac{3}{8}\) градус
= 39° + \(\frac{3 \times 60}{8} \) минут [1° = 60′]
= 39° + 22′ + \(\frac{1}{2}\) минут
= 39°22’30” [1′ = 60°].
Дополнительные ресурсы для CBSE Class 11
- Решения NCERT
- Решения NCERT Класс 11 Математика
- Решения NCERT, класс 11, физика
- Решения NCERT, класс 11, химический состав
- Решения NCERT, класс 11, биология
- Решения NCERT, класс 11, хинди
- Решения NCERT, класс 11, английский язык
- NCERT Solutions, класс 11, бизнес-исследования
- Решения NCERT, класс 11, бухгалтерский учет
- Решения NCERT, класс 11, психология
- Решения NCERT, класс 11, предпринимательство
- Решения NCERT Класс 11 Экономическое развитие Индии
- Решения NCERT, класс 11, информатика
Пример 3.
1 Класс 11 Математика Вопрос 3:
Колесо делает 360 оборотов за одну минуту. На сколько радиан он поворачивается за одну секунду?
Ответ:
Количество оборотов колеса за 1 минуту = 360
∴ Количество оборотов колеса за 1 секунду = \(\frac{360}{6}\) = 6
За один полный оборот , колесо поворачивается на угол 2π радиан.
Следовательно, за 6 полных оборотов он повернется на угол 6 × 2π радиан, т. е. 12π радиан
Таким образом, за одну секунду колесо поворачивается на угол 12π радиан.
Пример 3.1 Математика для 11 класса. Вопрос 4:
Найдите градусную меру угла, опирающегося на центр окружности радиусом 100 см и дугу длиной 22 см (Используйте π = \(\frac{22}{7 }\)).
Ответ:
Мы знаем, что в окружности радиуса r единицы, если дуга длины l единица образует угол θ радиан в центре, то θ = \(\frac{l}{r}\)
Следовательно, для r = 100 см, l = 22 см,
имеем
Таким образом, требуемый угол равен 12°36′.
Упражнение 3.1 Класс 11 Математика Вопрос 5:
В круге диаметром 40 см длина хорды составляет 20 см. Найдите длину малой дуги хорды.
Ответ:
Дано, диаметр = 40 см
∴ радиус (r) = \(\frac{40}{2}\) = 20 см
и длина хорды AB = 20 см
Таким образом, ∆OAB – равносторонний треугольник.
Мы знаем, что
θ = \(\frac{\text {Arc} A B}{\text {radius}}\)
⇒ Дуга AB = θ × r
= \(\ frac{\pi}{3}\) × 20 .
= \(\frac{20}{3}\) π см.
Пример 3.1 Класс 11 Математика Вопрос 6:
Если в двух окружностях дуги одинаковой длины образуют углы 60° и 75° в центре, найдите отношение их радиусов.
Ответ:
Пусть радиусы двух окружностей равны r 1 и r 2 .
Пусть дуга длины l образует угол 60° в центре окружности радиуса r 1 , а дуга длины l образует угол 75° в центре окружности радиуса r 2 .
Теперь 6o° = \(\frac{\pi}{3}\) радиан и
75° = \(\frac{5 \pi}{12}\) радиан
Мы знаем, что в окружности радиуса r единица, если дуга длины l единицы образует угол θ радиан в центре, то θ = \(\frac{l}{r}\) или l = rθ
∴ l = \(\frac{r_{1} \pi}{3}\) и
l = \(\frac{r_{2} 5 \pi}{12}\)
⇒ \(\frac{r_{1} \pi}{3}= \frac{r_{2} 5 \pi}{12}\)
⇒ r = \(\frac{r_{2} 5}{4}\)
\(\frac{r_{1}}{ r_{2}}=\frac{5}{4}\)
Таким образом, отношение радиусов равно 5 : 4.
Упражнение 3.1 Класс 11 Математика Вопрос 7:
Найдите угол в радианах, на который качается маятник, если его длина составляет 75 см, а кончик описывает дугу длиной
(i) 10 см
(ii) 15 см
(iii) 21 см.
Ответ:
Мы знаем, что в круге радиуса r единицы, если дуга длины l единица образует угол θ радиан в центре, то
θ = \(\frac{l}{r}\) .
Дано, что r = 75 см
(i) Здесь l = 10 см
θ = \(\frac{10}{75}\) радиан
= \(\frac{2}{15}\) радиан
(ii) Здесь l = 15 см
θ = \(\frac{15}{75}\) радиан
θ = \(\frac{ 1}{5}\) радиан
(iii) Здесь l = 21 см
θ = \(\frac{21}{75}\) радиан
= \(\frac{7}{75}\) радиан .
Пример 3.2 Класс 11 по математике Вопрос 1:
Найдите значения других пяти тригонометрических функций, если cos x = – \(\frac{1}{2} \) x лежит в третьем квадранте.
Ответ:
Пример 3.2 Математика для 11 класса Вопрос 2:
Найдите значения других пяти тригонометрических функций, если sin x = \(\frac{3}{5}\), x лежит во втором квадранте.
Ответ:
sin x = \(\frac{3}{5}\)
cosec x = \(\frac{1}{\sin x}=\frac{1}{\left(\ frac{3}{5}\right)}=\frac{5}{3}\)
sin 2 x + cos 2 x = 1
⇒ cos 2 x = 1 – sin 2 x
⇒ cos 2 x = 1 – (\(\frac{3}{5}\)) 2
⇒ cos 2 x = 1 – \(\frac{9}{25}\)
⇒ cos 2 x = \(\frac{16}{25}\)
⇒ ⇒ cos x = ± \(\frac{4}{5}\)
Поскольку x лежит во 2-м квадранте, значение cos x будет отрицательным
Упр.
значения остальных пяти тригонометрических функций, если cot x = \(\frac{3}{4}\), x лежит в третьем квадранте.
Ответ:
⇒ \(\frac{4}{3}=\frac{\sin x}{\frac{-3}{5}}\)
⇒ sin x = \(\left(\frac{4}{3}\right) \times\left(\frac{-3}{5}\right)=-\frac{4}{5}\)
⇒ cosec x = \(\frac{1}{\sin x}=-\frac{5}{4}\).
Пример 3.2 Математика для 11 класса. Вопрос 4:
Найдите значения других пяти тригонометрических функций, если sec x = \(\frac{13}{5}\), x лежит в четвертом квадранте.
Ответ:
Пример 3.2 Математика для 11 класса, вопрос 5:
Найдите значения других пяти тригонометрических функций, если tan x = \(\frac{5}{12}\), x лежит во втором квадранте.
Ответ:
tan x = – \(\frac{5}{12}\)
cot x = \(\frac{1}{\tan x}=\frac{1}{\left( -\frac{5}{12}\right)}=-\frac{12}{5}\)
1 + tan 2 x = sec 2 x
Пример 3.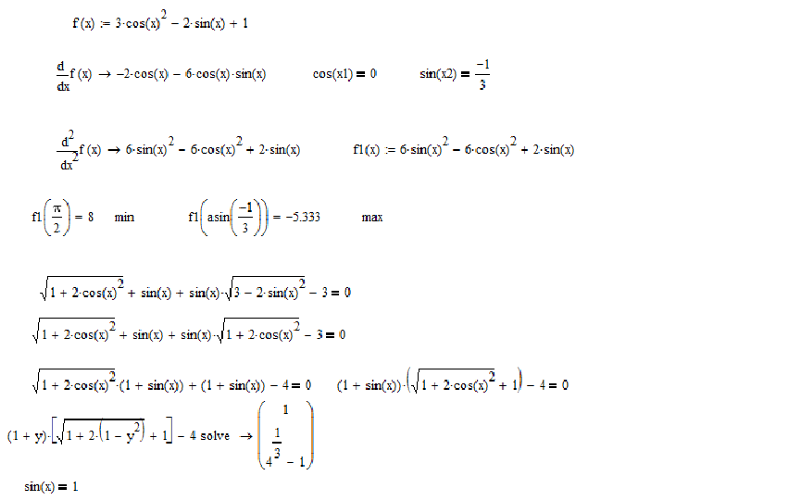
2 Класс 11 Математика Вопрос 6:
Найдите значение тригонометрической функции sin 765°.
Ответ:
Известно, что значения sin x повторяются через интервал 2π или 360°.
∴ sin 765° = sin (2 × 360° + 45°)
= sin 45° = 1
Пример 3.2 Математика для 11 класса Вопрос 7:
Найдите значение тригонометрической функции cosec (- 1410°)
Ответ:
Известно, что значения cosec x повторяются через интервал 2π или 360°.
∴ cosec (- 1410°) = cosec (- 1410° + 4 x 360°)
= cosec (- 1410° + 1440°)
= cosec 30° = 2.
Пример 3.2 Класс 11 Математика Вопрос 8:
Найдите значение тригонометрической функции tan \(\frac{19 \pi}{3}\).
Ответ:
Известно, что значения tan x повторяются через интервал π или 180°.
∴ \(\tan \frac{19 \pi}{3}=\tan 6 \frac{1}{3} \pi\)
= \(\tan \left(6 \pi+\frac{\pi {3}\right)=\tan \frac{\pi}{3}\)
= tan 60° = √3.
Пример 3.2 Математика для 11 класса. Вопрос 9:
Найдите значение тригонометрической функции sin \(\left(-\frac{11 \pi}{3}\right)\).
Ответ:
Известно, что значения ctg x повторяются через интервал π или 180°. 9{\circ}=\frac{\sqrt{3}}{2}\)
Пример 3.2 Математика 11 класса Вопрос 10:
Найдите значение тригонометрической функции кроватки \(\left(-\frac{15) \pi}{4}\справа)\).
Ответ:
Известно, что значения cot x повторяются через интервал ir или 1800.
∴ \(\cot \left(-\frac{15 \pi}{4}\right)=\ cot \left(-\frac{15 \pi}{4}+4 \pi\right)=\cot \frac{\pi}{4}\) = 1.
= \(\frac{1}{4}+\frac{1}{4}-1=-\frac{1}{2}\)
= R.H.S.
Значит доказано.
Упр. 3.3 Класс 11 Математика Вопрос 2:
Докажите, что: 2 sin 2 \(\frac{\pi}{6}\) + cosec 2 \(\frac{7 \pi}{6 }\) cos 2 \(\frac{\pi}{3}\) = \(\frac{3}{2}\)
Ответ:
Пример 3.
3 Класс 11 Математика Вопрос 3:
Докажите, что :cot 2 \(\frac{\pi}{6}\) + cosec \(\frac{5 \pi}{6}\) + 3 tan 9{2}\) + 1 + 8
= 1 + 1 + 8
= 10 = П.С.
Значит доказано.
Пример 3.3 Класс 11 Математика Вопрос 5:
Найдите значение: (i) sin 75°,
(ii) tan 15°
Ответ:
(i) sin 75° sin (45° + 30°)
= sin 45° cos 30° + cos 45° sin 30°
[∵ sin (x + y) = sin x cos y + cos x sin y]
= \(\left(\frac{1} {\ sqrt {2}} \ right) \ left (\ frac {\ sqrt {3}} {2} \ right) + \ left (\ frac {1} {\ sqrt {2}} \ right) \ left ( \frac{1}{2}\right)\)
= \(\frac{\sqrt{3}}{2 \sqrt{2}}+\frac{1}{2 \sqrt{2}}= \ гидроразрыва {\ sqrt {3} + 1} {2 \ sqrt {2}} \) 9{2} x}\)
= детская кроватка 2 x
= RHS
Отсюда доказано.
Пример 3.3 Класс 11 Математика Вопрос 9:
= 1
Ответ:
= 1 = RHS
Следовательно, доказано.
Пример 3.3 Класс 11 Математика Вопрос 10:
Докажите, что: sin (n + 1) x sin (n + 2) x + cos (n + 1) x cos (n + 2) x = cos x
Ans :
LHS = sin (n + 1) x sin (n + 2) x + cos (n + 1) x cos (n + 2) x
[По формуле cos (A – B) = cos A cos В + грех А грех В]
= cos [(n + 2) x + (n + 1) x]
= cos (4x + 2x – 4x – x)
= cos x = R.H.S.
Значит доказано.
Пример 3.3 Математика для 11 класса Вопрос 11:
Докажите, что: \(\cos \left(\frac{3 \pi}{4}+x\right)-\cos \left(\frac{3 \pi} {4}-x\right)=-\sqrt{2} \sin x\)
Ответ:
Известно, что
cos A – cos B = \(-2 \sin \left(\frac{ A+B}{2}\right) \cdot \sin \left(\frac{A-B}{2}\right)\)
∴ LHS= \(=\cos \left(\frac{3 \pi} {4}+x\right)-\cos\left(\frac{3 \pi}{4}-x\right)\)
= \(– 2 \sin \left\{\frac {\left(\frac{3 \pi}{4}+x\right)+\left(\frac{3 \pi}{4}-x \right)}{2}\right\} \cdot \sin \left\{\frac {\left(\frac{3 \pi}{4}+x\right)-\left(\frac{3 \pi {4}-x\right)}{2}\right\}\)
= – 2 sin (\(\frac{3 \pi}{4}\)) sin x
= – 2 sin ( — \(\frac{\pi}{4}\)) sin x
= — √2 sin x = R. H.S.
Значит доказано.
Пример 3.3 Класс 11 Математика Вопрос 12:
Докажите, что: sin 2 6x – sin 2 4x = sin 2x sin 10 x
Ответ:
Известно, что
sin A + sin B = 2 \(\sin \left(\frac{A-B}{2}\right) \cos \left(\frac{A-B}{2} \right)\)
sin A – sin B = 2 \(\cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right) \)
L.H.S.= sin 2 6x – sin 2 4x
= (sin 6x + sin 4x) (sin 6x – sin 4x)
= (2 sin 5x cos x) (2 cos 5x sin x)
= (2 sin 5x cos 5x) (2 sin x cos x)
= sin 10x sin 2x = R.H.S.
Значит доказано.
Пр.3.3 Класс 11 Математика Вопрос 13:
Докажите, что: cos 2 2x cos 2 6x = sin 4x sin 8x
Ответ:
\cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\)
cos A – cos = 2 \(\sin \left (\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)\)
∴ LHS = cos 2 2x – cos 2 6x
= (cos 2x + cos 6x) (cos 2x — 6x)
= \(\left[2 \cos \left(\frac{2 x+6 x}{2}\right) \cos \left(\frac{2 x-6 x}{2}\right)\right]\left[-2 \sin \left(\frac{2 x+6 x}{2}\right) \sin \frac{(2 x-6 x )}{2}\справа]\)
∴ L. H.S.= cos 2 2x – cos 2 6x
= (cos 2x + cos 6x) (cos 2x – 6x)
= [2 cos 4x cos (-2x)] [- 2 sin 4x sin (- 2x)]
= [2 cos 4x cos 2x] [- 2 sin 4x (- sin 2x)]
= (2 sin 4x cos 4x) (2 sin 2x cos 2x)
= sin 8x sin 4x
= R.H.S.
Значит доказано.
Упр. 3.3 Класс 11 Математика Вопрос 14:
Докажите, что: sin 2x + 2 sin 4x + sin 6x = 4 cos 6х
= [sin 2x + sin 6x] + 2 sin 4x
= \(\left[2 \sin \left(\frac{2 x+6 x}{2}\right) \cos \left(\frac{2) x-6 x}{2}\right)\right]\) + 2 sin 4x
[∵ sin A + sin B = 2 \(\sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\)]
= 2 sin 4x cos (- 2x) + 2 sin 4x
= 2 sin 4x cos 2x + 2 sin 4x
= 2 sin 4x ( cos 2x + 1)
= 2 sin 4x (2 cos 2 x – 1 + 1)
= 2 sin 4x (2 cos 2 x)
= 4 cos 2 x sin 4x
= R.H.S.
Значит доказано.
Пример 3.3 Класс 11 Математика Вопрос 15:
кроватка 4x (sin 5x + sin 3x) = кроватка x (sin 5x – sin 3x)
Ответ:
Пример 3. 3, класс 911, математика что: \(\frac{\cos 9 x-\cos 5 x}{\sin 17 x-\sin 3 x}=-\frac{\sin 2 x}{\cos 10 x}\)
Ответ:
Пример 3.3 Класс 11 Математика Вопрос 17:
Докажите, что: \(\frac{\sin 5 x+\sin 3 x}{\cos 5 x+\cos 3 x}\) = tan 4x
Ответ:
Известно, что
sin A + sin = 2 \(\sin\left(\frac{A+B}{2}\right) \cos\left(\frac{A-B}{2}\right)\)
cos A + cos = 2 \(\cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\)
∴ LHS = \(\frac {\ sin 5 x+\sin 3 x}{\cos 5 x+\cos 3 x}\)
= \(\frac{2 \sin\left(\frac{5 x+3 x}{2}\right ) \cos \left(\frac{5 x-3 x}{2}\right)}{2 \cos \left(\frac{5 x+3 x}{2}\right) \cos \left(\ frac{5 x-3 x}{2}\right)}\)
= \(\frac{2 \sin 4 x \cos x}{2 \cos 4 x \cos x}=\frac{\sin 4 х}{\cos 4 х}\) 9{2} x}\)
= \(\frac{2 \cos\left(\frac{x+3 x}{2}\right) \sin \left(\frac{x-3 x}{2) }\right)}{-\cos 2 x}\)
= \(\frac{2 \cos 2 x \sin (-x)}{-\cos 2 x}\)
= – 2 × ( — sin x) = 2 sin x
= R. H.S
Отсюда доказано.
Пример 3.3 Класс 11 Математика Вопрос 21:
Докажите, что: = детская кроватка 3x
Ответ:
Пример 3.3 Класс 11 Математика Вопрос 22:
Докажите, что: детская кроватка x детская кроватка 2x – детская кроватка 2x детская кроватка 3x – детская кроватка 3x детская кроватка x = 1 раскладушка 3x (раскладушка 2x + раскладушка x)
= раскладушка x раскладушка 2x – раскладушка (2x + x) (раскладушка 2x + раскладушка x)
= раскладушка x раскладушка 2x – \(\left[\frac{\cot 2 x \cot x-1}{\кроватка x+\кроватка 2 x}\right]\) (кроватка 2x + детская кроватка x)
[∵ детская кроватка (A + B) = \(\frac{\кроватка A \кроватка B-1}{ \раскладушка A+\раскладушка B}\)]
= раскладушка x раскладушка 2x – (раскладушка 2x раскладушка x – 1)
= 1 = R.H.S.
Значит доказано. 9{2} A}\)
Упр. 3.3 Класс 11 Математика Вопрос 24:
Докажите, что: cos 4x = 18 sin 2 x cos 2 x
Ответ: L. S.S. = cos 4x = cos 2(2x)
= 1 – 2 sin 2 2x [∵ cos 2A = 1 – 2 sin 2 A]
= 1 – 2(2 sin x cos x) 2 [∵ sin 2A = 2 sin A cos A]
= 1 – 8 sin 2 x cos 2 x
= R.H.S.
Значит доказано.
Пример 3.3 Класс 11 Математика Вопрос 25:
Докажите, что: cos 6x = 32 cos 6 x – 48 cos 4 x + 18 cos 2 x – 1
Ответ:
Мы знаем, что: cos 3x = 4 cos 3 x – 3cos, получить
cos 3(2x) = 4 cos 3 (2x) – 3 cos 2x
⇒ cos 6x = 4 (2cos 2 x – 1) 3 – 3 (2cos 1 х 9123) [∵ cos 2x = 2 cos 2 x – 1]
= 4 [8 cos 6 x – 12 cos 4 x + 6 cos 2 x – 1] – 6 cos 2 2 2 21031 [∵ (A — B) 3 = A 3 — 3A 2 B + 3AB 2 — B 3 ]
= 32 COS 6 x — 488 88 49 499 499 499 2 41239 41239 41239 41239 41239 41239 41239 41239 41239 41239 41239 41239 41239 41239 41239 4 4 4 32 32 39 41239 41239 4 = 32. cos 2 x – 4 – 6 cos 2 x + 3
⇒ cos 6x = 32 cos 6 x – 48 cos 4 x + 18 cos 1 x 9123
Пример 3.4 Математика для класса 11 Вопрос 1:
Найдите основное и общее решения уравнения, tan x = √3
Ответ:
tan x = √3
Известно, что:
tan \(\frac{\pi}{3}\) = √ 3 и
tan (\(\frac{4 \pi}{3}\)) = tan ( π + \(\frac{\pi}{3}\))
= tan \(\frac{\pi} {3}\) = √3
Таким образом, основными решениями являются x = \(\frac{\pi}{3}\) и \(\frac{4 \pi}{3}\).
Теперь tan x = tan \(\frac{\pi}{3}\)
⇒ x = nπ + \(\frac{\pi}{3}\), где n ∈ Z
Следовательно, общее решение есть x = nπ + \(\frac{\pi}{3}\), где n ∈ Z.
Пример 3.4 Математика для 11 класса Вопрос 2:
Найдите главное и общее решения уравнения: sec x = 2
Ответ:
sec x = 2
Известно, что:
sec \(\frac{\ pi}{3}\) = 2 и
сек \(\frac{5 \pi}{3}\) = sec (2π — \(\frac{\pi}{3}\))
= сек \( \frac{\pi}{3}\) = 2
Следовательно, главные решения равны x = \(\frac{\pi}{3}\) и \(\frac{5 \pi}{3}\) .
Теперь сек x = сек \(\frac{\pi}{3}\)
cos x = cos \(\frac{\pi}{3}\) [∵ sec x = \(\frac{1} {\ соз х} \)]
⇒ x = 2nπ ± \(\frac{\pi}{3}\), где n e Z
Следовательно, общее решение имеет вид x = 2nπ ± \(\frac{\pi}{3}\), где n ∈ Z.
Пример 3.4 Математика для 11 класса Вопрос 3:
Найдите главное и общее решения уравнения cot cot x = – √3.
Ans:
cot x = – √3
Пример 3.4 Класс 11 Математика Вопрос 4:
Найдите основное и общее решения cosec x = – 2
Ans:
x9 x9 –932 It известно, что:
cosec \(\frac{\pi}{6}\) = 2
Пример 3.4 Класс 11 Математика Вопрос 5:
Найдите общее решение уравнения: cos 4x = cos 2x
Ответ:
cos 4x = cos 2x
cos 4x — cos 2x = 0
— 2 sin \(\left(\frac{4 x+2 x}{2}\right)\) sin \(\left(\frac{4 x -2 x}{2}\right)\) = 0
[∵ cos A – cos B = 2 \sin \left(\frac{A+B}{2}\right) \sin \left(\frac {A-B}{2}\right)\(\)]
sin 3x sin x = 0
sin 3x = 0 or sin x = 0
3x = nπ или x = nπ, где n ∈ Z
x = \(\frac{n \pi}{3}\) или x = nπ, где n ∈ Z.
Упр. 3.4 Математика для 11 класса Вопрос 6:
Найдите общее решение уравнения cos 3x + cosx – cos 2x = 0
Ответ:
cos 3x + cos x – cos 2x = 0
2 cos \(\left(\frac{3 x+x}{2}\right)\) cos \( \left(\frac{3 xx}{2}\right)\) — cos 2x = 0
[∵ cos A + cos B = 2 \(\cos \left(\frac{A+B}{2} \right) \cos \left(\frac{A-B}{2}\right)\)]
2 cos 2x cos x – cos 2x = 0
cos 2x (2 cos x – 1) = 0
cos 2x = 0 или 2 cos x – 1 = 0
cos 2x = 0 или cos x = \(\frac{1{2}\)
∴ 2x = (2n + 1) \(\frac{\pi} {2}\) или cos x = cos \(\frac{\pi}{3}\), где n ∈ Z
x = (2n + 1) \(\frac{\pi}{4}\), или x = 2nπ ± \(\frac{\pi}{3}\), где n ∈ Z.
Упражнение 3.4, 11 класс, математика, вопрос 7:
Найдите общее решение уравнения sin 2x + cos x = 0
Ответ:
sin 2x + cos x = 0
⇒ 2sin x cos x + cos x = 0
⇒ cos x (2 sin x + 1) = 0
⇒ cos x = 0 или 2 sin x + 1 = 0
Теперь cos x = 0
⇒ x = (2n + 1) \(\frac{\pi}{2}\) , где n ∈ Z.
или 2 sin x + 1 = 0
⇒ sin x = – \(\frac{1}{2}\)
= – sin \(\frac{\pi}{6}\)
= sin (π + \(\frac{\pi}{6}\) )
= sin \(\frac{7 \pi}{6}\)
x = nπ + (- 1) n \(\frac{7 \pi}{6}\), где n ∈ Z
Следовательно, общее решение равно (2n + 1) \(\frac{\pi}{2}\) или nπ + (- 1) n \(\frac{7 \pi}{6}\), где n ∈ Z.
Пример 3.4 Класс 11 Математика Вопрос 8:
Найдите общее решение уравнения sec 2 2x = 1 – tan 2x.
ANS:
SEC 2 2x = 1 — TAN 2X
1 + TAN 2 2x = 1 — TAN 2X
TAN 2 X + TAN 2X = 0
=> TAN 2X 2x 2x 2x 2x 2x 2x 2x 2x 2x 2x (Tan 2. 1) = 0
=> tan 2x = 0 или tan 2x + 1 = 0
Теперь tan 2x = 0
=> tan 2x = tan 0
2x = nπ + 0, где n ∈ Z
x = \(\ frac{n \pi}{2}\), где n ∈ Z
или tan 2x + 1 = 0
= tan 2x = – 1
= – tan \(\frac{\pi}{4}\)
= тангенс (π — \(\ frac{\pi}{4}\))
= тангенс \(\frac{3 \pi}{4}\)
2x = nπ + \(\frac{ 3 \pi}{4}\), где n ∈ Z
x = \(\frac{n \pi}{2}+\frac{3 \pi}{8}\), где n ∈ Z
Поэтому , общее решение равно \(\frac{n \pi}{2}\) или \(\frac{n \pi}{2}+\frac{3 \pi}{8}\), где n ∈ Z.
Пример 3.4 Математика для 11 класса Вопрос 9:
Найдите общее решение уравнения sin x + sin 3x + sin 5x = 0
Ответ:
sin x + sin 3x + sin 5x = 0
⇒ (sin x + sin 5x) + sin 3x = 0
\(\left[2 \sin \left(\frac{x+5 x}{2}\right) \cos \left(\frac{x -5 x}{2}\right)\right]\) + sin 3x = 0
[∵ sin A + sin B = 2 sin \(\sin \left(\frac{A+B}{2}\ справа) \cos \left(\frac{A-B}{2}\right)\)]
2 sin 3x cos (2x) + sin 3x = 0
2 sin 3x cos 2x + sin 3x = 0
sin 3x ( 2 cos 2x +1) = 0
sin 3x = 0 или 2 cos 2x + 1 = 0
Теперь sin 3x = 0
⇒ 3x = nπ, где n ∈ Z
, т. е. x = \(\frac{n \pi {3}\), где n ∈ Z
или 2 cos 2x + 1 = 0
cos 2x = \(-\frac{1}{2}\)
= – cos \(\frac{\pi}{3}\)
= cos (π – \(\frac{\pi}{3}\))
потому что 2x = cos \(\frac{2 \pi}{3}\)
⇒ 2x = 2nπ ± \(\frac{2\pi {3}\), где n ∈ Z
⇒ x = nπ ± \(\frac{\pi}{3}\), где n ∈ Z
Следовательно, общее решение имеет вид \(\frac{n \pi}{3}\) или nπ ± \(\frac{\pi}{3}\), где n ∈ Z.
Разное Упражнение Класс 11 Математика Вопрос 1:
Докажите, что:
\(2 \cos \frac{\pi}{13} \cos \frac{9 \pi}{13}+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13}\) = 0
Ответ:
Отсюда доказано.
Разное Упражнение Класс 11 Математика Вопрос 2:
Докажите, что: (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0.
Ответ:
L.H.S. = (sin 3x + sin x) sin x + (cos 3x – cos x) cos x
= sin 3x sin x + sin 2 x + cos 3x cos x – cos 2 x
= cos 3x cos x + sin 3x sin x – (cos 2 x – sin 2 x)
= cos (3x – x) – cos 2x
[∵ cos(A – B) = cos A cos B + sin A sin B]
= cos 2x – cos 2x = 0
=R.H.S.
Значит доказано.
Разное Упражнение 11 класс Математика Вопрос 3:
Докажите, что:
(cos x + cos y) 2 + (sin x – sin y) 2 (3 = 4 cos 2 9123 \frac{x+y}{2}\right)\)
ANS:
L. H.S. = (COS X + COS Y) 2 + (SIN X — SIN Y) 2
= COS 2 X + COS 2 Y + 2 COS y + 2 Cos y + 2 Cos y + 2. + sin 2 x + sin 2 y – 2 sin x sin y
= (cos 2 x + sin 2 x) + (cos 2 y + sin 9 91 cos x cos y – sin x sin y)
= 1 + 1 + 2 cos (x + y)
[∵ cos (A + B) = (cos A cos B – sin A sin B)]
= 2 + 2 потому что (х + у)
= 2 [1 + потому что (х + у)] 9{2}\left(\frac{x+y}{2}\right)\) – 1]
[∵ cos 2A = 2 cos 2 A – 1]
= 4 c0s 2 \(\left (\frac{x+y}{2}\right)\)
= RHS
Значит доказано.
Разное Упражнение 11 класс Математика Вопрос 4:
Докажите, что:
(cos x – cos y) 2 + (sin x – sin y) 2 = 4 sin 9 x 2 912\frac {2}\)
Ответ:
LHS= (cos x – cos y) 2 + (sin x – sin y) 2
= cos 2 x + cos 2 y – 2 cos x cos y + sin 2 x + sin 2 y – 2 sin x sin y
= (cos 2 x 9 + sin 2) (cos 2 y + sin 2 y) – 2 [cos x cos y + sin x sin y]
= 1 + 1 – 2 [cos (x – y)]
= 2 [1 – {1 – 2 sin 2 \(\left(\frac{x-y}{2}\right)\)}]
[∵ cos 2A = 1 – 2 sin 2 A]
= 4 sin 2 \(\ влево (\ frac {x-y} {2} \ вправо) \)
= R. H.S.
Значит доказано.
Разное Упражнение Класс 11 Математика Вопрос 5:
Докажите, что: sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x
Ответ:
Известно, что sin A + sin B = 2 \(\sin\left(\frac{A+B}{2}\right) \cdot \cos \left(\frac{A-B}{2}\right)\)
∴ L.H.S. = (sin x + sin 3x) + (sin 5x + sin 7x)
= (sin x + sin 5x) + (sin 3x + sin 7x)
= \(2 \sin \left(\frac{x+5 x {2}\справа)\) . \(\cos\left(\frac{x-5x}{2}\right)+2\sin\left(\frac{3x+7x}{2}\right) \cos\left(\frac {3 x-7 x}{2}\справа)\)
= 2 sin 3x cos (- 2x) + 2 sin 5x cos (- 2x)
= 2 sin 3x cos 2x + 2 sin 5x cos 2x
= 2 cos 2x [sin 3x + sin 5x]
= 2 cos 2x [ латекс] 2 \sin \left(\frac{3 x+5 x}{2}\right) \cdot \cos \left(\frac{3 x-5 x}{2}\right)[/latex]
= 2 cos 2x [2 sin 4x . cos (- x)]
= 4 cos 2x sin 4x cos x
= R.H.S.
Значит доказано.
Разное Упражнение Класс 11 Математика Вопрос 6:
Докажите, что: \(\frac{(\sin 7 x+\sin 5 x)+(\sin 9 x+\sin 3 x)}{(\cos 7 x+\ cos 5 х)+(\cos 9x+\cos 3 x)}\) = tan 6x
Ответ:
Известно, что
Отсюда доказано.
Разное Упражнение Класс 11 Математика Вопрос 7:
Докажите, что: sin 3x + sin 2x – sin x = 4 sin x cos \(\frac{x}{2}\) cos \(\frac{3 x} {2}\).
Ответ:
L.H.S. = sin 3x + sin 2x – sin x
= sin 3x + (sin 2x – sin x)
Разное Упражнение Класс 11 Математика Вопрос 8:
Найдите sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) и tan \(\frac{x}{2}\) для tan x = — \(\frac{4}{3}\), x в квадранте II.
Ответ:
Разное Упражнение Класс 11 Математика Вопрос 9:
Найдите sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) и tan \(\frac{x}{2}\) для cos x = – \(\frac{1}{3}\), x в квадранте III.
Ответ:
Таким образом, соответствующие значения sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) и tan \(\frac{x} {2}\) равны \(\frac{\sqrt{6}}{5}\), \(\frac{\sqrt{3}}{3}\) и — √2.
Разное Упражнение 11 класс Математика Вопрос 10:
Найдите sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) и tan \(\frac{x}{2}\) для sin x = \( \frac{1}{4}\), x в квадранте II.
Ответ:
Таким образом, соответствующие значения sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) и tan \(\frac{x {2}\) представляют собой \(\sqrt{\frac{8+2 \sqrt{15}}{4}}\), \(\sqrt{\frac{8-2 \sqrt{15}}}{4 }}\) и 4 + √15.
त्रिकोणमितीय फलन प्रश्नावली 3.1 का हल हिंदी में
प्रश्न 1.
(i) 25 °
(II) — 47 ° 30 ′
(III) 240 °
(IV) 520 °
प्शFRHITRH 2.
निमчего ेडियनFRेडियन ेडियनFजчей ेडियन ेडियनFRशIst \(\frac { 22 }{ 7 }\)) का प्रयोग करें:
(i) \(\frac { 11 }{ 16 }\)
(ii) -4
(iii) \(\ frac { 5\ pi} {3} \)
(iv) \ (\ frac {7 \ pi} {6} \)
पказа 3 36034
एक पहिय मिनट मिनट 3 360934
. एक सेकंड में कितने रेडियन माप का कोण बनाएगा?
हल:
.
1 सेकण्ट में चहिया द्वारा बना कोण = \(\frac { 360\times 2\pi }{ 60 }\) = 12π र
प्रश्न 4.
एक वृत्त जिसकी त्रिज्य सेमी सेमी है है है है सेमी लंब की च वृत वृत Вивра के केन केन सेमी प कितने डिग डिग डिग डिग म क वृत के के केन केन्द्रравия (π = \(\frac { 22 }{ 7 }\) का प्रयोग कीजिए)
प्रश्न 5.
एक वृत्त जिसका व्यास 40 सेमी. है, की एक जीवा 20 सेमी. लंबाई की है तो इसके संगत छोटे चाप की लंबएई ज्थञात
हल:
व्यास = 40 सेमी
त्रिज्या = 20 सेमी
प्रश्न 6.
यदि दो वृत्तों के समान लंबाई वाले चाप अपने केन्द्रों पर क्रमशः 60° तथा 75° के कोण बनाते हों, तो उन्क लिन्याओं को अनुपात ज्ञात कीजिए।
प्रश्न 7.
75 सेमी लम्बाई वाले एक दोलायमान दोलक का एक सिरे से दूसरे सिरे तक दोन करने से जो कोण बनता है, उसका माप रेडियन में ज्ञात कीजिए, जबकि उसके नोक द्वारा बनाए गए चाय की Количество:
(i) 10 सेमी
(ii) 15 सेमी
(iii) 21 सेमी
Упражнение 3.1
Q.1: Рассчитайте измерение Radian3333333 (
903333333. 25∘
(ii). 240∘
(iii). −47∘30’
(iv). 520∘
Q. 2: Вычислите градусное измерение заданного градусного измерения: [Используйте π = \(\\ \frac { 22 }{ 7 } \)]
(i) \(\\ \frac { 11 }{ 16 } \)
(ii) -4
(iii) \(\frac { 5\pi }{ 3 } \)
(iv) \(\frac { 7\pi }{ 6 } \)
Q.3: За минуту колесо делает 360 оборотов. На сколько радиан он поворачивается за 1 секунду?
Q.4: Вычислите градусную меру угла, образуемого в центре окружности радиусом 100 м дугой длиной 22 м.
Q.5: По кругу диаметром 40 м длина хорды 20 м. Найдите длину малой дуги хорды.
Q.6: В двух окружностях дуги одинаковой длины образуют угол 60∘ и 75∘ в центре. Вычислите отношение их радиусов.
Q.7: Вычислите угол в радианах, на который качается маятник, если его длина равна 75 см, а его кончик описывает дугу длиной
(i) 10 см
(ii) 15 см
(iii) 21 см
Упражнение 3. 2
В.1: Вычислите значения пяти тригонометрических функций. если cosy = \(– \frac { 1 }{ 2 } \) и y лежит в 3 rd квадранте.
(I) Sec Y
(II) SIN Y
(III) COSEC Y
(IV). .2: Вычислите другие пять тригонометрических функций, если нам даны значения для sin y = \(\\ \frac { 3 }{ 5 } \), где y лежит во втором квадранте.
Q.3: Найдите значения других пяти тригонометрических функций, если coty=\(\\ \frac { 3 }{ 4 } \), где y лежит в третьем квадранте.
Q.4: Найдите значения других пяти тригонометрических, если secy=\(\\ \frac { 13 }{ 5 } \), где y лежит в четвертом квадранте.
Q.5: Найдите значения остальных пяти тригонометрических функций, если tan y = \(– \frac { 5 }{ 12 } \) и y лежит во втором квадранте.
Q. 6: Вычислите значение тригонометрической функции sin 765°.
Q.7: Вычислить значение тригонометрической функции cosec [-1410°]
Q.8: Вычислить значение тригонометрической функции tan \(\frac { 19\pi }{ 3 } \) .
Q.9: Вычислите значение тригонометрической функции sin \(-\frac { 11\pi }{ 3 } \).
Q.10: Вычислите значение тригонометрической функции кроватка \(-\frac { 15\pi }{ 4 } \)
Упражнение 3.3
Q.1: Докажите:
tan²\(\frac { \pi }{ 4 } \)= \(– \frac { 1 }{ 2 } \)
Q.2: Докажите:
2sin²\(\frac { \pi }{ 6 } \)+cosec²\(\frac { 7\pi }{ 6 } \)6cos²\(\frac { \pi }{ 3 } \)=\(\\ \frac { 3 }{ 2 } \ )
Q.3: Докажите:
cot²\(\frac { \pi }{ 6 } \)+cosec\(\frac { 5\pi }{ 6 } \)+3tan²latex s=2 ]\frac { \pi }{ 6 } [/латекс]=6
Q. 4: Докажите:
2sin²\(\frac { 3\pi }{ 4 } \)+2cos²\(\frac { \pi }{ 4 } \)+2sec²\(\frac { \pi }{ 3 } \)=10
Q.5: Рассчитайте значение:
(i). sin75∘
(ii). tan15∘
Вопрос 6: Докажите:
cos(\(\frac { \pi }{ 4 } \)–x)cos(\(\frac { \pi }{ 4 } \)– y)–sin(\(\frac { \pi}{4} \)–x)sin(\(\frac{\pi}{4} \)–y)=sin(x+y)
9{ 2 }x\)Q.9: Докажите:
\(cos(\frac { 3\pi }{ 2 } +x)cos(2\pi +x)[cot(\frac { 3\pi }{ 2 } -x)+cot(2\pi +x)]=1\)
Q.10: Докажите:
sin(n+1)xsin(n+2 )x+cos(n+1)xcos(n+2)x=cosx
Q.11 Докажите:
(\frac { 3\pi }{ 4 } -x)\)=−√2sinx
Q.12: Докажите:
sin²6x–sin²4x=sin2x sin10x
Q. 13: Prove:
cos²2x–cos²6x=sin4x sin8x
Q.14:Prove:
sin2x+2sin4x+sin6x=4cos²x sin4x
Q.15: Докажите:
cot4x(sin5x+sin3x)=cotx(sin5x–sin3x)
Q.16: Докажите:
\(\ fracx { cos9x-cos5x}} {-\ fracx3 cos9x-cos5x} frac { sin2x }{ cos10x } \)
Q.17: Докажите:
\(\frac { sin5x+sin3x }{ cos5x+cos3x } =tan4x\) 9{ 4 }x } \)
Q.24: Prove:
cos4x=1–8sin²xcos²x
Q.25: Prove:
cos6x=32cos 6 x–48cos 4 x+18cos 2 x−1
Упражнение 3.4
Найдите общие решения и принципиальные решения данного уравнения: sec x = 2
Q.3: Найдите общие решения и основные решения данного уравнения: cot = −√3
Q. 4: Найдите общие решения и основные решения данного уравнения: cosec x = -2
Q.5: Найдите общее решение данного уравнения: cos 4x = cos 2x
Q.6: Найдите общее решение данного уравнения: cos 3x + cos x – cos 2x = 0
Q.7: Найдите общее решение данного уравнения: sin 2x + cos x = 0
Q.8: Найдите общее решение данного уравнения: sec²2x=1–tan2x
Q.9: Найдите общее решение данного уравнения: sin x + sin 3x + sin 5x = 0
Разное Упражнение
Вопрос 1: Докажите, что: 3\pi }{ 13 } +cos\frac { 5\pi }{ 13 } =0\)
Q.2: Докажите, что:
9Q-3: Докажите, что:(cosx+cosy)²+(sinx–siny)²=4cos²\(\\ \frac { x+y }{ 2 } \)
Q-4: Докажите, что:
(cosx–cosy)²+(sinx–siny)²=4sin²\(\\ \frac { x-y } {2} \)
Q-5: Докажите, что:
SINX+SIN3X+SIN5X+SIN7X = 4COSXCOS2XCOS4X
333.