«Построение множеств с помощью кругов Эйлера»
Задание. Ученик по заданному логическому выражению построил круги Эйлера, до ошибся и неверно закрасил области.
а) Выполните правильно закрашивание кругов на схеме справа.
б) По начальному рисунку напишите логическое выражение.
Построение кругов Эйлера
1 вариант
№1. Заданы три множества А, В, С. Известно, что есть элементы, входящие в множества А, В, С одновременно. Построить круги Эйлера для множеств:
С & В | А
(А | С) & В
А | С | В
№2. Постройте круги Эйлера для множеств из таблицы.
A | тетради | учебники |
Б | тетради |
В | тетради & учебники |
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц по каждому запросу.
Расположите обозначения запросов в порядке возрастания количества страниц по каждому запросу.
№3. Постройте круги Эйлера для множеств из таблицы.
A | файлы & папки |
Б | файлы | папки |
В | файлы |
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке убывания количества страниц, по каждому запросу.
Построение кругов Эйлера
2 вариант
№1. Заданы три множества А, В, С. Известно, что есть элементы, входящие в множества А, В, С одновременно. Построить круги Эйлера для множеств:
А & С | В
(А | В) & С
А & В & С
№2. Постройте круги Эйлера для множеств из таблицы.
Постройте круги Эйлера для множеств из таблицы.
A | ручки | карандаши |
Б | ручки & карандаши |
В | ручки |
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке убывания количества страниц по каждому запросу.
№3. Постройте круги Эйлера для множеств из таблицы.
A | банты & ленты |
Б | банты |
В | банты | ленты |
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, по каждому запросу.
Построение кругов Эйлера
3 вариант
№1. Заданы три множества А, В, С. Известно, что есть элементы, входящие в множества А, В, С одновременно. Построить круги Эйлера для множеств:
А | С | В
А & В & С
В & (А | С)
№2. Постройте круги Эйлера для множеств из таблицы.
A | телевизор & холодильник |
Б | телевизор |
В | телевизор | холодильник |
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц по каждому запросу.
№3. Постройте круги Эйлера для множеств из таблицы.
A | клавиатура | мышь |
Б | клавиатура & мышь |
В | клавиатура |
В таблице приведены запросы к поисковому серверу.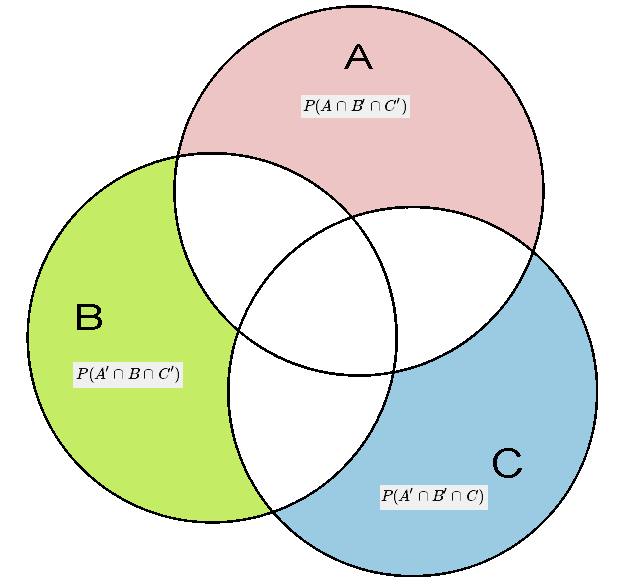 Расположите обозначения запросов в порядке убывания количества страниц, по каждому запросу.
Расположите обозначения запросов в порядке убывания количества страниц, по каждому запросу.
Построение кругов Эйлера
4 вариант
№1. Заданы три множества А, В, С. Известно, что есть элементы, входящие в множества А, В, С одновременно. Постройте круги Эйлера для множеств:
А & С & В
А | В & С
С & (А | В)
№2. Постройте круги Эйлера для множеств из таблицы.
A | маркер & фломастер |
Б | маркер | фломастер |
В | маркер |
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке убывания количества страниц по каждому запросу.
№3. Постройте круги Эйлера для множеств из таблицы.
A | открытка | визитка |
Б | открытка |
В | открытка & визитка |
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, по каждому запросу.
1.2. Операции над множествами. Круги Эйлера, Важность…
Привет, Вы узнаете про операции над множествами, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
операции над множествами, круги эйлера, двухместные операции над множествами, важность упорядоченности , настоятельно рекомендую прочитать все из категории Теория конечных автоматов.
Множества можно определять при помощи операций над некоторыми другими множествами и подмножествами. Пусть дана некоторая совокупность предметов, которую можно обозначить как множество
V ={ a, b, c, d, e, f, g, h, i, j, k }.
Предположим, что часть предметов, а именно: a, b, d и f имеют круглую форму, а часть – b, c, d, h, и i – окрашена в белый цвет. В этом случае говорят, что множество V имеет два подмножества
В результате получим четыре класса элементов:
С0 ={ e, g, j, k } – элементы, которые не обладают ни одним из названных свойств,
С1 ={ a, f } – элементы, обладающие только свойством А (круглые),
С2 ={ c, h, i } – элементы, обладающие только свойством В (белые),
С3 ={ b, d } – элементы, обладающие одновременно двумя свойствами.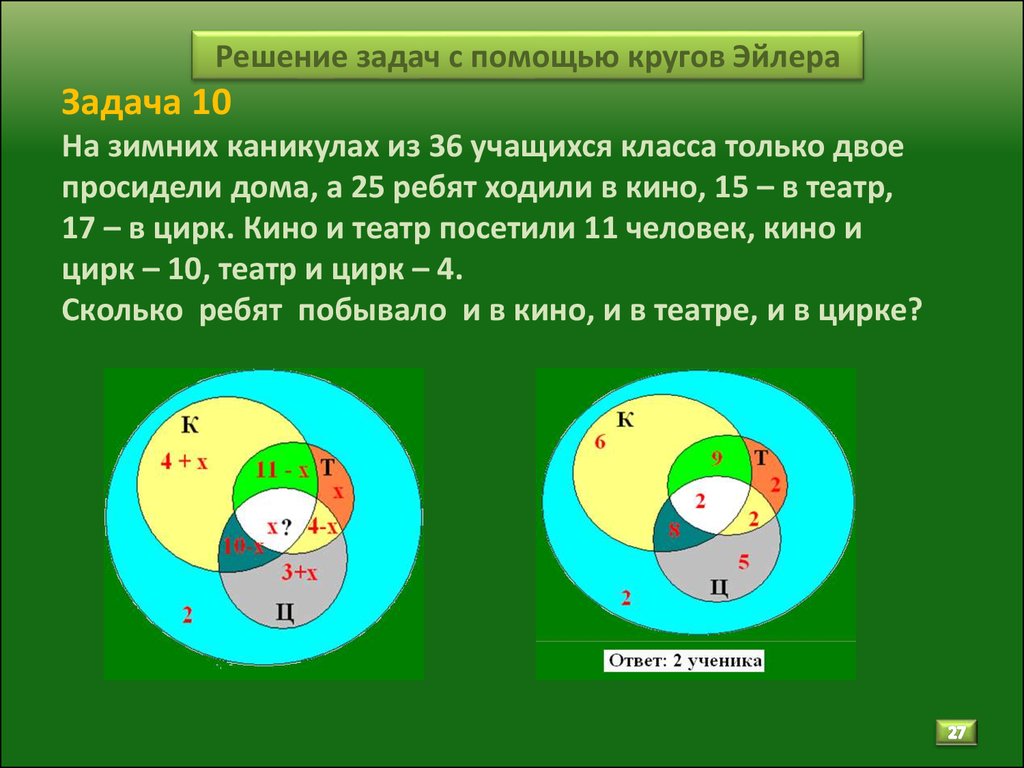
операции над множествами удобно изображать с помощью графической диаграммы Эйлера-Венна (рис. 1).
Рис. 1 . Диаграмма Эйлера-Венна для двух множеств А и В
Объединением множеств А = { a, b, d, f } и В = { b, c, d, h, i } назовем множество А ∪ В = { a, b, c, d, f, h, i }. Таким образом, объединением охватываются три класса элементов – С1, С2, С3, которые на диаграмме заштрихованы (рис. 2). При этом оба множества могут и не пересекаться, т.е. не иметь общих элементов. Логическую операцию объединения двух множеств можно охарактеризовать словами: элемент принадлежит множеству А или множеству В
х ∈ А ∪ В = (х ∈ А) ∨ (х ∈ В),
где ∨ – символ логической связки или, которая называется дизъюнкцией.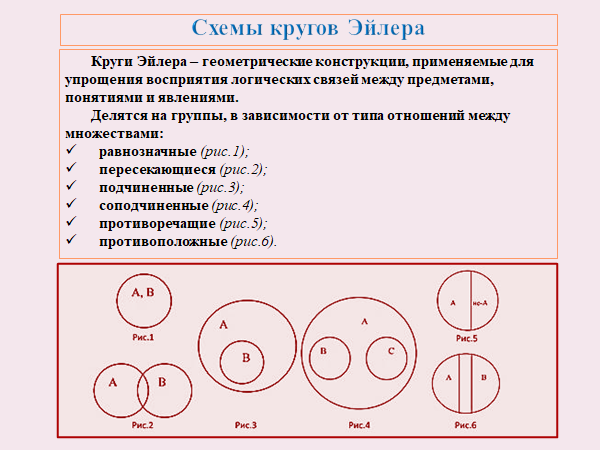
Пересечением множеств А и В называется множество K = А ∩В, содержащее те элементы из А и В, которые входят одновременно в оба множества. Для нашего примера будем иметь (рис. 3):
То, что элемент х принадлежит одновременно двум множествам А и В, можно выразить формулой
где ∧ – символ логической связки и, которая называется конъюнкцией.
Рис. 2. А ∪ В Рис. 3. А ∩ В
Рассмотрим области С1 и С3, образующие множество А (рис. 4). Тогда области С2 и С0 образуют множество элементов, не входящих в А (рис. 5). Это обозначается как .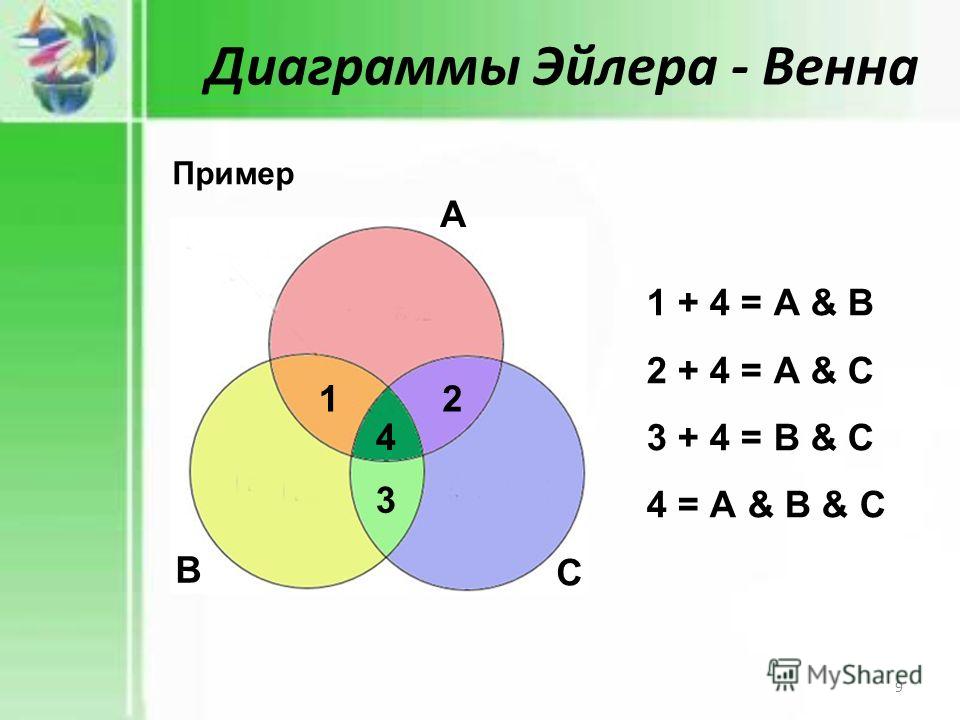 Об этом говорит сайт https://intellect.icu . Объединение или дизъюнкция множеств А и даст весь универсум а пересечение или конъюнкция даст нам нулевое множество
Об этом говорит сайт https://intellect.icu . Объединение или дизъюнкция множеств А и даст весь универсум а пересечение или конъюнкция даст нам нулевое множество
Рис. 4. А Рис. 5.
После рассмотрения операции инверсии (дополнения) все четыре области Сj на диаграмме можно выразить следующим образом:
Используя инверсию, можно представить любую множественную операцию, например объединение:
Операции дополнения или инверсии объединения и пересечения множеств называются соответственно стрелкой Пирса и штрихом Шеффера , которые обозначаются соответственно А↓В и А/В.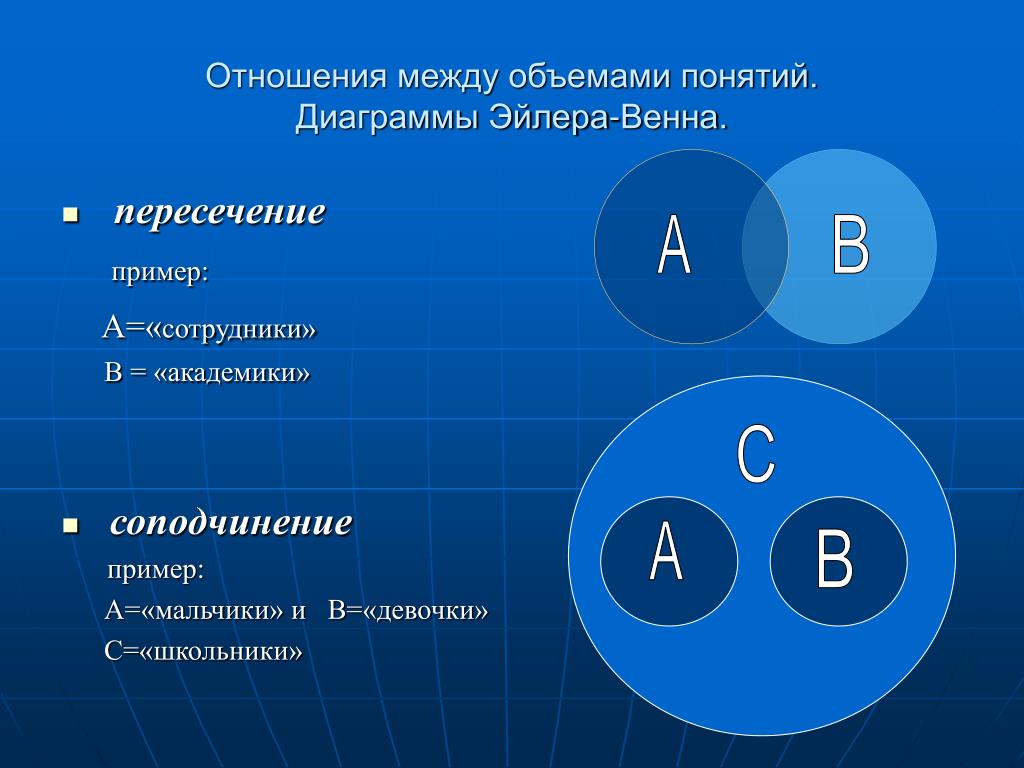 Диаграммы для этих операций представлены на рис. 6 и 7.
Диаграммы для этих операций представлены на рис. 6 и 7.
Рис. 6. А↓В Рис. 7. А/В
Рис. 8. ( В ← А ) Рис. 9. (В → А)
Разностью между множествами В и А называется совокупность тех элементов множества В, которые не вошли в множество А (рис. 8). Такая операция называется еще запретом А и обозначается ( В ← А ). Для нашего случая это будет область С2.
При этом
Рис. 10. (А ≡ В) Рис. 11. (А ⊕ В)
Дополнением к запрету служит импликация А. На диаграмме Эйлера-Венна это частичное включение множества В в множество А (рис. 9). Обозначается такая операция (В → А). При этом (В → А) = А
а b c
Рис. 12. (А ∪ В) ∩ (А ∪ С)
a (А ≡ B) b ((А≡ B)→(C ⊕ D))
c d
Рис.13. Диаграммы Венна для операций над четырьмя множествами
Аналогично определяются запрет В и импликация В
Остается привести еще две взаимно дополняющие операции – симметрическую разность или неравнозначность и эквивалентность или равнозначность.
Равнозначность определяется теми элементами множеств А и В, которые для них являются общими, а также элементами, не входящими ни в А, ни в В
. В нашем случае это будут области С0 и С3 (рис. 10). Обозначается равнозначность А º В или А ~ В.
Неравнозначность есть объединение двух разностей или двух запретов. Эта операция обозначается (А В). Таким образом,
На диаграмме Эйлера-Венна это области С1 и С2 (рис. 11). Неравнозначность имеет еще название строгая дизъюнкция. Эту операцию можно передать словами: «либо А, либо В».
Диаграммы Эйлера-Венна достаточно наглядно иллюстрируют операции над тремя и четырьмя множествами. Рассмотрим операцию (А ∪ В) ∩ (А ∪
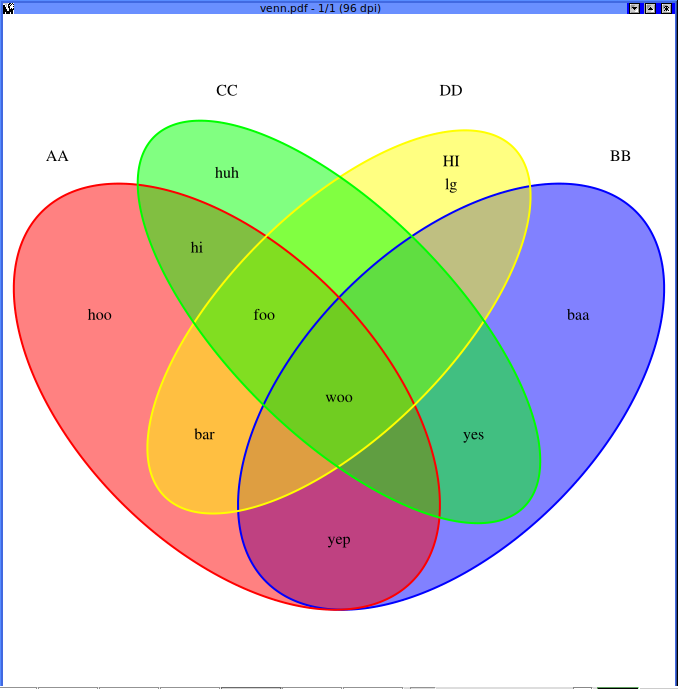
Для четырех множеств четыре круга Эйлера не дают полную диаграмму Венна, поскольку их пересечение дает только 14 областей, а необходимо 16.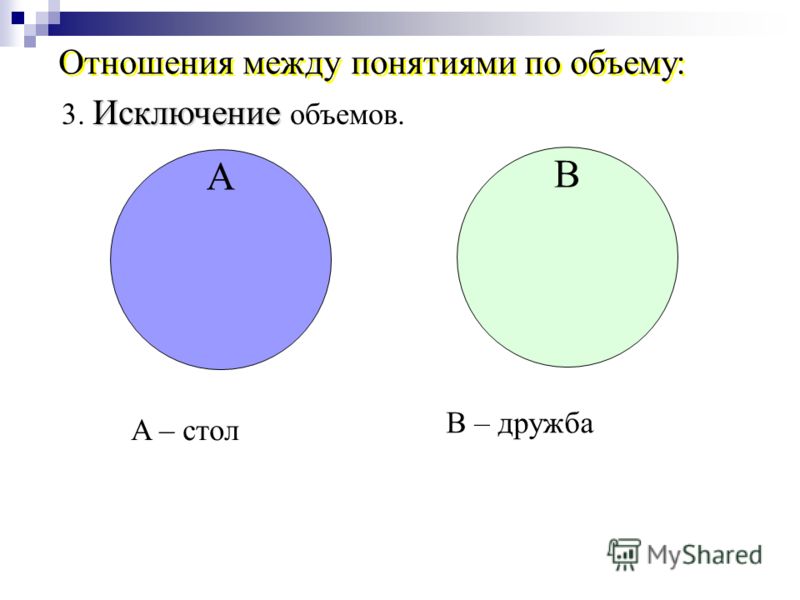 Поэтому круги необходимо деформировать в эллипсы. Покажем на примере построение диаграммы для выражения
Поэтому круги необходимо деформировать в эллипсы. Покажем на примере построение диаграммы для выражения
На рис. 13 изображены четыре диаграммы, соответствующие указанной последовательности операций. Последняя диаграмма (рис. 13d) является результирующей.
важность упорядоченности для двухместных операций над множествами.
Двухместные операции
— операции, в которых учувствуют два операнда. К двухместным операциям над множествами относятся:- Объединение ( ∪ )
- Пересечение ( ∩ )
- Разность ( \ )
- Исключающее ИЛИ, XOR ( ⊕ )
Упорядоченное множество может представляться в виде списка или массива. Операции над упорядоченными множествами могут выполняться быстрее, так как имеют меньшую временную сложность. Например, приведенные двухместные операции выполняются на неупорядоченном множестве за O(n2), а на упорядоченном — за O(n).
Примеры:
пример реализации на Java определения пересечения неупорядоченного множества
пример реализации на Java определения пересечения упорядоченного множества
См. также
- Отношения между множествами
- множество
- диаграмма Вена
Надеюсь, эта статья об операции над множествами, была вам интересна и не так слона для восприятия как могло показаться, удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое операции над множествами, круги эйлера, двухместные операции над множествами, важность упорядоченности и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория конечных автоматов
как выглядит, как изобразить множества, примеры решения задач
Содержание:
- Диаграмма Эйлера-Венна — что из себя представляет, где используется
-
Принципы построения, как изобразить множества
- Дополнение множества
- Объединение множеств
- Пересечение множеств
- Разность множеств
- Симметричная разность множеств
- Использование диаграмм Эйлера-Венна для доказательства логических равенств
-
Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна
- Как логические операции связаны с теорией множеств
- Примеры задач с решением
Содержание
- Диаграмма Эйлера-Венна — что из себя представляет, где используется
-
Принципы построения, как изобразить множества
- Дополнение множества
- Объединение множеств
- Пересечение множеств
- Разность множеств
- Симметричная разность множеств
- Использование диаграмм Эйлера-Венна для доказательства логических равенств
-
Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна
- Как логические операции связаны с теорией множеств
- Примеры задач с решением
Диаграмма Эйлера-Венна — что из себя представляет, где используется
Определение
Диаграмма Эйлера-Венна представляет собой геометрическую схему, предназначенную для представления моделей множеств и схем их взаимосвязей.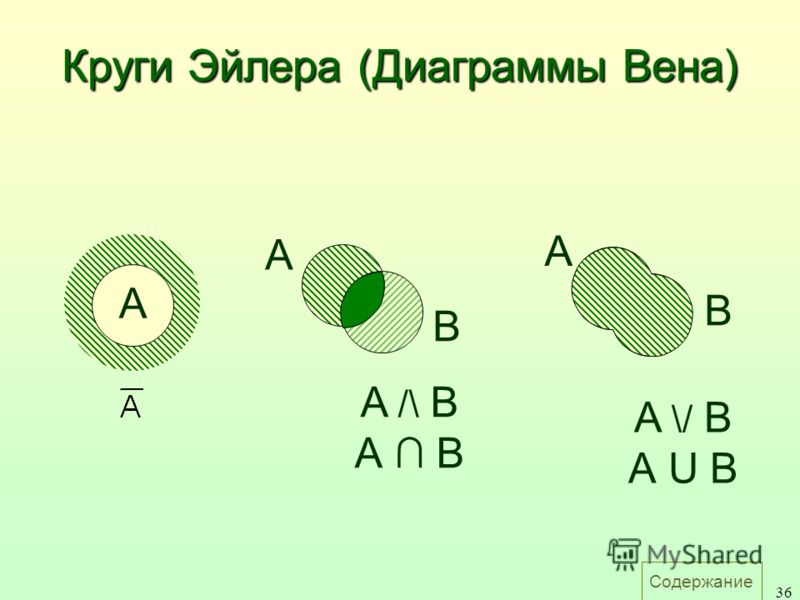
Благодаря данной диаграмме, приводят наглядное объяснение разных фактов о множествах. При таком методе универсальное множество представляют в виде прямоугольника, а для изображения подмножества используют круги. Широкое применение диаграммы Эйлера-Венна нашли в таких дисциплинах, как математика, логика, менеджмент, финансы и другие прикладные направления.
Примечание
Способы отражения отношений между множествами ранее отличались. Джон Венн применял в качестве обозначения множеств замкнутые фигуры, а Эйлер – круги.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Диаграммы Эйлера-Венна представляют собой важный частный случай кругов, которые изображал Эйлер. На диаграммах представлены все 2n комбинаций n свойств, что является конечной булевой алгеброй. Если n = 3, на диаграмме, как правило, изображают три круга с центрами, которые расположены в углах равностороннего треугольника, и совпадающими радиусами, ориентировочно равными длине сторон этого многоугольника.
Принципы построения, как изобразить множества
Определение
Построить диаграмму Эйлера-Венна – значит, составить большой прямоугольник, представляющий универсальное множество U, и разместить внутри него замкнутые фигуры в качестве обозначения множеств.
В том случае, когда требуется строить на диаграмме не более трех множеств, целесообразно использовать круги. Для изображения свыше четырех множеств применяют эллипсы. Пересечение фигур соответствует максимально общему случаю, согласно условиям задачи, и изображается должным образом на диаграмме.
Если предположить, что диаграмма содержит круг, обозначающий множество А, его центральная часть будет отражать истинность выражения А, а область вне круга – обозначать ложь. Те области, которые соответствуют истинным значениям, заштриховывают, что является отражением логической операции на диаграмме.
Согласно алгебре логики, конъюнкция множеств А и В соответствует истине в том случае, когда истинны оба эти множества.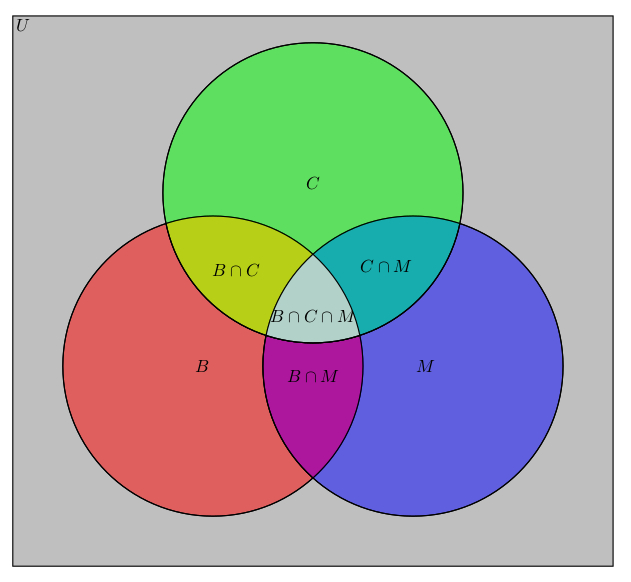 При этом на диаграмме отмечают участок пересечения множеств.
При этом на диаграмме отмечают участок пересечения множеств.
Применяя диаграммы Эйлера-Венна, доказывают любые алгебраические законы с помощью их графического изображения. Алгоритм построения:
- изображение диаграммы с заштрихованными множествами, которые представлены в левой части выражения;
- чертеж другой диаграммы с заштрихованными множествами, расположенными в правой части уравнения;
- сравнение заштрихованных областей на диаграммах: если это одна и та же область, то можно говорить об истинности тождества.
Данные диаграммы являются эффективным методом визуализации операций с множествами. Отдельные множества изображают в виде кругов, а универсальное множество представляют прямоугольником.
Дополнение множества
Источник: avatars.mds.yandex.net Источник: avatars.mds.yandex.netОбъединение множеств
Источник: avatars.mds.yandex.net Источник: avatars.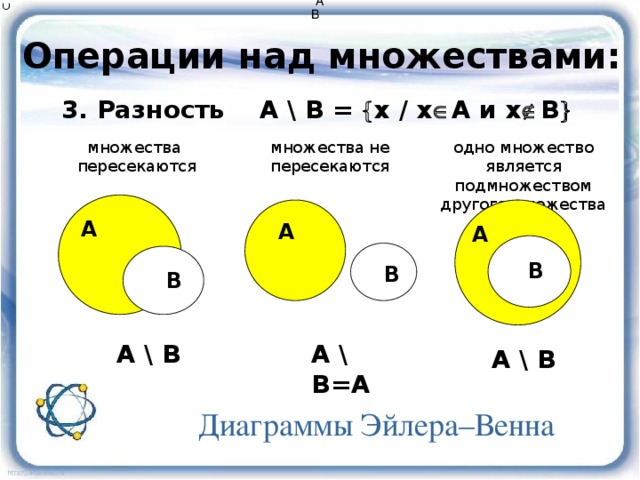 mds.yandex.net
mds.yandex.netПересечение множеств
Источник: avatars.mds.yandex.net Источник: avatars.mds.yandex.netРазность множеств
Источник: avatars.mds.yandex.net Источник: avatars.mds.yandex.netСимметричная разность множеств
Источник: avatars.mds.yandex.net Источник: avatars.mds.yandex.netИспользование диаграмм Эйлера-Венна для доказательства логических равенств
В качестве доказательства логического равенства подходит способ построения диаграмм Эйлера-Венна. Для примера можно представить доказательства следующего выражения: ¬(АvВ) = ¬А&¬В. Равенство демонстрирует запись закона де Моргана. В первую очередь следует наглядно изобразить левую часть уравнения. Для этого необходимо последовательно заштриховать серым цветом все круги, то есть применить дизъюнкцию. Отобразить инверсию можно с помощью закрашивания черным цветом области вне этих кругов.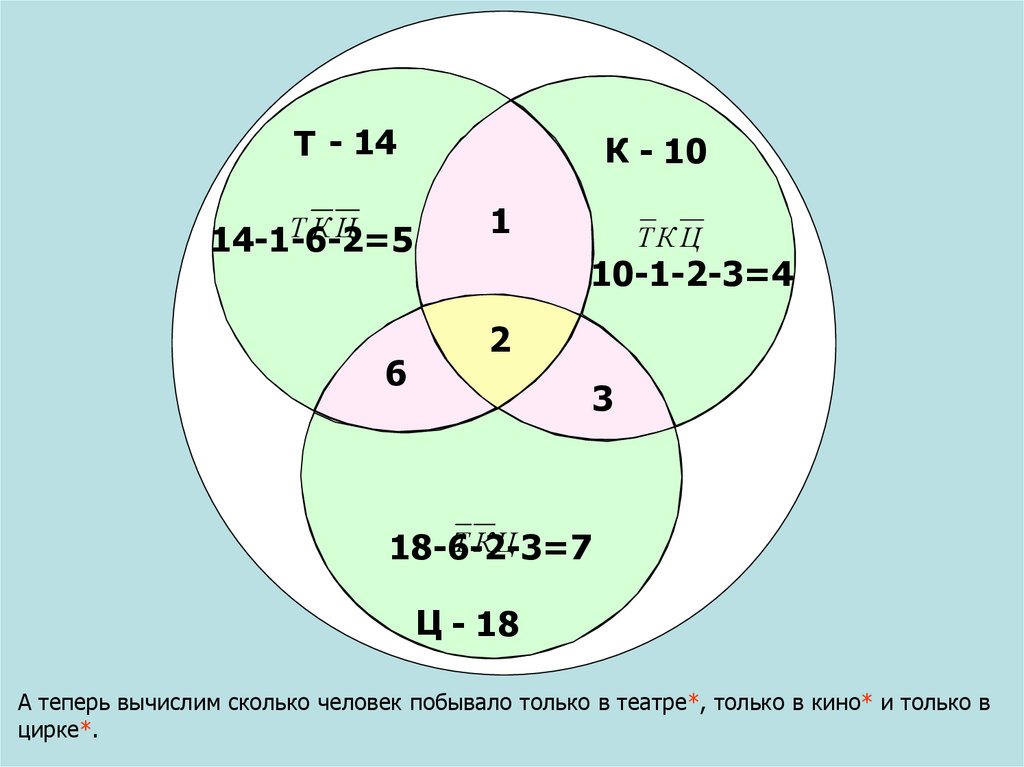
Далее следует визуально представить правую часть выражения. Последовательность действий в этом случае такова: необходимо заштриховать область, в которой отображается инверсия (¬А), с использованием серого цвета и аналогично закрасить область ¬В; отобразить конъюнкцию в виде пересечения этих серых областей. Результат такого наложения будет окрашен черным цветом.
Источник: urok.1sept.ru Источник: urok.1sept.ru Источник: urok.1sept.ruНа рисунке видно, что области, в которых отображены левая и правая части уравнения, равны друг другу. Таким образом, закономерность доказана.
Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна
Изучая тему поиска информации в глобальной сети Интернет, нельзя обойтись без примеров поисковых запросов, в которых использованы логические связки. Как правило, их смысл аналогичен союзам «и», «или» из русского языка.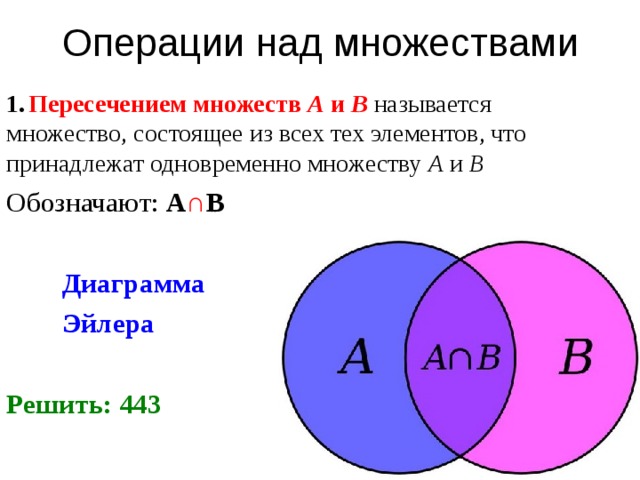 Принцип действия можно понять, если изобразить логические связи с помощью графической схемы или диаграммы Эйлера-Венна.
Принцип действия можно понять, если изобразить логические связи с помощью графической схемы или диаграммы Эйлера-Венна.
Как логические операции связаны с теорией множеств
Используя диаграммы Эйлера-Венна, принято наглядно демонстрировать связь логических действий и теории множеств. Операции логики можно задать с помощью таблиц истинности. В этом случае следует руководствоваться общим принципом.
На диаграмме в виде области круга под названием А отображают истинность определения А, то есть теоретически круг А обозначает все элементы, которые включены в данное множество. Таким образом, область за пределами круга А будет обозначать ложь соответствующего утверждения.
Понимание, какая область диаграммы отражает логическую операцию, возникает после того, как будут заштрихованы только те области, в которых значения логической операции на наборах А и В соответствуют истине. К примеру, импликация истинна при (00, 01 и 11).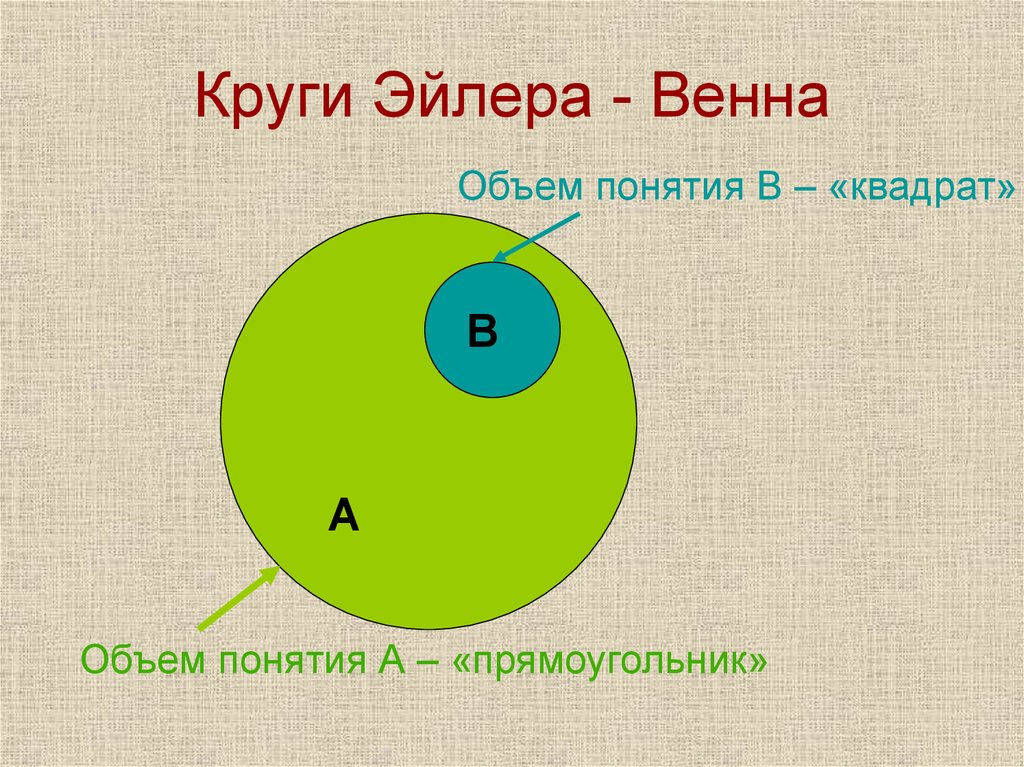
Необходимо заштриховать сначала область за пределами пары пересекающихся кругов в соответствии со значениями А=0, В=0. Затем закрасить область в круге В, которая относится к значениям А=0, В=1, и область, соответствующую и кругу А, и кругу В, то есть участок пересечения, отображающий значения А=1, В=1. Эти три области в комплексе являются графическим представлением логической импликации.
Примеры задач с решением
Диаграммы Эйлера-Венна могут содержать три и более круга. Преимуществом данного графического способа представления выражений является его высокая эффективность и наглядность. К примеру, можно изобразить диаграмму пересечений букв из русского, латинского и греческого алфавита:
Источник: avatars.mds.yandex.netПонять суть методики удобно на практике. Можно решить несколько задач с применением диаграмм Эйлера-Венна.
Задача 1
По условию есть таблица поисковых запросов. В ней представлены страницы по некоторому сегменту.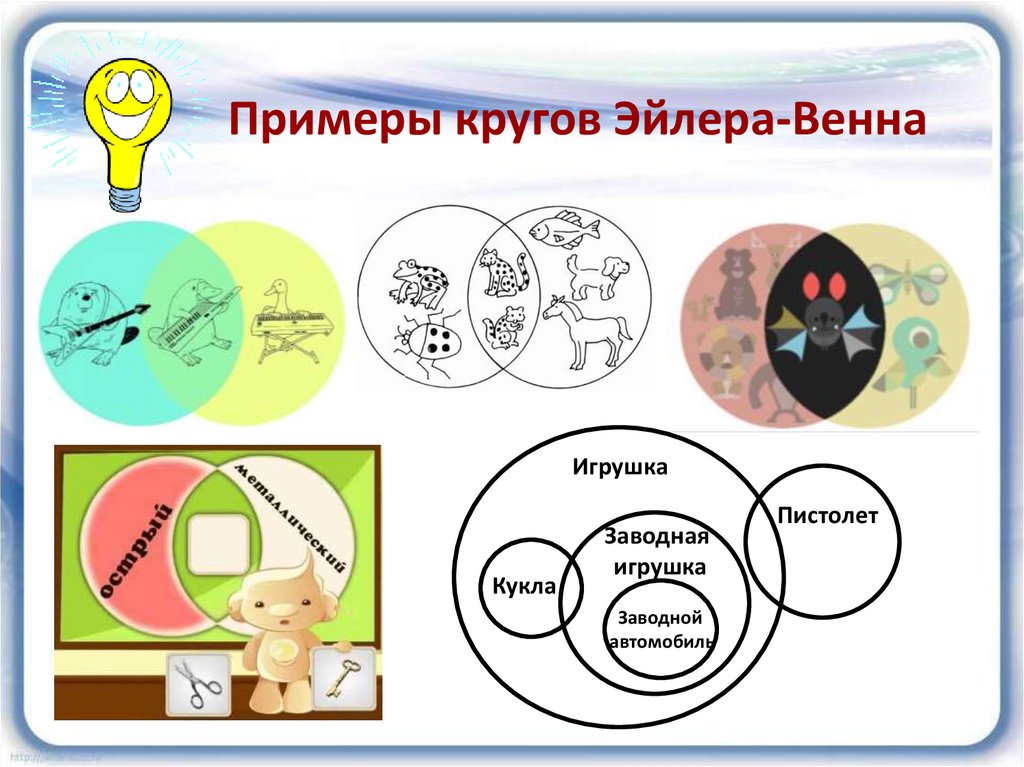 Требуется определить, сколько страниц в тысячах будет отображаться по запросу «Эсминец». Следует отметить, что запросы выполнялись практически в одно время, поэтому набор страниц с искомыми словами не менялся в процессе выполнения запросов.
Требуется определить, сколько страниц в тысячах будет отображаться по запросу «Эсминец». Следует отметить, что запросы выполнялись практически в одно время, поэтому набор страниц с искомыми словами не менялся в процессе выполнения запросов.
Решение
Допустим, что:
Ф – является числом страниц (в тысячах) в соответствии с запросом «Фрегат»;
Э – является числом страниц (в тысячах) в соответствии с запросом «Эсминец»;
Х – представляет собой число страниц (в тысячах) по запросу, в котором присутствует «Фрегат» и отсутствует «Эсминец»;
У – определяет число страниц (в тысячах) по запросу, в котором указано слово «Эсминец» и отсутствует слово «Фрегат».
Диаграмма для каждого поискового запроса будет иметь следующий вид:
Источник: urok.1sept.ruИсходя из информации по диаграммам, получим:
Х+900+У = Ф+У = 2100+У = 3400
Таким образом:
У = 3400-2100 = 1300
Э = 900+У = 900+1300= 2200
Ответ: по запросу «Эсминец» будет найдено 2200 страниц
Задача 2
Класс состоит из 36 учеников. Дети ходят на занятия в рамках математического, физического, химического кружка. Факультатив по математике посещают 18 учащихся, по физике – 14, по химии – 10. Также известно, что 2 ученика ходят на все три кружка, 8 – на математику и физику, 5 – на математику и химию, 3 – на физику и химию. Необходимо определить количество учеников, которые не посещают ни одного кружка.
Дети ходят на занятия в рамках математического, физического, химического кружка. Факультатив по математике посещают 18 учащихся, по физике – 14, по химии – 10. Также известно, что 2 ученика ходят на все три кружка, 8 – на математику и физику, 5 – на математику и химию, 3 – на физику и химию. Необходимо определить количество учеников, которые не посещают ни одного кружка.
Решение
Решить данную задачу можно с помощью удобного и наглядного метода в виде кругов Эйлера. Наибольшим кругом следует обозначить множество всех учащихся класса. Внутри этой окружности необходимо изобразить пересекающиеся множества в виде учащихся на факультативе по математике (М), физике (Ф), химии (Х).
Допустим, что:
МФХ – является множеством учеников, каждый из которых ходит на занятия во все три кружка;
МФ¬Х – определяет множество учащихся, которые посещают факультативы по математике и физике, но не ходят на занятия по химии.
¬М¬ФХ – представляет собой множество людей, каждый из которых посещает химический факультатив, но отказался от дополнительных занятий по физике и математике.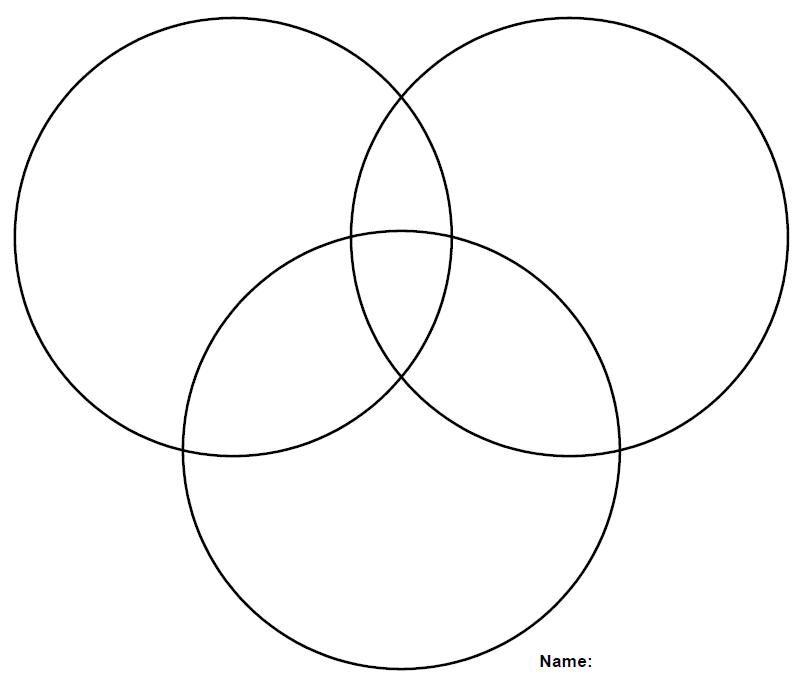
По аналогичному принципу можно ввести множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Согласно условиям задачи, пара учеников записаны во все три кружка. Поэтому в область МФХ требуется вписать число 2. Исходя из того, что 8 учащихся посещают факультативы по математике и физике, а из них двое школьников ходят во все кружки, то в области МФ¬Х следует отметить 6 человек (8-2). Аналогичным способом можно определить число учеников в остальных множествах:
Источник: urok.1sept.ruДалее требуется определить сумму учеников по всем областям:
7+6+3+2+4+1+5=28
Таким образом, всего 28 учащихся посещают факультативные занятия.
Поэтому:
36 – 28 = 8
Ответ: 8 учеников из класса не посещают ни одного кружка.
Задача 3
Когда закончились зимние каникулы, преподаватель поинтересовался у учеников, кто из них посещал театр, кино или цирк. Всего в классе 36 человек. По полученной информации, два ребенка не были ни в кино, ни в театре, ни в цирке. Кино посетили 25 школьников, театр – 11, цирк – 17. И в кино, и в театр сходили 6 человек, и в кино, и в цирк – 10, и в театр, и в цирк – 4. Необходимо посчитать, какое количество учащихся из класса посетили и кино, и театр, и цирк.
Кино посетили 25 школьников, театр – 11, цирк – 17. И в кино, и в театр сходили 6 человек, и в кино, и в цирк – 10, и в театр, и в цирк – 4. Необходимо посчитать, какое количество учащихся из класса посетили и кино, и театр, и цирк.
Решение
Предположим, что х представляет собой число учеников, которые посетили и кино, и театр, и цирк. В таком случае, можно изобразить диаграмму и определить число школьников для каждой области:
Источник: urok.1sept.ruОтвет: 1 ученик побывал и в кино, и в театре, и в цирке.
Насколько полезной была для вас статья?
Рейтинг: 3.00 (Голосов: 2)
Решение логических задач — как решать задачи на логику
Логика – это основа рационального мышления и фундамент для развития интеллекта ребенка. Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.
Эти умения пригодятся не только в учебе, но и в реальной жизни. Рассуждая логически, ребенок может грамотно выразить свое мнение, подойти к решению той или иной задачи более осознанно, дать обоснование всевозможным явлениям, быстро сориентироваться в ситуации.
Поэтому решение логических задач должно быть неотъемлемой частью детского развития и образования. А для того, чтобы щелкать их как орешки, нужно понимать, какими приемами и методами пользоваться при решении.
Самое главное в решении логических задач
Почти у любой задачи есть несколько вариантов решения. Чтобы легко справляться даже с самыми непростыми заданиями, надо знать, какой способ будет наиболее подходящим в той или иной ситуации.
Понимание разных методов позволяет находить оптимальный вариант решения, что особенно важно в условиях ограниченного времени.
Все задачи на развитие логики можно разделить на группы:
- Математические ребусы;
- Задачи на истинность утверждений;
- Задачи на перемещение, взвешивание или переливание;
- Задачи, которые решаются с конца;
- Работа с множествами;
- Задачи на сопоставление «Кто есть кто?»
Выбор способа решения зависит от того, к какой группе относится задание.
Известные техники решения логических задач
- Табличный метод (таблицы соответствий, истинности, совмещенные, кубические):
таблицы создают наглядность, прозрачность рассуждений, помогают сделать верные выводы. - Применение законов из алгебры логики: вводятся обозначения для простых высказываний и преобразовываются в некую формулу.
- Метод рассуждений: подходит для решения простых задач с небольшим количеством объектов. Последовательное рассуждение над каждым условием задачи приводит к правильному выводу.
- Черчение блок-схем: способ, подходящий для решения задач на переливание, взвешивание. Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении.
- Графический метод: подходит для решения задач на объединение или пересечение множеств. Самый популярный графический метод называется «Круги Эйлера». Нарисованная геометрическая схема наглядно показывает отношение между множествами.
- Метод «математический бильярд»: используется для решения задач на переливание жидкостей.
 Вычерчивается траектория движения бильярдного шара, который отталкивается от бортов стола в форме параллелограмма.
Вычерчивается траектория движения бильярдного шара, который отталкивается от бортов стола в форме параллелограмма.
Рассмотрим подробно самые распространенные способы, которые могут использовать в решении логических задач ученики начальных классов:
Табличный метод
Условия задачи и результаты записываем в специальную таблицу. На пересечении строк и столбцов ставим «+», если утверждения не противоречат друг другу и «-», если они расходятся.
Задача:
У Сони, Маши, Антона, Кости и Юры есть домашние животные. У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?
Решение:
Чертим таблицу, где названия столбцов – имена ребят, а названия строк – животные. Ставим в каждой ячейке знаки «+» или «-», опираясь на условия задачи:
1. Девочки собак не держат (ставим «-» на пересечении этих ячеек).
Девочки собак не держат (ставим «-» на пересечении этих ячеек).
2. У мальчиков нет попугаев (в этих ячейках тоже ставим «-»).
3. У Сони нет кошки (ставим «-»).
4. Значит, у Сони есть попугай (ставим «+»).
5. У Сони и Маши разные питомцы. Получается, у Маши нет попугая (ставим «-»), зато есть кошка (ставим «+»).
6. У Маши с Антоном одинаковые животные. Значит, у Антона тоже живет кошка (ставим «+») и нет собаки (ставим «-»).
7. У Антона с Костей разные питомцы, выходит, что у Кости нет кошки (ставим «-»), зато есть собака (ставим «+»).
8. У Кости с Юрой одинаковые животные, значит у Юры тоже собака (ставим «+»), а не кошка (ставим «-»).
Так мы узнали, какие питомцы живут у каждого из ребят (ячейки со знаком «+»).
Ответ: У Сони попугай, у Маши и Антона кошки, у Кости и Юры собаки.
Круги Эйлера
Чтобы было легче разобраться в условиях задачи и найти решение, чертим круги, каждый из которых – отдельное множество.
Задача:
Всему классу задали на лето читать книжки.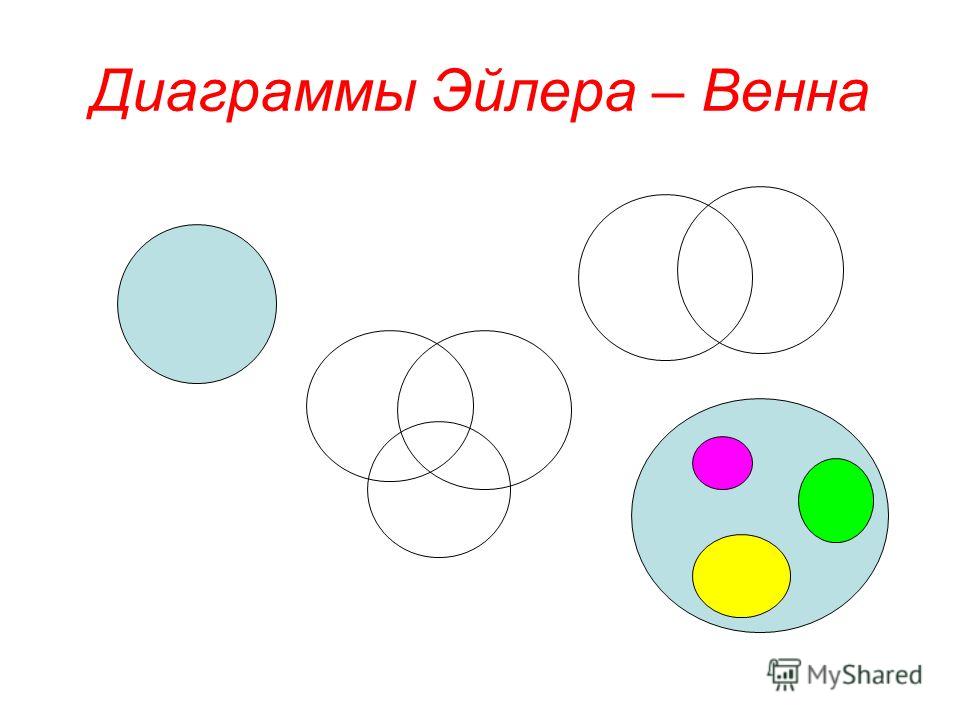 В списке литературы были такие произведения, как «Робинзон Крузо» Даниэля Дефо и «Белый клык» Джека Лондона. Известно, что 15 человек из класса прочитали «Робинзон Крузо», а остальные 11 – «Белый клык». Но среди них были 6 ребят, которые прочитали обе книги. Сколько человек прочитало только «Белый клык»?
В списке литературы были такие произведения, как «Робинзон Крузо» Даниэля Дефо и «Белый клык» Джека Лондона. Известно, что 15 человек из класса прочитали «Робинзон Крузо», а остальные 11 – «Белый клык». Но среди них были 6 ребят, которые прочитали обе книги. Сколько человек прочитало только «Белый клык»?
Решение:
Чертим два круга, каждый из которых – множество детей, прочитавших определенную книгу, а пересечение кругов – дети, прочитавшие обе книги.
1. 15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
2. 11 – 6 = 5 – дети, которые читали лишь «Белый клык».
Ответ: 5 человек.
Метод рассуждений
Поочередно рассматриваем каждое из условий задачи и делаем логические выводы.
Задача:
На столе стоят вазы: голубая, зеленая, розовая и оранжевая. Третьей в ряду стоит та ваза, название цвета которой содержит больше всего букв. А зеленая стоит между оранжевой и розовой. Какая ваза стоит последней?
Решение:
1. Больше всего букв в слове «оранжевая», значит она третья по счету.
Больше всего букв в слове «оранжевая», значит она третья по счету.
2. Если зеленая ваза стоит между оранжевой и розовой, значит, она будет второй в ряду, так как если ее поставить четвертой, то не останется места для розовой.
3. Соответственно, розовая будет стоять первой.
4. Остается голубая, она будет четвертой, то есть последней.
Ответ: голубая ваза.
Метод рассуждений «с конца»
Начинаем раскручивать клубок с конца, а затем сопоставляем результат с условиями задачи.
Задача:
Маме, папе и сыну вместе 125 лет. Когда родился сын, маме был 21 год. А папа старше мамы на 2 года. Сколько лет сейчас каждому из них?
Решение:
1. 21+2= 23 — было папе ( значит вместе родителям было 44 года)
2. (125 — 44) : 3 = 27 — возраст сына
3. 27 + 21 = 48 — возраст мамы
4. 48 + 2 = 50 — возраст папы
Ответ: 27, 48 и 50 лет.
Мы рассмотрели самые популярные и доступные методы, с помощью которых можно легко справиться с заданием. Главное – подобрать подходящий способ решения, который быстро приведет к правильному результату.
Главное – подобрать подходящий способ решения, который быстро приведет к правильному результату.
Для этого необходимо регулярно практиковаться и развивать свои способности. Отточить навыки решения подобных логических задач и многих других вы можете с помощью образовательной онлайн-платформы «Умназия».
Попробуйте решить вместе с ребенком задачу из раздела «логика» и переходите к регулярным занятиям на тренажере
Поробуйте решить задачу Умназии прямо сейчас!
Попробовать
Математика
Умназисты соревновались в поедании пирожков. Соревнование длилось ровно 45 минут. За это время все соревнующиеся в сумме съели 179 пирожков.
Посмотри на информацию о соревнующихся на рисунке. Можешь ли ты сказать, кто из умназистов занял почётное третье место?
Выбери ответ:
Третье место заняла Ума Коала.
Третье место занял Мышлен.
Третье место занял Грамотигр.
Третье место занял Ква-Квариус.
Третье место заняла Сообразебра.
ответить
Логика решения:
Мы знаем, что Мышлен ел по 1 пирожку в минуту, значит за 45 минут соревнования он съел 45 пирожков (1 х 45 = 45).
Если Мышлен съел на 10 пирожков больше, чем Сообразебра, то Сообразебра съела 35 пирожков (45 – 10 = 35).
Если Ума-Коала съела на 5 пирожков меньше, чем Сообразебра, то Ума-Коала съела 30 пирожков (35 – 5 = 30).
Чтобы выяснить, сколько съели Грамотигр и Ква-Квариус, сложим все пирожки, которые съели Мышлен, Ума-Коала и Сообразебра. Получается 45 + 35 + 30 = 110 пирожков.
От общего количества съеденных пирожков вычтем съеденное тремя умназистами: 179 – 110 = 69. Значит, Ква-Квариус и Грамотигр вместе съели 69 пирожков.
Из условия мы знаем, что Грамотигр съел пирожков в 2 раза больше, чем Ква-Квариус.
Допустим, Ква-Квариус съел 23 пирожка, тогда Грамотигр съел в два раза больше, то есть 23 х 2 = 46 пирожков.
Теперь снова сложим их пирожки, чтобы проверить себя: 23 + 46 = 69. Сходится.
Значит, Грамотигр (46 пирожков) занял первое место, Мышлен (45 пирожков) – второе, а Сообразебра (35 пирожков) – третье.
Если вам понравилось, было весело интересно и полезно, то ждем вас на нашей онлайн платформе!
Умназия сегодня — это:
1. Онлайн тренажер развития навыков мышления — логики, внимания, эрудиции.
2. Программа «Культурный код» по развитию кругозора. Для самых любознательных и тех, кого кажется уже ничем не удивить!
3. Курсы развития памяти. Хотите чтобы Ваш ребенок без труда учил стихи, запоминал иностранные слова и всегда помнил про день рождения бабушки? На курсах покажем и расскажем как же этого достичь.
4. Пять ступеней финансовой грамотности. Увлекательная история героя, которая полностью зависит от действий ребенка и не имеет определенного результата. Сможет ли он пройти все финансовые ловушки и освоить пятую ступень?
Ждем вас, будет весело и интересно!
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Читайте также:
- 15 сложных загадок на логику
- Загадки на логику с подвохом
- Логические загадки для детей
- Смешные логические загадки
- Загадки Эйнштейна на логику
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тесты по информатике для 7 класса онлайн
-
Информация и её свойства
14.09.2021 1720
Тест по информатике для 7 класса на тему: «Информация и её свойства»
-
Устройство компьютера
12.11.2016 96248
Тест по информатике для 7 класса по теме «Устройство компьютера» (УМК Босова Л.Л.)
-
Компьютерные объекты
18.
 10.2016
16947
10.2016
16947
Тест по теме «Компьютерные объекты» для 6 класса (УМК Л.Л. Босова)
-
Информатика 7 кл. Информация и информационные процессы
25.09.2017 25698
Тест для учеников 7 класса по темам: информация, её свойства, виды информации, информационные процессы.
-
Итоговый тест по информатике 7 класс. Босова Л.Л.
29.04.2021 7615 0
Итоговое тестирование по информатике 7 класс к учебнику Босовой. Тест включает в себя 12 заданий
-
Единицы измерения информации
08.
 10.2019
14551
10.2019
14551
Проверка знаний по теме «Единицы измерения информации». Информатика.
-
Файл и файловая система
13.12.2012 49952
Тест можно использовать для текущего контроля знаний по теме: «Файлы и файловая система» Подготовила: Шумилина Л. А.
-
Программное обеспечение компьютера
13.11.2016 48133
Тест по информатике для 7 класса по теме «Программное обеспечение компьютера»
-
Устройство компьютера — 7 класс
23.
 11.2016
28304
11.2016
28304
Тест по теме «Устройство компьютера» для 7 класса по 35 часовой программе.
-
Компьютерные вирусы и антивирусные программы
13.11.2016 14847
Тест по информатике для 7 класс на тему «Компьютерные вирусы и антивирусные программы»
-
Кодирование информации
08.10.2019 4903 0
Проверь свои знания в информатике по теме «Информация. Кодирование информации»
-
Информация и информационные процессы.
 7 класс. Информатика.
7 класс. Информатика.
06.11.2020 249 0
Тест по информатике. 7 класс по программе Л.Л.Босова. ФГОС. Раздел «Информация и информационные процессы»
-
Повторение изученного в 7 классе по информатике
29.06.2021 516 0
Данный тест предназначен для повторения изученного на уроках информатики в 7 классе
-
Итоговая контрольная работа по информатике 7 класс. Вариант 1
04.04.2019 3315
Годовая контрольная работа. Учебник Босовой Л.
 Л. Информатика 7 класс
Л. Информатика 7 класс -
Информация и информационные процессы (7 класс) — 1 вариант
22.10.2015 6212
Тест по темам «Информация и информационные процессы, история развития компьютерной техники» для 7 класса.
-
Логика высказываний
01.10.2019 2657
Тест по теме «Логика высказываний». Информатика 7 класс
-
Представление информации
16.11.2020 3441 0
Тест по информатике для обучающихся 7 класса на тему «Представление информации».

-
Тест на проверку читательской грамотности
15.06.2021 2315
Проверка читательской грамотности пользователя на уроке инфоматике.
-
Использование логических операций для построения поисковых запросов в Интернете
10.10.2019 405 0
Тест по теме «Использование логических операций для построения поисковых запросов в Интернете». Информатика 7 класс
-
Восприятие информации.Свойства информации.
26.
 11.2017
2163
0
11.2017
2163
0
Тест по теме «Информация, восприятие информации, свойства информации». Для учащихся 7 класса, изучающих информатику по учебнику Н.Г.Семакин.
-
Устройство Компьютера
09.10.2012 3590
Тренировочный тест, для прохождения тестирования на уроке информатики. Часть теста входит в поурочное тестирование, как контроль знаний
-
Информация и информационные процессы (7 класс) — 2 вариант
22.10.2015 3044 0
Тест по темам «Информация и информационные процессы, история развития компьютерной техники» для 7 класса.

-
Информатика 7 класс. Текстовые документы. Тест.
07.02.2019 5294
Тест проверяет знание основных понятий по теме «Текстовый документ». Учебник Босовой Л. Л.
-
Круги Эйлера
18.10.2020 1508 0
Тест проверяет умения решать задачи по теме «Запросы» из темы «Всемирная паутина»
-
Практикум 7-го класса.Глава 2. Компьютер как универсальное устройство для работы с информацией.
28.
 04.2017
2455
0
04.2017
2455
0
Это тестовые задания для самоконтроля, которые помогут вам подготовиться даже к самой сложной контрольной работе.
-
Единицы измерения информации
09.11.2021 285 0
Тест «Единицы измерения информации» предназначен для учащихся 7 классов, состоит из 5 вопросов.
-
Введение в информатику. 7 класс (Поляков, Еремин)
30.09.2017 2362 0
7 класс (Поляков, Еремин) — Устройство компьютера. Файловая система. Информация и данные, информационные процессы.
 Кодирование. Программое обеспечение
Кодирование. Программое обеспечение -
Алгоритмизация. 7 класс. Python — ввод и вывод данных, условия
02.02.2020 3431 0
Темы: Алгоритмы и исполнители, способы записи и свойства алгоритма. Блок-схемы. Python — начальный уровень
-
Итоговый тест по информатике 7 класс
19.05.2020 2398 0
Данный тест позволяет проверить проверить знания, полученные в 7 классе. По учебнику 7 класса под редакцией Босовой Л.Л.
-
7 класс «Измерение информации»
28.
 10.2020
4474
10.2020
4474
Тест позволит проверить знания по теме «Алфавитный подход к измерению информации. Единицы измерения информации».
-
Глава 4. Обработка текстовой информации.
29.04.2017 12846
Это тестовые задания для самоконтроля, которые помогут вам подготовиться даже к самой сложной контрольной работе.
-
Тест: «Информационные процессы. Всемирная паутина». (Информатика. 7 класс)
20.11.2021 35 0
Задание по теме: «Информационные процессы. Всемирная паутина» (Информатика 7 класс)
-
Как устроен персональный компьютер
02.
 02.2018
5798
02.2018
5798
Тест по теме » Как устроен персональный компьютер» к главе 2 учебника информатика 7 класс И. Г. Семакин
-
ЮНЫЙ ИНФОРМАТИК, 6-7 КЛАСС, 1 ТУР
02.12.2012 8207
Для развития любознательности, интереса к предмету информатики Внимательно прочитайте вопрос и выберите вариант ответа/
-
Операции над множествами
10.10.2019 1855 0
Тест по теме «Операции над множествами». Информатика 7 класс
-
Алгоритмизация.
 Ветвление. Блок-схемы
Ветвление. Блок-схемы
16.02.2020 5069
Темы: Алгоритмы и исполнители, алгоритмы ветвления. Блок-схемы алгоритмов
-
Компьютерная графика. 7 класс. I вариант
11.05.2015 26572
Тест содержит вопросы, составленные в соответствии с программой Л.Босовой ФГОС для 7 класса в аналогии с тестовыми заданиями автора учебника.
-
Алгоритм и исполнители
09.11.2016 16157
Тест по информатике для 6 класса по теме «Алгоритм и исполнители» (УМК Босова Л.
 Л.)
Л.) -
Тест для учеников 7 класса. Персональный компьютер.
12.11.2016 5747 0
Тест для 7 класса по теме «Персональный компьютер». Учебник Босовой Л.Л.
-
Логические операции И и ИЛИ
03.10.2019 980 0
Логика высказываний.Логичееские операции И и ИЛИ . Тест по информатике 7 класс.
-
Обработка графической информации
09.03.2020 6983
Тест по информатике.
 Тема: Обработка графической информации. 7 класс. УМК Босова Л.Л.
Тема: Обработка графической информации. 7 класс. УМК Босова Л.Л. -
Технология мультимедиа
14.05.2020 5026 0
Тест для 7 класса по теме Мультимедийные технологии. ФГОС по учебнику Л. Босовой
-
Информатика 7 класс (по учебнику Семакина)
24.05.2020 536 0
Тест из 10 вопросов позволит быстро освежить знания, полученные при изучении информатики в 7 классе.
-
Компьютер как универсальное устройство обработки информации
18.
 05.2015
5478
05.2015
5478
Данный тест охватывает весь материал по теме «Компьютер как универсальное устройство обработки информации» 7 класса. В нем присутствуют вопросы о программном обеспечении, устройствах компьютера и т.д.
-
Тест Информационное моделирование
19.10.2016 4555
Тест для 6 класса по информатике на тему Информационное моделирование (УМК Босова Л.Л.)
-
Графики и диаграммы
06.11.2016 11017
Тест по информатике для 6 класса на тему «Графики и диаграммы» (УМК Босова Л.
 Л.)
Л.) -
Итоговый тест по теме «Информация и информационные процессы»
24.10.2017 6614
Данный тест является итоговой проверкой знаний по раделу «Информация и информационные процессы» для учащихся 7 класса по программе Л.Л.Босовой 7 класс ФГОС
-
Алгоритмизация. 7 класс
21.02.2019 3054
Темы: Алгоритмы и исполнители, способы записи и свойства алгоритма. 7 класс, начало изучения алгоритмов
-
Оценка количественных параметров текстовых документов.
 Информатика. 7 класс.
Информатика. 7 класс.
09.03.2019 4140 0
Информатика 7 класс Тест проверяет умение рассчитывать объём текстового файла
-
Множества. Информатика 7 класс
10.10.2019 1141 0
Тест по теме «Множества». Информатика 7 класс Республика Беларусь
-
Проверочная работа «Количественные параметры информационных объектов»
06.06.2020 7 0
Описание работы Тест предназначен для обучающихся 7 класса. Работа состоит из 10 заданий с выбором ответа или кратким ответом, каждый верный ответ оценивается 1 баллом; Максимальное количество баллов 10.
 На выполнение теста отводится фиксированное время (30 минут).
На выполнение теста отводится фиксированное время (30 минут). -
Использование логических операций для построения поисковых запросов в Интернете
15.10.2021 52 0
Тест «Использование логических операций для построения поисковых запросов в Интернете». 7 класс. в тесте 5 вопросов с одним правильным ответомв каждом вопросе. после завершения теста сможете просмотреть на какие вопросы вы ответили верно, на какие неправильно.
-
Внутреннее устройство компьютера
28.10.2021 181 0
Тест предназначен для учащихся 7 класса. Тест на понимание особенностей устройств компьютера, умение читать интеллект карты.
 В помощь-интеллект карта из учебника информатики К.Ю. Полякова и Е.А. Еремина для 7 класса
В помощь-интеллект карта из учебника информатики К.Ю. Полякова и Е.А. Еремина для 7 класса -
Определение количества информации. Проверочная работа. Вариант 03
28.01.2022 117 0
Тестирование по теме «Измерение количества информации». Предназначено для обучающихся 7-8 классов с целью проверки и закрепления полученных знаний.
-
Промежуточная аттестация 7 класс. Босова Л.Л., Босова А.Ю
18.04.2022 662 0
Тест расчитан на 30-40 минут. Задания с выбором ответа и полным ответом.
-
Объекты.
 Системы объектов.
Системы объектов.
20.10.2013 1575 0
тест по теме «Объекты. Системы объектов». Тест направлен на оценку усвоения материала по теме.
-
Тест 1 по информатике по теме Электронные таблицы
07.02.2014 3760
тест для обучающихся 7-х классов по теме Электронные таблицы. Включает в себя 6 вопросов с выбором ответа или вводом своего варианта ответа
-
Правила записи арифметических выражений
03.12.2014 1051
Тест рассчитан для суммативного оценивания знаний учащихся 7 классов.
 Планируется использование теста в конце урока по теме «Правила записи арифметических выражений на языке Паскаль».
Планируется использование теста в конце урока по теме «Правила записи арифметических выражений на языке Паскаль». -
Информатика. 7 класс. Растровая и векторная графика. Общие сведения
11.02.2015 14423
Тест разработан для учащихся 7 класса при изучении темы «Общие сведения о растровой и векторной графики». Количество вопросов — 6, время ограничено 10 минутами
-
Компьютерная графика, общие сведения, 7 класс
27.02.2015 10510 0
Итоговый тест по теме «Компьютерная графика» для 7 класса.
-
Компьютерная графика.
 7 класс. II вариант
7 класс. II вариант
11.05.2015 4150 0
Тест содержит вопросы, составленные в соответствии с программой Л.Босовой ФГОС для 7 класса в аналогии с тестовыми заданиями автора учебника.
-
Основы алгоритмизации_1
06.08.2015 1812 0
Тест состоит из восьми вопросов на проверку таких понятий как алгоритм, свойство алгоритма, основные алгоритмические структуры
-
Информационные процессы (разбор ситуаций)
19.09.2015 1166 0
Тест по программе 7 класса для белорусских школ.
 использованы материалы «Рабочей тетради» автора Л. Овчинниковой
использованы материалы «Рабочей тетради» автора Л. Овчинниковой -
Тест для учеников 7 класса по информатике
19.10.2016 2759 0
Тест по теме: Измерение информации — алфавитный подход к измерению информации, 7 класс, по учебнику Босовой Л.Л.
-
Системы объектов
20.10.2016 4599
Тест для 6 класса (ФГОС) по УМК Босова Л.Л., тест проходят в качесте закрепления темы Система объектов
-
Тест для 6 класса «Схемы»
06.
 11.2016
4695
11.2016
4695
Тест по информатике для 6 класса на тему «Схемы» (УМК Босова Л.Л.)
-
Урок на тему: Программное обеспечение ПК. О системном ПО и системах программирования
08.11.2016 478 0
Урок-тест нацелен на формирование понятий о системном ПО и о системах программирования Задачи урока: 1. Образовательная – получить преставление о составе программного обеспечения компьютера: — назначении системного ПО, назначение ОС и программ, которые относятся к системному ПО; — назначении программ, которые относятся к прикладному ПО; — назначение систем программирования. 2. Развивающая – развить информационную культуру и умения определять, к какому программному обеспечению относится конкретная программа, развить навык работы с ЭОР.
 3. Воспитательная – воспитывать культуру работы в парах; воспитывать информационную культуру.
Тип урока: изучение нового материала.
(Автор УМК И.Г.Семакин и др.)
3. Воспитательная – воспитывать культуру работы в парах; воспитывать информационную культуру.
Тип урока: изучение нового материала.
(Автор УМК И.Г.Семакин и др.) -
Истрия развития ИКТ
12.11.2016 876 0
Тест по информатике для 7 класса на тему «История развития ИКТ» (УМК Босова Л.Л.)
-
Контрольная работа за 2 четверть (7 класс)
16.12.2016 2751
Контрольная работа по информатике для 7 класса за 2 четверть (учебник Н.Д.Угринович)
-
Тест для учеников 7 класса.
 Расчет информационного веса изображений.
Расчет информационного веса изображений.
14.01.2017 501 0
Тест для учеников 7 класса по учебнику Босовой Л.Л. Тема «Обработка графической информации».
-
Тест для учеников 7 класса. Расчет информационного веса текстовых фрагментов.
16.03.2017 616 0
Тест для учеников 7 класса по учебнику Босовой Л.Л. Тема «Обработка текстовой информации».
-
Практикум 7-го класса. Глава 1. Информация и информационные процессы.
26.
 04.2017
1071
0
04.2017
1071
0
Это тестовые задания для самоконтроля, которые помогут вам подготовиться даже к самой сложной контрольной работе.
-
Глава 3. Обработка графической информации.
29.04.2017 5164 0
Это тестовые задания для самоконтроля, которые помогут вам подготовиться даже к самой сложной контрольной работе.
-
Глава 1. Математические основы информатики.
03.05.2017 2142 0
Это тестовые задания для самоконтроля, которые помогут вам подготовиться даже к самой сложной контрольной работе.

-
Информатика шаг №1
05.02.2018 1048
Тест по информатике и ИКТ для 7-8 классов. Включает в себя темы: Инфомация, Интернет, Устройство компьютера. Время теста не ограниченно. Оставляйте свои комментарии.
-
Информатика шаг № 2
06.02.2018 266
На данной странице представлены ребусы, в которых в картинках зашифрованы термины по школьной дисциплине «Информатика». Ребусы по теме «История вычислительной техники».
-
Файл.
 Файловая система. Информатика. 7 класс.
Файловая система. Информатика. 7 класс.
11.04.2018 2406 0
Информатика Компьютер Хранение данных Файл Файловая система Основные понятия
-
Информатика. 7 класс.Маска имени файла
15.04.2018 776 0
Информатика. 7 класс. Файловая система. Тест.
-
Тест Обработка графической информации Информатика 7 класс
30.12.2018 5599 0
Информатика 7 класс Базовый уровень Тест Обработка графической информации
-
Информатика.
 7 класс. Обработка текстовой информации. Тест.
7 класс. Обработка текстовой информации. Тест.
10.03.2019 9642
Проверка знаний по теме «Обработка текстовой информации». Учебник Босовой Л. Л. Информатика 7 класс
-
Итоговая контрольная работа по информатике 7 класс. Вариант 2
05.04.2019 732
Годовая контрольная работа. Учебник Босовой Л. Л. Информатика 7 класс
-
Итоговая контрольная работа 7 класс
06.05.2019 343 0
Работа состоит из 12 заданий. За каждый правильный ответ, в зависимости от сложности задания дается один или более баллов.
 Баллы, получаемые вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше количество заданий и набрать как можно больше баллов.
Баллы, получаемые вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше количество заданий и набрать как можно больше баллов. -
Online Тест по Информатике для 7 класса
13.02.2020 105 0
Тест по информатике для 7 класса на казахском языке. На тему «Общий вопрос». Позволит проверить ваши знания.
-
Единицы измерения информации 7 класс Поляков К.Ю.
07.03.2020 168 0
Тест предназначен для учащихся 7 класса, обучающихся по программе К.Ю. Полякова, Е.А. Еремина при базовом изучении информатики (1 час в неделю)
-
Обработка текстовой информации
19.
 03.2020
48
0
03.2020
48
0
Тест по информатике «Обработка текстовой информации» предназначен для учащихся 7 класса, обучающихся по программе Босовой Л.Л. «Информатика. 7 класс!
-
контрольная работа № 4 Обработка текстовой информации
09.04.2020 340 0
Данный тест проверяет знания учащихся по теме Обработка текстовой информации 7 кл. по учебнику Информатика Босовой Л.
-
ВИРУСТАР жана АНТИВИРУСТАР
09.04.2020 60 0
Урматтуу окуучулар. Бул тест атайын сиздер үчүн түзүлдү.
 Ссылка боюнча тестке кирип, тест менен таанышып, андан кийин жообуңарды бергиле. Тест өтө кызыктуу. Тесттин жардамы менен өзүңөрдүн билимиңерди жогорулатасыңар. Тестке жооп берүү менин Ютуб каналыма каналыма кирип «ВИРУСТАР ЖАНА АНТИВИРУСТАР» деген видеосабагымды көрүп чыксаңар болот. Видеосабактарыма төмөнкү ссылка менен кириңиздер: https://www.youtube.com/channel/UCn-ibNWnjdVFVOLLQp8nPyQ?view_as=subscriber Чектөө жок. Бул тесттен кийин дагы көптөгөн тесттер болот. Тест тапшырууда баарыңарга ийгилик каалаймын.
Ссылка боюнча тестке кирип, тест менен таанышып, андан кийин жообуңарды бергиле. Тест өтө кызыктуу. Тесттин жардамы менен өзүңөрдүн билимиңерди жогорулатасыңар. Тестке жооп берүү менин Ютуб каналыма каналыма кирип «ВИРУСТАР ЖАНА АНТИВИРУСТАР» деген видеосабагымды көрүп чыксаңар болот. Видеосабактарыма төмөнкү ссылка менен кириңиздер: https://www.youtube.com/channel/UCn-ibNWnjdVFVOLLQp8nPyQ?view_as=subscriber Чектөө жок. Бул тесттен кийин дагы көптөгөн тесттер болот. Тест тапшырууда баарыңарга ийгилик каалаймын.
-
Тест «Текстовый редактор» 7 класс
12.04.2020 6680
Тест проверяет знание основных понятий по теме «Текстовый процессор». Учебник Босовой Л. Л.
-
Визуализация информации в текстовых документах (7 класс)
20.
 04.2020
1839
0
04.2020
1839
0
Данный тест составлен по рабочей тетради Л.Л. Босовой информатика 7 класс (ФГОС)
-
Контрольный тест «Мультимедиа» 7 кл
23.04.2020 1356 0
Контрольный тест по теме «Мультимедиа» для 7 кл. по информатике
-
Контрольная работа №4
25.04.2020 92 0
В тесте 17 вопросов по теме: «Обработка текстовой информации» (Информатика, 7 класс)
-
Контрольная работа «Обработка текстовой информации»
26.
 04.2020
597
0
04.2020
597
0
Тест представляет из себя контрольную работу по информатике в 7 классе по теме «Обработка текстовой информации»
-
Информатика. Мультимедиа. 7 класс.Босова
06.05.2020 14029
Тест предназначен для проверки знаний по теме «Мультимедиа» в курсе информатики 7 класса
-
Обработка текстовой информации
13.05.2020 86 0
Контрольная работа «Обработка текстовой информации» 7 класс (УМК Босова)
-
СОР № 1 по информатике для учащихся 7-х классов
14.
 05.2020
191
0
05.2020
191
0
СОР №2 по информатике для учащихся 7-х классов за раздел «Программирование решений»Колличество вопросов -4 вопросов Время прохождения -20 минМаксимальное колличество баллов -10 баллов После прохождения СОРа вы получаете свой баллы
-
Итоговый тест 7 класс по главам «Информация и информационные процессы. Компьютер, как универсальное устройство» Босова Л.Л.
22.05.2020 1203 0
Иоговый тест по темам курса информатики, объединенных в следующие тематические блоки: «Компьютер для начинающих», «Информация вокруг нас», «Информационные технологии». учебник 7 класс Босова Л.Л.
-
Итоговый тест по теме «Информация и информационные процессы»
14.
 10.2020
581
0
10.2020
581
0
Итоговый тест по теме «Информация и информационные процессы»
-
Информатика пробник
26.10.2020 5 0
Тренировочный тест по Информатике. Включает в себя 5 вопросов
-
Математический тест на применение в жизни
08.11.2020 180
Внимательно прочитай задание, решите задачу, можно использовать черновик, аккуратно введи ответ в строку ниже задания
-
Информация и информационные процессы.
 7 класс.
7 класс.
15.11.2020 577 0
Обобщение и систематизация основных понятий темы «Информация и информационные процессы». 7 класс.
| Miro
Шаблон диаграммы Эйлера помогает понять сложные иерархии и разобрать аргументы, идеи, системы и перекрывающиеся определения.
Эта диаграмма позволяет визуализировать все возможные связи между несколькими группами и разобраться в сложных отношениях. Например, вы можете использовать его, чтобы показать отношения между вирусами, людьми и другими организмами.
Вы также можете использовать диаграммы Эйлера для отображения отношений между разными людьми в организации или структур компьютерных сетей.
Короче говоря, диаграммы Эйлера полезны, когда вы хотите представить сложные иерархии или понять, как элементы в группе связаны друг с другом.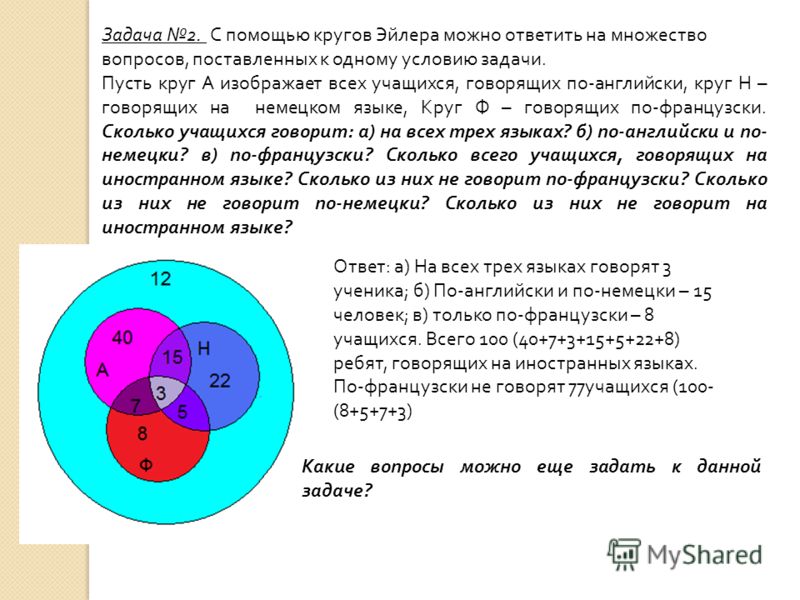
Продолжайте читать, чтобы узнать больше о нашем шаблоне диаграммы Эйлера.
Что такое диаграмма Эйлера?
Диаграммы Эйлера представляют собой визуальное представление существующих отношений между рядом элементов (наборов).
В математике множества представляют наборы объектов. Эти группы или «наборы» могут относиться к любой категории: люди, здания, автомобили, компьютерные сети или что-то еще.
Теория множеств утверждает, что группировка похожих элементов часто может упростить задачи, облегчая с ними работу.
Диаграммы Эйлера также могут представлять заданный сценарий с разных точек зрения. Например, они могут помочь вам визуализировать, как конкретное лечение влияет на пациентов из разных демографических групп.
Это полезно, чтобы понять влияние определенных условий, упростить сложную концепцию или сравнить различные подходы к решению проблемы.
Вы также можете использовать диаграммы Эйлера, чтобы деконструировать и визуализировать отношения между идеями в аргументе.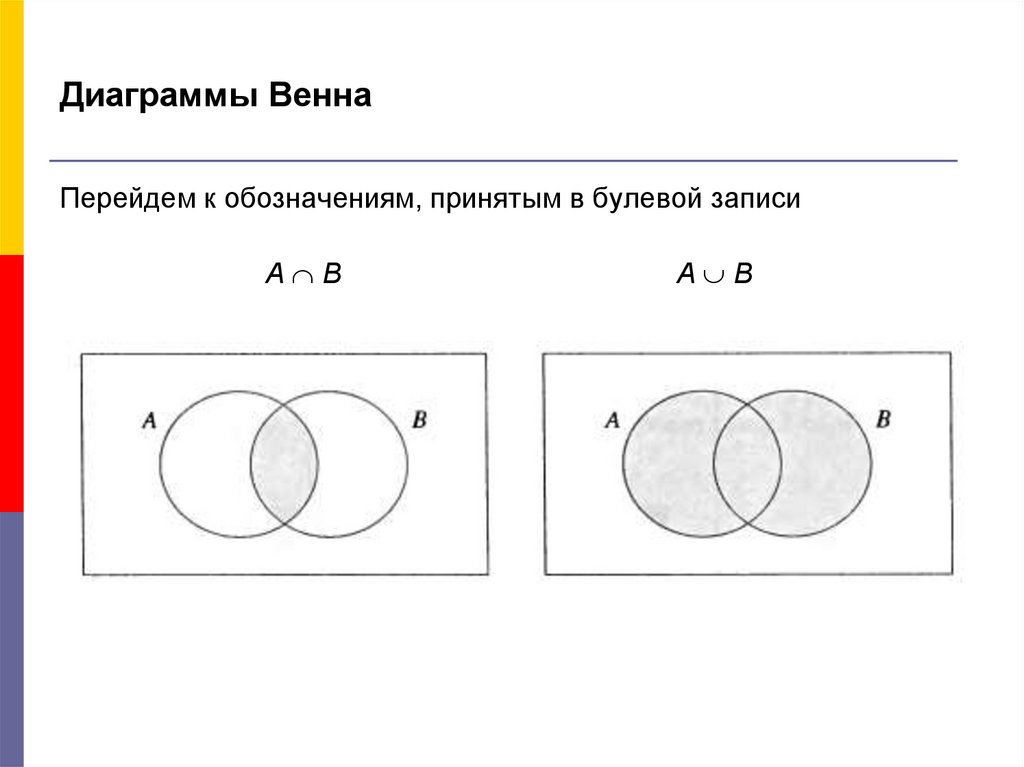
Преимущества реализации диаграммы Эйлера
Некоторые из основных преимуществ реализации диаграммы Эйлера включают:
Прояснение сложных взаимосвязей: Диаграммы Эйлера полезны, если вы хотите отобразить связи между большим количеством данных точки. Например, они могут помочь вам понять, как взаимосвязаны различные группы и категории.
Позволяет визуализировать вещи с разных точек зрения: Диаграммы Эйлера полезны в сложных мысленных экспериментах. Они позволяют вам изменить свою точку зрения и увидеть, как бы все изменилось, если бы у вас были другие входные данные.
Улучшает процесс принятия решений: Диаграммы Эйлера могут быть полезны, если вы хотите принять решение между различными вариантами действий. Например, они позволяют увидеть, как разные стратегии управления повлияют на компании из разных секторов.
Помогает лучше анализировать аргументы: Диаграммы Эйлера позволяют анализировать аргументы.
 Они позволяют раскрыть различные точки зрения и визуализировать вклад каждой части в целое.
Они позволяют раскрыть различные точки зрения и визуализировать вклад каждой части в целое.
Создайте свою собственную диаграмму Эйлера
С помощью Miro создать диаграмму Эйлера довольно просто. Сначала выберите шаблон диаграммы Эйлера. Затем выполните следующие действия:
Шаг 1. Введите названия категорий или групп, которые вы хотите классифицировать
Шаблон диаграммы Эйлера содержит предварительно созданные круги Эйлера или «ячейки», которые позволяют вам вводить названия групп. Вы можете добавлять имена к своей диаграмме Эйлера, просто вводя название категории в каждую ячейку.
Например, вы можете использовать готовые круги для представления «Людей», «Бактерий» и «Организмов» на диаграмме Эйлера.
Шаг 2. Назначьте отношения
После того, как вы добавили все имена различных групп на диаграмму Эйлера, назначьте отношение каждой группе и категории.
В данном примере «Люди» и «Бактерии» принадлежат к одной и той же категории «Организмы».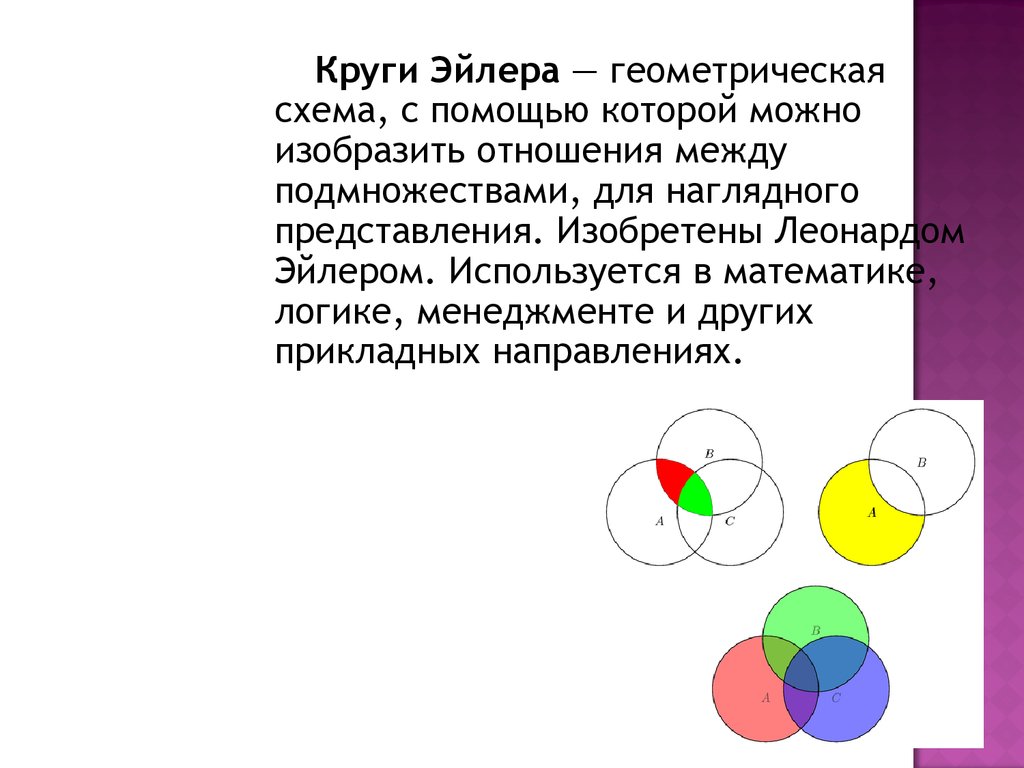 Вы можете добавить эту связь в диаграмму Эйлера.
Вы можете добавить эту связь в диаграмму Эйлера.
Вы также можете добавить отрицательную связь между «Люди» и «Бактерии». Это означает, что люди не являются бактериями.
В Miro вы можете изменить цвет данной категории, чтобы указать, является ли она положительной или отрицательной. Вы изменяете цвет кругов Эйлера, щелкая на палитре цветов и выбирая новый цвет для круга.
Шаг 3. Переместите эйлеровы круги соответствующим образом
После того, как вы добавили отношения между различными группами или кругами, переместите их соответствующим образом.
Этот шаг включает в себя перемещение соответствующих кругов в правильное положение и ориентацию. Вы можете перемещать круги, щелкая и перетаскивая их.
Вы также можете удалить круги, выбрав их и нажав «Удалить». Или вы можете отредактировать их, выбрав их и введя новое имя.
Если хотите, измените размер кругов, чтобы получить точное представление о вашей диаграмме. Например, если у категории много подкатегорий, вы можете изменить размер круга так, чтобы каждая категория помещалась в основной круг.
Реальный пример диаграммы Эйлера
Допустим, вы хотите понять экономические отношения между европейскими странами. Вы можете представить Европейский союз в виде одного круга. Затем внутри этого круга вы можете представить, как разные страны относятся друг к другу с точки зрения торговли. Вы можете разделить этот круг на разные секции, представляющие разные типы товаров, которыми страны торгуют друг с другом.
Например, Германия может покупать шведское вино и продавать пластмассовые изделия в Испанию. Тогда можно было бы, чтобы Франция покупала итальянский ликер, но продавала автомобили в Германию.
Вы можете добавить эти соотношения в свою диаграмму Эйлера, а затем использовать их, чтобы лучше понять, какие страны торгуют друг с другом.
Диаграмма Эйлера — значение, примеры, диаграмма Венна, как создать?
Диаграммы Эйлера — это общепринятое обозначение для отображения информации о множествах и их отношениях друг с другом.
Их часто изображают в виде групп (потенциально связанных) замкнутых кривых. Эти диаграммы допускают некоторое упущение множественных взаимодействий, позволяя им использовать в своих интересах пространственные качества удержания и непересекающихся кривых.
Эти диаграммы полезны в различных приложениях для представления теоретико-множественных данных, включая визуализацию статистических данных, построение основ диаграммной логики, разработку программного обеспечения и отображение результатов поисковых запросов в базе данных. Однако эти методы могут генерировать диаграммы только для ограниченной части всех мыслимых абстрактных описаний.
Содержание
- Что такое диаграмма Эйлера?
- Объяснение диаграммы Эйлера
- Steps to Create Euler Diagram
- Example
- Euler vs Venn Diagram
- Frequently Asked Questions (FAQs)
- Recommended Articles
- An Euler Diagram is a visual or diagrammatic representation of sets and their interactions with друг друга.
 Они состоят из простых замкнутых кривых на плоскости (обычно кругов), которые представляют наборы.
Они состоят из простых замкнутых кривых на плоскости (обычно кругов), которые представляют наборы. - Леонард Эйлер, швейцарский математик, создал концепцию.
- У них много общего с диаграммами Венна, но есть и небольшие различия.
- Это естественный способ представления данных в теории множеств. Визуализация статистических данных, создание основы для диаграммных рассуждений, разработка программного обеспечения и отображение результатов поисковых запросов в базе данных — все это примеры полезности диаграмм Эйлера.
Объяснение диаграммы Эйлера
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Диаграмма Эйлера (wallstreetmojo.com)
Диаграмма Эйлера — это представление замкнутых кругов или кривых, которые делят плоскость на отдельные, но соединенные подмножества. Их называют областями, каждая из которых окружена набором кривых. Общие примеры диаграмм Эйлера показывают теоретико-множественные отношения, где каждая кривая представляет набор, а каждая область представляет собой пересечение нескольких наборов. Представления, созданные с помощью онлайн-конструктора диаграмм Эйлера, могут иметь кривые любой геометрической формы. Ценность диаграммы заключается в том, как кривые перекрываются, а не в их размерах или формах. Следовательно, теоретико-множественные взаимодействия (пересечение, подмножество и непересекаемость) относятся к пространственным отношениям между областями, заключенными в каждой форме.
Их называют областями, каждая из которых окружена набором кривых. Общие примеры диаграмм Эйлера показывают теоретико-множественные отношения, где каждая кривая представляет набор, а каждая область представляет собой пересечение нескольких наборов. Представления, созданные с помощью онлайн-конструктора диаграмм Эйлера, могут иметь кривые любой геометрической формы. Ценность диаграммы заключается в том, как кривые перекрываются, а не в их размерах или формах. Следовательно, теоретико-множественные взаимодействия (пересечение, подмножество и непересекаемость) относятся к пространственным отношениям между областями, заключенными в каждой форме.
Швейцарский математик Леонард Эйлер (1707–1783) дал миру представление о диаграммах Эйлера, эйлеровых кругах и постоянной Эйлера. Здесь каждая кривая делит плоскость на две зоны или области. Внутренние части изображения представляют собой элементы множества, а внешние — элементы, не входящие в их состав. Кривые, не имеющие общих элементов, не пересекаются и являются непересекающимися множествами.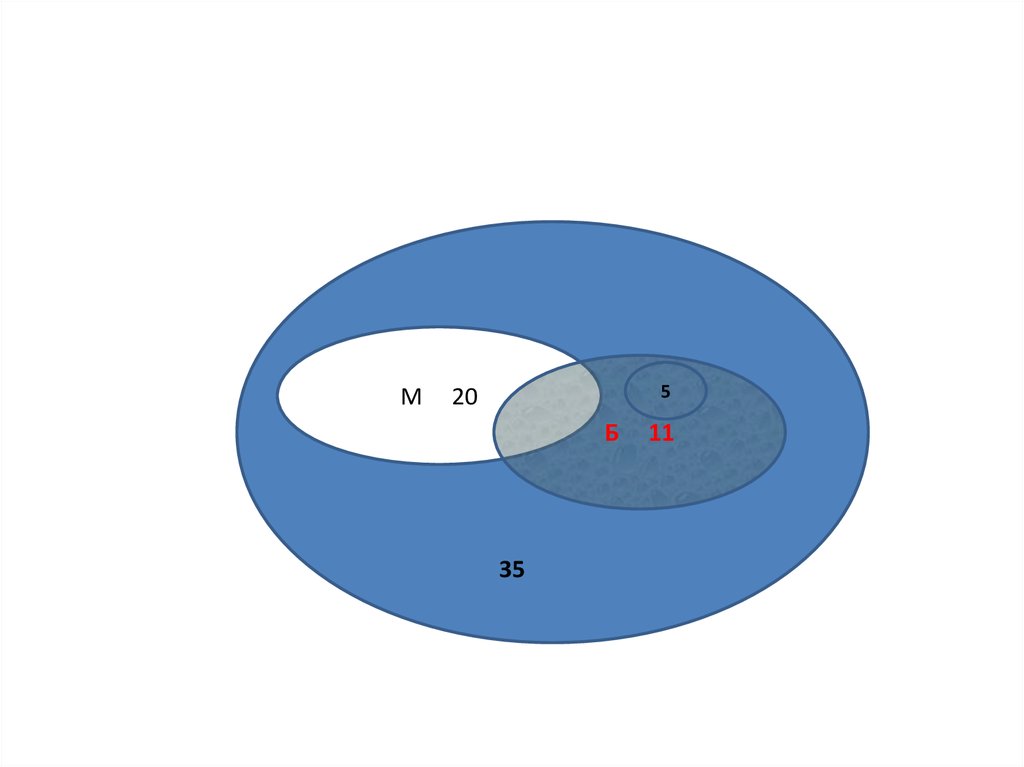 Те множества, которые пересекаются, имеют общие черты. В то же время кривая, полностью находящаяся внутри другой, является ее подмножеством. Люди могут использовать генератор диаграмм Эйлера, чтобы получить общее представление о том, как выглядят диаграммы.
Те множества, которые пересекаются, имеют общие черты. В то же время кривая, полностью находящаяся внутри другой, является ее подмножеством. Люди могут использовать генератор диаграмм Эйлера, чтобы получить общее представление о том, как выглядят диаграммы.
Шаги по созданию диаграммы Эйлера
Эти диаграммы полезны для убедительных логических рассуждений. В этих посылках метод определения правильности рассуждений, в которых фигурируют термины «все, некоторые и нет». Здесь первым шагом должно быть создание диаграммы для первой предпосылки. Затем над первой посылкой рисуется вторая посылка. Создатель диаграмм Эйлера помогает легко создавать эти диаграммы благодаря развитию технологий. А теперь можно делать выводы. Однако аргумент действителен тогда и только тогда, когда каждая мыслимая диаграмма изображает вывод аргумента и соответствует ему. Если хотя бы одна мыслимая диаграмма противоречит концовке, вывод не во всех случаях верен, а значит, утверждение неверно.
Пример
Ниже приведены некоторые аргументы, которые необходимо определить, являются ли они действительными или недействительными.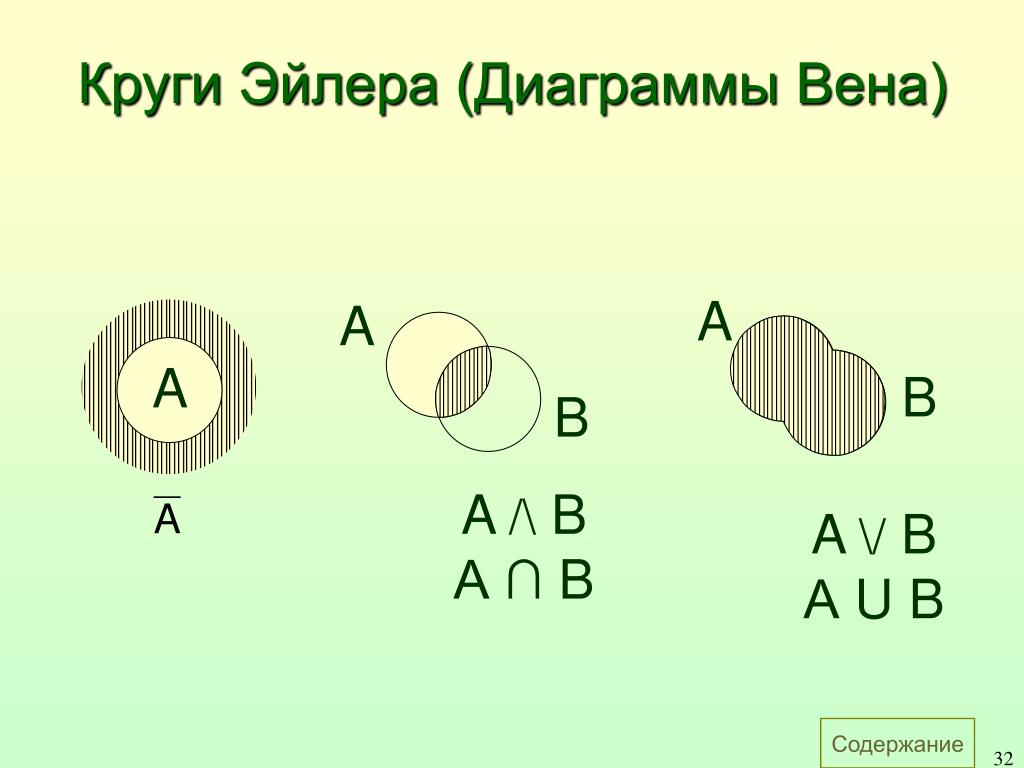
- Все гении, которые поют, не умеют читать.
- Все гении, которые не умеют читать, не могут учиться.
- Следовательно, Все гении, которые поют, непригодны для учебы.
Первым шагом будет создание диаграммы Эйлера для предпосылки первого аргумента.
Это будет:
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Диаграмма Эйлера (wallstreetmojo.com)
Следующим шагом является создание диаграммы посылки для второго аргумента, и единственный логический вывод:
Вы можете использовать это изображение на Ваш веб-сайт, шаблоны и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Диаграмма Эйлера (wallstreetmojo. com)
com)
для учебы» является действительным.
Диаграмма Эйлера и Венна
Понятия «диаграмма Эйлера» и «диаграмма Венна» Диаграмма Венна Диаграммы Венна относятся к схематическому представлению множеств с помощью кругов. Этот метод был введен английским логиком Джоном Венном в 1880 году. Он также известен как диаграммы множеств или логические диаграммы и используется в таких дисциплинах, как математика, статистика и бизнес-исследования. Однако на самом деле последняя является своего рода подклассом диаграмм Эйлера. В отличие от диаграмм Венна, которые должны отображать все потенциальные пересечения множества, другая должна представлять только их подмножество.
В рамках нового математического движения 1960-х годов диаграммы Венна и Эйлера использовались для обучения теории множеств. Последние изображают установленные отношения между кругами относительно отношений включения и исключения. Кроме того, он представляет пустоту либо затенением, либо устранением этой области из-за ее отсутствия.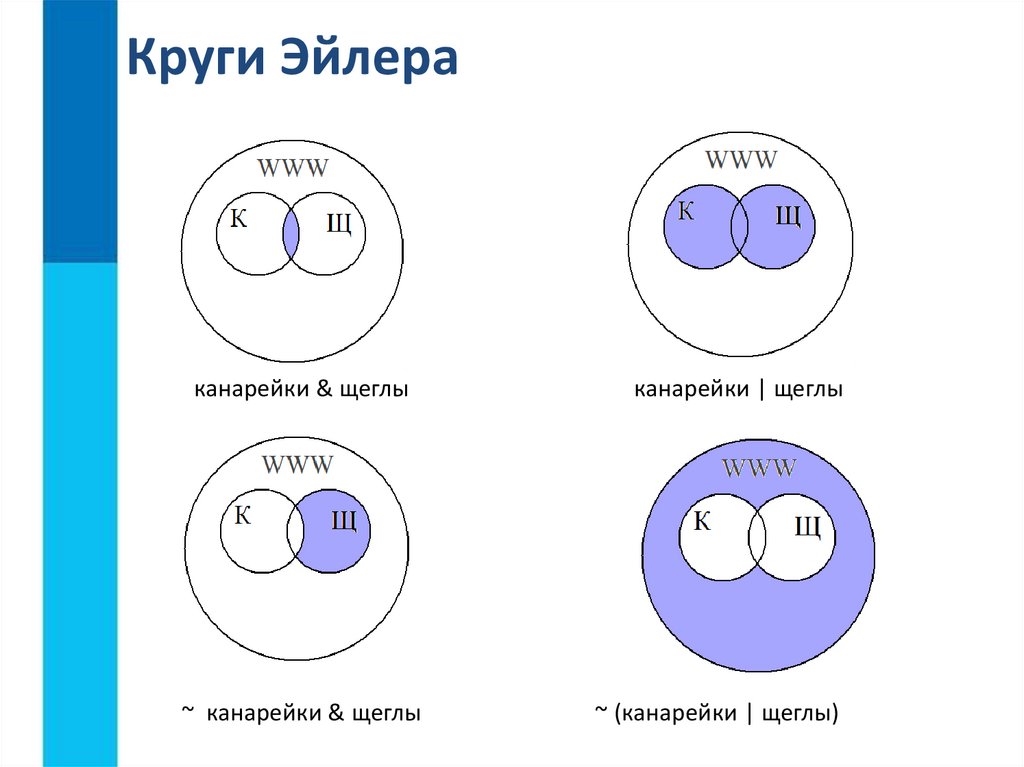 С другой стороны, диаграммы Венна содержат фиксированную конфигурацию круга и изображают отношения множества, указывая, что темные части символизируют пустое множество.
С другой стороны, диаграммы Венна содержат фиксированную конфигурацию круга и изображают отношения множества, указывая, что темные части символизируют пустое множество.
Если их метки не находятся в пересекающемся круге, перекрывающиеся круги на диаграммах Венна не обязательно показывают общность между наборами, а скорее вероятную логическую связь. То есть они содержат все возможные зоны перекрытия между элементами, представляющими кривые. Немногие различия, такие как эти, различают две темы; однако нельзя отрицать, что у них гораздо больше общего.
Часто задаваемые вопросы (FAQ)
Как узнать, действительна ли диаграмма Эйлера?
Аргумент диаграммы Эйлера верен тогда и только тогда, когда каждая мыслимая диаграмма изображает заключение этого аргумента. Если хотя бы одна мыслимая диаграмма противоречит заключению, вывод не во всех случаях верен, а рассуждение неверно.
Кто изобрел диаграмму Эйлера?
Эти диаграммы были построены Леонардом Эйлером, швейцарским математиком. Он является пионером различных открытий в различных математических дисциплинах и внес значительный вклад в науку, физику и астрономию. Диаграмма Эйлера — это схематическое представление множеств и отношений.
Он является пионером различных открытий в различных математических дисциплинах и внес значительный вклад в науку, физику и астрономию. Диаграмма Эйлера — это схематическое представление множеств и отношений.
Почему вы используете диаграмму Эйлера?
Они особенно удобны для объяснения сложных иерархий и перекрывающихся определений. Визуализация статистических данных, создание основы для диаграммных рассуждений, разработка программного обеспечения и отображение результатов поисковых запросов в базе данных — все это было выполнено с помощью этих диаграмм. Они также помогают в логических рассуждениях
Рекомендуемые статьи
Это руководство по диаграммам Эйлера. Мы объясняем шаги по созданию диаграммы Эйлера вместе с примером и ее отличиями от диаграммы Венна. Вы можете узнать больше из следующих статей —
- Диаграмма «рыбья кость» Диаграмма «рыбья кость»Диаграмма «рыбья кость» или диаграмма Исикавы — это современный инструмент управления качеством, который объясняет причинно-следственную связь для любой проблемы с качеством, которая возникла или может возникнуть.
 Подробнее
Подробнее - Диаграмма Венна в ExcelДиаграмма Венна в ExcelЕсть два способа создания Диаграмма Венна. 1) Создайте диаграмму Венна с помощью Excel Smart Art. 2) Создайте диаграмму Венна с помощью Excel Shapes.Подробнее две или более групп через пересекающиеся части кругов.Подробнее
nVenn: обобщенные, квазипропорциональные диаграммы Венна и Эйлера | Биоинформатика
Реферат
Мотивация
Диаграммы Венна и Эйлера широко используются для визуализации взаимосвязей между экспериментами и наборами данных. Однако представление более трех наборов данных при сохранении пропорций каждого региона по-прежнему невозможно с помощью существующих инструментов.
Результаты
Мы представляем алгоритм для отображения всех областей обобщенной n-мерной диаграммы Венна, сохраняя при этом площадь каждой области приблизительно пропорциональной количеству включенных элементов. Кроме того, отсутствие областей на диаграммах Эйлера приводит к упрощению представлений.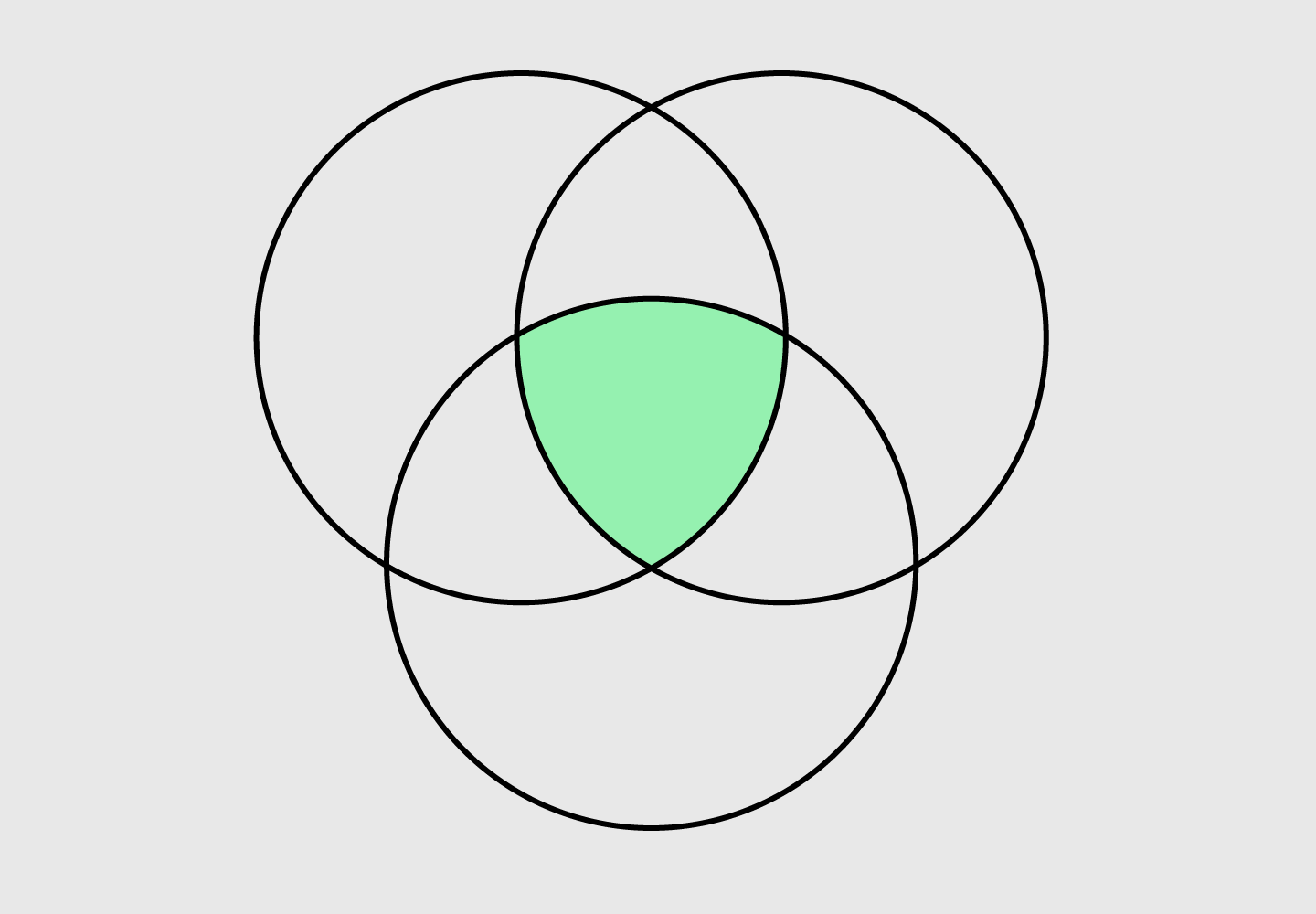 Алгоритм генерирует n-мерную диаграмму Венна и вставляет круги заданных областей в каждую область. Затем диаграмма перестраивается с помощью динамической самокорректирующейся симуляции, в которой каждая заданная граница сжимается до тех пор, пока не коснется кругов внутри. Этот алгоритм реализован в инструменте C++ (nVenn) с веб-интерфейсом или без него. Веб-интерфейс также предоставляет возможность анализа областей диаграммы.
Алгоритм генерирует n-мерную диаграмму Венна и вставляет круги заданных областей в каждую область. Затем диаграмма перестраивается с помощью динамической самокорректирующейся симуляции, в которой каждая заданная граница сжимается до тех пор, пока не коснется кругов внутри. Этот алгоритм реализован в инструменте C++ (nVenn) с веб-интерфейсом или без него. Веб-интерфейс также предоставляет возможность анализа областей диаграммы.
Доступность и реализация
Исходный код и предварительно скомпилированные двоичные файлы nVenn доступны по адресу https://github.com/vqf/nVenn. Доступ к веб-интерфейсу для шести комплектов можно получить по адресу http://degradome.uniovi.es/cgi-bin/nVenn/nvenn.cgi.
Дополнительная информация
Дополнительные данные доступны по адресу Биоинформатика онлайн.
1 Введение
Поставлена повторяющаяся задача интеллектуального анализа данных визуализации (Алсаллах и др. , 2016). В идеале цель этого анализа состоит в том, чтобы с первого взгляда найти наиболее важные взаимосвязи между наборами данных (Lex et al. , 2014). Диаграммы Венна и Эйлера являются популярным инструментом для этой цели, поскольку они представляют на одном рисунке все соответствующие перекрытия между наборами. Диаграммы Венна похожи на представления Эйлера, но они показывают все возможные пересечения между множествами, даже если они не существуют во входных данных. В области биоинформатики наборы могут, например, содержать гены, которые по-разному экспрессируются в различных условиях. Сходства в ответах на эти условия будут немедленно очевидны как пересечения, содержащие большее, чем ожидалось, количество элементов. По этой причине особенно полезно сделать площадь каждой области пропорциональной количеству содержащихся в ней элементов.
В идеале цель этого анализа состоит в том, чтобы с первого взгляда найти наиболее важные взаимосвязи между наборами данных (Lex et al. , 2014). Диаграммы Венна и Эйлера являются популярным инструментом для этой цели, поскольку они представляют на одном рисунке все соответствующие перекрытия между наборами. Диаграммы Венна похожи на представления Эйлера, но они показывают все возможные пересечения между множествами, даже если они не существуют во входных данных. В области биоинформатики наборы могут, например, содержать гены, которые по-разному экспрессируются в различных условиях. Сходства в ответах на эти условия будут немедленно очевидны как пересечения, содержащие большее, чем ожидалось, количество элементов. По этой причине особенно полезно сделать площадь каждой области пропорциональной количеству содержащихся в ней элементов.
Существует множество инструментов для автоматического создания диаграмм Эйлера, что отражает широкое использование этого представления в исследованиях.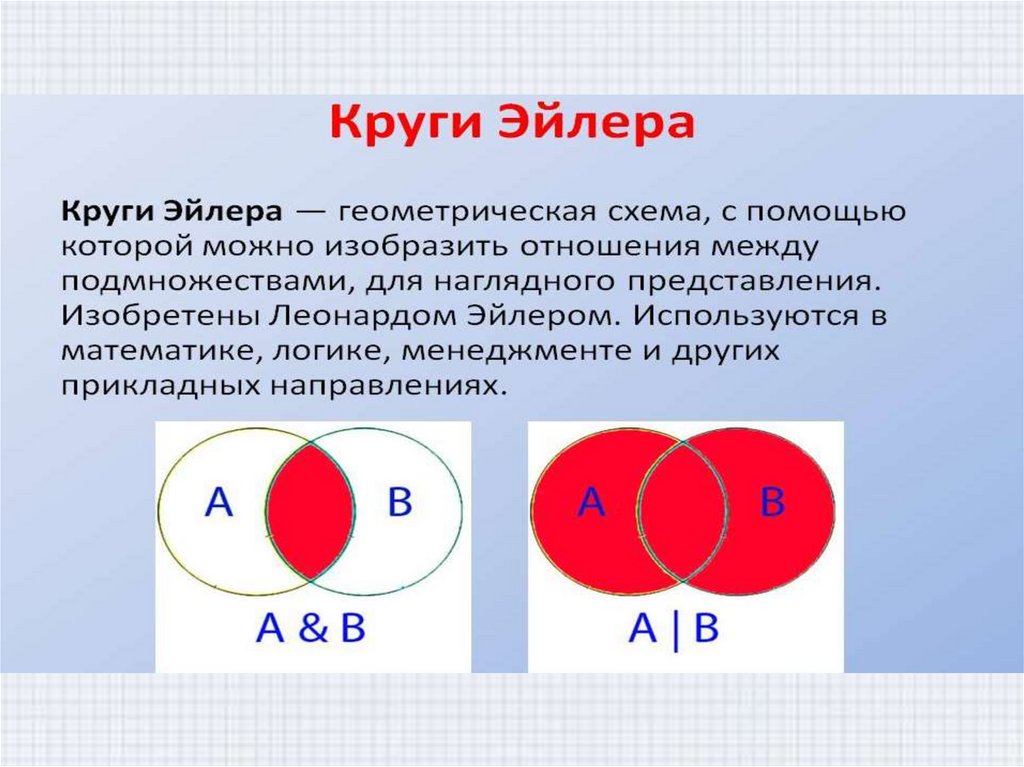 Большинство этих инструментов представляют до трех наборов и сохраняют области, приблизительно пропорциональные количеству элементов (например, Hulsen et al. , 2008, Micallef and Rodgers, 2014a). Представление более трех наборов при сохранении пропорциональности не является тривиальной задачей, поскольку симметричные формы набора недостаточно гибки. Некоторые инструменты обеспечивают приблизительную пропорциональность с помощью штрафных функций или других преобразований (например, Kestler 9).0246 и др. , 2008). Однако большинство инструментов просто представляют предварительно нарисованную n-множественную диаграмму Венна со вставленными числами, что, хотя и полезно, трудно интерпретировать (например, Bardou et al. , 2014, Heberle et al. , 2015).
Большинство этих инструментов представляют до трех наборов и сохраняют области, приблизительно пропорциональные количеству элементов (например, Hulsen et al. , 2008, Micallef and Rodgers, 2014a). Представление более трех наборов при сохранении пропорциональности не является тривиальной задачей, поскольку симметричные формы набора недостаточно гибки. Некоторые инструменты обеспечивают приблизительную пропорциональность с помощью штрафных функций или других преобразований (например, Kestler 9).0246 и др. , 2008). Однако большинство инструментов просто представляют предварительно нарисованную n-множественную диаграмму Венна со вставленными числами, что, хотя и полезно, трудно интерпретировать (например, Bardou et al. , 2014, Heberle et al. , 2015).
Интригующая разработка в создании пропорциональных диаграмм Эйлера была использована в eulerForce (Micallef and Rodgers, 2014b). Алгоритм, используемый в этом инструменте, выполняет физическое моделирование системы, настроенной для создания желаемого макета диаграммы Эйлера. Каждая кривая, охватывающая множество, концептуально представляется как ряд зарядов, соединенных пружинами. Управляя силами между этими виртуальными зарядами, eulerForce создает диаграммы Эйлера, которые являются правильными, гладкими и эстетически привлекательными. Однако площадями результирующих областей нелегко управлять, а использование более пяти кривых требует слишком больших вычислительных ресурсов. Эти ограничения иллюстрируют сложность представления нескольких наборов симметричными или простыми выпуклыми формами и учитывают пропорциональность каждой области.
Каждая кривая, охватывающая множество, концептуально представляется как ряд зарядов, соединенных пружинами. Управляя силами между этими виртуальными зарядами, eulerForce создает диаграммы Эйлера, которые являются правильными, гладкими и эстетически привлекательными. Однако площадями результирующих областей нелегко управлять, а использование более пяти кривых требует слишком больших вычислительных ресурсов. Эти ограничения иллюстрируют сложность представления нескольких наборов симметричными или простыми выпуклыми формами и учитывают пропорциональность каждой области.
Здесь мы представляем алгоритм для создания диаграмм Венна и Эйлера с произвольным количеством наборов. Каждая область на диаграмме содержит круг, площадь которого пропорциональна количеству элементов в этом пересечении. Мы также подготовили веб-интерфейс для создания пропорциональных диаграмм, содержащих до шести наборов.
2 Материалы и методы
Программа nVenn, написанная на C++, принимает на вход текст, описывающий размеры каждой области на диаграмме Венна, и выводит рисунок в формате SVG.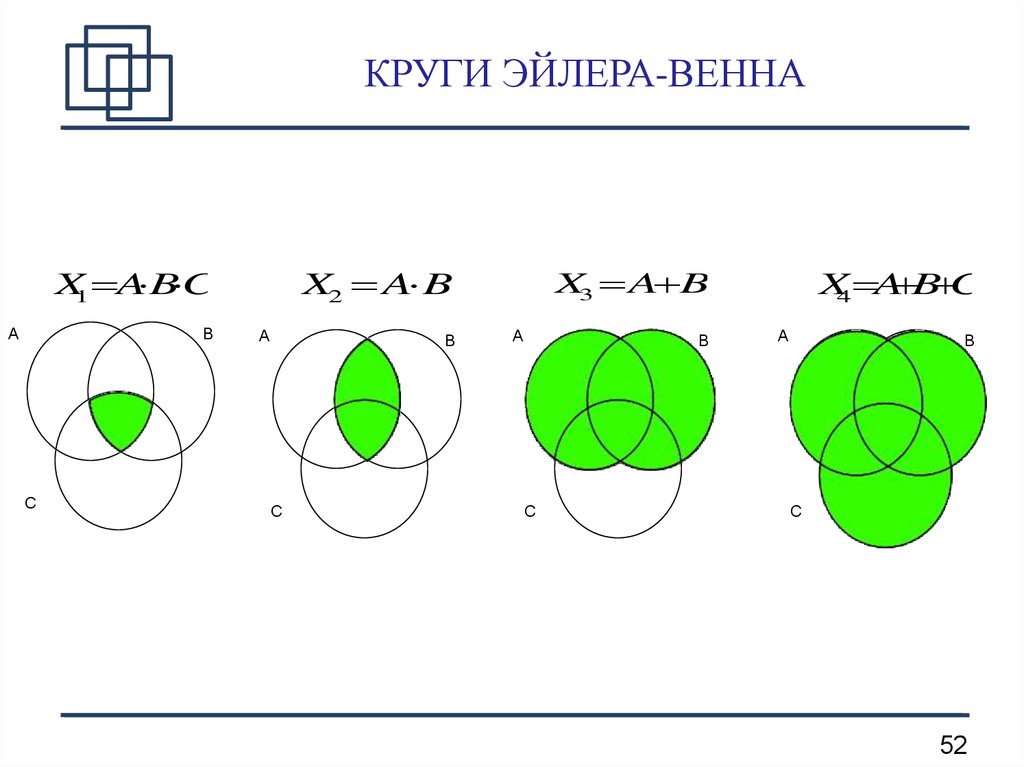 Шаги этого алгоритма показаны на рисунке 1. Вкратце,
Шаги этого алгоритма показаны на рисунке 1. Вкратце,
Рис. 1.
Открыть в новой вкладкеСкачать слайд
Алгоритм nVenn. Рисунок создан путем моделирования от обобщенной диаграммы Венна (вверху слева) до квазистатического решения (внизу в центре). Затем линии смягчаются, чтобы получить окончательную цифру (внизу слева). и др. , 2004). Во-первых, логическая решетка для n групп создается на основе изображения в Ruskey et al. (2006 г.). Эта решетка выражает каждую область как логический вектор, где каждый элемент представляет набор. Если эта позиция заполнена 1, область принадлежит набору, тогда как если она заполнена 0, она не принадлежит набору. Симметричная цепная декомпозиция гарантирует, что все области, принадлежащие набору, могут быть заключены в простую кривую, исключая при этом все области, не принадлежащие набору (дополнительный материал, раздел 1.1).
Затем каждая область сжимается посредством моделирования (рис.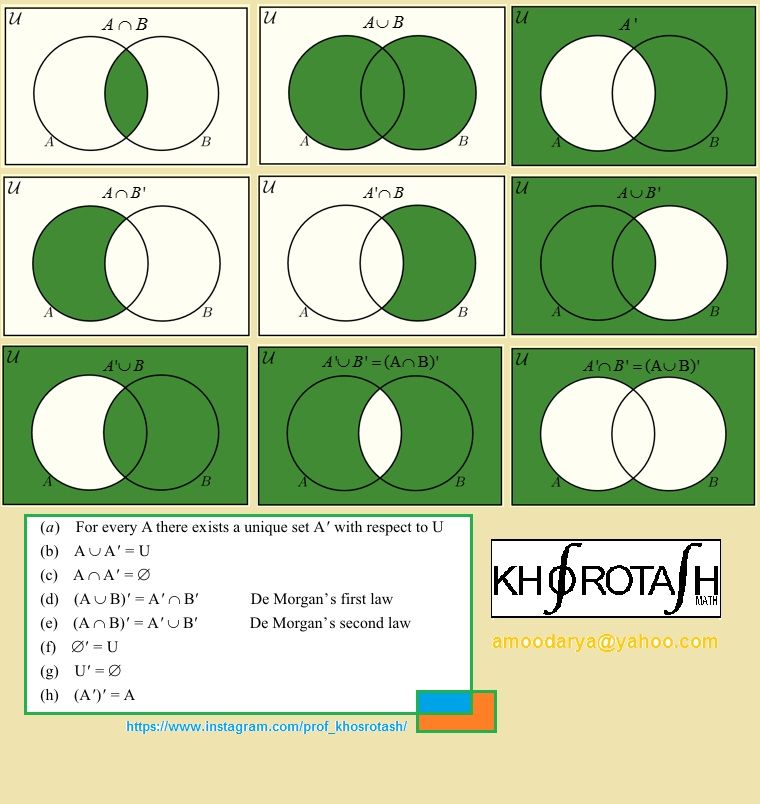 1, вверху в центре, вверху справа, внизу справа и внизу в центре). При этом каждая линия диаграммы заменяется большим количеством точек, соединенных пружинами (дополнительный материал, раздел 1.2). Внутренние круги перемещаются при контакте с точками линий и пружинами линий. Эта система моделируется с помощью простого движка, основанного на небольшой разнице во времени. Он включает в себя силы трения и демпфирования для ускорения сокращения линий.
1, вверху в центре, вверху справа, внизу справа и внизу в центре). При этом каждая линия диаграммы заменяется большим количеством точек, соединенных пружинами (дополнительный материал, раздел 1.2). Внутренние круги перемещаются при контакте с точками линий и пружинами линий. Эта система моделируется с помощью простого движка, основанного на небольшой разнице во времени. Он включает в себя силы трения и демпфирования для ускорения сокращения линий.
Наконец, сжатая диаграмма украшается с помощью моделирования, в котором фиксируются внутренние круги и добавляется сила притяжения пружины (дополнительный материал, раздел 1.1) между точками линии и кругами, так что линии более точно представляют каждую область (дополнительный фильм S1). , начиная с 20 секунды).
Конец каждого шага контролируется пользователем по-разному, в зависимости от интерфейса.
2.1 Интерфейсы
Текущая версия nVenn может использоваться с тремя различными интерфейсами: командная строка, графический вывод OpenGL и веб-интерфейс.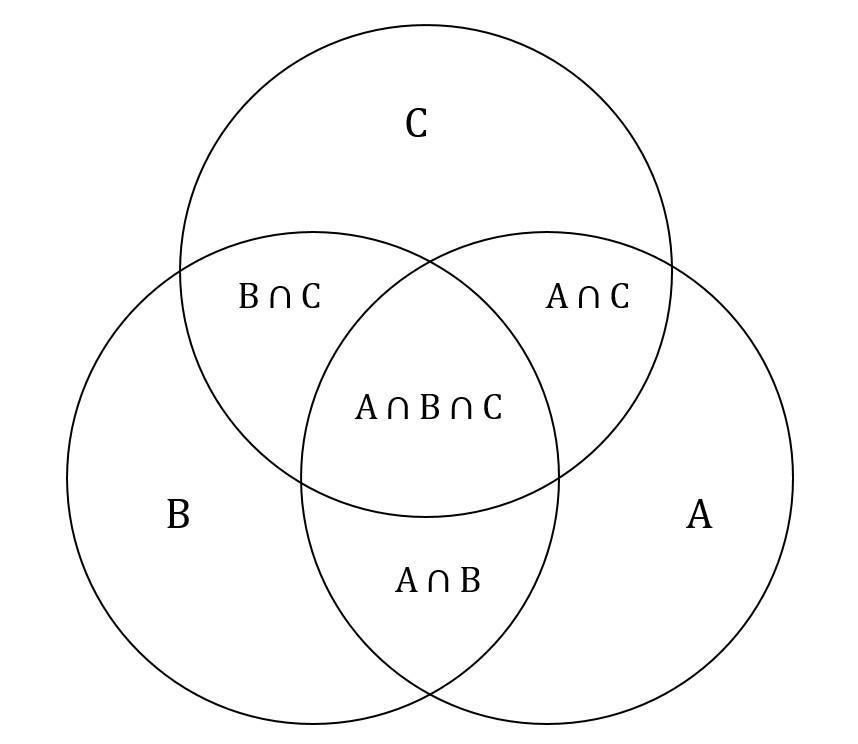 Хотя основные методы одинаковы, каждый вариант имеет свои требования и способы использования.
Хотя основные методы одинаковы, каждый вариант имеет свои требования и способы использования.
Эта версия принимает текстовый входной файл, описывающий каждую область на диаграмме (дополнительный рис. S1), и автоматически выполняет все три шага. Количество циклов на шаг зафиксировано в коде и подходит для большинства целей до шести подходов. В текущей версии основной шаг состоит из 7000 циклов. Программа автоматически сохраняет промежуточный результат, чтобы можно было добавить больше циклов, просто повторив эту процедуру для того же входного файла. Окончательное украшение выполняется в течение 200 циклов. Синтаксис для запуска этой версии:
./nVenn input_file [output_file_name=result]
При повторном выполнении может быть обработано неограниченное количество наборов. Однако следует отметить, что время, необходимое для завершения моделирования, быстро растет с увеличением количества наборов.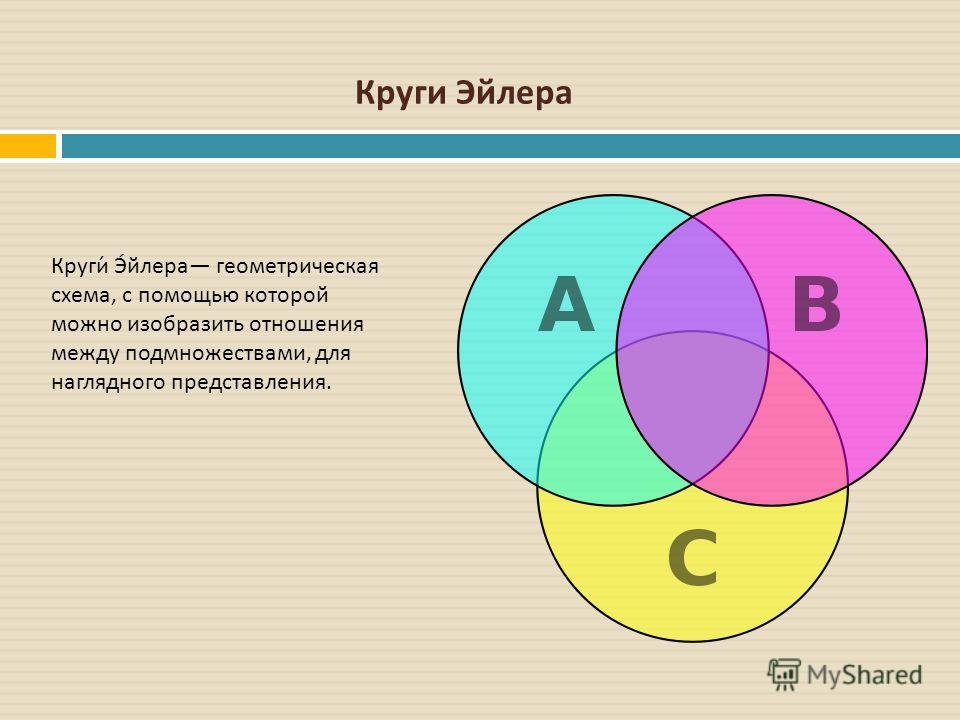 Эта версия использует стандартные библиотеки, поэтому легко компилируется в большинстве операционных систем. Для загрузки доступны предварительно скомпилированные версии x64 Linux Debian и Microsoft Windows.
Эта версия использует стандартные библиотеки, поэтому легко компилируется в большинстве операционных систем. Для загрузки доступны предварительно скомпилированные версии x64 Linux Debian и Microsoft Windows.
Также предоставляется графическая версия с использованием OpenGL. Входные данные для этого инструмента имеют тот же формат, что и версия для командной строки, хотя имена входных и выходных файлов фиксированы. Напротив, пользователь может в режиме реального времени решать, когда переходить от одной фазы к другой. Этот интерфейс также дает простой обзор процесса моделирования, как показано в дополнительном фильме S1.
Интерфейс OpenGL использует библиотеки, специфичные для Microsoft Windows. Предварительно скомпилированная версия для этой платформы доступна для скачивания.
2.1.3 Веб-интерфейс Эта версия использует более простой ввод и позволяет проводить дальнейший анализ выходной диаграммы.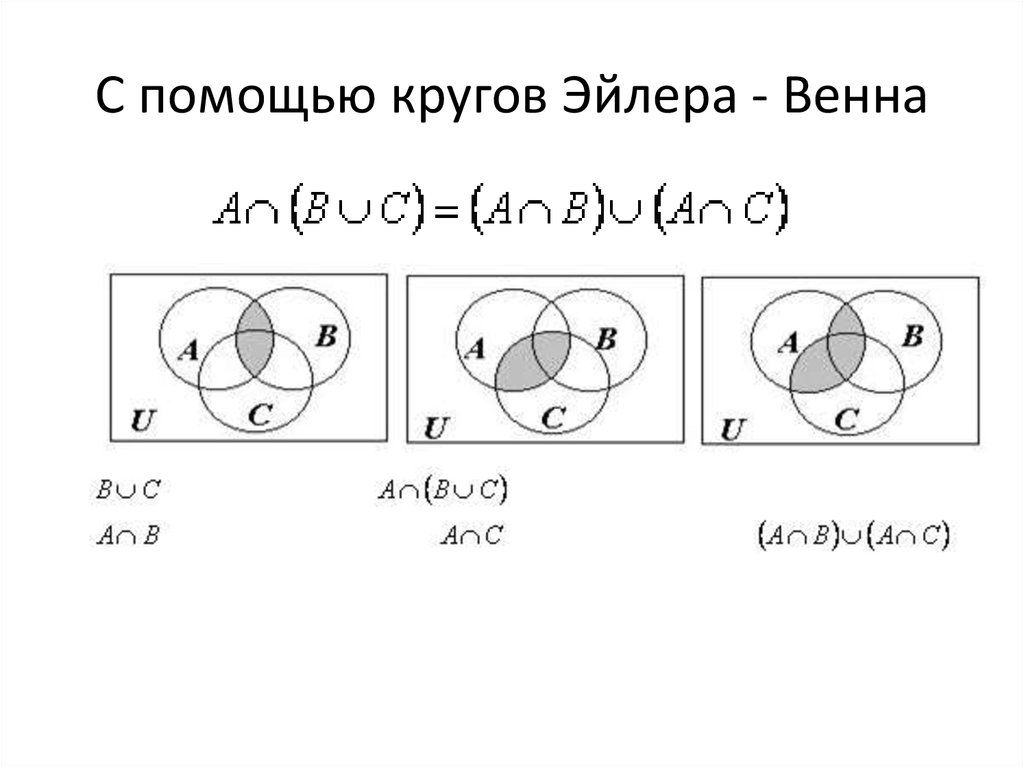 Таким образом, пользователи могут напрямую вводить элементы каждого набора в текстовые поля. Затем интерфейс вычисляет количество элементов в каждой области диаграммы, запускает nVenn и отображает результат. Кроме того, пользователи могут запросить свои данные для любого пересечения между наборами, установив флажки или щелкнув соответствующую область на выходном рисунке (рис. 2). Продолжительность симуляции фиксирована, но при повторном выполнении можно добавить больше циклов. В настоящее время интерфейс позволяет использовать до шести наборов, но система легко масштабируется до большего количества наборов.
Таким образом, пользователи могут напрямую вводить элементы каждого набора в текстовые поля. Затем интерфейс вычисляет количество элементов в каждой области диаграммы, запускает nVenn и отображает результат. Кроме того, пользователи могут запросить свои данные для любого пересечения между наборами, установив флажки или щелкнув соответствующую область на выходном рисунке (рис. 2). Продолжительность симуляции фиксирована, но при повторном выполнении можно добавить больше циклов. В настоящее время интерфейс позволяет использовать до шести наборов, но система легко масштабируется до большего количества наборов.
Рис. 2.
Открыть в новой вкладкеСкачать слайд
Протестировать диаграмму nVenn в веб-интерфейсе. Рисунок показан на правой панели с инструментами для манипулирования ниже. В текстовой области на верхней левой панели отображаются элементы, присутствующие только в наборах 4 и 5. Эту область можно выбрать, установив флажки (над текстовой областью) и щелкнув соответствующую область на рисунке (стрелка)
Интерфейс также позволяет настроить окончательную фигуру.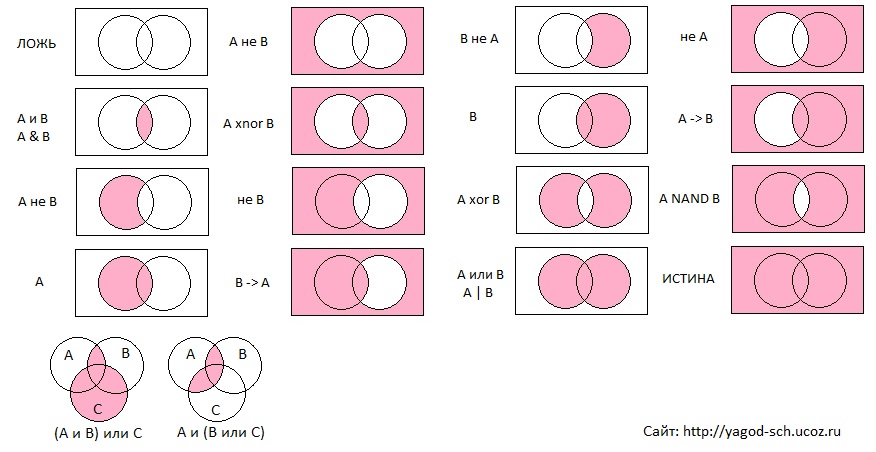 Пользователи могут добавлять или удалять метки, чтобы описать каждую область и показать, сколько элементов включено в нее. Цвет и непрозрачность каждого набора, а также ширину их границ также можно настроить. Выходной рисунок может быть сохранен в векторном формате (масштабируемая векторная графика, SVG) и в растровом формате (переносимая сетевая графика, PNG).
Пользователи могут добавлять или удалять метки, чтобы описать каждую область и показать, сколько элементов включено в нее. Цвет и непрозрачность каждого набора, а также ширину их границ также можно настроить. Выходной рисунок может быть сохранен в векторном формате (масштабируемая векторная графика, SVG) и в растровом формате (переносимая сетевая графика, PNG).
Веб-страница, взаимодействующая с nVenn, закодирована в стандартном HTML, CSS (с использованием мин. Bootstrap v.3.3.1) и javascript (с использованием мин. jQuery v.1.11.1). Мы также добавили пошаговое руководство по адресу верхняя панель навигации.
2.2 Тест
В качестве подтверждения концепции мы построили диаграмму Эйлера с помощью веб-интерфейса nVenn, используя гены, включенные в категорию GO системы врожденного иммунитета (GO: 0045087). Было сгенерировано шесть подмножеств с различными кодами доказательств GO: IBA (выведено из биологического аспекта предка), IC (выведено куратором), IDA (выведено из прямого анализа), IEA (выведено из электронной аннотации), ISS (выведено из последовательности или структурного анализа).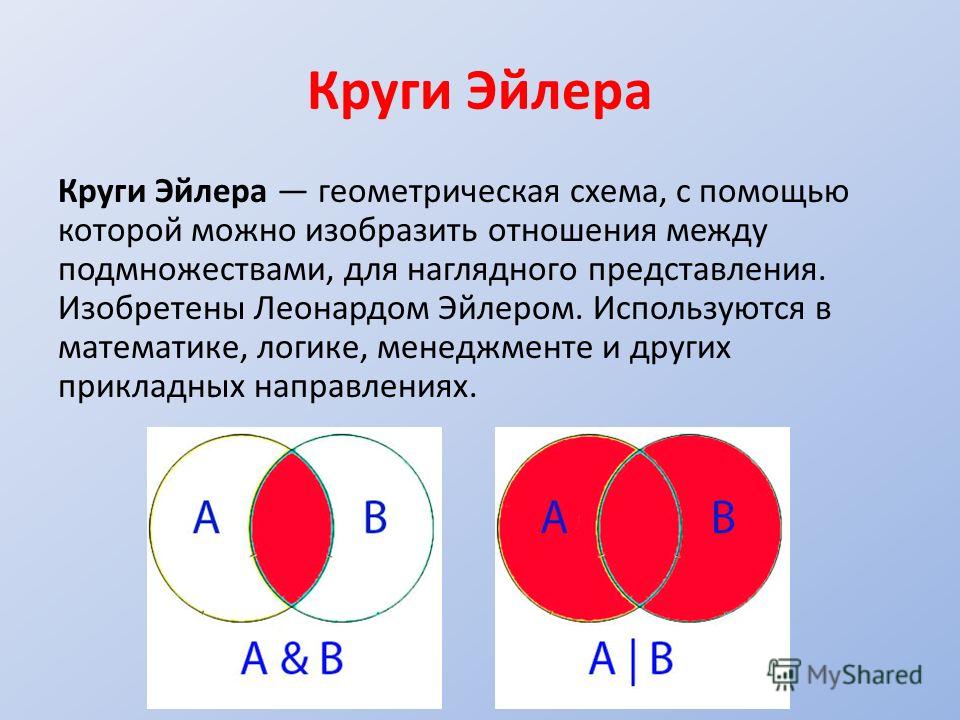 Сходство) и NAS (заявление об авторе, не подлежащем отслеживанию). Выполнение потребовало трех представлений для удовлетворительного результата (около 12 минут).
Сходство) и NAS (заявление об авторе, не подлежащем отслеживанию). Выполнение потребовало трех представлений для удовлетворительного результата (около 12 минут).
Результат показан на рис. 2 и дает краткий обзор различных размеров каждого подмножества, а также заметных корреляций между ними. Таким образом, пересечение групп IEA и ISS настолько велико, что делает ISS почти подмножеством IEA. Кроме того, количество элементов, общих только для этих подмножеств, непропорционально велико. На рис. 2 также показано, как пользователи могут анализировать каждый регион, просто нажимая на него.
3 Обсуждение
Целью nVenn является создание простых для интерпретации диаграмм Эйлера, которые передают информацию о неограниченном количестве множеств. Хотя такая возможность существует, на практике очень сложно интерпретировать диаграммы Венна для более чем шести наборов.
Основанный на моделировании алгоритм рисования наборов концептуально аналогичен алгоритму eulerForce, хотя последний моделирует только линии.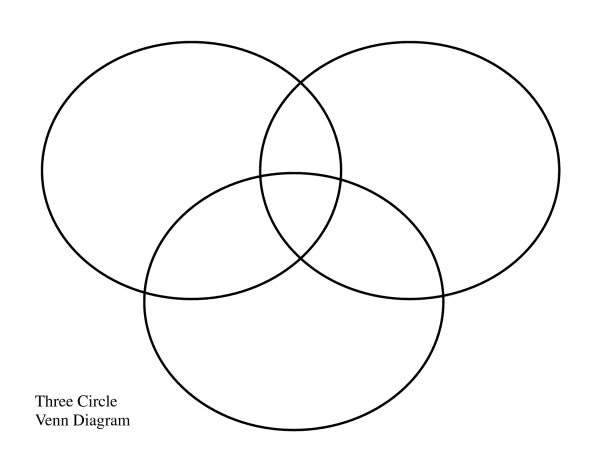 На самом деле цель eulerForce — построение правильных диаграмм Эйлера. Добиться пропорциональности с помощью этой программы было бы очень сложно, поскольку от пользователей требовалось бы указать координаты исходной диаграммы Эйлера и идеально сбалансировать внутренние силы. Напротив, использование внутренних кругов в nVenn позволяет пользователям напрямую контролировать размер каждой области. Это означает, что результирующие диаграммы не обязательно должны быть выпуклыми или строго правильными, как в случае с eulerForce. Однако мы добавили определенные шаги, чтобы упростить интерпретацию результатов.
На самом деле цель eulerForce — построение правильных диаграмм Эйлера. Добиться пропорциональности с помощью этой программы было бы очень сложно, поскольку от пользователей требовалось бы указать координаты исходной диаграммы Эйлера и идеально сбалансировать внутренние силы. Напротив, использование внутренних кругов в nVenn позволяет пользователям напрямую контролировать размер каждой области. Это означает, что результирующие диаграммы не обязательно должны быть выпуклыми или строго правильными, как в случае с eulerForce. Однако мы добавили определенные шаги, чтобы упростить интерпретацию результатов.
Таким образом, при разработке nVenn некоторые эстетические качества итоговой диаграммы взяли верх над строгой пропорциональностью. Во-первых, площадь каждой области больше, чем внутренний пропорциональный круг, что дает более гладкие кривые для каждого набора. Поэтому пользователи должны учитывать площади кругов, а не пустые места. В связи с этим большое количество наборов с небольшим количеством пересечений часто приводит к диаграммам с большими пустыми пространствами (дополнительный рис.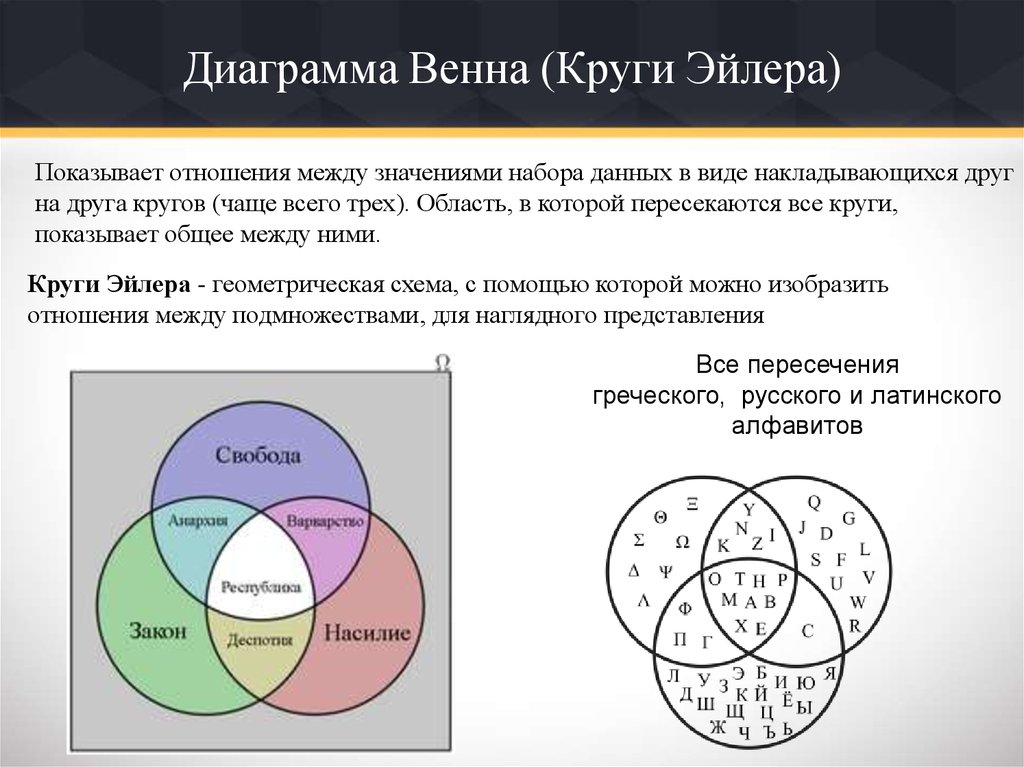 S2). Поскольку этот алгоритм решает сложную задачу упаковки кругов с дополнительными ограничениями, этот недостаток ожидаем и принят. Будущие версии nVenn могут включать случайные отклонения в начальных условиях, чтобы после нескольких запусков можно было исследовать несколько решений.
S2). Поскольку этот алгоритм решает сложную задачу упаковки кругов с дополнительными ограничениями, этот недостаток ожидаем и принят. Будущие версии nVenn могут включать случайные отклонения в начальных условиях, чтобы после нескольких запусков можно было исследовать несколько решений.
Дальнейшие отклонения от пропорциональности возникают, когда некоторые области слишком малы на итоговой фигуре. Чтобы избежать невидимых областей, минимальный радиус круга установлен равным 1% ширины или высоты диаграммы. Круги, радиус которых должен быть меньше указанного, будут казаться больше, чем ожидалось. Поскольку эти области было бы еще труднее интерпретировать на строгой диаграмме, это предостережение также принимается. Наконец, заданные линии отделены на разное расстояние от внутренних кругов. Эта функция сводит к минимуму перекрытия между линиями, чтобы можно было легко отслеживать каждую установленную линию.
Веб-интерфейс к nVenn предлагает дополнительные инструменты для анализа диаграмм, чтобы пользователи могли быстро узнать, какие элементы соответствуют каждому региону.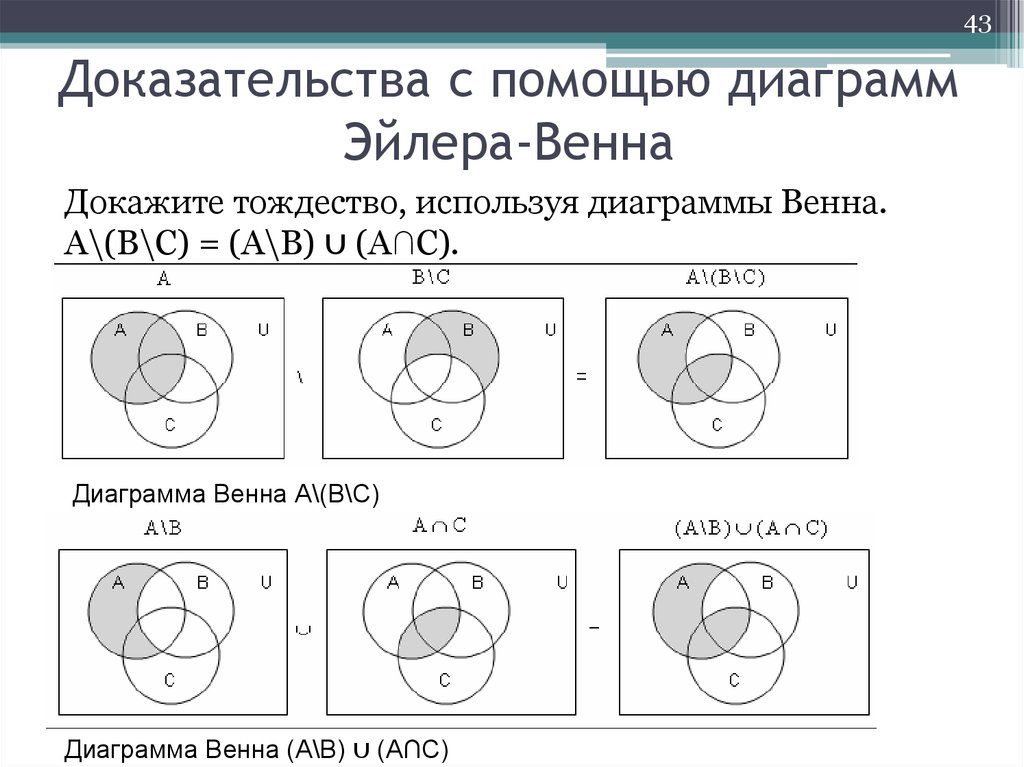 Мы разработали этот интерфейс, чтобы он был простым и интуитивно понятным, в надежде, что он может стать ценным инструментом для исследователей, пытающихся визуализировать сложные отношения между множествами.
Мы разработали этот интерфейс, чтобы он был простым и интуитивно понятным, в надежде, что он может стать ценным инструментом для исследователей, пытающихся визуализировать сложные отношения между множествами.
Благодарности
Мы благодарим Drs. Carlos López-Otín, Gloria Velasco и Magda R. Hamczyk за полезные обсуждения во время разработки этой рукописи.
Финансирование
Эта работа была поддержана Министерством экономики и конкурентоспособности Испании (SAF2014-59986-R, включая финансирование FEDER и программу Рамона и Кахала), Instituto de Salud Carlos III и Principado de Asturias, включая финансирование FEDER. .
Конфликт интересов : не объявлено.
Ссылки
Алсаллах
Б.
и др. (
2016
)
Современная визуализация декораций
.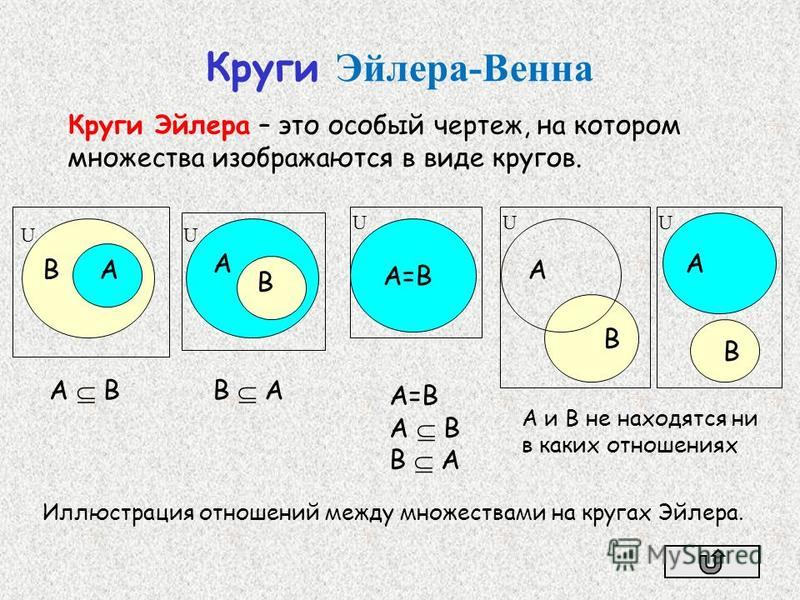
Вычисл. График Форум
,
35
,
234
–
260
.
Барду
P.
и др. (
2014
)
jvenn: интерактивный просмотрщик диаграмм Венна
.
BMC Биоинформатика
,
15
,
293.
Грин
К.
,
2 Клеманит0003
Д.Дж.
(
1976
)
Сильные версии теоремы Шпернера
.
Дж. Комбин. Теория Сер. А
,
20
,
80
–
88
.
Григгс
Дж.
и др. (
2004
)
Диаграммы Венна и симметричные цепные разложения в булевой решетке
.
Электронный J. Комбинированный
.,
11
. Исследовательская работа № R2.
Heberle
H.
и др. (
2015
)
Interactivenn: веб-инструмент для анализа множеств с помощью диаграмм Венна
.
BMC Bioinformatics
,
16
,
169.
Hulsen
T.
и др. (
2008
)
Biovenn – веб-приложение для сравнения и визуализации биологических списков с использованием диаграмм Венна, пропорциональных площади
.
BMC Genomics
,
9
,
488.
Kestler
H.A.
и др. (
2008
)
Vennmaster: диаграммы Эйлера, пропорциональные площади, для функционального анализа микрочипов
.
BMC Bioinformatics
,
9
,
67.
Lex
A.
и др. (
2014
)
Расстройство: визуализация пересекающихся множеств
.
IEEE Trans. Вис. вычисл. График
.,
20
,
1983
–
1992
.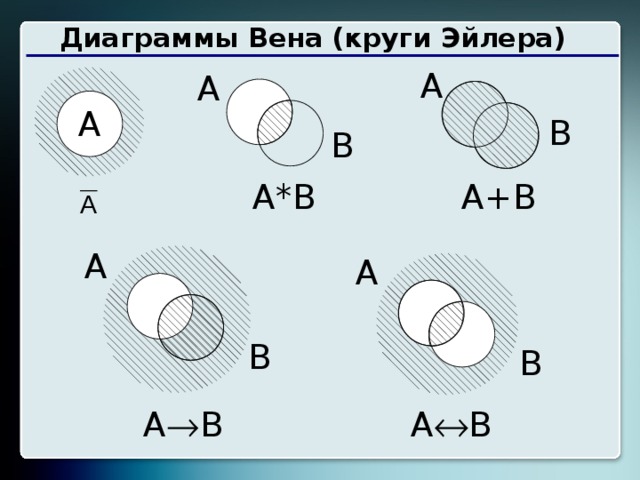
Микаллеф
Л.
,
Роджерс
П.
(
2014a
)
eulerape: построение пропорциональных площади трехмерных диаграмм Венна с использованием эллипсов
.
PLoS Один
,
9
,
e101717.
Микаллеф
Л.
,
Роджерс
П.
(
2014b
)
eulerForce: силовая компоновка для диаграмм Эйлера
.
Дж. Вис. Ланг. Вычисление
.,
25
,
924
–
934
.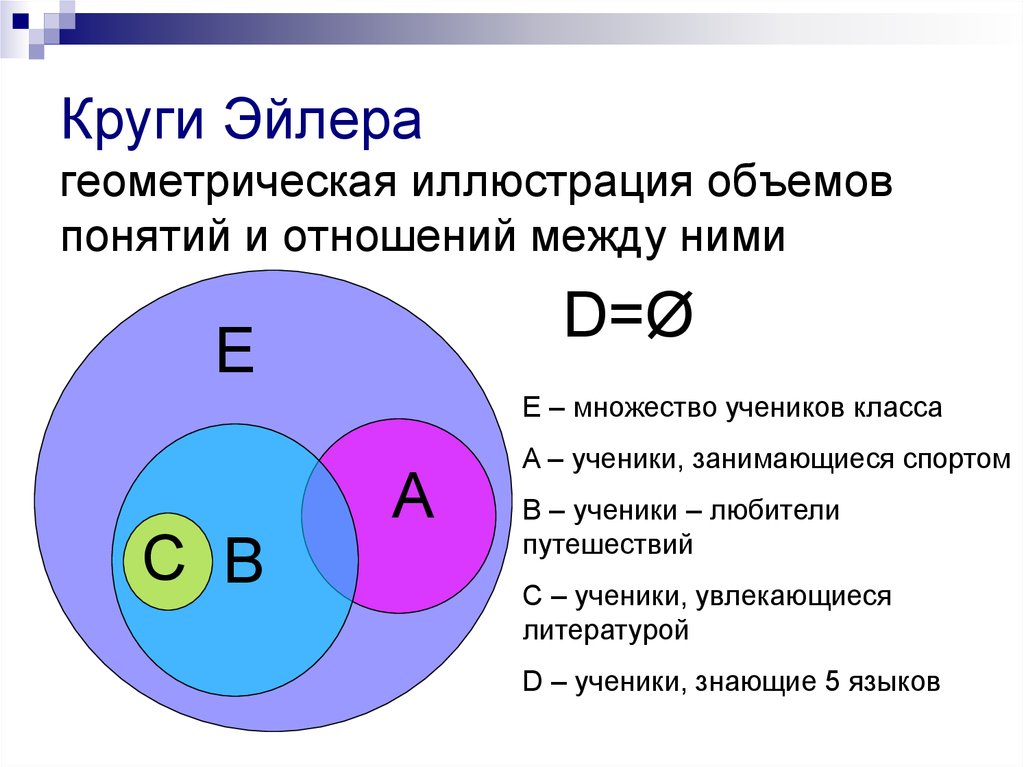
Ruskey
F.
и др. (
2006
)
Поиск простых симметричных диаграмм Венна
.
Уведомления Am. Мат. Соц
.,
53
,
1304
–
1312
.
© Автор(ы), 2018. Опубликовано Oxford University Press. Все права защищены. Для получения разрешений обращайтесь по электронной почте: [email protected]
© Автор(ы), 2018 г. Опубликовано Oxford University Press. Все права защищены. За разрешениями обращайтесь по электронной почте: [email protected]
Что такое диаграмма Венна
Что вам нужно для диаграммы Венна?
Я новичок в диаграммах Венна и хочу узнать больше.
Я хочу создать свою собственную диаграмму Венна в Lucidchart.
Я хочу сделать диаграмму Венна из шаблона Lucidchart.
Создавать диаграммы Венна очень просто и легко с помощью нашего конструктора диаграмм Венна. Изучите основы диаграмм Венна, а также их долгую историю, универсальные цели и способы использования, примеры и символы, а также шаги по их рисованию.
7 минут чтения
Хотите построить собственную диаграмму Венна? Попробуйте Люсидчарт. Это быстро, просто и совершенно бесплатно.
Построить диаграмму Венна
Что такое диаграмма Венна?
На диаграмме Венна используются перекрывающиеся круги или другие формы для иллюстрации логических отношений между двумя или более наборами элементов. Часто они служат для графической организации вещей, подчеркивая, чем они похожи и чем отличаются друг от друга.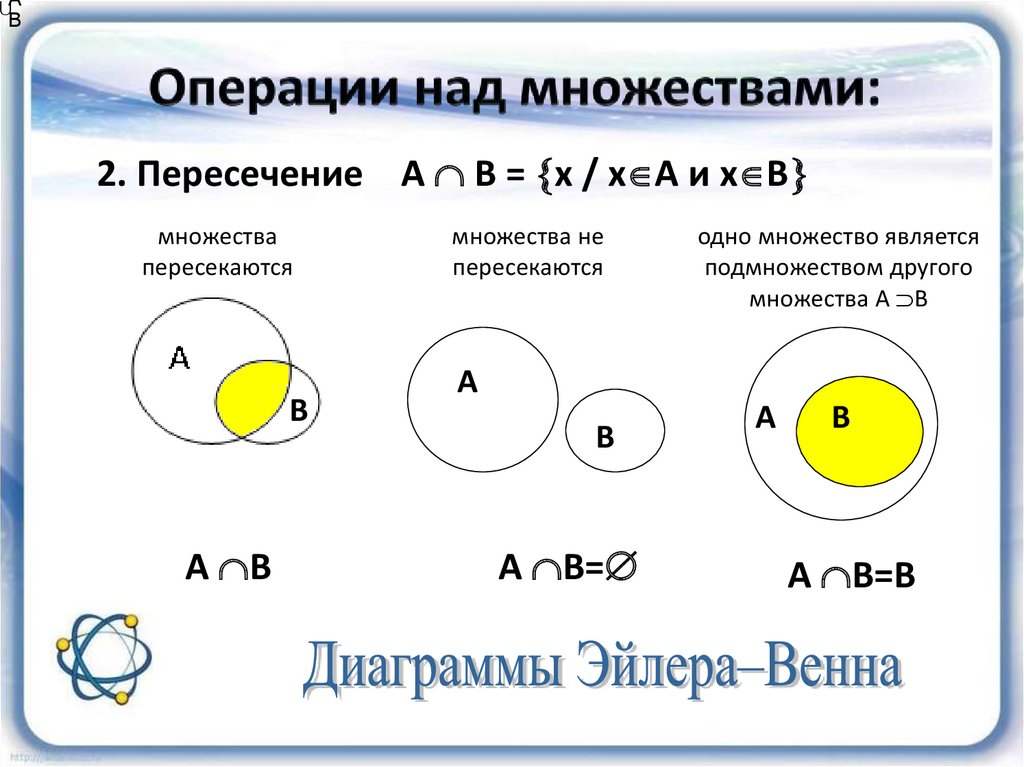
Диаграммы Венна, также называемые диаграммами множества или логическими диаграммами, широко используются в математике, статистике, логике, обучении, лингвистике, информатике и бизнесе. Многие люди впервые сталкиваются с ними в школе, когда изучают математику или логику, поскольку диаграммы Венна стали частью учебных программ «новой математики» в XIX веке.60-е годы. Это могут быть простые диаграммы, включающие два или три набора из нескольких элементов, или они могут стать довольно сложными, включая трехмерные презентации, по мере того, как они будут увеличиваться до шести или семи наборов и выше. Они используются для продумывания и изображения того, как элементы относятся к каждому из них в рамках определенной «вселенной» или сегмента. Диаграммы Венна позволяют пользователям визуализировать данные четкими и эффективными способами и поэтому обычно используются в презентациях и отчетах. Они тесно связаны с диаграммами Эйлера, которые отличаются отсутствием наборов, если в них нет элементов.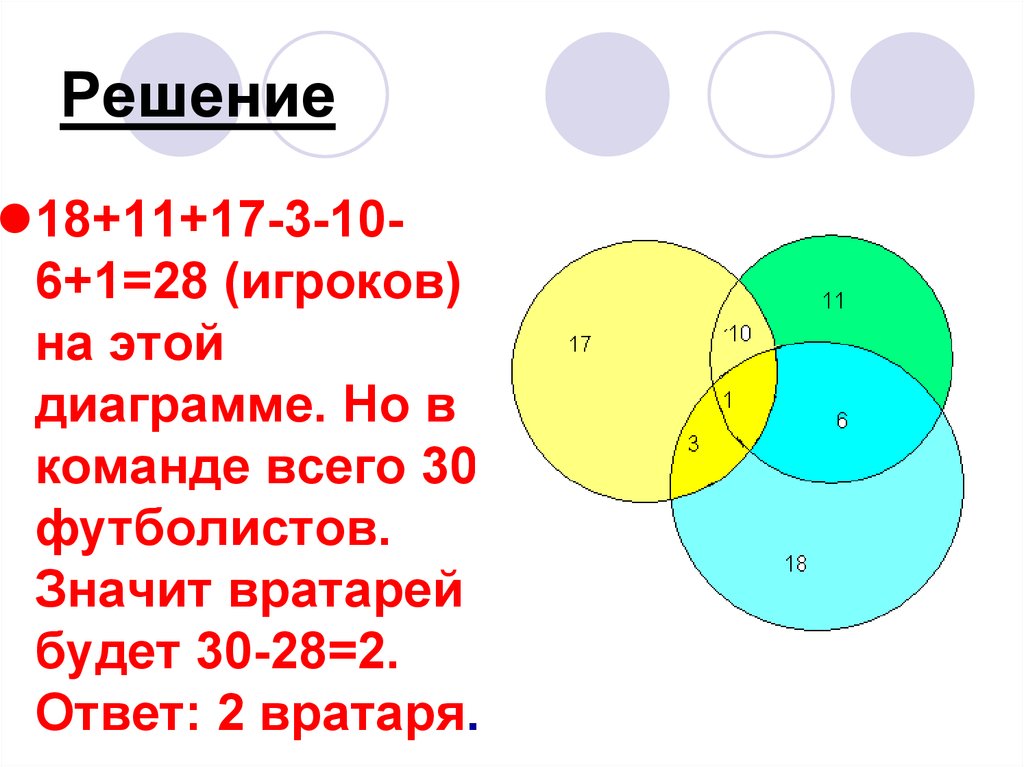 Диаграммы Венна показывают отношения, даже если множество пусто.
Диаграммы Венна показывают отношения, даже если множество пусто.
История диаграмм Венна
Диаграммы Венна названы в честь британского логика Джона Венна. Он написал о них в статье 1880 года, озаглавленной «О диаграммном и механическом представлении утверждений и рассуждений» в «Философском журнале» и «Журнале науки».
Но корни этого типа диаграмм уходят гораздо дальше, по крайней мере, на 600 лет. В 1200-х годах философ и логик Рамон Луллий (иногда пишется Луллий) с Майорки использовал аналогичный тип диаграммы, как писал автор М. Э. Барон в 1919 году.69 статей, прослеживающих их историю. Она также приписала немецкому математику и философу Готфриду Вильгельму фон Лейбницу создание подобных диаграмм в конце 1600-х годов.
В 1700-х годах швейцарский математик Леонард Эйлер (произносится как Ой-лер) изобрел то, что стало известно как диаграмма Эйлера, самый непосредственный предшественник диаграммы Венна.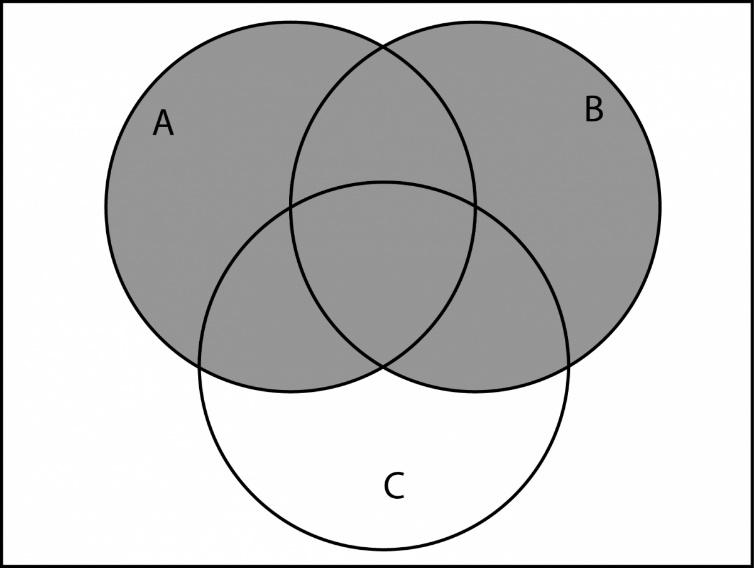 Фактически, Джон Венн называл свои собственные диаграммы Эйлеровыми кругами, а не диаграммами Венна. Термин «Диаграммы Венна» впервые был опубликован американским философом Кларенсом Ирвингом (К.И.) Льюисом в его 1918 книга, Обзор символической логики.
Фактически, Джон Венн называл свои собственные диаграммы Эйлеровыми кругами, а не диаграммами Венна. Термин «Диаграммы Венна» впервые был опубликован американским философом Кларенсом Ирвингом (К.И.) Льюисом в его 1918 книга, Обзор символической логики.
Диаграммы Венна продолжали развиваться в течение последних 60 лет благодаря достижениям экспертов Дэвида В. Хендерсона, Питера Гамбургера, Джерролда Григгса, Чарльза Э. «Чипа» Киллиана и Карлы Д. Сэвидж. Их работа касалась симметричных диаграмм Венна и их связи с простыми числами или числами, неделимыми другими числами, кроме 1 и самого числа. Одна такая симметричная диаграмма, основанная на простом числе 7, широко известна в математических кругах как Виктория.
Другими известными именами в разработке диаграмм Венна являются A.W.F. Эдвардс, Бранко Грюнбаум и Генри Джон Стивен Смит. Среди прочего, они изменили формы диаграмм, чтобы упростить отображение диаграмм Венна при увеличении количества наборов.
Пример Диаграмма Венна
Допустим, наша вселенная — это домашние животные, и мы хотим сравнить, на какого типа домашних животных согласится наша семья.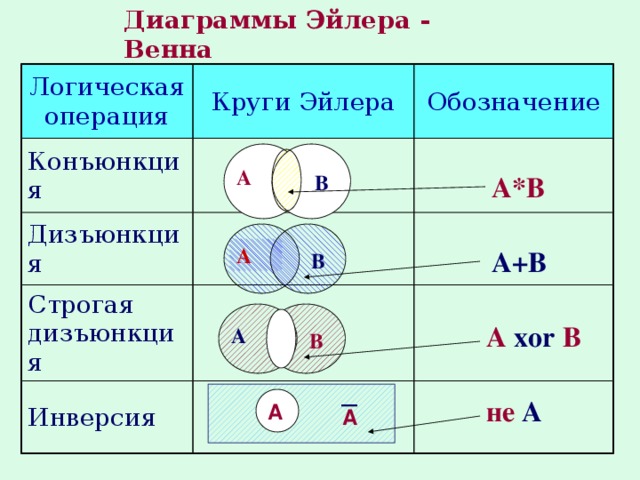
Набор А содержит мои предпочтения: собака, птица, хомяк.
Набор B содержит предпочтения члена семьи B: собака, кошка, рыба.
Набор C содержит предпочтения члена семьи C: собака, кошка, черепаха, змея.
Перекрытие или пересечение трех наборов содержит только собаку. Похоже, у нас появится собака.
Конечно, диаграммы Венна могут быть гораздо более сложными, поскольку они широко используются в различных областях.
Диаграмма Венна назначение и преимущества
- Для визуальной организации информации для просмотра взаимосвязей между наборами элементов, таких как общие черты и различия. Студенты и профессионалы могут использовать их, чтобы продумать логику концепции и изобразить отношения для визуальной коммуникации. Эта цель может варьироваться от элементарной до очень продвинутой.
- Чтобы сравнить два или более вариантов и четко увидеть, что у них общего, а что может их различать.
 Это может быть сделано для выбора важного продукта или услуги для покупки.
Это может быть сделано для выбора важного продукта или услуги для покупки. - Для решения сложных математических задач. Если вы математик, конечно.
- Чтобы сравнить наборы данных, найдите корреляции и предскажите вероятность определенных событий.
- Объяснять логику , стоящую за операторами или уравнениями, например, булеву логику поиска слов, включающую операторы «или» и «и», и то, как они сгруппированы.
С Lucidchart можно быстро и легко строить диаграммы. Начните бесплатную пробную версию сегодня, чтобы начать создавать и сотрудничать.
Создание диаграммы Венна
Варианты использования диаграммы Венна
- Математика: Диаграммы Венна обычно используются в школе для обучения основным математическим понятиям, таким как множества, объединения и пересечения.
 Они также используются в высшей математике для решения сложных задач, и о них много пишут в научных журналах. Теория множеств — это целая отрасль математики.
Они также используются в высшей математике для решения сложных задач, и о них много пишут в научных журналах. Теория множеств — это целая отрасль математики. - Статистика и вероятность: Специалисты по статистике используют диаграммы Венна для прогнозирования вероятности определенных событий. Это связано с областью предиктивной аналитики. Различные наборы данных можно сравнивать, чтобы найти степени общности и различий.
- Логика: Диаграммы Венна используются для определения достоверности конкретных аргументов и выводов. В дедуктивных рассуждениях, если посылки верны и форма аргумента верна, то вывод должен быть верным. Например, если все собаки — животные, а наш питомец Моджо — собака, то Моджо должен быть животным. Если мы назначаем переменные, то, скажем, собаки — это C, животные — это A, а Mojo — это B. В форме аргумента мы говорим: все C — это A. B — это C. Следовательно, B — это A. Связанная диаграмма в логике называется Таблица истинности, которая помещает переменные в столбцы, чтобы определить, что является логически правильным.
 Другая родственная диаграмма называется диаграммой Рэндольфа или R-диаграммой в честь математика Джона Ф. Рэндольфа. Он использует линии для определения наборов.
Другая родственная диаграмма называется диаграммой Рэндольфа или R-диаграммой в честь математика Джона Ф. Рэндольфа. Он использует линии для определения наборов. - Лингвистика: Диаграммы Венна использовались для изучения сходств и различий между языками.
- Обучение пониманию прочитанного: Учителя могут использовать диаграммы Венна, чтобы улучшить понимание прочитанного своими учениками. Учащиеся могут рисовать диаграммы, чтобы сравнивать и сопоставлять идеи, о которых они читают.
- Информатика: Программисты могут использовать диаграммы Венна для визуализации компьютерных языков и иерархий.
- Бизнес: Диаграммы Венна можно использовать для сравнения и противопоставления продуктов, услуг, процессов и почти всего, что может быть изображено в наборах. И они являются эффективным инструментом коммуникации, чтобы проиллюстрировать это сравнение.
Глоссарий диаграмм Венна
| Набор | Коллекция вещей. Учитывая универсальность диаграмм Венна, на самом деле все может быть что угодно. Вещи могут называться элементами, объектами, членами или подобными терминами. Учитывая универсальность диаграмм Венна, на самом деле все может быть что угодно. Вещи могут называться элементами, объектами, членами или подобными терминами. | |
| Союз | Все предметы в наборах. | |
| Пересечение | Перекрывающиеся элементы в наборах. Иногда называется подмножеством. | |
| Симметричная разность двух множеств | Все, кроме пересечения. | |
| Полная комплектация | Все, чего нет в наборе. | |
| Соответствующее дополнение | В одном наборе, в другом нет. | |
| Диаграмма Венна в масштабе | Также называется пропорциональной площади. Круги (или другие формы) имеют размер в соответствии с их пропорциональным представлением целого. | |
| Треугольник Рело | Форма, образованная пересечением трех кругов или фигур, например, на диаграмме Венна. | |
| Набор обозначений | Понятия, проиллюстрированные на диаграммах Венна, выражены математическими обозначениями, такими как наборы и подмножества (в скобках), объединения (с символом в виде буквы U) и пересечения (с символом перевернутой буквы U). | |
| Теория множеств | Давний раздел математики, занимающийся множествами. |
Более легкое примечание: диаграммы Венна появились на маленьком экране
Немногие диаграммы перешли в популярную культуру, но уважаемая диаграмма Венна сделала это.
- Драма: В телешоу CBS NUMB3RS, выходившем с 2005 по 2010 год, математический гений Чарльз Эппс использует диаграмму Венна, чтобы определить, какие подозреваемые соответствуют описанию и имеют историю насилия.
- Комедия: В программе NBC «Поздняя ночь с Сетом Мейерсом» у комика есть повторяющаяся процедура под названием «Диаграммы Венна», в которой он сравнивает два, казалось бы, не связанных между собой предмета, чтобы найти их забавную общность (он надеется).

Шаги по рисованию и использованию базовой диаграммы Венна
- Определите свою цель. Что вы сравниваете и почему? Это поможет вам определить наборы.
- Проведите мозговой штурм и перечислите предметы в своих наборах либо на бумаге, либо с помощью такой платформы, как Lucidchart.
- Теперь используйте свою диаграмму, чтобы сравнить и сопоставить наборы. Вы можете смотреть на вещи по-новому и быть в состоянии делать наблюдения, делать выбор, аргументировать или принимать решения.
Дополнительные ресурсы
- Шаблоны диаграмм Венна
- Как создать диаграмму Венна в Excel
- Как создать диаграмму Венна в PowerPoint
Lucidchart позволяет создавать профессионально выглядящие диаграммы Венна с помощью простого в использовании программного обеспечения . Поскольку все редактирование происходит в облаке, с коллегами легко работать над диаграммой Венна. Вы даже можете импортировать изображения и делиться своей схемой в цифровом виде или через печать.
Вы даже можете импортировать изображения и делиться своей схемой в цифровом виде или через печать.
Хотите построить собственную диаграмму Венна? Попробуйте Люсидчарт. Это быстро, просто и совершенно бесплатно.
Построить диаграмму Венна
Пути и схемы Эйлера и Гамильтона
Результаты обучения
- Определить, есть ли в графе путь Эйлера и/или цепь
- Используйте алгоритм Флери, чтобы найти схему Эйлера
- Добавление ребер в граф для создания схемы Эйлера, если таковой не существует
- Определите, есть ли в графе гамильтонова цепь или путь
- Найдите оптимальную гамильтонову схему для графа с помощью алгоритма грубой силы, алгоритма ближайшего соседа и алгоритма отсортированных ребер
- Определить связный граф, являющийся остовным деревом
- Используйте алгоритм Крускала для формирования остовного дерева и остовного дерева с минимальной стоимостью
На следующем уроке мы будем исследовать определенные типы путей в графе, которые называются эйлеровыми путями и цепями. Пути Эйлера — это оптимальный путь через граф. Они названы в его честь, потому что впервые их определил Эйлер.
Пути Эйлера — это оптимальный путь через граф. Они названы в его честь, потому что впервые их определил Эйлер.
Подсчитав количество вершин графа и их степень, мы можем определить, есть ли в графе эйлерова путь или цепь. Мы также изучим еще один алгоритм, который позволит нам найти схему Эйлера, как только мы определим, что граф имеет ее.
Цепи Эйлера
В первом разделе мы построили граф кенигсбергских мостов и спросили, можно ли пройти по каждому мосту один раз. Поскольку Эйлер первым изучил этот вопрос, эти типы путей названы в его честь.
Путь Эйлера
Путь Эйлера — это путь, который использует каждое ребро в графе без повторений. Будучи путем, он не должен возвращаться в начальную вершину.
Пример
В графе, показанном ниже, есть несколько путей Эйлера. Одним из таких путей является CABDCB. Путь показан стрелками вправо, порядок ребер пронумерован.
Схема Эйлера
Схема Эйлера — это схема, которая использует каждое ребро в графе без повторений. Будучи цепью, она должна начинаться и заканчиваться в одной и той же вершине.
Будучи цепью, она должна начинаться и заканчиваться в одной и той же вершине.
Пример
На приведенном ниже графике показано несколько возможных схем Эйлера. Вот пара, начинающаяся и заканчивающаяся в вершине A: ADEACEFCBA и AECABCFEDA. Второй показан стрелками.
Посмотрите на пример, используемый для путей Эйлера — есть ли в этом графе эйлерова цепь? Несколько попыток скажут вам «нет»; этот граф не имеет эйлеровой цепи. Когда мы работали с кратчайшими путями, нас интересовал оптимальный путь. Что касается путей и цепей Эйлера, нас в первую очередь интересует, является ли путь Эйлера или цепь существует .
Какое нам дело до существования схемы Эйлера? Вспомните нашего инспектора по газонам из начала главы. Инспектор по газонам заинтересован в том, чтобы гулять как можно меньше. Идеальной ситуацией была бы трасса, покрывающая все улицы без повторов. Это схема Эйлера! К счастью, Эйлер решил вопрос о том, будет ли существовать эйлеровский путь или цепь.
Теоремы Эйлера о путях и цепях
Граф будет содержать путь Эйлера, если он содержит не более двух вершин нечетной степени.
Граф будет содержать схему Эйлера, если все вершины имеют четную степень
Пример
В приведенном ниже графе вершины A и C имеют степень 4, так как в каждую вершину ведет 4 ребра. B имеет степень 2, D имеет степень 3, а E имеет степень 1. Этот граф содержит две вершины с нечетной степенью (D и E) и три вершины с четной степенью (A, B и C), поэтому теоремы Эйлера говорят нам об этом. граф имеет эйлеров путь, но не эйлеров цикл.
Пример
Есть ли схема Эйлера на графе инспектора жилищного строительства, который мы создали ранее в этой главе? Все выделенные вершины имеют нечетную степень. Поскольку вершин с нечетной степенью больше двух, на этом графе нет эйлеровых путей или эйлеровых цепей. К сожалению, нашему инспектору по газонам придется отступить.
Пример
Когда в одном и том же жилом комплексе идет снег, снегоочиститель должен вспахивать обе стороны каждой улицы. Для простоты предположим, что плуг выходит из строя достаточно рано, чтобы он мог игнорировать правила дорожного движения и двигаться по любой стороне улицы в любом направлении. Это можно визуализировать на графике, нарисовав два ребра для каждой улицы, представляющие две стороны улицы.
Для простоты предположим, что плуг выходит из строя достаточно рано, чтобы он мог игнорировать правила дорожного движения и двигаться по любой стороне улицы в любом направлении. Это можно визуализировать на графике, нарисовав два ребра для каждой улицы, представляющие две стороны улицы.
Обратите внимание, что все вершины в этом графе имеют четную степень, поэтому в этом графе есть эйлерова схема.
В следующем видео приведены дополнительные примеры определения пути Эйлера и схемы Эйлера для графа.
Алгоритм Флери
Теперь мы знаем, как определить, есть ли в графе эйлерова схема, но если да, то как ее найти? Хотя обычно можно найти схему Эйлера, просто вытащив карандаш и попытавшись найти ее, более формальным методом является алгоритм Флери.
804117647059″> Алгоритм Флери1. Начните с любой вершины при поиске схемы Эйлера. Если вы ищете путь Эйлера, начните с одной из двух вершин с нечетной степенью.
2. Выберите любое ребро, выходящее из вашей текущей вершины, при условии, что удаление этого ребра не разделит граф на два несвязанных множества ребер.
3. Добавьте это ребро к вашей схеме и удалите его из графа.
4. Продолжайте, пока не закончите.
Пример
Найдите на этом графе эйлеров цикл, используя алгоритм Флери, начиная с вершины A.
Попробуйте
Есть ли на приведенном ниже графе эйлеров цикл? Если да, то найдите.
В следующем видеоролике представлены дополнительные примеры использования алгоритма Флери для поиска схемы Эйлера.
Эйлеризация и задача китайского почтальона
Не в каждом графе есть эйлерова цепь или путь, но нашему инспектору по газонам все еще нужно проводить проверки. Ее цель — свести к минимуму количество пеших прогулок, которые ей приходится делать. Для этого ей придется дублировать некоторые ребра в графе, пока не будет существовать эйлерова схема.
Ее цель — свести к минимуму количество пеших прогулок, которые ей приходится делать. Для этого ей придется дублировать некоторые ребра в графе, пока не будет существовать эйлерова схема.
Эйлеризация
Эйлеризация — это процесс добавления ребер к графу для создания схемы Эйлера на графе. Для эйлеризации графа ребра дублируются, чтобы соединить пары вершин с нечетной степенью. Соединение двух вершин с нечетной степенью увеличивает степень каждой, давая им обеим четную степень. Когда две вершины с нечетной степенью не связаны напрямую, мы можем продублировать все ребра на пути, соединяющем их.
Обратите внимание, что мы можем дублировать ребра, а не создавать ребра там, где их раньше не было. Дублирование ребер означало бы пройти или проехать по дороге дважды, а создание ребра там, где его раньше не было, сродни прокладке новой дороги!
Пример
Для показанного прямоугольного графика показаны три возможные эйлеризации. Обратите внимание, что в каждом из этих случаев вершины, которые начинались с нечетных степеней, имеют четные степени после эйлеризации, что позволяет использовать эйлерову схему.
Обратите внимание, что в каждом из этих случаев вершины, которые начинались с нечетных степеней, имеют четные степени после эйлеризации, что позволяет использовать эйлерову схему.
В приведенном выше примере вы заметите, что для последней эйлеризации требовалось дублировать семь ребер, а для первых двух требовалось дублировать только пять ребер. Если бы мы эйлеризовали граф, чтобы найти пешеходный путь, нам нужна была бы эйлеризация с минимальным дублированием. Если бы ребра имели веса, представляющие расстояния или затраты, то мы хотели бы выбрать эйлеризацию с минимальным общим добавленным весом.
Попробуйте сейчас
Эйлеризуйте показанный граф, затем найдите эйлерову схему на эйлеризованном графе.
Пример
Снова взглянув на граф нашего инспектора газонов из примеров 1 и 8, мы увидим, что вершины с нечетной степенью выделены. С восемью вершинами нам всегда придется дублировать как минимум четыре ребра. В этом случае нам нужно продублировать пять ребер, так как две вершины нечетной степени не связаны напрямую. Без весов мы не можем быть уверены, что это эйлеризация, которая минимизирует пройденное расстояние, но выглядит довольно хорошо.
Без весов мы не можем быть уверены, что это эйлеризация, которая минимизирует пройденное расстояние, но выглядит довольно хорошо.
Задача нахождения оптимальной эйлеризации называется «задачей китайского почтальона» — название, данное американцем в честь китайского математика Мей-Ко Квана, который впервые изучил проблему в 1962 году, пытаясь найти оптимальные маршруты доставки для почтовых перевозчиков. Эта проблема важна при определении эффективных маршрутов для мусоровозов, школьных автобусов, контролеров парковки, дворников и т. д.
К сожалению, алгоритмы решения этой задачи достаточно сложны. Некоторые более простые случаи рассматриваются в упражнениях
В следующем видео показан другой взгляд на поиск эйлеризации задачи об инспекторе газонов.
Гамильтоновы схемы
Задача коммивояжера
В последнем разделе мы рассмотрели оптимизацию пешего маршрута для почтового перевозчика. Чем это отличается от требований драйвера доставки пакетов? В то время как почтовому перевозчику нужно было пройти по каждой улице (краю), чтобы доставить почту, водителю по доставке вместо этого нужно посетить каждое из набора мест доставки. Вместо того, чтобы искать схему, покрывающую каждое ребро один раз, доставщик пакетов заинтересован в схеме, которая посещает каждую вершину один раз.
Чем это отличается от требований драйвера доставки пакетов? В то время как почтовому перевозчику нужно было пройти по каждой улице (краю), чтобы доставить почту, водителю по доставке вместо этого нужно посетить каждое из набора мест доставки. Вместо того, чтобы искать схему, покрывающую каждое ребро один раз, доставщик пакетов заинтересован в схеме, которая посещает каждую вершину один раз.
Гамильтоновы цепи и пути
Гамильтоновы цепи — это цепи, которые посещают каждую вершину один раз без повторений. Будучи цепью, она должна начинаться и заканчиваться в одной и той же вершине. Гамильтонов путь также посещает каждую вершину один раз без повторений, но не обязательно должен начинаться и заканчиваться в одной и той же вершине.
Гамильтоновы цепи названы в честь Уильяма Роуэна Гамильтона, изучавшего их в 1800-х годах.
Пример
Одна гамильтонова цепь показана на графике ниже. На этом графе возможно несколько других гамильтоновых схем. Обратите внимание, что схема должна посетить каждую вершину только один раз; нет необходимости использовать каждое ребро.
Обратите внимание, что схема должна посетить каждую вершину только один раз; нет необходимости использовать каждое ребро.
Эта схема может быть обозначена последовательностью посещенных вершин, начинающихся и заканчивающихся в одной и той же вершине: ABFGCDHMLKJEA. Обратите внимание, что одна и та же схема может быть записана в обратном порядке или начинаться и заканчиваться в разных вершинах.
В отличие от схем Эйлера, не существует хорошей теоремы, позволяющей нам мгновенно определить, существует ли гамильтонова схема для всех графов.[1]
Пример
Существует ли гамильтонов путь или цепь на приведенном ниже графике?
Мы видим, что если мы доберемся до вершины E, то уже не сможем покинуть ее, не вернувшись в C, поэтому гамильтонова схема невозможна. Если мы начнем с вершины E, мы сможем найти несколько гамильтоновых путей, таких как ECDAB и ECABD
Попробуйте
С гамильтоновыми цепями наше внимание будет сосредоточено не на существовании, а на вопросе оптимизации; для данного графа, ребра которого имеют веса, можем ли мы найти оптимальную гамильтонову схему; тот, у которого наименьший общий вес.
Посмотрите это видео, чтобы увидеть отработку приведенных выше примеров.
Эта задача называется Задача коммивояжера (TSP), потому что вопрос можно сформулировать следующим образом: Предположим, что продавцу необходимо провести рекламную презентацию в четырех городах. Он просматривает стоимость авиабилетов между каждым городом и наносит затраты на график. В каком порядке он должен посетить каждый город по одному разу, а затем вернуться домой с наименьшей стоимостью?
Чтобы ответить на вопрос, как найти схему Гамильтона с наименьшей стоимостью, мы рассмотрим некоторые возможные подходы. Первый вариант, который может прийти на ум, — просто попробовать все возможные схемы.
вопрос можно сформулировать следующим образом: Предположим, что торговому представителю необходимо провести рекламную презентацию в четырех городах. Он просматривает стоимость авиабилетов между каждым городом и наносит затраты на график. В каком порядке он должен посетить каждый город по одному разу, а затем вернуться домой с наименьшей стоимостью?
Он просматривает стоимость авиабилетов между каждым городом и наносит затраты на график. В каком порядке он должен посетить каждый город по одному разу, а затем вернуться домой с наименьшей стоимостью?
Чтобы ответить на вопрос, как найти схему Гамильтона с наименьшей стоимостью, мы рассмотрим некоторые возможные подходы. Первый вариант, который может прийти на ум, — просто попробовать все возможные схемы.
Алгоритм грубой силы (также известный как полный перебор)
1. Перечислите все возможные гамильтоновы схемы
2. Найдите длину каждой цепи, добавив веса ребер
3. Выберите схему с минимальным общим весом.
Пример
Примените алгоритм грубой силы, чтобы найти гамильтонов контур минимальной стоимости на графике ниже.
Чтобы применить алгоритм грубой силы, мы перечисляем все возможные гамильтоновы схемы и вычисляем их вес:
| Цепь | Масса |
| АВСДА | 4+13+8+1 = 26 |
| АБДКА | 4+9+8+2 = 23 |
| АКБДА | 2+13+9+1 = 25 |
Примечание. Это уникальные цепи на этом графике. Все остальные возможные схемы обратны перечисленным или начинаются в другой вершине, но приводят к тем же весам.
Это уникальные цепи на этом графике. Все остальные возможные схемы обратны перечисленным или начинаются в другой вершине, но приводят к тем же весам.
Отсюда видно, что вторая схема, ABDCA, является оптимальной схемой.
Посмотрите, как эти примеры снова работают в следующем видео.
Попробуйте
Алгоритм грубой силы оптимален; он всегда будет давать гамильтонову схему с минимальным весом. Это эффективно? Чтобы ответить на этот вопрос, нам нужно рассмотреть, сколько гамильтоновых цепей может иметь граф. Для простоты давайте рассмотрим наихудший вариант, когда каждая вершина соединена с каждой другой вершиной. это называется полный график.
Предположим, у нас есть полный граф с пятью вершинами, подобный приведенному выше графу авиаперелетов. Из Сиэтла есть четыре города, которые мы можем посетить в первую очередь. Из каждого из них есть три варианта. В каждом из этих городов есть два возможных города, которые можно посетить в следующий раз. Тогда есть только один выбор для последнего города перед возвращением домой.
Из Сиэтла есть четыре города, которые мы можем посетить в первую очередь. Из каждого из них есть три варианта. В каждом из этих городов есть два возможных города, которые можно посетить в следующий раз. Тогда есть только один выбор для последнего города перед возвращением домой.
Это можно показать визуально:
Подсчитав количество маршрутов, мы видим, что существует [latex]4\cdot{3}\cdot{2}\cdot{1}[/latex] маршрутов. Для шести городов будет [latex]5\cdot{4}\cdot{3}\cdot{2}\cdot{1}[/latex] маршрутов.
Количество возможных цепей
Для N вершин в полном графе будет [латекс](n-1)!=(n-1)(n-2)(n-3)\dots {3}\cdot{2}\cdot{1}[/latex] маршруты. Половина из них является дубликатами в обратном порядке, поэтому существуют [латекс]\frac{(n-1)!}{2}[/latex] уникальные схемы.
Восклицательный знак ! читается как факториал и является сокращением для показанного продукта.
Пример
Сколько цепей будет в полном графе с 8 вершинами?
Полный граф с 8 вершинами будет иметь = 5040 возможных гамильтоновых цепей. Половина цепей являются дубликатами других цепей, но в обратном порядке, в результате чего остается 2520 уникальных маршрутов.
Половина цепей являются дубликатами других цепей, но в обратном порядке, в результате чего остается 2520 уникальных маршрутов.
Хотя это много, это не кажется необоснованно огромным. Но подумайте, что происходит с увеличением количества городов:
| Городов | Уникальные схемы Гамильтона |
| 9 | 8!/2 = 20 160 |
| 10 | 9!/2 = 181 440 |
| 11 | 10!/2 = 1 814 400 |
| 15 | 14!/2 = 43 589 145 600 |
| 20 | 19!/2 = 60 822 550 204 416 000 |
Посмотрите, как эти примеры снова работают в следующем видео.
Как видите, количество каналов растет очень быстро. Если бы компьютер просматривал один миллиард цепей в секунду, все равно потребовалось бы почти два года, чтобы изучить все возможные схемы только с 20 городами! Конечно Brute Force это , а не эффективный алгоритм.
Если бы компьютер просматривал один миллиард цепей в секунду, все равно потребовалось бы почти два года, чтобы изучить все возможные схемы только с 20 городами! Конечно Brute Force это , а не эффективный алгоритм.
Алгоритм ближайшего соседа (NNA)
1. Выберите начальную точку.
2. Перейти к ближайшей непосещенной вершине (ребру с наименьшим весом).
3. Повторяйте, пока цепь не будет завершена.
К сожалению, никто еще не нашел эффективного и оптимального алгоритма для решения TSP, и очень маловероятно, что кто-то когда-нибудь его найдет. Поскольку использовать грубую силу для решения проблемы нецелесообразно, вместо этого мы обратимся к 9.0019 эвристические алгоритмы ; эффективные алгоритмы, дающие приближенные решения. Другими словами, эвристические алгоритмы работают быстро, но могут создавать или не создавать оптимальную схему.
Пример
Рассмотрим наш предыдущий график, показанный справа.
Начиная с вершины A ближайшим соседом является вершина D с весом 1.
Из D ближайшим соседом является C с весом 8.
Из C наш единственный вариант — перейти к вершине B , единственная непосещенная вершина со стоимостью 13,
Из B мы возвращаемся в A с весом 4.
Получившаяся схема представляет собой ADCBA с общим весом [латекс]1+8+13+4 = 26[/латекс].
Посмотрите пример в следующем видео.
Мы нашли худшую схему на графике! Что случилось? К сожалению, хотя его очень легко реализовать, NNA представляет собой жадный алгоритм , то есть он рассматривает только немедленное решение, не учитывая последствия в будущем. В этом случае следование ребру AD заставило нас позже использовать очень дорогое ребро BC.
Пример
Рассмотрим еще раз нашего продавца. Начиная с Сиэтла, ближайший сосед (самый дешевый рейс) находится в Лос-Анджелесе по цене 70 долларов. Оттуда:
Начиная с Сиэтла, ближайший сосед (самый дешевый рейс) находится в Лос-Анджелесе по цене 70 долларов. Оттуда:
из Лос-Анджелеса в Чикаго: 100 долларов
из Чикаго в Атланту: 75 долларов
из Атланты в Даллас: 85 долларов
из Далласа в Сиэтл: 120 долларов
Общая стоимость: 450 долларов
3
3 оптимальная схема. Посмотрите этот пример еще раз в этом видео.
Возвращаясь к нашему первому примеру, как мы можем улучшить результат? Одним из вариантов было бы повторить алгоритм ближайшего соседа с другой начальной точкой, чтобы увидеть, изменился ли результат. Поскольку ближайший сосед очень быстр, сделать это несколько раз не составит большого труда.
Пример
Вернемся к графу из Примера 17.
Начиная с вершины A, получается схема с весом 26.
Начиная с вершины B, ближайшей соседней схемой является BADCB с весом 4+1+8 +13 = 26. Это та же схема, которую мы нашли, начиная с вершины A. Не лучше.
Начиная с вершины C ближайшей соседней схемой является CADBC с весом 2+1+9+13 = 25. Лучше!
Начиная с вершины D ближайшим соседним контуром является DACBA. Обратите внимание, что на самом деле это та же самая схема, которую мы нашли, начиная с C, просто написанная с другой начальной вершиной.
RNNA удалось создать немного лучшую схему с весом 25, но все же не оптимальную схему в данном случае. Обратите внимание, что даже если мы нашли схему, начав с вершины C, мы все равно могли написать схему, начинающуюся с вершины A: ADBCA или ACBDA.
Попробуйте
В таблице ниже показано время в миллисекундах, необходимое для отправки пакета данных между компьютерами в сети. Если бы данные нужно было отправлять последовательно на каждый компьютер, а уведомление должно было вернуться на исходный компьютер, мы бы решили TSP. Компьютеры помечены буквами A-F для удобства.
Компьютеры помечены буквами A-F для удобства.
А Б С Д Е Ф А — 44 34 12 40 41 Б 44 — 31 43 24 50 С 34 31 — 20 39 27 Д 12 43 20 — 11 17 Е 40 24 39 11 — 42 Ф 41 50 27 17 42 —
а. Найдите схему, созданную NNA, начиная с вершины B.
b. Найдите цепь, генерируемую RNNA.
Хотя, безусловно, лучше, чем базовый NNA, к сожалению, RNNA все еще жадный и будет давать очень плохие результаты для некоторых графиков. В качестве альтернативы наш следующий подход сделает шаг назад и взглянет на «общую картину» — он сначала выберет самые короткие ребра, а затем заполнит пробелы.
В качестве альтернативы наш следующий подход сделает шаг назад и взглянет на «общую картину» — он сначала выберет самые короткие ребра, а затем заполнит пробелы.
Пример
Используя четырехвершинный граф из предыдущего, мы можем использовать алгоритм Sorted Edges.
Самым дешевым ребром является AD со стоимостью 1. Мы выделяем это ребро, чтобы отметить его как выбранное.
Следующее самое короткое ребро — AC с весом 2, поэтому мы выделяем это ребро.
Для третьего ребра мы хотели бы добавить AB, но это дало бы вершине A степень 3, что недопустимо в гамильтоновой схеме. Следующим кратчайшим ребром является CD, но это ребро создало бы цепь ACDA, которая не включает вершину B, поэтому мы отбрасываем это ребро. Следующее самое короткое ребро — BD, поэтому мы добавляем это ребро к графу.
BAD
BAD
OK
Затем мы добавляем последнее ребро, чтобы завершить схему: ACBDA с весом 25.
Обратите внимание, что алгоритм не создал оптимальную схему в этом случае; оптимальная схема — это ACDBA с весом 23.
Хотя алгоритм Sorted Edge преодолевает некоторые недостатки NNA, он по-прежнему является только эвристическим алгоритмом и не гарантирует оптимальную схему.
Пример
Группа вашего учителя, Производная работа , совершает тур по барам в Орегоне. Расстояние движения показано ниже. Спланируйте эффективный маршрут, чтобы ваш учитель посетил все города и вернулся в исходное место. Используйте NNA, начиная с Портленда, а затем используйте Sorted Edges.
Эшленд Астория Изгиб Корваллис Кратерное озеро Юджин Ньюпорт Портленд Салем Приморская Эшленд – 374 200 223 108 178 252 285 240 356 Астория 374 – 255 166 433 199 135 95 136 17 Изгиб 200 255 – 128 277 128 180 160 131 247 Корваллис 223 166 128 – 430 47 52 84 40 155 Кратерное озеро 108 433 277 430 – 453 478 344 389 423 Юджин 178 199 128 47 453 – 91 110 64 181 Ньюпорт 252 135 180 52 478 91 – 114 83 117 Портленд 285 95 160 84 344 110 114 – 47 78 Салем 240 136 131 40 389 64 83 47 – 118 Приморский 356 17 247 155 423 181 117 78 118 –
Чтобы увидеть всю таблицу, прокрутите вправо
Используя NNA с большим количеством городов, может оказаться полезным отмечать города по мере их посещения, чтобы случайно не посетить их снова. . Глядя в ряду для Портленда, наименьшее расстояние составляет 47, до Салема. Следуя этой идее, наша схема будет такой:
. Глядя в ряду для Портленда, наименьшее расстояние составляет 47, до Салема. Следуя этой идее, наша схема будет такой:
Портленд — Салем 47
Салем к Corvallis 40
Corvallis to Eugene 47
Eugene to Newport 91
Newport to Seaside 117
Seaside to Astoria 17
Astoria to Bend 255
Bend To Ashland 200
Ashland To Crate.
Кратерное озеро в Портленд 344
Общая длина пути: 1266 миль
Используя Sorted Edges, вы можете счесть полезным нарисовать пустой граф, возможно, рисуя вершины по круговому шаблону. Добавление ребер к графу по мере их выбора поможет вам визуализировать любые цепи или вершины со степенью 3.
Начнем добавлять самые короткие ребра:
Побережье до Астории 17 миль
Корваллис до Салема 40 миль
Портленд до Салема 4 7 мили
от Корваллиса до Юджина 47 миль
График после добавления этих ребер показан справа. Следующее самое короткое ребро находится от Корваллиса до Ньюпорта на расстоянии 52 миль, но добавление этого ребра даст Корваллису степень 3.
Следующее самое короткое ребро находится от Корваллиса до Ньюпорта на расстоянии 52 миль, но добавление этого ребра даст Корваллису степень 3.
Продолжение продолжения, мы можем пропустить любую пару краев, которая содержит Салем или Корваллис, поскольку они оба уже имеют степень 2.
Портленд до приморья 78 миль
Eugene в Ньюпорт 91 миль
Портленд для Астории (Recubment замыкает цепь)
Ashland to Crater Lk 108 миль
График после добавления этих ребер показан справа. На этом этапе мы можем пропустить любую пару ребер, содержащую Salem, Seaside, Eugene, Portland или Corvallis, поскольку они уже имеют степень 2.
Newport to Astoria (Dize — Clos Lock Circuit)
Newport, чтобы изгибаться 180 миль
Bend в Ashland 200 миль
В этот момент единственный способ завершить схему:
Астория 433 мили. Последняя трасса, написанная для старта в Портленде:
Портленд, Салем, Корваллис, Юджин, Ньюпорт, Бенд, Эшленд, Кратер-Лейк, Астория, Сисайд, Портленд. Общая длина пути: 1241 миль.
Общая длина пути: 1241 миль.
Несмотря на то, что маршрут NNA лучше, ни один из алгоритмов не дал оптимального маршрута. Следующий маршрут может составить тур в 1069 миль:
Портленд, Астория, Сисайд, Ньюпорт, Корваллис, Юджин, Эшленд, Кратер Лейк, Бенд, Салем, Портленд
Посмотрите пример алгоритма ближайшего соседа для путешествия из города в город используя таблицу, разработанную в видео ниже.
В следующем видео мы используем ту же таблицу, но используем отсортированные ребра для планирования поездки.
Попробуйте
Найдите схему, созданную алгоритмом Sorted Edges, используя приведенный ниже график.
Spanning Trees
Компании требуется надежное подключение к Интернету и телефонной связи между ее пятью офисами (названными для простоты A, B, C, D и E) в Нью-Йорке, поэтому они решают арендовать выделенные линии у телефонной компании. Телефонная компания взимает плату за каждую установленную связь. Затраты в тысячах долларов в год показаны на графике.
В этом случае нам не нужно искать цепь или даже определенный путь; все, что нам нужно сделать, это убедиться, что мы можем позвонить из любого офиса в любой другой. Другими словами, нам нужно быть уверенным, что существует путь из любой вершины в любую другую вершину.
Связующее дерево
Связующее дерево — это связный граф, использующий все вершины, в которых нет циклов.
Другими словами, существует путь из любой вершины в любую другую вершину, но нет обходных путей.
Ниже показаны некоторые примеры остовных деревьев. Обратите внимание, что в деревьях нет циклов, и нормально иметь вершины со степенью выше двух.
Обычно у нас есть начальный график для работы, как в примере с телефоном выше. В этом случае мы формируем наше остовное дерево, находя подграф — новый граф, образованный с использованием всех вершин, но только некоторых ребер исходного графа. Ребра не будут созданы там, где их еще не было.
Конечно, любое случайное остовное дерево — это не совсем то, что нам нужно. Нам нужно связующее дерево с минимальной стоимостью (MCST) .
Покрывающее дерево с минимальной стоимостью (MCST)
Покрывающее дерево с минимальной стоимостью — это связующее дерево с наименьшим общим весом ребра.
Подход в стиле ближайшего соседа здесь не имеет особого смысла, поскольку нам не нужна схема, поэтому вместо этого мы воспользуемся подходом, аналогичным отсортированным ребрам.
Алгоритм Крускала
- Выберите самое дешевое неиспользуемое ребро в графе.
- Повторите шаг 1, добавив самое дешевое неиспользуемое ребро, если:
- добавление ребра создаст цепь
Повторите до тех пор, пока не будет сформировано дерево охраняющегося дерева
Пример
Использование нашего графа телефонной линии сверху, начинайте добавлять края:
ab 4 $
AE $ 5 OK
BE 6 $ 6 — Закрыть схема
AE $ 5 OK 9000 DC $7 OK
AC $8 OK
На этом мы останавливаемся – теперь все вершины соединены, поэтому мы сформировали остовное дерево стоимостью $24 тысячи в год.
Примечательно, что алгоритм Крускала оптимален и эффективен; мы гарантируем, что всегда будем производить оптимальный MCST.
Пример
Энергетической компании необходимо проложить обновленные распределительные линии, соединяющие десять городов Орегона внизу с электросетью. Как они могут минимизировать количество новой линии для прокладки?
Эшленд Астория Изгиб Корваллис Кратерное озеро Юджин Ньюпорт Портленд Салем Приморский Эшленд – 374 200 223 108 178 252 285 240 356 Астория 374 – 255 166 433 199 135 95 136 17 Изгиб 200 255 – 128 277 128 180 160 131 247 Корваллис 223 166 128 – 430 47 52 84 40 155 Кратерное озеро 108 433 277 430 – 453 478 344 389 423 Юджин 178 199 128 47 453 – 91 110 64 181 Ньюпорт 252 135 180 52 478 91 – 114 83 117 Портленд 285 95 160 84 344 110 114 – 47 78 Салем 240 136 131 40 389 64 83 47 – 118 Приморский 356 17 247 155 423 181 117 78 118 –
Чтобы увидеть всю таблицу, прокрутите вправо
Используя алгоритм Крускала, мы добавляем ребра от самых дешевых к самым дорогим, отбрасывая все, что замыкает цепь. Мы останавливаемся, когда граф связен.
Мы останавливаемся, когда граф связен.
Seaside to Astoria 17 Milescorvallis to Salem 40 миль
Портленд до Салема 47 миль
Corvallis to Eugene 47 миль
Corvallis To Newport 52 миль
Салем в Евгении. График до этого момента показан ниже.
Продолжение,
Ньюпорт — Салем отклонить
Corvallis to Portland Reject
Eugene to Newport Отказ
Портленд в Astoria Отказ
Ashland To Crater LK 108 миль
Eugen
Поверните к Юджину 128 миль
Bend to Salem Rejuct
Astoria to Newport Rejuct
Салема в Astoria Отказ
Corvallis to Seaside Отказ
Портленд на изгиб DRIED
ASTORIA TO CORVALLIS Recure
EUGEN график. Общая длина кабеля для прокладки составит 695 миль.
Посмотрите приведенный выше пример, отработанный в следующем видео, без таблицы.
Теперь мы представляем тот же пример с таблицей в следующем видео.
Попробуйте
Найдите остовное дерево минимальной стоимости на графике ниже, используя алгоритм Крускала.
[1] Есть некоторые теоремы, которые можно использовать в конкретных обстоятельствах, например, теорема Дирака, которая утверждает, что гамильтонова цепь должна существовать на графе с n вершин, если каждая вершина имеет степень n /2 или выше.
ggVennDiagram: интуитивно понятный, простой в использовании и настраиваемый пакет R для создания диаграммы Венна
Введение
Диаграмма Венна — это широко используемая диаграмма, показывающая отношения между несколькими наборами. В биомедицинских исследованиях диаграмма Венна часто используется для определения принадлежности различных типов данных, таких как соединения, гены, пути и виды. Когда количество наборов меньше пяти, диаграммы Венна, вероятно, являются наиболее интуитивно понятной формой визуализации данных, превосходящей тепловые карты и таблицы.
Когда количество наборов меньше пяти, диаграммы Венна, вероятно, являются наиболее интуитивно понятной формой визуализации данных, превосходящей тепловые карты и таблицы.
В среде R, одной из самых популярных платформ для визуализации биомедицинских данных, доступно множество пакетов для построения диаграммы Венна, включая VennDiagram (Chen and Boutros, 2011), ColorfulVennPlot (Noma and Manvae, 2013), venn (Dusa, 2020), nVennR (Quesada, 2021), eulerr (Larsson, 2020), venneuler (Wilkinson, 2011), RVenn (Akyol, 2019) и gplots (Warnes et al., 2020), и это лишь некоторые из них (см. Таблицу 1). для сравнения функций этих пакетов). Как одно из самых популярных программ, VennDiagram поддерживает несколько форматов ввода, а также может генерировать диаграммы Эйлера в дополнение к диаграммам Венна. Кроме того, venn поддерживает рисование диаграмм Венна, содержащих до семи наборов. RVenn был разработан как систематический и простой в использовании метод вычисления пересекающихся и перекрывающихся элементов в диаграммах Венна. Невозможно разработать современный инструмент Венна, не используя сильные стороны вышеупомянутых инструментов.
Невозможно разработать современный инструмент Венна, не используя сильные стороны вышеупомянутых инструментов.
Таблица 1. Сравнение функций доступных в настоящее время инструментов построения графиков Венна (пакеты R и веб-инструменты).
Однако у вышеупомянутых программных пакетов есть и свои недостатки. Прежде всего, эти пакеты имеют ограничения в отображении различий между различными регионами на диаграмме Венна, несмотря на возможность отображения исходных наборов. ColorfulVennPlot и venn поддерживают заполнение областей, но пользователям необходимо вручную указывать цвета для каждой области, что делает их слишком сложными для использования обычными пользователями. Кроме того, в большинстве этих пакетов отсутствует полная поддержка грамматики графики, что приводит к невозможности адекватной интеграции в популярную экосистему ggplot2. Кроме того, входные данные некоторых пакетов очень неясны; таким образом, получение квалифицированных входных данных занимает много времени.
Принимая во внимание это, мы разработали ggVennDiagram, интуитивно понятный, простой в использовании и настраиваемый пакет R для создания диаграмм Венна, который поддерживает график Венна с двумя-семью множествами и генерирует цифры публикационного качества с минимальными затратами. Кроме того, мы также разработали всеобъемлющую структуру данных Венна, чтобы упростить расширение диаграмм Венна и облегчить представление новой диаграммы в будущем.
Результаты и обсуждение
Рабочий процесс ggVennDiagram
Основная функция «ggVennDiagram()» принимает ввод списка и выводит объект ggplot . Измеряя длину входного списка, он автоматически применяет внутренние функции для построения графика в два этапа: предварительная обработка данных и визуализация. Второй шаг зависит от функций ggplot2; поэтому мы в основном сосредоточимся на объяснении первого шага следующим образом.
Предварительная обработка данных затем может быть разделена на две процедуры: генерация формы, которая определяет края наборов Венна и областей, и вычисление значения области, которое вычисляет элементы области и выполняет необходимые статистические данные, такие как подсчет и вычисление процентов.
Поскольку возвращаемые данные после предварительной обработки данных совместимы с объектом sf , эти данные напрямую передаются в функции «geom_sf()»/«geom_sf_label()»/«geom_sf_text()», изначально предоставляемые ggplot2. Цвета заливки сопоставляются с количеством элементов региона, а легенда цветной полосы создается автоматически, чтобы показать разницу между различными регионами (рис. 1А).
Рисунок 1. Дизайн ggVennDiagram. (A) Компоненты диаграммы Венна. SetEdge , SetLabel и регион выделены зеленым текстовым полем. (B) Логическая структура ggVennDiagram. Диаграмма Венна, построенная этим пакетом, представляет собой объект ggplot , в котором хранится объект VennPlotData . Объект VennPlotData дополнительно скомпилирован с помощью простых функций, описанных в sf, и объекта Venn / Polygon , представленного в RVenn.
Генерация формы
В ggVennDiagram мы рассматривали все ребра, метки и многоугольники как простые элементы, которые ссылаются на стандарт описания того, как объекты реального мира могут быть представлены в компьютерах, с акцентом на пространственную геометрию эти объекты. Всего в R реализовано 15 типов простых функций, три из которых используются для описания всех компонентов диаграммы Венна.
Всего в R реализовано 15 типов простых функций, три из которых используются для описания всех компонентов диаграммы Венна.
Во-первых, ребра множеств наследуются от LINESTRING , представляющей собой последовательность точек, соединенных прямыми несамопересекающимися линиями. Во-вторых, все возможные пересекающиеся области наследуются от POLYGON , который образован последовательностью замкнутых точек. В-третьих, метки наборов наследуются от POINT , которая является единственной точкой, используемой для привязки короткого текста. Простые функции заключаются в определении координат компонентов графика Венна. Это первый раз, когда простые функции используются в диаграмме Венна. Такой дизайн расширяет возможности описания компонентов диаграммы Венна, позволяя вычислять области пересечения и перекрытия между различными наборами.
Чтобы упростить вычисление простых функций, мы вводим объект класса S4 Polygon , который расширяет объект класса S4 Venn , производный от RVenn. Поскольку эти методы реализованы в RVenn, методы операций над множествами реализованы для объекта Polygon , что приводит к унифицированным функциям операций над множествами для объекта Set Venn и объекта формы Polygon .
Поскольку эти методы реализованы в RVenn, методы операций над множествами реализованы для объекта Polygon , что приводит к унифицированным функциям операций над множествами для объекта Set Venn и объекта формы Polygon .
Форма, используемая в диаграмме Венна с менее чем четырьмя наборами, может быть простой структурой, такой как круг или эллипс, но когда диаграмма Венна имеет более четырех наборов, требуются неправильные многоугольники. Трудно создавать неправильные многоугольники с помощью простых геометрических функций. Поэтому ggVennDiagram разработан так, чтобы иметь встроенный предварительно обработанный набор данных формы, импортированный из venn, VennDiagram и некоторых онлайн-материалов, что, несомненно, повышает эффективность генерации формы на стороне пользователя.
Вычисление значения региона
Вычисление значения региона зависит от пакета RVenn и новых функций, написанных для его определенного объекта Venn . Всего на диаграмме Венна 2 n — 1 областей, где n указывает количество наборов. Элемент и его номер в каждом регионе хранятся с идентификаторами регионов в таблице и соединяются с объектом формы региона с помощью уникальных идентификаторов. Точно так же член и его номер в наборе назначаются SetEdge через уникальные идентификаторы параллельно. При этом для последующего построения графика создается полный объект VennPlotData (рис. 1В).
Элемент и его номер в каждом регионе хранятся с идентификаторами регионов в таблице и соединяются с объектом формы региона с помощью уникальных идентификаторов. Точно так же член и его номер в наборе назначаются SetEdge через уникальные идентификаторы параллельно. При этом для последующего построения графика создается полный объект VennPlotData (рис. 1В).
Поэтапная самонастройка диаграмм Венна
После предварительной обработки данных ggVennDiagram вызывает собственные функции ggplot2 для рисования диаграмм Венна в четырех слоях (рис. 2A, B). Первый слой должен отображать количество членов в каждом регионе, с заливкой градиентным цветом, демонстрирующей различия в количестве членов в разных регионах. Второй слой должен показать установленные края. Когда для рисования диаграммы Венна используется неправильный многоугольник, а не эллипс и окружность, ребра множеств необходимы для различения границ между различными множествами. Третий слой предназначен для отображения меток наборов, а четвертый уровень — для отображения меток регионов. Пользователям доступна функция предварительной обработки данных. Таким образом, для тех, кто знаком с синтаксисом ggplot2, легко изменить детали изображения, включая цвет заливки области, цвет/толщину линии, стиль текста и т. д. (рис. 2C, D).
Пользователям доступна функция предварительной обработки данных. Таким образом, для тех, кто знаком с синтаксисом ggplot2, легко изменить детали изображения, включая цвет заливки области, цвет/толщину линии, стиль текста и т. д. (рис. 2C, D).
Рис. 2. Метод построения графика ggVennDiagram. Способ по умолчанию (A) и возвращаемый график (B) , когда пользователь вызывает «ggVennDiagram()» со списком из четырех наборов генов («gene_list»). (C,D) Пошаговая самостоятельная настройка графика Венна с использованием обычных функций ggplot2.
Новые фигуры в диаграммах Венна
Как было отмечено выше, для построения диаграммы Венна используется набор встроенных форм из ggVennDiagram. По умолчанию при вызове основной функции «ggVennDiagram()» используется только наиболее подходящая форма. Однако другие применимые формы могут быть указаны в пошаговом графике, который был описан в предыдущем разделе (рис. 3А). Кроме того, ggVennDiagram предоставляет ряд функций, помогающих пользователям создавать новые формы, когда им известны координаты формы. Например, диаграмма Венна с шестью множествами может состоять только из шести треугольников (рис. 3В). Для этого нам достаточно передать координаты вершины и задать координаты метки в функции «triangle()» и «label_position()» соответственно, а затем построить VennPlotData с функцией-конструктором «VennPlotData()» (рис. 1B). Сгенерированный объект VennPlotData теперь может соединяться с установленными и рассчитанными значениями региона с помощью функции «plotData_add_venn()», а полученные данные можно использовать для пошаговой настройки диаграммы Венна (рис. 3B).
Например, диаграмма Венна с шестью множествами может состоять только из шести треугольников (рис. 3В). Для этого нам достаточно передать координаты вершины и задать координаты метки в функции «triangle()» и «label_position()» соответственно, а затем построить VennPlotData с функцией-конструктором «VennPlotData()» (рис. 1B). Сгенерированный объект VennPlotData теперь может соединяться с установленными и рассчитанными значениями региона с помощью функции «plotData_add_venn()», а полученные данные можно использовать для пошаговой настройки диаграммы Венна (рис. 3B).
Рисунок 3. Применение новых форм и поддержка диаграммы Венна до семи наборов в ggVennDiagram. (A) Прямоугольник со скругленными углами используется для построения диаграммы Венна с четырьмя множествами. (B) Треугольник используется для построения диаграммы Венна с шестью множествами. (C–E) Диаграммы Венна с пятью, шестью и семью наборами, построенные на основе ggVennDiagram. Воспроизводимые примеры доступны из виньеток, прилагаемых к упаковке.
Воспроизводимые примеры доступны из виньеток, прилагаемых к упаковке.
Диаграмма Венна с более чем четырьмя наборами
Начиная с версии 1.0, ggVennDiagram поддерживает диаграммы Венна с числом наборов до семи (рис. 3C–E). Эта функция зависит от форм, импортированных из другого пакета R (Dusa, 2020). Однако мы настаиваем на том, что диаграммы Венна с более чем четырьмя наборами могут быть не лучшим выбором для отображения их взаимосвязей.
На сегодняшний день существует три основных метода отображения отношений множества: диаграмма Венна, диаграмма Эйлера и график UpSet (Conway et al., 2017). График UpSet — это современный метод визуализации для количественного анализа наборов (Lex et al., 2014), который поддерживает неограниченное количество наборов. Когда количество наборов очень велико, более оправдан выбор графика UpSet.
Интеграция ggVennDiagram в конвейеры анализа биоинформатики
Первая версия ggVennDiagram была выпущена 9 октября.2019 г. (версия 0.3). С тех пор он применяется во многих областях биомедицинских исследований. Например, Кук и др. (2020) использовали ggVennDiagram, чтобы показать перекрывающиеся дифференциально экспрессируемые гены в течение трех периодов выборки (1-й, 3-й и 5-й дни) как в корне, так и в побеге канолы. Кроме того, Харрис и соавт. (2020) использовали ggVennDiagram, чтобы показать, что 22,5% дифференциально экспрессируемых генов были общими для мышей, получавших лечение, и пациентов-людей. Кроме того, Магуайр и соавт. (2020) использовали ggVennDiagram, чтобы подтвердить, что их новый метод имеет низкую систематическую ошибку и более чувствителен, чем три других метода подготовки библиотеки малых РНК. Кроме того, ggVennDiagram также используется для анализа различий между несколькими пространственно разнообразными образцами пероральной метаболомики (Ciurli et al., 2021) и для сравнения однонуклеотидных вариантов между опухолевыми и неопухолевыми тканями (Horny et al., 2021). На данный момент ggVennDiagram цитировался более чем в 20 рецензируемых статьях и препринтах в открытом доступе, полученных Google Scholar.
(версия 0.3). С тех пор он применяется во многих областях биомедицинских исследований. Например, Кук и др. (2020) использовали ggVennDiagram, чтобы показать перекрывающиеся дифференциально экспрессируемые гены в течение трех периодов выборки (1-й, 3-й и 5-й дни) как в корне, так и в побеге канолы. Кроме того, Харрис и соавт. (2020) использовали ggVennDiagram, чтобы показать, что 22,5% дифференциально экспрессируемых генов были общими для мышей, получавших лечение, и пациентов-людей. Кроме того, Магуайр и соавт. (2020) использовали ggVennDiagram, чтобы подтвердить, что их новый метод имеет низкую систематическую ошибку и более чувствителен, чем три других метода подготовки библиотеки малых РНК. Кроме того, ggVennDiagram также используется для анализа различий между несколькими пространственно разнообразными образцами пероральной метаболомики (Ciurli et al., 2021) и для сравнения однонуклеотидных вариантов между опухолевыми и неопухолевыми тканями (Horny et al., 2021). На данный момент ggVennDiagram цитировался более чем в 20 рецензируемых статьях и препринтах в открытом доступе, полученных Google Scholar. Можно предположить, что ggVennDiagram имеет очень широкий спектр сценариев применения в биомедицинских исследованиях.
Можно предположить, что ggVennDiagram имеет очень широкий спектр сценариев применения в биомедицинских исследованиях.
Сравнение функций доступных в настоящее время инструментов построения графика Венна
В таблице 1 представлены функции доступных в настоящее время инструментов построения графика Венна (см. также Рисунок 4 для сравнения графиков, созданных этими инструментами). В первую очередь оценивалась поддержка грамматики графики девятью пакетами R и двумя веб-инструментами. Грамматика графики — это общая схема визуализации данных, которая разбивает графики на семантические компоненты, такие как масштабы и слои. За исключением ggVennDiagram, ни один из этих инструментов полностью не поддерживает эту функцию при построении диаграмм Венна.
Рисунок 4. Графики, сгенерированные инструментами, перечисленными в Таблице 1. Используемые инструменты: ggVennDiagram, VennDiagram, ColorfulVennPlot, venn, nVennR, eulerr, RVenn, gplots, InteractiveVenn и Venny (A–K) соответственно. За исключением venn (D) , venneuler (G) и RVenn (H) , все графики генерируются с минимальной конфигурацией (с использованием параметров по умолчанию) и теми же входными данными, которые представляют собой моделируемый ген из четырех наборов. список. Входные данные для venn — это именованный вектор, а входные данные для venneuler — уточненное выражение. Поскольку RVenn не поддерживает графики Венна с четырьмя наборами, используются только три набора списка генов.2340 (Н) .
За исключением venn (D) , venneuler (G) и RVenn (H) , все графики генерируются с минимальной конфигурацией (с использованием параметров по умолчанию) и теми же входными данными, которые представляют собой моделируемый ген из четырех наборов. список. Входные данные для venn — это именованный вектор, а входные данные для venneuler — уточненное выражение. Поскольку RVenn не поддерживает графики Венна с четырьмя наборами, используются только три набора списка генов.2340 (Н) .
Кроме того, ggVennDiagram лидирует в следующих трех аспектах производительности обработки данных. (1) Мы можем получить доступ к членам региона, запросив объект VennPlotData . (2) Следует отметить, что мы реализуем только ввод списка (как формат ввода). Этот дизайн достаточно прост для понимания и подготовки, и в нем легко хранить элементы набора, что необходимо для расчета элементов региона. (3) С помощью дизайна многослойного объекта ggVennDiagram может сохранять графические данные в VennPlotData (рис. 1B), что позволяет запрашивать и повторно использовать целевые данные.
1B), что позволяет запрашивать и повторно использовать целевые данные.
Кроме того, ggVennDiagram лучше в четырех аспектах визуализации. (1) Заполнение области позволяет пользователю легко определить различия между различными частями диаграммы Венна, и это одна из ключевых особенностей ggVennDiagram. Хотя несколько других инструментов имеют эту функцию, только ggVennDiagram является полностью автоматическим, поскольку он управляется эстетическим отображением ggplot2. (2) ggVennDiagram имеет встроенные формы, состоящие из кругов, эллипсов и т. д. Кроме того, мы также предоставляем функции, помогающие пользователям импортировать самоопределяемые формы (рис. 3A, B). (3) ggVennDiagram поддерживает диаграммы Венна с количеством наборов от двух до семи, что достаточно для повседневного использования. (4) Элемент управления в ggVennDiagram можно применять для установки края/метки и заливки/метки области, чтобы было удобно задавать их цвет/тип/размер линии и т. д. (рис. 1А, 2Б, Г, 3А–Д). ).
).
Примечательно, что несколько инструментов поддерживают как диаграммы Венна, так и диаграммы Эйлера. Однако у диаграммы Эйлера есть два недостатка: во-первых, она пропорциональна площади, но человеческий глаз менее чувствителен к площади, чем к цвету; во-вторых, он показывает только соответствующие отношения, но иногда невозможно показать все области пересечения, просто используя простые геометрические фигуры, такие как круги и эллипсы. Поэтому мы полагаем, что более целесообразно использовать цветовую заливку для отображения различия между разными областями в обычных медико-биологических исследованиях.
В целом, ggVennDiagram интегрирует и оптимизирует метод построения диаграммы Венна, демонстрируя многочисленные преимущества в производительности по сравнению с существующими инструментами. По сравнению с веб-инструментом сценарии R легче интегрировать в существующие конвейеры биоинформатического анализа для реализации автоматизации и пакетного рисования диаграмм Венна. Поэтому необходимо и полезно развивать ggVennDiagram.
Поэтому необходимо и полезно развивать ggVennDiagram.
Заявление о доступности данных
Пакет ggVennDiagram R имеет открытый исходный код и находится в свободном доступе на CRAN (https://cran.r-project.org/package=ggVennDiagram) и GitHub (https://github.com/gaospecial/ggVennDiagram). ). ggVennDiagram в основном требует пакетов R (> 3.5.0), ggplot2 и sf, и его полная функциональность также зависит от пакета plotly.
Вклад автора
C-HG, GY и PC написали эту рукопись. C-HG реализовал этот пакет с помощью GY. ПК руководил проектом. Все авторы внесли свой вклад в статью и одобрили представленную версию.
Финансирование
Эта работа была поддержана Национальным фондом естественных наук Китая (32100090, 41877029 и 41961130383), стипендией Royal Society-Newton Advanced Fellowship (NAFR11
), Национальной программой ключевых исследований Китая (2020YFC1806803), Wuhan Applied Foundational Пограничный проект (2019)020701011469) и Фонды фундаментальных исследований для центральных университетов (2662021JC012).

Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Примечания издателя
Все претензии, изложенные в этой статье, принадлежат исключительно авторам и не обязательно представляют претензии их дочерних организаций, издателя, редакторов и рецензентов. Любой продукт, который может быть оценен в этой статье, или претензии, которые могут быть сделаны его производителем, не гарантируются и не поддерживаются издателем.
Благодарности
Мы благодарим Адриана Душу за то, что он позволил нам повторно использовать данные «venn:::sets» в его пакете venn, и это очень важно для включения диаграмм Венна из пяти-семи наборов в ggVennDiagram. Мы также благодарим пользователя GitHub Yi Liu (@liuyigh) за его вклад в курирование кода. Выражаем огромную благодарность лингвисту Пинг Лю из Сельскохозяйственного университета Хуажонг, Ухань, Китай, за ее работу по редактированию и полировке английского языка.
Ссылки
Акьол, Т. Ю. (2019). RVenn: набор операций для многих наборов. Доступно в Интернете по адресу: https://CRAN.R-project.org/package=RVenn (по состоянию на 1 мая 2021 г.).
Google Scholar
Чен Х. и Бутрос П. К. (2011). VennDiagram: пакет для создания диаграмм Венна и Эйлера с широкими возможностями настройки в R. BMC Bioinform. 12:35. doi: 10.1186/1471-2105-12-35
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Чурли А., Либл М., Деркс Рико. JE, Neefjes, JJC, and Giera, M. (2021). Выборка с пространственным разрешением для нецелевой метаболомики: новый инструмент для анализа слюны. iScience 24:102768. doi: 10.1016/j.isci.2021.102768
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Конвей, Дж. Р., Лекс, А., и Геленборг, Н. (2017). UpSetR: пакет R для визуализации пересекающихся множеств и их свойств. Биоинформатика 33, 2938–2940. doi: 10.1093/bioinformatics/btx364
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Кук Дж. , Дуглас Г. М., Чжан Дж., Глик Б. Р., Лангилле М. Г. И., Лю К.-Х. и др. (2020). Транскриптомное профилирование ответов Brassica napus на синегнойная палочка . Врожденный иммунитет. 27, 143–157. doi: 10.1177/1753425
, Дуглас Г. М., Чжан Дж., Глик Б. Р., Лангилле М. Г. И., Лю К.-Х. и др. (2020). Транскриптомное профилирование ответов Brassica napus на синегнойная палочка . Врожденный иммунитет. 27, 143–157. doi: 10.1177/1753425
0512 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Дуса, А. (2020). Венн: рисовать диаграммы Венна. Доступно в Интернете по адресу: https://CRAN.R-project.org/package=venn (по состоянию на 1 мая 2021 г.).
Google Scholar
Гао, К.-Х. (2021). ggVennDiagram: реализация ggplot2 диаграммы Венна. Доступно в Интернете по адресу: https://github.com/gaospecial/ggVennDiagram (по состоянию на 1 мая 2021 г.).
Google Scholar
Харрис С.Э., Пулман Т.М., Арванити А., Кокс Р.Д., Гатеркол Л.Л. и Томлинсон Дж.В. (2020). Американская диета с синдромом ожирения, вызванным образом жизни, у самцов и самок грызунов повторяет клинические и транскриптомные особенности неалкогольной жировой болезни печени и неалкогольного стеатогепатита. утра. Дж. Физиол. Гастроинтест. Физиол печени. 319, G345–G360. doi: 10.1152/ajpgi.00055.2020
утра. Дж. Физиол. Гастроинтест. Физиол печени. 319, G345–G360. doi: 10.1152/ajpgi.00055.2020
PubMed Abstract | Полный текст перекрестной ссылки | Академия Google
Heberle, H., Meirelles, G.V., da Silva, F.R., Telles, G.P., and Minghim, R. (2015). InteractiVenn: веб-инструмент для анализа наборов с помощью диаграмм Венна. БМК Биоинформ. 16:169. doi: 10.1186/s12859-015-0611-3
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Хорни К., Герхардт П., Хебель-Черуни А., Вюльбек К., Ютикал Дж. и Беккер Дж. К. (2021). Мутационный ландшафт клеточных линий карциномы Меркеля, ассоциированных с вирусом и УФ-излучением, сравним с опухолевой тканью. Раков 13:649. doi: 10.3390/cancers13040649
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Ларссон, Дж. (2020). eulerr: пропорциональные площади диаграммы Эйлера и Венна с эллипсами. Доступно в Интернете по адресу: https://CRAN.R-project. org/package=eulerr (по состоянию на 1 мая 2021 г.).
org/package=eulerr (по состоянию на 1 мая 2021 г.).
Google Scholar
Лекс А., Геленборг Н., Стробельт Х., Вюйлемо Р. и Пфистер Х. (2014). UpSet: визуализация пересекающихся наборов. IEEE Trans. Вис. вычисл. График 20, 1983–1992 гг. doi: 10.1109/TVCG.2014.2346248
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Магуайр С., Ломан Г. Дж. С. и Гуан С. (2020). Метод подготовки библиотеки малых РНК с низким смещением и чувствительностью с использованием рандомизированного лигирования шин. Рез. нуклеиновых кислот. 48:e80. doi: 10.1093/nar/gkaa480
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Нома, Э., и Манве, А. (2013). красочныйVennPlot: рисуйте и добавляйте пользовательские раскраски к диаграммам Венна для 2-мерных, 3-мерных и 4-мерных данных. Доступно в Интернете по адресу: https://CRAN.R-project.org/package=colorfulVennPlot (по состоянию на 1 мая 2021 г.).
Google Scholar
Oliveros, JC (2007).

 Компьютеры помечены буквами A-F для удобства.
Компьютеры помечены буквами A-F для удобства. В качестве альтернативы наш следующий подход сделает шаг назад и взглянет на «общую картину» — он сначала выберет самые короткие ребра, а затем заполнит пробелы.
В качестве альтернативы наш следующий подход сделает шаг назад и взглянет на «общую картину» — он сначала выберет самые короткие ребра, а затем заполнит пробелы.
 . Глядя в ряду для Портленда, наименьшее расстояние составляет 47, до Салема. Следуя этой идее, наша схема будет такой:
. Глядя в ряду для Портленда, наименьшее расстояние составляет 47, до Салема. Следуя этой идее, наша схема будет такой: Следующее самое короткое ребро находится от Корваллиса до Ньюпорта на расстоянии 52 миль, но добавление этого ребра даст Корваллису степень 3.
Следующее самое короткое ребро находится от Корваллиса до Ньюпорта на расстоянии 52 миль, но добавление этого ребра даст Корваллису степень 3. Общая длина пути: 1241 миль.
Общая длина пути: 1241 миль.


 Мы останавливаемся, когда граф связен.
Мы останавливаемся, когда граф связен.
 Когда количество наборов меньше пяти, диаграммы Венна, вероятно, являются наиболее интуитивно понятной формой визуализации данных, превосходящей тепловые карты и таблицы.
Когда количество наборов меньше пяти, диаграммы Венна, вероятно, являются наиболее интуитивно понятной формой визуализации данных, превосходящей тепловые карты и таблицы. Невозможно разработать современный инструмент Венна, не используя сильные стороны вышеупомянутых инструментов.
Невозможно разработать современный инструмент Венна, не используя сильные стороны вышеупомянутых инструментов.

 Всего в R реализовано 15 типов простых функций, три из которых используются для описания всех компонентов диаграммы Венна.
Всего в R реализовано 15 типов простых функций, три из которых используются для описания всех компонентов диаграммы Венна. Поскольку эти методы реализованы в RVenn, методы операций над множествами реализованы для объекта Polygon , что приводит к унифицированным функциям операций над множествами для объекта Set Venn и объекта формы Polygon .
Поскольку эти методы реализованы в RVenn, методы операций над множествами реализованы для объекта Polygon , что приводит к унифицированным функциям операций над множествами для объекта Set Venn и объекта формы Polygon . Элемент и его номер в каждом регионе хранятся с идентификаторами регионов в таблице и соединяются с объектом формы региона с помощью уникальных идентификаторов. Точно так же член и его номер в наборе назначаются SetEdge через уникальные идентификаторы параллельно. При этом для последующего построения графика создается полный объект VennPlotData (рис. 1В).
Элемент и его номер в каждом регионе хранятся с идентификаторами регионов в таблице и соединяются с объектом формы региона с помощью уникальных идентификаторов. Точно так же член и его номер в наборе назначаются SetEdge через уникальные идентификаторы параллельно. При этом для последующего построения графика создается полный объект VennPlotData (рис. 1В). Пользователям доступна функция предварительной обработки данных. Таким образом, для тех, кто знаком с синтаксисом ggplot2, легко изменить детали изображения, включая цвет заливки области, цвет/толщину линии, стиль текста и т. д. (рис. 2C, D).
Пользователям доступна функция предварительной обработки данных. Таким образом, для тех, кто знаком с синтаксисом ggplot2, легко изменить детали изображения, включая цвет заливки области, цвет/толщину линии, стиль текста и т. д. (рис. 2C, D). Например, диаграмма Венна с шестью множествами может состоять только из шести треугольников (рис. 3В). Для этого нам достаточно передать координаты вершины и задать координаты метки в функции «triangle()» и «label_position()» соответственно, а затем построить VennPlotData с функцией-конструктором «VennPlotData()» (рис. 1B). Сгенерированный объект VennPlotData теперь может соединяться с установленными и рассчитанными значениями региона с помощью функции «plotData_add_venn()», а полученные данные можно использовать для пошаговой настройки диаграммы Венна (рис. 3B).
Например, диаграмма Венна с шестью множествами может состоять только из шести треугольников (рис. 3В). Для этого нам достаточно передать координаты вершины и задать координаты метки в функции «triangle()» и «label_position()» соответственно, а затем построить VennPlotData с функцией-конструктором «VennPlotData()» (рис. 1B). Сгенерированный объект VennPlotData теперь может соединяться с установленными и рассчитанными значениями региона с помощью функции «plotData_add_venn()», а полученные данные можно использовать для пошаговой настройки диаграммы Венна (рис. 3B). Воспроизводимые примеры доступны из виньеток, прилагаемых к упаковке.
Воспроизводимые примеры доступны из виньеток, прилагаемых к упаковке. (версия 0.3). С тех пор он применяется во многих областях биомедицинских исследований. Например, Кук и др. (2020) использовали ggVennDiagram, чтобы показать перекрывающиеся дифференциально экспрессируемые гены в течение трех периодов выборки (1-й, 3-й и 5-й дни) как в корне, так и в побеге канолы. Кроме того, Харрис и соавт. (2020) использовали ggVennDiagram, чтобы показать, что 22,5% дифференциально экспрессируемых генов были общими для мышей, получавших лечение, и пациентов-людей. Кроме того, Магуайр и соавт. (2020) использовали ggVennDiagram, чтобы подтвердить, что их новый метод имеет низкую систематическую ошибку и более чувствителен, чем три других метода подготовки библиотеки малых РНК. Кроме того, ggVennDiagram также используется для анализа различий между несколькими пространственно разнообразными образцами пероральной метаболомики (Ciurli et al., 2021) и для сравнения однонуклеотидных вариантов между опухолевыми и неопухолевыми тканями (Horny et al., 2021). На данный момент ggVennDiagram цитировался более чем в 20 рецензируемых статьях и препринтах в открытом доступе, полученных Google Scholar.
(версия 0.3). С тех пор он применяется во многих областях биомедицинских исследований. Например, Кук и др. (2020) использовали ggVennDiagram, чтобы показать перекрывающиеся дифференциально экспрессируемые гены в течение трех периодов выборки (1-й, 3-й и 5-й дни) как в корне, так и в побеге канолы. Кроме того, Харрис и соавт. (2020) использовали ggVennDiagram, чтобы показать, что 22,5% дифференциально экспрессируемых генов были общими для мышей, получавших лечение, и пациентов-людей. Кроме того, Магуайр и соавт. (2020) использовали ggVennDiagram, чтобы подтвердить, что их новый метод имеет низкую систематическую ошибку и более чувствителен, чем три других метода подготовки библиотеки малых РНК. Кроме того, ggVennDiagram также используется для анализа различий между несколькими пространственно разнообразными образцами пероральной метаболомики (Ciurli et al., 2021) и для сравнения однонуклеотидных вариантов между опухолевыми и неопухолевыми тканями (Horny et al., 2021). На данный момент ggVennDiagram цитировался более чем в 20 рецензируемых статьях и препринтах в открытом доступе, полученных Google Scholar. Можно предположить, что ggVennDiagram имеет очень широкий спектр сценариев применения в биомедицинских исследованиях.
Можно предположить, что ggVennDiagram имеет очень широкий спектр сценариев применения в биомедицинских исследованиях. За исключением venn (D) , venneuler (G) и RVenn (H) , все графики генерируются с минимальной конфигурацией (с использованием параметров по умолчанию) и теми же входными данными, которые представляют собой моделируемый ген из четырех наборов. список. Входные данные для venn — это именованный вектор, а входные данные для venneuler — уточненное выражение. Поскольку RVenn не поддерживает графики Венна с четырьмя наборами, используются только три набора списка генов.2340 (Н) .
За исключением venn (D) , venneuler (G) и RVenn (H) , все графики генерируются с минимальной конфигурацией (с использованием параметров по умолчанию) и теми же входными данными, которые представляют собой моделируемый ген из четырех наборов. список. Входные данные для venn — это именованный вектор, а входные данные для venneuler — уточненное выражение. Поскольку RVenn не поддерживает графики Венна с четырьмя наборами, используются только три набора списка генов.2340 (Н) . 1B), что позволяет запрашивать и повторно использовать целевые данные.
1B), что позволяет запрашивать и повторно использовать целевые данные. ).
). Поэтому необходимо и полезно развивать ggVennDiagram.
Поэтому необходимо и полезно развивать ggVennDiagram.
 , Дуглас Г. М., Чжан Дж., Глик Б. Р., Лангилле М. Г. И., Лю К.-Х. и др. (2020). Транскриптомное профилирование ответов Brassica napus на синегнойная палочка . Врожденный иммунитет. 27, 143–157. doi: 10.1177/1753425
, Дуглас Г. М., Чжан Дж., Глик Б. Р., Лангилле М. Г. И., Лю К.-Х. и др. (2020). Транскриптомное профилирование ответов Brassica napus на синегнойная палочка . Врожденный иммунитет. 27, 143–157. doi: 10.1177/1753425PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Дуса, А. (2020). Венн: рисовать диаграммы Венна. Доступно в Интернете по адресу: https://CRAN.R-project.org/package=venn (по состоянию на 1 мая 2021 г.).
Google Scholar
Гао, К.-Х. (2021). ggVennDiagram: реализация ggplot2 диаграммы Венна. Доступно в Интернете по адресу: https://github.com/gaospecial/ggVennDiagram (по состоянию на 1 мая 2021 г.).
Google Scholar
Харрис С.Э., Пулман Т.М., Арванити А., Кокс Р.Д., Гатеркол Л.Л. и Томлинсон Дж.В. (2020). Американская диета с синдромом ожирения, вызванным образом жизни, у самцов и самок грызунов повторяет клинические и транскриптомные особенности неалкогольной жировой болезни печени и неалкогольного стеатогепатита. утра. Дж. Физиол. Гастроинтест. Физиол печени. 319, G345–G360. doi: 10.1152/ajpgi.00055.2020
утра. Дж. Физиол. Гастроинтест. Физиол печени. 319, G345–G360. doi: 10.1152/ajpgi.00055.2020
PubMed Abstract | Полный текст перекрестной ссылки | Академия Google
Heberle, H., Meirelles, G.V., da Silva, F.R., Telles, G.P., and Minghim, R. (2015). InteractiVenn: веб-инструмент для анализа наборов с помощью диаграмм Венна. БМК Биоинформ. 16:169. doi: 10.1186/s12859-015-0611-3
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Хорни К., Герхардт П., Хебель-Черуни А., Вюльбек К., Ютикал Дж. и Беккер Дж. К. (2021). Мутационный ландшафт клеточных линий карциномы Меркеля, ассоциированных с вирусом и УФ-излучением, сравним с опухолевой тканью. Раков 13:649. doi: 10.3390/cancers13040649
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Ларссон, Дж. (2020). eulerr: пропорциональные площади диаграммы Эйлера и Венна с эллипсами. Доступно в Интернете по адресу: https://CRAN.R-project. org/package=eulerr (по состоянию на 1 мая 2021 г.).
org/package=eulerr (по состоянию на 1 мая 2021 г.).
Google Scholar
Лекс А., Геленборг Н., Стробельт Х., Вюйлемо Р. и Пфистер Х. (2014). UpSet: визуализация пересекающихся наборов. IEEE Trans. Вис. вычисл. График 20, 1983–1992 гг. doi: 10.1109/TVCG.2014.2346248
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Магуайр С., Ломан Г. Дж. С. и Гуан С. (2020). Метод подготовки библиотеки малых РНК с низким смещением и чувствительностью с использованием рандомизированного лигирования шин. Рез. нуклеиновых кислот. 48:e80. doi: 10.1093/nar/gkaa480
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Нома, Э., и Манве, А. (2013). красочныйVennPlot: рисуйте и добавляйте пользовательские раскраски к диаграммам Венна для 2-мерных, 3-мерных и 4-мерных данных. Доступно в Интернете по адресу: https://CRAN.R-project.org/package=colorfulVennPlot (по состоянию на 1 мая 2021 г.).
Google Scholar
Oliveros, JC (2007).

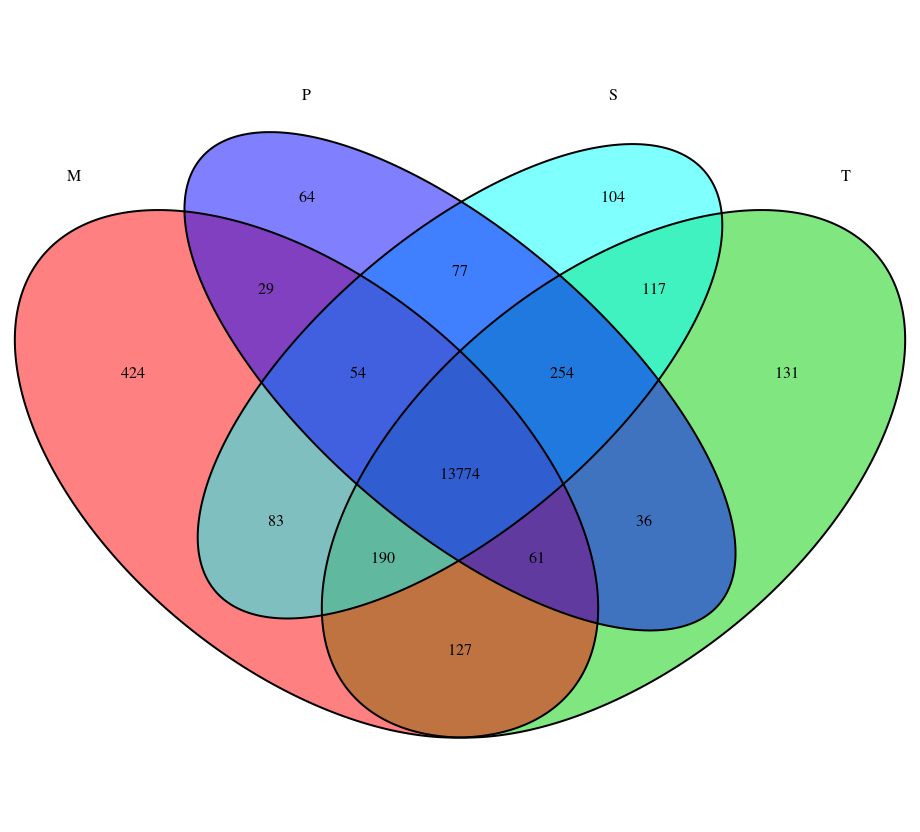 Вычерчивается траектория движения бильярдного шара, который отталкивается от бортов стола в форме параллелограмма.
Вычерчивается траектория движения бильярдного шара, который отталкивается от бортов стола в форме параллелограмма.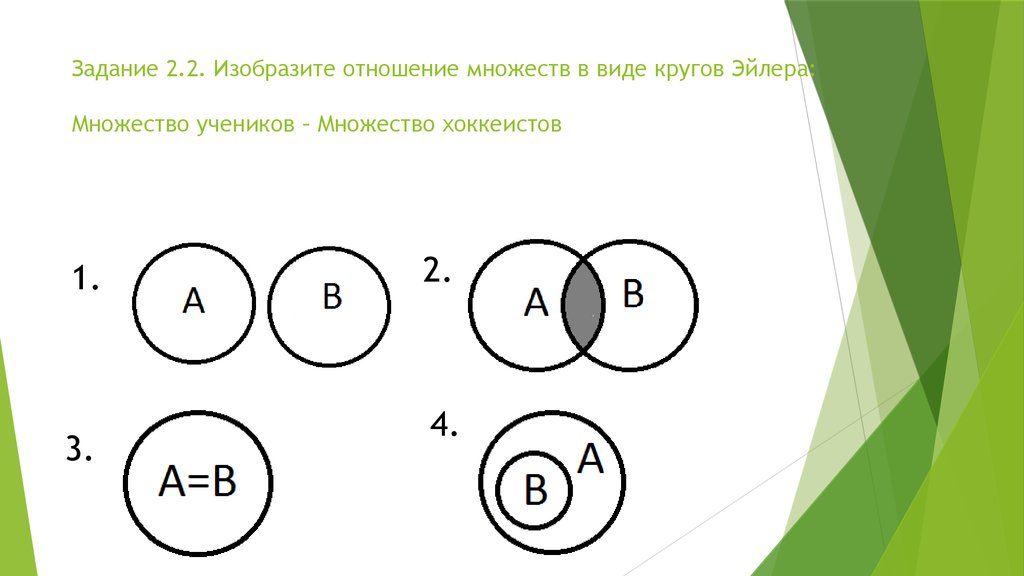 spb.ru
spb.ru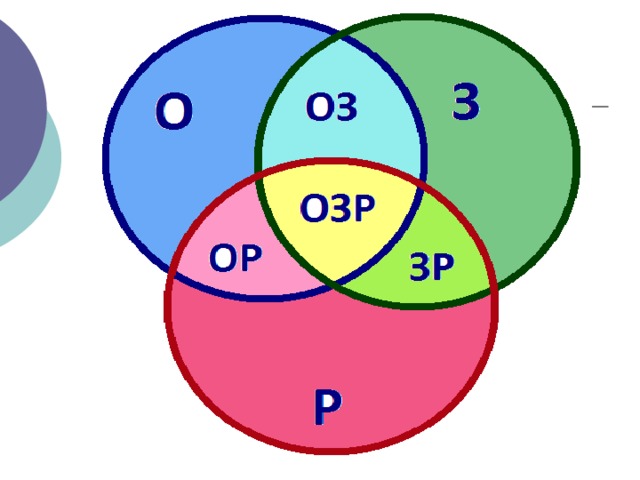 Актуальные
материалы размещены на другой странице.
Актуальные
материалы размещены на другой странице.
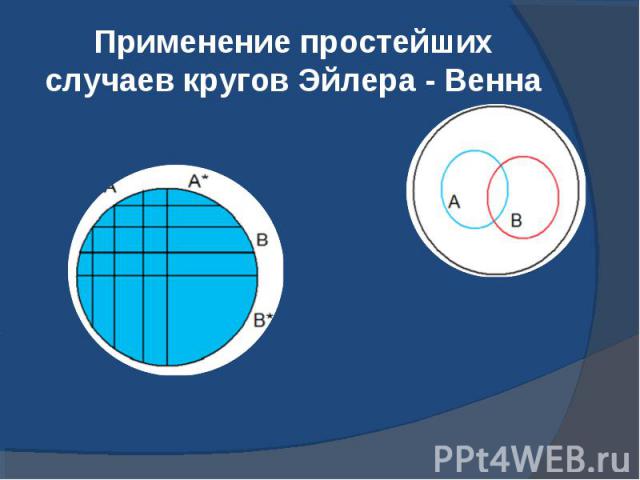 09.2020
09.2020
 11.2018
11.2018
 Кабанов)
03.08.2020
Кабанов)
03.08.2020
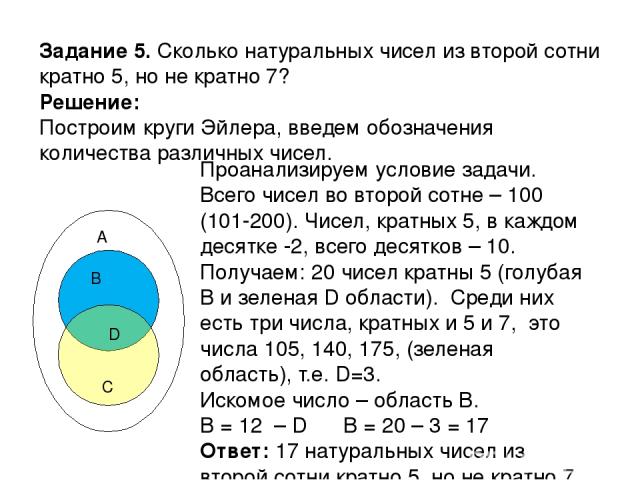 Кабанов)
21.07.2019
Кабанов)
21.07.2019
 Коротков)
25.12.2018
Коротков)
25.12.2018
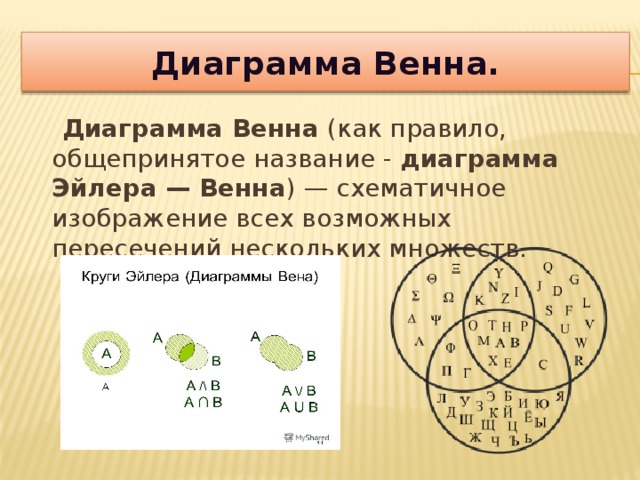 08.2019
08.2019
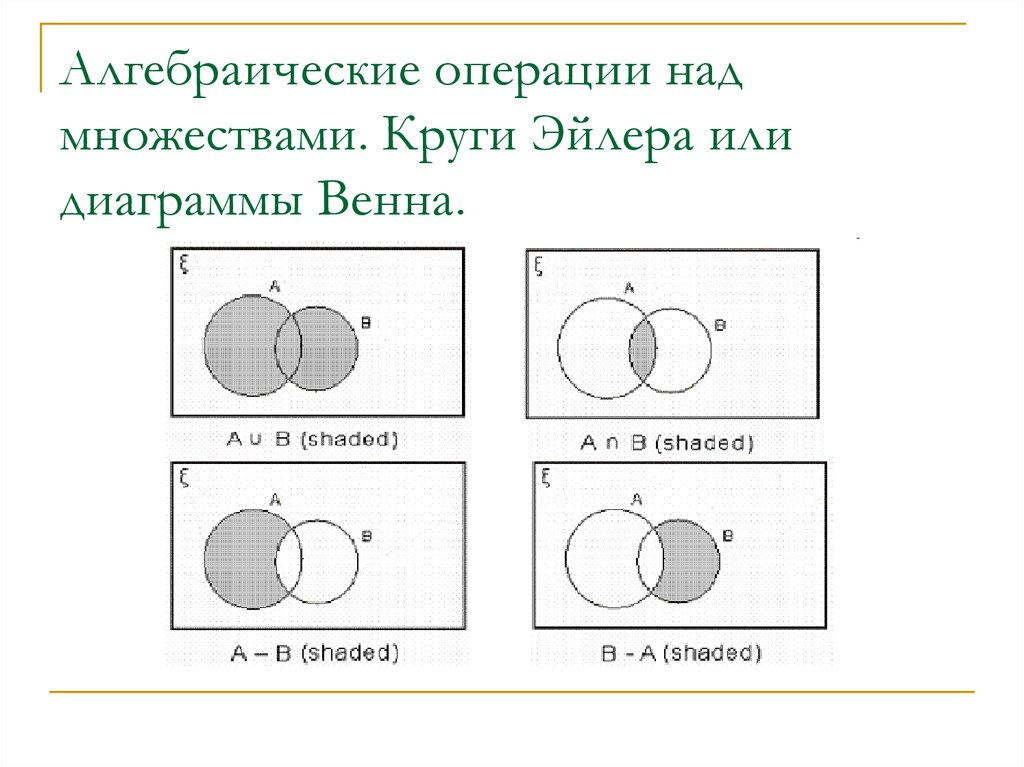 08.2019
08.2019
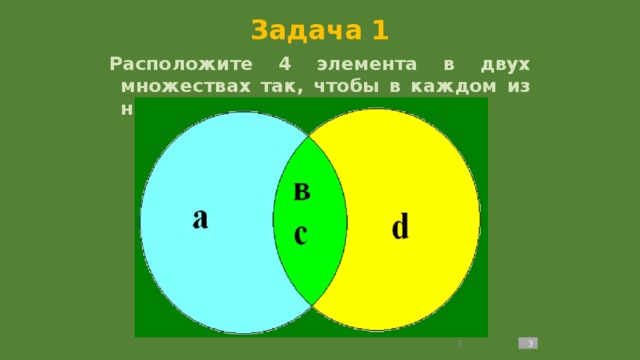 2018
2018
 09.2016
09.2016
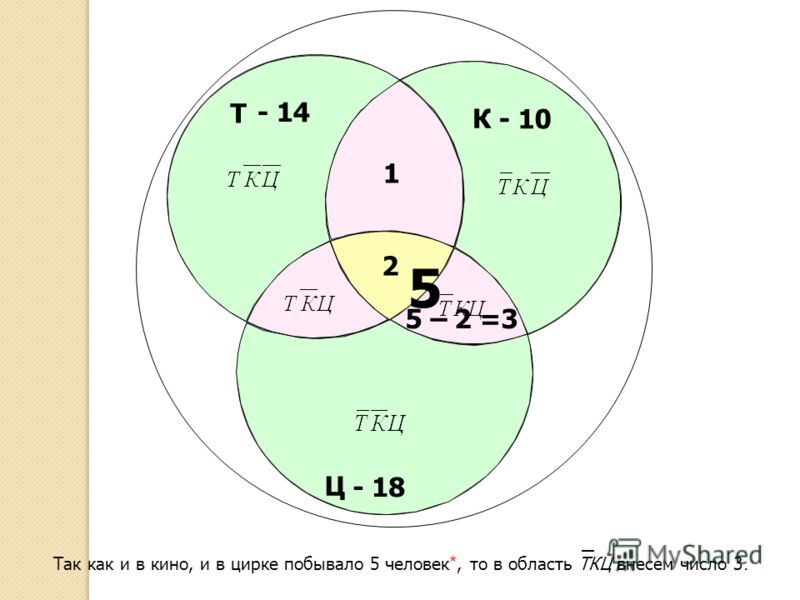 09.2014
09.2014
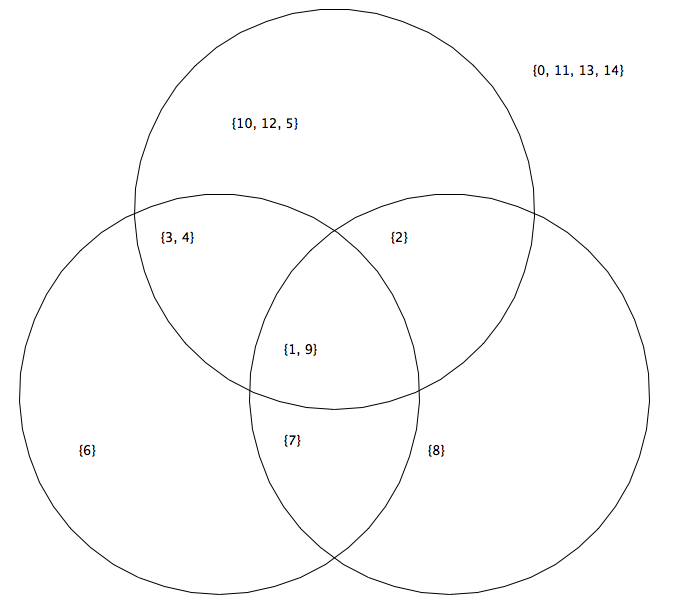
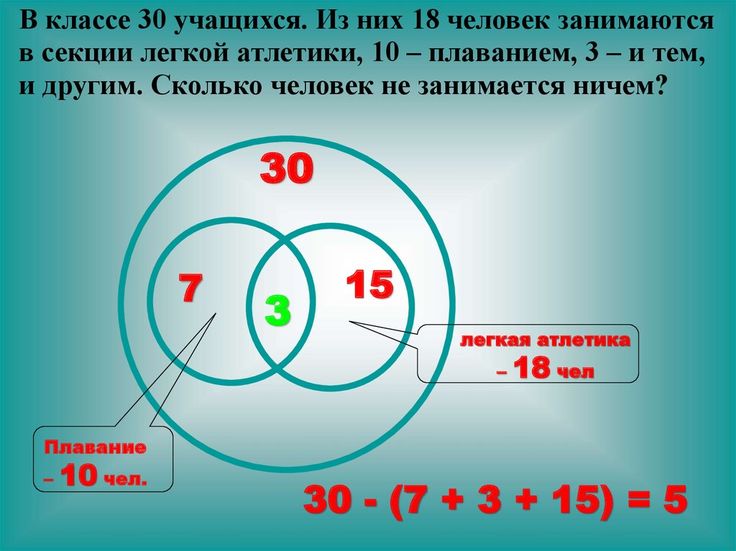 Поляков
Поляков
 10.2016
16947
10.2016
16947
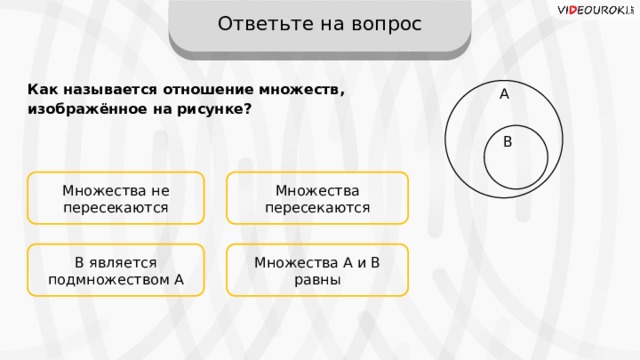 10.2019
14551
10.2019
14551
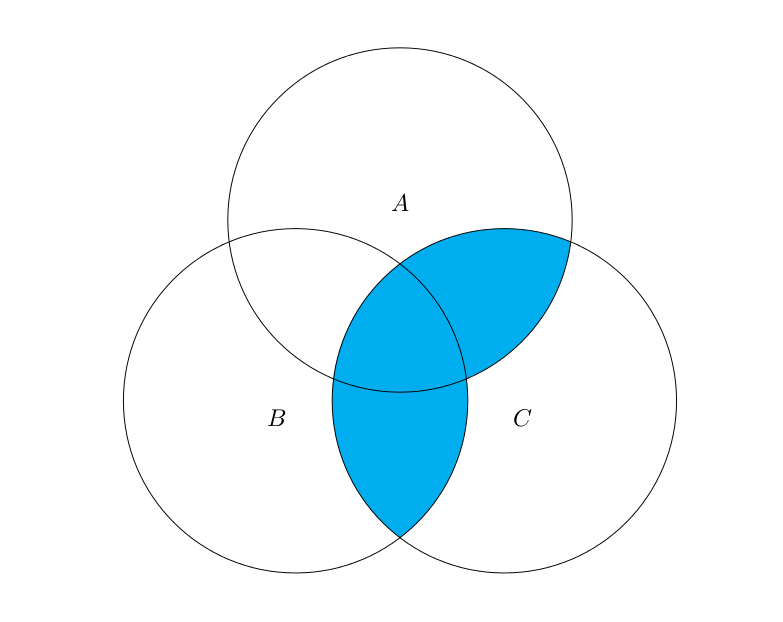 11.2016
28304
11.2016
28304
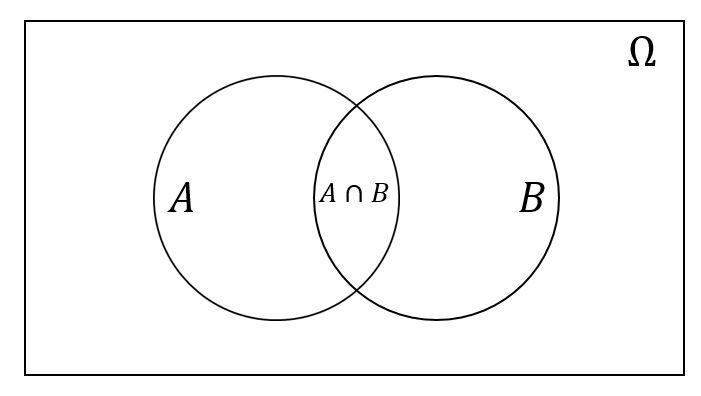 7 класс. Информатика.
7 класс. Информатика.
 Л. Информатика 7 класс
Л. Информатика 7 класс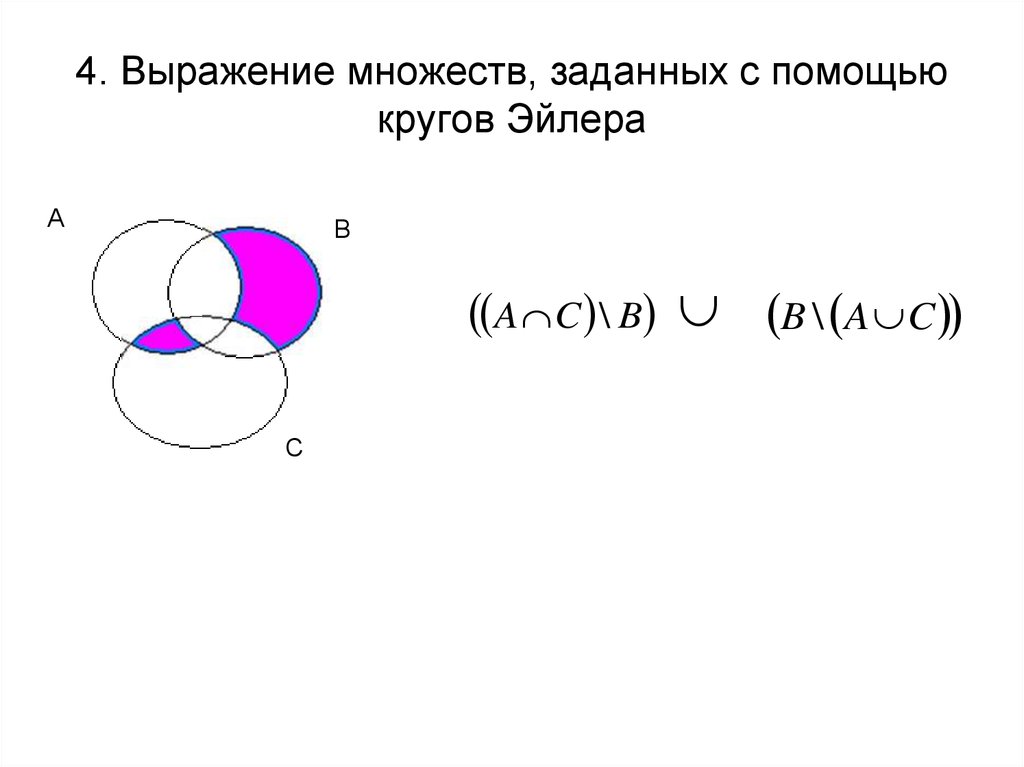
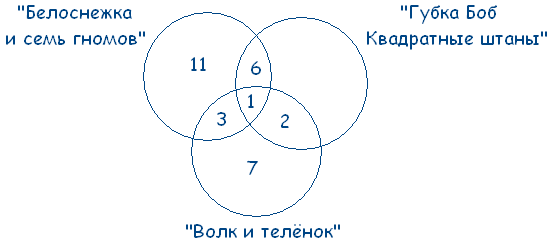 11.2017
2163
0
11.2017
2163
0
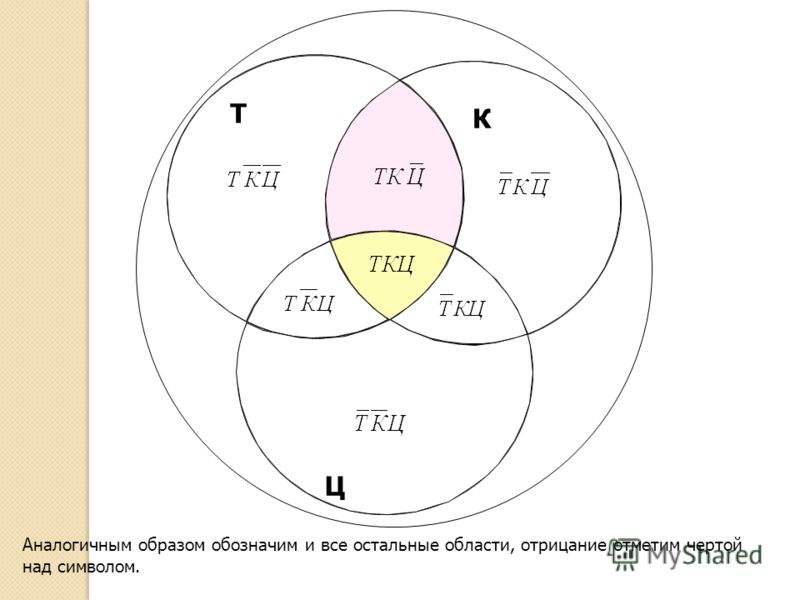
 04.2017
2455
0
04.2017
2455
0
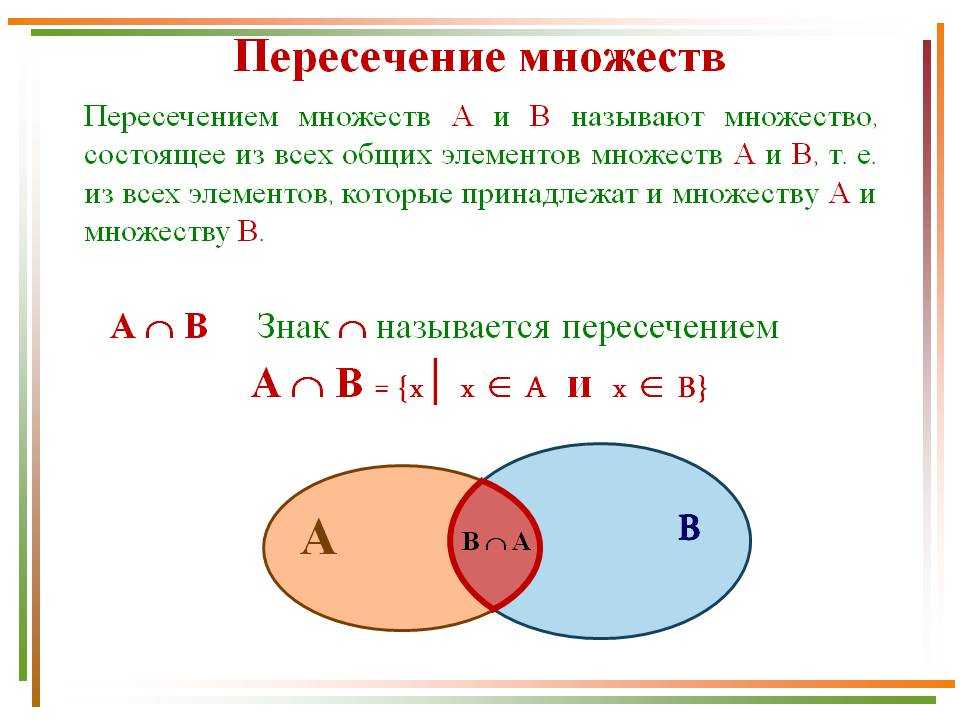 Кодирование. Программое обеспечение
Кодирование. Программое обеспечение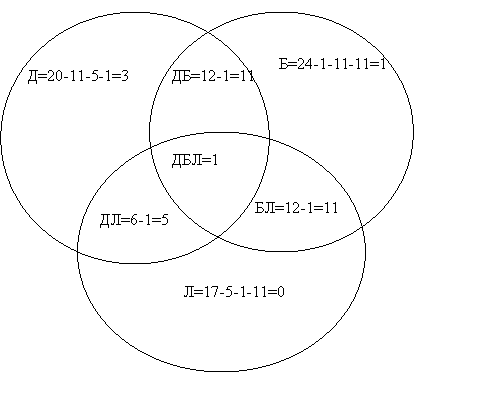 10.2020
4474
10.2020
4474
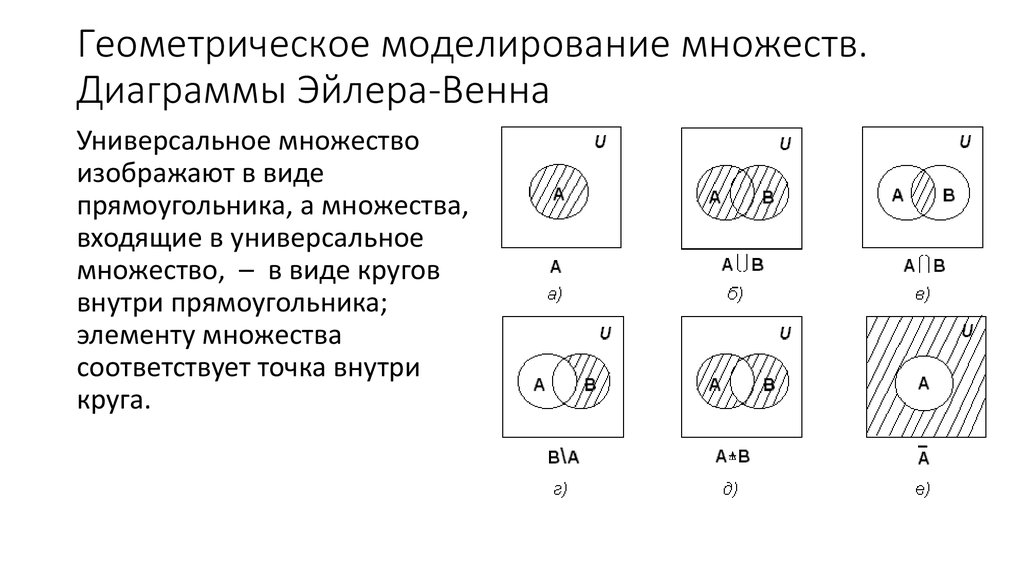 02.2018
5798
02.2018
5798
 Ветвление. Блок-схемы
Ветвление. Блок-схемы
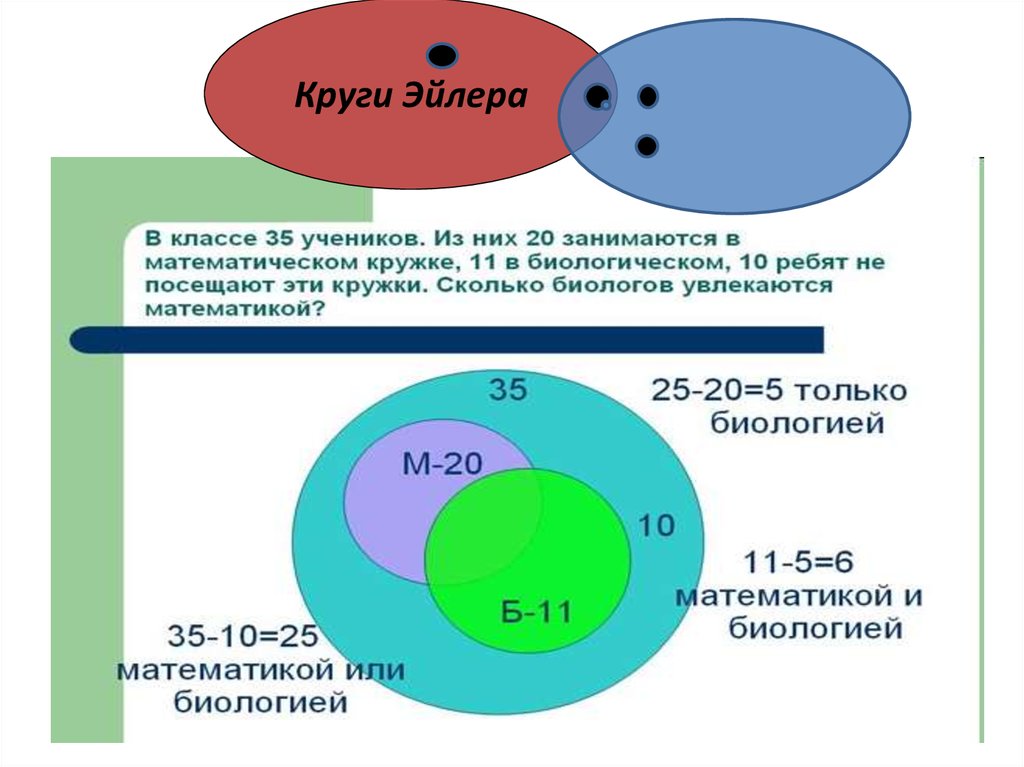 Л.)
Л.)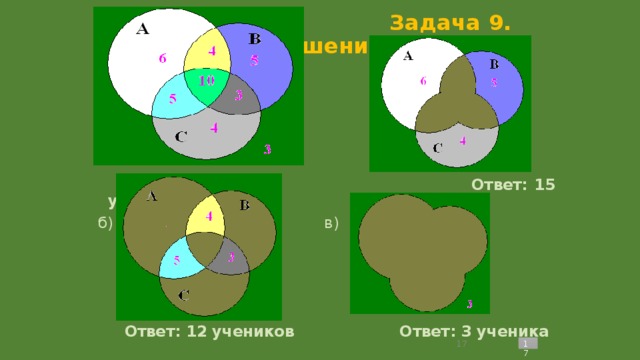 Тема: Обработка графической информации. 7 класс. УМК Босова Л.Л.
Тема: Обработка графической информации. 7 класс. УМК Босова Л.Л. 05.2015
5478
05.2015
5478
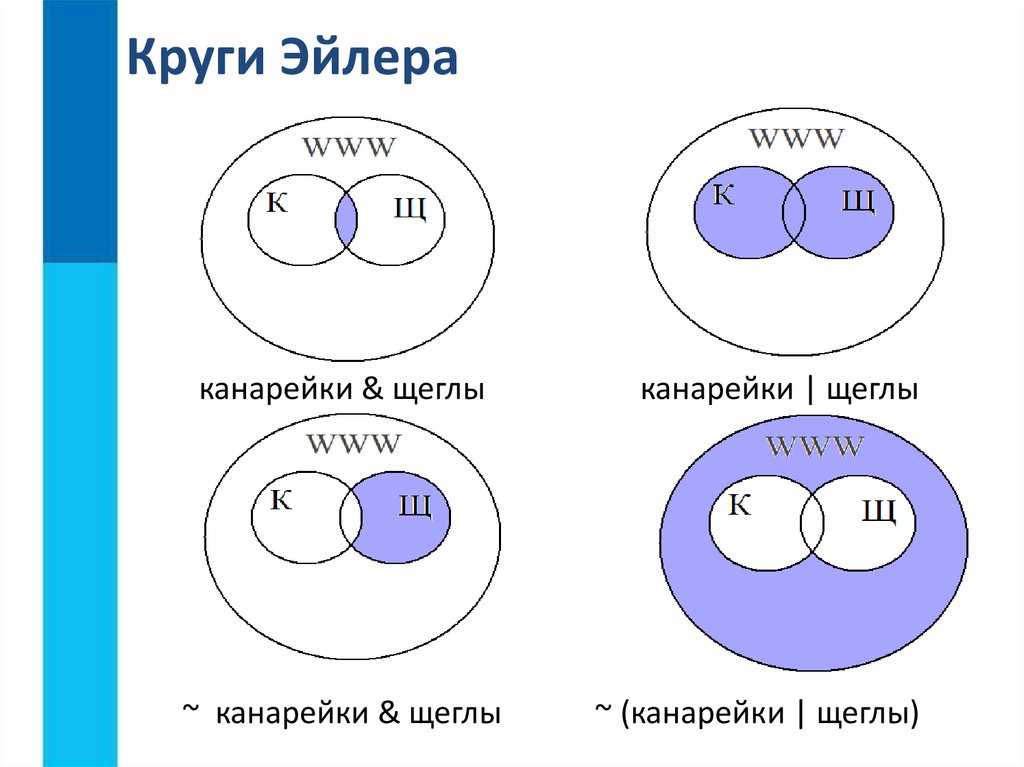 Л.)
Л.)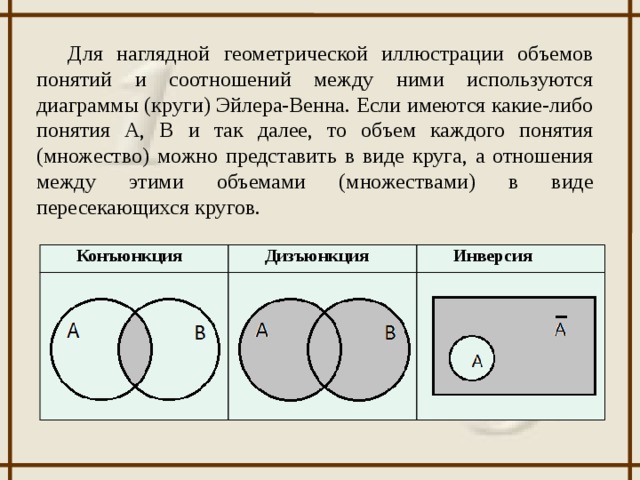 Информатика. 7 класс.
Информатика. 7 класс.
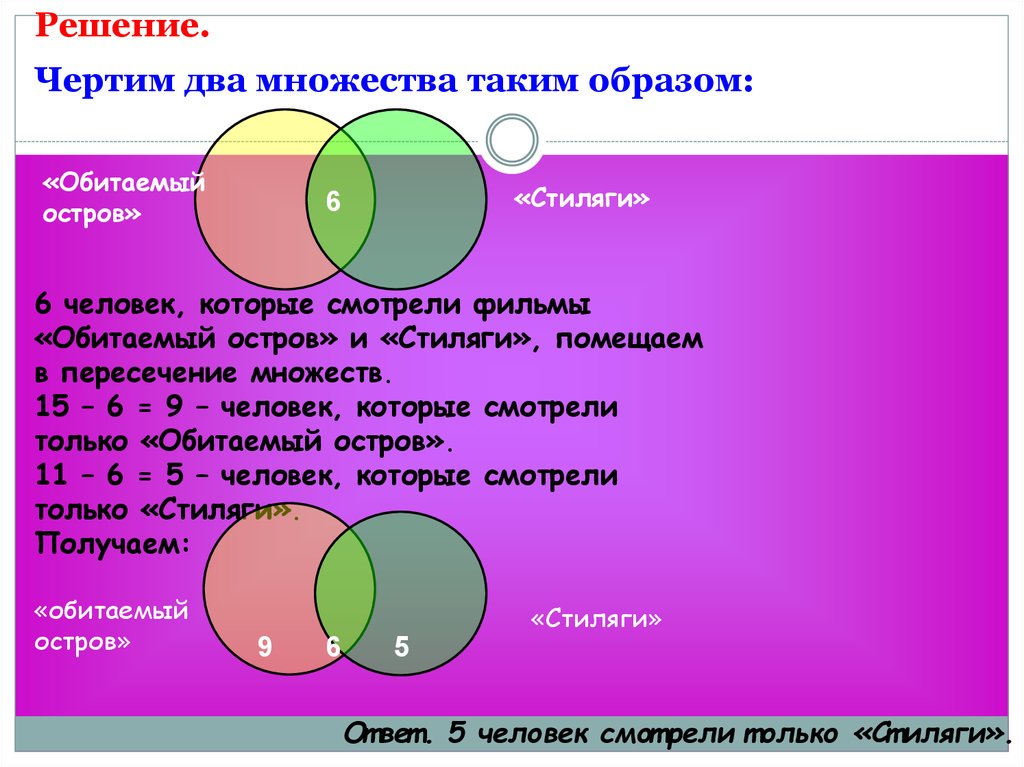 На выполнение теста отводится фиксированное время (30 минут).
На выполнение теста отводится фиксированное время (30 минут). В помощь-интеллект карта из учебника информатики К.Ю. Полякова и Е.А. Еремина для 7 класса
В помощь-интеллект карта из учебника информатики К.Ю. Полякова и Е.А. Еремина для 7 класса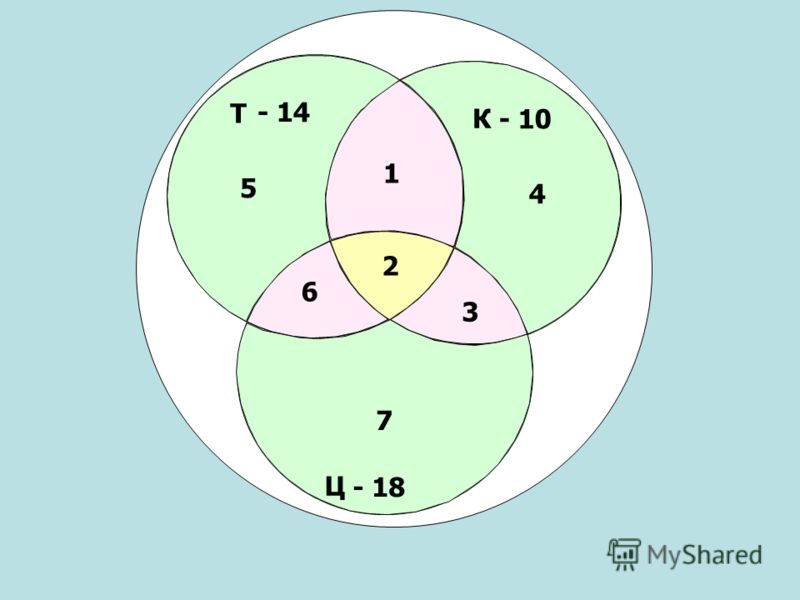 Системы объектов.
Системы объектов.
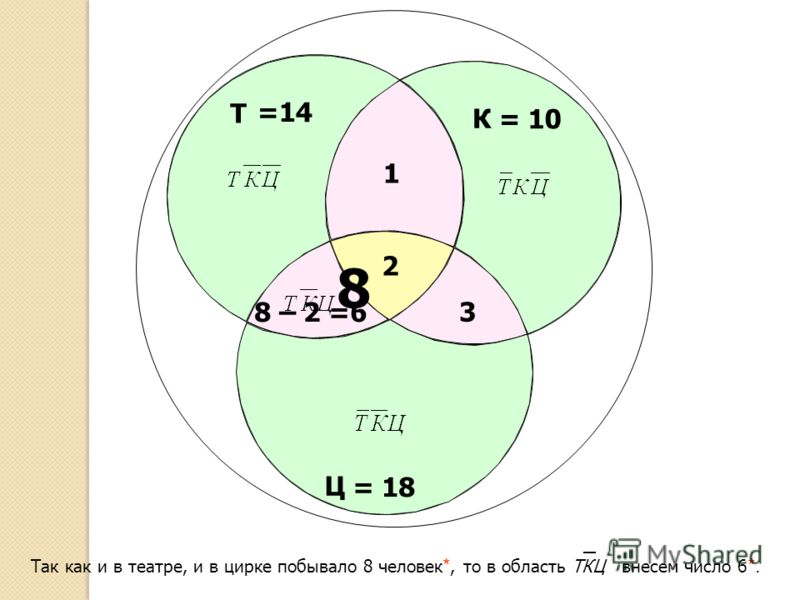 Планируется использование теста в конце урока по теме «Правила записи арифметических выражений на языке Паскаль».
Планируется использование теста в конце урока по теме «Правила записи арифметических выражений на языке Паскаль».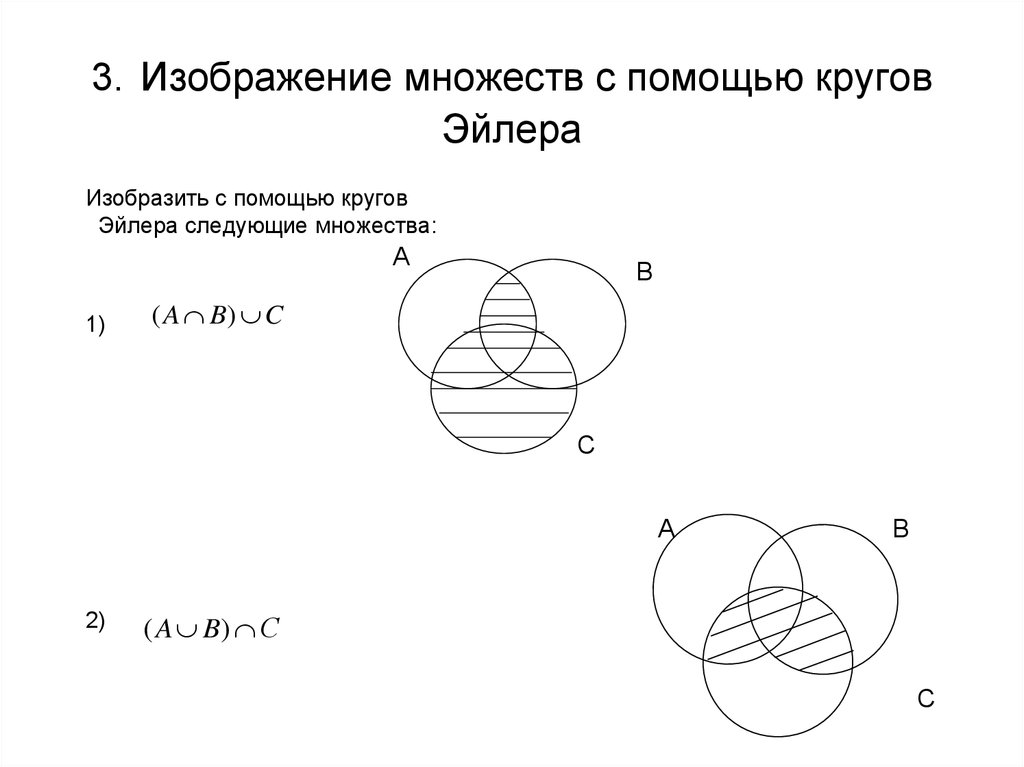 7 класс. II вариант
7 класс. II вариант
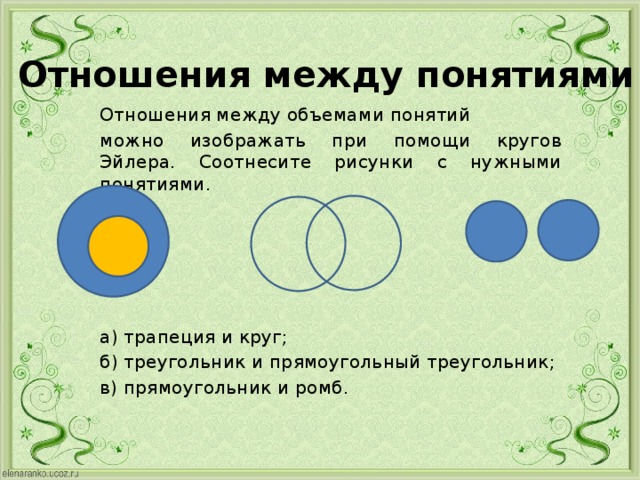 использованы материалы «Рабочей тетради» автора Л. Овчинниковой
использованы материалы «Рабочей тетради» автора Л. Овчинниковой 11.2016
4695
11.2016
4695
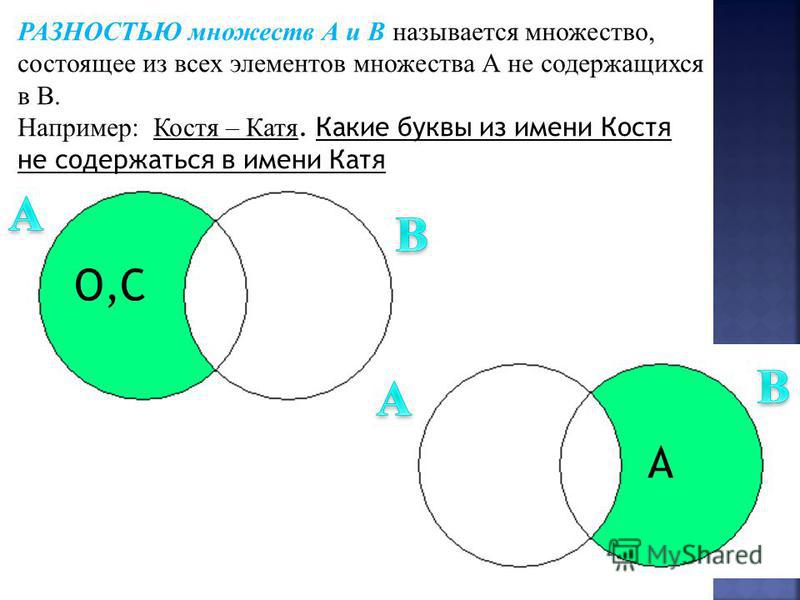 3. Воспитательная – воспитывать культуру работы в парах; воспитывать информационную культуру.
Тип урока: изучение нового материала.
(Автор УМК И.Г.Семакин и др.)
3. Воспитательная – воспитывать культуру работы в парах; воспитывать информационную культуру.
Тип урока: изучение нового материала.
(Автор УМК И.Г.Семакин и др.)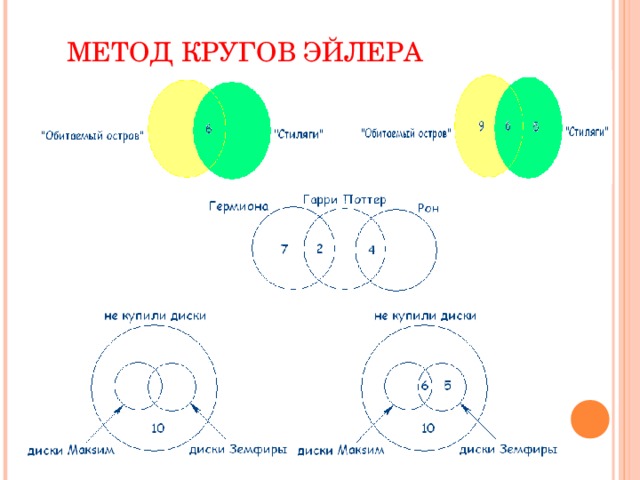 Расчет информационного веса изображений.
Расчет информационного веса изображений.
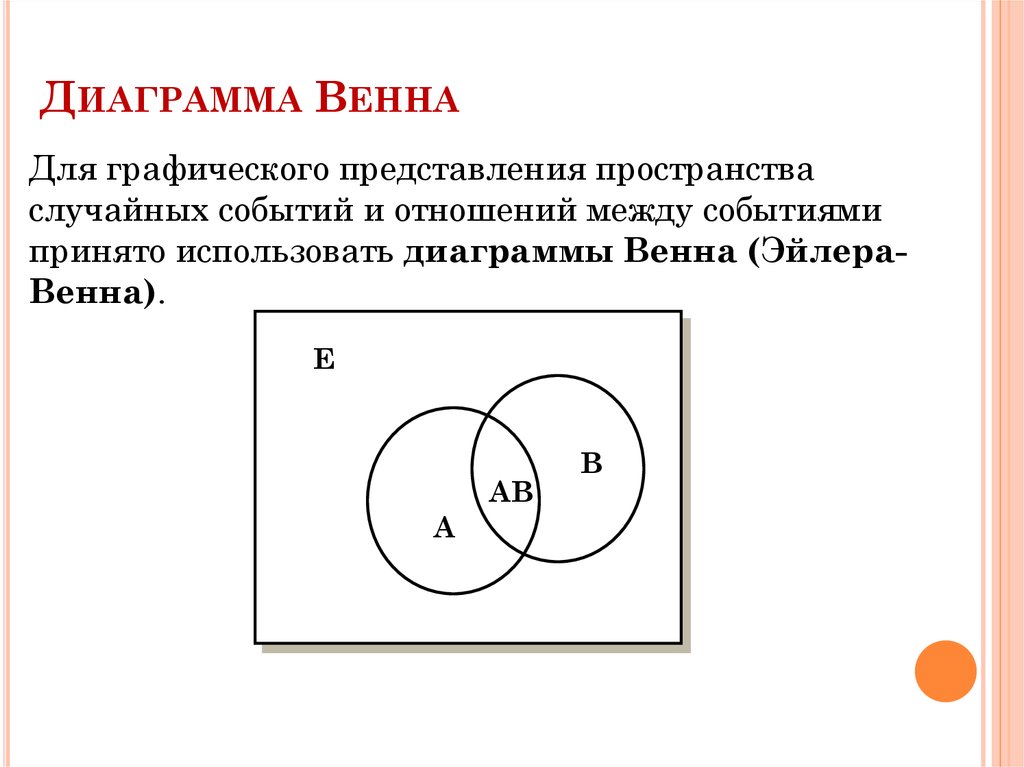 04.2017
1071
0
04.2017
1071
0
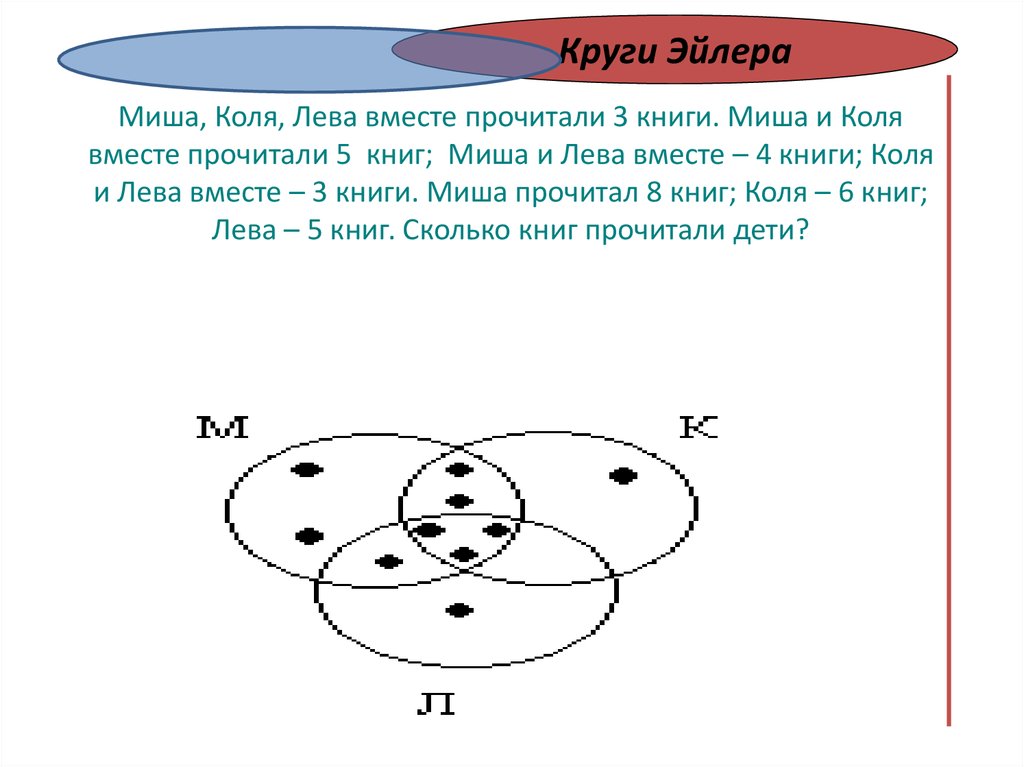
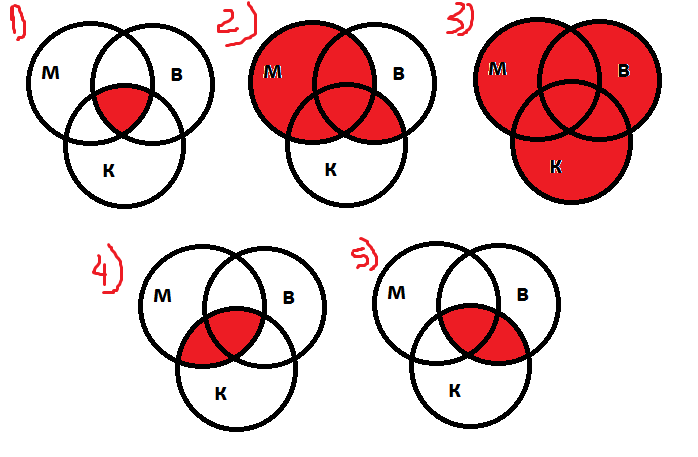 Файловая система. Информатика. 7 класс.
Файловая система. Информатика. 7 класс.
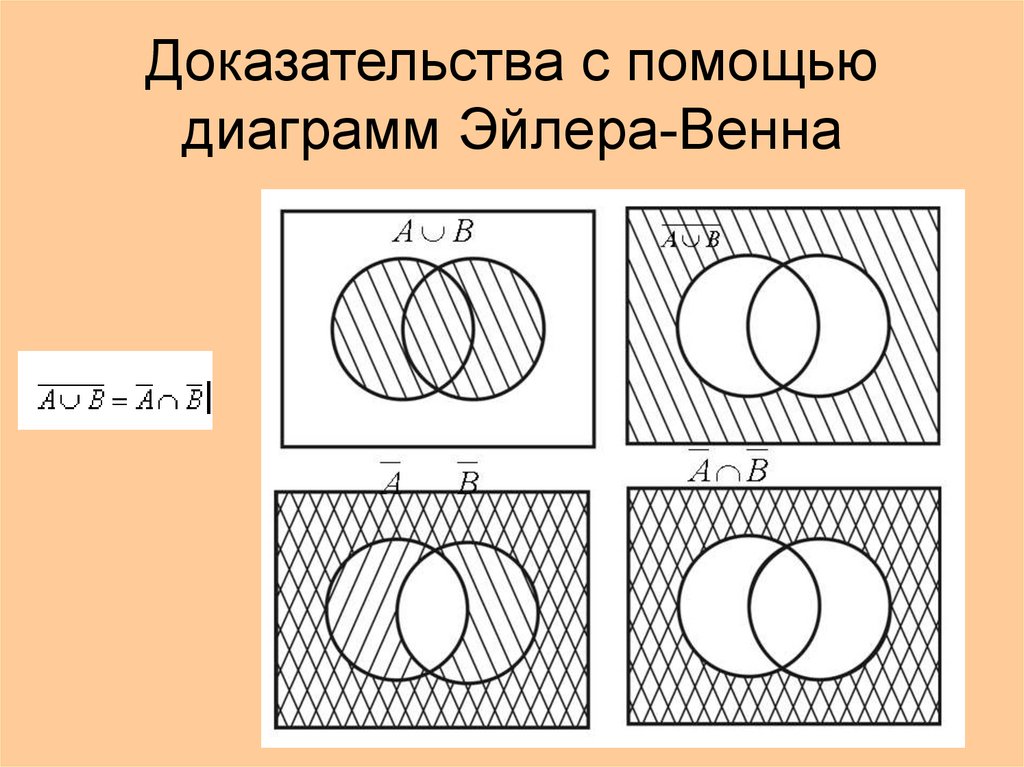 7 класс. Обработка текстовой информации. Тест.
7 класс. Обработка текстовой информации. Тест.
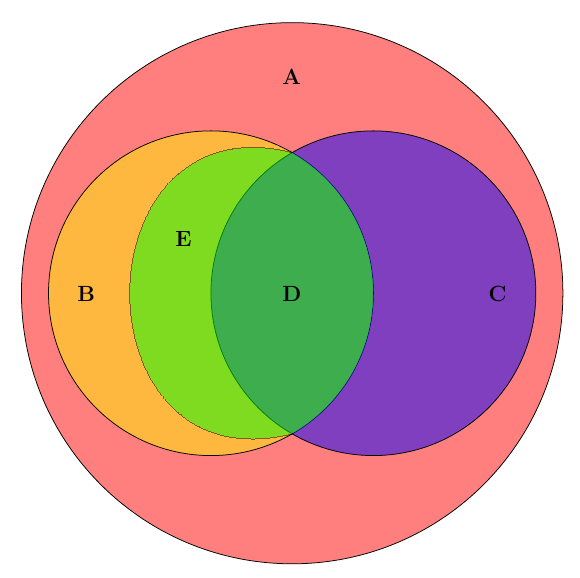 Баллы, получаемые вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше количество заданий и набрать как можно больше баллов.
Баллы, получаемые вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше количество заданий и набрать как можно больше баллов.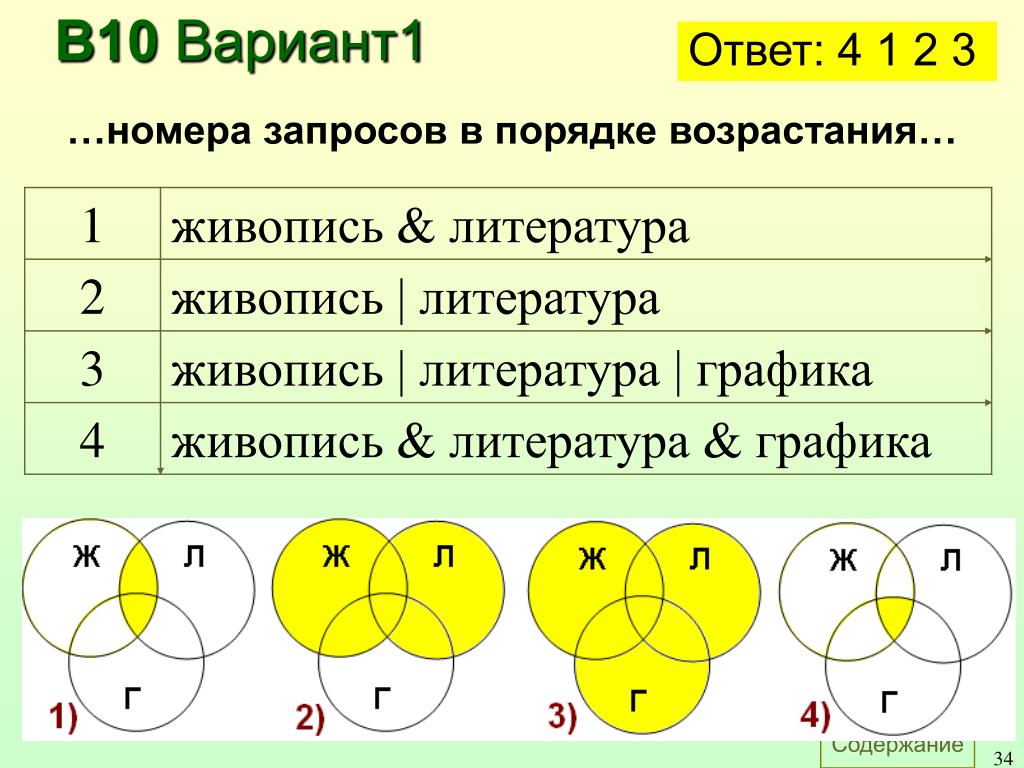 03.2020
48
0
03.2020
48
0
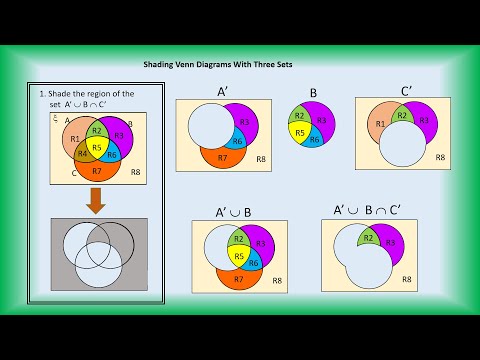 Ссылка боюнча тестке кирип, тест менен таанышып, андан кийин жообуңарды бергиле. Тест өтө кызыктуу. Тесттин жардамы менен өзүңөрдүн билимиңерди жогорулатасыңар. Тестке жооп берүү менин Ютуб каналыма каналыма кирип «ВИРУСТАР ЖАНА АНТИВИРУСТАР» деген видеосабагымды көрүп чыксаңар болот. Видеосабактарыма төмөнкү ссылка менен кириңиздер: https://www.youtube.com/channel/UCn-ibNWnjdVFVOLLQp8nPyQ?view_as=subscriber Чектөө жок. Бул тесттен кийин дагы көптөгөн тесттер болот. Тест тапшырууда баарыңарга ийгилик каалаймын.
Ссылка боюнча тестке кирип, тест менен таанышып, андан кийин жообуңарды бергиле. Тест өтө кызыктуу. Тесттин жардамы менен өзүңөрдүн билимиңерди жогорулатасыңар. Тестке жооп берүү менин Ютуб каналыма каналыма кирип «ВИРУСТАР ЖАНА АНТИВИРУСТАР» деген видеосабагымды көрүп чыксаңар болот. Видеосабактарыма төмөнкү ссылка менен кириңиздер: https://www.youtube.com/channel/UCn-ibNWnjdVFVOLLQp8nPyQ?view_as=subscriber Чектөө жок. Бул тесттен кийин дагы көптөгөн тесттер болот. Тест тапшырууда баарыңарга ийгилик каалаймын.
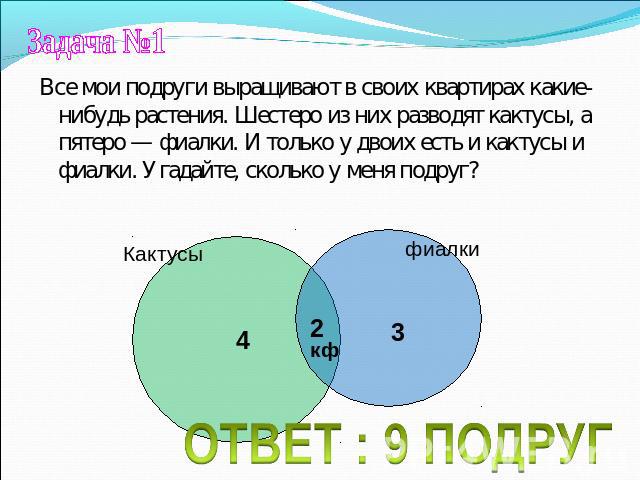 04.2020
1839
0
04.2020
1839
0
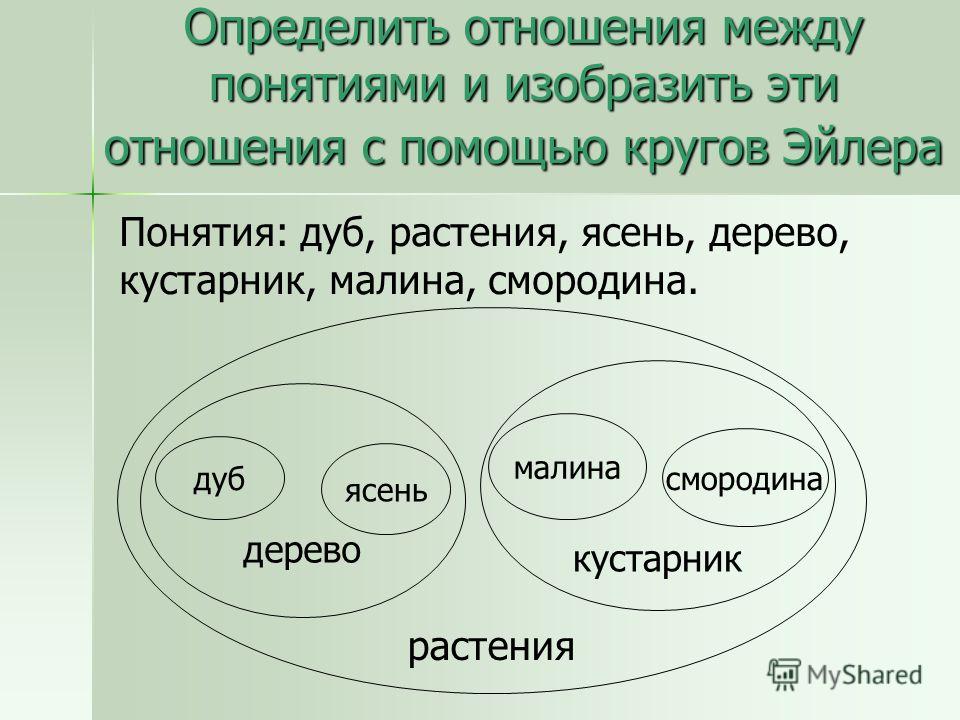 04.2020
597
0
04.2020
597
0
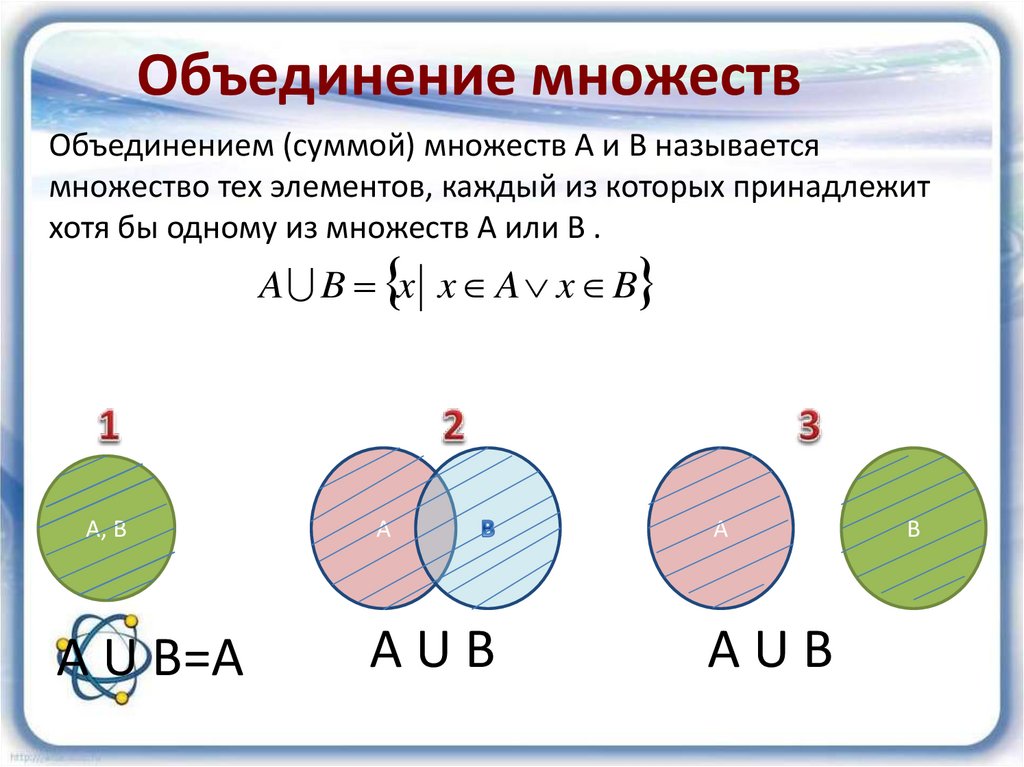 05.2020
191
0
05.2020
191
0
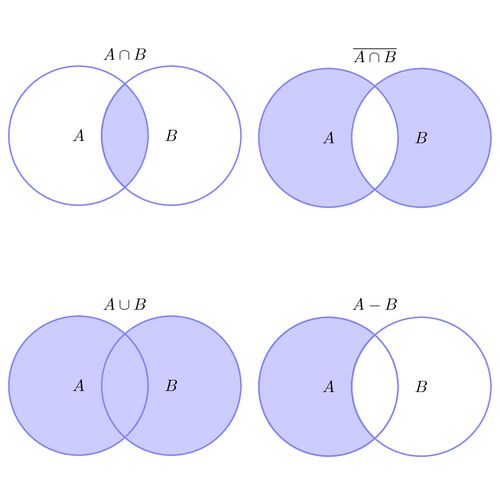 10.2020
581
0
10.2020
581
0
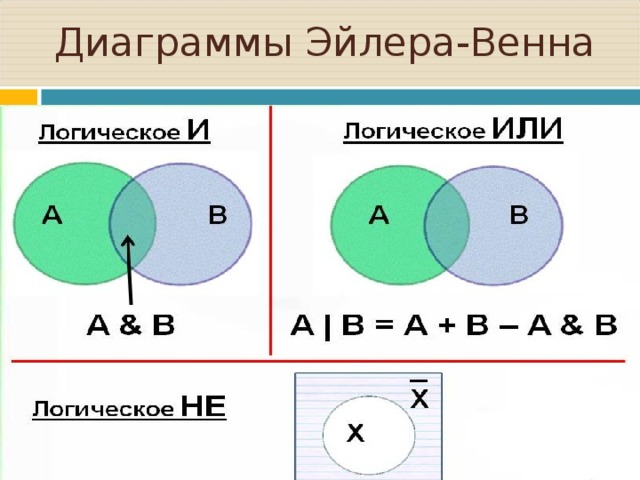 7 класс.
7 класс.
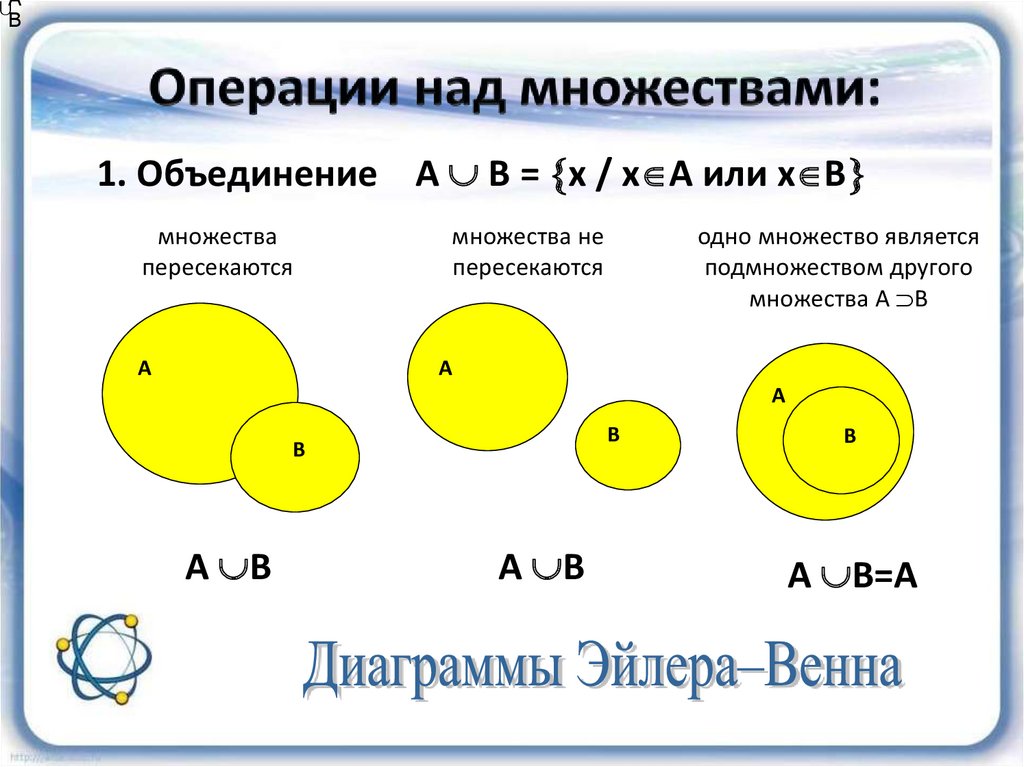 Они позволяют раскрыть различные точки зрения и визуализировать вклад каждой части в целое.
Они позволяют раскрыть различные точки зрения и визуализировать вклад каждой части в целое.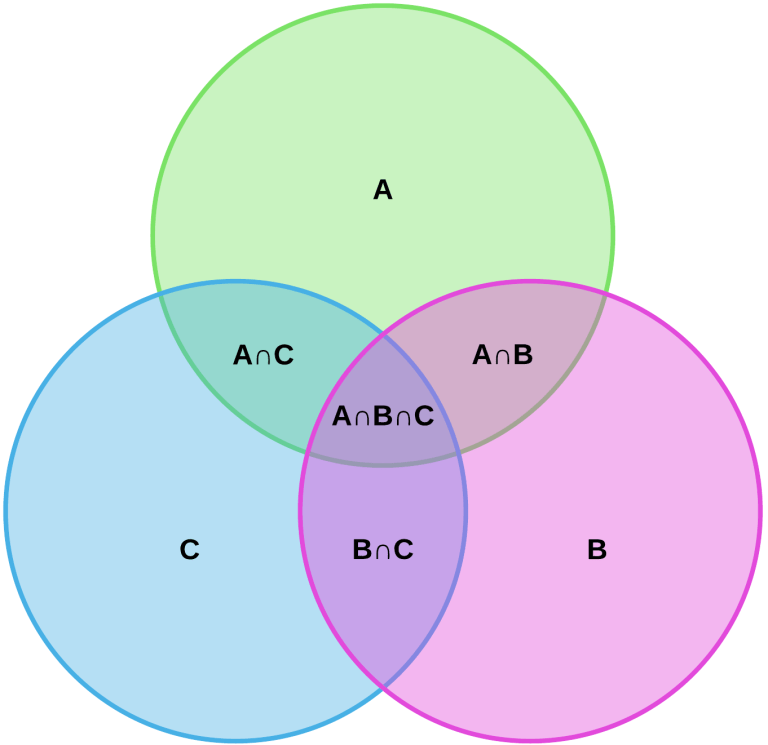 Их часто изображают в виде групп (потенциально связанных) замкнутых кривых. Эти диаграммы допускают некоторое упущение множественных взаимодействий, позволяя им использовать в своих интересах пространственные качества удержания и непересекающихся кривых.
Их часто изображают в виде групп (потенциально связанных) замкнутых кривых. Эти диаграммы допускают некоторое упущение множественных взаимодействий, позволяя им использовать в своих интересах пространственные качества удержания и непересекающихся кривых. Они состоят из простых замкнутых кривых на плоскости (обычно кругов), которые представляют наборы.
Они состоят из простых замкнутых кривых на плоскости (обычно кругов), которые представляют наборы.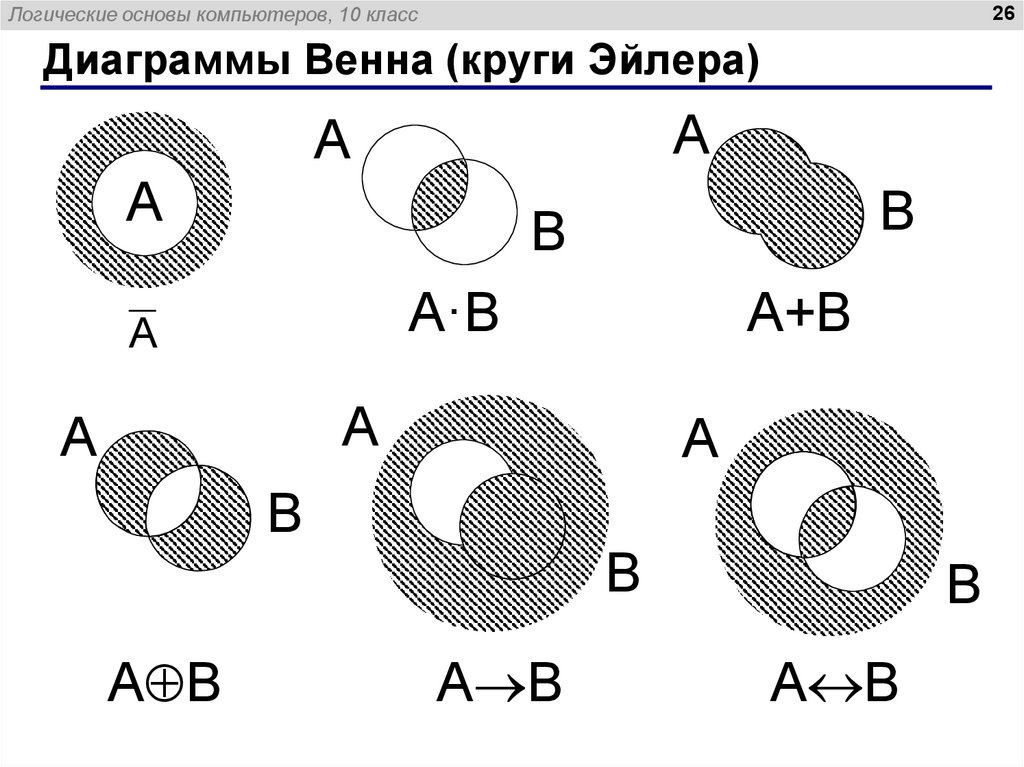 Подробнее
Подробнее