Синус и косинус равны не табличному значению. Как решить уравнение? Часть 2
Синус равен не стандартному значению
В прошлой статье мы разобрали как решать простейшие тригонометрические уравнения со стандартными значениями, т.е. вот эти:
Но бывает так, что нужно решить уравнение, в котором синус равен не табличному значению. Например, как решить уравнение \(\sinx= \frac{1}{3}\)? Давайте обо всем по порядку.
Сначала действуем, как и при решении стандартных уравнений:
1. Чертим оси и тригонометрический круг
2. На оси синусов отмечаем нужное значение
3. Проводим к оси перпендикуляр
А что дальше? Какие значения будут получаться на круге? Не \(\frac{π}{6}\), не \(\frac {π}{4}\), и даже не \(\frac{π}{7}\) — вообще никакие привычные числа не подходят. Однако при этом очевидно, что значения эти есть.
Но как их записать? Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin\frac{1}{3}\). Почему? Да потому что синус равен \(\frac{1}{3}\) .
Ок, значение правой точки найдено, как найти значение левой? Давайте подумаем. Значение дуги от нуля до правой точки равно \(\arcsin\frac{1}{3}\).
Но дуга от \(π\) до левой точки имеет такую же длину:
Значит, если мы пройдем от \(π\) против часовой стрелки на величину \(\arcsin\frac{1}{3}\) мы попадем в левую точку. Иными словами, значение в левой точке равно \(π-\arcsin\frac{1}{3}\).
Теперь мы можем записать все корни уравнения: \( \left[ \begin{gathered} x_1=\arcsin\frac{1}{3}+2πn\\ x_2=π-\arcsin\frac{1}{3}+2πn, \, n∈Z\end{gathered}\right.\). Не понимаешь откуда появилось «\(2πn\)» и «\(n∈Z\)» ? Смотри это и это видео!
Готово.
Без арксинусов решить уравнение \(\sinx=\frac{1}{3}\) не получилось бы, потому что мы не смогли бы записать итоговый ответ.
С арксинусом – бесконечное количество.
Алгоритм решения простейших уравнений с синусом
Шаг 1. Построить окружность и оси синусов и косинусов.
Шаг 2. Отметить на оси синусов значение, которому синус должен быть равен.
Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.
Шаг 4. Найти по одному значению каждой из полученных точек на круге. Если синус равен не стандартному числу, то правую точку на круге можно отметить, как \(\arcsina\), а левую как \(π-\arcsina\).
Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn\), \(n∈Z\), где \(t_0\) – как раз те значения точек, которые вы нашли в шаге 4.
Пример: \(\sinx=-\frac{\sqrt{2}}{4}\)
Или если воспользоваться свойством арксинуса \(\arcsin(-a)=-\arcsina\):
Ответ: \( \left[ \begin{gathered} x=π+\arcsin\frac{\sqrt{2}}{4}+2πn\\ x=-\arcsin\frac{\sqrt{2}}{4}+2πn, \, n∈Z\end{gathered}\right.\)
Как делать не надо:
\(\sinx=\frac{1}{2}\)
Ответ: \( \left[ \begin{gathered} x=\arcsin\frac{1}{2}+2πn\\ x=π-\arcsin\frac{1}{2}+2πn, \, n∈Z\end{gathered}\right.\)
Это стандартное уравнение — его можно решить с помощью круга, либо просто вычислить \(\arcsin\frac{1}{2}= \frac{π}{6}\). В любом случае корректным ответом здесь будет:
\( \left[ \begin{gathered} x=\frac{π}{6}+2πn\\ x=\frac{5π}{6}+2πn, \, \end{gathered}\right.\) \(n∈Z\)
Запомните! В математике принято вычислять ответы до конца, поэтому если арксинус берется для стандартной точки и может быть посчитан – его надо вычислить.
Потому что ответ с \(\arcsin\frac{1}{2}\) и тому подобным будет выглядеть столь же странно, как ответ \(x=\frac{6}{3}\) в линейном уравнении \(3x=6\).
Больше примеров использования алгоритма читай в этой статье: простейшие уравнения с синусом и косинусом.
Косинус равен не стандартному значению
Предположим, надо решить уравнение \(\cosx=\frac{1}{3}\). Как это сделать?
Тут логика такая же, как и в уравнении с синусом: косинус одной трети равняться может, следовательно, и значение должно быть таким, при котором косинус будет равен \(\frac{1}{3}\). Очевидное решение — использовать арккосинус.
Несложно заметить, что дуга от нуля до нижней точки имеет такую же длину, как и от нуля до верхней, но только она откладывается в отрицательном направлении (по часовой стрелке). Поэтому одно из значений второй точки: \(-\arccos\frac{1}{3}\)
И теперь можно записать общий ответ: \(x=±\arccos\frac{1}{3}+2πn\), \(n∈Z\).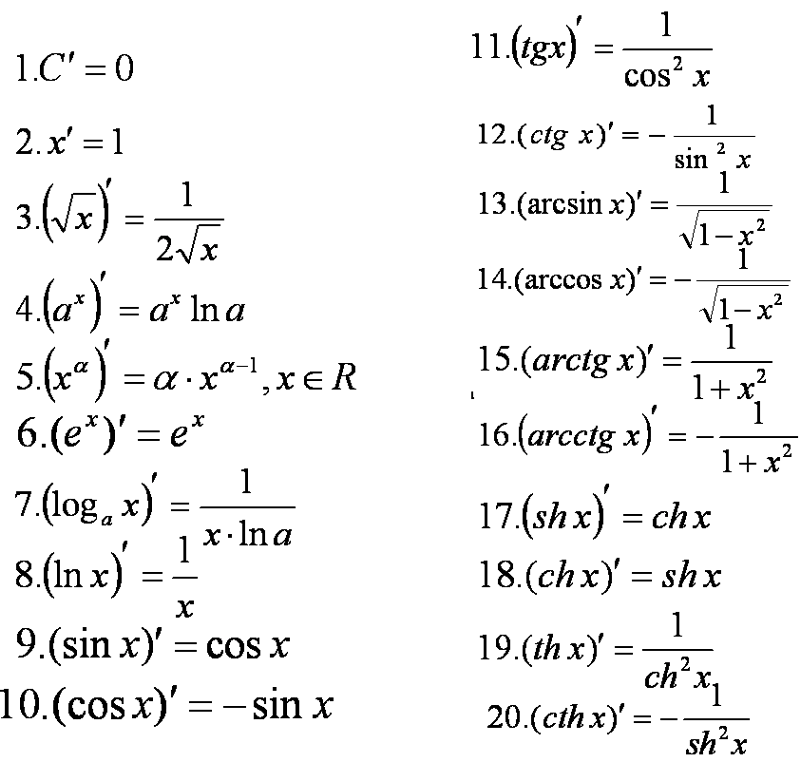
Алгоритм решения простейших уравнений с косинусом
Шаг 1. Построить окружность и оси синусов и косинусов.
Шаг 2. Отметить на оси косинусов значение, которому косинус должен быть равен.
Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.
Шаг 4. Найти по одному значению каждой из полученных точек на круге. Если косинус равен не стандартному числу, то верхнюю точку на круге можно отметить, как \(\arccosa\), а нижнюю как \(-\arccosa\).
Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn\), \(n∈Z\), где \(t_0\) – как раз те значения точек, которые вы нашли в шаге 4.
Пример: \(\cosx=-\frac{8}{7}\).
Решение:
Важно быть начеку, а не штампованно везде писать аркфункции.
Пересечения с окружность нет, значит и решений нет.
Пример: \(\cosx=-\frac{3}{4}\).
Или если применить формулу \(\arccos(-a)=π-\arccosa\)
Ответ: \(π±\arccos \frac{3}{4}+2πn\), \(n∈Z\).
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Арксинус
Арксинус, записывается как арксинус или синус -1 (не путать с ) — функция обратного синуса.
Диаграмма Arcsin
График y = arcsin(x) показан ниже:
Область определения y = arcsin(x) равна , а ее диапазон равен . Одно из свойств обратных функций состоит в том, что если точка (a, b) находится на графике функции f, то точка (b, a) находится на графике обратной функции. Это фактически означает, что график обратной функции является отражением графика функции через прямую y = x. Мы можем увидеть это, если посмотрим на график y = sin(x) ниже:
Обратите внимание, что синус имеет обратный только в ограниченной области , выделенной красным, и что эта ограниченная область является диапазоном y = arcsin(x). Причина, по которой область определения y = sin(x) должна быть ограничена, заключается в том, что для того, чтобы функция имела обратную, функция должна быть взаимно однозначной, что означает, что никакая горизонтальная линия не может пересекать график функции. больше чем единожды. Поскольку синус является периодической функцией, без ограничения области определения горизонтальная линия будет периодически пересекать функцию бесконечно много раз.
Калькулятор арксинуса
Ниже приведен калькулятор для определения либо значения арккоса числа от -1 до 1, либо значения косинуса угла.
| угловой синус | = | деградировать | ||
Использование специальных углов для нахождения арксинуса
Хотя мы можем найти значение арксинуса для любого значения x в интервале [-1, 1], существуют определенные углы, которые часто используются в тригонометрии (0°, 30°, 45°, 60°, 90°, их кратные и эквиваленты в радианах), значения синуса и арксинуса которых стоит запомнить. Ниже приведена таблица, показывающая эти углы (θ) как в радианах, так и в градусах, а также их соответствующие значения синусов, sin(θ).
| θ | -90° | -60° | -45° | -30° | 0° | 30° | 45° | 60° | 90° |
| sin(θ) | -1 | 0 | 1 |
Один из методов, который может помочь в запоминании этих значений, состоит в том, чтобы выразить все значения sin(θ) в виде дробей, содержащих квадратный корень.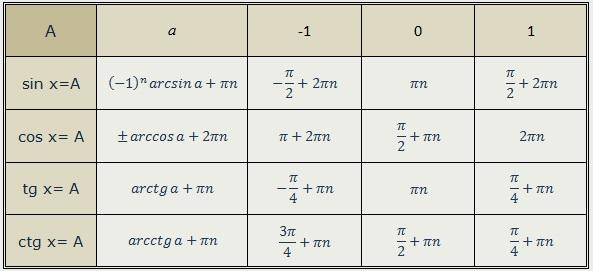
Начиная с 0° и заканчивая 90°, sin(0°) = 0 = . Последующие значения sin(30°), sin(45°), sin(60°) и sin(90°) следуют шаблону, так что используя значение sin(0°) в качестве эталона, чтобы найти значения синуса для последующих углов, мы просто увеличиваем число под знаком радикала в числителе на 1, как показано ниже.
| θ | 0° | 30° | 45° | 60° | 90° |
| sin(θ) |
Значения синуса от 0° до -90° следуют той же схеме, за исключением того, что значения отрицательные, а не положительные, поскольку синус отрицателен в квадранте IV. Этот шаблон периодически повторяется для соответствующих угловых измерений, и мы можем определить значения sin(θ) на основе положения θ в единичной окружности, принимая во внимание знак синуса: синус положительный в квадрантах I и II и отрицательный в квадрантах III и IV.
После того, как мы запомнили значения, или если у нас есть какая-то ссылка, становится относительно просто распознавать и определять значения синуса или арксинуса для специальных углов.
Пример:
Найти arcsin(), arcsin() и arcsin(3) в радианах.
, .
, .
arcsin(3) не определено, потому что 3 не находится в интервале -1≤arcsin(θ)≤1, области определения arcsin(x).
Обратные свойства
Как правило, функции и их обратные свойства демонстрируют отношение
f(f -1 (x)) = x и f -1 (f(x)) = x
при условии, что x находится в области определения функции. То же самое верно для sin(x) и arcsin(x) в пределах их соответствующих ограниченных областей:
sin(arcsin(x)) = x для всех x в [-1, 1]
и
arcsin(sin (x)) = x, для всех x в [ ]
Эти свойства позволяют нам оценить композицию тригонометрических функций.
Композиция арксинуса и синуса
Если x находится в области определения, вычисление композиции арксинуса и синуса относительно просто.
Примеры:
1.
2.
Если x не входит в область значений, нам необходимо определить опорный угол, а также соответствующий квадрант. Учитывая arcsin(sin() ), мы не можем оценить это, как мы сделали выше, потому что x не находится внутри [ ], поэтому решение не может быть . Чтобы оценить это, нам сначала нужно определить sin() перед использованием arcsin:
3.
В приведенном выше примере опорный угол равен , а sin() равен . Однако находится в квадранте III, где sin отрицателен, поэтому sin() = , и единственный угол в области определения arcsin(x), синус которого равен .
Композиция других тригонометрических функций
Мы также можем составить композиции, используя все другие тригонометрические функции: косинус, тангенс, косеканс, секанс и котангенс.
Пример:
Найти cos(arcsin()).
Так как это не одно из соотношений для специальных углов, мы можем использовать прямоугольный треугольник, чтобы найти значение этой композиции.
Учитывая arcsin()=θ, мы можем найти, что sin(θ)=. Прямоугольный треугольник ниже показывает θ и отношение его противоположной стороны к гипотенузе треугольника.
Чтобы найти косинус, нам нужно найти прилежащую сторону, так как cos(θ)=. Пусть b длина смежной стороны. Using the Pythagorean Theorem,
3 2 + b 2 = 5 2
9 + b 2 = 25
b 2 = 16
b = 4
We know that arcsin () = θ, поэтому мы можем переписать задачу и найти cos(θ), используя треугольник, который мы построили выше, и тот факт, что cos(θ)=:
cos(arcsin()) = cos(θ) =
Тот же процесс можно использовать с переменным выражением.
Пример:
Найти tan(arcsin(2x)).
Учитывая arcsin(2x) = θ, мы можем найти, что sin(θ) = и построить следующий треугольник:
Чтобы найти касательную, нам нужно найти смежную сторону, поскольку tan(θ)=. Пусть b длина смежной стороны.