Элементарные функции и их графики
Понятие функции — одно из ключевых в математике. О нём подробно рассказано в статье «Что такое функция».
И конечно, в задачах части 2 Профильного ЕГЭ по математике без них не обойтись. А если вы выбрали технический или экономический вуз — первая же лекция по матанализу будет посвящена именно элементарным функциями и их графикам.
Но это не всё. Математические функции, изучением которых мы занимаемся, — это не что-то такое выдуманное или существующее только в замкнутом пространстве учебника. Они являются отражением реальных взаимосвязей и процессов, происходящих в природе и обществе.
Существует всего пять типов элементарных функций:
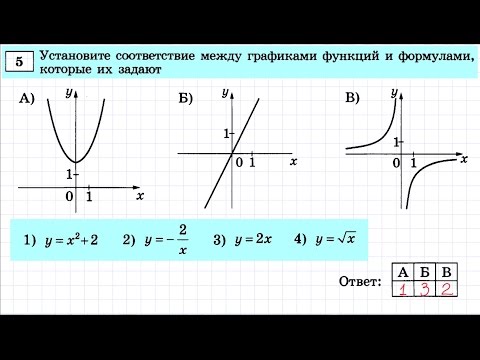
1. Степенные
К этому типу относятся линейные, квадратичные, кубические, , , . Все они содержат выражения вида xα.
2. Показательные
Это функции вида y = ax.
3. Логарифмические
y = logax.
4. Тригонометрические
В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы.
5. Обратные тригонометрические
Содержат arcsinx, arccosx, arctgx, arcctgx.
Элементарными они называются, потому что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x2 · ex — произведение квадратичной и показательной функций; y = sin(ax) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.
Графики и свойства основных элементарных функций следует знать наизусть.
Степенные функции
| 1. Линейная функция y = x | |
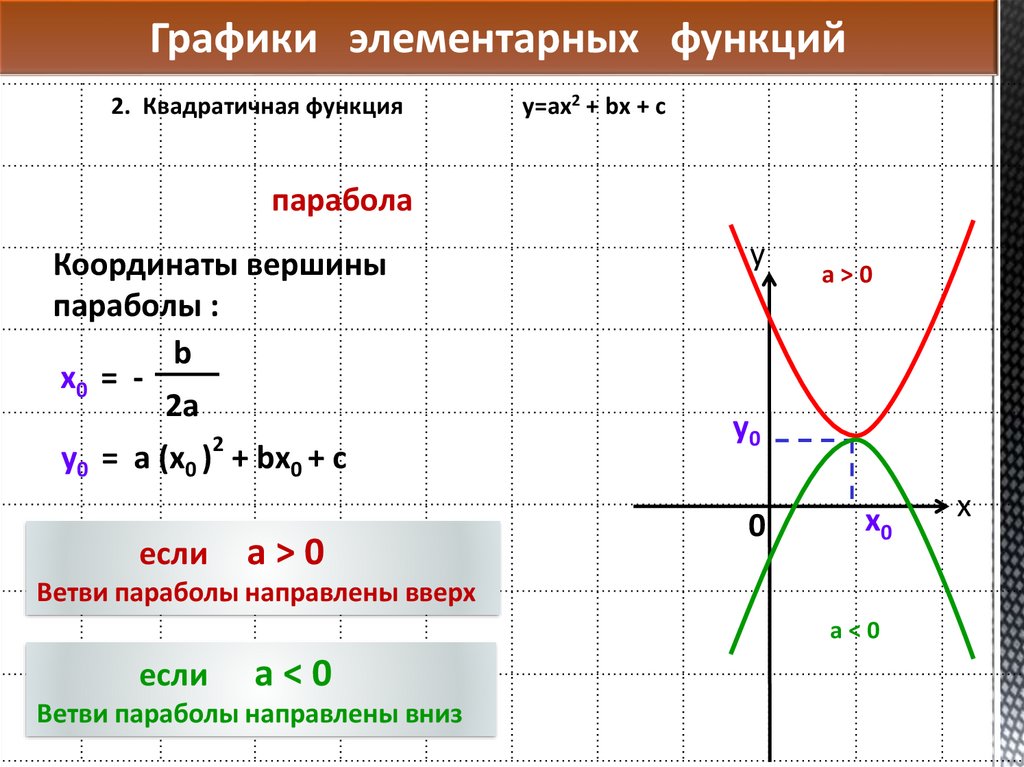
| 2. Квадратичная парабола y = x2 | |
| 3. Функция y = xn, n — натуральное, n > 1 n — чётное n = 2, 4, 6,… | |
| n — нечётное n = 3, 5, 7,… | |
| 4.Гипербола | |
| 5. | |
| 6. |
Показательная функция y = ax
| a > 1 | |
| 0 < a < 1 |
Логарифмическая функция y = logax
| a > 1 | |
| 0 < a < 1 |
Тригонометрические функции
1.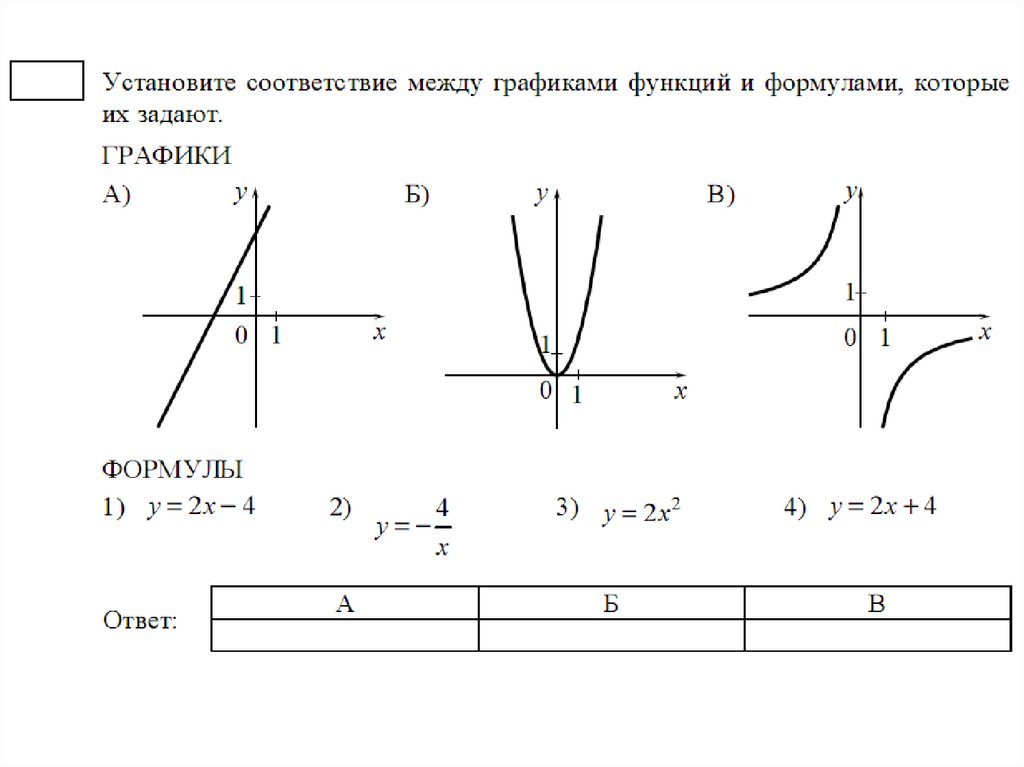 | |
| 2. | |
| 3. | |
| 4. |
Обратные тригонометрические функции
| 1. | |
| 2. | |
| 3. | |
| 4. |
Выше приведены основные, «базовые» графики. А как будут выглядеть, например, графики функций y = sin(2x) или y = 4x
Обратите внимание: уравнения, которые вы решаете, обычно относятся к одному из этих пяти типов. Для каждого типа — свои способы решения. Это и понятно: они основаны на тех или иных свойствах функций.
Почему в уравнении 3x = 35 мы можем «отбросить» основания и записать, что x = 5? Да потому что показательная функция y = 3x возрастает и каждое значение принимает только один раз.
Почему уравнение имеет бесконечно много решений, которые записываются в виде серии: , где n — целое? Потому что функция y = sinx — периодическая, то есть каждое свое значение принимает бесконечно много раз.
Зная графики элементарных функций, вы уже не запутаетесь с ОДЗ уравнений и неравенств. Вы сможете решать сложные задачи графически — а это часто во много раз легче и быстрее, чем аналитически.
Есть еще и такие уравнения, где слева и справа стоят функции разных типов. Для их решения есть графический способ, а также специальные приемы, о которых рассказывается в статье «Метод оценки».
Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Элементарные функции и их графики» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 08.04.2023
Графики функций и их построение — ЗФТШ, МФТИ
Одним из разделов школьной математики является изучение функциональных зависимостей или функций.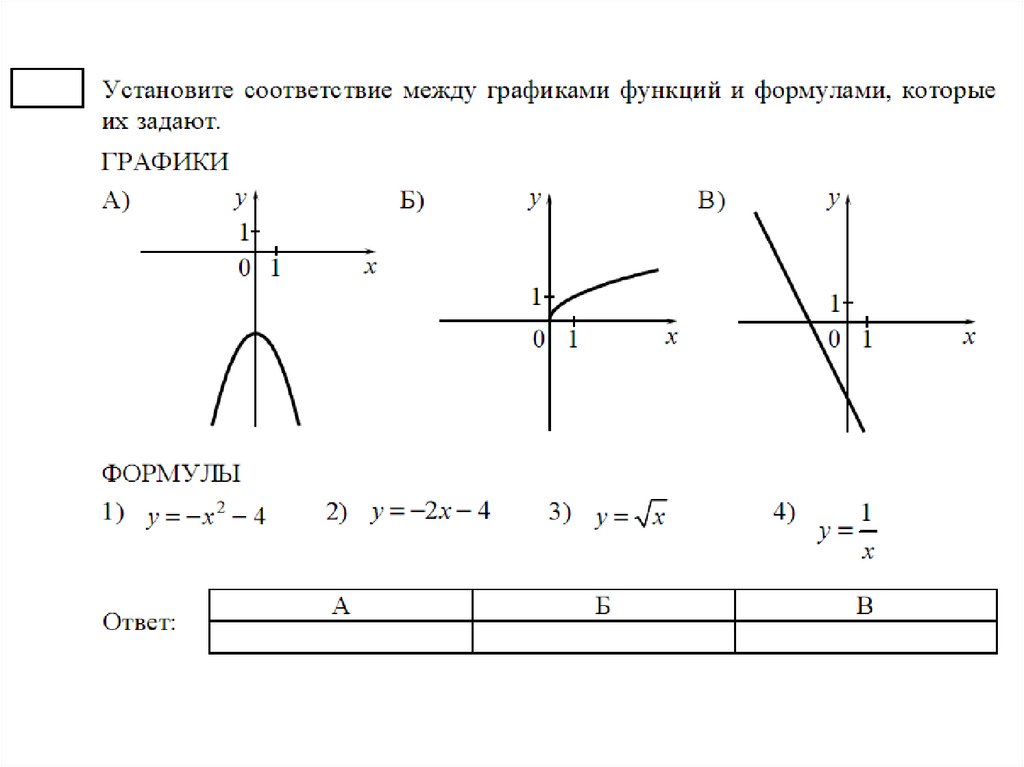
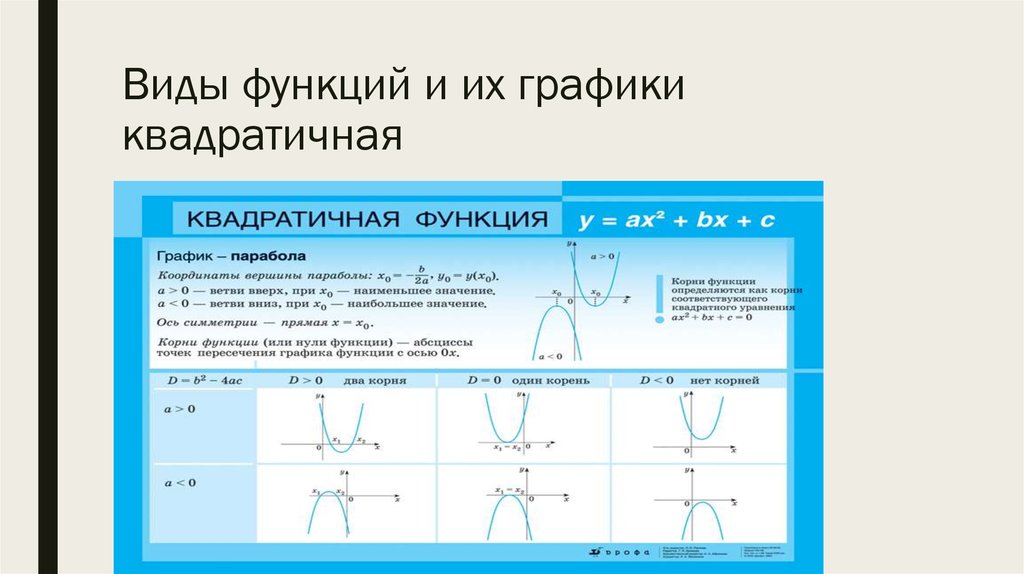
Напомним, что функцией математики называют зависимость величины от одной или нескольких других величин. При этом независимые переменные величины принято называть аргументами, а зависимые – функциями. При этом важно не забывать, что каждому значению аргумента (или аргументов) ставится в соответствие единственное значение зависимой переменной (функции). Наглядно функции изображают с помощью графика – специального набора точек на плоскости. Пусть имеется функция $$ y=f\left(x\right)$$ одной переменной $$ x$$. На плоскости введём декартову систему координат $$ xOy$$ и рассмотрим множество точек $$ G$$ с координатами $$ (x,f(x\left)\right)$$, где $$ x$$ принадлежит некоторому множеству $$ M$$, которое называется областью определения функции. А множество $$ G$$ называется графиком функции $$ y=f\left(x\right)$$ (рис. 1).
В школьном курсе математики вы изучали такие типы функций:
- Линейные функции $$ f\left(x\right)=kx+b$$.
 {n}$$ при натуральных $$ n$$.
{n}$$ при натуральных $$ n$$. - Степенные функции вида $$ f\left(x\right)=\sqrt[n]{x}$$ при натуральных $$ n$$.
- Обратная пропорциональность $$ f\left(x\right)={\displaystyle \frac{k}{x}}$$, $$ k\ne 0$$.
График линейной функции можно построить по двум точкам, поскольку это прямая линия. Однако стоит заметить, что не всякая прямая будет графиком линейной функции. Если взять вертикальную прямую $$ x=a$$, то такая линия не может быть графиком никакой функции (рис. 2).
Действительно, здесь одному значению переменной $$ x$$ ставится в соответствие несколько значений переменной $$ y$$. Итак,
Напомним геометрический смысл коэффициентов $$ k$$ и $$ b$$ в уравнении прямой $$ y=kx+b:$$ $$ k=\mathrm{tg} \alpha $$ – тангенс угла наклона прямой к оси $$ Ox$$, $$ b$$ – ордината точки пересечения прямой с осью $$ Oy$$. Поэтому две невертикальные прямые $$ y={k}_{1}x+{b}_{1}$$ и $$ y={k}_{2}x+{b}_{2}$$:
- параллельны ⟺ $$ {k}_{1}={k}_{2}$$ и $$ {b}_{1}\ne {b}_{2}$$;
- совпадают ⟺ $$ {k}_{1}={k}_{2}$$ и $$ {b}_{1}={b}_{2}$$;
- перпендикулярны ⟺ $$ {k}_{1}{k}_{2}=-1$$.
 {n}$$, но при этом $$ x$$ и $$ y$$ меняются местами. Для чётных $$ n$$ при этом еще нужно учесть ОДЗ $$ x\ge 0$$. Поэтому график функции $$ f\left(x\right)=\sqrt[n]{x}$$ имеет следующий вид в зависимости от чётности натурального числа $$ n$$ (рис. 7, 8):
{n}$$, но при этом $$ x$$ и $$ y$$ меняются местами. Для чётных $$ n$$ при этом еще нужно учесть ОДЗ $$ x\ge 0$$. Поэтому график функции $$ f\left(x\right)=\sqrt[n]{x}$$ имеет следующий вид в зависимости от чётности натурального числа $$ n$$ (рис. 7, 8):Рассмотрим теперь функции вида $$ f\left(x\right)=\frac{k}{x}$$.
Поскольку функция $$ f$$ нечётна, то график должен быть симметричным относительно начала координат. Схематический вид графика этой функции показан на рисунке 9.
Если $$ k
Покажем, как меняется график функции $$ f\left(x\right)={\displaystyle \frac{k}{x}}$$ при изменении параметра $$ k$$. Если $$ \left|{k}_{2}\right|>\left|{k}_{1}\right|$$, то линия $$ f\left(x\right)={\displaystyle \frac{{k}_{2}}{x}}$$ более удалена от осей координат, чем $$ f\left(x\right)={\displaystyle \frac{{k}_{1}}{x}}$$. Схематично это изображено на рис. 11, 12.
графических функций — Как графические функции?
Графические функции — это процесс построения графика (кривой) соответствующей функции.
 Графики основных функций, таких как линейные, квадратичные, кубические и т. д., довольно просты, графические функции, которые являются сложными, такими как рациональные, логарифмические и т. д., требуют некоторых навыков и некоторых математических понятий для понимания.
Графики основных функций, таких как линейные, квадратичные, кубические и т. д., довольно просты, графические функции, которые являются сложными, такими как рациональные, логарифмические и т. д., требуют некоторых навыков и некоторых математических понятий для понимания.Давайте посмотрим процесс графического отображения функций вместе с примерами.
1. Что подразумевается под графическими функциями? 2. Основные графические функции 3. График сложных функций 4. Графические функции с помощью преобразований 5. Часто задаваемые вопросы о графических функциях Что подразумевается под графическими функциями?
Графические функции рисует кривую, представляющую функцию на координатной плоскости.
 Если кривая (график) представляет собой функцию, то каждая точка кривой удовлетворяет уравнению функции. Например, следующий график представляет линейную функцию f(x) = -x+ 2.
Если кривая (график) представляет собой функцию, то каждая точка кривой удовлетворяет уравнению функции. Например, следующий график представляет линейную функцию f(x) = -x+ 2.Возьмем любую точку на этой прямой, скажем, (-1, 3). Подставим (-1, 3) = (x, y) (т. е. x = -1 и y = 3) в функцию f(x) = -x + 2 (заметим, что ее можно записать как y = — х + 2). Затем
3 = -(-1) + 2
3 = 1 + 2
3 = 3, таким образом, (-1, 3) удовлетворяет функции.Таким же образом можно попробовать взять разные точки и проверить, удовлетворяют ли они функции. Каждая точка на линии (обычно называемая «кривой») удовлетворяет этой функции. Рисование таких кривых, представляющих функции, известно как графическое отображение функций.
Основные функции построения графиков
Графики основных функций, таких как линейные функции и квадратичные функции, очень просты. Основная идея графических функций
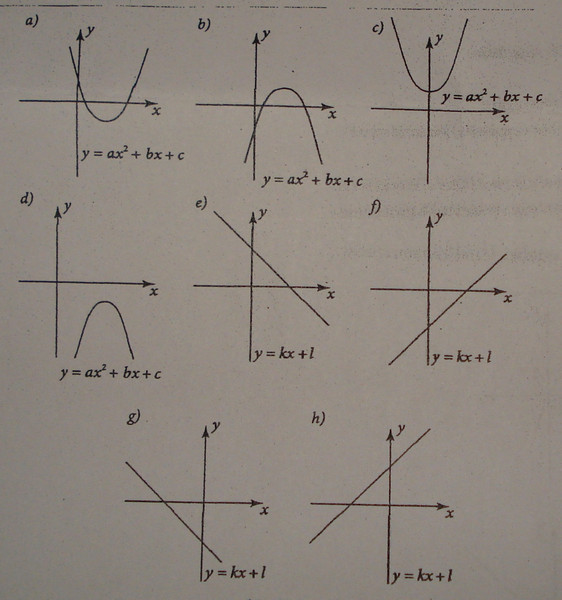
- Определение формы, если возможно. Например, если это линейная функция вида f(x) = ax + b, то ее график будет линией; если это квадратичная функция вида f(x) = ax 2 + bx + c, то это парабола.

- нахождение на нем некоторых точек путем подстановки некоторых случайных значений x и нахождение соответствующих значений y путем подстановки каждого значения в функцию.
Вот несколько примеров.
Графики линейных функций
Построим график той же линейной функции, что и в предыдущем разделе (f(x) = -x + 2). Для этого мы создаем таблицу значений, взяв несколько случайных чисел для x, скажем, x = 0 и x = 1. Затем подставьте каждое из них в y = -x + 2, чтобы вычислить значения y.
х и 0 -0 + 2 = 2 1 -1 + 2 = 1 Таким образом, на прямой есть две точки (0, 2) и (1, 1). Если мы нанесем их на график и соединим их прямой линией (продолжив линию с обеих сторон), мы получим ее график, как показано в предыдущем разделе.
График квадратичных функций
Для построения графика квадратичной функции мы можем найти на ней несколько случайных точек.
 Но это может не дать идеальной U-образной кривой. Это потому, что для получения идеальной U-образной кривой нам нужно, где она поворачивает. т. е. надо найти его вершину. Найдя вершину, мы можем найти две или три случайные точки с каждой стороны вершины, и они помогут в построении графика функции.
Но это может не дать идеальной U-образной кривой. Это потому, что для получения идеальной U-образной кривой нам нужно, где она поворачивает. т. е. надо найти его вершину. Найдя вершину, мы можем найти две или три случайные точки с каждой стороны вершины, и они помогут в построении графика функции.Пример: График квадратичной функции f(x) = x 2 — 2x + 5.
Решение:
Сравнение с f(x) = ax 2 , a + c + bx = 1, b = -2 и c = 5.
Координата x вершины: h = -b/2a = -(-2)/2(1) = 1.
Координата y есть, f(1) = 1 2 — 2(1) + 5 = 4.
Следовательно, вершина (1, 4).
Возьмем два случайных числа по обе стороны от 1 (координата x вершины) и создадим таблицу. Затем мы можем вычислить координаты y с помощью функции.
х и -1 (-1) 2 — 2(-1) + 5 = 8 0 0 2 — 2(0) + 5 = 5 Вершина: 1 4 2 2 2 — 2(2) + 5 = 5 3 3 2 — 2(3) + 5 = 8 Теперь мы нанесем точки (-1, 8), (0, 5), (1, 4), (2, 5) и (3, 8) на лист графика, соединим их, и продлите кривую с обеих сторон.

График сложных функций
Графические функции сравнительно просты, если каждый их домен и диапазон представляет собой набор всех действительных чисел. Но это НЕ относится ко всем типам функций. Есть некоторые сложные функции, для которых необходимо учитывать домен, диапазон, асимптоты и дыры при их построении. Самые популярные такие функции:
- Рациональные функции. Его родительская функция имеет форму f(x) = 1/x (которая называется обратной функцией).
- Экспоненциальные функции. Его родительская функция имеет вид f(x) = a x .
- Логарифмические функции. Его родительская функция имеет вид f(x) = log x.
Просто представьте, как выглядят графики родительских функций каждой из этих функций.
В каждом из этих случаев за графических функций , мы выполняем следующие шаги:
- Найдите область определения и диапазон функции и помните об этом при построении кривой.

- Найдите точки пересечения x и y и нанесите их на график.
- Определите отверстия, если они есть.
- Найдите асимптоты (вертикальную, горизонтальную и наклонную) и нарисуйте их пунктирными линиями, чтобы мы могли разбить график по этим линиям и убедиться, что график их не касается.
- Постройте таблицу значений, взяв несколько случайных чисел для x (по обе стороны от точки пересечения x и/или по обе стороны от вертикальной асимптоты), рассчитайте соответствующие значения y.
- Нанесите точки из таблицы и соедините их, учитывая асимптоты, домен и диапазон.
Давайте посмотрим, как построить график функции в различных случаях, используя описанные выше шаги.
График рациональных функций
Построим график рациональной функции f(x) = (x + 1) / (x — 2). Мы следуем вышеуказанным шагам и рисуем график этой функции.
График экспоненциальных функций
Рассмотрим экспоненциальную функцию f(x) = 2 -x + 2.
 Мы построим ее график, используя те же шаги, что и упомянутые выше.
Мы построим ее график, используя те же шаги, что и упомянутые выше.- Его областью определения является множество всех действительных чисел (R), а его диапазон равен y > 2. Чтобы узнать, как их найти, нажмите здесь.
- Не имеет вертикальных асимптот. Но у него есть горизонтальная асимптота при y = 2, .
- Он не имеет x-перехватов. Его y-пересечение равно (0, 3).
- Без отверстий.
- У нас нет данных о VA или x-intercept. Пока у нас есть только одно значение (0, 3). Итак, давайте возьмем несколько случайных чисел по обе стороны от x = 0 и составим таблицу.
х и -2 2 -(-2) + 2 = 6 -1 2 -(-1) + 2 = 4 0 3 (г-целое) 1 2 -1 + 2 = 2,5 2 2 -2 + 2 = 2,25 - Нанесем всю информацию на график.

Графики логарифмических функций
Мы построим график логарифмической функции, скажем, f(x) = 2 log 2 x — 2. Теперь мы построим ее график, выполнив действия, описанные ранее.
Точно так же вы можете увидеть, как построить график нелинейных функций, функции тождества, функции модуля, полиномиальной функции, функции нуля, функции наибольшего целого числа, постоянной функции, тригонометрических функций, функции дробной части и т. д., нажав на соответствующие ссылки.
Графические функции с помощью преобразований
Мы можем построить графики функций, применяя преобразования к графикам родительских функций. Вот родительские функции нескольких важных типов функций.
- Линейная функция: f(x) = x
- Квадратичная функция: f(x) = x 2
- Кубические функции: f(x) = x 3
- Функция квадратного корня: f(x) = √x
- Функция кубического корня: f(x) = ∛x
- Функция абсолютного значения: f(x) = |x|
- Обратная функция: f(x) = 1/x
- Экспоненциальная функция: f(x) = a x , 0 < a < 1
- Логарифмическая функция: f(x) = log x
Нам нужно иметь представление о том, как выглядит график каждой из этих родительских функций (нажав на соответствующие ссылки).
 Затем мы можем применить следующие преобразования для построения графика данной функции.
Затем мы можем применить следующие преобразования для построения графика данной функции.Трансформация Изменение графика f(x) + с Сдвигает график функции c единиц вверх. ф(х) — с Сдвигает график функции c единиц вниз. ф(х + с) Сдвигает график функции c единиц влево. ф(х — в) Смещает график функции c единиц вправо. -ф(х) Отражает график функции по оси X (в перевернутом виде). ф(-х) Отражает график функции по оси Y (т. е. левая и правая части меняются местами). ф(акс) Горизонтальное расширение с коэффициентом 1/a. а ф(х) Вертикальное расширение в a. Чтобы подробно понять, как построить график функций с помощью преобразований, нажмите здесь.

Важные примечания по графическим функциям:
- f(ax) ≠ a f(x). Оба могут иметь разные значения.
- Значение x, используемое для построения графика любой функции f(x), может быть целым числом, действительным числом или десятичным числом.
- График функции никогда не должен касаться асимптот.
- Не выбирайте значения x в таблице, которых НЕТ в домене функции.
☛ Похожие темы:
- Калькулятор графических функций
- Введение в графику
- Визуализация функций с помощью графиков
Часто задаваемые вопросы о графических функциях
Как графически отображать функции?
Для графических функций нам нужно построить его асимптоты, его точки пересечения x и y, дыры и несколько точек на нем, построив таблицу значений. Затем просто присоединитесь к точке, не касаясь асимптот и сохраняя примечание области определения и диапазона функции.

Какие этапы построения графика линейной функции?
Шаги построения графика линейной функции приведены ниже:
- Убедитесь, что линейная функция имеет форму y=mx+b.
- Теперь b откладывается по оси Y.
- м переводится в дробь.
- Теперь линия продлевается от b с использованием наклона.
- Линию можно продолжить, используя m в качестве направляющего фактора.
Альтернативный вариант:
Любые две точки на прямой определяют линию. Итак, чтобы нарисовать линейную функцию, нам нужно всего лишь две точки на ней. Чтобы отобразить это, просто создайте таблицу значений с двумя столбцами x и y, возьмите несколько случайных чисел для x и вычислите соответствующие значения y, подставив каждое из них в функцию. Затем просто нанесите точки на график, соедините их линией и бесконечно продлите линию с обеих сторон.
Как построить график кусочной функции?
Кусочная функция определяется по-разному (с помощью разных уравнений) на разных интервалах.
 Нам просто нужно рассматривать каждое уравнение как другую функцию в заданной области и отображать ее так же, как мы изображаем нормальную функцию. Чтобы узнать больше о построении графика кусочной функции, нажмите здесь.
Нам просто нужно рассматривать каждое уравнение как другую функцию в заданной области и отображать ее так же, как мы изображаем нормальную функцию. Чтобы узнать больше о построении графика кусочной функции, нажмите здесь.Как идентифицировать функции с помощью графиков?
Вот несколько приемов для определения функций по графикам:
- Если график представляет собой линию, то это линейная функция, имеющая вид f(x) = ax + b.
- Если график имеет форму идеальной буквы U или перевернутой буквы U, то он является квадратичной функцией и имеет вид f(x) = ax 2 + bx + c.
- Если на графике есть две кривые, симметричные относительно наклонной линии, то это рациональная функция, которая обычно имеет вид f(x) = (ax + b) / (cx + d).
- Если график имеет форму V или перевернутой буквы V, то это функция абсолютного значения и имеет вид f(x) = a |bx + c| + д.
- Если график состоит из нескольких горизонтальных линий, то он представляет собой функцию нижнего или верхнего предела.

- Если график с одной кривой возрастает или убывает с вертикальной асимптотой, то это логарифмическая функция.
- Если график с одной кривой возрастает или убывает с горизонтальной асимптотой, то это экспоненциальная функция.
- Если на графике несколько волн, это может быть одна из тригонометрических функций:
Функция синуса
Функция косинуса
Функция тангенса
Функция косеканса
Функция секанса
Функция котангенса
Как узнать, является ли график функцией?
Функция всегда проходит тест вертикальной линии. Чтобы использовать этот тест, просто возьмите вертикальную линию (или просто вертикальную палочку) и проведите ее по графику слева направо по горизонтали. Ни в какой момент времени линия не должна пересекать график более чем в одной точке, чтобы график представлял функцию.
Как использовать график для решения уравнения?
Сначала определите тип функции, взглянув на график. Возьмем его общее уравнение.
 Используйте некоторые точки на графике и общее уравнение, чтобы определить точное уравнение функции.
Используйте некоторые точки на графике и общее уравнение, чтобы определить точное уравнение функции.Как нарисовать график уравнения?
Чтобы нарисовать график уравнения функции, сделайте следующее:
- Нанесите различные точки уравнения.
- Соедините точки и сформируйте кривую. Полученная таким образом кривая является графиком данного уравнения.
Типы графиков функций
Функция в математике — это особый тип отношения с некоторыми правилами. Функция f, например, представляет собой отношение непустого множества A к непустому множеству B, где областью определения f является A и никакие две различные упорядоченные пары в f не имеют одинаковый первый элемент. Кроме того, у нас есть различные типы функций, которые можно определить на основе их свойств.
Функции: Функция представляет собой отношение между набором входных данных и набором выходных данных, при этом каждый вход связан ровно с одним выходом.

Предположим, у нас есть множества P и Q. Отображение из P в Q будет функцией, только если каждому элементу в множестве P соответствует только один элемент из множества Q.
Графы. В математике, а точнее в теории графов, граф — это структура, состоящая из набора объектов, некоторые из которых каким-то образом «связаны». Объекты соответствуют математическим абстракциям, известным как вершины, а каждая пара связанных вершин известна как ребро. График функции — это множество всех точек плоскости вида (x, f(x)). График f можно также определить как график уравнения y = f. (Икс). В результате график функции является подмножеством графика уравнения.
Типы функций и их графики
Существует несколько типов алгебраических функций, каждая со своим набором характеристик. Многие из этих алгебраических функций можно определить, просто изучив их график.
В зависимости от типа отображаемой функции существуют различные типы графиков.

График линейной функции
График функции возведения в квадрат
График кубической функции
График функции квадратного корня
График обратной функции
График ступенчатой функции
График кусочной функции
Линейный график 1. 42 - Определение формы, если возможно. Например, если это линейная функция вида f(x) = ax + b, то ее график будет линией; если это квадратичная функция вида f(x) = ax 2 + bx + c, то это парабола.
Область определения функции возведения в квадрат представляет собой набор всех действительных чисел, соответствующих оси x.
Поскольку график имеет U-образную форму, диапазон функции возведения в квадрат — все неотрицательные действительные числа.
Поскольку функция симметрична относительно оси Y, она является четной функцией.
Точка пересечения функции возведения в квадрат находится в точке (0, 0).
График функции возведения в квадрат имеет относительный минимум в точке (0, 0).
Кубическая функция является своеобразной функцией.
В начале координат кубическая функция симметрична.
Область определения кубической функции — это множество всех действительных чисел.
Поскольку функция имеет интервал между ними, диапазон кубической функции представляет собой набор всех действительных чисел (-∞,∞)
Точка пересечения графика находится в точке (0, 0).
Область определения состоит из набора неотрицательных действительных чисел (0, ∞).
Диапазон состоит из набора неотрицательных действительных чисел (0, ∞).
Точка пересечения графика находится в точке (0, 0).
Возрастает между интервалами (0,∞).
Домен представляет собой совокупность всех действительных чисел.
Диапазон функции представляет собой набор всех целых чисел.
Точка пересечения по оси X равна [0, 1], а точка пересечения по оси Y равна (0, 0).
Между каждой парой целых чисел график остается постоянным.
Для каждого значения y график перемещается на одну единицу по вертикали.
Все линейные функции имеют вид f(x)=ax+b, где a и b — действительные числа, а an не равно нулю. Графики этих функций всегда будут прямыми линиями. Это означает, что линейная функция является полиномиальной функцией первой степени:
2. График функции возведения в квадрат
График функции возведения в квадрат обычно называют параболой, которая представляет собой U-образную кривую.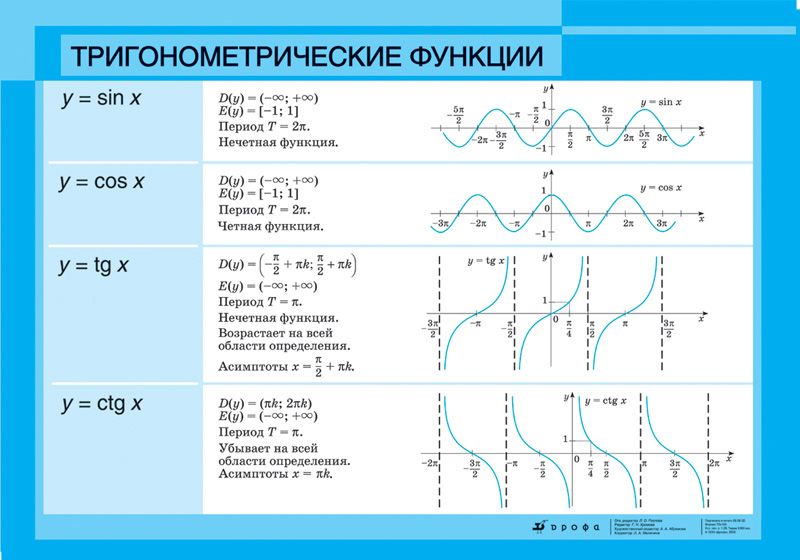 Функция возведения в квадрат f(x) = x2. Диаграмма показана ниже.
Функция возведения в квадрат f(x) = x2. Диаграмма показана ниже.
Свойства функции возведения в квадрат
3. График кубической функции
В отличие от функции возведения в квадрат график кубической функции имеет как положительные, так и отрицательные стороны.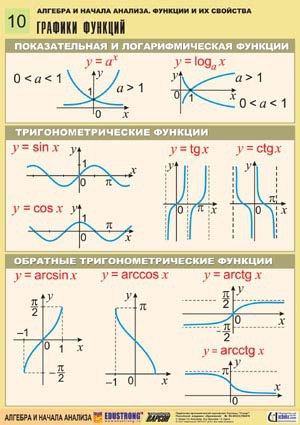 f(x) = x3
f(x) = x3
График кубической функции выглядит так.
Свойства кубической функции
4. График функции извлечения квадратного корня
График функции f(x), где x равно x.
f(x) = x
График функции возведения в квадрат показан ниже.
Как мы видим, график имеет положительную сторону как для x, так и для f(x).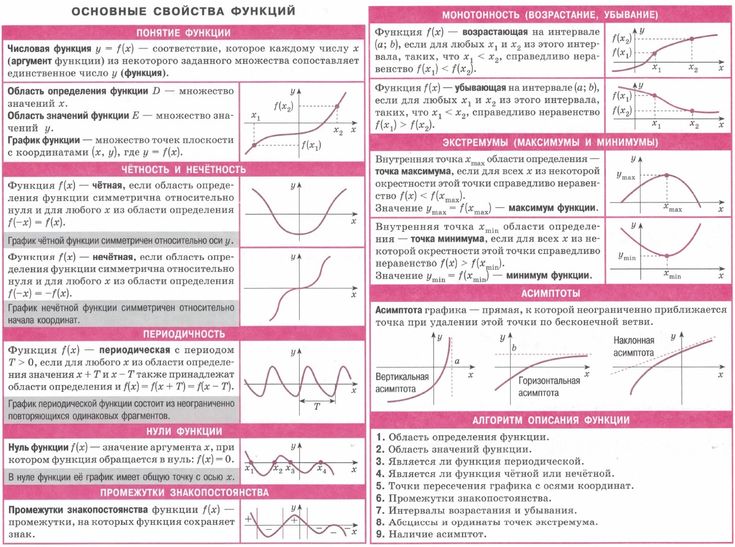
Свойства функции возведения в квадрат
5. График обратной функции
Пусть f(x) — функция f(x) = 1x, известная как обратная функция. Обратный график показан ниже.
Хотя обратная функция симметрична относительно начала координат, она никогда не касается его.
6. График ступенчатой функции
График ступенчатой функции напоминает лестничную клетку со ступенями.
Пусть f(x) = [[x]] + 1 Обозначим ступенчатую функцию. [[x]] обозначает значение, которое «больше или равно x».
График ступенчатой функции показан ниже.
Шаг Свойства функции
7. График кусочной функции
Кусочные функции, также известные как функции, определяемые частями, представляют собой функции, которые имеют различные выражения в зависимости от того, где находится независимая переменная в интервале.
Когда x больше или равно 0, f(x) равно x, а когда x меньше 0, f(x) равно -x.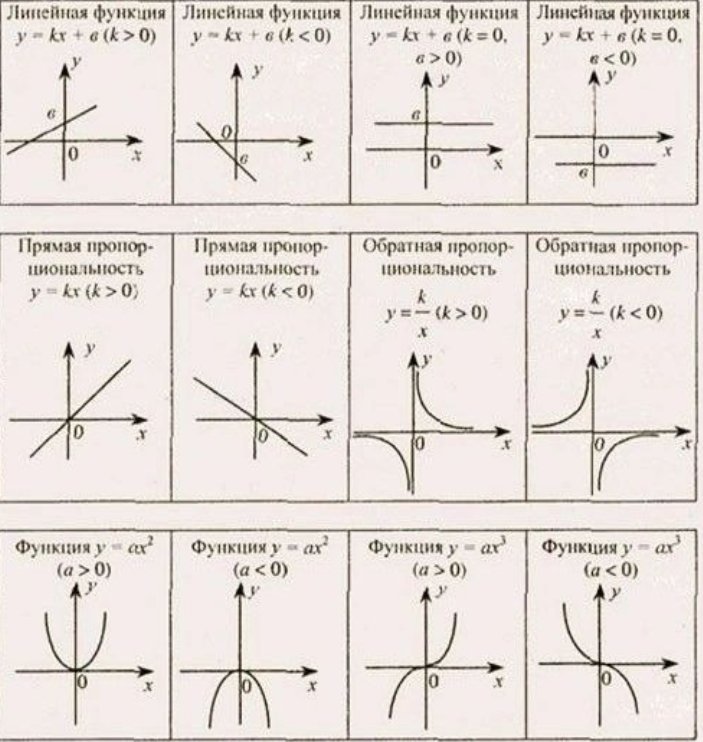

 {n}$$ при натуральных $$ n$$.
{n}$$ при натуральных $$ n$$.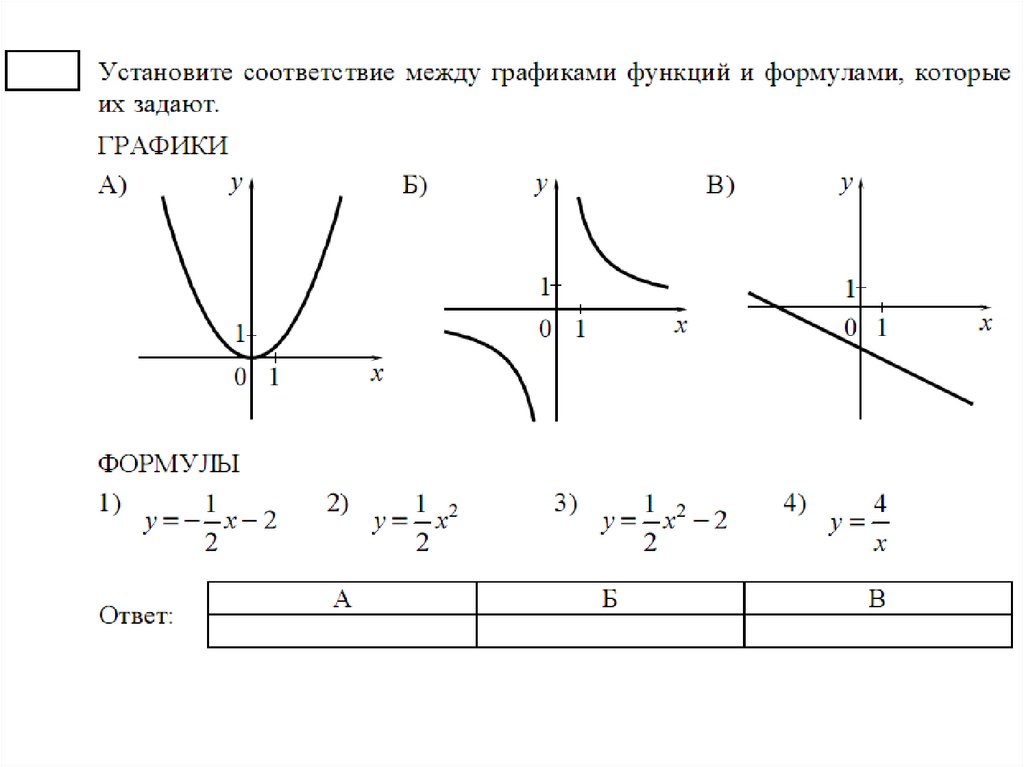 {n}$$, но при этом $$ x$$ и $$ y$$ меняются местами. Для чётных $$ n$$ при этом еще нужно учесть ОДЗ $$ x\ge 0$$. Поэтому график функции $$ f\left(x\right)=\sqrt[n]{x}$$ имеет следующий вид в зависимости от чётности натурального числа $$ n$$ (рис. 7, 8):
{n}$$, но при этом $$ x$$ и $$ y$$ меняются местами. Для чётных $$ n$$ при этом еще нужно учесть ОДЗ $$ x\ge 0$$. Поэтому график функции $$ f\left(x\right)=\sqrt[n]{x}$$ имеет следующий вид в зависимости от чётности натурального числа $$ n$$ (рис. 7, 8): Графики основных функций, таких как линейные, квадратичные, кубические и т. д., довольно просты, графические функции, которые являются сложными, такими как рациональные, логарифмические и т. д., требуют некоторых навыков и некоторых математических понятий для понимания.
Графики основных функций, таких как линейные, квадратичные, кубические и т. д., довольно просты, графические функции, которые являются сложными, такими как рациональные, логарифмические и т. д., требуют некоторых навыков и некоторых математических понятий для понимания.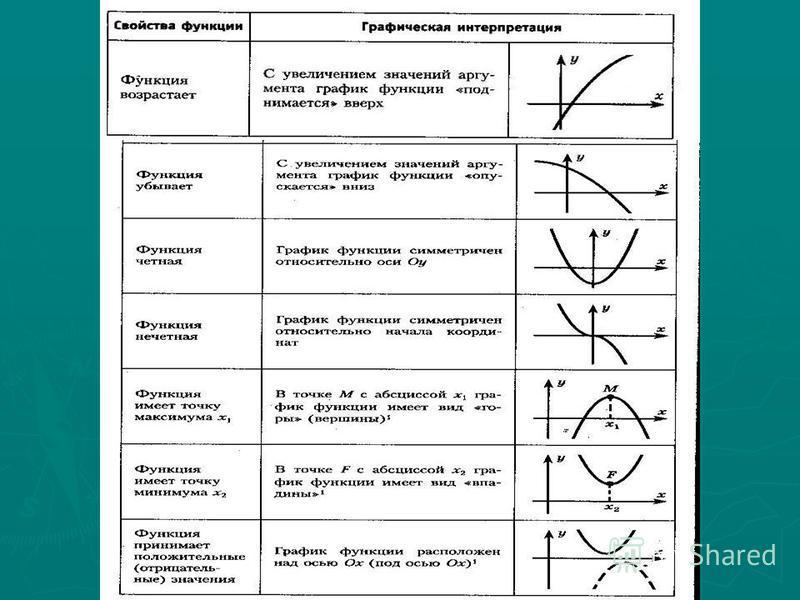 Если кривая (график) представляет собой функцию, то каждая точка кривой удовлетворяет уравнению функции. Например, следующий график представляет линейную функцию f(x) = -x+ 2.
Если кривая (график) представляет собой функцию, то каждая точка кривой удовлетворяет уравнению функции. Например, следующий график представляет линейную функцию f(x) = -x+ 2.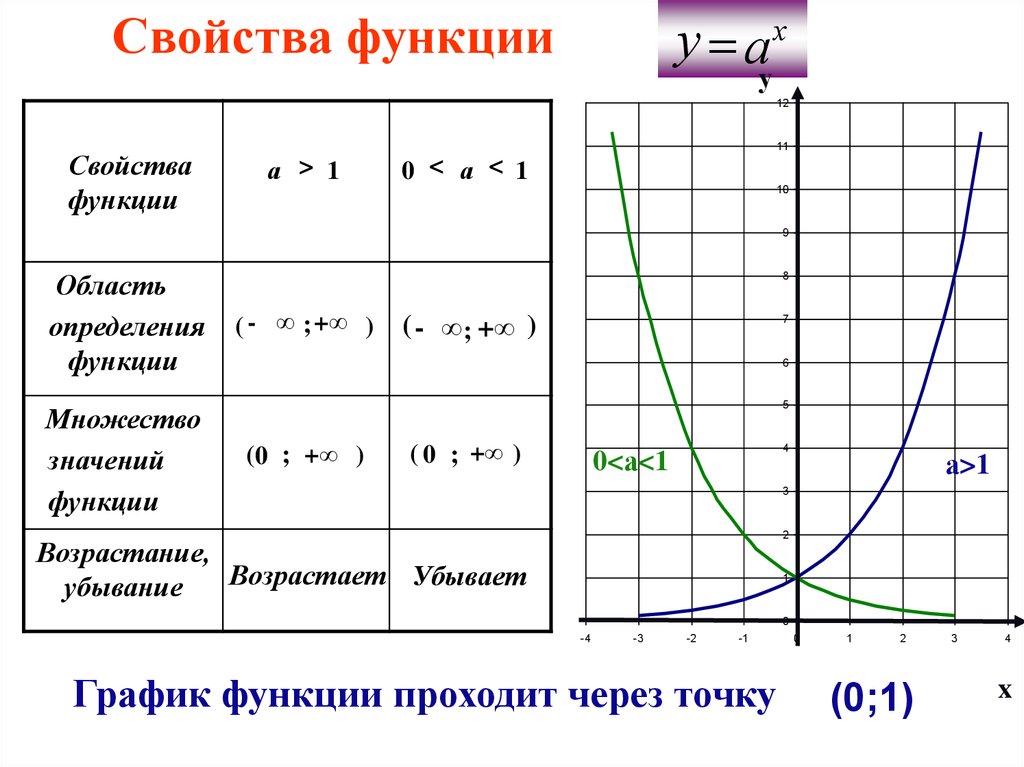
 Но это может не дать идеальной U-образной кривой. Это потому, что для получения идеальной U-образной кривой нам нужно, где она поворачивает. т. е. надо найти его вершину. Найдя вершину, мы можем найти две или три случайные точки с каждой стороны вершины, и они помогут в построении графика функции.
Но это может не дать идеальной U-образной кривой. Это потому, что для получения идеальной U-образной кривой нам нужно, где она поворачивает. т. е. надо найти его вершину. Найдя вершину, мы можем найти две или три случайные точки с каждой стороны вершины, и они помогут в построении графика функции.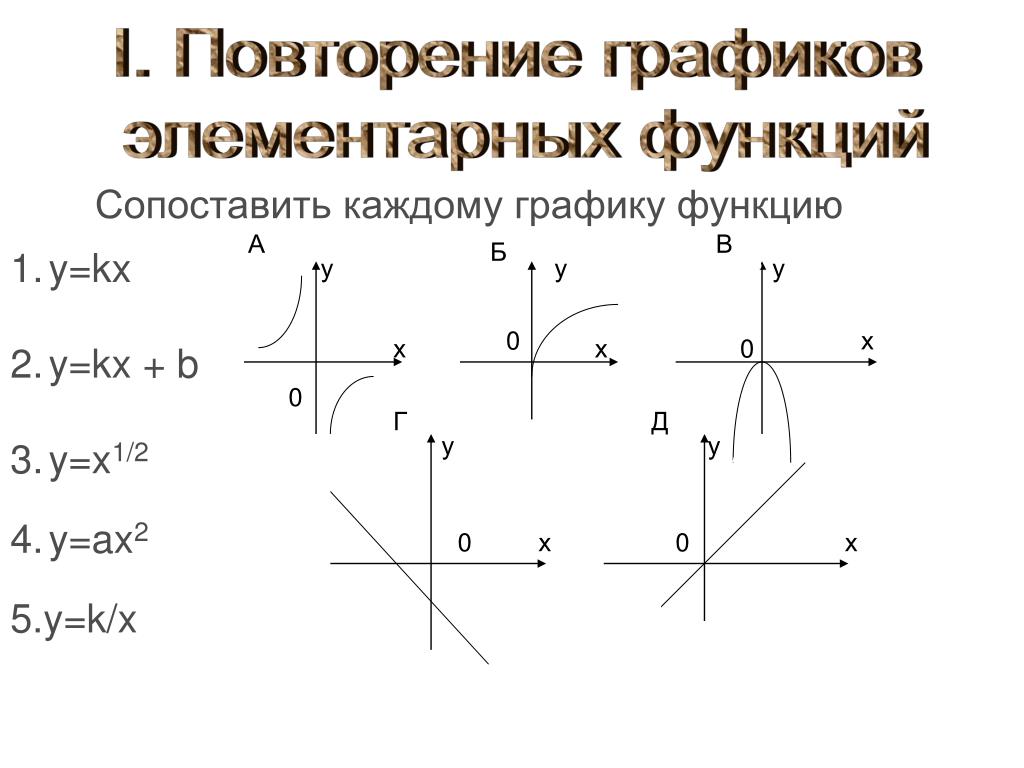

 Мы построим ее график, используя те же шаги, что и упомянутые выше.
Мы построим ее график, используя те же шаги, что и упомянутые выше.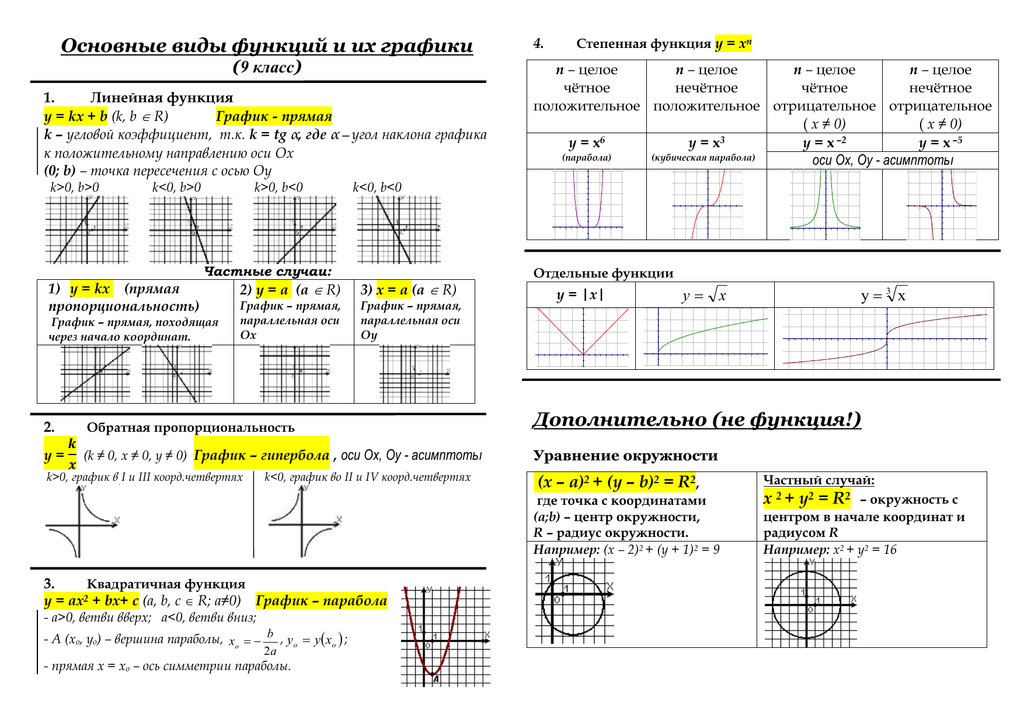
 Затем мы можем применить следующие преобразования для построения графика данной функции.
Затем мы можем применить следующие преобразования для построения графика данной функции.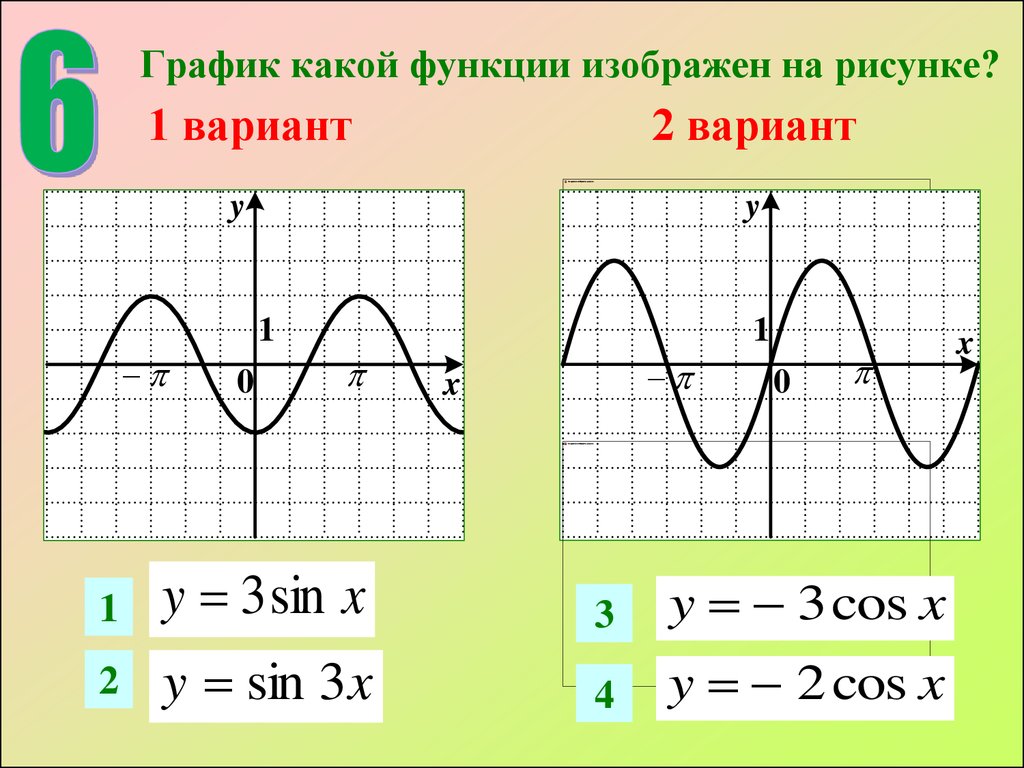
 Нам просто нужно рассматривать каждое уравнение как другую функцию в заданной области и отображать ее так же, как мы изображаем нормальную функцию. Чтобы узнать больше о построении графика кусочной функции, нажмите здесь.
Нам просто нужно рассматривать каждое уравнение как другую функцию в заданной области и отображать ее так же, как мы изображаем нормальную функцию. Чтобы узнать больше о построении графика кусочной функции, нажмите здесь.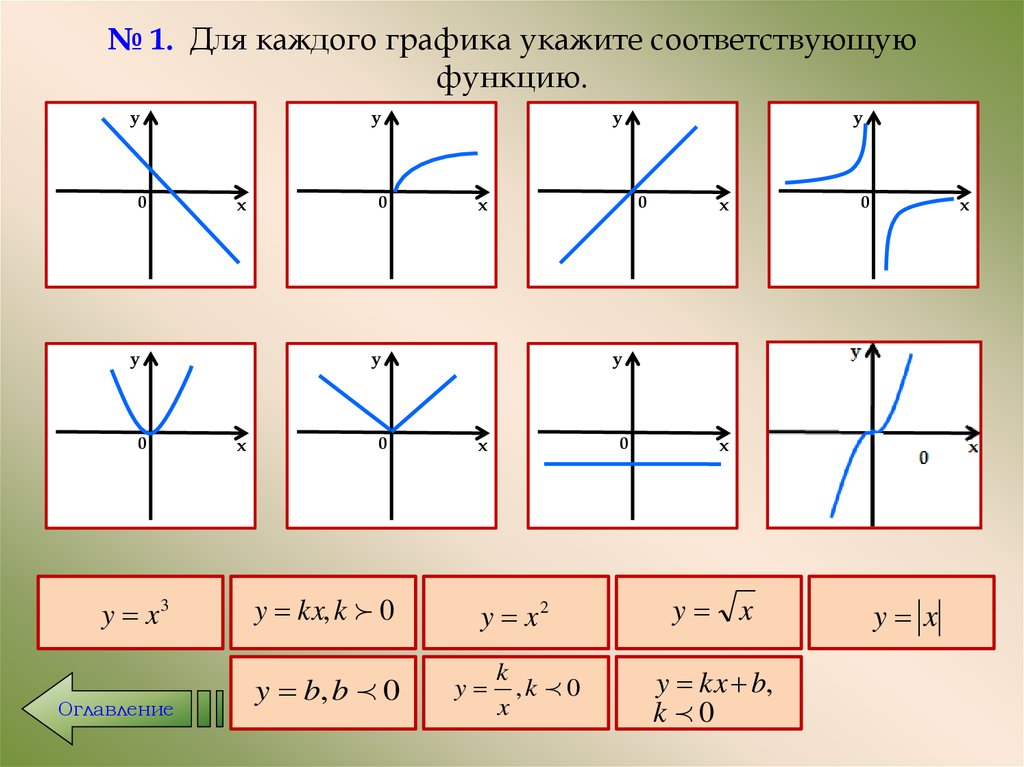
 Используйте некоторые точки на графике и общее уравнение, чтобы определить точное уравнение функции.
Используйте некоторые точки на графике и общее уравнение, чтобы определить точное уравнение функции.
