Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3.  ВЫЧИТАНИЕ§ 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5.  СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ§ 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ Контрольные вопросы ГЛАВА VI § 1.  ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ§ 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3.  КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК§ 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4.  СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросыГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4.  СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК§ 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2.  ПРЕДЕЛ ФУНКЦИИ§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1.  ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК§ 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1.  2 α = 1, называемое основным тригонометрическим тождеством.Доказательство. Формулы сложения. Для любых углов α и β справедливы равенства:
Для любых углов α и β таких, что α ≠ π/2 + πk, β ≠ π/2 + πn, α + β ≠ π/2 + πm (k, n, m принадлежат множеству Z), справедливо:
Для любых углов α и β таких, что α ≠ π/2 + πk, β ≠ π/2 + πn, α – β ≠ π/2 + πm (k, n, m принадлежат множеству Z), справедливо:
Для любых углов α и β таких, что α ≠ πk, β ≠ πn, α + β ≠ πm (k, n, m принадлежат множеству Z), справедливо:
Для любых углов α и β таких, что α ≠ πk, β ≠ πn, α – β ≠ πm (k, n, m принадлежат множеству Z), справедливо:
Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет свое название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс. Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет свое название. Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства. 1 четверть: sin:+ cos:+ tg, ctg:+ Тригонометрические формулы двойного угла, понижения степени и половинного аргумента.
Понижение степени cos2t=21+cos2t; sin2t=21−cos2t Формулы половинного аргумента Универсальная тригонометрическая подстановка. . Универсальной тригонометрической подстановкой называются выражение тригонометрических функций через тангенс половинного аргумента. Эти формулы позволяют выразить любую тригонометрическую функцию через тангенс половинного угла. Это дает возможность свести любое тригонометрическое уравнение к алгебраическому относительно этого тангенса. Пусть t = , тогда , , , . При использовании этих формул следует иметь в виду, что они имеют смысл только тогда, когда определен тангенс половинного угла, т.е. при ; в формуле для tg α требуется, кроме того, чтобы t не равнялось 1, а в формуле для ctg α – чтобы t не равнялось 0. Формула двойного угла — MathCracker.comКалькуляторы Геометрия Инструкции: Используйте эту формулу двойного угла для вычисления тригонометрических значений двойного угла для заданного угла \(\theta\) в форме ниже: Угол в радианах \(\theta\) (например, ‘1’, ‘2pi’ и т.  д.) =Один интересный момент в тригонометрических функциях заключается в том, что есть способ вычислить значение тригонометрической функцией двойного данного угла, используя относительно простые формулы, используя так называемые формулы двойного угла. 92(\тета)}\] Что хорошо в этих формулах, так это то, что если вы знаете тригонометрические значения угла \(\theta\), вы можете использовать приведенные выше формулы для вычисления тригонометрических формул для \(2\theta\). Итак, скажем, что вы знаете тригонометрические значения для 30 о , то вы можете использовать приведенные выше формулы для вычисления тригонометрических значений для 60 9о) = \ displaystyle 2 \ cdot \ frac {\ sqrt {2}} {2} \ cdot \ frac {\ sqrt {2}} {2} = 2 \ cdot \ frac {2} {4} = 1 \] Для чего вы используете двойной угол? Мы говорили, что двойной угол может быть очень полезен для расчетов, но на самом деле это скорее теоретическое применение. Формулы двойного угла чрезвычайно полезны в тождествах, используемых для обеспечения возможности определенного вычисления тригонометрических интегралов. Тесно связанные и концептуально эквивалентные, вы можете использовать эти формулы половинного угла для вычисления тригонометрического значения половинного угла \(\frac{\theta}{2}\) с учетом тригонометрических значений \(\theta\). Пример вычисления двойного угла (включая двойной тангенс угла) Вопрос : Используйте формулу двойного угла для синуса, косинуса и тангенса для исходного угла: \(\theta = \frac{\pi}{8} \). Решение: Нам дан угол \(\theta = \frac{\pi{}}{8}\) радиан. Для нахождения угла используются следующие формулы двойного угла. тригонометрические значения соответствующего двойного угла \(2\theta\). Для синуса: \[ \begin{array}{ccl} \sin(2\theta) & = & \displaystyle \sin(2 \cdot \frac{\pi{}}{8}) \\\\ \\\\ & = & \displaystyle 2 \sin(\frac{\pi{}}{8}) \cos(\frac{\pi{}}{8}) \\\\ \\\\ & = & \displaystyle 2 \times 0,383 \times 0,924 \\\\ \\\\ & = & 1 \end{массив}\] Теперь для косинуса: 92(\frac{\pi{}}{8})} \\\\ \\\\ & = & \displaystyle \frac{2 \times 0,414}{1-0,1714} \\\\ \\\\ & = & 0,999 \end{массив}\] Таким образом, исходя из заданного угла \(\theta = \frac{\pi{}}{8}\) радиан, соответствующий двойной угол
выражения: \(\sin(2\theta) = 1\), \(\cos(2\theta) = 0,707\) и \(\tan(2\theta) = 0,999\). Формула двойного угла Калькулятор геометрии Геометрические решатели Объяснение урока: двухугольные и полуугловые тождестваВ этом объяснении мы узнаем, как использовать тождества двойного угла и половинного угла для оценки тригонометрических значений. Тождества двойного угла дают cos2𝜃 и sin2𝜃 через cos𝜃 и грех𝜃. Они являются частным случаем тождеств суммы, коскоссинсин(𝜃+𝜃′)=𝜃𝜃′−𝜃𝜃′ и sinsincossin(𝜃+𝜃′)=𝜃𝜃′+𝜃𝜃′, а именно, когда 𝜃=𝜃′. Двухугловые тождества могут быть просто производные от них, как показано ниже: Идентичность: двухугольные тождества Для любого действительного числа 𝜃 мы имеем
Coscossinsincossin2𝜃 = 𝜃 — 𝜃, 2𝜃 = 2𝜃𝜃. для 𝜃 ≠ (45,135,225,315)+𝑛360𝜃 ≠ 𝜋4,3𝜋4,5𝜋4,7𝜋4+2𝑛𝜋∘∘∘∘∘, у нас есть tantantan2𝜃=(2𝜃)1−𝜃. Здесь стоит ненадолго остановиться и подумать о соответствующих признаках cos2𝜃, sin2𝜃 и tan2𝜃 как функции от 𝜃. Как показано на следующем рисунке, если мы допустим, что 𝜃 находится в полуквадрант единичного круга, то 2𝜃 в целом квадрант. Например, когда 0≤𝜃≤45∘ (или 0≤𝜃≤𝜋4), мы имеем 0≤2𝜃≤90∘ (или 0≤𝜃≤𝜋2). В таком случае, соз𝜃, грех𝜃, загар𝜃, cos2𝜃, sin2𝜃 и tan2𝜃 все неотрицательно, а tan2𝜃 не определен для 𝜃=45∘. Проверим, что это согласуется с тождествами двойного угла. Первое тождество равно coscossin2𝜃=𝜃−𝜃. Поскольку |𝜃|≥|𝜃|коссин, имеем cossin𝜃≥𝜃, и, таким образом, cossin𝜃−𝜃≥0, что действительно соответствует чтобы cos2𝜃 был неотрицательным. Из второго тождества sincossin2𝜃=2𝜃𝜃 получаем, что sin2𝜃
неотрицательна, если cos𝜃 и
sin𝜃 имеют одинаковый знак или один из них равен нулю. Наконец, поскольку косинус𝜃>𝜃≥0 когда 0≤𝜃45∘, у нас есть 0≤𝜃=𝜃𝜃1tansincos, что приводит к 1−𝜃>0tan, и, таким образом, тантантан2𝜃=2𝜃1−𝜃≥0. Аналогичные рассуждения можно применить ко всем 8 полуквадрантам единичного круга. (для 4 полуквадрантов внизу круга значения 2𝜃 тогда больше, чем 360∘ или 2𝜋 рад) и покажите, что тождества двойного угла выполняются для любых значений 𝜃. Мы также можем использовать эти два числа, чтобы вывести формулу для tan(2𝜃). В таком случае, чисто в плане загара𝜃, tansincossoscossIndIvingThroughOutbyCostantantan (2𝜃) = (2𝜃) (2𝜃) = 2𝜃𝜃𝜃 — 𝜃𝜃 == 2 (𝜃) (1) — = 2𝜃1 — 𝜃, sincoscossciscoscoscossincosos давая нам тантантан(2𝜃)=2𝜃1−𝜃 и cotcotcot(2𝜃)=𝜃−12𝜃. Давайте посмотрим на нашем первом примере, как использовать эти двухугольные тождества для
упростить тригонометрические выражения. Пример 1. Упрощение тригонометрических выражений с использованием тождеств с двойными угламиУпростить 1−2𝑥1+2𝑥.coscos ОтветНапомним, что coscossin2𝑥=𝑥−𝑥, который мы можно использовать для упрощения числителя и знаменателя: 1−2𝑥=1−𝑥−𝑥=1−𝑥+𝑥=2𝑥,coscossincossinsin где мы использовали тождество Пифагора 1−𝑥=𝑥cossin. В знаменателе, теперь с тождеством 1−𝑥=𝑥sincos, 1+2𝑥=1+𝑥−𝑥=1+−𝑥=2𝑥.coscossincossincos Следовательно, 1−2𝑥1+2𝑥=2𝑥2𝑥=𝑥.coscossincostan Обратим внимание на два тождества, которые мы получили из coscossin2𝜃=𝜃−𝜃 в предыдущий пример. Идентификация: Идентичность, полученная из идентичности с двойным углом cos 2 𝜃 = cos2 𝜃 — sin 2 𝜃Для любого действительного числа 𝜃 имеем 1+2𝜃=2𝜃,1−2𝜃=2𝜃.coscoscossin Теперь мы рассмотрим пример того, как мы можем упростить тригонометрическое выражение с помощью
используя тождество двойного угла в противоположном направлении. Пример 2. Упрощение тригонометрических выражений с использованием двуугольных тождествУпростить sinsin𝑥−𝑥. ОтветЗаметим, что мы можем исключить грех𝑥: sinsinsinsin𝑥−𝑥=𝑥1−𝑥. Пифагорейское тождество cossin𝑥+𝑥=1 дает 1−𝑥=𝑥sincos. Подставив это в лиды к sinsinsincossincos𝑥−𝑥=𝑥𝑥=(𝑥𝑥). Используя тождество двойного угла sinsincos2𝑥=2𝑥𝑥, мы находим, что sincossin𝑥𝑥=2𝑥2. Замена дает sinsinsinsin𝑥−𝑥=2𝑥2=14(2𝑥). Теперь оценим тригонометрическое выражение, используя тождество двойного угла. Пример 3. Использование двухугольных тождеств для вычисления тригонометрического выраженияНайдите без использования калькулятора значение sincos2𝐵22𝐵 учитывая cos𝐵=45, где 3𝜋2𝐵2𝜋. Ответ Чтобы применить формулы двойного угла, нам нужно знать значение sin𝐵. Пифагорейская идентичность
синкос𝐵+𝐵=1
можно решить дать
sincos𝐵=1−𝐵=1−45=925. Итак, sin𝐵 равно 35 или −35. Информация о расположении 𝐵 говорит нам, что он находится в 4-м квадранте, где синус отрицателен. Следовательно, грех𝐵=−35. Использование тождеств двойного угла sinsincos2𝐵=2𝐵𝐵 и coscossin2𝐵=𝐵−𝐵, находим, что Sincossincoscossin2𝐵22𝐵 = 2𝐵𝐵2𝐵 — 𝐵 = 2 — 2 — = — = — 127. Конечно альтернатива состоит в том, чтобы заметить, что нас просят оценить tan2𝐵2 и используйте формулу двойного угла для касательных. До сих пор мы использовали тождества с двойным углом. Полуугольные тождества могут можно вывести из них, просто поняв, что разница между рассмотрением один угол и его двойник, а рассмотрение угла и его половины — это просто вопрос перспектива. Использование тождества 2𝜃=1+2𝜃coscos
которое мы получили из тождества двойного угла
coscossin2𝜃=𝜃−𝜃 и
подставляя в 2𝜃=𝜑 и
𝜃=𝜑2, получаем
2𝜑2=1+𝜑𝜑2=±1+𝜑2. Начиная с другого тождества, полученного из тождества двойного угла coscossin2𝜃=𝜃−𝜃 (т. е. 2𝜃=1−2𝜃sincos), мы находим, что 2𝜑2=1−𝜑𝜑2=±1−𝜑2.sincossincos Наконец, чтобы найти tan𝜑2, мы используем выражения мы только что установили для cos𝜑2 и sin𝜑2 написав tansincoscoscoscos𝜑2==±1−𝜑2⋅±21+𝜑=±1−𝜑1+𝜑. С помощью трех полуугловых тождеств, которые мы получили выше, мы видим, что абсолютные значения трех тригонометрических функций половины угла зависят только от значения косинуса этого угла. Однако «±» показывает, что их знаки не определены. Это означает, что мы сможем написать правильный знак в тождестве, только если мы знаем, в какой четверти находится половина угла. Это происходит из-за того, что угол не полностью определяется своим косинусом
ценить. Возьмем, к примеру
𝜑=140∘,
𝜑=220∘,
𝜑=500∘,
и 𝜑=580∘. Пока у нас есть
coscoscoscos𝜑=𝜑=𝜑=𝜑, мы видим, что
coscoscos𝜑2=𝜑2=−𝜑2=−𝜑2
и sinsinsinsin𝜑2=𝜑2=−𝜑2=−𝜑2, как показано в следующем
диаграмма. Давайте теперь посмотрим, как можно переписать тождество касательной половины угла так, чтобы знак определяется. Начиная с тансинкос𝜑2=, умножаем числитель и знаменатель дроби в правой части на 2𝜑2cos, что дает tansincoscos𝜑2=22. Числитель можно переписать как sin𝜑, используя двуугольные тождества 2𝜃𝜃=2𝜃sincossin (с 2𝜃=𝜑 и 𝜃=𝜑2) и знаменатель как 1+𝜑cos с использованием тождества 1+2𝜃=2𝜃coscos (с 2𝜃=𝜑 и 𝜃=𝜑2), производная от двойного угла тождество coscossin2𝜃=𝜃−𝜃. Отсюда имеем тансинкос𝜑2=𝜑1+𝜑. Начиная снова с тансинкос𝜑2=, теперь умножаем числитель и знаменатель дроби в правой части на 2𝜑2sin. Мы получили tansinsincos𝜑2=22. Используя здесь тождество 1−2𝜃=2𝜃cossin,
мы можем переписать 2𝜑2sin как
1−𝜑cos и, как прежде,
2𝜑2𝜑2sincos как
грех𝜑. Следовательно, мы находим, что
танкосин𝜑2=1−𝜑𝜑. Стоит отметить, что перестановка tancoscos𝜑2=±1−𝜑1+𝜑 путем умножения правой части уравнения либо 1+𝜑1+𝜑coscos, либо 1−𝜑1−𝜑coscos ведет к тансинкос𝜑2=±|𝜑|1+𝜑 и танкосин𝜑2=±1−𝜑|𝜑|. Изучение соответствующих знаков tan𝜑2 и sin𝜑 как приведенной в следующей таблице, мы делаем вывод, что загар𝜑2 и грех𝜑 всегда имеют один и тот же знак. Это позволяет установить тождества тансинкос𝜑2=𝜑1+𝜑 и танкосин𝜑2=1−𝜑𝜑.
Повторим только что полученные тождества полууглов. Идентичность: полуугловые тождестваДля любого действительного числа 𝜃 мы имеем коссинкос𝜃2=±1+𝜃2,𝜃2=±1−𝜃2. Для 𝜃≠180+𝑛360(𝜃≠𝜋+2𝑛𝜋)∘∘, где 𝑛 — целое число, имеем tancoscostansincos𝜃2=±1−𝜃1+𝜃,𝜃2=𝜃1+𝜃. Для 𝜃≠(0,180)+𝑛360(𝜃≠(0,𝜋)+2𝑛𝜋)∘∘ имеем танкосин𝜃2=1−𝜃𝜃. Давайте посмотрим, как использовать тождества половинного угла в следующем пример. Пример 4. Вычисление функции косинуса для половинного угла с учетом функции косинуса и квадрант углаНайдите значение cos𝜃2 дано cos𝜃=1517, где 0𝜃90∘∘, без использования калькулятора. ОтветНапомним тождество половинного угла coscos𝜃2=±1+𝜃2. Нам говорят, что 0𝜃90∘∘. Следовательно, 0𝜃245∘∘ и cos𝜃2>0. Это означает, что у нас есть coscos𝜃2=1+𝜃2 поскольку −1+𝜃2≤0.cos Найдем значение cos𝜃2 по формуле
подставляя значение cos𝜃 в указанное выше
уравнение:
cos𝜃2=1+2=322×17=1617=4√17. Эту дробь можно рационализировать, умножив ее на √17√17, что дает cos𝜃2=4√1717. Наконец, давайте посмотрим на нашем последнем примере, как двойной угол и половинный угол тождества можно использовать для нахождения точного значения некоторых тригонометрических функций. Пример 5. Нахождение точного значения тригонометрического выраженияИспользуя формулы половинного угла или иным образом, найдите точное значение загар𝜋8. ОтветУгол 𝜋8 радиан не является одним из специальных углов, тригонометрические отношения которых хорошо известны. Однако мы замечаем, что это половина значения этих специальных углов, а именно половина 𝜋4 радиана. Используя тождество половинного угла тансинкос𝜃2=𝜃1+𝜃, мы находим, что tansincos𝜋8=1+. Так как sincos𝜋4=𝜋4=1√2, у нас есть tan𝜋8=1+=1√2+1.√√ Умножение правой части на √2−1√2−1
дает
tan𝜋8=√2−12−1=√2−1. |
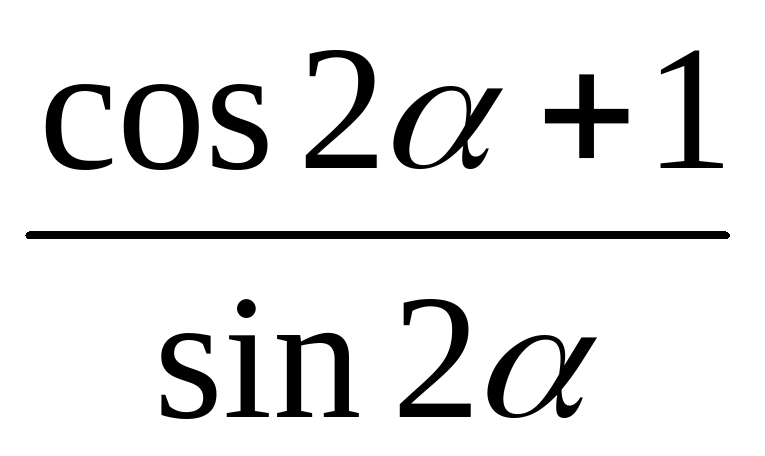
Я имею в виду, что тригонометрические таблицы вычисляются не с использованием двойного угла, начиная с некоторых известных углов, а вместо этого с использованием приближения Тейлора.
Это имеет место для 0≤𝜃≤45∘.
coscoscos
