Cos между векторами: Найти косинус угла между векторами (3;-1) и (1;2)

Содержание

Векторы и матрицы | Вводный курс ML

Все курсы > Вводный курс > Занятие 12

Содержание занятия

Ещё на первом занятии мы упомянули, что в уравнении может быть несколько независимых переменных.

$$y = w_1 \times x_1 + w_2 \times x_2 + w_0 $$

Такое уравнение нельзя изобразить на координатной плоскости (имеющей два измерения, x и y), потому что в нем три переменных, а значит три измерения. Нужен график, имеющий три плоскости.

С помощью этого графика мы можем представить зависимость обхвата шеи не только от роста, но и, например, от веса.

На самом деле измерений может быть и больше, просто так как мы живём в трёхмерном пространстве, представить четыре и более измерений мы не можем. Математически же это вполне возможно.

Данные как векторы и матрицы

Помимо того, что мы можем представить данные на графике (по крайней мере вплоть до третьего измерения), мы также можем представить их в форме вектора. Вектор, по сути, это набор чисел, описывающих координаты наших данных.

Если взять несколько точек и соответственно несколько векторов,

то получится набор чисел, называемых матрицей.

Из сказанного выше очевидно, что любой вектор — не что иное как матрица, в которой один столбец или одна строка.

Область математики, изучающая векторы и матрицы, называется линейной алгеброй.

На этом занятии мы рассмотрим два аспекта векторных и матричных вычислений. Во-первых, посмотрим на удобный способ умножения одного вектора на другой. Во-вторых, посмотрим как мы можем рассчитать угол между двумя векторами.

Умножение векторов

Вспомним, как мы делали прогноз с помощью нашей модели. Мы умножали вес (наклон) на значение независимой переменной и прибавляли ошибку (сдвиг). Когда у нас несколько независимых переменных и несколько весов, нам нужно их попарно перемножить и сложить произведения.

Если представить и веса, и значения независимых переменных с помощью векторов, то можно воспользоваться инструментом, который называется скалярным произведением векторов (dot product), чтобы получить прогнозное значение (ŷ).

Работа над ошибками. На видео представлена иная схема расположения векторов (см. скриншот ниже), а именно вектор-столбец весов мы умножаем на вектор-строку данных.

Результат вычислений от этого не меняется, однако исправленное положение векторов математически более точное.

Как мы узнаем на следующем курсе, перемножать можно не только векторы, но и матрицы. При этом при нахождении произведения двух матриц мы умножаем строки первой матрицы на столбцы второй. И здесь положение множителей будет иметь значение для вычисления конечного результата.

Поэтому и векторы, которые являются частным случаем матрицы с одной строкой или одним столбцом, правильнее расположить именно таким образом.

Добавлю, что если вы не вполне поняли, что это значит, ничего страшного, на следующем курсе мы во всем разберемся.

Скалярное произведение векторов на Питоне

На Питоне это реализовано с помощью библиотеки Numpy. До сих пор мы создавали массивы Numpy в, скажем так, служебных целях, чтобы использовать их, например, в моделях Scikit-learn.

Сегодня рассмотрим эти массивы сами по себе. По сути, массив Numpy (Numpy array), это и есть вектор или матрица. Давайте посмотрим, как создать такой массив, и как перемножить два вектора.

Вначале откроем ноутбук к этому занятию⧉

Вначале разберемся с основами работы с массивами.

import numpy as np

# предположим мы записали наши данные

# роста, веса и обхвата шеи одного человека в список

data = [1.72, 54, 36.2]

# убедимся, что это список с помощью функции type()

type(data)

# преобразуем список в массив Numpy

data_Numpy = np. array(data)

data_Numpy

array([ 1.72, 54. , 36.2 ])

# если у нас несколько наблюдений, то нужна матрица, т.е.

# по сути, несколько векторов

data_matrix = np.array([[1.72, 54, 36.2], [1.74, 58, 36.3], [1.68, 52, 32.9]])

data_matrix

array([[ 1.72, 54. , 36.2 ],

[ 1.74, 58. , 36.3 ],

[ 1.68, 52. , 32.9 ]])

# мы можем посмотреть размерность матрицы (количество строк и столбцов)

data_matrix.shape

(3, 3)

Теперь мы готовы умножить один вектор на другой.

# даны два вектора в виде массивов Numpy

a = np.array([1.72, 54]) # вектор данных

w = np.array([19.86, 0.05]) # вектор весов

# перемножим их вручную

1.72 * 19.86 + 54 * 0.05

36.8592

# используем скалярное произведение векторов

np.dot(a, w)

36.8592

Именно благодаря скалярному произведению векторов компьютер так эффективно перемножает веса и данные и минимизирует функцию потерь.

Теперь посмотрим на угол между векторами.

Угол между векторами

Представление данных в форме вектора имеет ещё одно полезное свойство. Мы можем измерить близость двух векторов или угол между ними. Чем угол меньше, тем они ближе.

Посмотрим на формулу.

$$ \cos(\theta )={\mathbf {b} \cdot \mathbf {c} \over \|\mathbf {b} \|\|\mathbf {c} \|} $$

В этой формуле мы умножаем один вектор на другой и делим на произведение их длин. Результатом будет косинус угла θ между ними. Зная косинус, мы можем найти сам угол в градусах.

Косинусное сходство с помощью Питона

В первую очередь найдем косинус угла по формуле, приведенной выше.

# даны два вектора (данные двух человек)

# нам нужно понять, насколько они схожи

b = np.array([1.72, 54, 36.2])

c = np.array([1.56, 47, 30.0])

# вначале выполним операции в числителе формулы

numerator = np.dot(b, c)

# теперь займемся знаменателем и

# (1) рассчитаем длины (по большому счету, это теорема Пифагора)

bLen = np. linalg.norm(b)

cLen = np.linalg.norm(c)

# (2) перемножим их

denominator = bLen * cLen

# посмотрим, чему равен косинус угла между векторами

cosine = numerator/denominator

cosine

0.9997468709497721

Теперь рассчитаем угол в градусах

# для этого вначале вычислим угол в радианах

angle_radians = np.arccos(cosine)

# затем в градусах

angle_degrees = angle_radians * 360/2/np.pi

angle_degrees

1.2891925481394304

Как мы видим угол чрезвычайно мал, а значит векторы очень близки друг к другу.

Мы будем на практике применять косинусное сходство или близость векторов, например, при построении рекомендательных систем для сопутствующих товаров в интернет-магазине.

Когда вы покупаете, например, холодильник, то микроволновую печь вам рекомендуют именно потому, что вектор ваших покупок очень близок к вектору покупок тех, кто купил микроволновку.

Подведем итог

На этом занятии мы узнали, что данные можно представить в виде вектора и матрицы. Это создает новые возможности для вычислений и преобразования данных.

В частности, мы посмотрели на то, как умножить один вектор на другой через скалярное произведение векторов, а также научились вычислять косинусное сходство между двумя векторами.

Вопросы для закрепления

Какие два вектора мы перемножаем для того, чтобы сделать прогноз?

Посмотреть правильный ответ

Ответ: вектор весов и вектор данных (ну и еще прибавляем ошибку).

Какое расстояние (сходство) помогает определить близость векторов?

Посмотреть правильный ответ

Ответ: косинусное расстояние

Дополнительные упражнения⧉ вы найдете в конце ноутбука.

Последний штрих

Прежде чем перейти к построению моделей остается последний штрих: научиться разделять данные, на которых мы будем обучать модель.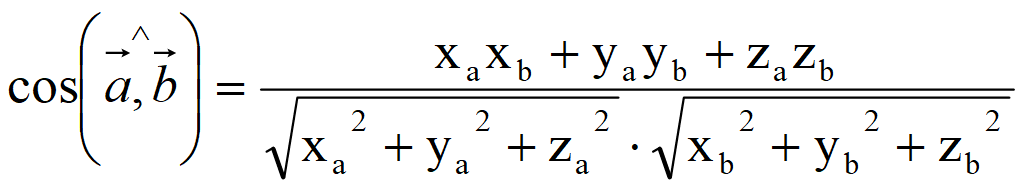

Нахождение угла между векторами, примеры и решения — Студопедия

Пусть на плоскости или в трехмерном пространстве заданы два ненулевых вектора и . Отложим от произвольной точки O векторы и . Тогда справедливо следующее определение.

Определение.

Углом между векторами и называется угол между лучами OA и OB.

Угол между векторами и будем обозначать как .

Угол между векторами может принимать значения от 0 до или, что то же самое, от до .

когда векторы и сонаправленные, когда векторы и противоположно направленные.

Определение.

Векторы и называются перпендикулярными, если угол между ними равен ( радиан).

Если хотя бы один из векторов и нулевой, то угол не определен.

Нахождение угла между векторами, примеры и решения.

Косинус угла между векторами и , а значит и сам угол, в общем случае может быть найден либо с использованием скалярного произведения векторов, либо с использованием теоремы косинусов для треугольника, построенного на векторах и .

Разберем эти случаи.

По определению скалярное произведение векторов есть . Если векторы и ненулевые, то можно разделить обе части последнего равенства на произведение длин векторов и , и мы получим формулу для нахождения косинуса угла между ненулевыми векторами: . Эту формулу можно использовать, если известны длины векторов и их скалярное произведение.

Пример.

Вычислите косинус угла между векторами и , а также найдите сам угол, если длины векторов и равны 3 и 6 соответственно, а их скалярное произведение равно -9.

Решение.

В условии задачи даны все величины необходимые для применения формулы . Вычисляем косинус угла между векторами и : .

Теперь находим угол между векторами: .

Ответ:

Существуют задачи, где векторы заданы координатами в прямоугольной системе координат на плоскости или в пространстве. В этих случаях для нахождения косинуса угла между векторами можно использовать все ту же формулу , но в координатной форме. Получим ее.

Длина вектора есть корень квадратный из суммы квадратов его координат, скалярное произведение векторов равно сумме произведений соответствующих координат. Следовательно, формула для вычисления косинуса угла между векторами на плоскости имеет вид , а для векторов в трехмерном пространстве — .

Пример.

Найдите угол между векторами , заданными в прямоугольной системе координат.

Решение.

Можно сразу воспользоваться формулой :

А можно для нахождения косинуса угла между векторами использовать формулу , предварительно вычислив длины векторов и скалярное произведение по координатам:

Ответ:

К предыдущему случаю сводится задача, когда даны координаты трех точек (например А, В и С) в прямоугольной системе координат и требуется найти какой-нибудь угол (например, ).

Действительно, угол равен углу между векторами и . Координаты этих векторов вычисляются как разность соответствующих координат точек конца и начала вектора.

Пример.

На плоскости в декартовой системе координат заданы координаты трех точек . Найдите косинус угла между векторами и .

Решение.

Определим координаты векторов и по координатам заданных точек:

Теперь воспользуемся формулой для нахождения косинуса угла между векторами на плоскости в координатах:

Ответ:

Угол между векторами и также можно вычислить по теореме косинусов. Если отложить от точки O векторы и , то по теореме косинусов в треугольнике ОАВ мы можем записать , что эквивалентно равенству , откуда находим косинус угла между векторами . Для применения полученной формулы нам нужны лишь длины векторов и , которые легко находятся по координатам векторов и . Однако, этот метод практически не используется, так как косинус угла между векторами проще найти по формуле .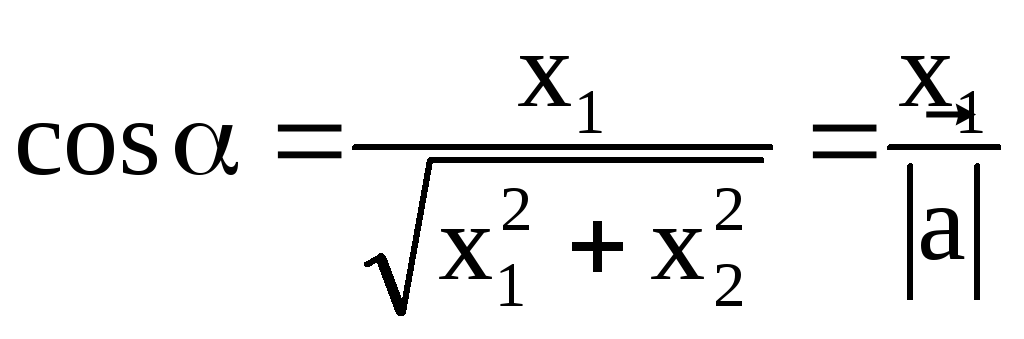

Вычисление ортогональной проекции(сво-во проекции):

Проекция вектора на ось l равна произведению модуля вектора на косинус угла φ между вектором и осью, т.е. пр cosφ.

Док-во: Если φ= < , то пр_l =+ = *cos φ.

Если φ> (φ≤ ), то пр_l =- =- * cos( –φ) = cosφ (см.рис10)

Если φ= , то пр_l = 0 = соs φ.

Следствие: Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нуле, если этот угол – прямой.

Следствие: Проекции равных векторов на одну и ту же ось равны между собой.

Вычисление ортогональной проекции суммы векторов (сво-во проекции):

Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.

Док-во: Пусть, например, = + + . Имеем пр_l =+ =+ + — , т.е. пр_l( + + ) = пр_l + пр_l + пр_l (см. рис11)

РИС. 11

Вычисление произведения вектора на число:

При умножеии вектора на число λ его проекция на ось так же умножается на это число, т.е. пр_l (λ* )= λ* пр_l .

Док-во: При λ > 0 имеем пр_l (λ* )= *cos φ = λ* φ = λ*пр_l

При λl (λ* )= *cos( –φ)=- * (-cosφ) = * cosφ= λ *пр_l .

Свойство справедливо и при

Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.

Урок Видео: Угол между двумя векторами в пространстве

Стенограмма видео

Угол между двумя векторами в пространстве Космос

В этом видео мы научимся как мы можем найти угол между любыми двумя векторами в пространстве, используя точку товар. И мы увидим, как это сделать в несколько ситуаций, например, с заданными составными формами вектора или заданным графическое представление векторов.

Для этого мы сначала собираемся нужно напомнить пару фактов о векторах. Во-первых, мы знаем, как найти точку произведение двух векторов одинаковой размерности. Если 𝐮 — вектор с компонентами 𝐮 один, 𝐮 два, до 𝐮 𝑛 и 𝐯 вектор с компонентами 𝐯 один, 𝐯 два, вверх в 𝐯 𝑛, то скалярное произведение между 𝐮 и 𝐯 равно сумме произведений соответствующих компонентов. 𝐮 точка 𝐯 это 𝐮 один 𝐯 один плюс 𝐮 два 𝐯 два и суммируем до 𝐮 𝑛 раз 𝐯 𝑛. И мы видели несколько разных способов мы можем применить скалярное произведение.

Например, если 𝜃 — угол между векторами 𝐮 и 𝐯, то мы знаем, что cos 𝜃 будет равен точке произведение между 𝐮 и 𝐯, деленное на величину 𝐮, умноженную на величину 𝐯. И стоит отметить, что второй способ просмотра этой формулы. Если мы позволим 𝐮 шляпе быть единичным вектором указывающий в том же направлении, что и вектор 𝐮, а 𝐯 — единичный вектор, указывающий в том же направлении, что и вектор 𝐯, поэтому шляпа 𝐮 равна 𝐮, деленной на величину 𝐮 а 𝐯 шляпа 𝐯 делится на величину 𝐯 — тогда косинус 𝜃 тоже будет равно скалярному произведению между шляпой 𝐮 и шляпой 𝐯.

Это дает нам красивую геометрическую интерпретация скалярного произведения.

Вот эту формулу мы и собираемся используйте, чтобы найти угол между нашими двумя векторами. Вычислим это выражение и затем возьмите обратные косинусы обеих частей уравнения. Однако есть одна вещь, которая стоит указывая здесь на нашу ценность 𝜃. Мы вспоминаем, если мы работаем в градусов, то функция арккосинуса будет иметь диапазон от нуля до 180 степени включительно. Итак, если мы возьмем только обратный cos этого выражения, наш ответ всегда будет между 0 и 180 градусами включительно.

И это дает полезный результат геометрически. Если мы нарисуем векторы 𝐮 и 𝐯 начиная с той же точки, то, используя эту формулу, чтобы найти значение 𝜃, мы всегда будет получать меньший угол. И, конечно же, мы можем найти другой ракурс прямо из эскиза. Сумма этих двух углов дает нам 360. Значит угол будет 360 градусов минус 𝜃. И альтернативный метод видения почему это верно, если подумать о том, что происходит, когда мы берем обратный стороны уравнения.

Мы знаем, что есть несколько решений за это. И мы также знаем, что если 𝜃 является решение этого, то 360 минус 𝜃 также является решением, потому что cos 𝜃 равен равно косинусу 360 минус 𝜃. Последнее, что мы собираемся указать вытекает из того, что все, что мы только что обсудили, верно, если бы вместо этого мы работали в радианы. Однако наши значения 𝜃 будут диапазон между нулем и 𝜋 вместо этого. Давайте теперь посмотрим на несколько примеров того, как мы собираемся применить это, чтобы найти угол между двумя векторами.

Учитывая, что модуль вектора 𝐀 равно 35, а модуль вектора 𝐁 равен 23, а скалярное произведение между 𝐀 и 𝐁 равно равный отрицательному корню 805 из двух, деленному на два, определяют меру меньшего угол между двумя векторами.

В этом вопросе нам дается информация о векторах 𝐀 и 𝐁. И нас просят определить меньший угол между этими двумя векторами. Иногда в этих вопросах мы нравится рисовать картину происходящего. Однако информация, которую мы данные о наших векторах не позволят нам нарисовать картинку. Мы не знаем компонентов векторы 𝐀 и 𝐁. Вместо этого мы знаем только их модуль и их скалярное произведение.

Так что нам придется полагаться полностью по нашей формуле. Помните, это говорит нам, является ли 𝜃 угол между двумя векторами 𝐀 и 𝐁, то cos вектора 𝜃 будет равен точке произведение между 𝐀 и 𝐁, деленное на модуль 𝐀, умноженный на модуль 𝐁. И мы бы нашли значение 𝜃 взяв арккосинус обеих частей этого уравнения. И это дает нам полезный результат потому что функция арккосинуса имеет диапазон от нуля до 180 градусов.

Поэтому это не имеет большого значения как мы рисуем наши векторы 𝐀 и 𝐁.

Если значение 𝜃 между нулем и 180, это всегда будет давать нам меньший угол между этими двумя векторами. Единственная возможная оговорка к этому было бы, если бы наши векторы указывали в прямо противоположных направлениях. Тогда угол, измеренный в обоих направления будут равны 180 градусам. Однако, как мы увидим, это не что происходит в этом вопросе.

Теперь найдем меньший угол между нашими двумя векторами 𝐀 и 𝐁. Он решает уравнение, потому что 𝜃 будет равно скалярному произведению между 𝐀 и 𝐁, деленному на модуль 𝐀 раз больше модуля 𝐁. В вопросе нам говорят точку произведение между 𝐀 и 𝐁 равно отрицательному корню 805 два из двух, модуль 𝐀 равно 35, а модуль 𝐁 равен 23. Таким образом, мы можем подставить эти значения прямо в нашу формулу, что дает нам, потому что 𝜃 отрицательный корень 805 два над двумя все разделить на 35 умножить на 23,

Мы можем упростить это. Помните, что деление на число так же, как умножение на обратное этому числу, что дает нам cos 𝜃 отрицательный корень 805 два разделить на два раза 35 раз 23. И если бы мы должны были оценить 35 раз 23, мы увидели бы, что оно в точности равно 805. Поэтому мы можем их отменить, оставив нам с cos 𝜃 равно отрицательному корню два из двух.

И, наконец, мы можем решить для нашего значение 𝜃, взяв обратный cos обеих частей уравнения. Помните, мы знаем, что это даст нам меньший угол между нашими двумя векторами. Это дает нам 𝜃 является обратным cos отрицательного корня два из двух, который мы можем вычислить, составляет 135 градусов.

Давайте теперь посмотрим на пример того, как мы будет вычислять угол между двумя векторами, учитывая формы их компонентов.

Найдите угол 𝜃 между векторы 𝐕 четыре, два, минус один и 𝐖 восемь, четыре, минус два.

В этом вопросе нам дано два вектора в компонентной форме. И нас просят найти угол 𝜃 между этими двумя векторами. Для этого мы знаем формулу нахождение угла между любыми двумя векторами. Напомним, если 𝜃 — это угол между векторами 𝐕 и 𝐖, то 𝜃 удовлетворяет уравнению, потому что коэффициент 𝜃 равен скалярное произведение между 𝐕 и 𝐖, деленное на модуль 𝐕, умноженный на модуль 𝐖.

А так как нам даны 𝐕 и 𝐖 в составной форме, мы можем рассчитать все эти значения. Таким образом, мы можем найти наше значение 𝜃. Начнем с вычисления точки продукт между 𝐕 и 𝐖. Итак, мы хотим найти скалярное произведение между векторами четыре, два, минус один и восемь, четыре, минус два. Помните, чтобы найти точечный продукт между двумя векторами, нам нужно перемножить соответствующие компоненты вместе и затем добавьте все это вместе.

Умножение первых компонентов каждый вектор вместе, мы получаем четыре раза по восемь. Умножая вторые компоненты, мы получаем дважды четыре. И умножение третьего компоненты, мы получаем минус один раз минус два. Таким образом, скалярное произведение этих двух векторы будут суммой этих трех произведений. И мы можем оценить это выражение. Мы получаем скалярное произведение между 𝐕 а 𝐖 равно 42.

Однако дело не только в этом. нам нужно вычислить. Также необходимо найти модуль 𝐕 и модуль 𝐖. Для этого мы сначала собираемся нужно вспомнить, как мы находим модуль вектора. Помните, модуль вектора — квадратный корень из суммы квадратов его компонентов. Другими словами, модуль вектор 𝐚, 𝐛, 𝐜 представляет собой квадратный корень из 𝐚 в квадрате плюс 𝐛 в квадрате плюс 𝐜 в квадрате. И мы знаем компоненты 𝐕 четыре, два и отрицательная единица. Итак, модуль 𝐕 — это квадрат корень из четырех в квадрате плюс два в квадрате плюс минус один в квадрате.

И если мы вычислим это выражение, мы видим, что оно равно квадратному корню из 21. Затем мы можем сделать то же самое вещь, чтобы найти модуль 𝐖. Он равен квадратному корню из восемь в квадрате плюс четыре в квадрате плюс минус два все в квадрате. И если бы мы оценили и упростив это выражение, мы увидели бы, что модуль 𝐖 равен двум корням из 21. Теперь, когда мы нашли точку произведение между 𝐕 и 𝐖 и модулем 𝐕 и модулем 𝐖, мы можем подставьте их в наше уравнение с участием 𝜃.

Мы показали скалярное произведение между 𝐕 и 𝐖 равны 42, модуль 𝐕 равен корню 21, а модуль 𝐖 равен двум корням. 21. Следовательно, косинус 𝜃 больше 42. корень 21 умножить на два корня 21. Однако, если мы начнем вычислять это выражение, мы видим что-то интересное. В знаменателе этого выражение, корень 21, умноженный на два, корень 21 упрощает, чтобы дать нам 42. И 42 на 42 равно единице. Таким образом, все наше уравнение упрощается чтобы дать нам cos 𝜃 равен единице, и мы можем найти 𝜃. Возьмем арккосинус обоих стороны уравнения, что дает нам 𝜃 обратный cos единицы, который, как мы знаем, равен нулю градусов.

На этом мы могли бы остановиться; Однако, это дает нам полезную информацию. Если угол между 𝐕 и 𝐖 равен ноль градусов, то 𝐕 и 𝐖 указывают в одном направлении. Другими словами, мы также показали что векторы 𝐕 и 𝐖 параллельны. И в самом деле, мы могли бы прямо доказать это. Мы увидели бы, что наш вектор 𝐖 равен всего в два раза больше вектора 𝐕. И есть полезный результат, который мы можем получить от этого. Поскольку наш скаляр положителен, угол между этими двумя векторами будет равен нулю. Однако, если этот скаляр был отрицательный, то угол между ними будет 180 градусов, потому что тогда наши векторы указывали бы прямо в противоположные стороны. В любом случае, мы смогли показать угол 𝜃 между векторами 𝐕 и 𝐖, данный нам в вопросе, был равен нулю градусов.

Давайте посмотрим еще один пример нахождение угла между двумя векторами.

Найдите угол 𝜃 между векторов 𝐯 равно 𝐢 и 𝐰 равно трем 𝐢 плюс два 𝐣 плюс четыре 𝐤. Дайте правильный ответ на два десятичные разряды.

В этом вопросе нам дано два векторы 𝐯 и 𝐰 через единичные векторы направлений 𝐢, 𝐣 и 𝐤. И нас просят найти угол 𝜃 между этими двумя векторами. И нам нужно дать ответ на два десятичных знака.

Для этого мы можем начать с вспоминая, что у нас есть формула для нахождения угла между двумя векторами. Поскольку 𝜃 — это угол между векторов 𝐯 и 𝐰, cos 𝜃 должен быть равен скалярному произведению между 𝐯 и 𝐰 разделить на величину 𝐯, умноженную на величину 𝐰. Итак, чтобы найти значение 𝜃, нам нужно чтобы найти скалярное произведение между 𝐯 и 𝐰, величину 𝐯 и величину 𝐰. Тогда все, что нам нужно сделать, это взять арккосинус обеих частей уравнения.

Существует несколько способов делая это. Например, мы могли бы работать напрямую с обозначением вектора единичного направления для 𝐯 и 𝐰. Однако мы могли бы также написать эти векторов покомпонентно, взяв коэффициенты единичного направления векторы. Любой метод будет работать; это личные предпочтения, которые мы будем использовать.

Мы будем писать 𝐯 и 𝐰 по компонентам. 𝐯 — вектор единица, ноль, нуль а 𝐰 — вектор три, два, четыре. Теперь начнем находить значения нашего уравнения. Начнем с скалярного произведения между 𝐯 и 𝐰. Помните, чтобы найти скалярное произведение двух векторов, нам нужно найти произведение соответствующих компонент, а затем сложите результаты вместе. В этом случае первая составляющая 𝐯 умножить на первый компонент 𝐰 один раз три, второй компонент 𝐯 раз второй компонент 𝐰 равен нулю, умноженному на два, а третий компонент 𝐯 умножить на третий компонент 𝐰 ноль умножить на четыре.

Таким образом, скалярное произведение равно сумме это один раз два плюс ноль раз два плюс ноль раз четыре. И мы можем просто вычислить это выражение. Второй и третий термины нуль. Так что это просто дает нам три. Теперь мы хотим найти величину из двух наших векторов. Начнем с величины 𝐯. Помните, 𝐯 — это единица вектор направления 𝐢. И помните, 𝐢 — это единица направленный вектор. Он имеет величину один.

Теперь, чтобы найти величину 𝐰, труднее. Итак, мы напишем это в компоненте обозначение. И мы вспомним, чтобы найти величина вектора, нам нужно найти квадратный корень из суммы квадратов компоненты. Таким образом, величина вектора 𝐚, 𝐛, 𝐜 будет квадратным корнем из 𝐚 в квадрате плюс 𝐛 в квадрате плюс 𝐜 в квадрате. Итак, для вектора 𝐰 это будет квадратный корень из трех в квадрате плюс два в квадрате плюс четыре в квадрате, что мы можем вычислить равно квадратному корню из 29.

Теперь, когда мы нашли эти значения, мы можно подставить их в наше уравнение для 𝜃. Мы показали скалярное произведение между 𝐯 и 𝐰 равны трем, величина 𝐯 равна единице, а величина 𝐰 равна корню. 29. Таким образом, мы должны иметь cos 𝜃 три разделить на один, умноженный на квадратный корень из 29. И теперь мы можем решить 𝜃 с помощью взяв обратный cos обеих частей нашего уравнения. Это дает нам, что 𝜃 является обратный косос трех деленный на корень 29. И если мы посчитаем это и округлим наш ответ до двух знаков после запятой, мы видим, что 𝜃 составляет 56,15 градусов.

Давайте теперь посмотрим на пример того, как мы найдет угол между двумя векторами, заданными на диаграмме.

Найдите угол между векторами показано на следующей диаграмме.

В этом вопросе нам нужно найти угол между двумя векторами. И нам даны эти векторы на диаграмма. И мы также можем видеть угол между двумя векторами, данными на нашей диаграмме. У нас есть несколько различных вариантов как мы могли вычислить это. Например, мы могли бы просто сделать это с помощью тригонометрии. Однако у нас также есть формула для нахождение угла между двумя векторами. Напомним, если 𝜃 — это угол между двумя векторами 𝐮 и 𝐯, то cos 𝜃 будет равен скалярному произведению 𝐮 и 𝐯, деленное на величину 𝐮, умноженную на величину 𝐯. Затем мы можем использовать это, чтобы решить для значение 𝜃, взяв арккосинус обеих частей уравнения.

Чтобы ответить на этот вопрос, мы нужно будет найти скалярное произведение между нашими векторами 𝐮 и 𝐯 и величина 𝐮 и величина 𝐯. И для этого нам понадобится чтобы записать наши векторы в компонентной форме. Мы сделаем это с помощью диаграмма. Начнем с нашего вектора 𝐮. Мы могли видеть на нашей диаграмме это начинается в начале координат, а затем в конечной точке имеет отрицательную 𝑥-координату два корня три. Таким образом, изменение 𝑥 отрицательно два корень три. Точно так же мы можем видеть его 𝑦-координата начинается с нуля и заканчивается на двойке, а ее изменение в 𝑦 равно двум. Таким образом, мы можем представить 𝐮 как вектор с горизонтальной составляющей минус два, корень три и вертикальная составляющая два.

Мы можем сделать то же самое для вектор 𝐯. Мы видим, что он начинается в начале а затем заканчивается на 𝑥-координате минус два и начинается в начале координат и заканчивается на 𝑦-координате минус два. Таким образом, изменение 𝑥 отрицательно два, а изменение у отрицательно два. Итак, 𝐯 — это отрицательный вектор два, минус два. Теперь нам нужно найти скалярное произведение этих двух векторов и их величины.

Начнем с вычисления точки произведение между 𝐮 и 𝐯. Помните, чтобы найти скалярное произведение из двух векторов, нам нужно найти произведения соответствующих компонент, а затем добавить все это вместе. Итак, умножаем первые компоненты из 𝐮 и 𝐯 вместе, чтобы дать нам минус два корня три раза минус два. Затем мы добавляем продукты их вторые компоненты. Это два умножить на минус два. И если мы вычислим это выражение, мы видим, что оно равно четырем корням из трех минус четыре.

Но это еще не все. Нам еще нужно найти величину 𝐮 и величину 𝐯. Начнем с поиска величина 𝐮. Помните, мы можем найти это по извлекая квадратный корень из суммы квадратов компонентов.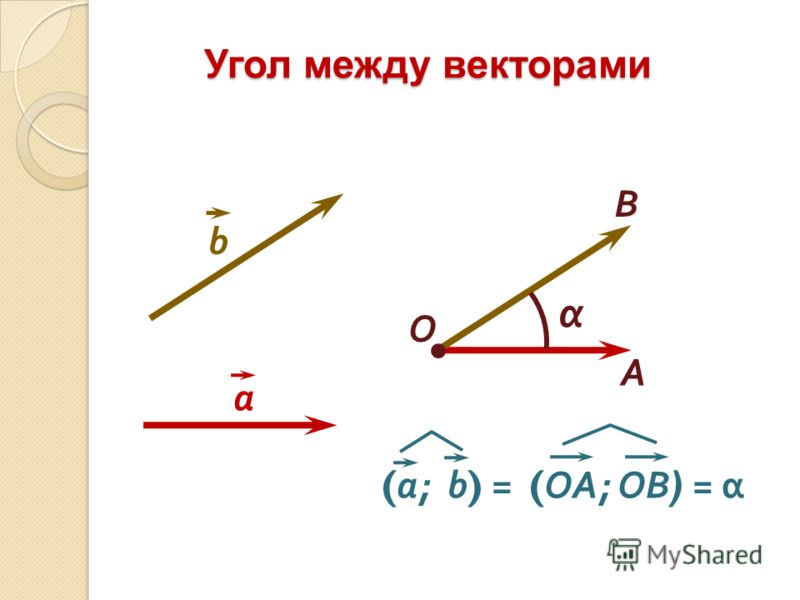 Таким образом, величина 𝐮 равна квадратный корень из минус двух корень три все в квадрате плюс два в квадрате, что мы можем вычисления, дает нам квадратный корень из 12 плюс четыре, что составляет корень 16, который конечно как раз равно четырем. Затем мы можем сделать то же самое для найдите величину 𝐯. Возводим в квадрат каждую компоненту 𝐯, добавляем вместе и извлеките квадратный корень. Величина 𝐯 — это квадрат корень из минус двух в квадрате плюс минус два в квадрате, что, конечно, упрощает чтобы получить квадратный корень из четырех плюс четыре, что равно корню из восьми.

И теперь, когда мы все это нашли значений, мы готовы подставить их в наше уравнение для 𝜃. Подстановка в 𝐮 точки 𝐯 равно четырем корень три минус четыре, величина 𝐮 равна четырем, а величина 𝐯 равна корню восемь, мы получаем потому что 𝜃 равно четырем корень три минус четыре все разделить на четыре корня восемь. И здесь стоит отметить, что мы можно упростить это выражение, чтобы получить корень шесть минус корень два, все деленное на четыре. Однако в этом нет необходимости, поскольку все, что нам нужно сделать сейчас, это взять арккосинус обеих частей уравнения.

Это дает нам, что 𝜃 — это обратный косой корня шесть минус корень два, деленный на четыре, что, как мы можем вычислить, дает нам 75 градусов. И это наш окончательный ответ потому что, если мы посмотрим на нашу диаграмму, есть два возможных угла между векторами 𝐯 и 𝐮. Угол показан на нашем диаграмма, и есть угол, который мы могли бы взять в противоположном направлении. Однако этот вторичный угол, показанный в зеленом больше 75 градусов, поэтому он не может быть 75 градусов. На самом деле это будет 360 минус 75. градусов. Таким образом, мы смогли показать угол между двумя векторами на нашей диаграмме 𝐮 и 𝐯 равен 75 градусам.

Давайте теперь пройдемся по одному последнему пример того, как мы можем использовать нашу формулу для поиска информации о векторах.

Угол между вектором 𝐀 и вектор 𝐁 равен 22 градусам. Если величина вектора 𝐀 равна равно троекратной величине вектора 𝐁 равно 25,2, найдите точку произведение между 𝐀 и 𝐁 с точностью до сотых.

В этом вопросе нам дается информация о двух векторах 𝐀 и 𝐁. Во-первых, нам говорят угол между эти два вектора равны 22 градусам. Далее нам также сообщается информация об их величинах. Мы знаем, что величина 𝐀 равна равно 25,2, и мы знаем, что трехкратная величина 𝐁 также равна 25.2. Таким образом, величина 𝐀 равна трем раз больше, чем величина 𝐁. Нам нужно использовать это, чтобы найти точку произведение 𝐀 и 𝐁. И нам нужно дать ответ на ближайшая сотая.

Чтобы ответить на этот вопрос, нам нужно обратите внимание, что мы знаем формулу, которая связывает угол между двумя векторами с их скалярное произведение. Напомним, если 𝜃 — это угол между двумя векторами 𝐀 и 𝐁, то мы знаем, что cos вектора 𝜃 должен быть равен скалярное произведение между 𝐀 и 𝐁, деленное на величину 𝐀, умноженную на величину 𝐁. И в этом вопросе мы уже знать некоторые из этих значений. Например, нам говорят угол между нашими двумя векторами составляет 22 градуса. Далее нам также сообщается величина 𝐀 равно 25,2.

А еще мы могли бы найти величину 𝐁, используя информацию, предоставленную нам в вопросе. Один из способов сделать это — заметить что трехкратная величина 𝐁 равна 25,2. Затем мы можем решить это, чтобы найти величину 𝐁, разделив обе части нашего уравнения на три. И вычисляя это, мы получаем величина 𝐁 равна 8,4. Так что, по сути, единственный неизвестный в это уравнение представляет собой скалярное произведение между 𝐀 и 𝐁. И это именно то, что мы спросили вычислять.

Подставим угол 𝜃 равен 22 градусам, величина 𝐀 равна 25,2, а величина 𝐁 равный 8,4 в наше уравнение. Это дает нам cos 22 градуса должен быть равен скалярному произведению между 𝐀 и 𝐁, деленному на 25,2, умноженному на 8,4. И теперь мы можем просто изменить это уравнение для скалярного произведения между 𝐀 и 𝐁. Умножаем через в 25,2 раза 8.4. Это дает нам 𝐀 точка 𝐁 равна 25,2. раз в 8,4 раза больше, чем 22 градуса. И мы можем вычислить это до ближайшая сотая или до двух знаков после запятой. равно 196.27.

Давайте теперь пройдемся по ключевым моментам это видео. Во-первых, мы знаем, является ли 𝜃 углом между двумя векторами 𝐮 и 𝐯, то cos 𝜃 будет равен скалярному произведению 𝐮 и 𝐯, деленное на величину 𝐮, умноженную на величину 𝐯. И это работает до тех пор, пока ни вектор 𝐮 или 𝐯 равен нулю. И взять скалярное произведение 𝐮 и 𝐯, нам нужно, чтобы они имели одинаковую размерность. Мы также можем использовать эту формулу для найти угол между двумя векторами, взяв арккосинус обеих сторон это уравнение. Но нам нужно быть осторожными потому что функция арккосинуса имеет диапазон от нуля до 180 градусов включительно, или, если мы работаем в радианах, от нуля до 𝜋 включительно. Таким образом, этот метод даст нам меньший из двух углов между нашими векторами 𝐮 и 𝐯.

math — Угол между двумя векторами в R

Если вы хотите вычислить угол между несколькими переменными, вы можете использовать следующую функцию, которая является расширением решения, предоставленного @Graeme Walsh.

 углов <- функция(матрица){
  ## Вычисление векторного произведения матрицы
  cross.product <- t(matrix)%*%matrix
  ## нижний и верхний треугольник векторного произведения — это скалярные произведения векторов
  dot. products<- cross.product[lower.tri(cross.product)]
  ## Рассчитать нормы L2
  temp <- подавлять предупреждения (diag (sqrt (cross.product)))
  temp <- temp%*%t(temp)
  L2.norms <- temp[lower.tri(temp)]
  ## Значения арккосинуса для каждой пары переменных
  low.t <- acos(dot.products/L2.norms)
  ## Создать пустую матрицу для представления результатов
  result.matrix <- matrix(NA,ncol = dim(matrix)[2],nrow=dim(matrix)[2])
  ## Заполните матрицу значениями арккосинуса и присвойте диагональным значениям ноль «0»
  result.matrix[нижний.tri(result.matrix)] <- нижний.t
  diag(результат.матрица) <- 0
  результирующая.матрица[верхняя.три(результат.матрица)] <- t(результат.матрица)[верхняя.три(т(результат.матрица))]
  ## Получить результирующую матрицу
  возврат (результат.матрица)
}

Кроме того, если вы отцентрировали входные переменные по центру и получили косинусные значения приведенной выше матрицы результатов, вы получите точную матрицу корреляции переменных.

Вот приложение функции.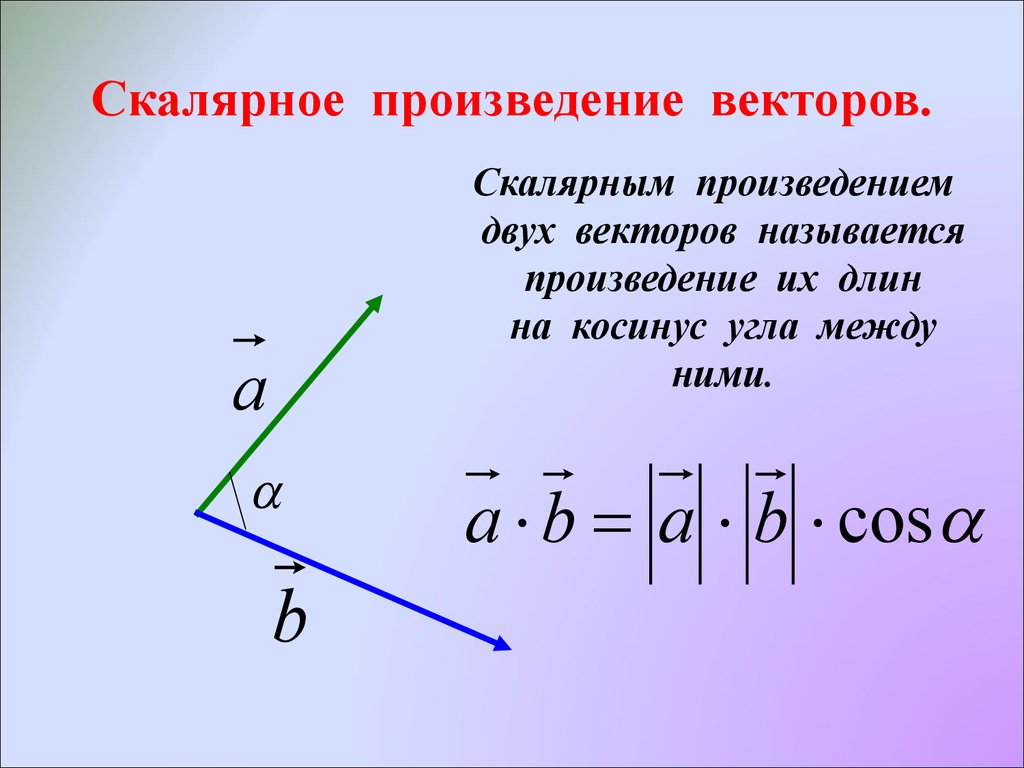

 комплект семян(123)
п <- 100
м <- 5
# Генерируем набор случайных величин
mt <- матрица (rnorm (n * m), nrow = n, ncol = m)
# Среднецентрированная матрица
mt.c <- шкала (mt, шкала = F)
# Углы косинуса
cosine.angles <- углы (матрица = mt)
> косинус.углы
 [1] [2] [3] [4] [5]
[1,] 0,000000 1,6308191,686037 1,618119 1,751859
[2,] 1,630819 0,000000 1,554695 1,523353 1,712214
[3,] 1,686037 1,554695 0,000000 1,619723 1,581786
[4,] 1,618119 1,523353 1,619723 0,000000 1,593681
[5,] 1,751859 1,712214 1,581786 1,593681 0,000000
# Углы косинуса центрированных данных
centered.cosine.angles <- angles(matrix = mt.c)
> центр.косинус.углы
 [1] [2] [3] [4] [5]
[1,] 0,000000 1,620349 1,700334 1,614890 1,764721
[2,] 1,620349 0,000000 1,540213 1,526950 1,701793
[3,] 1,700334 1,540213 0,000000 1,615677 1,595647
[4,] 1,614890 1,526950 1,615677 0,000000 1,5
 [5,] 1,764721 1,701793 1,595647 1,5 0,000000
# Это даст вам матрицу корреляции
потому что (углы (матрица = mt.c))
 [1] [2] [3] [4] [5]
[1,] 1,00000000 -0,04953215 -0,12917601 -0,04407900 -0,19271110
[2,] -0,04953215 1,00000000 0,03057903 0,04383271 -0,13062219
[3,] -0,12917601 0,03057903 1,00000000 -0,04486571 -0,02484838
[4,] -0,04407900 0,04383271 -0,04486571 1,00000000 -0,01925986
[5,] -0,19271110 -0,13062219 -0,02484838 -0,01925986 1,00000000
# Исходная корреляционная матрица
кор (мт)
 [1] [2] [3] [4] [5]
[1,] 1,00000000 -0,04953215 -0,12917601 -0,04407900 -0,19271110
[2,] -0,04953215 1,00000000 0,03057903 0,04383271 -0,13062219
[3,] -0,12917601 0,03057903 1,00000000 -0,04486571 -0,02484838
[4,] -0,04407900 0,04383271 -0,04486571 1,00000000 -0,01925986
[5,] -0,19271110 -0,13062219 -0,02484838 -0,01925986 1,00000000
# Проверяем, равны ли они
all.No related posts.