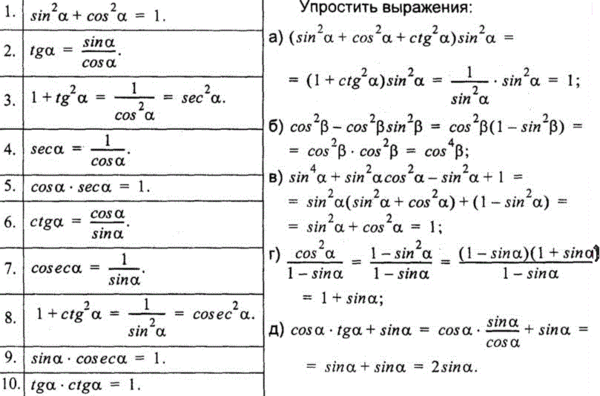PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.
1 Электростатика - 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 4.
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5. 6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
1 Электростатика
6 СТОЗдесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см.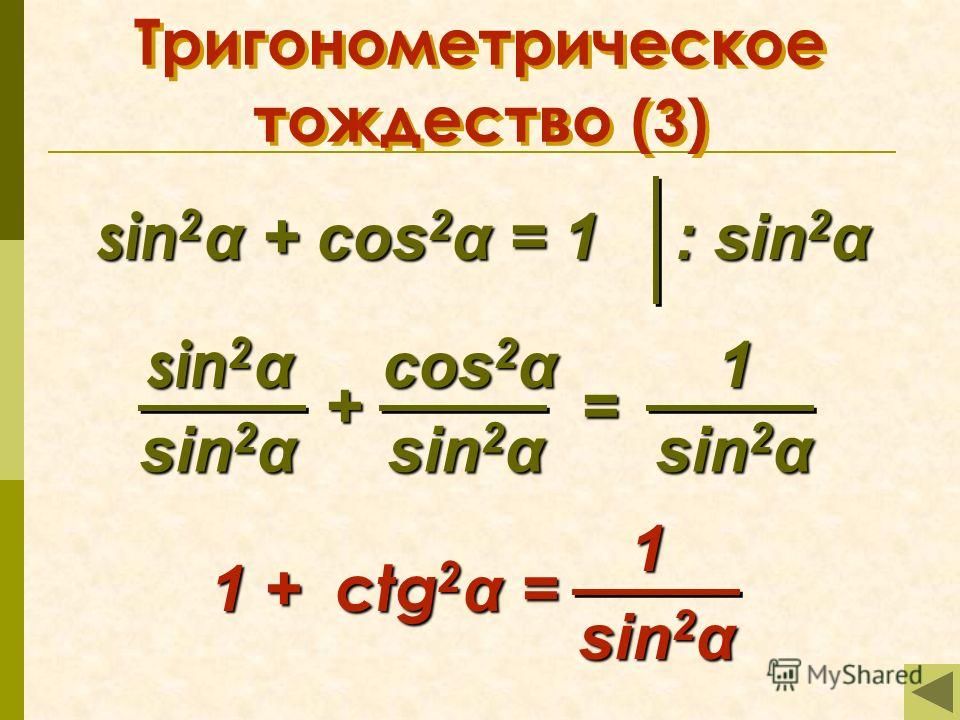
справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Чему равно произведение sin и cos. Сумма и разность синусов и косинусов: вывод формул, примеры
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 .
Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Yandex.RTB R-A-339285-1
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
Формулы суммы и разности для косинусов
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.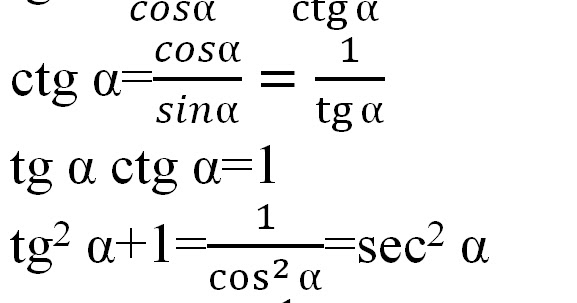
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению.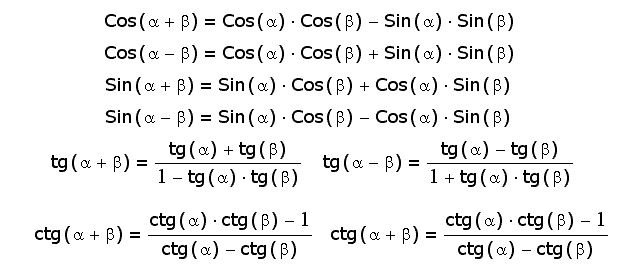
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники.
Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов.
Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов.
Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы.
Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице.
Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники.
Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу.
То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету.
Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
Самые часто задаваемые вопросы
Возможно ли, изготовить печать на документе по предоставленному образцу? Ответ Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Какие виды оплаты вы принимаете?
Ответ
Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.
Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами?
Ответ
В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день.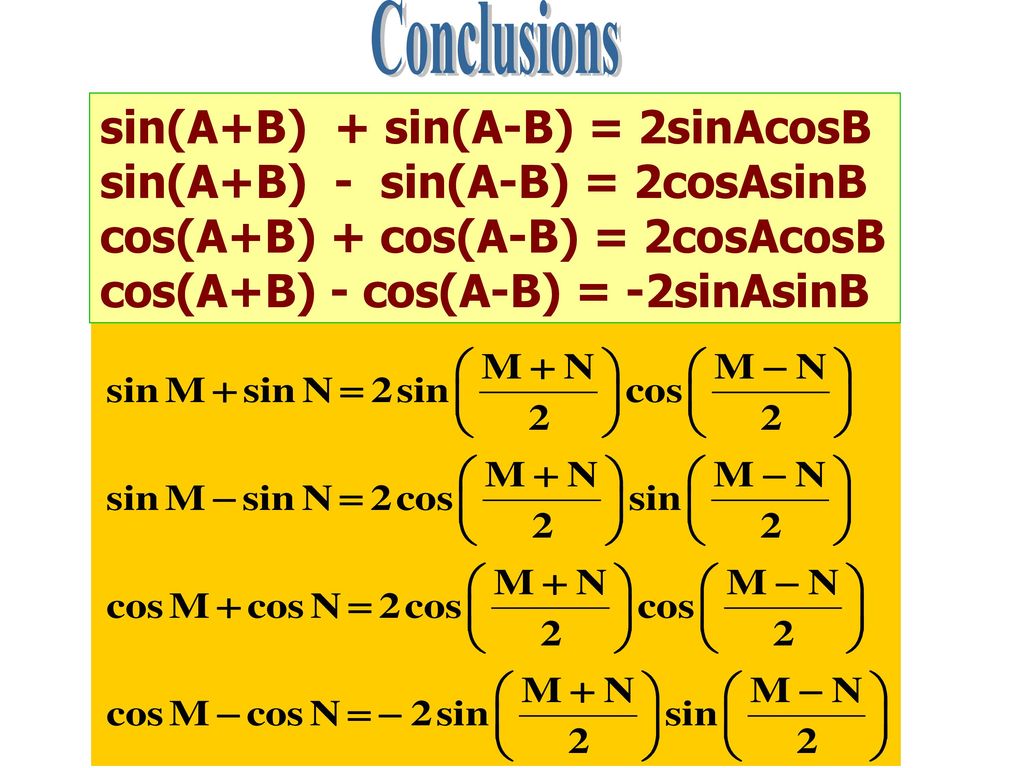
Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.
Что делать при обнаружении в документе опечаток и ошибок?
Ответ
Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.
Что нужно сделать, чтобы заказать диплом в вашей компании?
Ответ
Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.
Последние отзывы
Алексей:
Мне нужно было приобрести диплом для устройства на работу по профессии менеджер. И самое главное, что и опыт, и навыки у меня есть, но без документа я не могу, никуда устроится. Попав на ваш сайт, все-таки решился на покупку диплома. Диплом был выполнен за 2 дня!! Теперь у меня есть работа, о которой я раньше и не мечтал!! Спасибо!
Косинус суммы и разности двух углов
В этом параграфе будут доказаны следующие две формулы:
cos (α + β) = cos α cos β — sin α sin β, (1)
cos (α — β) = cos α cos β + sin α sin β. (2)
Косинус суммы (разности) двух углов равен произведению косинусов этих углов минус (плюс) произведение синусов этих углов.
Нам удобнее будет начать с доказательства формулы (2). Для простоты изложения предположим сначала, что углы α и β удовлетворяют следующим условиям:
1) каждый из этих углов неотрицателен и меньше 2π :
0 α 2π, 0 β
2) α > β .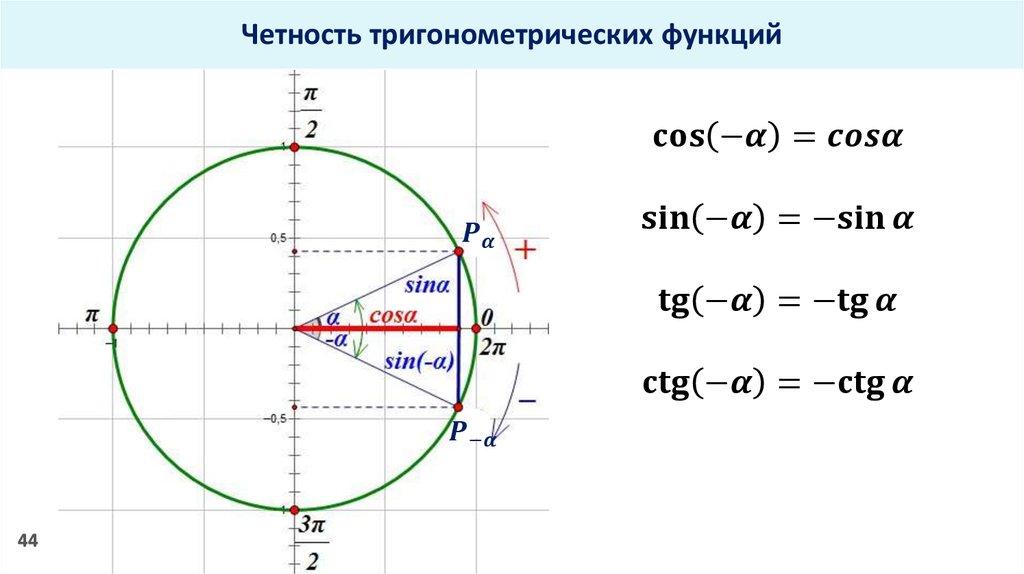
Пусть положительная часть оси 0х является общей начальной стороной углов α и β .
Конечные стороны этих углов обозначим соответственно через 0А и 0В. Очевидно, что угол α — β можно рассматривать как такой угол, на который нужно повернуть луч 0В вокруг точки 0 против часовой стрелки, чтобы его направление совпало с направлением луча 0А.
На лучах 0А и 0В отметим точки М и N, отстоящие от начала координат 0 на расстоянии 1, так что 0М = 0N = 1.
В системе координат х0у точка М имеет координаты (cos α, sin α ), а точка N — координаты (cos β , sin β ). Поэтому квадрат расстояния между ними равен:
d 1 2 = (cos α — cos β) 2 + (sin α — sin β) 2 = cos 2 α — 2 cos α cos β +
+ cos 2 β + sin 2 α — 2sin α sin β + sin 2 β = .
При вычислениях мы воспользовались тождеством
sin 2 φ + cos 2 φ = 1 .
Теперь рассмотрим другую систему координат В0С, которая получается путем поворота осей 0х и 0у вокруг точки 0 против часовой стрелки на угол β .
В этой системе координат точка М имеет координаты (cos (α — β ), sin (α — β )), а точка N -координаты (1,0). Поэтому квадрат расстояния между ними равен:
d 2 2 = 2 + 2 = cos 2 (α — β) — 2 cos (α — β) + 1 +
+ sin 2 (α — β) = 2 .
Но расстояние между точками М и N не зависит от того, относительно какой системы координат мы рассматриваем эти точки. Поэтому
d 1 2 = d 2 2
2 (1 — cos α cos β — sin α sin β) = 2 .
Отсюда и вытекает формула (2).
Теперь следует вспомнить о тех двух ограничениях, которые мы наложили для простоты изложения на углы α и β .
Требование, чтобы каждый из углов α и β был неотрицательным, на самом деле не существенно. Ведь к любому из этих углов можно прибавить угол, кратный 2я, что никак не отразится на справедливости формулы (2). Точно так же от каждого из данных углов можно вычесть угол, кратный 2π .
Поэтому можно считать, что 0 α
2π
, 0 β
2π
.
Не существенным оказывается и условие α > β . Действительно, если α β , то β >α ; поэтому, учитывая четность функции cos х , получаем:
cos (α — β) = cos (β — α) = cos β cos α + sin β sin α,
что по существу совпадает с формулой (2). Таким образом, формула
cos (α — β) = cos α cos β + sin α sin β
верна для любых углов α и β . В частности, заменяя в ней β на —β и учитывая, что функция cos х является четной, а функция sin х нечетной, получаем:
cos (α + β) = cos [α — (- β)] =cos α cos (-β) + sin α sin (-β) =
= cos α cos β — sin α sin β,
что доказывает формулу (1).
Итак, формулы (1) и (2) доказаны.
Примеры.
1) cos 75° = cos (30° + 45°) = cos 30° cos 45°-sin 30°-sin 45° =
2) cos 15° = cos (45° — 30°) = cos 45° cos 30° + sin 45° sin 30° =
Упражнения
1 .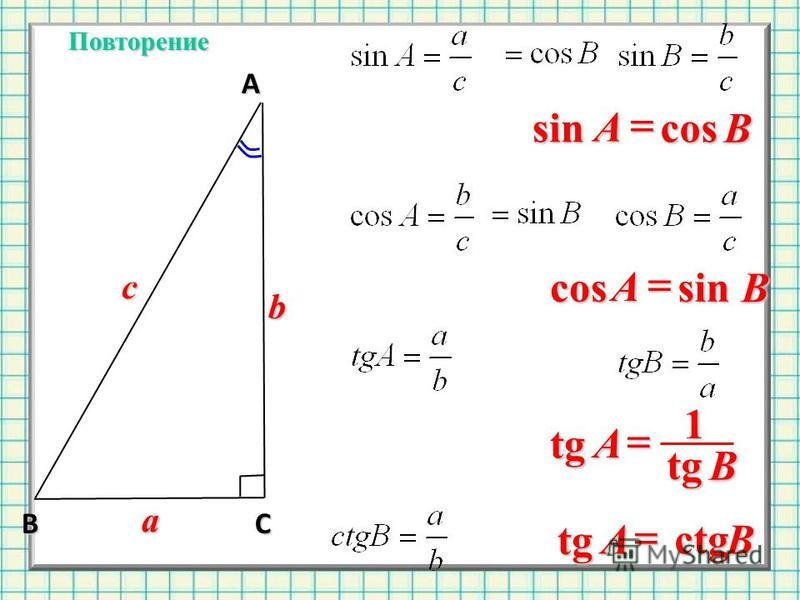
Вычислить, не пользуясь тригонометрическими таблицами:
a) cos 17° cos 43° — sin 17° sin 43°;
б) sin 3° sin 42° — cos 39° cos 42°;
в) cos 29° cos 74° + sin 29° sin 74°;
г) sin 97° sin 37° + cos 37° cos 97°;
д) cos 3π / 8 cos π / 8 + sin 3π / 8 sin π / 8 ;
e) sin 3π / 5 sin 7π / 5 — cos 3π / 5 cos 7π / 5 .
2.Упростить выражения:
a). cos (α + π / 3 ) + cos (π / 3 — α ) .
б). cos (36° + α ) cos (24° — α ) + sin (36° + α ) sin (α — 24°).
в). sin (π / 4 — α ) sin (π / 4 + α ) — cos (π / 4 + α ) cos (π / 4 — α )
г) cos 2α + tg α sin 2α .
3 . Вычислить :
a) cos (α — β) , если
cos α = — 2 / 5 , sin β = — 5 / 13 ;
90° α β
б) cos (α + π / 6), если cos α = 0,6;
3π / 2 α
4 . Найти cos (α + β) и cos (α — β) ,если известно, что sin α = 7 / 25 , cos β = — 5 / 13 и оба угла (α и β ) оканчиваются в одной и той же четверти.
5 .Вычислить:
а). cos [ arcsin 1 / 3 + arccos 2 / 3 ]
б). cos [ arcsin 1 / 3 — arccos (- 2 / 3)] .
в). cos [ arctg 1 / 2 + arccos (- 2) ]
Варенье из бузины: польза и вред
Узнать встретимся ли мы. Сонник дома солнца. Как правильно сформулировать вопрос в процессе гадания
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Как считать формулы приведения. Синус (sin x) и косинус (cos x) – свойства, графики, формулы
Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду.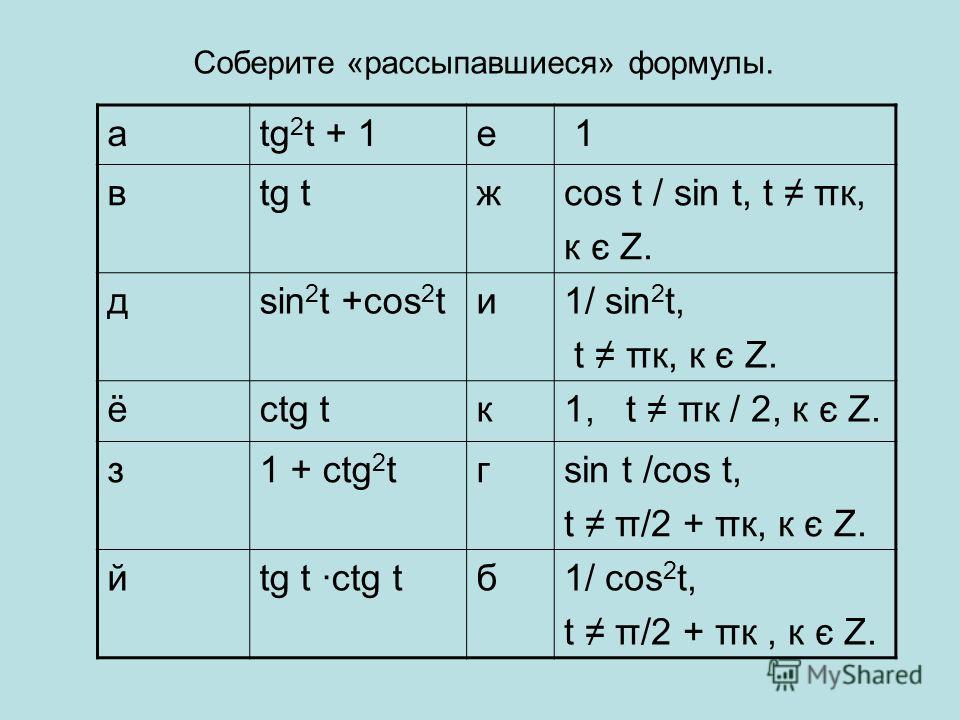
О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
угол альфа лежит пределах от 0 до 90 градусов
* * *
Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.
Напомню их:
2. Запомните следующее:
функция изменяется на кофункцию
функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.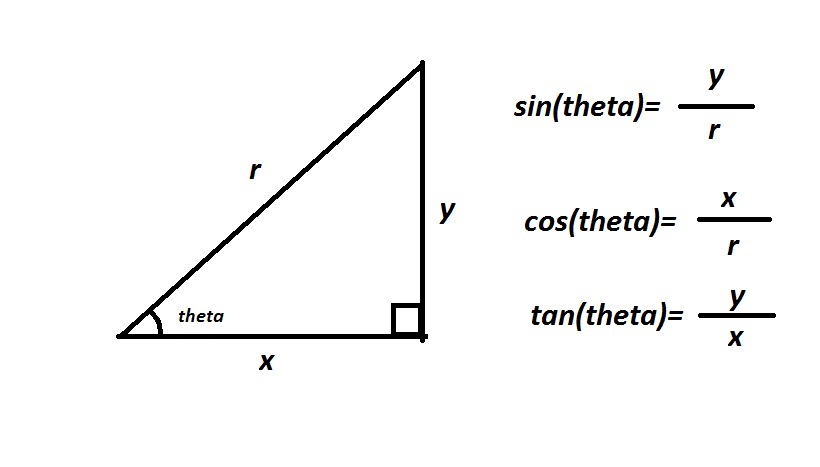
Вот и всё!
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
***
В статье на решение был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
С центром в точке A .
α — угол, выраженный в радианах.
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.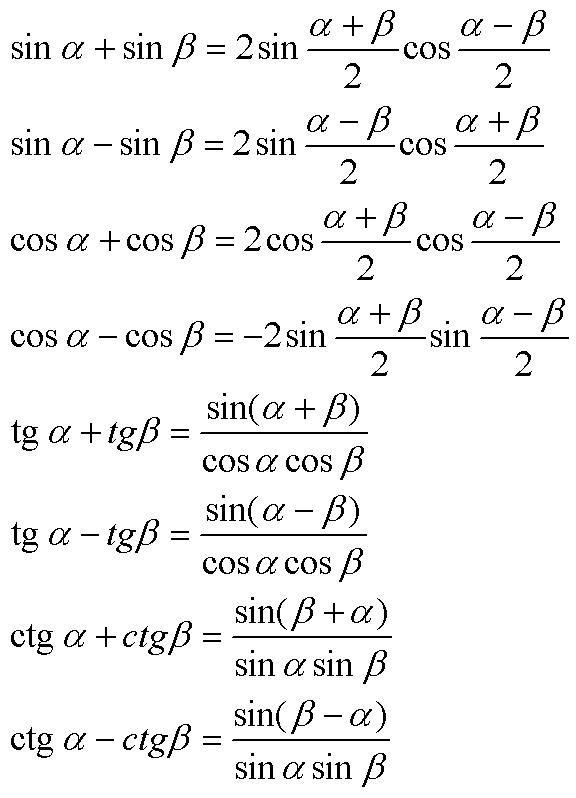
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
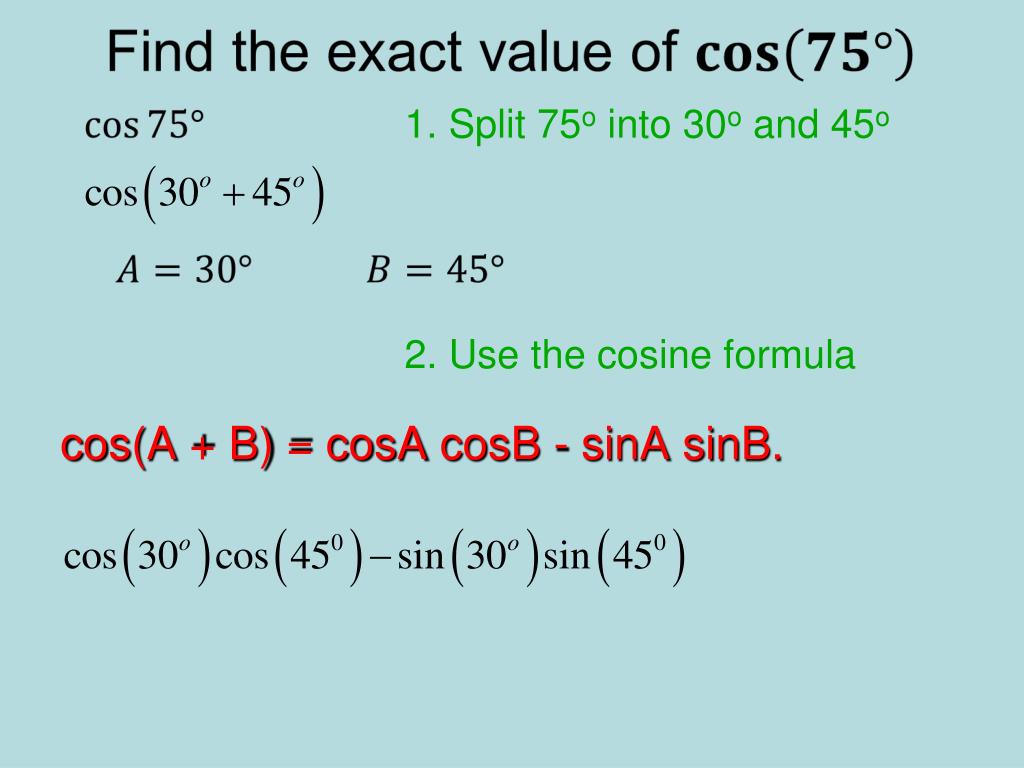
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Для использования формул приведения существует два правила.
1.
Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет.
2. Правило «каким ты был, таким ты и остался».
Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Вычислить Sin(150˚)
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен +. Значит у приведенной функции тоже будет знак «плюс». Это мы применили второе правило.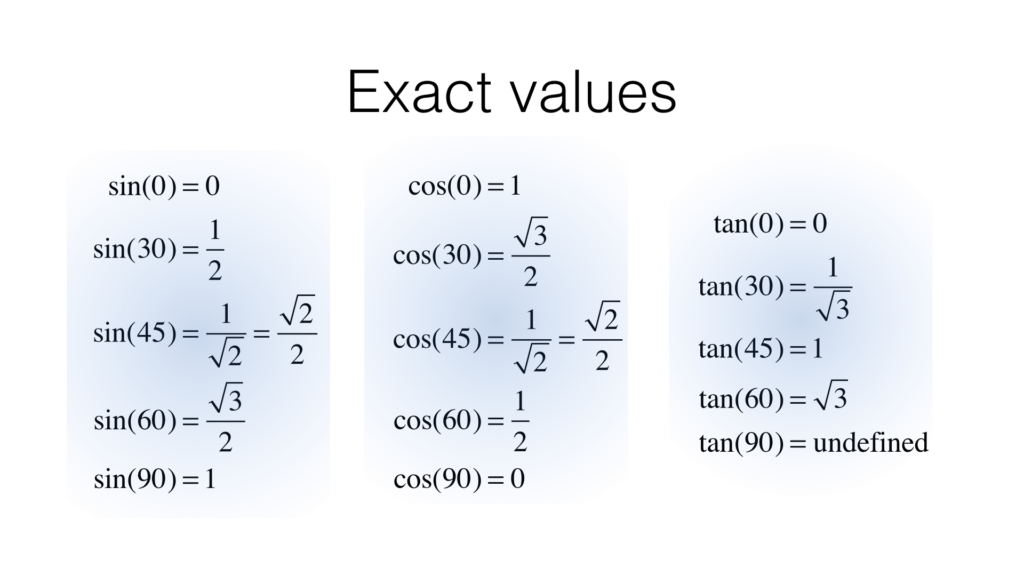
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
При желании все формулы приведения можно свести в одну таблицу. Но все же легче запомнить эти два правила и пользоваться ими.
Определение. Формулами приведения называют формулы, которые позволяют перейти от тригонометрических функций вида к функциям аргумента . С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.
Формулы приведения:
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg.
Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет
2. Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Пример:
Вычислить
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен «+». Значит у приведенной функции тоже будет знак «+». Это мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
Тригонометрия.Формулы приведения.
Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода. Это очень легко!
Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.
Разберем в каждой четверти функции sin(a) и cos(a).
Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.
В первой четверти видно, что функция sin(a)>0
И функция cos(a)>0
Первую четверть можно описать через градусную меру, как (90-α) или (360+α).
Во второй четверти видно, что функция sin(a)>0 , потому что ось Y положительна в этой четверти.
А функция cos(a) , потому что ось X отрицательна в этой четверти.
Вторую четверть можно описать через градусную меру, как (90+α) или (180-α).
В третьей четверти видно, что функции sin(a) Третья четверть можно описать через градусную меру, как (180+α) или (270-α).
В четвертой четверти видно, что функция sin(a) , потому что ось Y отрицательна в этой четверти.
А функция cos(a)>0 , потому что ось X положительна в этой четверти.
Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).
Теперь рассмотрим сами формулы приведения.
Запомним простой алгоритм :
1. Четверть. (Всегда смотрите в какой вы четверти находитесь).
2. Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
3. Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется .
И так начнем разбирать по четвертям данный алгоритм.
Выясни чему будет равно выражение cos(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
Будет cos(90-α) = sin(α)
Выясни чему будет равно выражение sin(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
Будет sin(90-α) = cos(α)
Выясни чему будет равно выражение cos(360+α)
Рассуждаем по алгоритму:
1.
Четверть первая.
2. В первой четверти знак у функции косинуса положительный.
Будет cos(360+α) = cos(α)
Выясни чему будет равно выражение sin(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(360+α) = sin(α)
Выясни чему будет равно выражение cos(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90+α) = -sin(α)
Выясни чему будет равно выражение sin(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90+α) = cos(α)
Выясни чему будет равно выражение cos(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.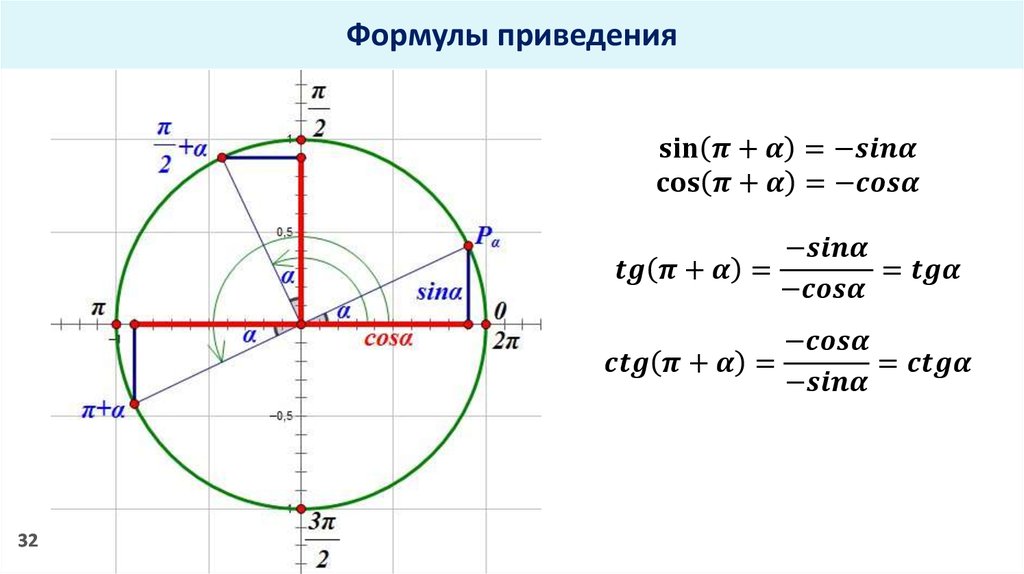
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(180-α) = cos(α)
Выясни чему будет равно выражение sin(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(180-α) = sin(α)
Рассуждаю про третью и четвертую четверть подобным образом составим таблицу:
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Sin, Cos, Tan — тригонометрия
Все ресурсы по тригонометрии
6 диагностических тестов 155 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Тригонометрия Помощь » Тригонометрические операции » Sin, Cos, Tan
Найдите значение тригонометрической функции в виде дроби для треугольника .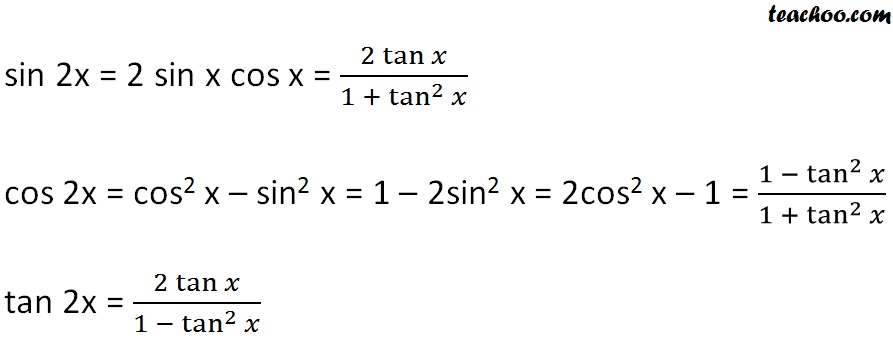
Что такое косинус?
Возможные ответы:
Правильный ответ:
Объяснение:
Косинус угла — это значение прилежащего катета к гипотенузе.
Следовательно:
Сообщить об ошибке
Каково значение ?
Возможные ответы:
Правильный ответ:
Объяснение:
Решите каждое условие отдельно.
Добавьте оба термина.
Сообщить об ошибке
Определите значение .
Возможные ответы:
Правильный ответ:
Объяснение:
Переписать в терминах синусов и косинусов.
Упростите сложную дробь.
Сообщить об ошибке
Найдите значение .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти значение , решите каждое условие отдельно.
Суммируйте два члена.
Сообщить об ошибке
Выберите коэффициент, который даст Tan B.
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Пояснение:
Нам нужен Tan B. Длины каких сторон соответствуют этому соотношению?
Сообщить об ошибке
Рассчитать .
Возможные ответы:
Правильный ответ:
Объяснение:
Функция тангенса имеет период единиц.
То есть
для всех.
Так как , мы можем переписать исходное выражение следующим образом:
Следовательно,
Отчет о ошибке
Расчет.
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала переведите заданную меру угла из радиан в градусы:
Затем вспомните, что лежит в четвертом квадранте единичной окружности, где косинус положителен. Кроме того, опорный угол равен
Следовательно, все, что требуется, — это признать из этих наблюдений, что
,
что есть .
Следовательно,
Сообщить об ошибке
Что получится, если максимально упростить следующее выражение?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку это нечетная функция, мы можем переписать второй член в выражении.
.
Теперь мы используем формулу двойного угла, чтобы расширить первый член.
.
Поскольку они обратны, .
Сообщить об ошибке
Округлить до сотых.
Используйте свой калькулятор, чтобы найти:
Возможные ответы:
Ни один из вышеперечисленных
Правильный ответ:
. Объяснение:
Перед подключением функции к калькулятору убедитесь, что режим калькулятора установлен на градусы,
Подставьте , что равно .
Сообщить об ошибке
Округлить до сотых.
Используйте свой калькулятор, чтобы найти:
Возможные ответы:
Ни один из вышеперечисленных
Правильный ответ:
.
Объяснение:
Перед подключением функции к калькулятору убедитесь, что режим калькулятора установлен на радианы,
подключите
, что равно
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Учитесь по концепции
Правило All Sin Tan Cos
Правило All Sin Tan Cos помогает нам оценивать различные тригонометрические отношения в разных квадрантах.
«Правило all sin tan cos» можно легко запомнить, используя следующие фразы.
«All Sliver Tea Cups»
или
«Все студенты принимают исчисление»
или
«Все студенты принимают кофе»
«Все греховное загар» Также известно, как правило «. Формула ASTC в тригонометрии.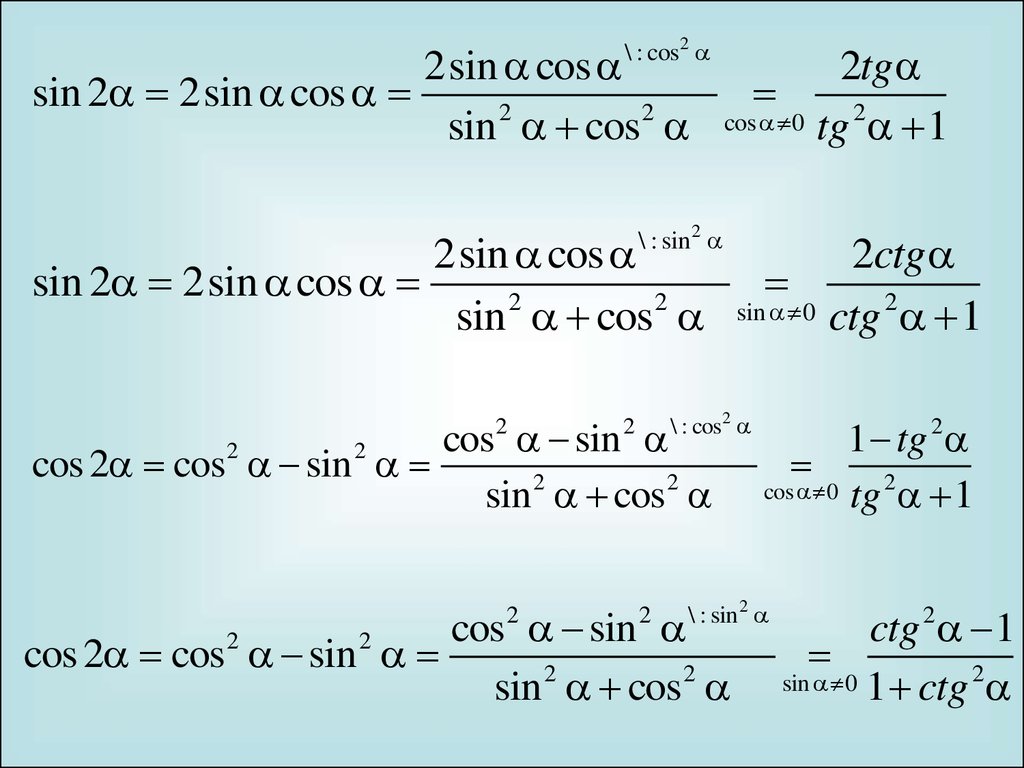
Форма ASTC четко объяснена на рисунке ниже.
Точнее,
В первом квадранте (от 0° до 90°) все тригонометрические соотношения положительны.
Во втором квадранте (от 90° до 180°) sin и csc положительны, а остальные тригонометрические отношения отрицательны.
В третьем квадранте (от 180° до 270°) tan и cot положительны, а остальные тригонометрические отношения отрицательны.
В четвертом квадранте (от 270° до 360°) cos и sec положительны, а остальные тригонометрические отношения отрицательны.
Важные преобразования
При наличии углов 90° и 270° в тригонометрических соотношениях в виде
(90° + θ)
(90° — θ)
(270° + 05) 90
(270° — θ)
Мы должны сделать следующие преобразования:
sin θ <------> cos θ
tan θ <------> cot θ
csc θ < ------> сек θ
Например,
sin (270° + θ) = — cos θ
cos (90° — θ) = sin θ
Для углов 0° или 360° и 180° указанные выше преобразования выполнять не следует.
Разделение квадрантов
(90° — θ) ——-> I квадрант
(90° + θ) и (180° — θ) ——-> II квадрант
(180° + θ) и (270° — θ) ——-> III квадрант
(270° + θ), (360° — θ) и (- θ) —- —> IV квадрант
Правило All Sin Tan Cos — практические вопросы
Вопрос 1:
Оценка: cos (270° — θ)
Ответ :
Чтобы вычислить cos (270° — θ), мы должны учитывать следующие важные моменты.
(i) (270° — θ) попадет в III квадрант.
(ii) Когда у нас будет 270°, «cos» станет «sin»
(iii) В третьем квадранте знак «cos» отрицательный.
С учетом вышеизложенного имеем
cos (270° — θ) = — sin θ
Вопрос 2 :
Вычислить : sin (180° + θ)
Ответ :
Чтобы вычислить sin (180° + θ), мы должны учитывать следующие важные моменты.
(i) (180° + θ) попадет в III квадрант.
(ii) Когда у нас есть 180°, «sin» не изменится
(iii) В III четверти знак «sin» отрицательный.
Учитывая вышеизложенное, мы имеем
sin (180° + θ) = — sin θ
На основании двух приведенных выше примеров мы можем оценить следующие тригонометрические соотношения.
sin (-θ) = — sin θ cos (-θ) = cos θ tan (-θ) = — tan θ csc (-θ) = — csc θ ) сек (-θ) sec θ cot (-θ) = — cot θ sin (90°-θ) = cos θ cos (90°-θ) = sin θ tan (90°-θ) = 9 0cot 0θ5 csc (90°-θ) = sec θ сек (90°-θ) = csc θ cot (90°-θ) = tan θ sin (90°+θ) = cos θ cos 90 (90°+θ) = -sin θ tan (90°+θ) = -cot θ csc (90°+θ) = sec θ sec (90°+θ) = -csc θ cot (90°+-θ) = tan θ sin (180°-θ) = sin θ cos (180°-θ) = -cos θ tan (180°-θ) = -tan θ | csc (180°-θ) = csc θ сек (180°-θ) = -sec θ cot (180°-θ) = -cot θ cos (180°+θ) = -cos θ tan (180°+θ) = tan θ csc (180°+θ) = -csc θ сек (180°+θ) = -sec θ csc (180°+θ) = cot θ sin (270°-θ) = -cos θ cos (270°-θ) = -sin θ tan (270°-θ) = cot θ csc (270°-θ) = 07-04 сек θ 3 θ) = -csc θcot (270°-θ) = tan θ sin (270°+θ) = -cos θ cos (270°+θ) 0 = 9 sin 3 θ 0 = 9 sin 3 θ 270°+θ) = -cot θ csc (270°+θ) = -сек θ сек (270°+θ) = cos θ cot (270°+θ) = -tan θ |
Углы больше или равны 360°
Если угол равен или больше 360°, мы должны разделить данный угол на 360 и взять остаток.
Например,
(i) Рассмотрим угол 450°.
Когда мы делим 450° на 360, мы получаем остаток 90°.
Следовательно, 450° = 90°
(ii) Рассмотрим угол 360°
Когда мы делим 360° на 360, мы получаем остаток 0°.
Следовательно, 360° = 0°
На основании двух приведенных выше примеров мы можем оценить следующие тригонометрические отношения.
sin (360° — θ) = sin (0° — θ) = sin (- θ) = — sin θ
cos (360° — θ) = cos (0° — θ) = cos (- θ) = cos θ
тангенс (360° — θ) = тангенс (0° — θ) = тангенс (- θ) = — тангенс θ
csc (360° — θ) = csc (0° — θ) = csc ( — θ) = — csc θ
сек (360° — θ) = сек (0° — θ) = сек (- θ) = сек θ — COT θ
Тригонометрические отношения углов, превышающие или равные 360 ° — Практические задачи
Задача 1:
Оценка:
TAN 735 °
Решение:
. 360°.
Итак, мы должны разделить 735° на 360 и взять остаток.
При делении 735° на 360 в остатке 15°.
Следовательно,
735° = 15° ——> tan 735° = tan 15°
Следовательно, tan 735° равен tan 15°.
Задача 2 :
Оценка :
cos (-870°)
Решение :
Поскольку заданный угол (-870°) имеет отрицательный знак в четвертом квадранте, мы должны принять его .
В четвертом квадранте «cos» положителен.
Итак, у нас есть cos (-870°) = cos 870°.
Заданные 870° больше, чем 360°.
Итак, мы должны разделить 870° на 360 и взять остаток.
При делении 870° на 360 в остатке 150°.
Следовательно,
870° = 150° ——> cos 870° = cos 150°
cos 870° = cos (180° — 30°)
cos 0 870° 0 5 0 0 —
cos 870 = — √3 / 2
Следовательно, cos 870° равен — √3/2.
Задача 3 :
Найдите значение :
(sin 780 sin 480° + cos 120° cos 60°)
Решение:
Найдем значение каждого тригонометрического соотношения для заданного угла.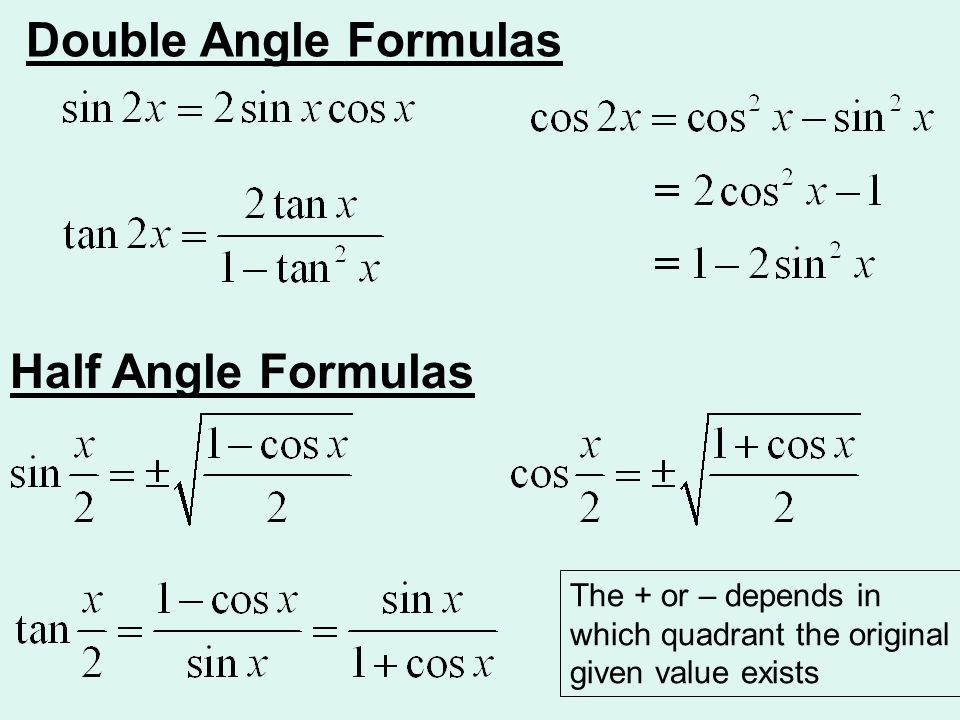
sin 780° = sin 60° = √3 / 2
sin 480° = sin 120° = sin (180° — 60°) = sin 60° = √03/2 cos 1 0 9 0 180° — 60°) = — cos 60° = — 1/2
cos 60° = 1/2
sin780 sin480° + cos120° cos60° равно
= (√3/3) x (√3/2) x (√3/2) /2) + (-1/2) x (1/2)
= (3/4) — (1/4)
= (3-1) / 4
= 2 / 4
= 1/2
Следовательно, значение данного тригонометрического выражения равно 1/2.
Задача 4 :
Упрощение :
cot (90°-θ) sin (180°+θ) сек(360°-θ) / tan(180°+θ) сек(-θ) cos(90 °+θ)
Решение:
Используя формулу ASTC, мы имеем
cot (90°-θ) = tan θ
sin (180°+θ) = — sin θ
-θ) = сек θ
tan(180°+θ) = tan θ
сек(-θ) = сек θ
cos(90°+θ) = — sin θ
Тогда данное выражение имеет вид sec θ x -sin θ)
= 1
Следовательно, упрощение данного тригонометрического выражения равно 1.
Задача 5 :
(180°-θ) + cot(90°+θ) csc(270°-θ)
Решение:
Используя формулу ASTC, мы имеем
с (360°-θ) = с θ
tan (180°-θ) = — tan θ
cot (90°+θ) = — tan θ
csc (270 °-θ-) sec θ
Тогда данное выражение имеет вид
= 0
Следовательно, упрощение данного тригонометрического выражения равно 0.
Помимо материалов, приведенных в этом разделе, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Пожалуйста, отправьте ваш отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
При решении тригонометрических выражений, таких как синус, косинус и тангенс, очень важно понимать, что Excel использует радианы, а не градусов для выполнения этих вычислений! Если угол в градусах вы должны сначала преобразовать его в радианы. Есть два простых способа сделать это.
Excel использует несколько встроенных триггерных функций. Те, которые вы будете использовать чаще всего отображаются в таблице ниже. Обратите внимание, что аргументы для функций SIN(), COS() и TAN() по умолчанию радиан . Кроме того, функции ASIN(), ACOS() и ATAN() возвращаемые значения в виде радиан . (При работе со степенями вам потребуется правильно используйте функции ГРАДУСЫ() и РАДИАНЫ() для преобразования в правильные единицы измерения.)
Ниже приведены несколько примеров задач, связанных с тригонометрией, и способы их решения. Решение для высоты дерева, ч , находим . Снимок экрана ниже показано, как мы использовали Excel, чтобы определить, что высота дерево 47 м. Обратите внимание на использование функции RADIANS() в пример выше. Мы можем переписать это уравнение как
. Снимок экрана ниже показано, как мы использовали Excel, чтобы определить, что угол запуска угол наклона 14,04°. Обратите внимание на использование ГРАДУСОВ() и РАДИАНОВ(). функцию в приведенном выше примере. Обратите внимание на приведенный ниже снимок экрана, что эта идентичность верна. когда q дано в радианах и градусов . Обратите внимание на единицы измерения угла q размещены в разных ячейках, чем числа. Если мы поместим числа и единицы в одну ячейку, Excel не сможет расшифровать число и поэтому мы не будем иметь возможность ссылаться на ячейки для использования в любом уравнении! |
Отображение символов 
Например, выражение Excel, используемое для преобразования
270° в радианах будет RADIANS(270), что
равняется 4,712389 радианам
5) равно 0,07074, косинусу 1,5 радиана
мы использовали Excel, чтобы решить их.
Использование арксинуса
(обратный синус) мы можем найти угол a
используя уравнение