Что такое хорда окружности в геометрии, её определение и свойства
Хорда в переводе с греческого означает «струна». Это понятие широко применяется в разных областях науки — в математике, биологии и других.
В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.
…
Как построить геометрическую хорду
Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.
Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.
В этом случае радиус разделит её на две идентичные половины.
Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.
Свойства
Существует ряд закономерностей, связывающих между собой хорды и центр круга:
- Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
- Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.
- Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности. И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
- Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
- Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга.
 Такая ось проходит через центр и делит её на две равные части.
Такая ось проходит через центр и делит её на две равные части. - Отрезок с наименьшей длиной представляет собой точку.
- Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.
Взаимосвязь с радиусом и диаметром
Вышеуказанные математические понятия связаны между собой следующими закономерностями:
- Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
- С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
- Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
- Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
- Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.

- Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.
Хорда и радиус
Между этими понятиями существуют следующие связи:
- Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
- Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
- Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
- Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
- Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
- Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.

Отношения со вписанными углами
Углы, вписанные в окружность, подчиняются следующим правилам:
- Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
- Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
- Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
- Вписанный угол, который опирается на диаметр круга, является прямым.
- Равные между собой по размеру отрезки стягивают равные центральные углы.
- Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
- Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.

Взаимодействия с дугой
Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:
- Две равные между собой хорды стягивают равные дуги.
- Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
- Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.
Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.
ДИАМЕТРЫ И ХОРДЫ | Математика
ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР
АДАМАР
ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР
Скачать всю книгу Ж. АДАМАР «ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ» в хорошем качестве
Ниже посмотрите текст для быстрого ознакомления(формулы отображаются не корректно):
61. На основании определения, данного в п. 19а, сказанное в п. 9
может быть сформулировано так:
Теорема. Всякий диаметр служит осью симметрии для
окружности и для круга.
Отсюда видно, что окружность имеет бесчисленное множество
осей симметрииг
ДИАМЕТРЫ И ХОРДЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР
62. Хордой называется отрезок, соединяющий концы дуги окружности.
Эта дуга, как говорят, стягивается хордой. Следует заметить,
что всякая хорда стягивает две различные дуги — одну меньшую, а
другую большую полуокружности (или обе равные полуокружности,
если хорда есть диаметр).
63. Теорема. Диаметр, перпендикулярный хорде, делит эту
хорду и каждую из стягиваемых ею дуг на две равные части.
В самом деле, диаметр окружности О, перпендикулярный к хорде
АВ, служит осью симметрии, с одной стороны, окружности, а с другой
стороны, — равнобедренного треугольника ОАВ\ следовательно,
он является осью симметрии и для образованной ими фигуры в целом.
Следствие. Каждые два из пяти следующих условий:
1°. быгь перпендикулярным хорде,
2°. проходить через центр,
3°. проходить через середину хорды,
4°, 5°. проходить через середину одной из двух стягиваемых дуг, —
определяют прямую.
Все определённые таким образом прямые сливаются в одну.
Геометрическое место середин ряда параллельных хорд есть
диаметр, перпендикулярный к этим хордам.
Касательная параллельна тем хордам, которые делятся диаметром,
проведённым в точку касания, на две равные части.
Теорема. Две дуги окружности, заключённые между двумя
параллельными прямыми, равны (черт. 64).
Действительно, эти дуги симметричны друг с другом относительно
диаметра, перпендикулярного к обеим параллельным прямым.
64. Теорема. Если в плоскости окружности дана некоторая
точка Pf то из всех точек, лежащих на окружности, точка, наиболее
близкая к Р, и точка, наиболее удалённая от Р, представляют
собой основание нормалей к окружности (п. 60), проходящих
60), проходящих
через точку Р.
Если А —та из двух точек, которая расположена на полупрямой
ОР, а В — та точка, которая лежит на противоположной полупрямой
(черт. 65 и 66), то расстояние РА равно разности ОР и
радиуса, а расстояние РВ — сумме тех же длин. Следовательно, любая
70ДИАМЕТРЫ И ХОРДЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР
точка М окружности находится от точки Рна расстоянии, большем РА
и меньшем РВ, как третья сторона треугольника ОРМ.
Расстояние РМ постоянно увеличивается, когда точка М описывает
окружность, перемещаясь из А в В, потому что сторона РМ
треугольника ОРМ лежит против угла, который всё время увеличивается
и заключён между двумя сторонами постоянной длины.
Следствие. Диаметр есть наибольшая хорда окружности.
Если, в самом деле, совместить точку Р с точкой А, то хорда РМ
будет, очевидно, меньше диаметра РВ.
65. Теорема. В одном круге или в двух равных кругах:
1°. равным дугам соответствуют равные хорды, и обратно;
2°. из двух неравных дуг, меньших полуокружности, большая
из двух неравных дуг, меньших полуокружности, большая
дуга соответствует большей хорде.
1°. Если мы совместим две равные дуги, совмещая их концы, то
совместятся и хорды.
Обратно, если хорды равны, то центральные углы равны по
третьему признаку равенства треугольников, и, следовательно, дуги
также равны.
2°. Если дуга АВ меньше дуги А!ВТ (черт. 67) и, следовательно,
угол АОВ меньше угла АтОВт, то хорда АВ будет меньше А!В’, как
это показывает теорема п. 28, применённая к треугольникам ОАВ
и ОА!В\
66. Теорема. В одном и том же круге или в двух равных
кругах:
1°. две равные хорды одинаково удалены от центра, и обратно;
2°. из двух неравных хорд большая менее удалена от центра.
1°. Две равные хорды в одном и том же круге соответствуют
двум равным дугам; достаточно наложить друг на друга эти две дуги,
чтобы убедиться, что середины обеих хорд находятся на одинаковом
расстоянии от центра.
Обратно, если две хорды АВ и А’В’ круга О (черт. 68) одинаково
68) одинаково
отстоят от центра, прямоугольные треугольники ОНА и ОН А’ имеют
равные гипотенузы и равные катеты О Н — О Н ] следовательно, Н А —
= НА’ и АВ — АГВГ.
71 ДИАМЕТРЫ И ХОРДЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР
2°. Предположим, что хорда АВ больше хорды А’В’ (черт. 69).
Отсюда следует, что угол АОВ больше угла АгОВ\ и если опустить
перпендикуляры ОН и ОН’, то угол АОН больше угла А’ОНг.
Но в таком случае угол О АН, являющийся дополнением первого
угла, меньше угла ОАтНг, представляющего собой дополнение второго.
Два прямоугольных треугольника ОНА и ОН’Ат имеют, таким образом,
равные гипотенузы и неравные острые углы, откуда следует (п. 35),
что 0#<0#’.
67. Представим себе хорду ММГ (черт. 70), которая перемещается
таким образом, что расстояние её от центра, вначале меньшее радиуса,
увеличивается и становится равным
этому радиусу. Предположим для определённости,
что эта хорда перемещается,
оставаясь перпендикулярной к определённому
диаметру ОА.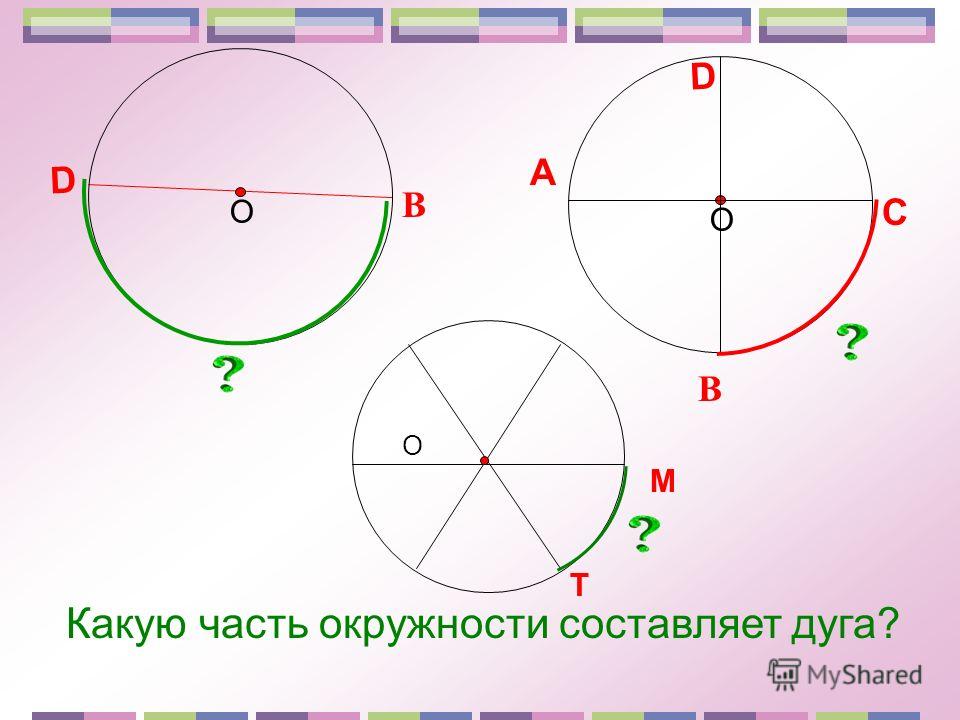
Длина ММГ уменьшается по мере того,
как хорда приближается к касательной
в точке А, на основании предыдущей
теоремы, и точку М можно взять настолько
близко к точке А (иначе говоря хорду,
настолько близко к касательной), что
эта длина будет сколь угодно малой, так
как ЛШ'<2ЖА.
Мы видим, что точки М и М! безгранично приближаются одна
к другой и стремятся слиться с точкой А; мы выражаем это обстоятельство
следующими словами: касательная имеет с окружностью
две общие точки, сливающиеся в А. Мы увидим, что такой способ
выражения позволяет проще сформулировать некоторые теоремы.
УПРАЖНЕНИЯ.
50. Окружность проходит через две данные точки А и В. Пусть С —
одна из точек, в которой эта окружность встречает данную прямую, перпендикулярную
к прямой АВ. Найти геометрическое место точек, диаметрально-
противоположных точке С, если окружность, изменяясь, всё время
проходит через точки Л и 5 (использовать упражнение 34).
51. Если разделить £орду на три равные части и соединить с центром
точки деления, то соответствующий центральный угол не разделится на три
равные части (доказать).
Какая из трёх частей угла будет наибольшей (использовать упражнение
7)? Обобщить на случай большего числа частей.
52. Если две хорды на одной окружности равны между собой, то расстояния
от точки пересечения этих хорд или их продолжений до концов той и
другой хорды соответственно равны между собой (доказать).
53. Найти геометрическое место середин хорд данной окружности,
имеющих данную длину.
54. Найти наименьшую хорду окружности, которую можно провести
через данную точку, находящуюся внутри этой окружности.
72 ДИАМЕТРЫ И ХОРДЫ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР
ДИАМЕТРЫ И ХОРДЫ
Хорда окружности — определение, свойства, теорема » Kupuk.net
Термин «хорда» используется в различных науках. Например, в биологии это означает скелетный гибкий стержень, в математике — отрезок, вписанный в окружность.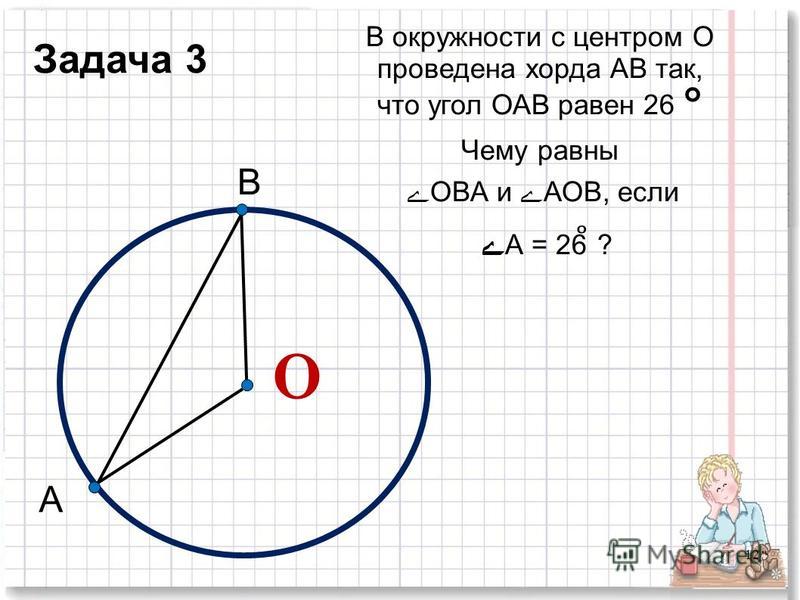 В геометрии хорда окружности — это отрезок, который соединяет две точки окружности. Она является частью секущей, проведенной через окружность.
В геометрии хорда окружности — это отрезок, который соединяет две точки окружности. Она является частью секущей, проведенной через окружность.
Хорда в геометрии
Каждая хорда имеет свою длину. Ее можно определить с помощью теоремы синусов. То есть длина хорды окружности зависит от радиуса и вписанного угла, опирающегося на данный отрезок. Формула для определения длины выглядит следующим образом: B*A = R*2 * sin α, где R — радиус, AB — это хорда, α — вписанный угол. Также длину можно вычислить через другую формулу, которая выводится из теоремы Пифагора: B*A = R*2 * sin α/2 , где AB — это хорда, α — центральный угол, который опирается на данный отрезок, R — радиус.
Если рассматривать хорды в совокупности с дугами, то получаются новые объекты. Например, в кругу можно дополнительно выделить две области: сектор и сегмент. Сектор образуется с помощью двух радиусов и дуги.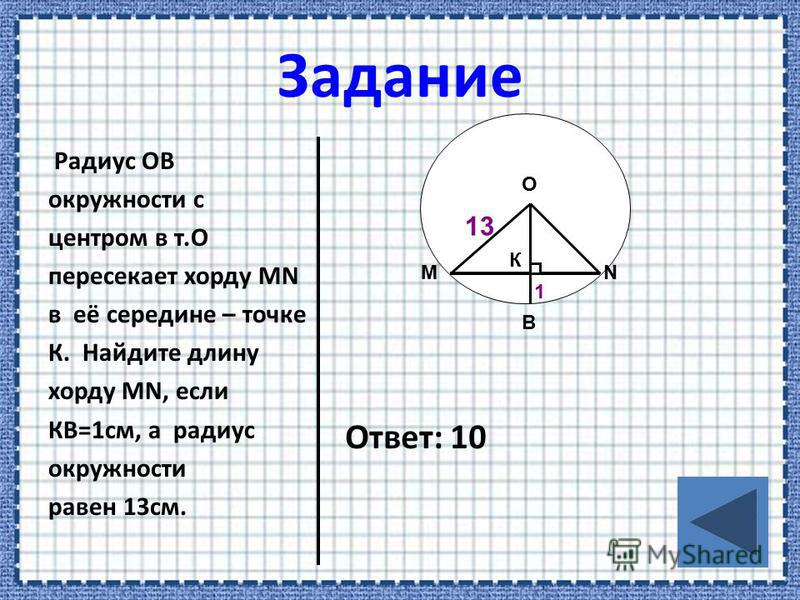 Для сектора можно вычислить площадь, а если он является частью конуса, то еще и высоту. Сегмент, в свою очередь, это область, состоящая из отрезка и дуги.
Для сектора можно вычислить площадь, а если он является частью конуса, то еще и высоту. Сегмент, в свою очередь, это область, состоящая из отрезка и дуги.
Для того чтобы проверить правильность своего решения в нахождении длины, можно обратиться к онлайн-калькуляторам в интернете. Они представлены в виде таблицы, в которую нужно вписать только известные параметры, а программа сама выполнит необходимые вычисления.
Это очень полезная функция, так как не приходится вспоминать различные уравнения и производить сложные расчеты.
Свойства отрезка окружности
Для решения геометрических задач необходимо знать свойства хорды окружности. Для нее характерны такие показатели:
Помимо основных свойств отрезка круга, нужно выделить еще одно важное свойство. Оно отражено в теореме о пересекающихся хордах.
Ключевая теорема
Имеется круг с центром в точке O и радиусом R. Для теоремы нужно в круг вписать две прямые, пускай это будут хорды BA и CD, которые пересекаются в точке E. Перед тем как перейти к доказательству, нужно сформулировать определение теоремы. Оно звучит следующим образом: если хорды пересекаются в некоторой точке, которая делит их на отрезки, то произведения длин отрезков первой хорды равно произведению длин отрезков второй хорды. Для наглядности можно записать эту формулу: AE*BE= EC*ED. Теперь можно перейти к доказательству.
Для наглядности можно записать эту формулу: AE*BE= EC*ED. Теперь можно перейти к доказательству.
Проведем отрезки CB и AD. Рассмотрим треугольники CEB и DEA. Известно, что углы CEB и DEA равны как вертикальные углы, DCB и BAD равны за следствием с теоремы про вписанные углы, которые опираются на одну и ту же дугу. Треугольники CEB и DEA подобны (первый признак подобия треугольников). Тогда выходит пропорциональное соотношение BE/ED = EC/EA. Отсюда AE*BE= EC*ED.
Помимо взаимодействия с внутренними элементами окружности, для хорды еще существуют свойства при пересечении с секущейся и касательными прямыми. Для этого необходимо рассмотреть понятия касательная и секущая и определить главные закономерности.
Касательная — это прямая, которая соприкасается с кругом только в одной точке. И если к ней провести радиус круга, то они будут перпендикулярны. В свою очередь, секущая — это прямая, которая проходит через две точки круга. При взаимодействии этих прямых можно заметить некоторые закономерности.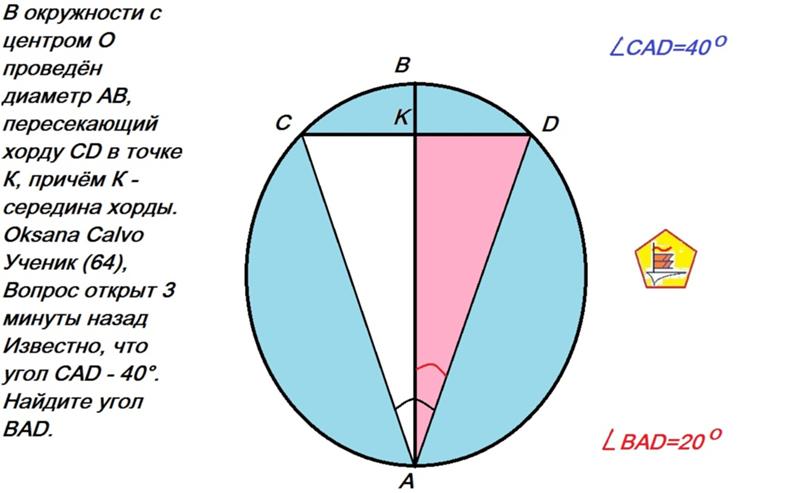
Касательная и секущая
Существует теорема о двух касательных, которые проведены с одной точки. В ней говорится о том, что если есть две прямые OK и ON, которые проведены с точки O, будут равны между собой. Перейдем к доказательству теоремы.
Рассмотрим два прямоугольных треугольника AFD и AED. Поскольку катеты DF и DE будут равны как радиусы круга, а AD — общая гипотенуза, то между собой данные треугольники будут равны за признаком равенства треугольников, с чего выходит, что AF = AE.
Если возникает ситуация, когда пересекаются касательная и секущая, то в этом случае также можно вывести закономерность. Рассмотрим теорему и докажем, что AB 2 = AD*AC.
Предположим у нас есть касательная AB и секущая AD, которые берут начало с одной точки A. Обратим внимание на угол ABC, он спирается на дугу BC, значит, за свойством значение его угла будет равно половине градусной меры дуги, на которую он опирается.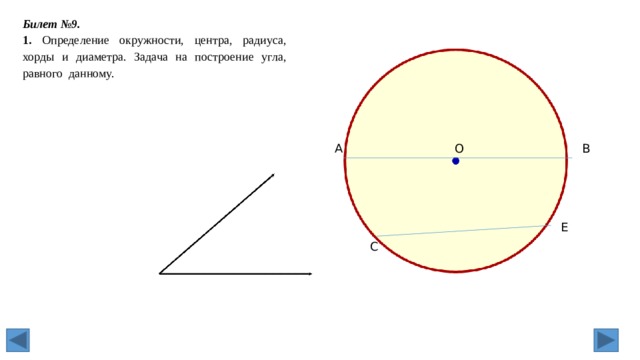 За свойством вписанного угла, величина угла BDC также будет равно половине дуги BC. Таким образом, треугольники ABD и ABC будут подобны за признаком подобия треугольников, так как угол A — общий, а угол ABC равен углу BDC. Опираясь на теорию, получаем соотношение: AB/CA = DA/AB, переписав это соотношение в правильную форму, получаем равенство AB 2 = AD*AC, что и требовалось доказать.
За свойством вписанного угла, величина угла BDC также будет равно половине дуги BC. Таким образом, треугольники ABD и ABC будут подобны за признаком подобия треугольников, так как угол A — общий, а угол ABC равен углу BDC. Опираясь на теорию, получаем соотношение: AB/CA = DA/AB, переписав это соотношение в правильную форму, получаем равенство AB 2 = AD*AC, что и требовалось доказать.
Как есть теорема про две касательные, так есть и теорема про две секущие. Она так же просто формулируется, как и остальные теоремы. Поэтому рассмотрим доказательство и убедимся, что AB*AC = AE*AD.
Проведем две прямые через точку A, получим две секущие AC и AE. Дорисуем две хорды, соединяя точки C и B, B и D. Получим два треугольника ABD И CEA. Обратим внимание на вписанный четырехугольник BDCE. За свойством вписанных четырехугольников узнаем, что значения углов BDE и ECB в сумме будут давать 180 градусов. И сумма значений углов BDA и BDE также равна 180, за свойством смежных углов.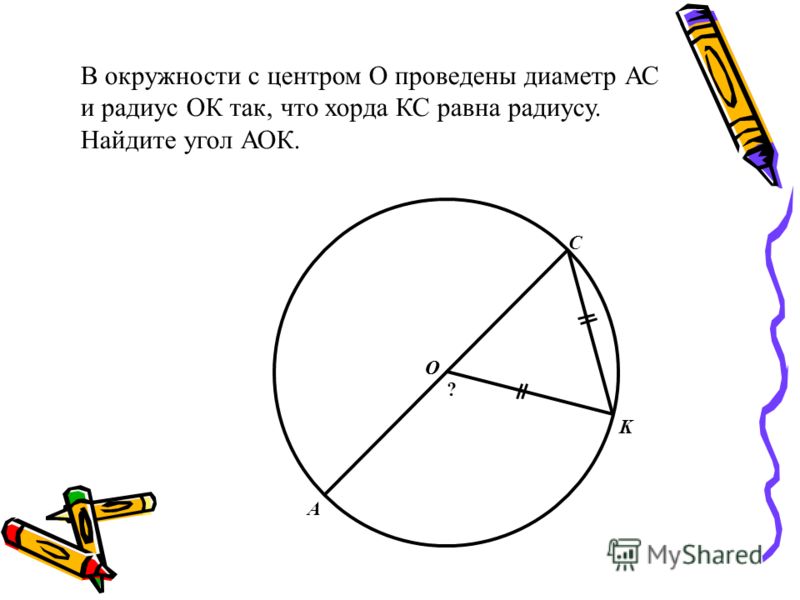
Отсюда можно получить два уравнения, из которых будет выведено, что углы ECB и BDA будут равны: BDA + BDE = 180; BDE + ECB = 180. Все это записываем в систему уравнений, отнимаем первое от второго, получаем результат, что ECB = BDA.
Если вернутся к треугольникам ABD И CEA, то теперь можно сказать, что они подобны, так как угол А — общий, а углы ECA и BDA — равны. Теперь можно записать соотношение сторон: AB/AE = AD/AC. В итоге получим, что AB*AC = AE*AD.
Решение задач
При решении задач, связанных с окружностью, хорда часто выступает главным элементом, опираясь на который можно найти остальные неизвестные элементы. В каждой второй задаче задаются два параметра, чтобы найти третий неизвестный. В задачах, которые, связанные с кругом, хорда — это обязательный элемент:
- Найти высоту детали, которая была получена путем сгибания заготовки в дугу.
 В начальных данных обязательно присутствует хорда и длина дуги.
В начальных данных обязательно присутствует хорда и длина дуги. - Дана развертка, нужно найти длину части кольца. Задается хорда и диаметр.
- Также можно находить длину хорды. В случае если заданы уравнения прямой и окружности, которые пересекаются.
Для решения задач с отрезком в окружности удобно использовать схематические рисунки. Их рисуют с помощью линейки и циркуля, и принцип решения задач становится более наглядным.
Дайте определение окружности. Объясните, что такое центр, радиус, хорда и диаметр окружности. — Студопедия.Нет
Ответ: Окружность — это геометрическое место точек плоскости, равноудаленных от одной точки плоскости.
Центр окружности — точка плоскости, равноудаленная от всех точек окружности.
Радиус окружности — равные отрезки, соединяющие центр с точками окружности.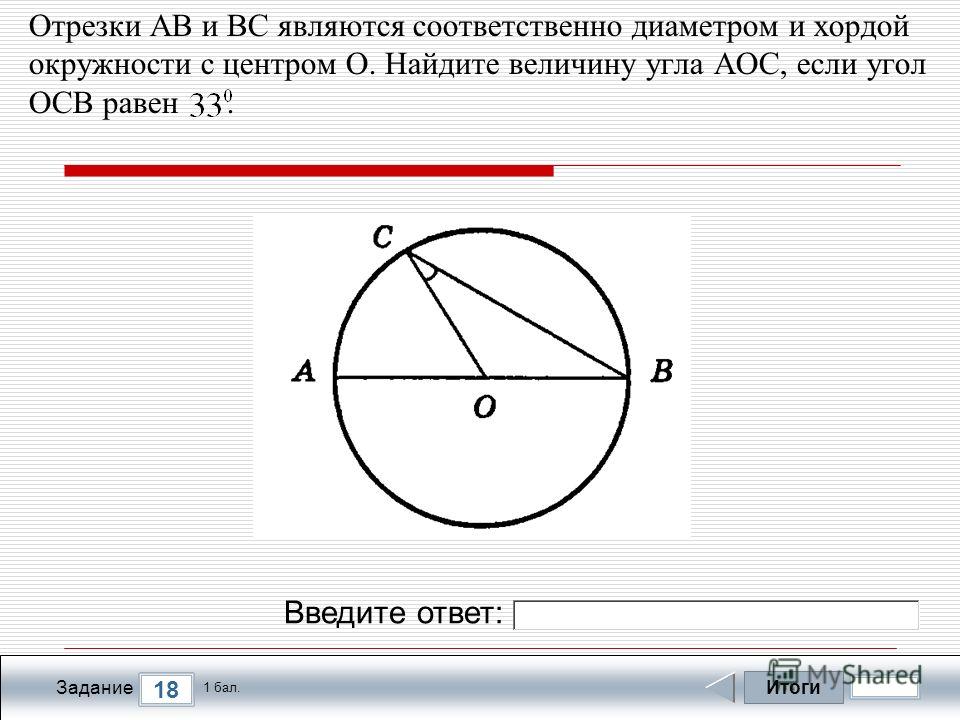
Хорда — отрезок, соединяющий любые две точки окружности.
Диаметр окружности — хорда, проходящая через центр.
Докажите свойство углов при основании равнобедренного треугольника.
Доказательство: Пусть BD — биссектриса АВС, тогда по первому признаку равенства треугольников ABD = CBD (т. к. угол ABD= углу CBD, AB=CB, сторона BD — общая) , следовательно 1)BD — медиана и высота, 2)углы при основании равны.
Билет №7
Дайте определение прямоугольного треугольника и сформулируйте его свойства.
Ответ: Прямоугольный треугольник— треугольник один из углов которого прямой.
Объясните решение задачи на построение: Построить биссектрису данного угла.
Ответ: 1. Провести окружность произвольного радиуса с центром в вершине угла.
Построить две окружности этого же радиуса с центром в точках пересечения первой окружности и сторонами угла.
Построить такой луч из вершины угла, чтобы он проходил через точку пересечения окружностей из второго шага.
Билет №8
Дайте определение параллельных прямых и сформулируйте признаки параллельных двух прямых.
Ответ: Параллельные прямые — это две непересекающиеся прямые, лежащие в одной плоскости. Параллельные прямые записываются через знак параллельности «||».
1 Две прямые, параллельные третьей* параллельны.
II. Если внутренние накрест лежащие углы равны, то прямые параллельны
III. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны.
IV. Если соответственные углы равны, то прямые параллельны.
Объясните решение задачи на построение: Построить середину данного отрезка.
Ответ: Замерить длину отрезка. Разделить длину пополам, отмерить от любого края отрезка эту половину и поставить черточку. . Если нужно проведите прямую перпендикулярную вашему отрезку.
. Если нужно проведите прямую перпендикулярную вашему отрезку.
Билет№9
Дайте определение внешнего угла треугольника и сформулируйте его свойство.
Ответ:Внешний угол треугольникапри данной вершине — это угол,
Докажите свойство накрест лежащих углов при параллельных прямых
Ответ: Дано: а║b, с — секущая, ∠1 и ∠2 — внутренние накрест лежащие.
Доказать: ∠1 = ∠2.
Доказательство:
Предположим, что ∠1 ≠ ∠2.
Тогда можно построить ∠ВАК = ∠2. Так как углы ВАК и ∠2 внутренние накрест лежащие при пересечении прямых b и АК секущей с, то b║АК.
Получилось, что через точку А проходят две прямые, параллельные прямой b, что противоречит аксиоме о параллельных прямых.
Значит, предположение неверно и
∠1 = ∠2.
Билет №10
Сформулируйте признаки равенства треугольников.
Ответ:
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Докажите свойство соответственных углов при параллельных прямых.
Ответ: Ответ не нашёл!
Билет №11
Сформулируйте признаки равенства прямоугольных треугольников.
Ответ: Если гипотенуза и катет одного прямоугольного треугольника равен гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны
Докажите свойство односторонних углов при параллельных прямых.
Сумма односторонних углов, образованных пересечением двух параллельных прямых третьей, равна 180°.
Доказательство:
Пусть параллельные прямые а и b пересечены секущей АВ.
Тогда соответственные ∠1 и ∠2 будут равны,
∠2 и ∠3 – смежные, поэтому ∠2 + ∠3 = 180°.
Из равенств ∠1 = ∠2 и ∠2 + ∠3 = 180° следует, что
сумма односторонних углов ∠1 + ∠3 = 180°.
Билет №12
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы./ / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. / / Длина хорды, центральный угол в ° (угловых градусах) и радианах при делении окружности единичного диаметра на равные сегменты. Поделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Окружность и круг. Обобщение 8 класс онлайн-подготовка на Ростелеком Лицей
Основные определения
Определение окружности: множество точек, удаленных от данной на одно и то же расстояние. Поэтому для рисования окружности удобно использовать циркуль – острие размещается в центре окружности, а ширина его раствора определяет радиус окружности (см. рис. 1).
Рис. 1. Окружность
Круг отличается от окружностью тем, что круг – это множество точек, удаленных от данной на расстояние не больше, чем радиус соответствующей окружности, которая ограничивает этот круг (см. рис. 2).
Рис. 2. Круг
Если корову привязать к колышку, то через некоторое время она выест вокруг себя круг травы, радиус которой будет равен длине веревки.
Окружность является частью круга, но иногда возникает необходимость рассмотреть круг без его границы. Такой круг называют открытым (см. рис. 3).
рис. 3).
Рис. 3. Открытый круг
Хорда – это отрезок, соединяющий две любые точки окружности (см. рис. 4). Если хорда проходит через центр, то ее называют диаметром (см. рис. 4). Понятно, что диаметр – это самая длинная хорда.
Рис. 4. Хорда и диаметр
Надо отметить, что слова «радиус» и «диаметр» используются в двух смыслах. Соединим центр и произвольную точку окружности отрезком. Такой отрезок называется радиусом (см. рис. 5). Его длина называется не длиной радиуса, а просто радиусом.
Рис. 5. Радиус
То же самое относится к диаметру – это и отрезок, хорда – проходящая через центр и его длина. Ясно, что диаметр равен двум радиусам. Радиус и диаметр обозначают большими или малыми буквами и соответственно.
Число
Одна из главных особенностей окружности – это то, что любая окружность задается всего одним параметром (с точностью до расположения) – радиусом (см. рис. 6).
Рис.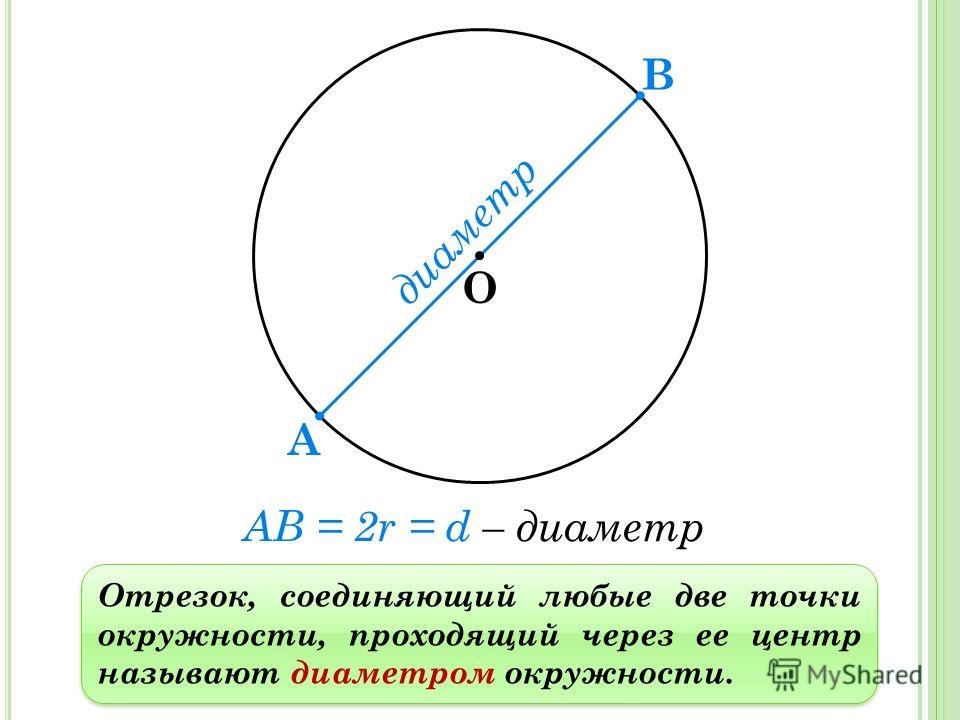 6. Окружность задается радиусом
6. Окружность задается радиусом
Кроме того, все окружности подобны друг другу (см. рис. 7).
Рис. 7. Окружности подобны
Это означает, что если в несколько раз увеличить или уменьшить радиус или диаметр окружности, то ровно во столько же раз изменится длина окружности . Это означает, что отношение длины окружности к диаметру для любой окружности одно и то же:
Эта величина не является рациональным числом, т. е. ее нельзя точно записать в виде отношения двух целых чисел, конечной десятичной или хотя бы периодической десятичной дроби.
Поэтому для этого числа ввели специальный символ , которым обозначается это иррациональное число. Несложно оценить эту величину.
Если описать вокруг окружности квадрат и вписать в нее квадрат (см. рис. 8), то можно получить такую оценку (периметр вписанного квадрата меньше длины окружности, а описанного – больше):
Рис. 8. Вокруг окружности описали и вписали квадрат
Длина стороны вписанного квадрата равна:
Тогда:
Длина стороны описанного квадрата равна:
Тогда:
Тогда:
Если увеличивать количество сторон вписанного и описанного правильных многоугольников, все больше и больше приближая их к окружности, то получаемая оценка числа будет все точнее и точнее.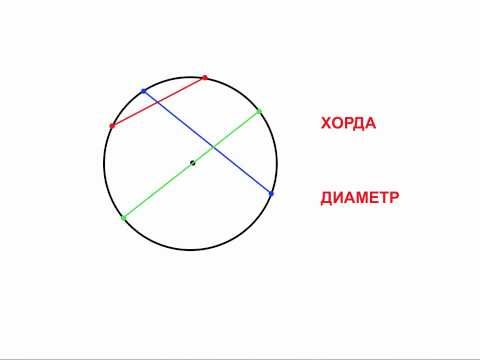
При решении задач и мы будем чаще всего использовать приближение , если иное не оговорено в условии.
Приближения числа
Архимед для уточнения значения числа увеличивал число вершин в правильных многоугольниках, которые он вписывал в окружность и описывал вокруг окружности. Это очень трудоемкий процесс.
Архимед дошел до -угольников, что дало ему возможность показать, что число находится в интервале:
Это соответствует точности два знака после запятой в десятичной записи, что мы обычно и используем в расчетах:
Существуют алгебраические способы оценки этого отношения без использования геометрических фигур. Например, число равно сумме такого бесконечного ряда:
Это равенство открыл индийский математик Мадхава примерно в году.
Чем больше дробей в скобках взять для расчета, тем точнее мы получим десятичное приближение числа . Проблема в том, что такой ряд очень медленно приближается к числу (говорят, что он медленно сходится). Нужно взять около дробей в скобках, чтобы получить оценку Архимеда. Однако сам Мадхава немного улучшил свою формулу и получил точных знаков после запятой для числа.
Нужно взять около дробей в скобках, чтобы получить оценку Архимеда. Однако сам Мадхава немного улучшил свою формулу и получил точных знаков после запятой для числа.
Развитие математических методов в целом давало и новые возможности уточнения значения числа . Например, Исаак Ньютон предложил удобную формулу, которая использует тригонометрические функции. В XIX веке получили уже более знаков числа .
В эпоху компьютеров стало возможным вычислить невероятное число знаков десятичного разложения числа . Сейчас они оцениваются триллионами или больше.
Длина окружности
Итак, определение числа – это отношение длины окружности к ее диаметру:
Переписывая это выражение в привычном виде, получаем известную формулу длины окружности:
Таким образом, формула длины окружности не требует какого-то доказательства, а представляет собой эквивалентное определение числа .
Рассмотрим пример задачи, для решения которой пригодится формула длины окружности.
Задача 1. Какое расстояние нужно проплыть, чтобы перебраться в диаметрально противоположную точку берега круглого озера, длина береговой линии которого равна км?
Решение
Нам необходимо вычислить диаметр окружности, длина которой равна . Формула:
Подумаем о том, что даже достаточно «круглое» озеро в реальности все-таки отличается от настоящего круга. Тот факт, что в условии дана длина берега км, наводит на мысль, что это тоже сильно приближенное значение. Тогда привычное приближение будет совершенно излишним и мы вполне можем считать:
Тогда пловцу придется преодолеть путь:
Более того, в условиях такой низкой точности вполне оправданно считать этот диаметр приблизительно метров.
Ответ: м.
Задача 2. Какого диаметра необходимо изготовить колесо, чтобы длина его обода была см?
Решение
Задача аналогична предыдущей и решается с помощью той же самой формулы:
Разница в точности вычислений.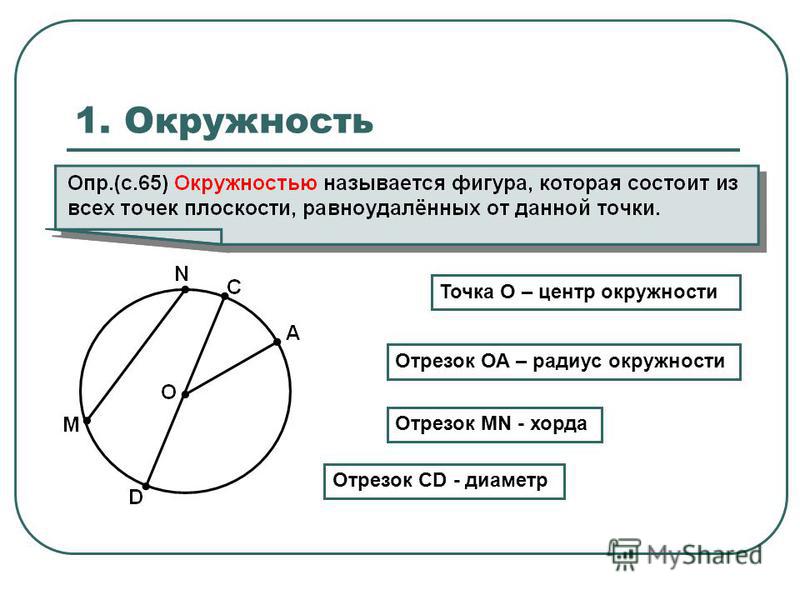 Размеры даны в см, и, следовательно, наш результат не должен иметь погрешность больше см.
Размеры даны в см, и, следовательно, наш результат не должен иметь погрешность больше см.
Подставим различные приближения в формулу:
Необходимой точности мы достигли только при приближении:
Ответ: см.
Дуга окружности
Иногда требуется найти длину не всей окружности, а только ее части – дуги (см. рис. 9). Дуга окружности, кроме линейной меры (длины), имеет и градусную меру, которая совпадает с градусной мерой соответствующего центрального угла.
Рис. 9. Дуга окружности
Понятно, что длина дуги пропорциональна градусной мере. Если градусная мера равна , то длина дуги равна длины окружности, т. е.:
Для произвольного угла получаем формулу длины дуги:
Если же значение угла дано в радианах, то формула принимает вид:
(так как рад).
Площадь круга
Формула площади круга, в отличие от формулы длины окружности, уже требует доказательства. Одним из первых его вариантов является доказательство, которое придумал Архимед.
Одним из первых его вариантов является доказательство, которое придумал Архимед.
Сводится оно к тому, что, разрезая круг на части, Архимед складывает из них фигуры, приближающиеся к прямоугольнику, и вычисляет его площадь.
Разрезав пиццу на 8 частей, можно сложить из нее фигуру, достаточно близкую к прямоугольнику (см. рис. 10) (по рисунку, конечно, больше похоже на параллелограмм, но по мере увеличения количества кусков, на которые мы круг разрезаем, угол между сторонами будет все ближе к прямому).
Рис. 10. Пиццу разрезали на 8 частей и сложили из нее фигуру, достаточно близкую к прямоугольнику
Боковые стороны здесь равны радиусу, а верхняя и нижняя являются половинами окружности, т. е. длина каждой – .Тогда площадь этой фигуры примерно равна:
На самом деле, это равенство уже точное. Пиццу очень мелко делить не получится, поэтому перейдем к обычному кругу.
Делим его на большее количество частей и складываем по тому же принципу. Получаем фигуры, все больше похожие на прямоугольник со сторонами и .
Получаем фигуры, все больше похожие на прямоугольник со сторонами и .
Не вызывает сомнения, что можно сложить фигуру, близкую к прямоугольнику с любой точностью. Но площади всех этих фигур равны площади исходного круга. Следовательно, его площадь:
Сектор и сегмент
Часть круга, ограниченная двумя радиусами, называется сектором (см. рис. 11).
Рис. 11. Сектор
Понятно, что площадь сектора пропорциональна углу между радиусами. Если угол равен , то сектор совпадает с целым кругом, если угол равен , то сектор – это половина круга. Если угол равен , то площадь такого сектора равна от площади круга:
Для произвольного угла получаем формулу площади сектора:
Опять же, если угол дан в радианах, то:
Часть круга, которую отсекает хорда, называется сегментом (см. рис. 12).
Рис. 12. Сегмент
Названия похожи, старайтесь не путать. Сегмент, как и сектор, определяется радиусом и величиной центрального угла или равной ей градусной мерой дуги.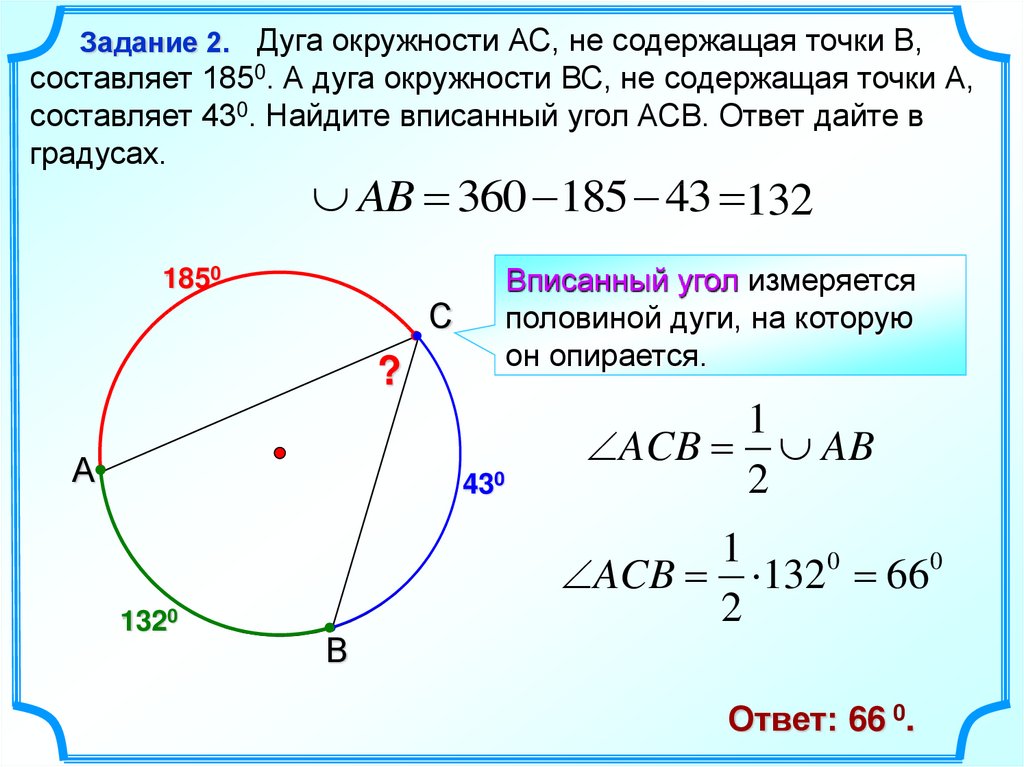
Видно, что сегмент является частью соответствующего сектора. Его площадь обычно находят как разность площадей сектора и равнобедренного треугольника:
Задача 3. Найти длину дуги окружности радиуса м, градусная мера которой равна . Найти площади соответствующих сектора и сегмента (см. рис. 13).
Рис. 13. Иллюстрация к задаче 3
Решение
Найдем длину дуги:
Такая запись считается конечной и пишется в ответ.
Можно вычислить это значение приближенно, если необходимо:
Найдем площадь сектора:
Для вычисления площади сегмента нам понадобится площадь равнобедренного треугольника. Воспользуемся формулой:
Найдем площадь сегмента:
Ответ: .
При небольших углах сектор почти целиком состоит из треугольника, а на сегмент приходится совсем небольшая часть.
Взаимное расположение окружности и прямой
Мы рассмотрели основные характеристики окружности и круга: радиус, диаметр, длину окружности, площадь. Рассмотрели характеристики частей окружности и круга: дуги, сектора и сегмента.
Рассмотрели характеристики частей окружности и круга: дуги, сектора и сегмента.
Теперь рассмотрим взаимное расположение окружности и прямой. Это важно хотя бы по той причине, что все многоугольники состоят из отрезков, т. е. частей прямых. А значит, любая задача на окружность и многоугольник сводится к изучению взаимного расположения окружности и прямой.
Для окружности и прямой существует три типа возможного расположения (см. рис. 14):
- прямая пересекает окружность в двух точках;
- прямая касается окружности в одной точке;
- прямая и окружность не имеют общих точек.
Рис. 14. Три типа возможного расположения окружности и прямой
Опустим перпендикуляр из центра на прямую. Его длина – это расстояние от центра до окружности.
Легко видеть следующее (см. рис. 15):
- В случае пересечения прямой и окружности – это расстояние меньше радиуса. В самом деле, в равнобедренном треугольнике высота меньше его боковых сторон.

- Если расстояние больше радиуса, то прямая не имеет общих точек с окружностью. В самом деле, основание перпендикуляра находится вне окружности. Любая наклонная длиннее перпендикуляра, значит, любая точка прямой находится от еще дальше, чем .
- В случае касания расстояние от центра до прямой равно радиусу.
Рис. 15. Расстояние от центра до окружности меньше радиуса; равно радиусу; больше радиуса окружности
Несложно убедиться, что это в самом деле так. Если не перпендикуляр, то это наклонная. Но тогда должен существовать перпендикуляр , который должен быть короче, чем , что невозможно.
Верно и обратное: если прямая проходит через конец радиуса и перпендикулярна ему, то она является касательной (см. рис. 16). В этом случае надо показать, что общая точка единственная. Если бы это было не так, т. е. была бы вторая точка, то мы получили бы первый случай, только в равнобедренном треугольнике было бы два прямых угла, что невозможно.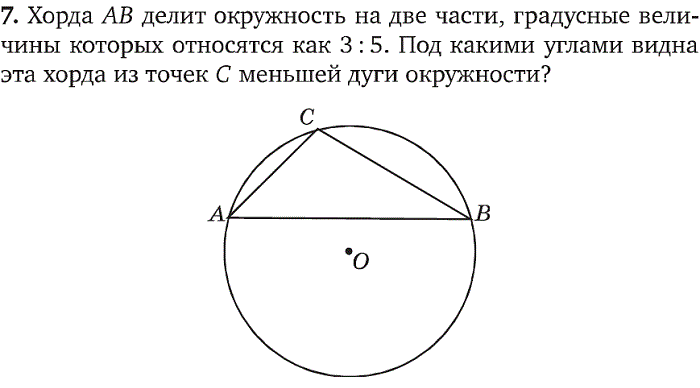 Перпендикулярность касательной к радиусу, проведенному в точку касания, очень важный факт, и мы будем часто использовать его в решении задач.
Перпендикулярность касательной к радиусу, проведенному в точку касания, очень важный факт, и мы будем часто использовать его в решении задач.
Рис. 16. Касательная
Из перпендикулярности касательной и радиуса следует еще один важный факт. Проведем из точки вне окружности две касательные. Получили два треугольника, и . Они прямоугольные, так как касательные перпендикулярны радиусам и равны по катету и гипотенузе (см. рис. 17).
Рис. 17. Отрезки касательных, проведенных из одной точки
Нам здесь важно, что тогда равными получаются отрезки касательных и , а также углы и . Эти факты тоже часто используются при решении различных задач.
Центральный и вписанный углы
В уроке о вписанных и описанных многоугольниках мы рассмотрели понятие центрального и вписанного углов.
Центральный угол имеет вершину в центре окружности, а вписанный – на самой окружности (см. рис. 18).
Рис. 18. Центральный угол и вписанный угол
Центральный угол опирается на дугу и равен ее градусной мере. Вписанный угол опирается на ту же дугу и равен половине ее градусной меры (несложно доказать, что он равен половине соответствующего центрального угла и, как следствие, половине дуги, на которую опирается).
Вписанный угол опирается на ту же дугу и равен половине ее градусной меры (несложно доказать, что он равен половине соответствующего центрального угла и, как следствие, половине дуги, на которую опирается).
Отсюда мы получили два важных следствия:
- Вписанный угол, опирающийся на диаметр, является прямым, потому как опирается на дугу в .
- Вписанные углы, опирающиеся на одну и ту же дугу, равны друг другу.
Свойство хорд
Проведем две хорды окружности так, чтобы они пересеклись (см. рис. 19).
Рис. 19. Две хорды пересекаются
Понятно, что углы равны как вертикальные. Но нужно заметить, что угол . Это так, потому что они опираются на одну и ту же дугу .
Рис. 20. Равные пары углов: и
Но тогда два треугольника, которые мы получили, подобны. Таким образом, две хорды, пересекаясь, образуют подобные треугольники и . Из подобия треугольников следует:
Что можно переписать так:
Произведения отрезков хорд, которые получаются при пересечении, равны.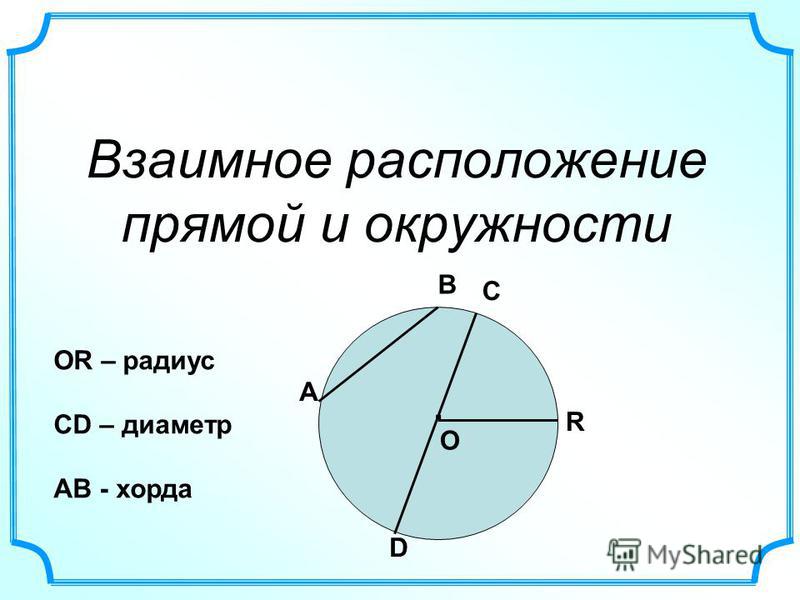
Список литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 8 класс. Учебник. – М.: издательство «Просвещение», 2018.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 8 класс. Учебник. – М.: издательство «Просвещение», 2018.
- Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия, 8 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал ru.onlinemschool.com (Источник)
- Интернет-портал yaklass.ru (Источник)
- Интернет-портал yaklass.ru (Источник)
Домашнее задание
- Центральный угол больше вписанного угла, опирающегося на ту же дугу, на . Найти градусную меру вписанного угла.
- Найти длину дуги окружности радиуса , если ее градусная мера равна .
- Площадь круга, описанного около равностороннего треугольника, больше площади вписанного в него круга на .
 Найти радиус вписанного круга.
Найти радиус вписанного круга.
Диаметр и хорды — PSAT Math
Все математические ресурсы PSAT
10 диагностических тестов 421 практический тест Вопрос дня Карточки Learn by Concept
PSAT Math Help » Геометрия » Плоская геометрия » Круги » Диаметр и хорды
Радиус круга выше равен , а мера – . Какова длина хорды?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить задачу с хордами, нарисуйте прямоугольные треугольники, используя хорду, радиусы и линию, соединяющую центр окружности с хордой под прямым углом.
Теперь хорда делится на две равные части, а угол AOB делится пополам. Вместо одного угла в 120 градусов теперь у вас есть два треугольника 30-60-90. Треугольники 30-60-90 характеризуются соотношением сторон:
Треугольники 30-60-90 характеризуются соотношением сторон:
Итак, чтобы найти длину хорды, сначала найдите длину каждой половины. Поскольку треугольники в вашем круге подобны треугольнику 30-60-90 выше, вы можете установить пропорцию. Гипотенуза нашего треугольника равна 6 (радиус окружности), поэтому она больше 2 (гипотенуза нашего модельного треугольника 30-60-90). Половина хорды окружности – это катет треугольника, расположенный напротив угла 60 градусов (120 / 2), поэтому он соответствует стороне модельного треугольника.
Следовательно,
Поскольку x равен половине хорды, ответ равен .
Сообщить об ошибке
Пусть представляет собой площадь круга и представляет его длину окружности. Какое из следующих уравнений выражается через ?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула площади круга , а формула длины окружности .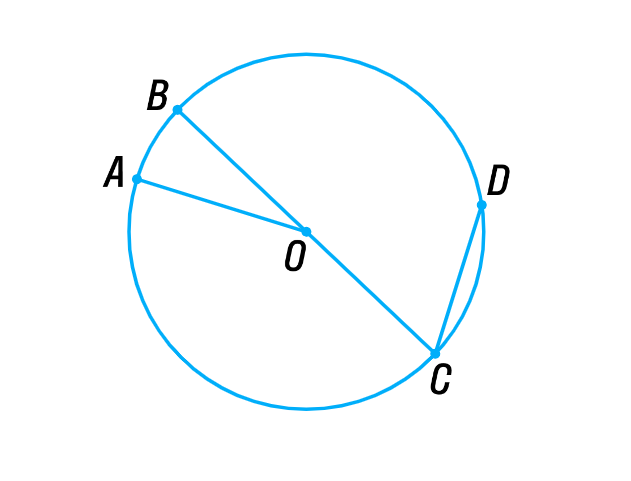 Если мы решим для C через r, мы получим
Если мы решим для C через r, мы получим
.
Затем мы можем подставить это значение r в формулу площади:
Сообщить об ошибке
Если площадь той же окружности в четыре раза больше, чем длина окружности круг, каков диаметр круга?
Возможные ответы:
4
16
32
8
2
54 Правильный ответ:40004 16
Объяснение:
Задайте площадь круга, равную четырехкратной длине окружности πr 2 = 4(2 πr ).
Вычеркните оба символа π и по одному r с каждой стороны, и у вас останется r = 4(2), поэтому r = 8 и, следовательно, d = 16. периметр круга равен 36 π. Каков диаметр круга?
Возможные ответы:
72
3
36
18
6
Правильный ответ: 20
36904 Объяснение:Периметр круга = 2 πr = πd
Следовательно, d = 36
Сообщить об ошибке
Если площадь круга, касающегося квадрата на рисунке выше, равна , каково ближайшее значение к площадь квадрата?
Возможные ответы:
Правильный ответ:
Объяснение:
Получите радиус круга из площади.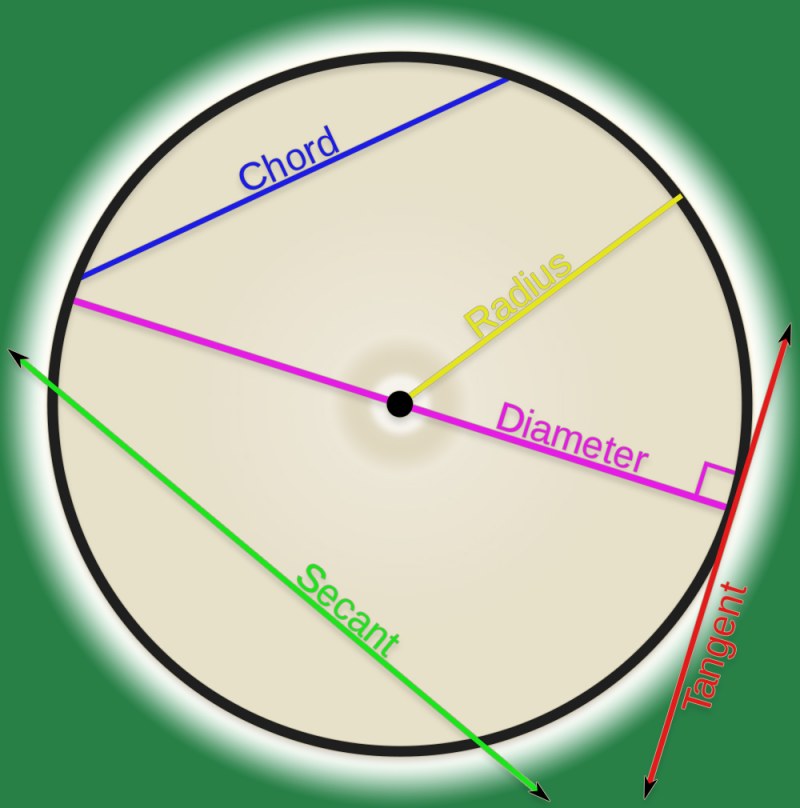
Разделите квадрат на 4 треугольника, соединив противоположные углы. Эти треугольники будут иметь прямой угол в центре квадрата, образованный двумя радиусами круга, и двумя углами по 45 градусов в углах квадрата. Поскольку у вас есть треугольник 45-45-90, вы можете рассчитать стороны треугольников как , , и . Радиусы окружности (от центра до углов квадрата) будут 9. Гипотенуза (сторона квадрата) должна быть .
Тогда площадь квадрата равна .
Сообщить об ошибке
Две стороны прямоугольного треугольника имеют соответственно 3 и 4 длины. Чему равна площадь окружности, описанной около треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы окружность содержала все 3 вершины, гипотенуза должна быть равна диаметру окружности. Гипотенуза и, следовательно, диаметр равны 5, так как это должен быть прямоугольный треугольник 3-4-5.
Уравнение площади круга: A = πr 2 .
Сообщить об ошибке
Примечание. Рисунок выполнен НЕ в масштабе.
В приведенном выше круге длина дуги равна и . Каков диаметр круга?
Возможные ответы:
Правильный ответ:
Объяснение:
Назовите диаметр . Так как , является кругом и является кругом с окружностью .
– это длина, поэтому
Сообщить об ошибке
Примечание. Рисунок выполнен НЕ в масштабе.
В приведенном выше круге длина дуги равна 10 и . Укажите диаметр круга. (Ближайшая десятая).
Возможные ответы:
Недостаточно информации для ответа на вопрос.
Правильный ответ:
Объяснение:
Назовите диаметр .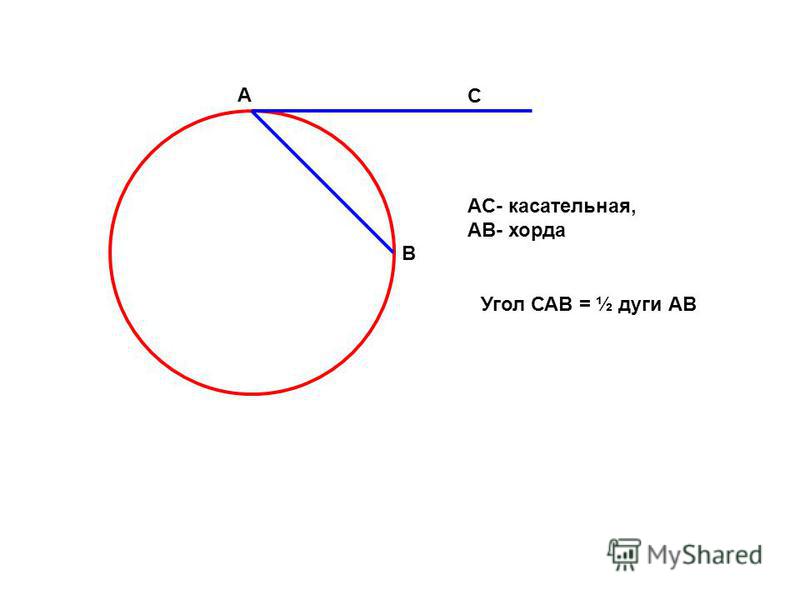 Так как , это круг с окружностью . Поскольку его длина равна 10, длина окружности в 5 раз больше, или 50. Следовательно, установите в формуле длины окружности:
Так как , это круг с окружностью . Поскольку его длина равна 10, длина окружности в 5 раз больше, или 50. Следовательно, установите в формуле длины окружности:
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы PSAT Math3
10 диагностических тестов 421 практический тест Вопрос дня Карточки Учитесь по концепции
Хорды окружности – объяснение и примеры
Из этой статьи вы узнаете:
- Что такое хорда окружности.
- Свойства хорды и; и
- Как найти длину хорды, используя различные формулы.
Что такое хорда окружности?
По определению, хорда — это прямая линия, соединяющая 2 точки на окружности. Диаметр окружности считается самой длинной хордой, потому что она соединяется с точками на окружности окружности.
В круге ниже AB, CD и EF являются хордами круга.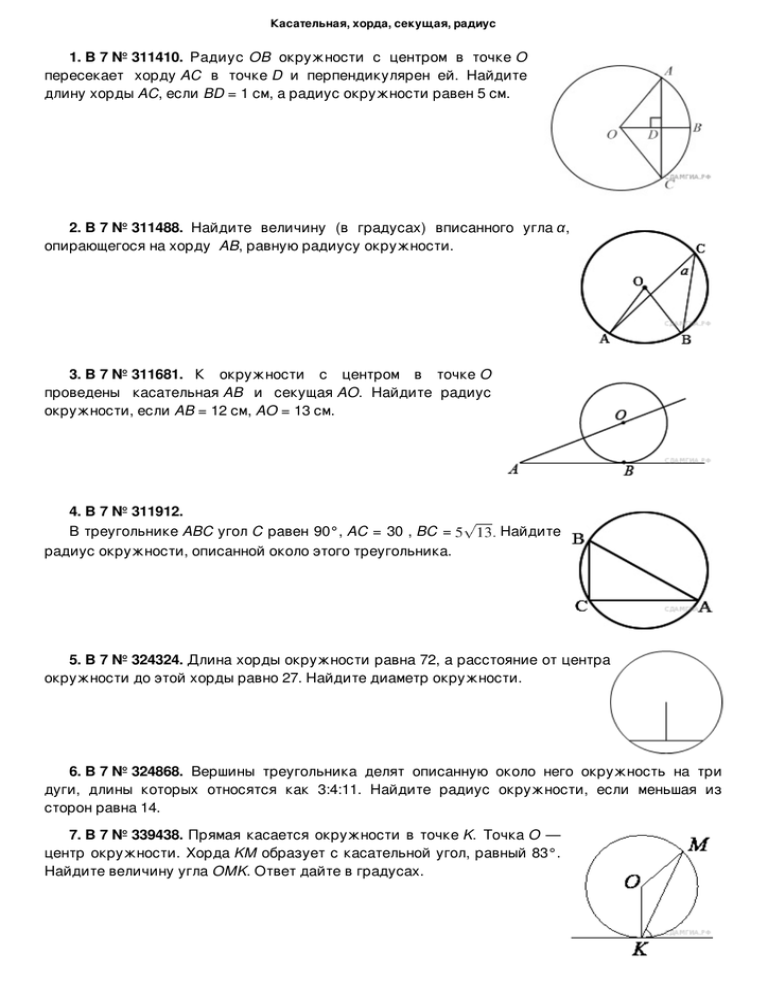 Хорда CD — это диаметр окружности.
Хорда CD — это диаметр окружности.
Свойства хорды
- Радиус окружности — это биссектриса хорды.
- Длина хорды увеличивается по мере уменьшения перпендикулярного расстояния от центра окружности до хорды и наоборот.
- Диаметр — это самая длинная хорда окружности, при этом расстояние по перпендикуляру от центра окружности до хорды равно нулю.
- Два радиуса, соединяющие концы хорды с центром окружности, образуют равнобедренный треугольник.
- Две хорды равны по длине, если они равноудалены от центра окружности. Например, хорда AB равна хорде CD , если PQ = QR.
Как найти хорду окружности?
Есть две формулы для определения длины хорды. Каждая формула используется в зависимости от предоставленной информации.
- Длина хорды, заданная радиусом и расстоянием до центра окружности.
Если длина радиуса и расстояние между центром и хордой известны, то формула для определения длины хорды имеет вид:
Длина хорды = 2√ (r 2 – d 2 )
Где r = радиус окружности, а d = расстояние по перпендикуляру от центра окружности до хорды.
На приведенном выше рисунке длина хорды PQ = 2√ (r 2 – d 2 )
- Длина хорды, если известны радиус и центральный угол
Если известны радиус и центральный угол хорды, то длина хорды определяется как
Длина хорды = 2 × r × синус (C/2)
= 2r синус (C/2)
Где r = радиус окружности
C = угол, образуемый в центре хордой
d = расстояние по перпендикуляру от центра окружности до хорды.
Давайте разработаем несколько примеров с хордой окружности.
Пример 1
Радиус окружности равен 14 см, а расстояние по перпендикуляру от хорды до центра равно 8 см. Найдите длину хорды.
Решение
При заданном радиусе r = 14 см и перпендикулярном расстоянии d = 8 см
По формуле Длина хорды = 2√(r 2 −d 2 )
Длина хорды = 2√ (14 2 −8 2 )
= 2√ (196 − 64)
= 2√ (132)
= 2 х 11,5
= 23 см 2 хорд,
Пример 2
Расстояние по перпендикуляру от центра окружности до хорды равно 8 м. Вычислите длину хорды, если диаметр окружности равен 34 м.
Вычислите длину хорды, если диаметр окружности равен 34 м.
Решение
Учитывая расстояние, d = 8 м.
Диаметр, D = 34 м. Итак, радиус r = D/2 = 34/2 = 17 м
Длина хорды = 2√ (R 2 -D 2 )
по замене,
Длина хорда = 2√ (17 2 — 8 2 )
= 2чина (289 – 64)
= 2√ (225)
= 2 х 15
= 30
Итак, длина хорды 30 м.
Пример 3
Длина хорды окружности 40 дюймов. Предположим, что перпендикулярное расстояние от центра до хорды составляет 15 дюймов. Каков радиус хорды?
Решение
Дано, длина хорды = 40 дюймов.
Расстояние, d = 15 дюймов
Радиус, r =?
по формуле, длина хорды = 2√ (r 2 -D 2 )
40 = 2√ (R 2 — 15 2 )
40 = 2чина − 225)
Квадрат с обеих сторон
1600 = 4 (r 2 – 225)
1600 = 4r 2 – 900
Доп.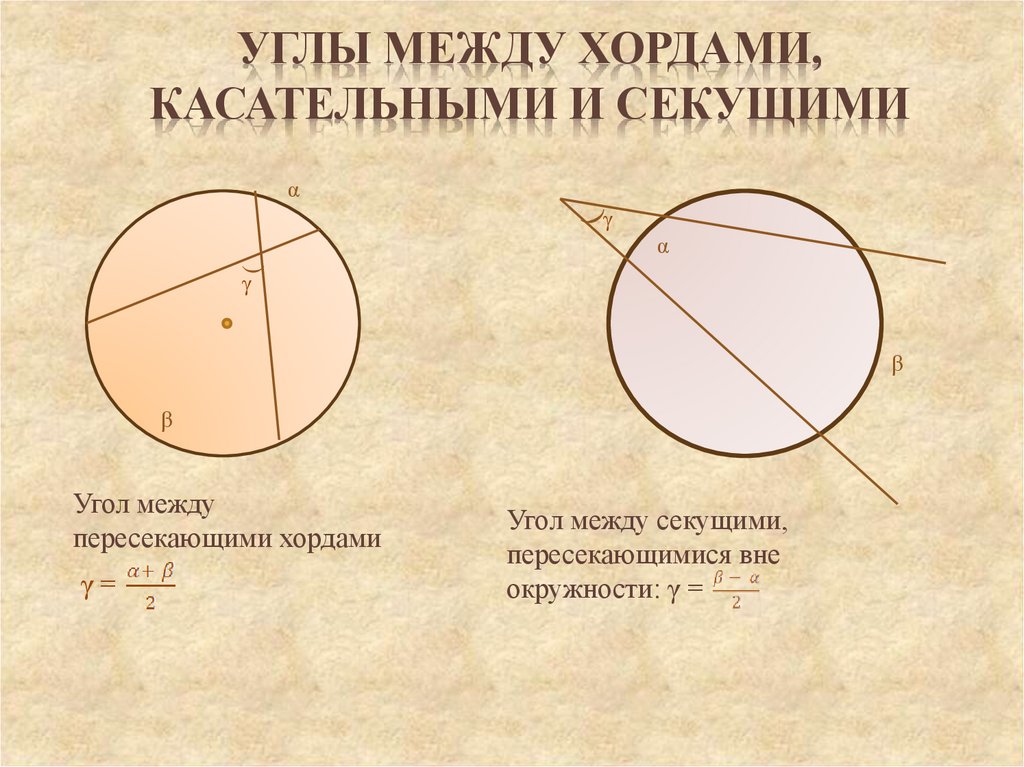
2500 = 4R 2
Разделив обе стороны на 4, мы получаем,
R 2 = 625
√r 2 = √625
R = -25 или 25
Длина не может быть отрицательное число, поэтому мы выбираем только положительные 25.
Следовательно, радиус круга равен 25 дюймам.
Пример 4
Учитывая, что радиус показанного ниже круга равен 10 ярдам, а длина PQ равна 16 ярдам. Рассчитать расстояние ОМ .
Решение
PQ = длина хорды = 16 ярдов.
Радиус, r = 10 ярдов.
ОМ = расстояние, d =?
Длина хорда = 2√ (r 2 -D 2 )
16 = 2√ (10 2 — D 2 )
16 = 2чина (100 — D 2 )
Квадрат с обеих сторон.
256 = 4(100 − d 2 )
256 = 400 − 4d 2
Вычесть 400 с обеих сторон.
-144 = − 4d 2
Разделите обе части на -4.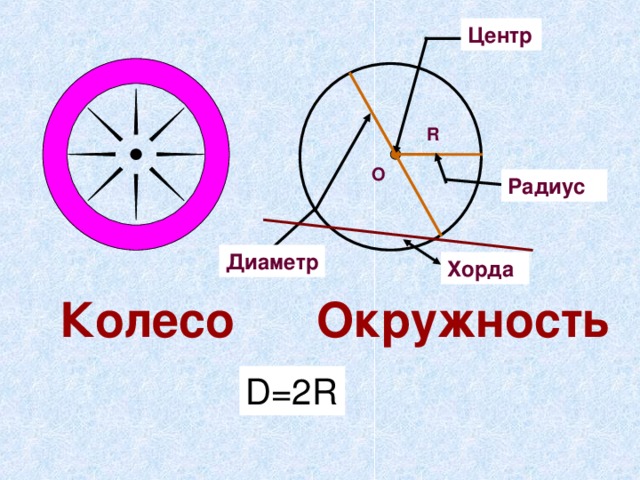
36 = d 2
d = -6 или 6.
Таким образом, перпендикулярное расстояние равно 6 ярдам.
Пример 5:
Рассчитайте длину хорды PQ в круге, показанном ниже.
Решение
Учитывая центральный угол, C = 80 0
Радиус окружности, r = 28 см
Длина хорды PQ =?
По формуле длина хорды = 2r синуса (С/2)
Подставить.
Длина хорды = 2r синуса (C/2)
= 2 x 28 x синус (80/2)
= 56 x синус 40
= 56 x 0,6428
= 36
, поэтому длина хорда PQ 36 см.Пример 6
Рассчитайте длину хорды и центральный угол хорды в круге, показанном ниже.
Раствор
Дано,
Перпендикулярное расстояние, d = 40 мм.
Радиус, r = 90 мм.
Длина хорды = 2√ (R 2 — D 2 )
= 2√ (90 2 — 40 2 )
= 2 √ (8100 — 1600)
= 2чина.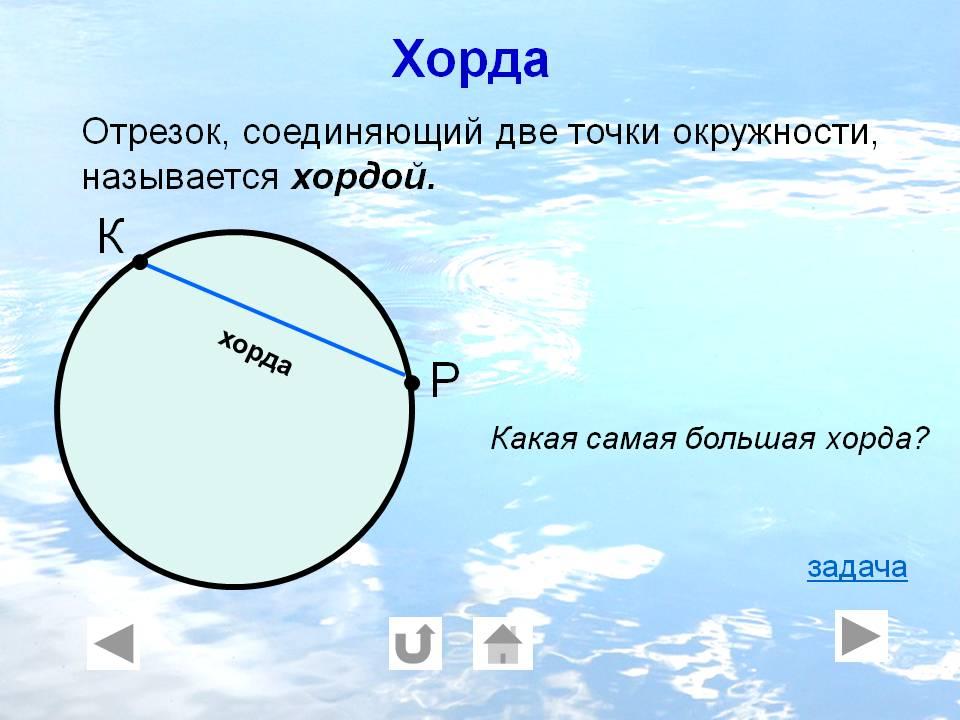 6500
6500
= 2 x 80,6
= 161,2
Итак, длина хорды равна 161,2 мм
Теперь вычислите угол, образуемый хордой.
Длина хорды = 2r синуса (C/2)
161,2 = 2 x 90 синус (C/2)
161,2 = 180 синус (C/2)
Разделите обе части на 180.
0,8956 = синус (C/2)
.
C/2 = 63,6 градуса
Умножьте обе стороны на 2
C = 127,2 градуса.
Итак, центральный угол, образуемый хордой, равен 127,2 градуса.
|
Длина хорды при разделении на равные сегменты
Калькулятор длины хорды
радиус (м, фут. .)
.)
нет. отрезки
Длину — L — хорды при делении окружности на равное количество отрезков можно рассчитать по таблице ниже. Длина хорды — L — в таблице указана для «единичного круга» с радиусом = 1 .
Чтобы вычислить фактическую длину хорды, умножьте длину «единичного круга» — L — на радиус фактического круга.
Пример — длина хорды
Окружность радиусом 3 м разделена на 24 сегмента . Из приведенной ниже таблицы: длина — L — одной хорды в «единичной окружности» с 24 сегментами составляет 0,2611 единиц .
Длина хорды для окружности с радиусом 3 м может быть рассчитана как
0,2611 (3 м) = 0,7833 м
Суммарная длина всех хорд в окружности может быть рассчитана как
8 (0,7833 м) 24
= 6.2653 (3m)
= 18.7959 m
The circumference of the circle can be calculated as
C = 2 π r
= 2 π (3 m)
= 18,8496 M
| Количество сегментов — n — | Центральный угол — θ — | — однолетний угол — θ — | LANGE of Single CORD — θ — | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| degrees | radians | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 180. 0000 0000 | 3.1416 | 2.0000 | 4.0000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 90.0000 | 1.5708 | 1.4142 | 5.6569 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 60.0000 | 1,0472 | 1,0000 | 6.0000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 45.00008|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.7854 | 0.7654 | 6.1229 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 36.0000 | 0.6283 | 0.6180 | 6.1803 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 30.0000 | 0.5236 | 0.5176 | 6.2117 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | 25,7143 | 0,4488 | 0,4450 | 6,2306 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | 22,5000 7 0,9 0757 9,3927 0,3927 0,3 | 6.2429 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | 20.0000 | 0.3491 | 0.3473 | 6.2513 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | 18. 0000 0000 | 0.3142 | 0.3129 | 6.2574 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | 16.3636 | 0.2856 | 0,2846 | 6.2619 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | 15,0000 | 0,2618 | 0,2611 | 6,2653 | 777777790707ter9щенный069426 | 13.8462 | 0.2417 | 0.2411 | 6.2679 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | 12.8571 | 0.2244 | 0.2239 | 6.2700 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | 12.0000 | 0.2094 | 0.2091 | 6.2717 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | 11,2500 | 0,1963 | 0,1960 | 6,2731 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 8 19 | 780707 | 0.1848 | 0.1845 | 6.2742 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | 10.0000 | 0.1745 | 0.1743 | 6.2752 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | 9.4737 | 0. 1653 1653 | 0.1652 | 6.2760 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | 9.0000 | 0.1571 | 0.1569 | 6.2767 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | 8.5714 | 0.1496 | 0.1495 | 6.2773 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | 8.1818 | 0.1428 | 0.1427 | 6.2778 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | 7.8261 | 0.1366 | 0.1365 | 6.2783 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | 7.5000 | 0.1309 | 0.1308 | 6.2787 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50 | 7.2000 | 0.1257 | 0.1256 | 6.2791 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52 | 6.9231 | 0.1208 | 0.1208 | 6.2794 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 54 | 6.6667 | 0.1164 | 0.1163 | 6.2796 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 56 | 6.4286 | 0.1122 | 0.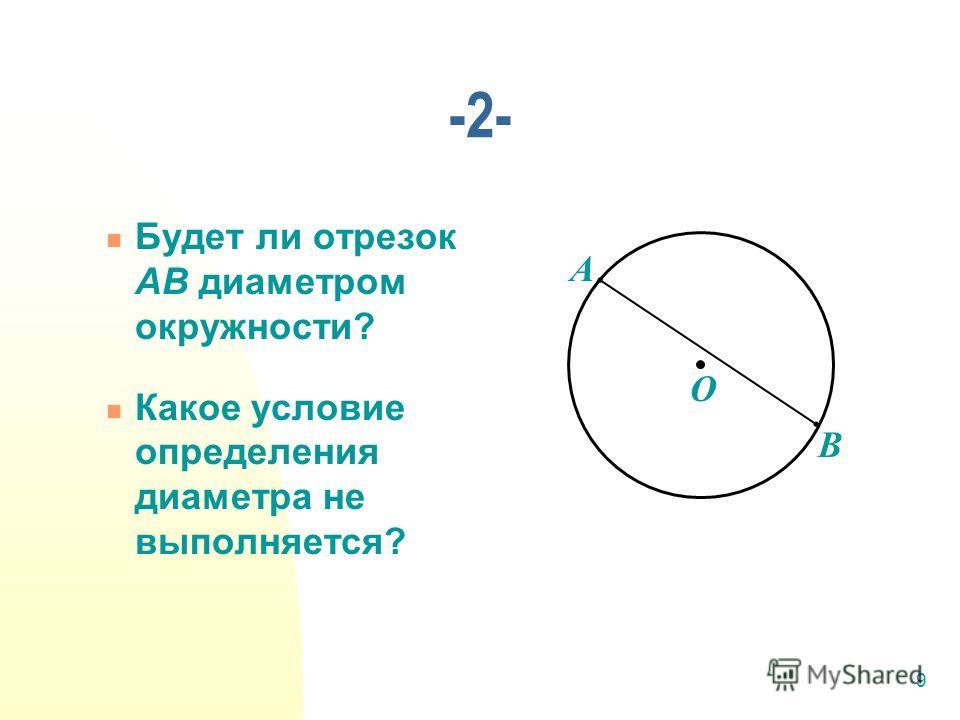 1121 1121 | 6.2799 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 58 | 6,2069 | 0,1083 | 0,1083 | 6,2801 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 09 6097 | 75 0.10470.1047 | 6.2803 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 62 | 5.8065 | 0.1013 | 0.1013 | 6.2805 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 | 5.6250 | 0.0982 | 0.0981 | 6.2807 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 | 5.4545 | 0,0952 | 0,0952 | 6,2808 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | 5,2941 | 0,0924 | 070740 0 0 0 0 0 09ще — | 740||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | 5.1429 | 0.0898 | 0.0897 | 6.2811 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 | 5.0000 | 0.0873 | 0.0872 | 6.2812 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 | 4.8649 | 0.0849 | 0.0849 | 6.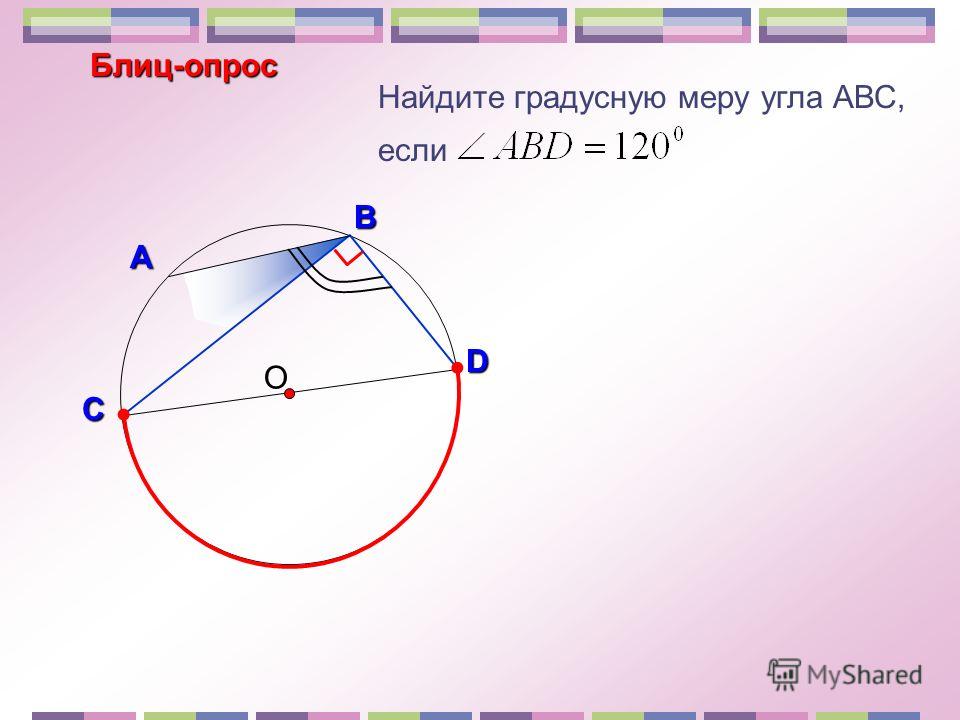 2813 2813 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 76 | 4.7368 | 0.0827 | 0.0826 | 6.2814 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 78 | 4.6154 | 0.0806 | 0.0805 | 6.2815 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 | 4.5000 | 0.0785 | 0.0785 | 6.2816 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 82 | 4.3902 | 0.0766 | 0.0766 | 6.2816 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 84 | 4,2857 | 0,0748 | 0,0748 | 6,2817 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86 | 0.0730 | 6.2818 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 | 4.0909 | 0.0714 | 0.0714 | 6.2819 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 | 4.0000 | 0.0698 | 0.0698 | 6.2819 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 92 | 3.9130 | 0,0683 | 0,0683 | 6.2820 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 94 | 3,8298 | 0,0668 | 0,068 | 9070,068 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,068 | 0,068 | 0,068 | 0,068 | .|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 96 | 3.7500 | 0.0654 | 0.0654 | 6.2821 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 98 | 3.6735 | 0.0641 | 0.0641 | 6.2821 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 100 | 3.6000 | 0.0628 | 0.0628 | 6,2822 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 102 | 3,5294 | 0,0616 | 0,0616 | 6,2822 9 709 | 10970495 3.46150.0604 | 0.0604 | 6.2822 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| 106 | 3.3962 | 0.0593 | 0.0593 | 6.2823 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 108 | 3.3333 | 0.0582 | 0.0582 | 6.2823 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 110 | 3.2727 | 0.0571 | 0.0571 | 6.2823 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 112 | 3.2143 | 0.0561 | 0.0561 | 6.2824 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 114 | 3. 1579 1579 | 0.0551 | 0.0551 | 6.2824 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 116 | 3.1034 | 0.0542 | 0.0542 | 6.2824 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 118 | 3.0508 | 0.0532 | 0,0532 | 6.2824 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 120 | 3,0000 | 0,0524 | 0,0524 | 9095 6.28925255999995 0,0524 9095 6,28675592525592555555755555575552559255558925ще.0708|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 122 | 2.9508 | 0.0515 | 0.0515 | 6.2825 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 124 | 2.9032 | 0.0507 | 0.0507 | 6.2825 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 126 | 2.8571 | 0.0499 | 0.0499 | 6.2825 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 128 | 2,8125 | 0,0491 | 0,0491 | 6,2826 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1307070707970808 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 130707070707970808 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 130707070707 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 130707070707 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13070707 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. 2 2 | 0.0483 | 0.0483 | 6.2826 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 132 | 2.7273 | 0.0476 | 0.0476 | 6.2826 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 134 | 2.6866 | 0.0469 | 0.0469 | 6.2826 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 136 | 2.6471 | 0.0462 | 0.0462 | 6.2826 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 138 | 2.6087 | 0.0455 | 0.0455 | 6.2826 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 140 | 2.5714 | 0.0449 | 0.0449 | 6.2827 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 142 | 2.5352 | 0.0442 | 0.0442 | 6.2827 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 144 | 2.5000 | 0.0436 | 0,0436 | 6,2827 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 146 | 2,4658 | 0,0430 | 0,0430 | 909148 | 2.4324 | 0.0425 | 0.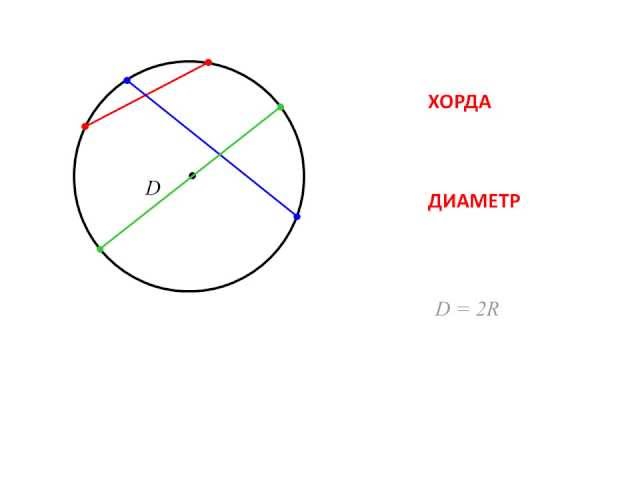 0425 0425 | 6.2827 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 150 | 2.4000 | 0.0419 | 0.0419 | 6.2827 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 152 | 2.3684 | 0.0413 | 0.0413 | 6.2827 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 154 | 2.3377 | 0.0408 | 0.0408 | 6.2827 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 156 | 2.3077 | 0.0403 | 0.0403 | 6.2828 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 158 | 2.2785 | 0.0398 | 0.0398 | 6.2828 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 160 | 2.2500 | 0.0393 | 0.0393 | 6.2828 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 162 | 2.2222 | 0,0388 | 0,0388 | 6.2828 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 164 | 2,1951 | 0,0383 | 1 0,07070707070707070707070707070707070707070707070707070709н.0695 6.2828 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 166 | 2.1687 | 0.0379 | 0.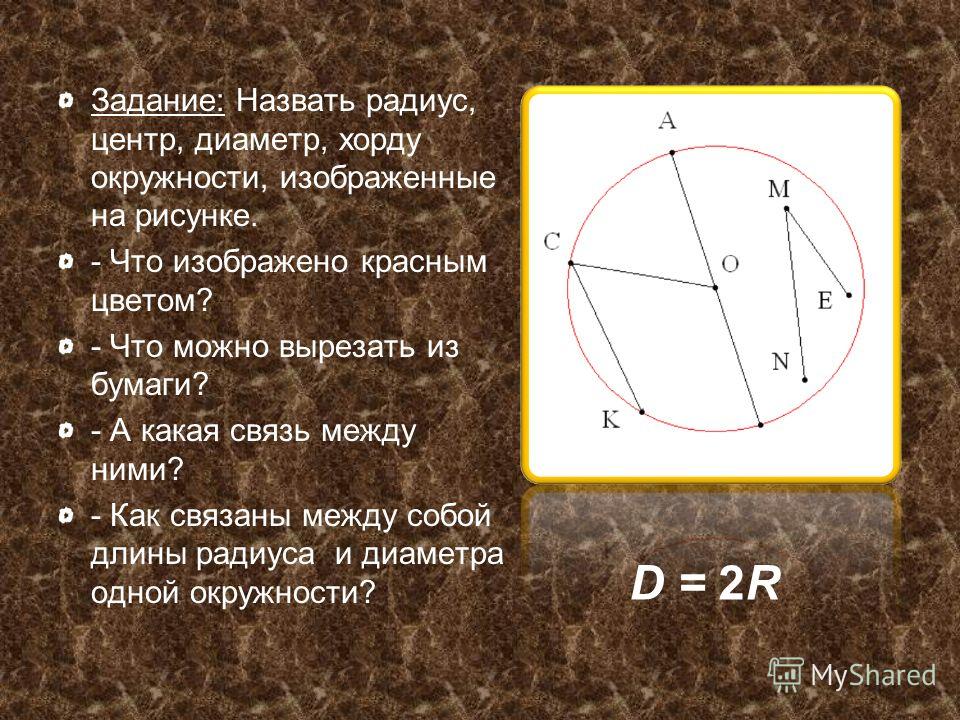 0378 0378 | 6.2828 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 168 | 2.1429 | 0.0374 | 0.0374 | 6.2828 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 170 | 2.1176 | 0.0370 | 0.0370 | 6,2828 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 172 | 2,0930 | 0,0365 | 0,0365 | 9 0978 174 | 2.0690 | 0.0361 | 0.0361 | 6.2828 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 176 | 2.0455 | 0.0357 | 0.0357 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 178 | 2.0225 | 0.0353 | 0.0353 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 180 | 2,0000 | 0,0349 | 0,0349 | 6,2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 182 | 9067,97878987707070707070707070707070707 чем5 0.03450.0345 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 184 | 1.9565 | 0.0341 | 0.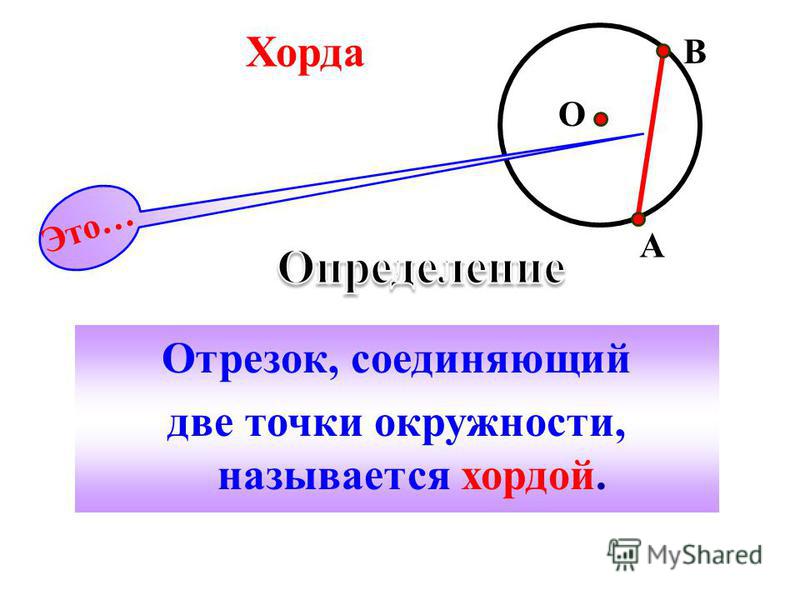 0341 0341 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 186 | 1.9355 | 0.0338 | 0.0338 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 188 | 1.9149 | 0,0334 | 0,0334 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 190 | 1,8947 | 0,0331 | 070707 | 0,0331 | 070707 | 0,0331 | 070707 | 0,0331 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| .0695 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 192 | 1.8750 | 0.0327 | 0.0327 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 194 | 1.8557 | 0.0324 | 0.0324 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 196 | 1.8367 | 0.0321 | 0.0321 | 6,2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 198 | 1,8182 | 0,0317 | 0,0317 | 4 200 | 1.8000 | 0.0314 | 0.0314 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 202 | 1. 7822 7822 | 0.0311 | 0.0311 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 204 | 1.7647 | 0.0308 | 0.0308 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 206 | 1.7476 | 0.0305 | 0.0305 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 208 | 1.7308 | 0.0302 | 0.0302 | 6.2829 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 210 | 1.7143 | 0.0299 | 0.0299 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 212 | 1.6981 | 0.0296 | 0.0296 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 214 | 1.6822 | 0.0294 | 0.0294 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 216 | 1.6667 | 0.0291 | 0.0291 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 218 | 1.6514 | 0.0288 | 0.0288 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 220 | 1.6364 | 0. 0286 0286 | 0.0286 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 222 | 1.6216 | 0.0283 | 0.0283 | 6,2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 224 | 1,6071 | 0,0280 | 0,0280 | 9 0978 909 830 9005 226 | 1.5929 | 0.0278 | 0.0278 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 228 | 1.5789 | 0.0276 | 0.0276 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 230 | 1.5652 | 0.0273 | 0.0273 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 232 | 1.5517 | 0.0271 | 0.0271 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 234 | 1.5385 | 0.0269 | 0.0269 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 236 | 1.5254 | 0.0266 | 0.0266 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 238 | 1.5126 | 0.0264 | 0.0264 | 6.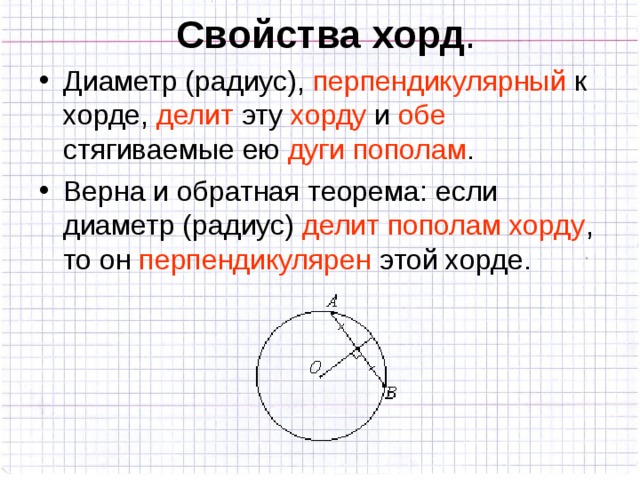 2830 2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 240 | 1.5000 | 0,0262 | 0,0262 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 242 | 1,4876 | 0,0260 | 9876 0,076607.0695 6.2830 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 244 | 1.4754 | 0.0258 | 0.0258 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 246 | 1.4634 | 0.0255 | 0.0255 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 248 | 1.4516 | 0.0253 | 0.0253 | 6,2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 250 | 1,4400 | 0,0251 | 0,0251 | 9 09 830 9005 252 | 1.4286 | 0.0249 | 0.0249 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 254 | 1.4173 | 0.0247 | 0.0247 | 6.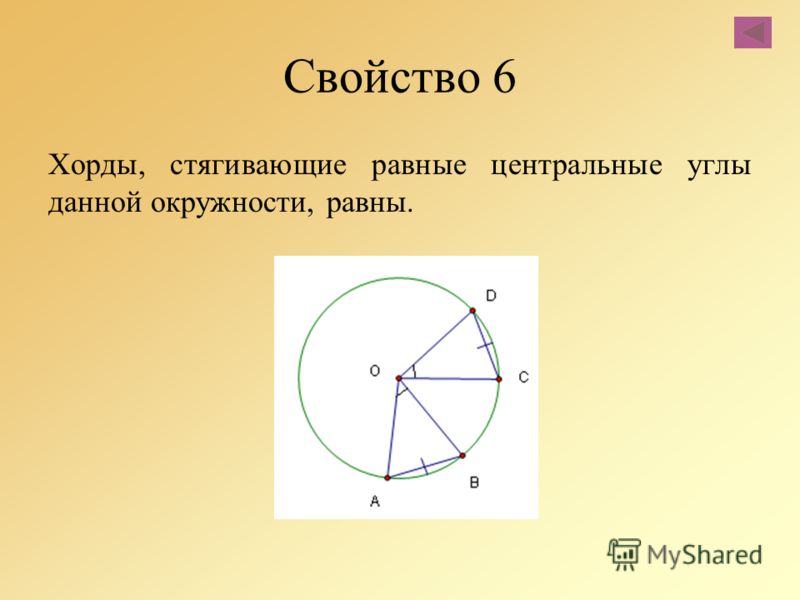 2830 2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 256 | 1.4063 | 0.0245 | 0.0245 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 258 | 1,3953 | 0,0244 | 0,0244 | 6,2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 260 | 1,388888888888888888888696996969696969696 |
| 0.0242 | 6.2830 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 262 | 1.3740 | 0.0240 | 0.0240 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 264 | 1.3636 | 0.0238 | 0.0238 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 266 | 1.3534 | 0,0236 | 0,0236 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 268 | 1,3433 | 0,0234 | 0,0744074407440744074407440744074407440744074407440707 9074 074. 0749074. 9074 074 | 7070,0234 | 95074434 0,074. 9074.9074. 9074.9074. | .0695 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 270 | 1.3333 | 0.0233 | 0.0233 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 272 | 1.3235 | 0.0231 | 0.0231 | 6.2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 274 | 1.3139 | 0.0229 | 0.0229 | 6,2830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 276 | 1,3043 | 0,0228 | 0,0228 | 9 09830 278 | 1.2950 | 0.0226 | 0.0226 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 280 | 1.2857 | 0.0224 | 0.0224 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 282 | 1.2766 | 0.0223 | 0.0223 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 284 | 1,2676 | 0,0221 | 0,0221 | 6,2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 286 | 1.2555555757979797979797797777777777777777755555555555555555555555555555рой5 0.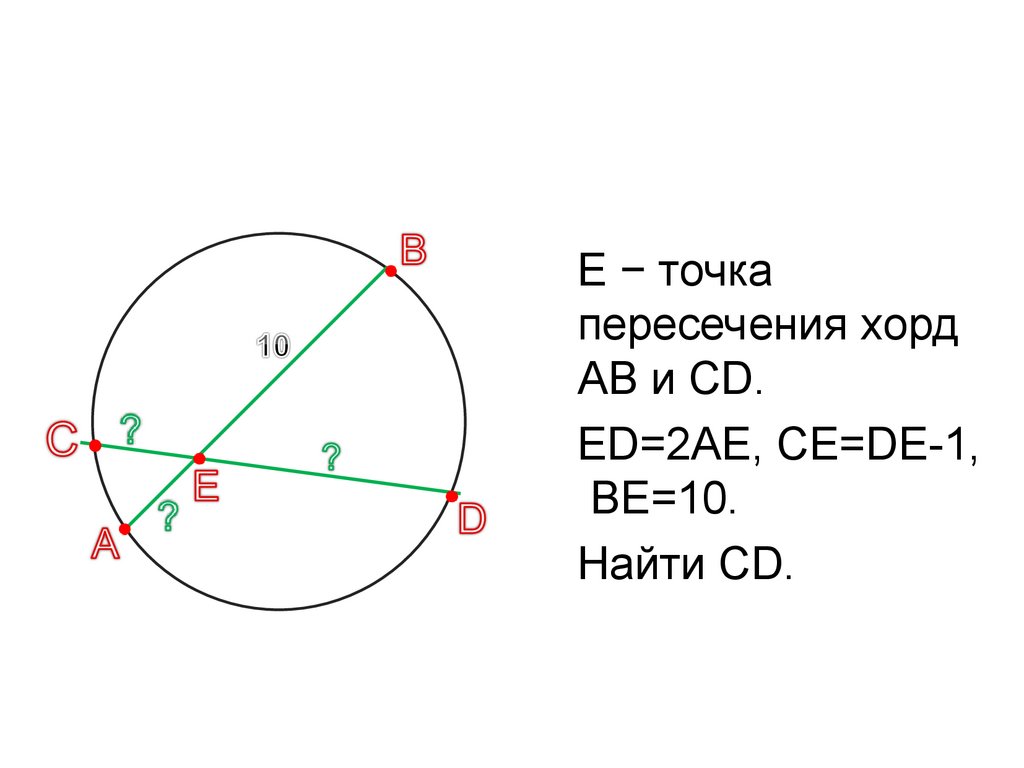 0220 0220 | 0.0220 | 6.2831 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 288 | 1.2500 | 0.0218 | 0.0218 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 290 | 1.2414 | 0.0217 | 0.0217 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 292 | 1.2329 | 0.0215 | 0.0215 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 294 | 1.2245 | 0.0214 | 0.0214 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 296 | 1.2162 | 0.0212 | 0.0212 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 298 | 1.2081 | 0.0211 | 0.0211 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 300 | 1.2000 | 0.0209 | 0.0209 | 6,2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 302 | 1,1921 | 0,0208 | 0,0208 | 909 831 9005 304 | 1.1842 | 0.0207 | 0.0207 | 6.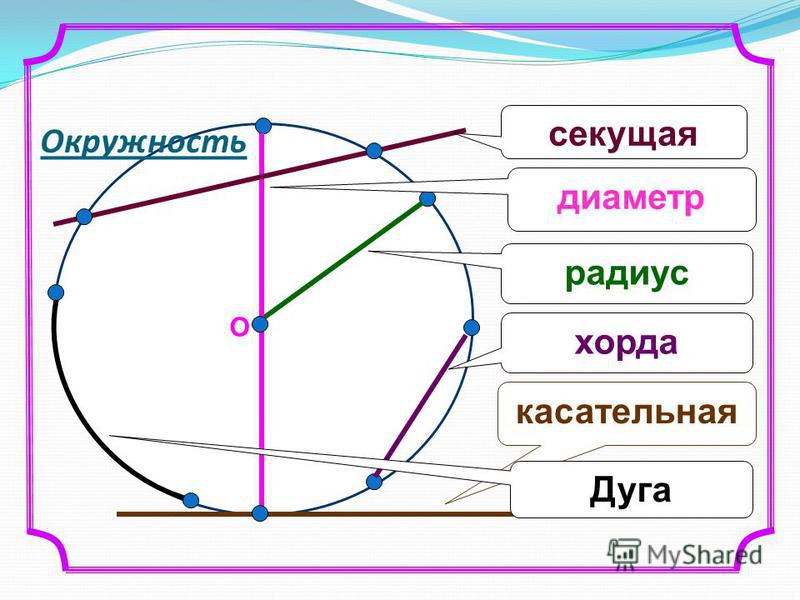 2831 2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 306 | 1.1765 | 0.0205 | 0.0205 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 308 | 1.1688 | 0.0204 | 0.0204 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 310 | 1.1613 | 0.0203 | 0.0203 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 312 | 1.1538 | 0.0201 | 0.0201 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 314 | 1.1465 | 0.0200 | 0.0200 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 316 | 1.1392 | 0.0199 | 0.0199 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 318 | 1.1321 | 0.0198 | 0.0198 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 320 | 1.1250 | 0.0196 | 0.0196 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 322 | 1.1180 | 0.0195 | 0.0195 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 324 | 1.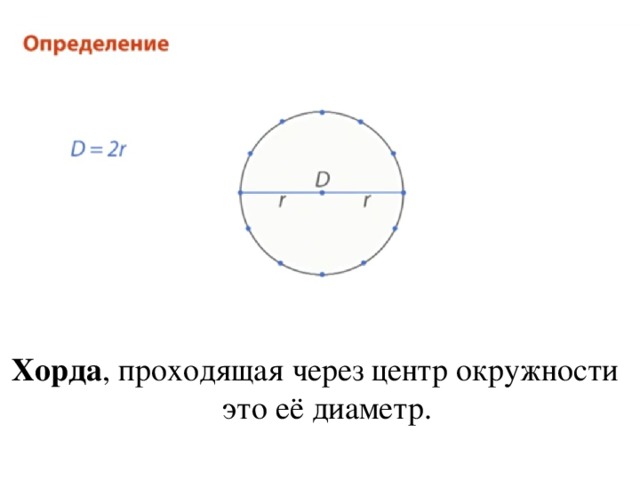 1111 1111 | 0.0194 | 0.0194 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 326 | 1.1043 | 0.0193 | 0.0193 | 6,2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 328 | 1,0976 | 0,0192 | 0,0192 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.0909 | 0.0190 | 0.0190 | 6.2831 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 332 | 1.0843 | 0.0189 | 0.0189 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 334 | 1.0778 | 0.0188 | 0.0188 | 6.2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 336 | 1,0714 | 0,0187 | 0,0187 | 6,2831 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 338 | 1,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695 1,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695,0695,0706997
Q2 a Является ли каждый диаметр окружности также хордой b Является ли каждая хорда окружности также диаметром…Перейти к
Главная >
Решения НЦЭРТ
Класс 6
Математика
>
Глава 4. Вопрос 3 Упражнение 4.6 Q2) (a) Является ли каждый диаметр окружности хордой? (б) Каждая хорда окружности также является диаметром? Ответ: Решение 2: (a) Да, каждый диаметр окружности является хордой. (b) Нет, каждая хорда окружности не является диаметром . Стенограмма видео Здравствуйте, студенты. Добро пожаловать в обучение. Так что да, вопрос в том, что каждый диаметр круга также я вырезал, да, каждый круг вырезается. Итак, второй вопрос заключается в том, что каждая четверть круга также является диаметром. Нет, это не диаметр круга. Хорошо. Спасибо Связанные вопросы По рисунку определите: (а) центр окружности (б) три радиуса (в) диаметр (г) хорду (д) две точки. Q1) По рисунку определите: (a) центр окружности (b) три радиуса (c) диаметр (d) хорду (e)… а) Является ли каждый диаметр окружности также хордой? (б) Является ли каждая хорда окружности также диаметром? Начертите любой круг и отметьте (а) его центр (б) радиус (в) диаметр (г) сектор (д) сегмент (е) точку… Q3) Нарисуйте любой круг и отметьте (а) его центр (б) радиус (в) диаметр (г) сектор (д) сегмент (е) … Q4) Верно или неверно: (а) Два диаметра круга обязательно пересекаются. (б) Центр … Фейсбук WhatsApp Копировать ссылку Было ли это полезно? Упражнение Упражнение 4. Упражнение 4.2 Упражнение 4.3 Упражнение 4.4 Упражнение 4.5 Упражнение 4.6 Главы Знание наших чисел Целые числа Игра с числами Основные геометрические идеи Понимание элементарных форм Интеллекционеры Фракции 9000 Decimals RATLING Mens 4. Симметрия Практическая геометрия Курсы Быстрые ссылки Условия и политика Условия и политика 2022 © Quality Tutorials Pvt Ltd Все права защищены Круги — определение, площадь, окружность, формула, дуга, большой сектор, малый сегмент и хорда← Список тем Уровень: Базовый Будь то колеса автомобиля, рябь, которая образуется, когда капля дождя падает на пруд, космические тела, такие как планеты, продукты питания, такие как пицца и пончики, монеты или даже браслеты, круг существовал всегда. Понимание круга в геометрических терминах: Определение круга:когда кривая линия, концы которой соединены друг с другом, образует круглую фигуру, все точки которой равноудалены от фиксированной точки или центра, круг сформирован. Важные термины, относящиеся к окружности: • Хорда: Это отрезок, концы которого лежат на самой окружности. • Касательная: Это линия, которая касается окружности ровно в одной внешней точке и перпендикулярна радиусу. Это расстояние между центром круга и его границей. Это половина диаметра. • Диаметр:Это линия, проходящая через центр окружности и заканчивающаяся на границе окружности. Диаметр в два раза больше радиуса. • Окружность:Это периметр круга. • Центр:Точка, находящаяся точно в центре круга, равноудаленная от всех возможных точек на границе круга. • Район:Пространство, ограниченное границей круга, называется площадью круга. • Секанс:Это линия, которая пересекает окружность в двух точках на границе. • Дуга: Часть окружности называется дугой. • Сектор:Относится к области круга, ограниченной дугой и двумя радиусами. • Сегмент:Часть окружности, ограниченная секущей или хордой и дугой. Большой сектор, Малый сектор, Большая дуга, Малая дуга и Большой сегмент, Малый сегмент:Окружность: Граница любой замкнутой геометрической фигуры называется ее периметром. Формула для расчета длины окружности = π x диаметр = π x 2 x радиус π читается как число Пи, и его значение равно 3,14159.265358….(округлено до 3,14) Круги — Решено Пример:Q.1) Если радиус круга равен 7 см, какова будет длина его окружности? Решение: Мы знаем, что длина окружности = π x 2 x радиус Круги — Решено Пример: Q. Решение: Мы знаем, что длина окружности = = π x диаметр Площадь круга относится к области, ограниченной окружностью круга. Формула для вычисления площади круга = π x радиус 2 Круги – решено Пример:Q.3) Если длина окружности 44 см, найдите площадь круг. Решение: Мы знаем, что длина окружности = π x 2 x радиус Окружности — решено Пример: Q. Решение: Мы знаем, что угол, вписанный в окружность, прямой, а меньшие стороны треугольника равны 21 см и 28 см. Круги – решено Пример: В. |

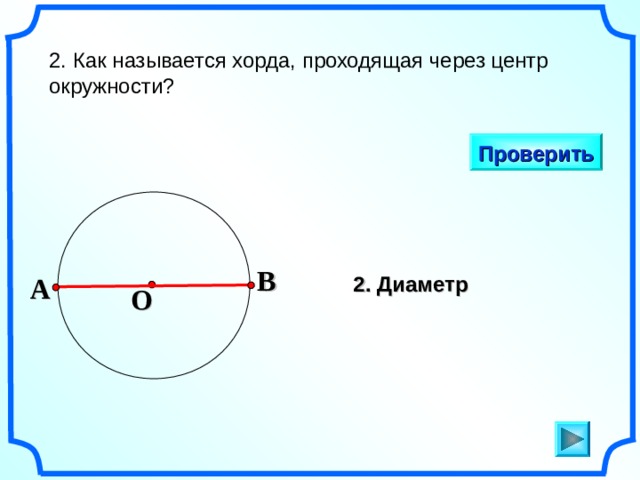 Такая ось проходит через центр и делит её на две равные части.
Такая ось проходит через центр и делит её на две равные части.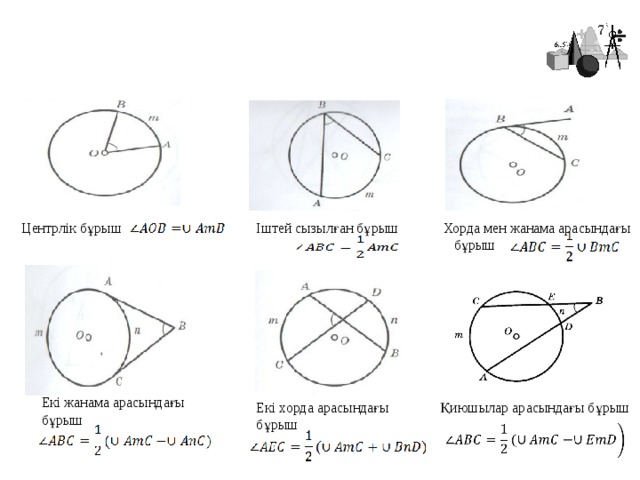
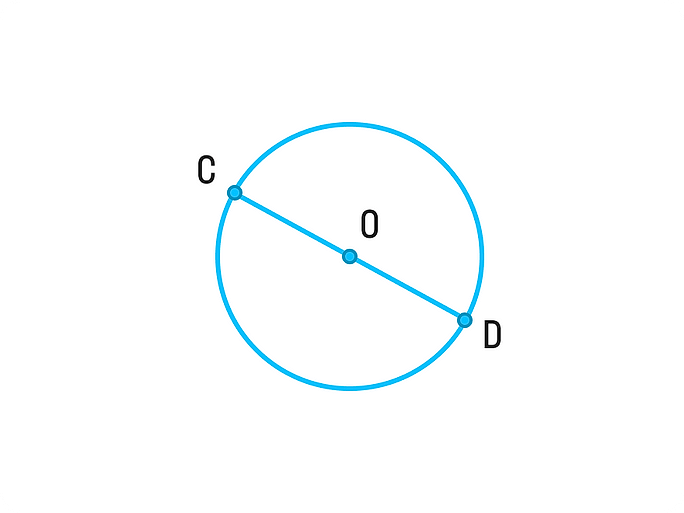

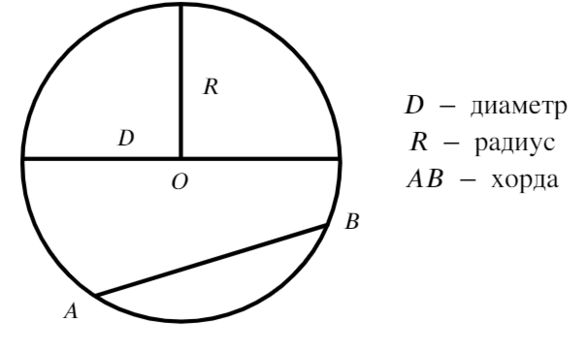 В начальных данных обязательно присутствует хорда и длина дуги.
В начальных данных обязательно присутствует хорда и длина дуги.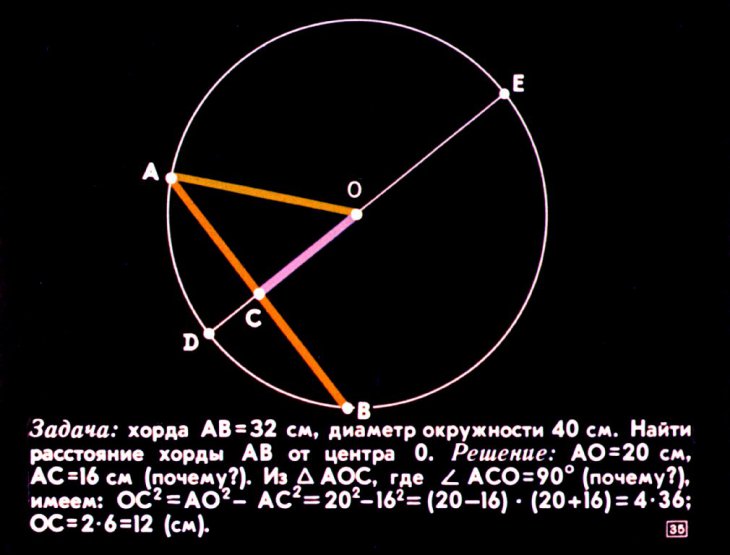
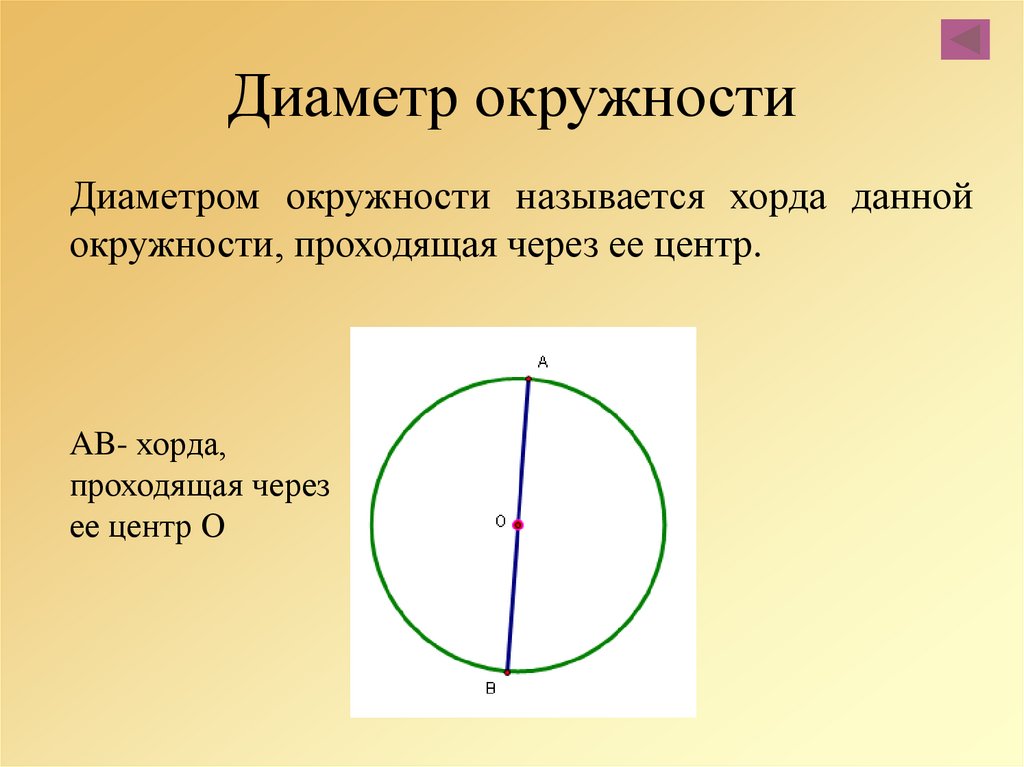 Опа-на! Не путаем диаметр и радиус!
Опа-на! Не путаем диаметр и радиус!
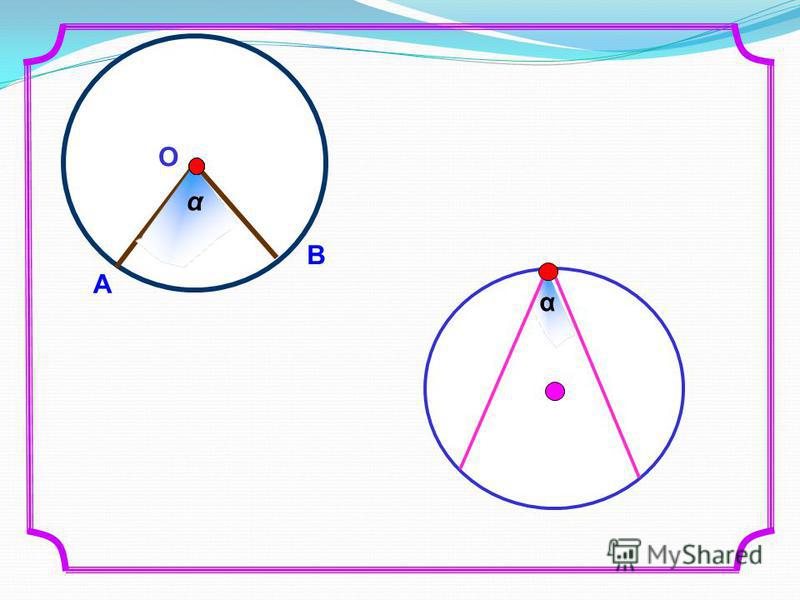 Введите свой запрос:
Введите свой запрос: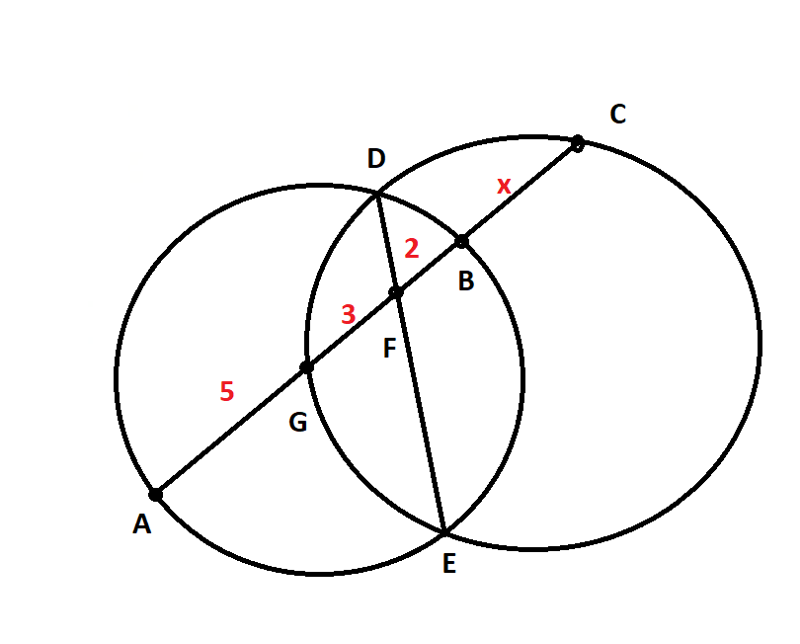
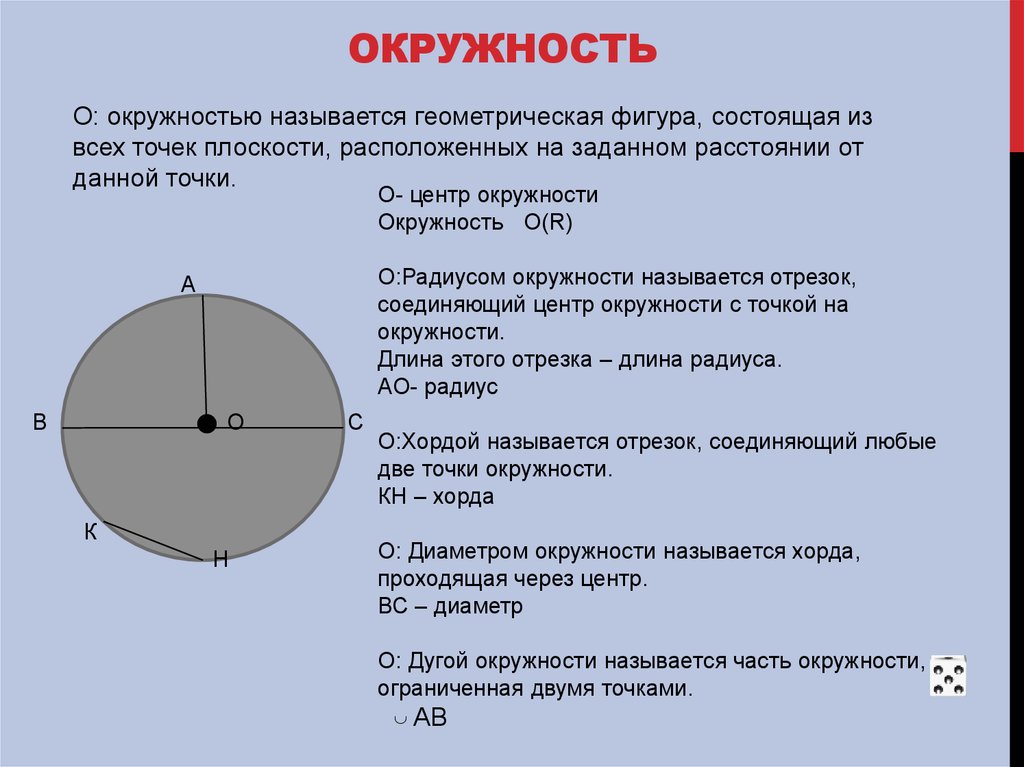 Найти радиус вписанного круга.
Найти радиус вписанного круга.
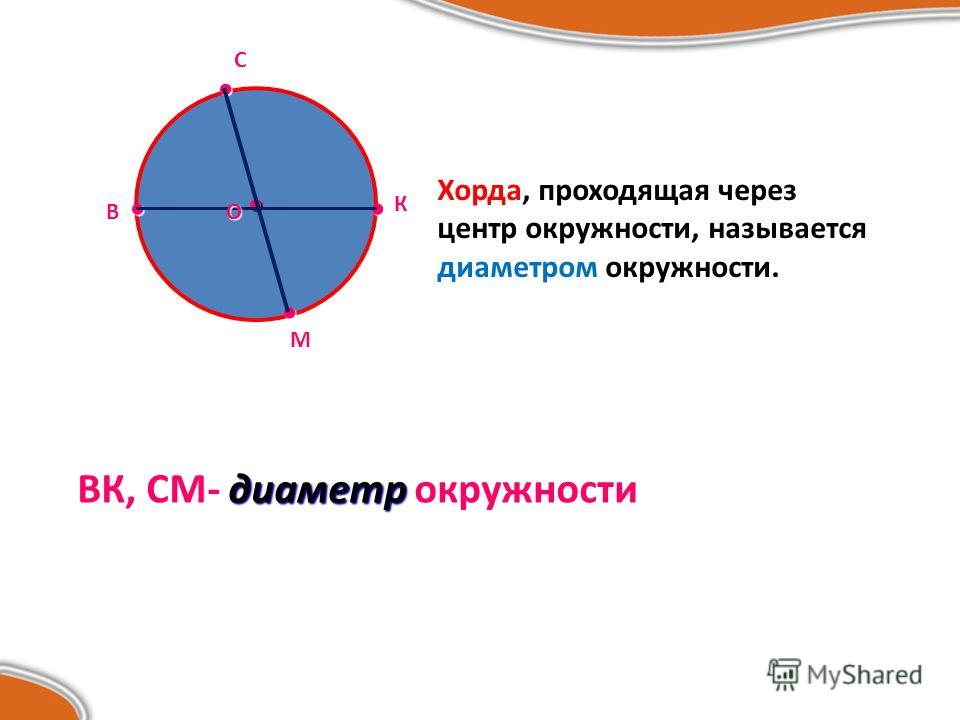

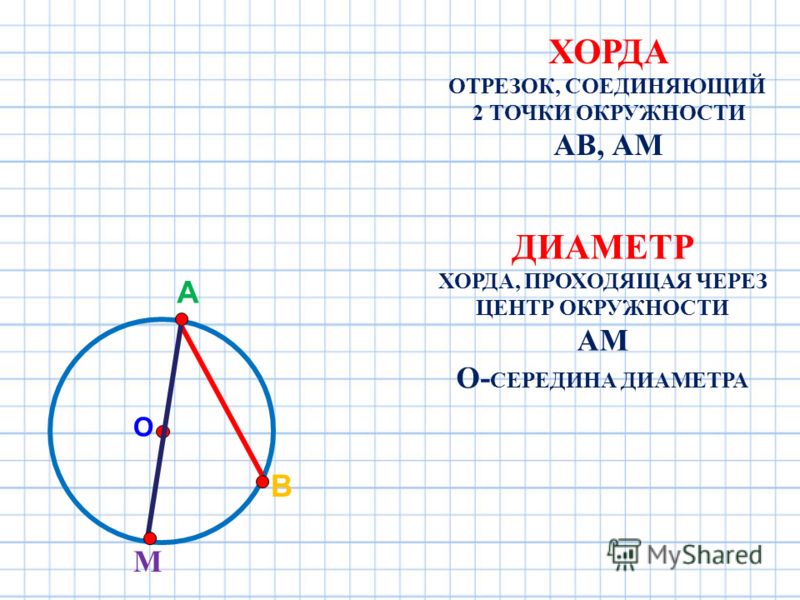
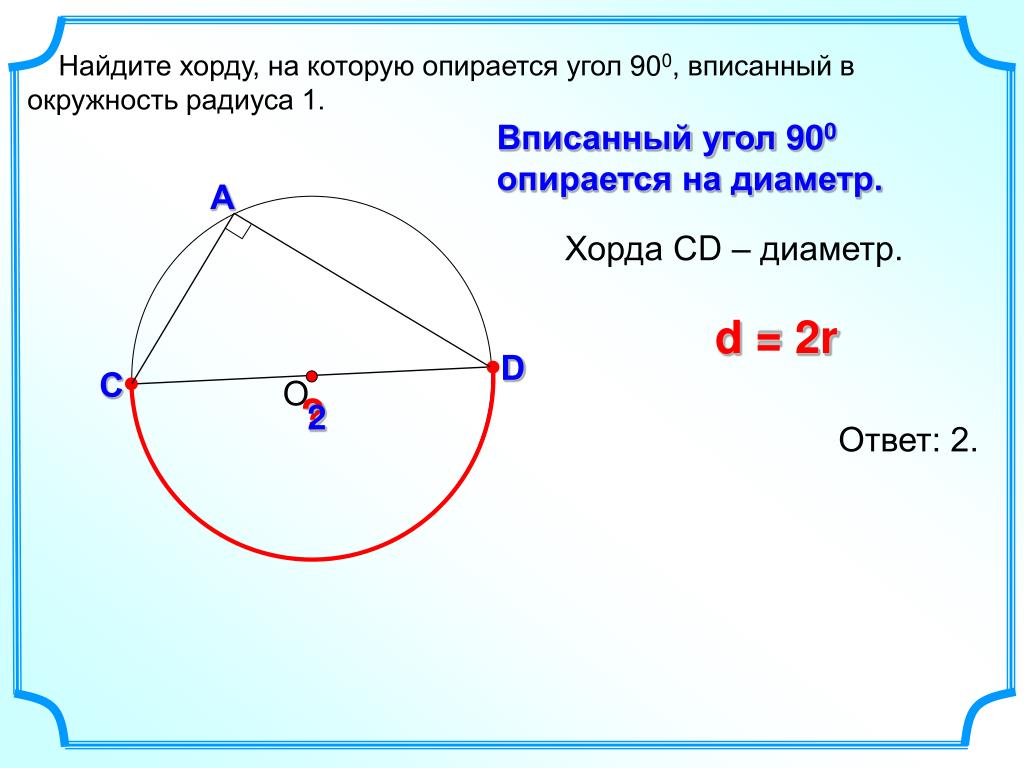
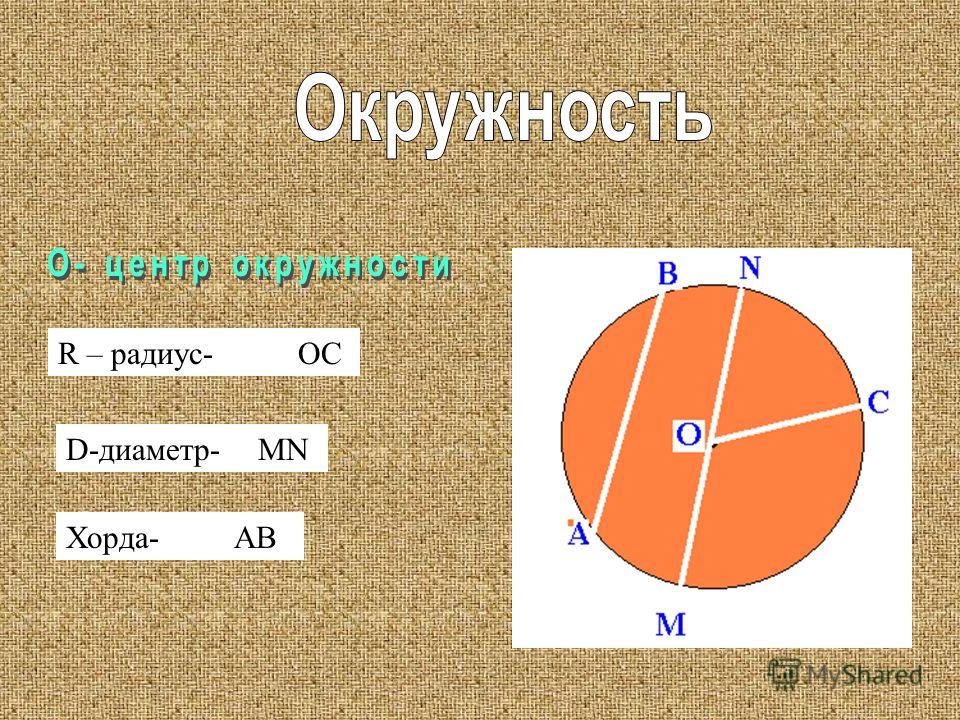
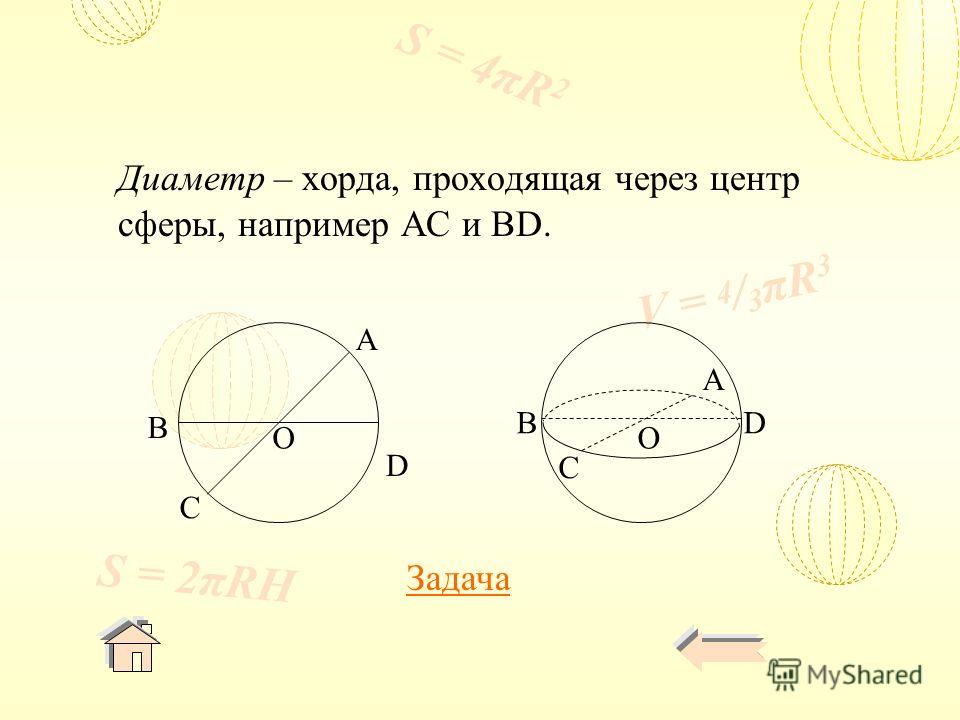
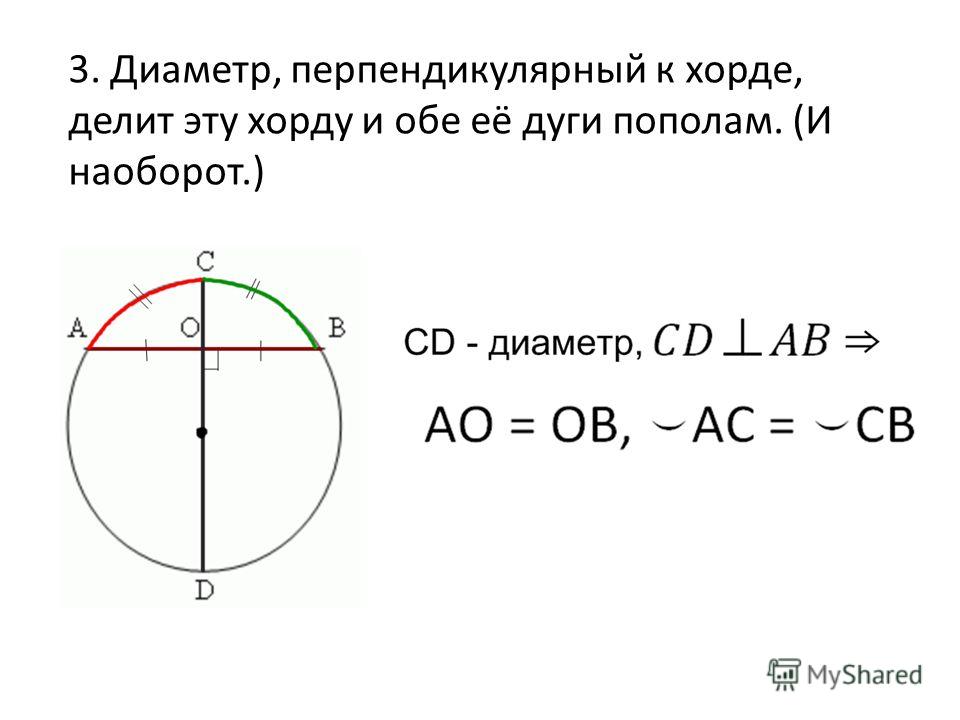

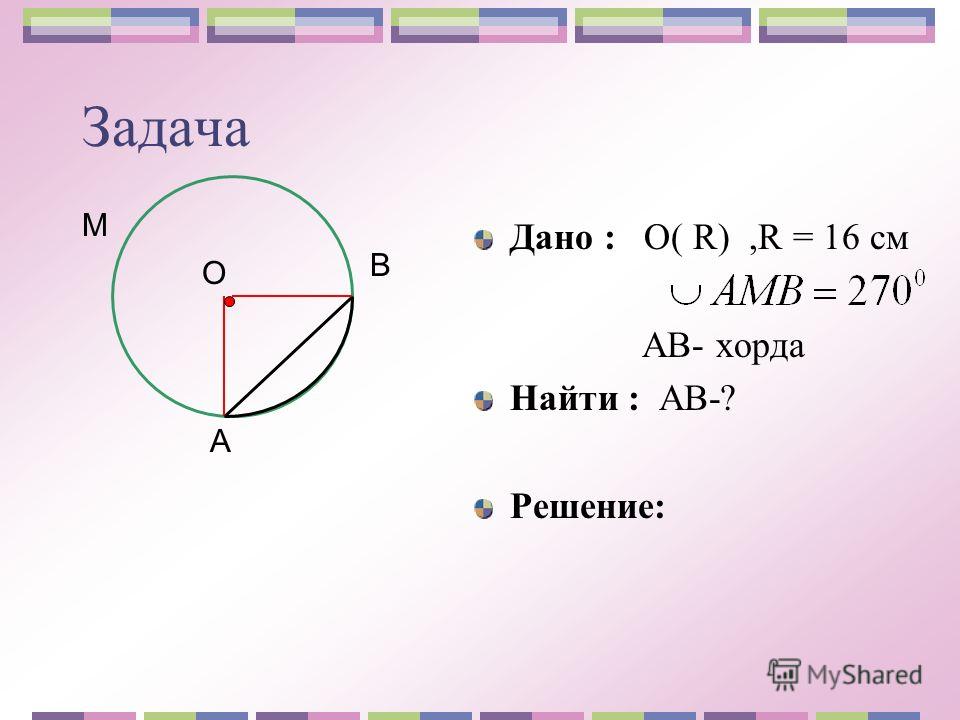
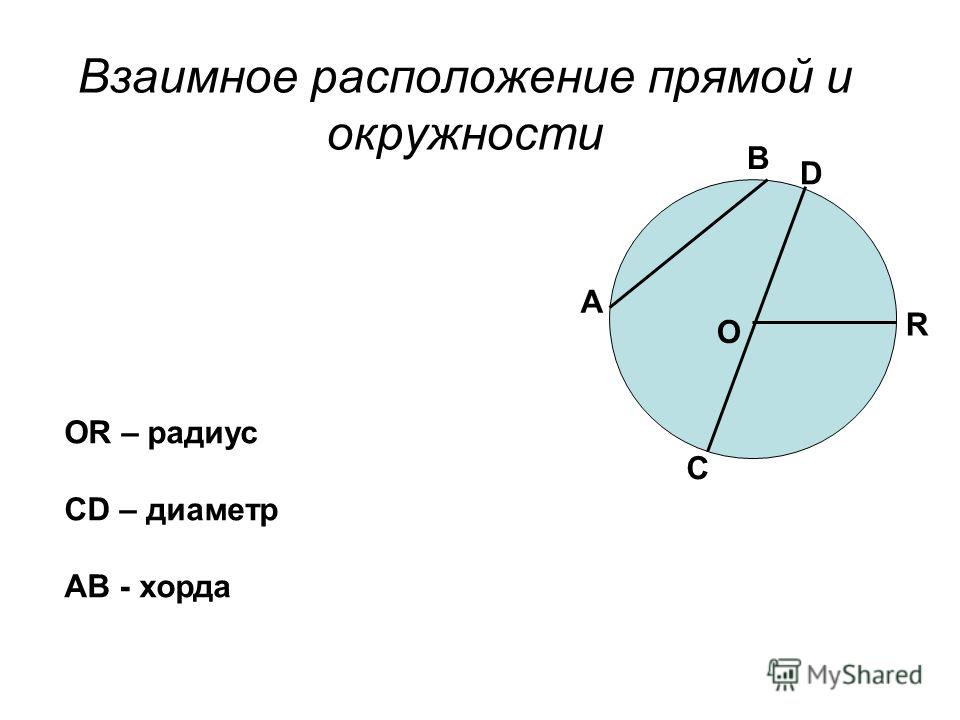



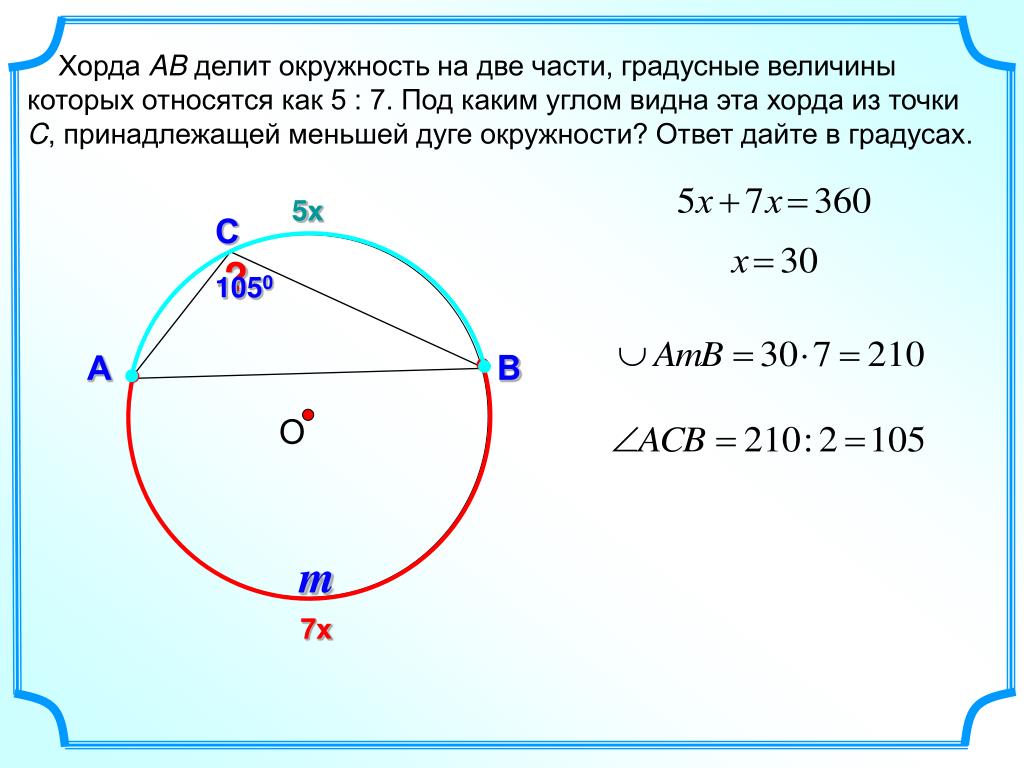

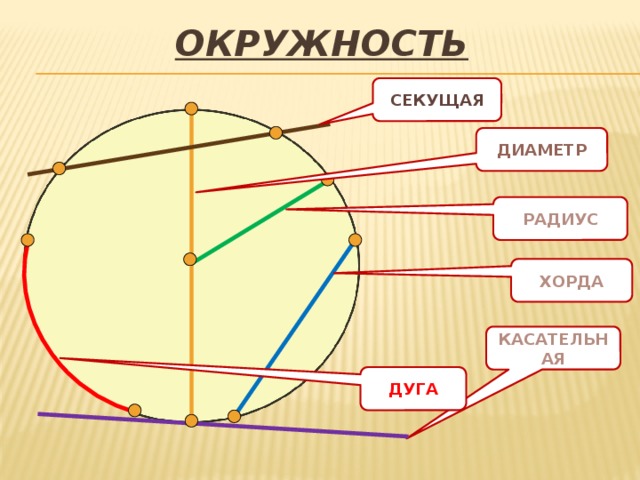
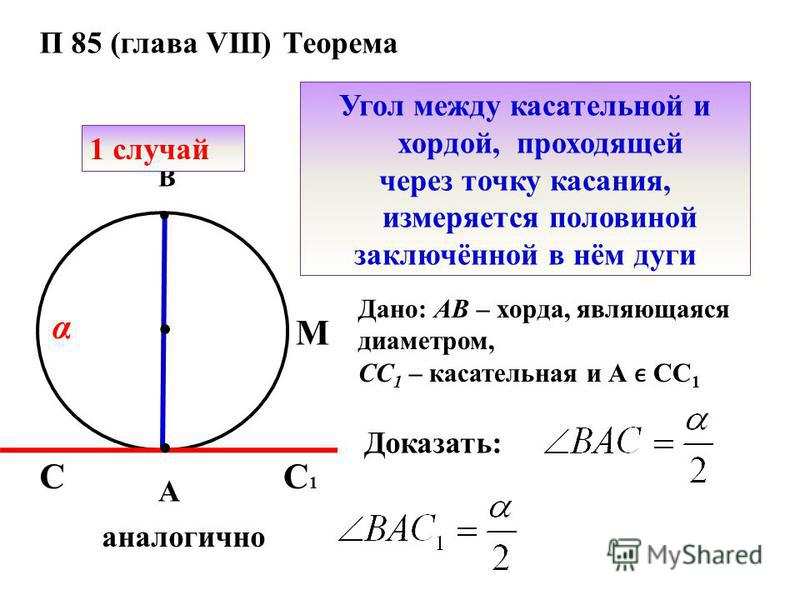
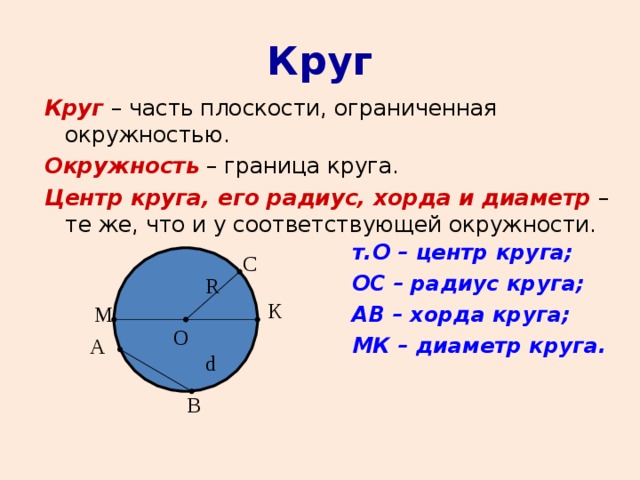 0707
0707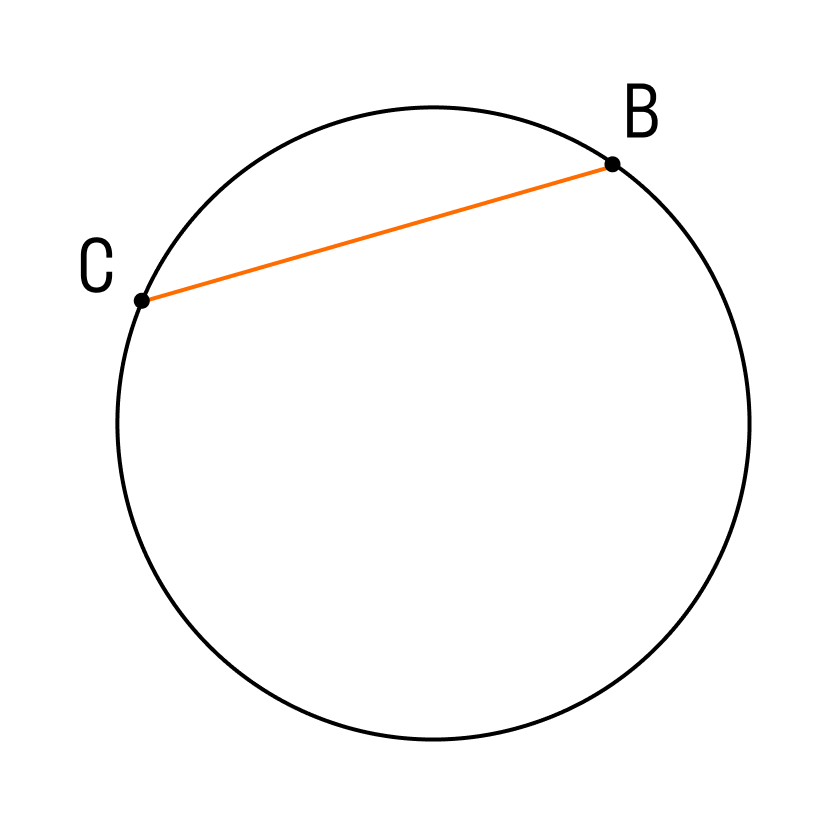 2831
2831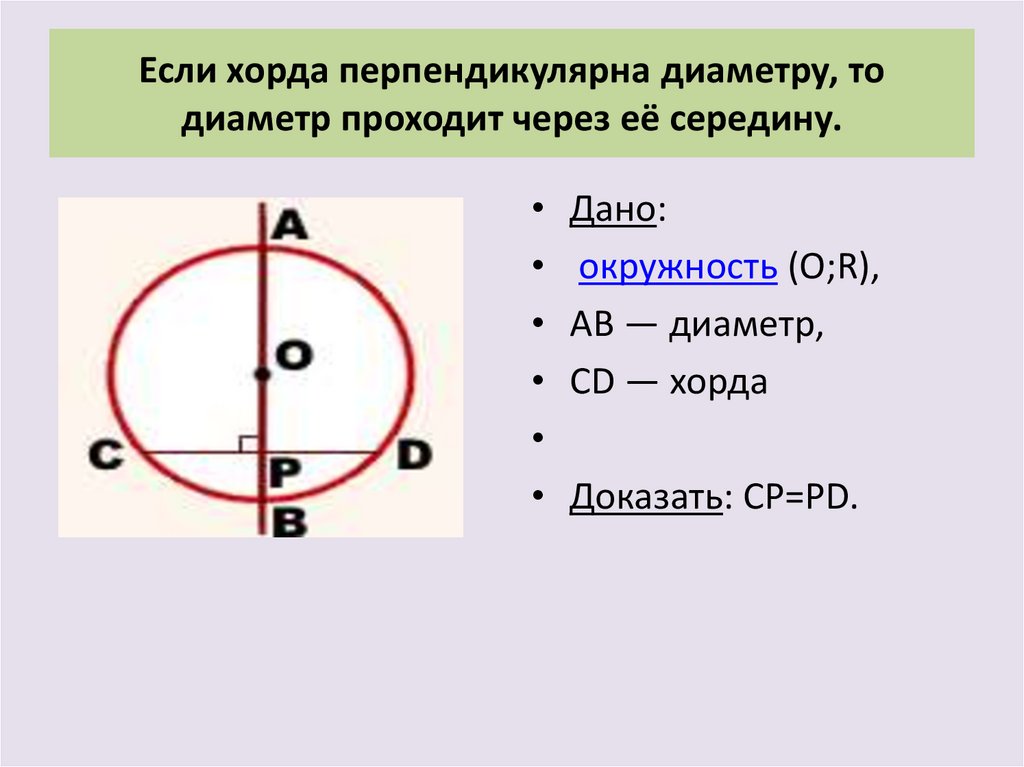 0176
0176 5
5 Основные геометрические идеи
>
Упражнение 4.6
>
Вопрос 3
Основные геометрические идеи
>
Упражнение 4.6
>
Вопрос 3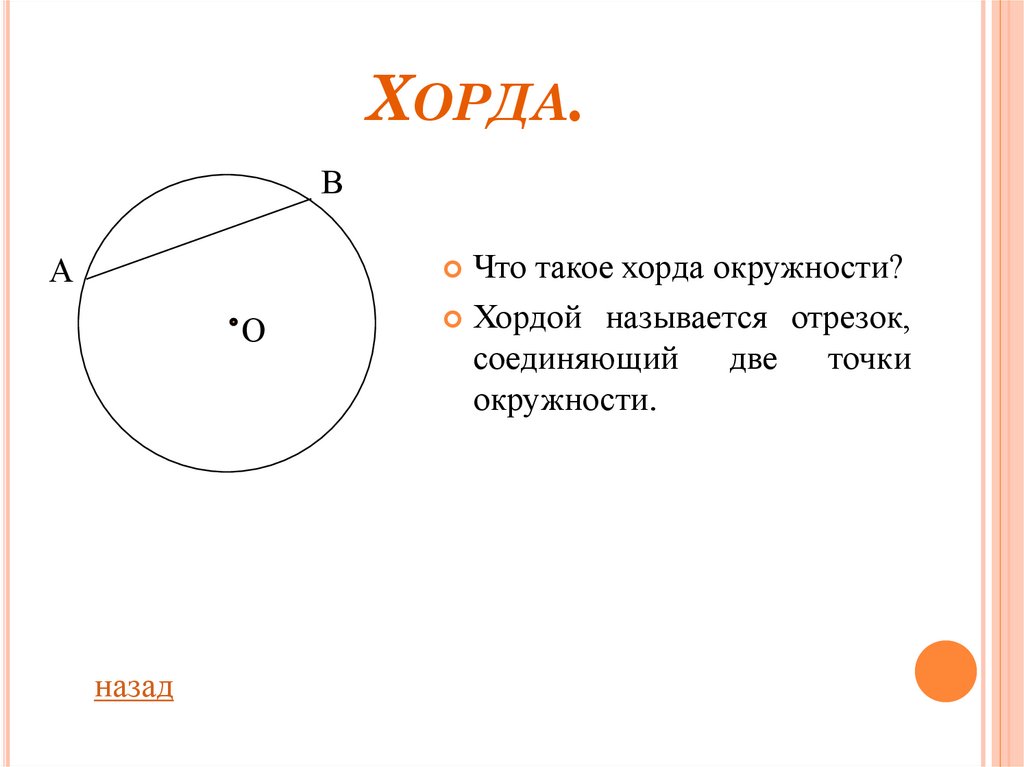 ..
..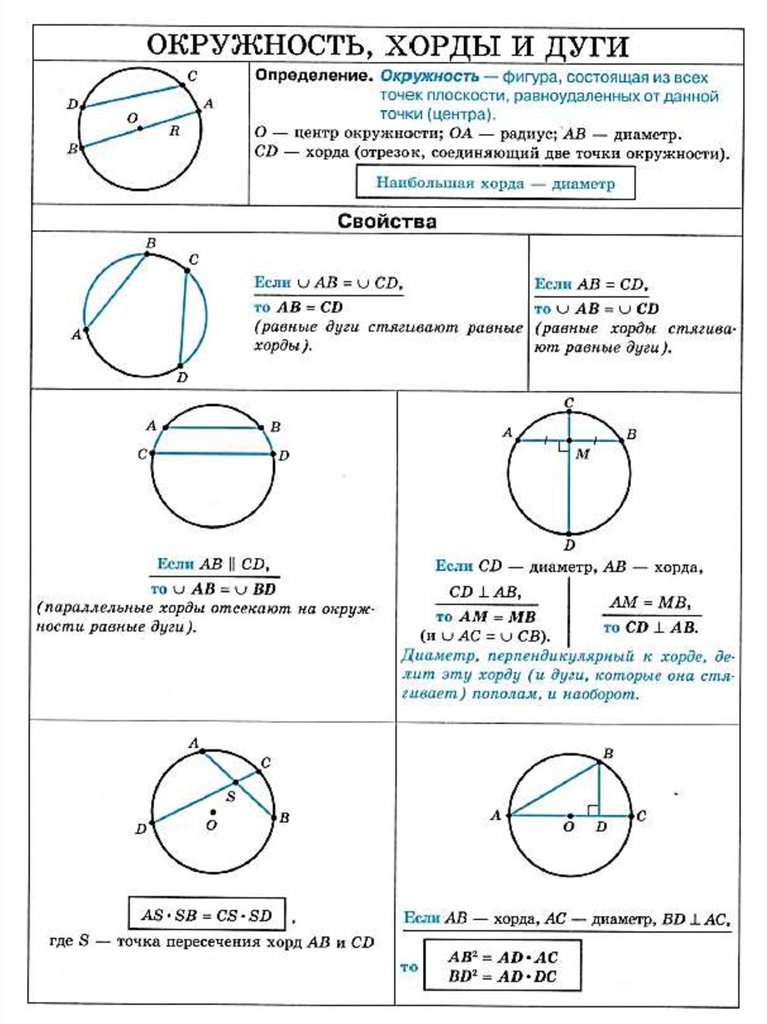 1
1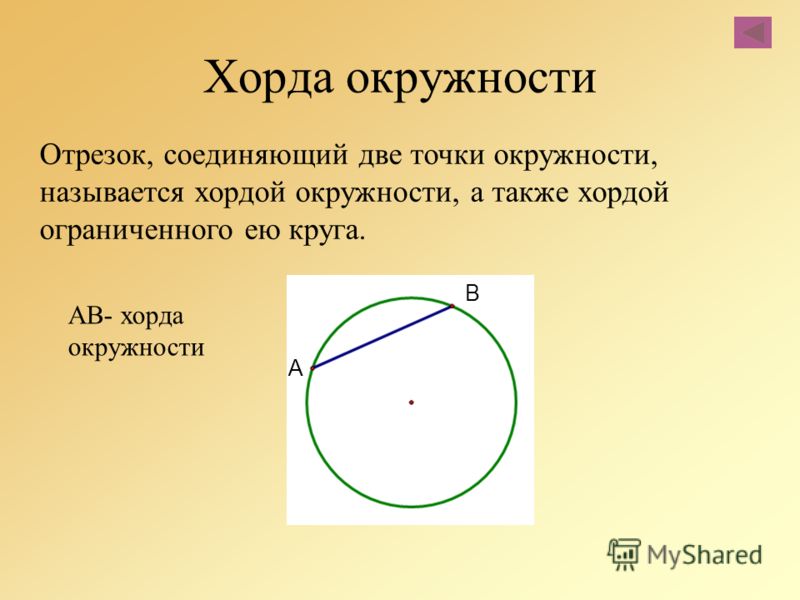 в нашей жизни с незапамятных времен. Он, несомненно, проник в нашу повседневную жизнь благодаря своей ошеломляющей универсальности. Термин круг происходит от греческого слова 9.4042 киркос , что означает обруч или круг. На него также повлияло латинское слово circulus , что снова означает кольцо. Она очаровывала математиков с незапамятных времен и представляет собой форму, которую видят, изучают, находят и используют вне теории.
в нашей жизни с незапамятных времен. Он, несомненно, проник в нашу повседневную жизнь благодаря своей ошеломляющей универсальности. Термин круг происходит от греческого слова 9.4042 киркос , что означает обруч или круг. На него также повлияло латинское слово circulus , что снова означает кольцо. Она очаровывала математиков с незапамятных времен и представляет собой форму, которую видят, изучают, находят и используют вне теории.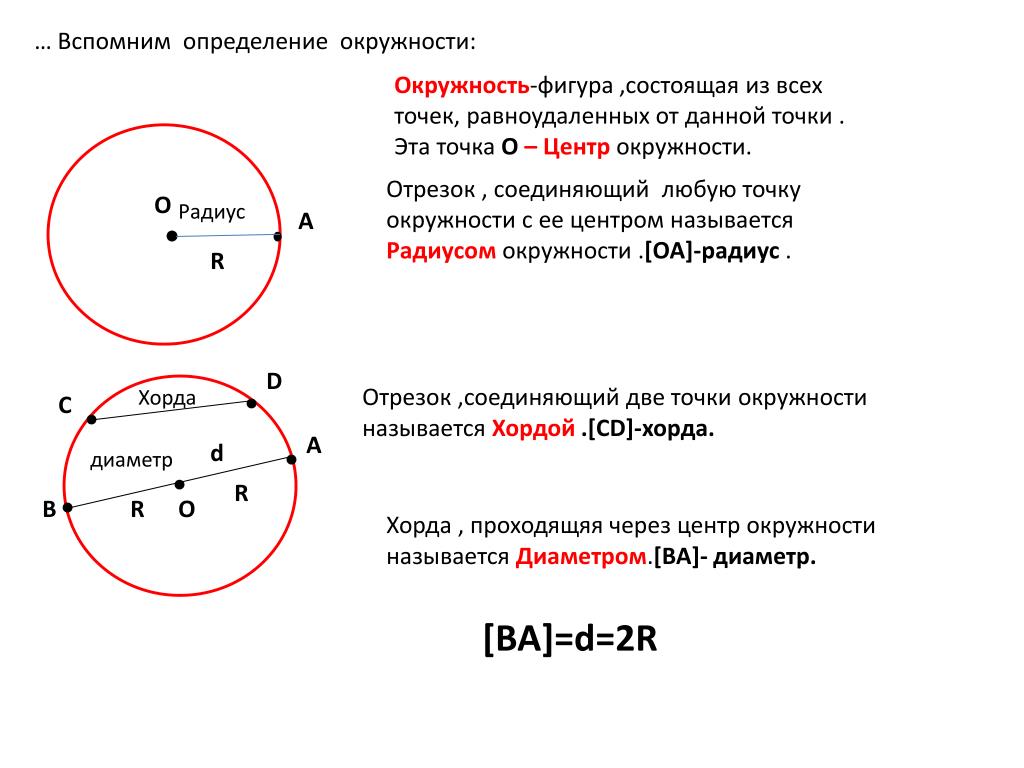
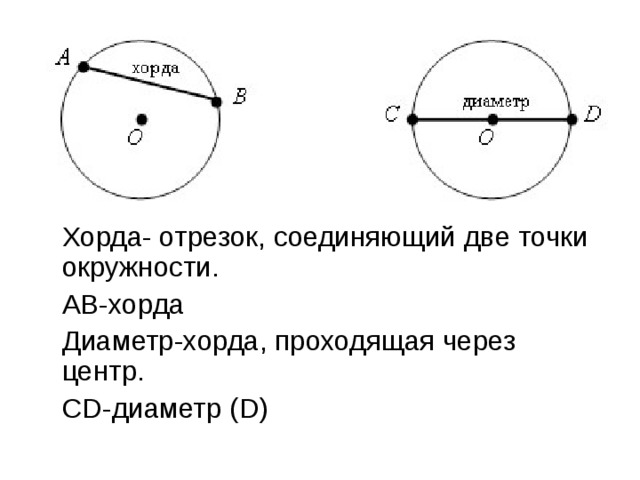 Точно так же в контексте круга периметр называется окружностью .
Точно так же в контексте круга периметр называется окружностью .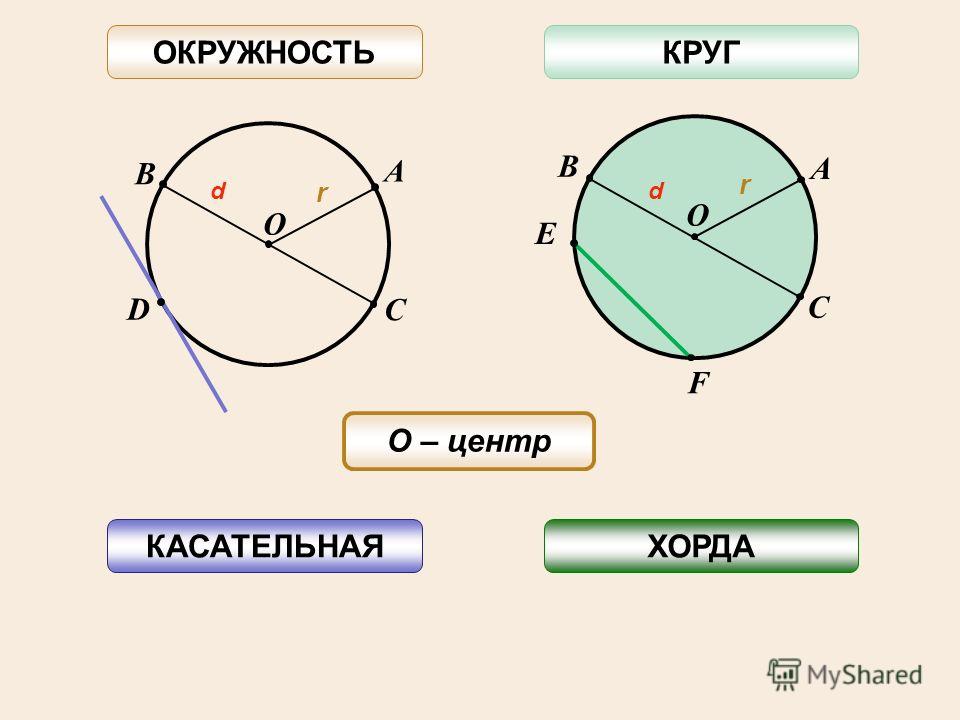 2) Пешеходная дорожка имеет форму кольца, внутренняя окружность которого составляет 440 м, а внешняя окружность — 616 м. Найдите толщину дорожки.
2) Пешеходная дорожка имеет форму кольца, внутренняя окружность которого составляет 440 м, а внешняя окружность — 616 м. Найдите толщину дорожки.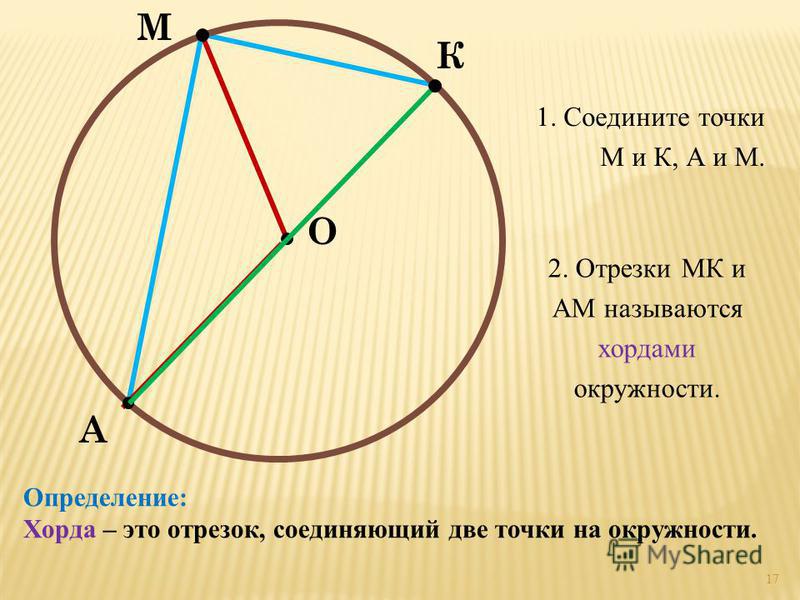 4) Самый длинный прямоугольный треугольник вписан в окружность. сторона как диаметр того же круга. Если две меньшие стороны треугольника равны 21 см и 28 см соответственно, то какова площадь круга?
4) Самый длинный прямоугольный треугольник вписан в окружность. сторона как диаметр того же круга. Если две меньшие стороны треугольника равны 21 см и 28 см соответственно, то какова площадь круга?