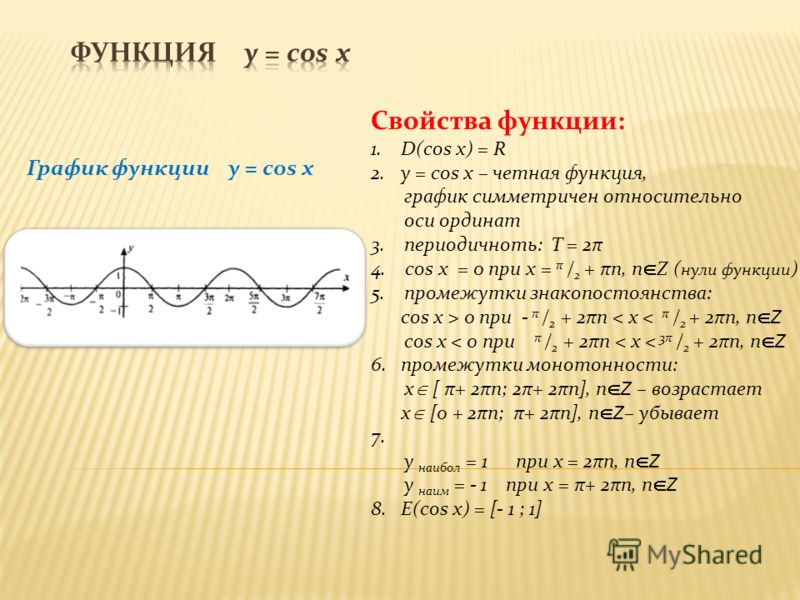
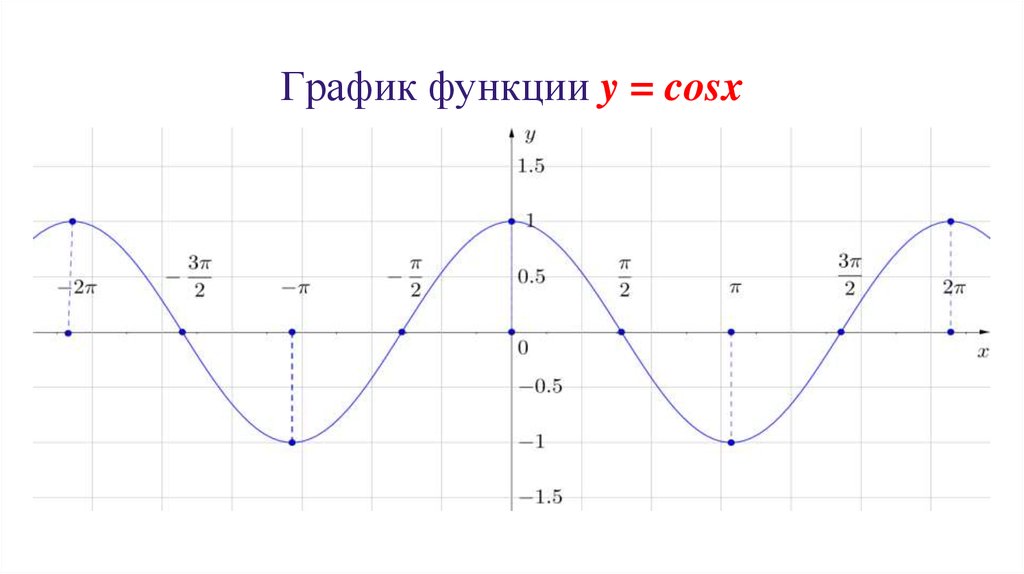
График функции y = cosx. 11-й класс
Тема урока: “Функция у=cosx”Урок №1
Цели урока: Ознакомить учащихся со свойствами функции у=cosx, обучение построению графика функции у=cosx, чтению этого графика, использование свойств и графика функции при решении уравнений и неравенств.
Задачи урока.
Образовательная – формирование функциональных представлений на наглядном материале, формирование умений построения графиков функции у=cosx, формировать навыки свободного чтения графиков, умение отражать свойства функции на графике.
Развивающая – формирование способности анализировать, обобщать полученные знания. Формирование логического мышления.
Воспитательная – активизировать интерес к
получению новых знаний, воспитание графической
культуры, формирование точности и аккуратности
при выполнении чертежей.
Оснащене: мультимедийный проектор, экран, операционная система Microsoft Windows 98/Me/2000/XP, программа MS Office 2003: Power Point, Microsoft Word, Microsoft Excel.
Ход урока
| № | Этап урока | Демонстрация слайдов | Время |
| 1 | Организационный момент. Приветствие | 1 |
|
| 2 | Объявление темы и цели урока | Слайд №2 |
2 |
| 3 | Актуализация опорных знаний Выполнение
устных упражнений. |
Фронтальный опрос |
5 |
| 4 | Изложение нового материала Задача на построение графика у =cosx на отрезке Обсуждение свойств функции у =cosx на отрезке Задача на построение эскиза графика функции у = cosх Обсуждение свойств функции у = cosx |
Слайд №3
Слайд №4 Занесение свойств в таблицу |
12 |
| 5 | Закрепление первичных знаний. Решение задач по учебнику №708, №709 |
Решение проходит в сопровождении cлайда №4 | 5 |
| 6 | Задача на построение графика
функции со сдвигом вдоль оси ординат и вдоль оси
абсцисс. Обсуждение свойств функции |
Слайд №5
Слайд №6 |
9 |
| 7 | Самостоятельная работа по учебнику | №710 (1;3), №711 (1;3), №711 (1;3) |
6 |
8 |
Подведение итогов.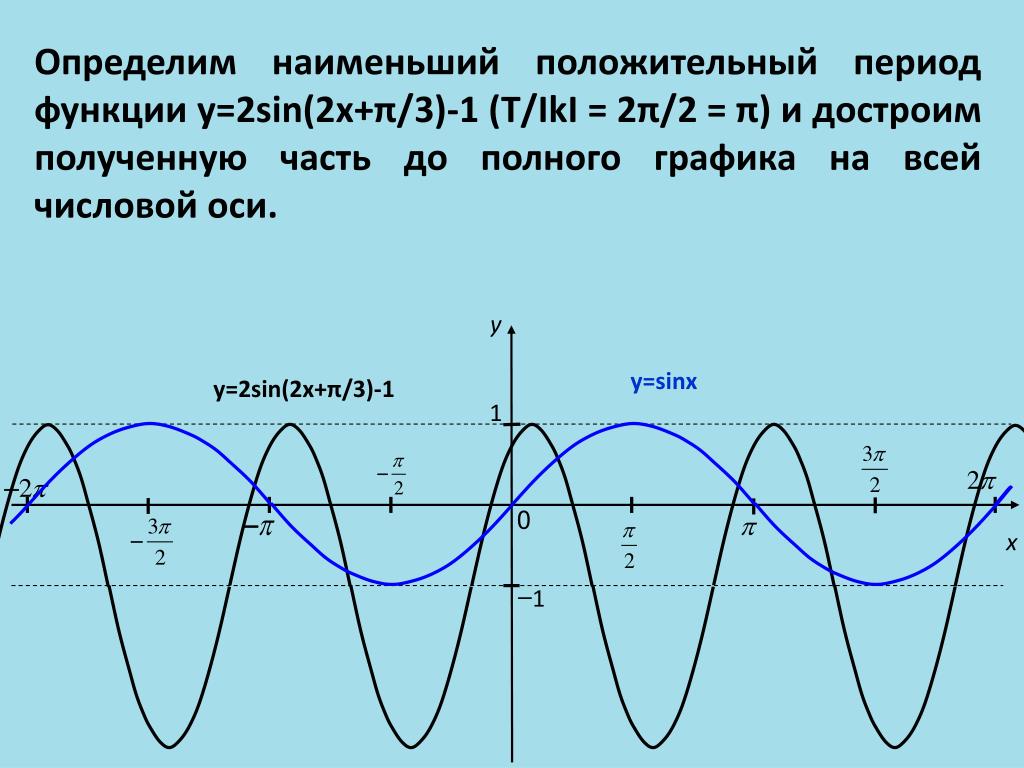 Итоги урока. Выставление оценок. |
3 |
|
| 9 | Домашнее задание | Дополнительно №717 (1) |
2 |
Цель урока: Ознакомить учащихся со свойствами функции у=cosx, обучение построению графика функции у=cosx, чтению этого графика, использование свойств и графика функции при решении уравнений и неравенств.
1. Организационный момент. Приветствие.
2. Объявление темы и цели урока сопровождается слайдом №2
3. Актуализация опорных знаний
Актуализация опорных знаний
Выполнение устных упражнений.
- Повторить определение тригонометрических функций и знаки значений этих функций.
- Обратить внимание учащихся на то, что для любого действительного числа можно указать соответствующую точку на единичной окружности, а следовательно ее абсциссу и ординату, т.е. косинус и синус числа х: у = cosx и у = sinx, область определения которых – все действительные числа.
Затем учащиеся отвечают на вопросы:
- При каких значениях х функция у=cosx принимает значение, равное 0? 1? -1?
- Может ли функция у=cosx принимать значение больше 1, меньше -1?
- При каких значениях х функция у=cosx принимает наибольшее (наименьшее) значение?
- Каково множество значений функции у=cosx?
Ответы на эти и следующие вопросы
сопровождаются иллюстрацией на единичной
окружности.
Повторив знаки значений тригонометрических функций в каждой четверти координатной плоскости, учащимся предлагается показать несколько точек единичной окружности, соответствующих числам, косинус которых положительное (отрицательное) число. Затем ответить на вопросы:
1) Какой знак имеет значение функции у=cosx, если х=, х=,
0<х<, 0<х<, <х<, <х<2.5?
2) Укажите несколько значений х, при которых значения функции у = cosx положительны, отрицательны.
3) Можно ли назвать все значения числа , косинус которых положителен, отрицателен?
4) Можно ли назвать все значения аргумента х, при которых значения функции у = cosx положительны, отрицательны?
5) Четная или нечетная функция у= cosx.
6) Чему равен период этой функции?
4. Изложение нового материала.
Обобщение и конкретизация знаний полученных
ранее: исследование области определения,
множества значений, четности, периодичности
позволяет построить график сначала на отрезке, затем на
отрезке , а
затем на всей числовой прямой.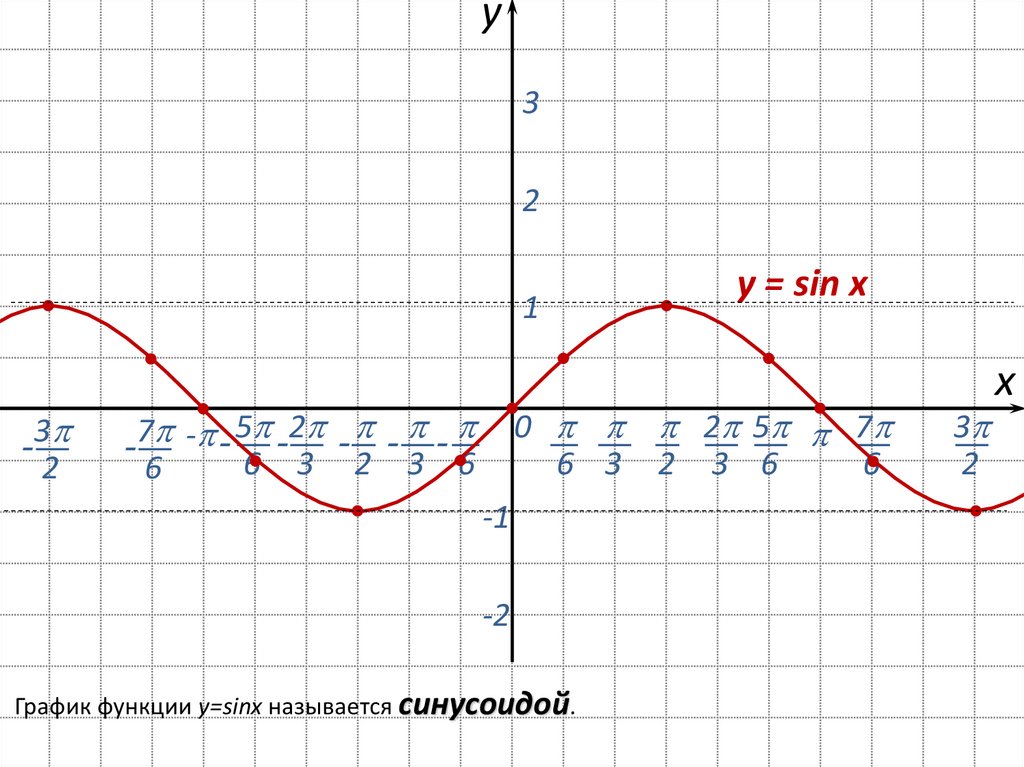
Затем учащиеся учатся изображать эскиз графика функции у= cosx по точкам (0;1), (;0),
(:-1), (;0), (;1) и обобщают свойства функции, записывая их в таблицу.
Проверяем с помощью слайда №4.
(На этом этапе выдаются опорные конспекты (приложение 1))
5. Закрепление первичных знаний.
С помощью эскиза графика функции у=cosx учащиеся отвечают на вопросы №708, с помощью таблицы свойств функции у=cosх отвечают на вопросы №709
6. Задача на построение графика функции со сдвигом вдоль оси ординат и вдоль оси абсцисс.
1. Слайд №5, 6
Слайд №6
В ходе беседы обсуждаются свойства этих функций.
7. Самостоятельная работа по учебнику
№710(1;3), №711(1;3), №711(1;3), №710
Разбить данный отрезок на два отрезка так, чтобы на одном из них функция у = cosx возрастала, а на другом убывала:
1)
— убывает; — возрастает
3)
— убывает; — возрастает
№711(1;3)
Используя свойство возрастания или убывания функции у = cosx, сравнить числа:
1)
, на отрезке функция у
= cosx убывает; ,
следовательно, .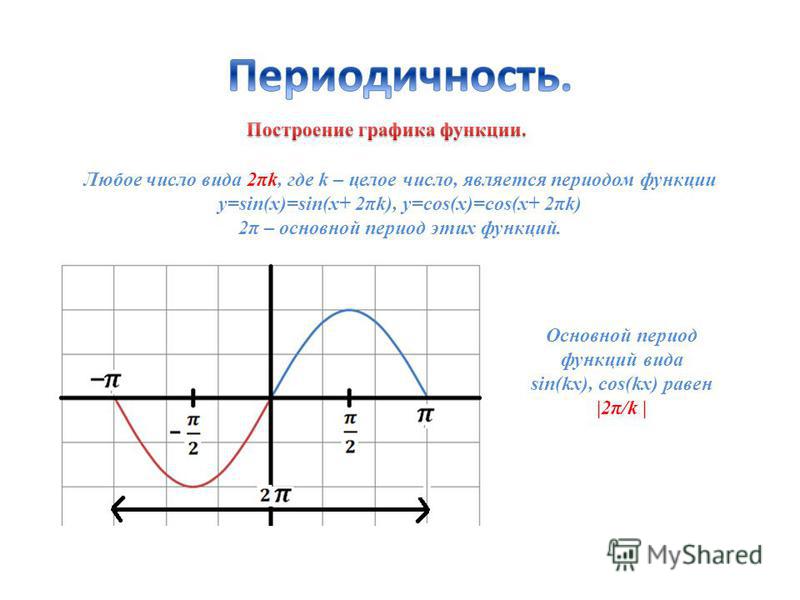
3) cos и cos
, , на отрезке функция у = cosx возрастает;
<, следовательно, cos < cos
№712 (1;3)
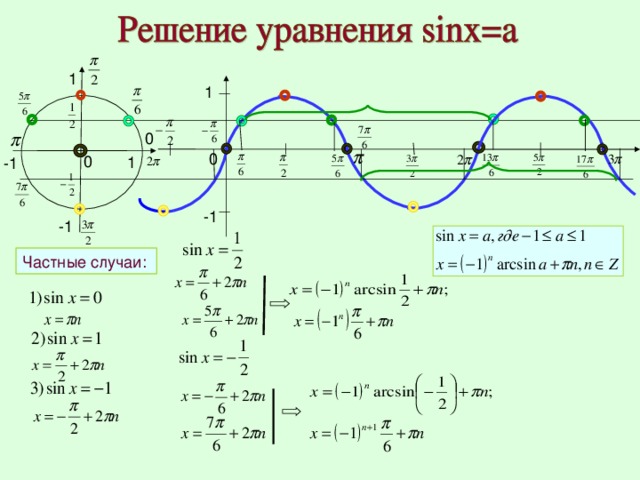
Найти все корни уравнения, принадлежащие отрезку :
1) cosx = х = ±+2n, nZ
Ответ: ; ; .
2) cosx = — х = ±
Ответ:
8. Подведение итогов.
Выставление оценок.
На уроке научились строить график функции у = cosx, читать свойства этого графика, строить эскиз графика, решать задачи связанные с использованием графика и свойств функции у = cosx.
9. Домашнее задание.
§40 №710(2;4), №711(2;4), №711(2;4). Построить графики функций у =cosx на и описать свойства этой функции.
Дополнительно №717(1).
Тема: “Функция у=cosx”
Урок №2
Цели урока: Повторить правила построения
графика функции у=cosx, научиться применять
приемы преобразования графика, чтению этого
графика, использование свойств и графика функции
при решении уравнений и неравенств.
Задачи урока.
Образовательная – формирование функциональных представлений на наглядном материале, формирование умений построения графиков функции у=cosx при различных преобразованиях, формировать навыки свободного чтения графиков, умение отражать свойства функции на графике.
Развивающая – формирование способности анализировать, обобщать полученные знания. Формирование логического мышления.
Воспитательная – активизировать интерес к получению новых знаний, воспитание графической культуры, формирование точности и аккуратности при выполнении чертежей.
Оснащене: мультимедийный проектор, экран, операционная система Microsoft Windows 98/Me/2000/XP, программа MS Office 2003: Power Point, Microsoft Word, Microsoft Excel.
Ход урока
| № | Этап урока | Демонстрация слайдов | Время |
| 1 | Организационный момент. Приветствие Приветствие |
1 | |
| 2 | Объявление темы и цели урока | Слайд №2 |
2 |
| 3 | Проверка домашнего задания | №717(1), Слайд №7 |
5 |
| 4 | Изложение нового материала Задача на построение графика путем сжатия и растяжения к оси ОХ Обсуждение свойств функции у =k·cosx при k>1 и 0<k<1. Задача на построение графика путем сжатия и растяжения к ори ОУ Обсуждение свойств функции у = cos(k·x) при k>1 и
0<k<1. |
Слайд №8, 9 |
12 |
| 5 | Закрепление первичных знаний. Решение
задач по учебнику №713(1;3), №715(1) №716(1) |
№717(2) учебник стр. 208. При решении №715(1), №716(1) использовать построенный график функции у = cos2x. Слайд №10 | 5 |
| 6 | Задача на построение графика функции симметричного относительно оси абсцисс. Обсуждение свойств функции | Слайд №11 |
6 |
| 7 | Самостоятельная работа. Решение
тестовых задач Решение
тестовых задач |
Тест XL, тест Word |
9 |
| 8 | Подведение итогов. Итоги
урока. Выставление оценок |
3 | |
| 9 | Домашнее задание | §40 №717(3), №713(4), №715(4), №716(2). Дополнительно №717(2) |
2 |
Цели урока: Повторить правила построения
графика функции у=cosx, научиться применять
приемы преобразования графика, чтению этого
графика, использование свойств и графика функции
при решении уравнений и неравенств.
1. Организационный момент. Приветствие.
2. Объявление темы и цели урока сопровождается слайдом №2.
3. Проверка домашнего задания
Слайд №7
4. Изложение нового материала
1. Задача на построение графика путем сжатия и растяжения к оси ОХ.
Обсуждение свойств функции у =k·cosx при k>1 и 0<k<1.
Слайд № 8
2. Задача на построение графика путем сжатия и растяжения к оси ОУ.
Обсуждение свойств функции у = cos(kx) при k>1 и 0<k<1.
Слайд № 9
5. Закрепление первичных знаний
Решение задач по учебнику №713(1;3), №715(1) №716(1)
Задание №715(1) №716(1) проверяем с помощью слайда №10
6. Задача на построение графика функции симметричного относительно оси абсцисс
Обсуждение свойств функции. Слайд №11 (использовать опорный конспект (приложение 1))
7. Самостоятельная работа
Самостоятельная работа
Решение тестовых задач. (Половина учащихся решает тесты в XL (приложение 2), за компьютерами, вторая половина на раздаточном материале (приложение 3). Затем учащиеся меняются местами.)
8. Итоги урока.
В результате изучения темы учащиеся научились строить график функции у = cosх, читать свойства функции, строить графики функции используя различные преобразования, читать свойства графиков с преобразованиями, решать простейшие задачи используя графики и свойства функции у = cosх.
Выставление оценок.
9. Домашнее задание.
§40 №717(3), №713(4), №715(4), №716(2). Дополнительно №719(2) (Проверка слайд №13)
В начале следующего урока можно предложить учащимся выполнить работу по построению графиков на готовых раздаточных материалах (приложение 4).
Постройте график функции y cos x 2. Графики тригонометрических функций кратных углов.
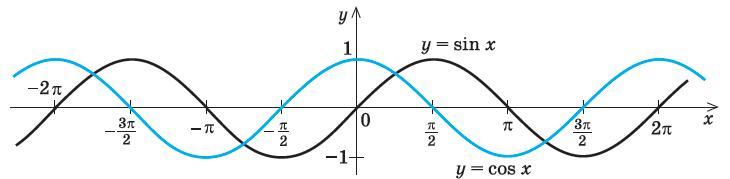 Свойства функции cos(x)
Свойства функции cos(x)Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у
= sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.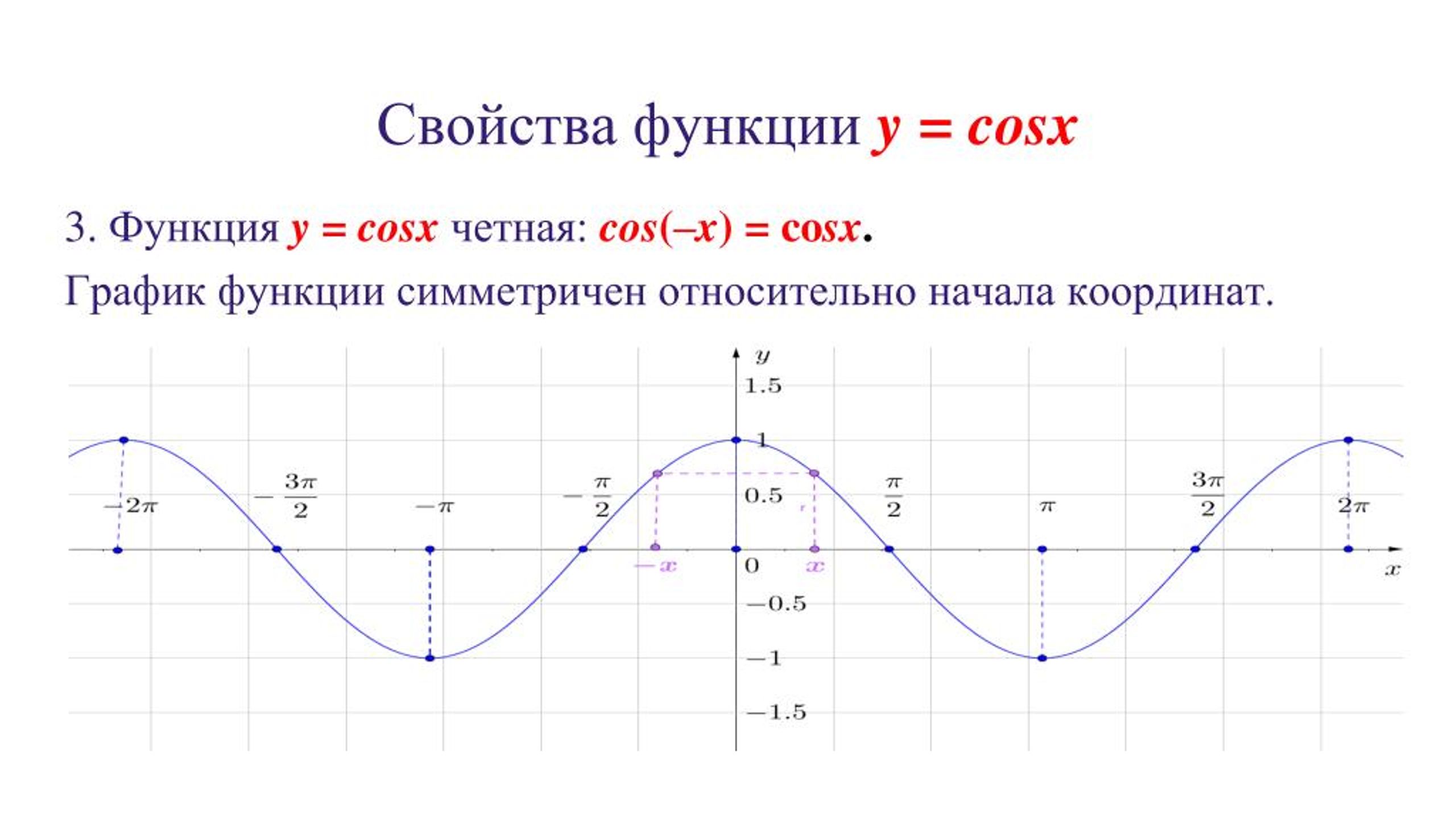
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.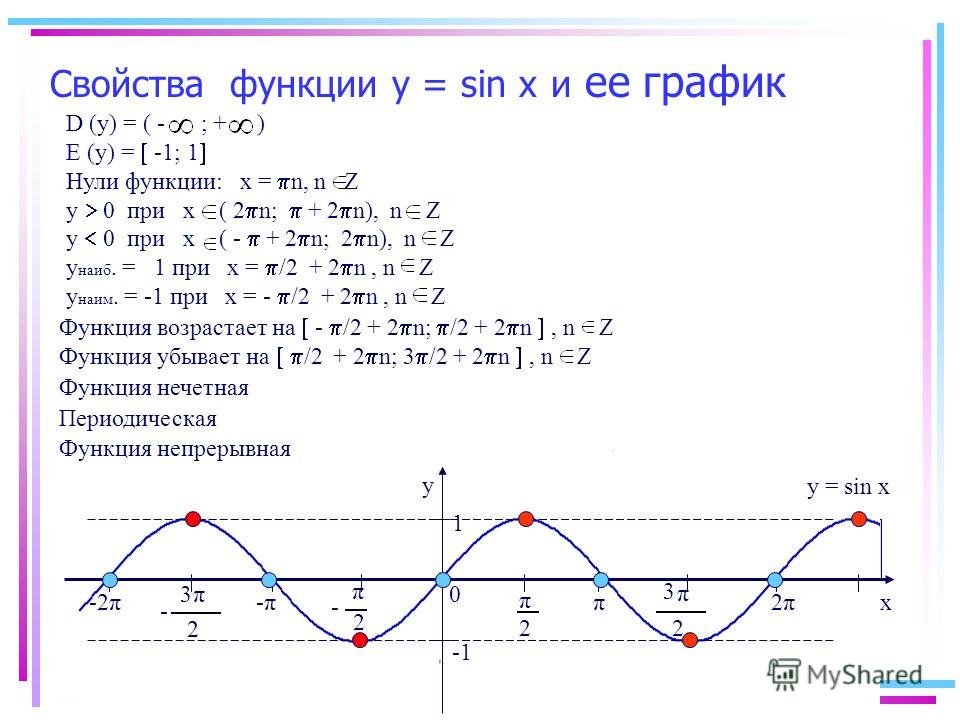
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой). Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).
«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…
«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
Оцените свои умения. Точки максимума функции.
«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.
«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом. Условия параллельности и перпендикулярности двух прямых. Угол между графиками функций. Уравнение касательной к графику функции в точке. Пусть функция дифференцируема в точке. Пусть прямые заданы уравнениями и.
Всего в теме 25 презентаций
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6. 1″
1″
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
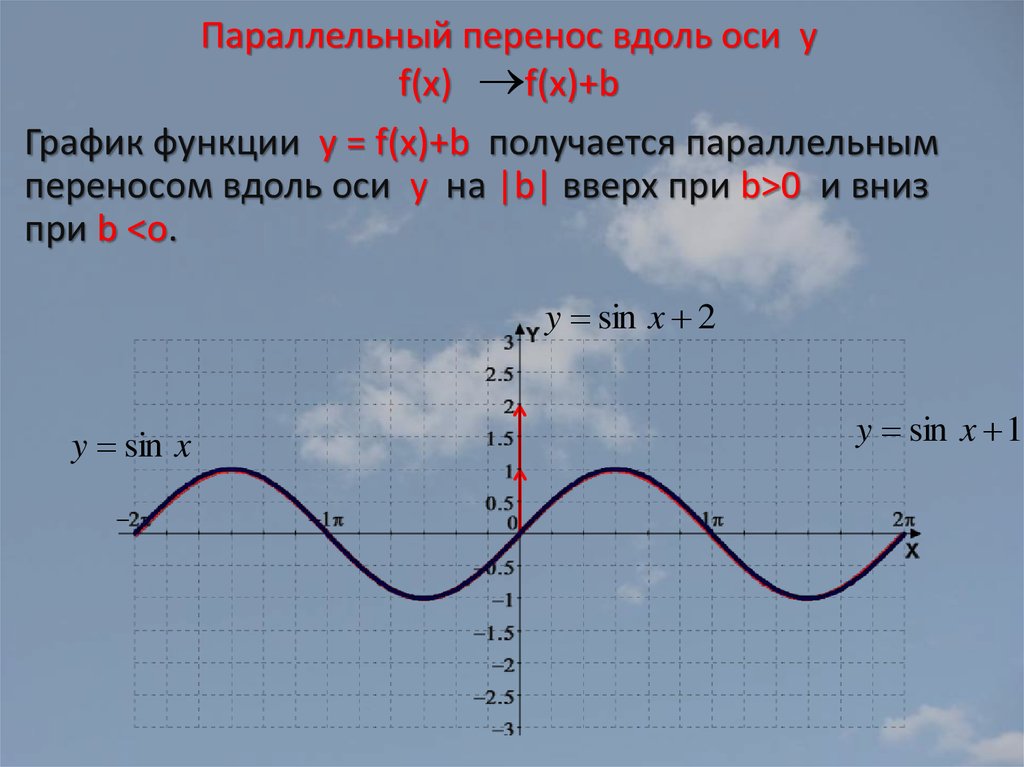
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.

- Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
- Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.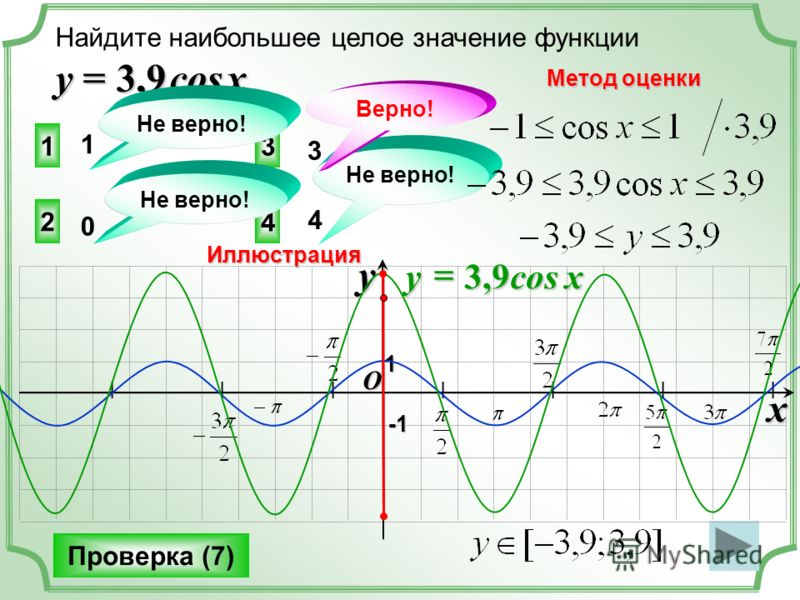
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
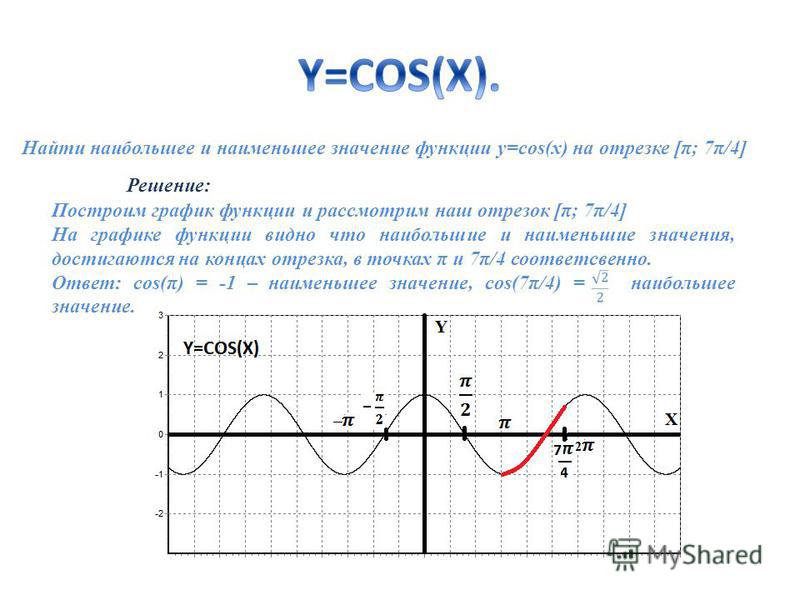
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке [- π/6; 5π/4].
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Коля, Дима и Саша собрали. 2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
с одного берега реки на другой можно попасть через остров воспользовавшись двумя из пяти существующих мостов за какое наименьшее время можно…
Пользуйтесь нашим приложением
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.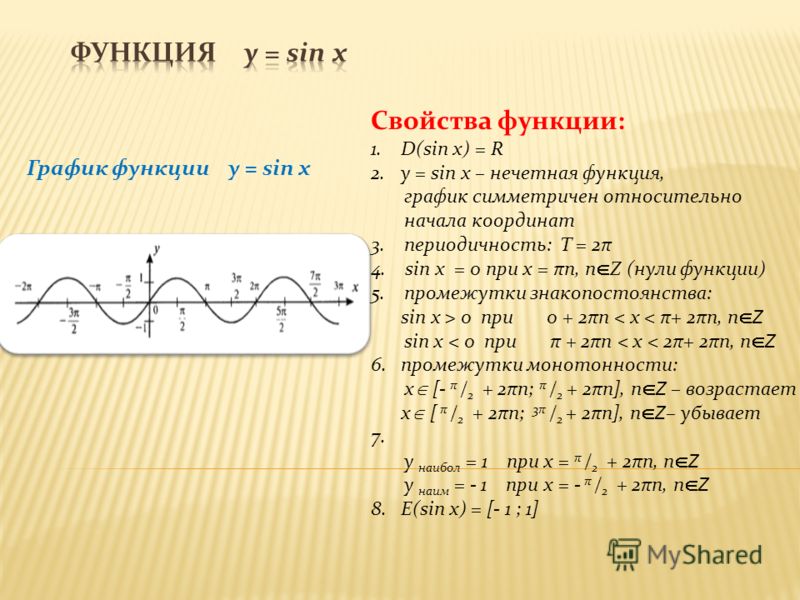 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
графическое представление функции 1+cos(x)
Программное обеспечение для построения кривых онлайн , также известное как графопостроитель ,
представляет собой онлайн-построитель кривых , который позволяет отображать функции в режиме онлайн. Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функционального исследования ,
позволяет получить графическое представление функции г. из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функционального исследования ,
позволяет получить графическое представление функции г. из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
В графическом калькуляторе для записи математических функций должны использоваться следующие операторы: 9Для мощности
Это программное обеспечение для построения кривых позволяет использовать следующие обычные математические функции :
- абс (абсолютное значение), график абсолютного значения
- арккос (арккосинус), арккосинус графика
- арксинуса (арксинуса), арксинус графика г.
- арктангенс (арктангенс), арктангенс графика
- ч (гиперболический косинус), построить гиперболический косинус
- косинус (косинус), график косинус
- косек (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- эксп (экспоненциальная), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- г.
 (синус),
график синуса
(синус),
график синуса - sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- абс. (абсолютное значение), график абсолютного значения г.
- арккос (арккосинус), арккосинус графика
- арксинуса (арксинуса), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ч (гиперболический косинус), построить гиперболический косинус г.
- косинус (косинус), график косинус
- косек (косеканс), косеканс участка
- котанг (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс г.
- cube_root (кубический корень), построить кубический корень
- эксп (экспоненциальная), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика г.
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тан (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс

- Графические функции онлайн
Этот онлайн плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .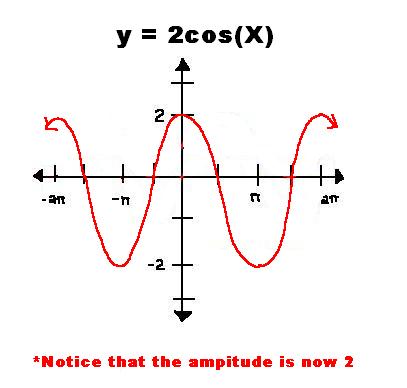
Для представления функций используется переменная «x».
Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
г.Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.
9Онлайн-плоттер 1811 имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.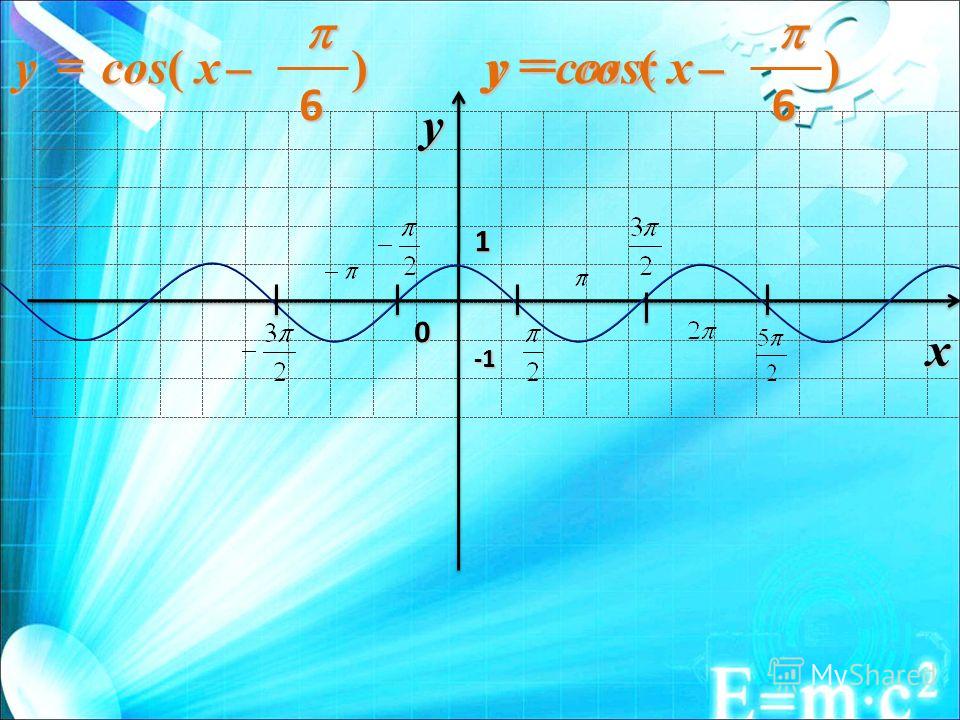
- Проведение касательной функции к точке
- График производной функции
Онлайн-плоттер позволяет провести тангенс функции в точке , чтобы сделать это, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
г. Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.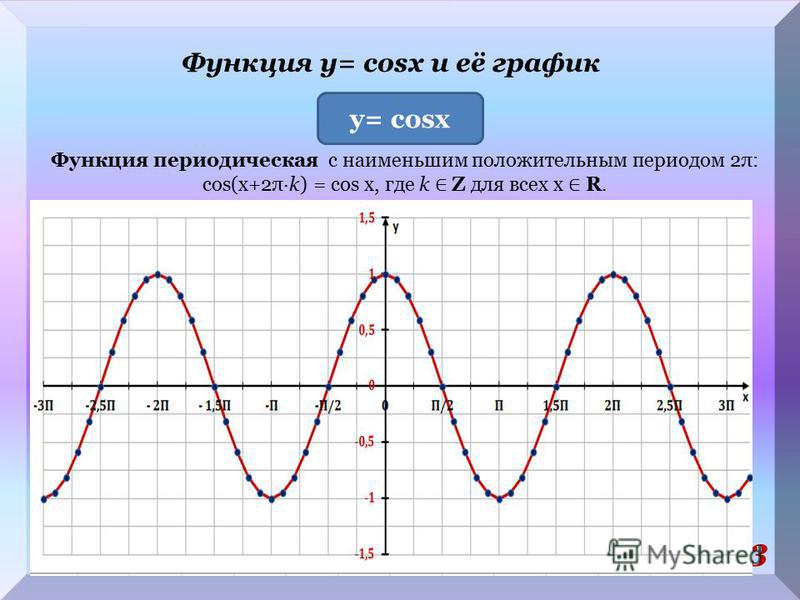
9Построитель кривых 1811 также можно использовать для вычисления производной функции и к участок он для этой цели, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
г. Плоттер позволяет рисовать параметрическую кривую , для этого,
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.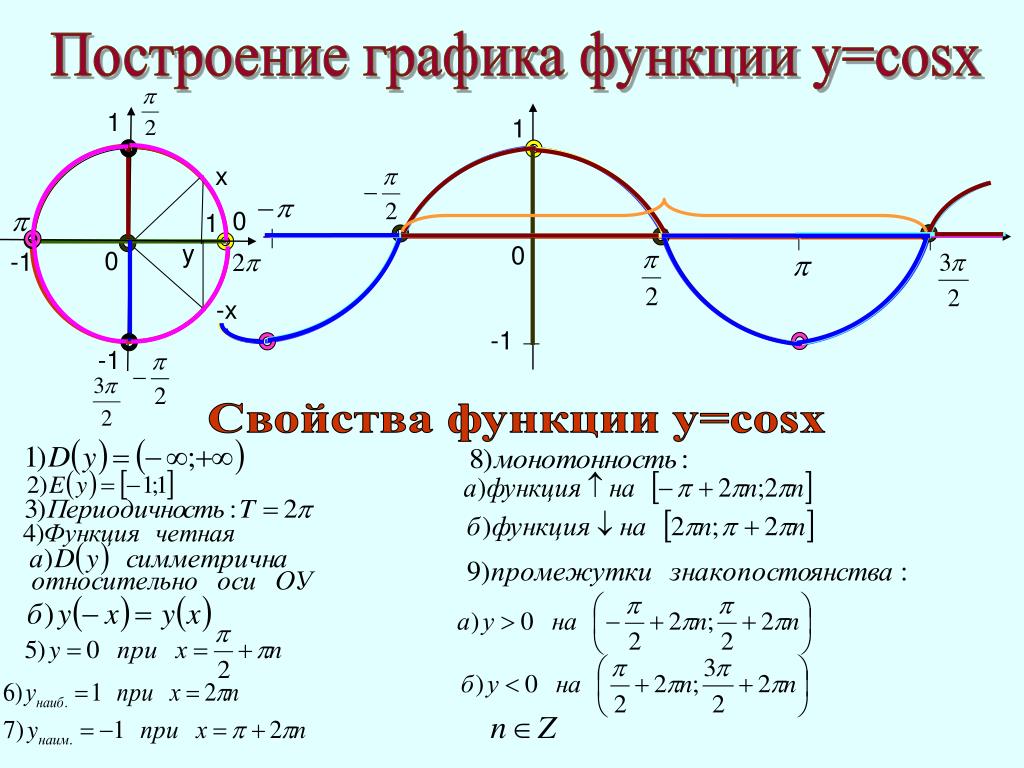
Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика.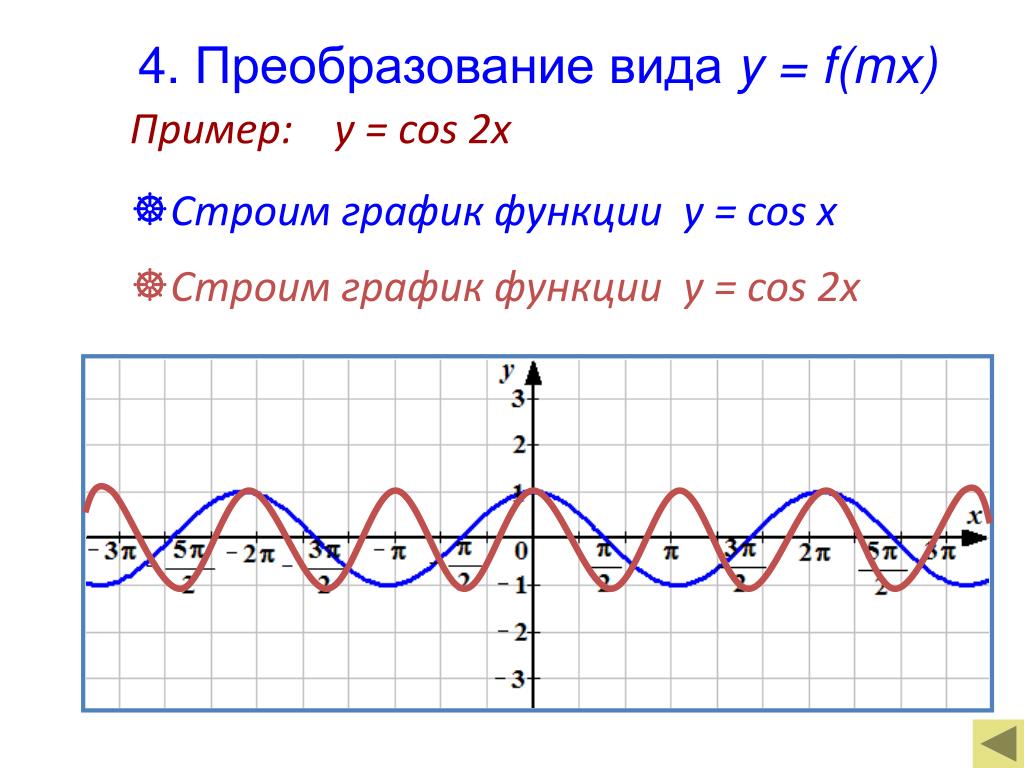 Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых, г.
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.
2.2: Графики функций секанса и косеканса
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 59548
- OpenStax
- OpenStax
Цели обучения
- Анализ графиков \(y=\sec x\) и \(y=\csc x\).
- Графические варианты \(y=\sec x\) и \(y=\csc x\).
Анализ графиков \(y = \sec x\) и \(y = \csc x\)
Функция секущей определялась обратным тождеством \(sec \, x=\dfrac{1}{\cos Икс}\). Обратите внимание, что функция не определена, когда косинус равен \(0\), что приводит к вертикальным асимптотам при \(\dfrac{\pi}{2}\), \(\dfrac{3\pi}{2}\) и т. д. , Поскольку косинус никогда не превышает \(1\) по абсолютной величине, секанс, являющийся обратной величиной, никогда не будет меньше \(1\) по абсолютной величине.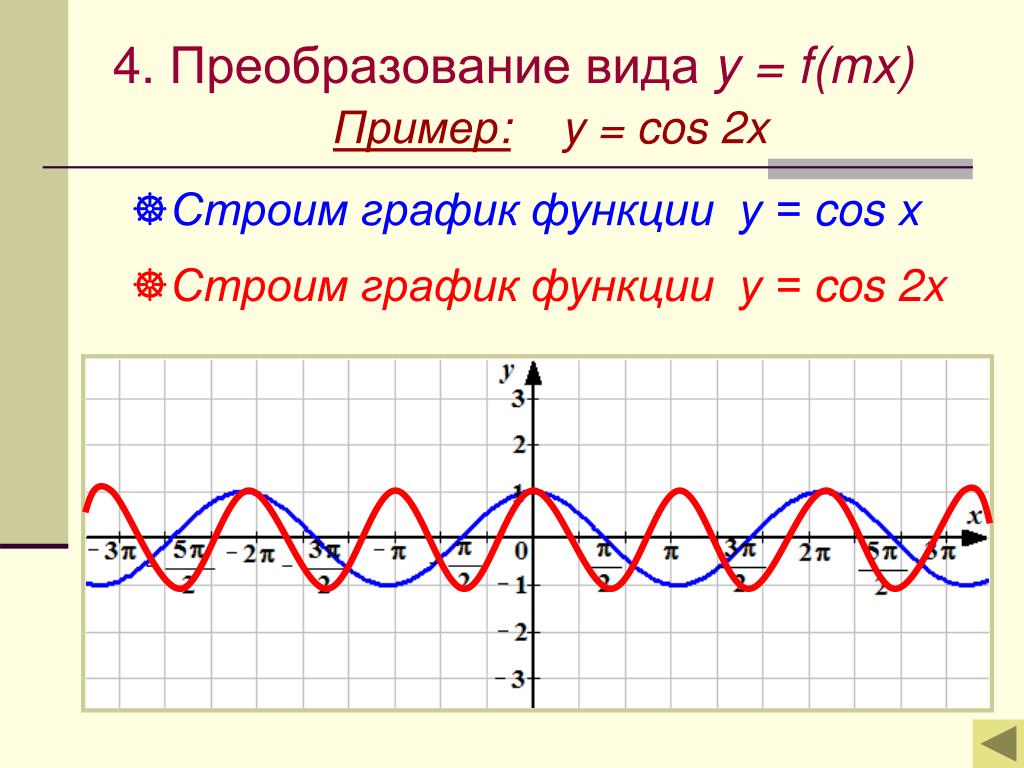
Мы можем построить график \(y=\sec x\), наблюдая за графиком функции косинуса, потому что эти две функции обратны друг другу. См. рисунок \(\PageIndex{1}\). График косинуса показан пунктирной оранжевой волной, чтобы мы могли видеть взаимосвязь. Там, где график функции косинуса уменьшается, график функции секанса увеличивается. Там, где график функции косинуса увеличивается, график функции секанса уменьшается. Когда функция косинуса равна нулю, секанс не определен.
График секущих имеет вертикальные асимптоты при каждом значении \(x\), где график косинуса пересекает ось \(x\) — это потому, что значение, обратное 0, не определено. Мы показываем их на графике ниже пунктирными вертикальными линиями, но не будем явно показывать все асимптоты на всех последующих графиках, включающих секанс и косеканс.
Обратите внимание, что поскольку косинус является четной функцией, секанс также является четной функцией. То есть \(\sec(-x)=\sec x\).
Рисунок \(\PageIndex{1}\): График секущей функции, \(f(x)=\sec x=\dfrac{1}{\cos x}\) Поскольку не существует максимальных или минимальных значений функции тангенса, термин амплитуда не может быть интерпретирован так же, как для функций синуса и косинуса. Вместо этого мы будем использовать фразу коэффициент растяжения/сжатия при обращении к константе \(A\).
Вместо этого мы будем использовать фразу коэффициент растяжения/сжатия при обращении к константе \(A\).
ОСОБЕННОСТИ ГРАФИКА \(Y = A \sec(Bx)\)
- Коэффициент растяжения равен \(| A |\).
- Период равен \(\dfrac{2\pi}{| B |}\).
- Домен равен \(x≠\dfrac{\pi}{2| B |}k\), где \(k\) — нечетное целое число. г.
- Диапазон равен \((−∞,−|A|]∪[|A|,∞)\).
- Вертикальные асимптоты находятся в точке \(x=\dfrac{\pi}{2| B |}k\), где \(k\) — нечетное целое число.
- Нет амплитуды.
- \(y=A\sec(Bx)\) — четная функция, потому что косинус — четная функция.
Аналогично секансу, косеканс определяется взаимной тождественностью \(\csc x=\dfrac{1}{\sin x}\). Обратите внимание, что функция не определена, когда синус равен \(0\), что приводит к вертикальной асимптоте на графике в точках \(0\), \(\pi\) и т. д. Поскольку синус никогда не превышает \(1 \) по абсолютной величине, косеканс, будучи обратным, никогда не будет меньше \(1\) по абсолютной величине.
Мы можем построить график \(y=\csc x\), наблюдая за графиком функции синуса, потому что эти две функции являются обратными друг другу. См. рисунок \(\PageIndex{2}\). График синуса показан пунктирной оранжевой волной, чтобы мы могли видеть взаимосвязь. Там, где график функции синуса уменьшается, график функции косеканса увеличивается. Там, где график функции синуса увеличивается, график функции косеканса уменьшается.
График косеканса имеет вертикальные асимптоты при каждом значении \(x\), где график синусов пересекает ось \(x\); мы показываем это на графике ниже пунктирными вертикальными линиями.
Обратите внимание, что, поскольку синус является нечетной функцией, функция косеканса также является нечетной функцией. То есть \(\csc(-x)=-\csc x\).
График косеканса, показанный на рисунке \(\PageIndex{2}\), аналогичен графику секанса.
Рисунок \(\PageIndex{2}\): График функции косеканса, \(f(x)=\csc x=\frac{1}{\sin x}\)ОСОБЕННОСТИ ГРАФИКА \(Y = A \csc(Bx)\)
- Коэффициент растяжения равен \(| A |\).

- Период равен \(\dfrac{2\pi}{|B|}\). г.
- Домен равен \(x≠\dfrac{\pi}{|B|}k\), где \(k\) — целое число.
- Диапазон равен \((−∞,−|A|]∪[|A|,∞)\).
- Асимптоты находятся в точке \(x=\dfrac{\pi}{| B |}k\), где \(k\) — целое число.
- \(y=A\csc(Bx)\) — нечетная функция, потому что синус — нечетная функция.
Графики вариаций \(y = \sec x\) и \(y= \csc x\)
Для сдвинутых, сжатых и/или растянутых версий функций секанса и косеканса мы определяем вертикальные асимптоты, а также оценивайте функции для нескольких точек (в частности, локальных экстремумов). Если мы хотим построить график только одного периода, мы можем выбрать интервал для периода более чем одним способом. Процедура для секанса очень похожа, потому что идентичность кофункций означает, что график секанса совпадает с графиком косеканса, сдвинутым на полпериода влево. Вертикальный и фазовый сдвиги могут применяться к функции косеканса так же, как к секансу и другим функциям. Уравнения становятся следующими.
Уравнения становятся следующими.
\[y=A\sec(Bx−C)+D \nonumber\]
\[y=A\csc(Bx−C)+D \nonumber\]
ОСОБЕННОСТИ ГРАФИКА \(Y = A\sec(Bx−C)+D\)
- Коэффициент растяжения равен \(|A|\).
- Период равен \(\dfrac{2\pi}{|B|}\).
- Домен равен \(x≠\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), где \(k\) — нечетное целое число.
- Диапазон равен \((−∞,−|A|]∪[|A|,∞)\).
- Вертикальные асимптоты находятся в точке \(x=\dfrac{C}{B}+\dfrac{π}{2| B |}k\), где \(k\) — нечетное целое число. г.
- Нет амплитуды.
- \(y=A\sec(Bx)\) — четная функция, потому что косинус — четная функция.
ОСОБЕННОСТИ ГРАФИКА \(Y = A\csc(Bx−C)+D\)
- Коэффициент растяжения равен \(|A|\).
- Период равен \(\dfrac{2\pi}{|B|}\).
- Домен равен \(x≠\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), где \(k\) — целое число.
- Диапазон равен \((−∞,−|A|]∪[|A|,∞)\).
- Вертикальные асимптоты находятся в точке \(x=\dfrac{C}{B}+\dfrac{\pi}{|B|}k\), где \(k\) — целое число.
 г.
г. - Нет амплитуды.
- \(y=A\csc(Bx)\) — нечетная функция, потому что синус — нечетная функция.
HOWTO: Для функции вида \(y=A\sec(Bx)\) постройте график одного периода
- Нарисуйте функцию \(y=A\cos(Bx)\).
- Нарисуйте вертикальные асимптоты там, где кривая пересекает среднюю линию, являющуюся осью \(x\)
- Закрасьте секущую между асимптотами. Там, где кривая косинуса имеет максимум, кривая секущей будет иметь восходящую U. Там, где кривая косинуса имеет минимум, кривая секущей будет иметь нисходящую U. г.
Пример \(\PageIndex{1}\): построение графика изменения секущей функции
Постройте график одного периода \(f(x)=2,5\sec(0,4x)\).
Решение
- Шаг 1. Нарисуйте график функции \(f(x)=2,5\cos(0,4x)\). \(A=2,5\), поэтому коэффициент растяжения равен \(2,5\). \(B=0,4\), поэтому \(P=\dfrac{2\pi}{0,4}=5\pi\). Период составляет \(5\pi\) единиц.
 Разделив это на 4, мы получим \(\dfrac{5\pi}{4}\). Каждый раз, когда мы проходим расстояние \(\dfrac{5\pi}{4}\), мы будем на максимуме, на средней линии или на минимуме. г.
Разделив это на 4, мы получим \(\dfrac{5\pi}{4}\). Каждый раз, когда мы проходим расстояние \(\dfrac{5\pi}{4}\), мы будем на максимуме, на средней линии или на минимуме. г. - Шаг 2. Нарисуйте вертикальные асимптоты там, где кривая пересекает среднюю линию, являющуюся осью \(x\)
- Шаг 3. Заполните секущую между асимптотами. Там, где кривая косинуса имеет максимум, кривая секущей будет иметь восходящую U. Если кривая косинуса имеет минимум, кривая секущей будет иметь нисходящую U. На рисунке \(\PageIndex{3}\) показан график. Зеленая пунктирная кривая — функция косинуса, которая действует как «каркас» секущей. Синие пунктирные линии — вертикальные асимптоты. Красные кривые — функция секущей. г.
Рисунок \(\PageIndex{3}\)
Обратите внимание, что на приведенном выше графике зеленая и синяя пунктирные линии не являются частью графика секущих, мы просто используем их для получения графика секущих. Только красные кривые представляют собой секущую, как показано ниже.
Упражнение \(\PageIndex{1}\)
Постройте график одного периода \(f(x)=−2,5\sec(0,4x)\).
- Ответить
Это вертикальное отражение предыдущего графика, поскольку \(A\) отрицательное значение.
г. Рисунок \(\PageIndex{4}\)
Вопросы и ответы: Вертикальный сдвиг и растяжение/сжатие влияют на диапазон секущей?
Да. Диапазон \(f(x)=A\sec(Bx−C)+D\) равен \((−∞,−|A|+D]∪[|A|+D,∞)\).
Для функции вида \(f(x)=A\sec(Bx−C)+D\) начертите один период.
- Нарисуйте график \(f(x)=A\cos(Bx−C)+D\)
- Нарисуйте вертикальные асимптоты, которые возникают там, где кривая косинуса проходит через свою среднюю линию в точке \(y=D\) г.
- Закрасьте секущую между асимптотами. Там, где кривая косинуса имеет максимум, кривая секущей будет иметь направленную вверх U. Там, где кривая косинуса имеет минимум, кривая секущей будет иметь направленную вниз U.
Пример \(\PageIndex{2}\): построение графика изменения секущей функции
График одного периода \(y=\sec \left (2x−\dfrac{\pi}{2} \right )+ 3\).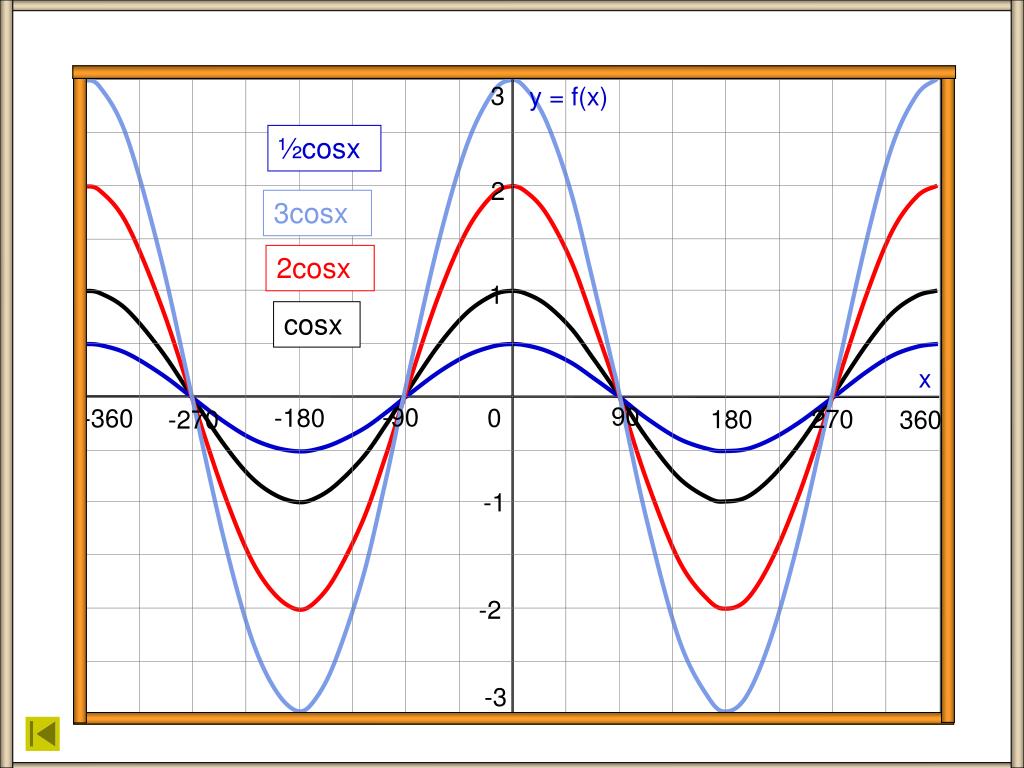
Решение
- Шаг 1. Нарисуйте кривую \(y=\cos \left (2x−\dfrac{\pi}{2} \right )+3\). Коэффициент растяжения/сжатия равен \(| A |=1\), поэтому амплитуда равна 1. \(B=2\), поэтому период равен \(\dfrac{2\pi}{2}=\pi\). Разделение периода на 4 дает \(\dfrac{\pi}{4}\). Каждый раз, когда мы проходим это расстояние, мы будем находиться на максимуме, на средней линии или на минимуме. Чтобы найти фазовый сдвиг, решаем уравнение \(2x−\dfrac{\pi}{2}=0\), которое имеет решение \(x=\dfrac{\pi}{4}\). Имеется фазовый сдвиг \(\dfrac{\pi}{4}\) вправо. Это означает, что мы можем «начать» косинусоидальную кривую с максимума, расположенного в точке \(\left(\dfrac{\pi}{4},4\right)\). Средняя линия — это горизонтальная линия \(y=3\). г.
- Шаг 2. Нарисуйте вертикальные асимптоты, которые возникают там, где кривая косинуса проходит через среднюю линию \(y=3\).
- Шаг 3. Заполните секущую между асимптотами. Там, где кривая косинуса имеет максимум, кривая секущей будет иметь направленную вверх U.
 Там, где кривая косинуса имеет минимум, кривая секущей будет иметь направленную вниз U. На рисунке \(\PageIndex{5}\) показан график. Зеленая кривая — функция косинуса, а вертикальные синие линии — вертикальные асимптоты. Кривая \(y=\sec \left (2x−\dfrac{\pi}{2} \right )+3\) выделена красным цветом. г.
Там, где кривая косинуса имеет минимум, кривая секущей будет иметь направленную вниз U. На рисунке \(\PageIndex{5}\) показан график. Зеленая кривая — функция косинуса, а вертикальные синие линии — вертикальные асимптоты. Кривая \(y=\sec \left (2x−\dfrac{\pi}{2} \right )+3\) выделена красным цветом. г.
Рисунок \(\PageIndex{5}\)
Упражнение \(\PageIndex{2}\)
Постройте график одного периода \(f(x)=−6\sec(4x+2)−8\).
- Ответить
- Рисунок \(\PageIndex{6}\)
Q&A: Областью определения \(\csc \, x\) были заданы все \(x\), такие что \(x≠k\pi\) для любого целого числа \(k\). Будет ли областью \(y=A\csc(Bx−C)+D\) быть \(x≠\dfrac{C+k\pi}{B}\)?
Да. Исключенные точки области следуют вертикальным асимптотам. Их расположение показывает сдвиг по горизонтали и сжатие или расширение, подразумеваемые преобразованием входных данных исходной функции.
Дана функция вида \(y=A\csc(Bx)\), постройте график за один период.
- Нарисуйте функцию \(y=A\sin(Bx)\).
- Нарисуйте вертикальные асимптоты там, где кривая пересекает среднюю линию, являющуюся осью \(x\)
- Закрасьте косеканс между асимптотами. Там, где синусоида имеет максимум, косеканс будет иметь восходящую U. Там, где синусоида имеет минимум, косеканс будет иметь нисходящую U.
Пример \(\PageIndex{3}\): построение графика изменения функции косеканса
Постройте график одного периода \(f(x)=−3\csc(4x)\).
Решение
- Шаг 1. Нарисуйте график функции \(f(x)=−3\sin(4x)\). \(| A |=| −3 |=3\), поэтому амплитуда равна 3. \(B=4\), поэтому \(P=\dfrac{2\pi}{4}=\dfrac{\pi {2}\). Период составляет \(\dfrac{\pi}{2}\) единиц. Разделение периода на 4 дает \(\dfrac{\pi}{8}\). Каждый раз, когда мы проходим расстояние \(\dfrac{\pi}{8}\), синусоида будет иметь максимум, находиться на средней линии или иметь минимум. Значение \(C\) равно 0, поэтому фазового сдвига нет, мы можем «начать» кривую на средней линии в точке \(x=0\).
 Значение \(D\) равно 0, поэтому смещения по вертикали нет — средняя линия является осью \(x\). г.
Значение \(D\) равно 0, поэтому смещения по вертикали нет — средняя линия является осью \(x\). г. - Шаг 2. Нарисуйте вертикальные асимптоты там, где кривая пересекает среднюю линию, являющуюся осью \(x\).
- Шаг 3. Заполните кривую косеканса между асимптотами. Там, где синусоида имеет максимум, кривая косеканса будет иметь восходящий U. Там, где синусоида имеет минимум, косеканс будет иметь нисходящий U. На рисунке \(\PageIndex{7}\) показан график за один период. .
Упражнение \(\PageIndex{3}\)
График \(f(x)=0,5\csc(2x)\) не менее чем за два периода.
- Ответить
Рисунок \(\PageIndex{8}\)
Для заданной функции вида \(f(x)=A \csc(Bx−C)+D\) построить график одного периода
- Начертить график функции \(f(x)=A\sin(Bx −С)+D\)
- Нарисуйте вертикальные асимптоты, которые возникают там, где синусоида проходит через свою среднюю линию в точке \(y=D\)
- Закрасьте косеканс между асимптотами.
 Там, где синусоидальная кривая имеет максимум, косеканс будет иметь восходящую U. Там, где синусоида имеет минимум, косеканс будет иметь нисходящую U. г.
Там, где синусоидальная кривая имеет максимум, косеканс будет иметь восходящую U. Там, где синусоида имеет минимум, косеканс будет иметь нисходящую U. г.
Пример \(\PageIndex{4}\): построение графика вертикально растянутого, горизонтально сжатого и вертикально сдвинутого косеканса
Нарисуйте график \(y=2\csc \left (\dfrac{\pi}{2} х \справа )+1\).
Решение
- Шаг 1. Нарисуйте график функции \(y=2\sin \left (\dfrac{\pi}{2}x \right )+1\). \(| A |=2\), поэтому амплитуда равна 2. Период равен \(\dfrac{2\pi}{| B |}=\dfrac{2\pi}{\dfrac{\pi}{2} }=2\pi⋅\dfrac{2}{\pi}=4\). Разделение периода на 4 дает 1. Каждый раз, когда мы перемещаем единицу на 1, синусоида будет иметь максимум, находиться на средней линии или иметь минимум. Чтобы найти фазовый сдвиг, мы решаем уравнение \(\dfrac{\pi}{2}x=0\), которое имеет решение \(x=0\). Мы можем «начать» синусоиду с точки \(x=0\) на средней линии, которая находится в точке \(y=1\). г.
- Шаг 2. Нарисуйте вертикальные асимптоты, которые возникают там, где синусоида проходит через свою среднюю линию в точке \(y=1\).
- Шаг 3. Заполните кривую косеканса между асимптотами. Там, где синусоида имеет максимум, косеканс будет иметь восходящую U. Там, где синусоида имеет минимум, косеканс будет иметь нисходящую U.
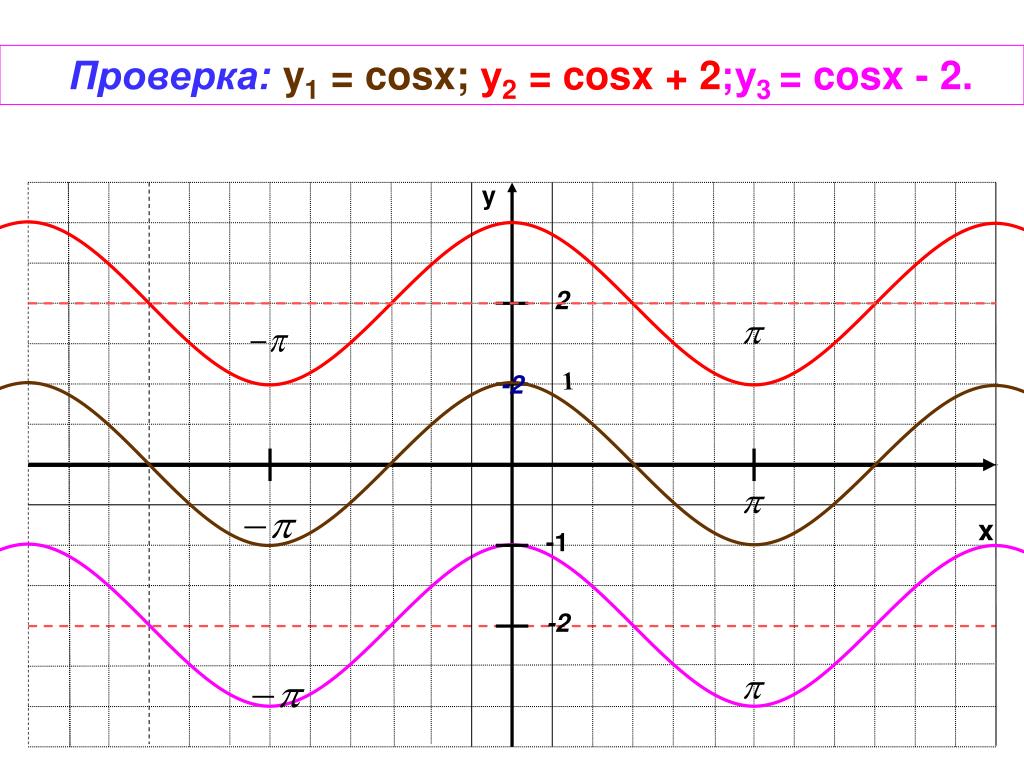
График для этой функции показан на рисунке \(\PageIndex{9}\) темно-синим цветом. Оранжевая пунктирная линия — это синусоида, а пунктирные вертикальные синяя и зеленая линии — вертикальные асимптоты.
Рисунок \(\PageIndex{9}\): Преобразованная функция косекансаАнализ
Вертикальные асимптоты, показанные на графике, отмечают один период функции, а локальные экстремумы на этом интервале показаны точками . Обратите внимание, как график преобразованного косеканса соотносится с графиком \(f(x)=2\sin\left (\frac{\pi}{2}x \right)+1\), показанным оранжевой пунктирной волной .
Упражнение \(\PageIndex{4}\)
Учитывая график \(f(x)=2\cos\left (\frac{\pi}{2}x \right )+1\), показанный на На рисунке \(\PageIndex{10}\) нарисуйте график \(g(x)=2\sec \left (\dfrac{\pi}{2}x \right )+1\) на тех же осях.
Рисунок \(\PageIndex{10}\)- Ответ
- Рисунок \(\PageIndex{18}\)
Ключевые уравнения
| Сдвинутая, сжатая и/или растянутая функция секанса | \(y=A \sec(Bx−C)+D\) |
| Сдвинутая, сжатая и/или растянутая функция косеканса | \(y=A\csc(Bx−C)+D\) |
Ключевые понятия
- Секанс и косеканс являются периодическими функциями с периодом \(2\pi\).
- \(f( x )=A\sec( Bx−C )+D\) дает сдвинутый, сжатый и/или растянутый график функции секущей. См. Пример \(\PageIndex{4}\) и Пример \(\PageIndex{5}\).
- \(f( x )=A\csc( Bx−C )+D\) дает сдвинутый, сжатый и/или растянутый график функции косеканса.



 11.16
11.16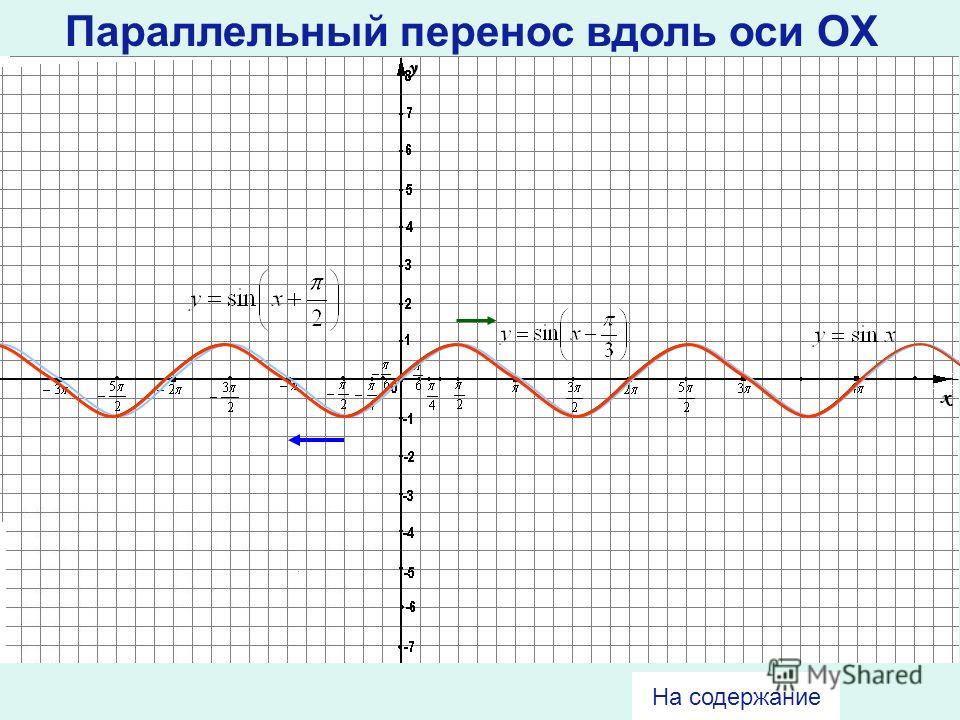 (синус),
график синуса
(синус),
график синуса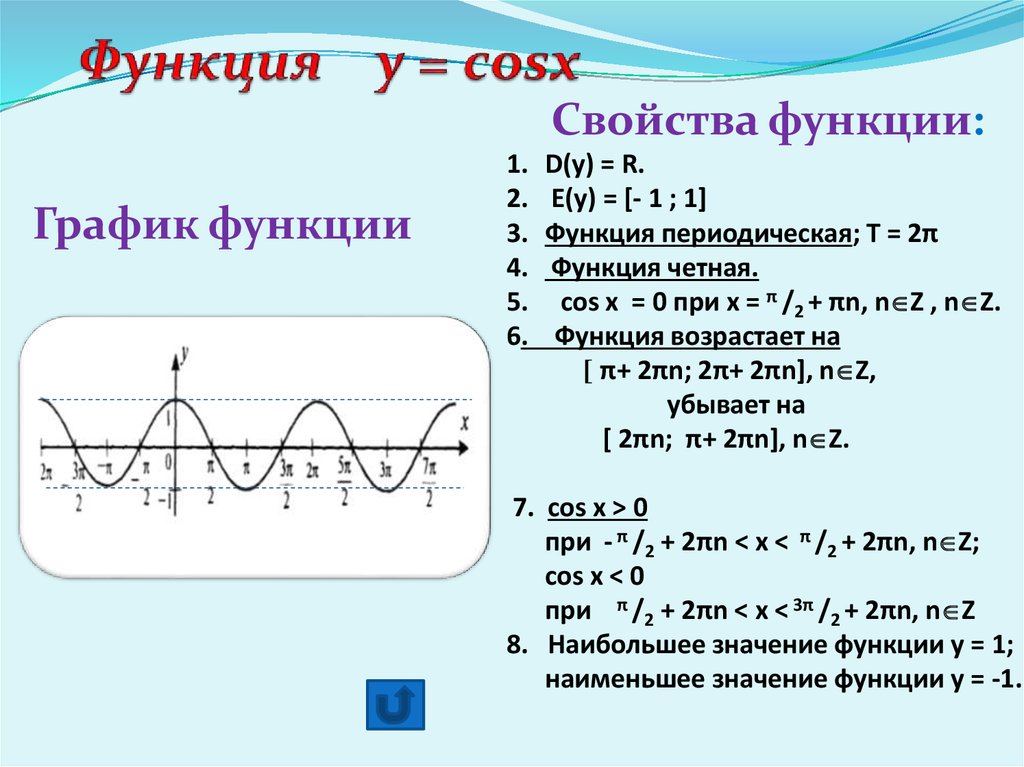

 Разделив это на 4, мы получим \(\dfrac{5\pi}{4}\). Каждый раз, когда мы проходим расстояние \(\dfrac{5\pi}{4}\), мы будем на максимуме, на средней линии или на минимуме.
Разделив это на 4, мы получим \(\dfrac{5\pi}{4}\). Каждый раз, когда мы проходим расстояние \(\dfrac{5\pi}{4}\), мы будем на максимуме, на средней линии или на минимуме.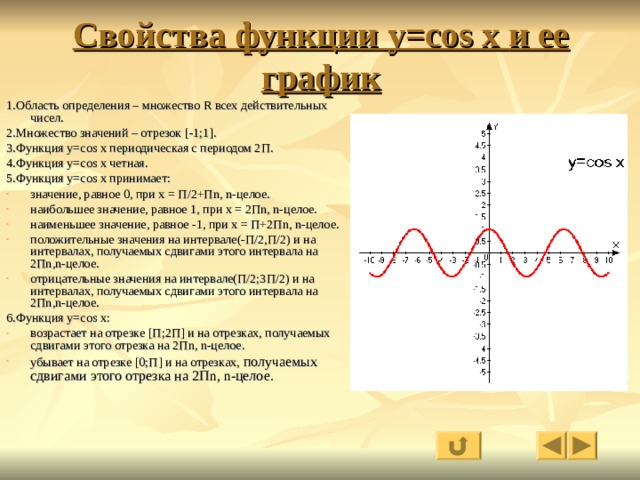 Там, где кривая косинуса имеет минимум, кривая секущей будет иметь направленную вниз U. На рисунке \(\PageIndex{5}\) показан график. Зеленая кривая — функция косинуса, а вертикальные синие линии — вертикальные асимптоты. Кривая \(y=\sec \left (2x−\dfrac{\pi}{2} \right )+3\) выделена красным цветом.
Там, где кривая косинуса имеет минимум, кривая секущей будет иметь направленную вниз U. На рисунке \(\PageIndex{5}\) показан график. Зеленая кривая — функция косинуса, а вертикальные синие линии — вертикальные асимптоты. Кривая \(y=\sec \left (2x−\dfrac{\pi}{2} \right )+3\) выделена красным цветом. Значение \(D\) равно 0, поэтому смещения по вертикали нет — средняя линия является осью \(x\).
Значение \(D\) равно 0, поэтому смещения по вертикали нет — средняя линия является осью \(x\). Там, где синусоидальная кривая имеет максимум, косеканс будет иметь восходящую U. Там, где синусоида имеет минимум, косеканс будет иметь нисходящую U.
Там, где синусоидальная кривая имеет максимум, косеканс будет иметь восходящую U. Там, где синусоида имеет минимум, косеканс будет иметь нисходящую U.