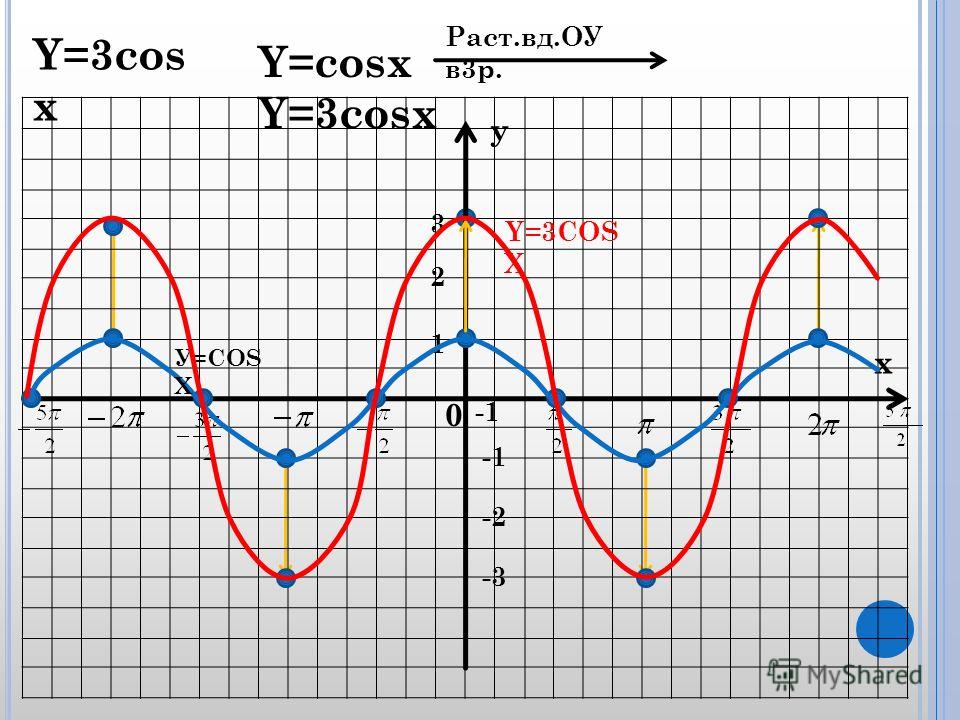
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | ||
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | загар((5pi)/3) | ||
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Cos(x) Cos(2x) Cos(4x)
Кос(х) Кос(2х) Кос(4х) Дата: Сб, 20 сентября 1997 г. , 10:02:27 -06:00 (CST)
, 10:02:27 -06:00 (CST) Тема: математика
Имя: Тан
Кто спрашивает: Студент
Уровень: средний
Вопрос:
Сколько существует различных острых углов x, для которых cosx cos2x cos4x=1/8?
Привет Тан,
У нас есть два решения для вас. В первом решении мы расширяем ваше уравнение, чтобы получить полином седьмой степени от cos(x), и используем правило знаков Декарта, чтобы доказать, что существует три положительных решения. Второе решение использует только тригонометрию и не только показывает, что существует ровно три решения, но и находит их явно. 93 -т -1/8.
Поскольку cos(x) неотрицательна для острых углов, мы ищем положительные нули g(t)
Теперь используйте Правило знаков Декарта , которое гласит:
Пусть P(x) — многочлен с действительными коэффициентами, записанными в убывающих степенях x. Подсчитайте количество перемен знаков в знаках коэффициентов.
- Количество положительных действительных нулей равно количеству перемен знака или равно этому числу, уменьшенному на четное число.

- Количество отрицательных вещественных нулей равно количеству перемен знака в P(-x) или равно этому числу, уменьшенному на четное число.
- g(1/2)=f(Pi/3)=0 дает один ноль.
- g(1)=f(0)>0 и g(sqrt(3)/2)=f(Pi/6)
Таким образом, поскольку g(t) имеет по крайней мере два положительных действительных нуля, их должно быть три. Следовательно, существуют три острых угла x, для которых cos(x)cos(2x)cos(4x)=1/8.
Крис и Харли.
Решение 2.
Сначала мы покажем, что cos(x) cos(2x) cos(4x) = 1/8 тогда и только тогда, когда sin(8x) = sin(x) и sin(x) # 0. (Здесь я использую # для обозначения не равного .)
Доказательство:
Предположим, что cos(x) cos(2x) cos(4x) =1/8, тогда очевидно sin(x) # 0. Умножьте обе части cos(x) cos(2x) cos(4x) =1/8 на 8sin( x), чтобы получить 8sin(x)cos(x) cos(2x) cos(4x) =sin(x).

Сейчас
8sin(x)cos(x) cos(2x) cos(4x) =sin(x)
тогда и только тогда, когда
4sin(2x)cos(2x)cos(4x)=sin(x)
тогда и только тогда, когда
2sin(4x)cos(4x)=sin(x)
тогда и только тогда, когда
грех (8х) = грех (х).Наоборот, если sin(8x) = sin(x) и sin(x) # 0, то 8sin(x)cos(x) cos(2x) cos(4x) =sin(x) и деление на 8sin(x) дает cos( х) cos(2x) cos(4x) =1/8.
Используя тригонометрическое тождество
sin(p)-sin(q) = 2 sin((p-q)/2)cos((p+q)/2),
sin(8x) — sin(x)=0 тогда и только тогда, когда
2cos(9x/2)sin(7x/2)=0cos(9x/2)=0 дает 9x/2=Pi/2, 3Pi/2, 5Pi/2,…
что для острых углов дает x=Pi/9 и x=Pi/3.
sin(7x/2)=0 дает 7x/2=0, Pi, 2Pi,…
что для острых углов дает x=0 и x=2Pi/7.
Но sin(x)#0, поэтому решения равны x=Pi/9, Pi/3 и 2Pi/7.
Харагаури.
Перейти в центр математики Чтобы вернуться на предыдущую страницу, используйте кнопку «Назад» вашего браузера.